Climate Trends Impact on the Snowfall Regime in Mediterranean Mountain Areas: Future Scenario Assessment in Sierra Nevada (Spain)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
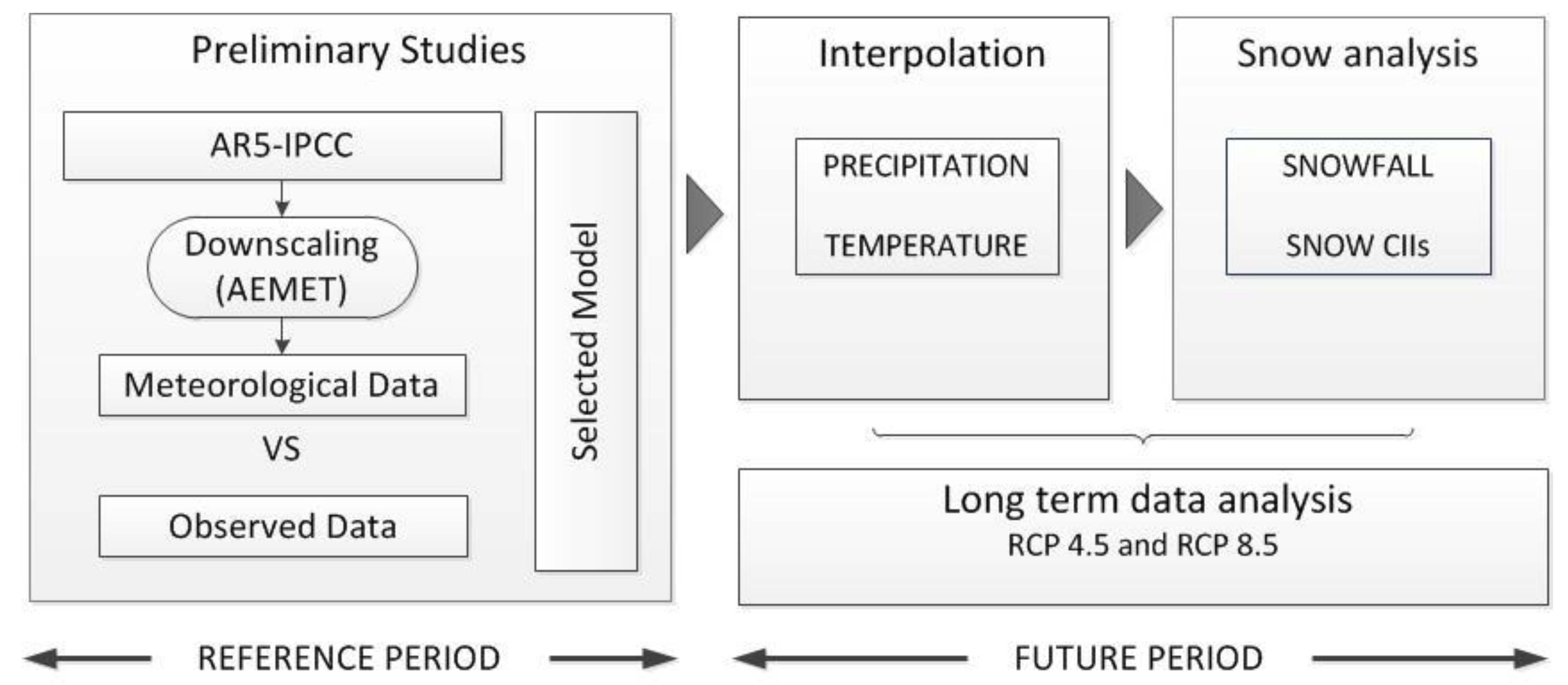
2.2. Overall Study Design
2.3. Data Sources
2.4. Interpolation of Meteorological Variables
2.5. Snowfall Analysis and Snow Climate Indicators
- Snowfall days indicator (Dsnowfall): number of days each year in which snowfall is higher than 0.5 mm.
- Snowfall intensity (Isnowfall): relationship between the annual snowfall and the snowfall days indicator, as outlined by Equation (2).
2.6. Long-Term Data Analysis
3. Results
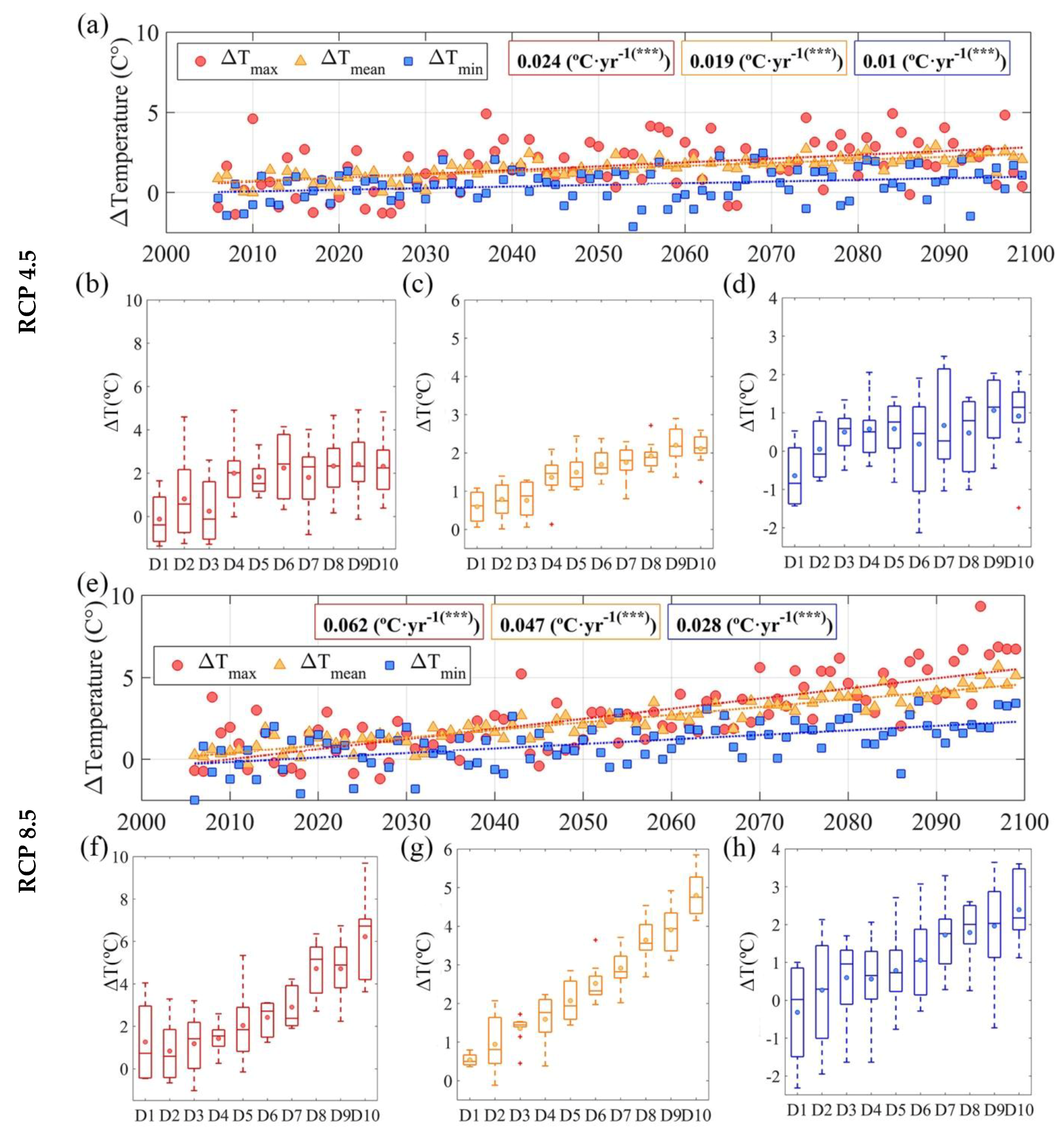
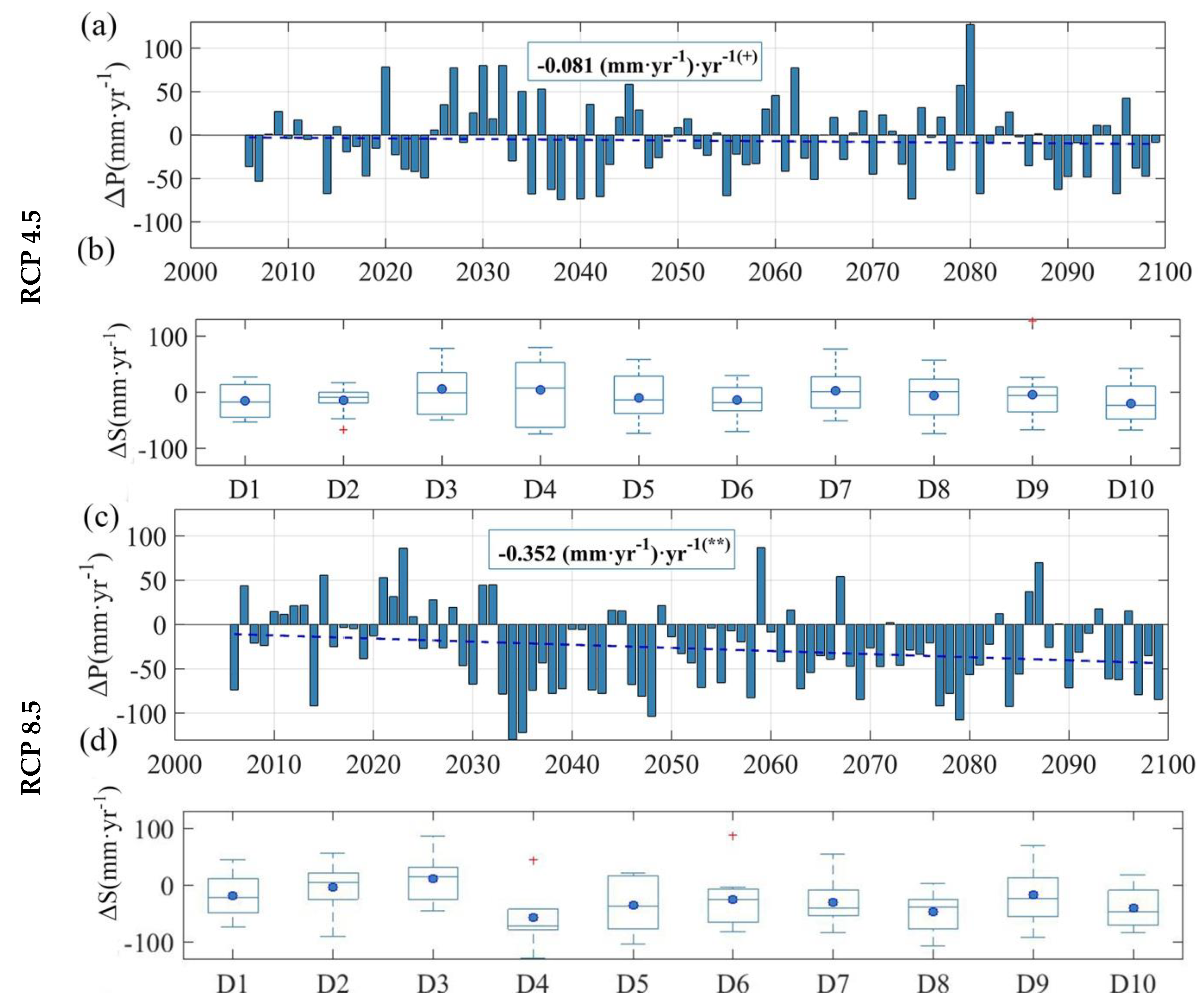
3.1. Long-Term Precipitation and Temperature Analysis for Future Scenarios
3.2. Long-Term Snowfall Analysis for Future Scenarios
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303. [Google Scholar] [CrossRef] [PubMed]
- Mote, P.W. Trends in snow water equivalent in the Pacific Northwest and their climatic causes. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
- Hamlet, A.F.; Mote, P.W.; Clark, M.P.; Lettenmaier, D.P.; Hamlet, A.F.; Mote, P.W.; Clark, M.P.; Lettenmaier, D.P. Effects of Temperature and Precipitation Variability on Snowpack Trends in the Western United States. J. Clim. 2015, 48, 4545–4561. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Woods, R.A.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Chang. 2014, 4, 583. [Google Scholar] [CrossRef]
- Kevin, E. Trenberth Changes in precipitation with climate change. Clim. Res. Clim Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Chou, C.; Lan, C.-W.; Chou, C.; Lan, C.-W. Changes in the Annual Range of Precipitation under Global Warming. J. Clim. 2012, 25, 222–235. [Google Scholar] [CrossRef]
- Solomon, S.; Quin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.; Tignort, M.; Miller, H. Climate Change: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2017. [Google Scholar]
- Groisman, P.Y.; Knight, R.W.; Easterling, D.R.; Karl, T.R.; Hegerl, G.C.; Razuvaev, V.N. Trends in Intense Precipitation in the Climate Record. J. Clim. 2005, 18, 1326–1350. [Google Scholar] [CrossRef]
- Norrant, C.; Douguédroit, A. Monthly and daily precipitation trends in the Mediterranean (1950–2000). Theor. Appl. Climatol. 2006, 83, 89–106. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Wijngaard, J.B.; Können, G.P.; Böhm, R.; Demarée, G.; Gocheva, A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C.; et al. Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int. J. Climatol. 2002, 22, 1441–1453. [Google Scholar] [CrossRef] [Green Version]
- New, M.; Todd, M.; Hulme, M.; Jones, P. Precipitation measurements and trends in the twentieth century. Int. J. Climatol. 2001, 21, 1889–1922. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Palazón, M.J.; Pimentel, R.; Herrero, J.; Aguilar, C.; Perales, J.M.; Polo, M.J. Extreme values of snow-related variables in Mediterranean regions: Trends and long-term forecasting in Sierra Nevada (Spain). Proc. Int. Assoc. Hydrol. Sci. 2015, 369, 157–162. [Google Scholar] [CrossRef]
- Beniston, M. Climatic Change in Mountain Regions: A Review of Possible Impacts. Clim. Chang. 2003, 59, 5–31. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Gelfan, A.; Gustafsson, D.; Motovilov, Y.; Arheimer, B.; Kalugin, A.; Krylenko, I.; Lavrenov, A. Climate change impact on the water regime of two great Arctic rivers: Modeling and uncertainty issues. Clim. Chang. 2017, 141, 499–515. [Google Scholar] [CrossRef]
- Eisner, S.; Flörke, M.; Chamorro, A.; Daggupati, P.; Donnelly, C.; Huang, J.; Hundecha, Y.; Koch, H.; Kalugin, A.; Krylenko, I.; et al. An ensemble analysis of climate change impacts on streamflow seasonality across 11 large river basins. Clim. Chang. 2017, 141, 401–417. [Google Scholar] [CrossRef]
- Soares, M.B.; Alexander, M.; Dessai, S. Sectoral use of climate information in Europe: A synoptic overview. Clim. Serv. 2018, 9, 5–20. [Google Scholar] [CrossRef]
- Damm, A.; Greuell, W.; Landgren, O.; Prettenthaler, F. Impacts of +2 °C global warming on winter tourism demand in Europe. Clim. Serv. 2017, 7, 31–46. [Google Scholar] [CrossRef]
- Donnelly, C.; Greuell, W.; Andersson, J.; Gerten, D.; Pisacane, G.; Roudier, P.; Ludwig, F. Impacts of climate change on European hydrology at 1.5, 2 and 3 degrees mean global warming above preindustrial level. Clim. Chang. 2017, 143, 13–26. [Google Scholar] [CrossRef]
- Steininger, K.W.; Bednar-Friedl, B.; Formayer, H.; König, M. Consistent economic cross-sectoral climate change impact scenario analysis: Method and application to Austria. Clim. Serv. 2016, 1, 39–52. [Google Scholar] [CrossRef]
- Fayad, A.; Gascoin, S.; Faour, G.; López-Moreno, J.I.; Drapeau, L.; Page, M.L.; Escadafal, R. Snow hydrology in Mediterranean mountain regions: A review. J. Hydrol. 2017, 551, 374–396. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Gascoin, S.; Herrero, J.; Sproles, E.A.; Pons, M.; Alonso-González, E.; Hanich, L.; Boudhar, A.; Musselman, K.N.; Molotch, N.P.; et al. Different sensitivities of snowpacks to warming in Mediterranean climate mountain areas. Environ. Res. Lett. 2017, 12, 074006. [Google Scholar] [CrossRef]
- Möller, L.; Hanke, B.; Lubinski, L.; Kollig, C. For Life, for the Future. Biosphere Reserves and Climate Change; German Commission for UNESCO (DUK): Bonn, Germany; ISBN 978-3-940785-27-5.
- Danco, J.F.; DeAngelis, A.M.; Raney, B.K.; Broccoli, A.J. Effects of a Warming Climate on Daily Snowfall Events in the Northern Hemisphere. J. Clim. 2016, 29, 6295–6318. [Google Scholar] [CrossRef]
- Blanca, G.; Cueto, M.; Martínez-Lirola, M.J.; Molero-Mesa, J. Threatened vascular flora of Sierra Nevada (Southern Spain). Biol. Conserv. 1998, 85, 269–285. [Google Scholar] [CrossRef]
- Heywood, V. Endemism and biodiversity of the flora and vegetation of Sierra Nevada: Environmental consequences. In Sierra Nevada. Conservaci6n y Desarrollo Sostenible; University of Granada: Granada, Spain, 1996; pp. 191–201. [Google Scholar]
- Pimentel, R.; Herrero, J.; Polo, M.J. Subgrid parameterization of snow distribution at a Mediterranean site using terrestrial photography. Hydrol. Earth Syst. Sci. 2017, 21, 805–820. [Google Scholar] [CrossRef] [Green Version]
- Lorite, J.; Navarro, F.B.; Valle, F. Estimation of threatened orophytic flora and priority of its conservation in the Baetic range (S. Spain). Plant Biosyst. 2007, 141, 1–14. [Google Scholar] [CrossRef]
- Myers, N.; Mittermeier, R.A.; Mittermeier, C.G.; da Fonseca, G.A.B.; Kent, J. Biodiversity hotspots for conservation priorities. Nature 2000, 403, 853–858. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Palazon, M.J.; Pimentel, R.; Herrero, J.; Polo, M.J. Modelado el régimen de humedad media del suelo en el área de Sierra Nevada a diferentes escalas temporales. In Estudios de la Zona no Saturada; Martinez Perez, S., Merlín, A.S., Eds.; Universidad de Alcalá, Servicio de Publicaciones: Madrid, Spain, 2015; Volumen XII, pp. 221–226. [Google Scholar]
- Boé, J.; Terray, L. Can metric-based approaches really improve multi-model climate projections? The case of summer temperature change in France. Clim. Dyn. 2015, 45, 1913–1928. [Google Scholar] [CrossRef]
- Knutti, R.; Furrer, R.; Tebaldi, C.; Cermak, J.; Meehl, G.A.; Knutti, R.; Furrer, R.; Tebaldi, C.; Cermak, J.; Meehl, G.A. Challenges in Combining Projections from Multiple Climate Models. J. Clim. 2010, 23, 2739–2758. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Mearns, L.O.; Giorgi, F.; Mearns, L.O. Calculation of Average, Uncertainty Range, and Reliability of Regional Climate Changes from AOGCM Simulations via the “Reliability Ensemble Averaging” (REA) Method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Tebaldi, C.; Smith, R.L.; Nychka, D.; Mearns, L.O.; Tebaldi, C.; Smith, R.L.; Nychka, D.; Mearns, L.O. Quantifying Uncertainty in Projections of Regional Climate Change: A Bayesian Approach to the Analysis of Multimodel Ensembles. J. Clim. 2005, 18, 1524–1540. [Google Scholar] [CrossRef] [Green Version]
- Block, K.; Mauritsen, T. Forcing and feedback in the MPI-ESM-LR coupled model under abruptly quadrupled CO2. J. Adv. Model. Earth Syst. 2013, 5, 676–691. [Google Scholar] [CrossRef]
- Zorita, E.; von Storch, H.; Zorita, E.; von Storch, H. The Analog Method as a Simple Statistical Downscaling Technique: Comparison with More Complicated Methods. J. Clim. 1999, 12, 2474–2489. [Google Scholar] [CrossRef]
- Stevens, B.; Giorgetta, M.; Esch, M.; Mauritsen, T.; Crueger, T.; Rast, S.; Salzmann, M.; Schmidt, H.; Bader, J.; Block, K.; et al. Atmospheric component of the MPI-M Earth System Model: ECHAM6. J. Adv. Model. Earth Syst. 2013, 5, 146–172. [Google Scholar] [CrossRef] [Green Version]
- Jungclaus, J.H.; Fischer, N.; Haak, H.; Lohmann, K.; Marotzke, J.; Matei, D.; Mikolajewicz, U.; Notz, D.; von Storch, J.S. Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM) the ocean component of the MPI-Earth system model. J. Adv. Model. Earth Syst. 2013, 5, 422–446. [Google Scholar] [CrossRef] [Green Version]
- Jones, C.; Robertson, E.; Arora, V.; Friedlingstein, P.; Shevliakova, E.; Bopp, L.; Brovkin, V.; Hajima, T.; Kato, E.; Kawamiya, M.; et al. Twenty-First-Century Compatible CO2 Emissions and Airborne Fraction Simulated by CMIP5 Earth System Models under Four Representative Concentration Pathways. J. Clim. 2013, 26, 4398–4413. [Google Scholar] [CrossRef]
- Maier-Reimer, E.; Kriest, I.; Segschneider, J.; Wetzel, P. The HAMburg Ocean Carbon Cycle Model HAMOCC5.1-Technical Description Release 1.1; Max-Planck-Inst. für Meteorologie: Hamburg, Germany, 2005. [Google Scholar] [CrossRef]
- Kaminski, T.; Knorr, W.; Schürmann, G.; Scholze, M.; Rayner, P.J.; Zaehle, S.; Blessing, S.; Dorigo, W.; Gayler, V.; Giering, R.; et al. The BETHY/JSBACH Carbon Cycle Data Assimilation System: Experiences and challenges. J. Geophys. Res. Biogeosci. 2013, 118, 1414–1426. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- Petisco, S.E.; Martín, J.; Gel, D. Método de estima de precipitación mediante “downscaling”. In Nota técnica n.o 11 del Servicio de Variabilidad y Predicción del Clima; INM: Madrid, Spain, 2005. [Google Scholar]
- Petisco, S.E.; Martín, J.M. Escenarios de temperatura y precipitación para la España peninsular y Baleares durante el período 2001–2100 basados en “downscaling” estadístico mediante métodos de análogos. In Proceedings of the XXIX Jornadas Científicas de la Asociación Meteorológica Española, Pamplona, Spain, 24–26 April 2006. [Google Scholar]
- Agnew, M.; Palutikof, J. GIS-based construction of baseline climatologies for the Mediterranean using terrain variables. Clim. Res. 2000, 14, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Herrero, J.; Aguilar, C.; Polo, M.J.; Losada, M.A. Mapping of meteorological variables for runoff generation forecast in distributed hydrological modeling. In Proceedings of the Hydraulic Measurements & Experimental Methods Conference, Lake Placid, NY, USA, 10–12 September 2007; pp. 606–611. [Google Scholar]
- Creutin, J.D.; Obled, C. Objective analyses and mapping techniques for rainfall fields: An objective comparison. Water Resour. Res. 1982, 18, 413–431. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P.; De Bièvre, B.; Wyseure, G. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef] [Green Version]
- Susong, D.; Marks, D.; Garen, D. Methods for developing time-series climate surfaces to drive topographically distributed energy- and water-balance models. Hydrol. Process. 1999, 13, 2003–2021. [Google Scholar] [CrossRef]
- Garen, D.C.; Marks, D. Spatially distributed energy balance snowmelt modelling in a mountainous river basin: Estimation of meteorological inputs and verification of model results. J. Hydrol. 2005, 315, 126–153. [Google Scholar] [CrossRef]
- Aguilar, C.; Herrero, J.; Polo, M.J. Topographic effects on solar radiation distribution in mountainous watersheds and their influence on reference evapotranspiration estimates at watershed scale. Hydrol. Earth Syst. Sci. 2010, 14, 2479–2494. [Google Scholar] [CrossRef] [Green Version]
- Herrero, J.; Polo, M.J. Evaposublimation from the snow in the Mediterranean mountains of Sierra Nevada (Spain). Cryosphere 2016, 10, 2981–2998. [Google Scholar] [CrossRef] [Green Version]
- Pimentel, R.; Herrero, J.; Polo, M. Quantifying Snow Cover Distribution in Semiarid Regions Combining Satellite and Terrestrial Imagery. Remote Sens. 2017, 9, 995. [Google Scholar] [CrossRef]
- Dai, A. Temperature and Pressure Dependence of the Rain-Snow Phase Transition over Land and Ocean. Geophys. Res. Lett. 2008, 10. [Google Scholar] [CrossRef]
- Lundquist, J.D.; Neiman, P.J.; Martner, B.; White, A.B.; Gottas, D.J.; Ralph, F.M.; Lundquist, J.D.; Neiman, P.J.; Martner, B.; White, A.B.; et al. Rain versus Snow in the Sierra Nevada, California: Comparing Doppler Profiling Radar and Surface Observations of Melting Level. J. Hydrometeorol. 2008, 9, 194–211. [Google Scholar] [CrossRef] [Green Version]
- Klos, P.Z.; Link, T.E.; Abatzoglou, J.T. Extent of the rain-snow transition zone in the western U.S. under historic and projected climate. Geophys. Res. Lett. 2014, 41, 4560–4568. [Google Scholar] [CrossRef] [Green Version]
- Rajagopal, S.; Harpold, A.A. Testing and Improving Temperature Thresholds for Snow and Rain Prediction in the Western United States. JAWRA J. Am. Water Resour. Assoc. 2016, 52, 1142–1154. [Google Scholar] [CrossRef]
- Hatchett, B.; Daudert, B.; Garner, C.; Oakley, N.; Putnam, A.; White, A. Winter Snow Level Rise in the Northern Sierra Nevada from 2008 to 2017. Water 2017, 9, 899. [Google Scholar] [CrossRef]
- Motoyama, H.; Motoyama, H. Simulation of Seasonal Snowcover Based on Air Temperature and Precipitation. J. Appl. Meteorol. 1990, 29, 1104–1110. [Google Scholar] [CrossRef] [Green Version]
- Lynch-Stieglitz, M. The Development and Validation of a Simple Snow Model for the GISS GCM. J. Clim. 1994, 7, 1842–1855. [Google Scholar] [CrossRef] [Green Version]
- Marks, D.; Winstral, A.; Reba, M.; Pomeroy, J.; Kumar, M. An evaluation of methods for determining during-storm precipitation phase and the rain/snow transition elevation at the surface in a mountain basin. Adv. Water Resour. 2013, 55, 98–110. [Google Scholar] [CrossRef]
- Herrero, J.; Polo, M.J.; Moñino, A.; Losada, M.A. An energy balance snowmelt model in a Mediterranean site. J. Hydrol. 2009, 371, 98–107. [Google Scholar] [CrossRef]
- Yang, Z.-L.; Dickinson, R.E.; Robock, A.; Vinnikov, K.Y.; Yang, Z.-L.; Dickinson, R.E.; Robock, A.; Vinnikov, K.Y. Validation of the Snow Submodel of the Biosphere–Atmosphere Transfer Scheme with Russian Snow Cover and Meteorological Observational Data. J. Clim. 1997, 10, 353–373. [Google Scholar] [CrossRef] [Green Version]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference; Chapman & Hall/CRC Edition: London, UK, 2011; ISBN 9781420077612. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-PLUS; Springer Science & Business Media: Berlin, Germany, 2013; ISBN 9781441930088. [Google Scholar]
- Esteban-Parra, M.J.; Rodrigo, F.S.; Castro-Diez, Y. Spatial and temporal patterns of precipitation in Spain for the period 1880–1992. Int. J. Climatol. 1998, 18, 1557–1574. [Google Scholar] [CrossRef] [Green Version]
- Shuttleworth, W.J. The challenges of developing a changing world. Eos Trans. Am. Geophys. Union 1996, 77, 347. [Google Scholar] [CrossRef]
- Maheras, P.; Balafoutis, C.; Vafiadis, M. Precipitation in the Central Mediterranean during the last century. Theor. Appl. Climatol. 1992, 45, 209–216. [Google Scholar] [CrossRef]
- Gampe, D.; Nikulin, G.; Ludwig, R. Using an ensemble of regional climate models to assess climate change impacts on water scarcity in European river basins. Sci. Total Environ. 2016, 573, 1503–1518. [Google Scholar] [CrossRef] [PubMed]
- Molina-Navarro, E.; Andersen, H.E.; Nielsen, A.; Thodsen, H.; Trolle, D. Quantifying the combined effects of land use and climate changes on stream flow and nutrient loads: A modelling approach in the Odense Fjord catchment (Denmark). Sci. Total Environ. 2018, 621, 253–264. [Google Scholar] [CrossRef] [PubMed]
- Tan, M.L.; Ibrahim, A.L.; Yusop, Z.; Chua, V.P.; Chan, N.W. Climate change impacts under CMIP5 RCP scenarios on water resources of the Kelantan River Basin, Malaysia. Atmos. Res. 2017, 189, 1–10. [Google Scholar] [CrossRef]
- Dimri, A.P.; Kumar, D.; Choudhary, A.; Maharana, P. Future changes over the Himalayas: Maximum and minimum temperature. Glob. Planet. Chang. 2018, 162, 212–234. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Scherer, M.; Ashfaq, M. Response of snow-dependent hydrologic extremes to continued global warming. Nat. Clim. Chang. 2013, 3, 379–384. [Google Scholar] [CrossRef] [PubMed]
- Verfaillie, D.; Lafaysse, M.; Déqué, M.; Eckert, N.; Lejeune, Y.; Morin, S. Multi-component ensembles of future meteorological and natural snow conditions for 1500 m altitude in the Chartreuse mountain range, Northern French Alps. Cryosphere 2018, 125194, 1249–1271. [Google Scholar] [CrossRef]
- Marty, C.; Schlögl, S.; Bavay, M.; Lehning, M. How much can we save? Impact of different emission scenarios on future snow cover in the Alps. Cryosphere 2017, 11, 517–529. [Google Scholar] [CrossRef]
- Meza, F.J.; Wilks, D.S.; Gurovich, L.; Bambach, N. Impacts of Climate Change on Irrigated Agriculture in the Maipo Basin, Chile: Reliability of Water Rights and Changes in the Demand for Irrigation. J. Water Resour. Plan. Manag. 2012, 138, 421–430. [Google Scholar] [CrossRef]
- Vicuña, S.; Garreaud, R.D.; McPhee, J. Climate change impacts on the hydrology of a snowmelt driven basin in semiarid Chile. Clim. Chang. 2011, 105, 469–488. [Google Scholar] [CrossRef]
- Cayan, D.; Tyree, M.; Kunkel, K.E.; Castro, C.; Gershunov, A.; Barsugli, J.; Ray, A.J.; Overpeck, J.; Anderson, M.; Russell, J.; et al. Future Climate: Projected Average. In Assessment of Climate Change in the Southwest United States: A Report Prepared for the National Climate Assessment; A Report by the Southwest Climate Alliance; Garfin, G., Jardine, A., Merideth, R., Black, M., LeRoy, S., Eds.; Island Press: Washington, DC, USA, 2013; pp. 101–125. [Google Scholar]
- Kay, A.L. A review of snow in Britain: The historical picture and future projections. Prog. Phys. Geog. 2016, 40, 676–698. [Google Scholar] [CrossRef] [Green Version]
- Monaghan, A.J.; Bromwich, D.H.; Schneider, D.P. Twentieth century Antarctic air temperature and snowfall simulations by IPCC climate models. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Polade, S.D.; Gershunov, A.; Cayan, D.R.; Dettinger, M.D.; Pierce, D.W. Precipitation in a warming world: Assessing projected hydro-climate changes in California and other Mediterranean climate regions. Sci. Rep. 2017, 7, 10783. [Google Scholar] [CrossRef] [PubMed]
- Berg, N.; Hall, A. Increased Interannual Precipitation Extremes over California under Climate Change. J. Clim. 2015, 28, 6324–6334. [Google Scholar] [CrossRef]
- Valdés-Pineda, R.; Pizarro, R.; García-Chevesich, P.; Valdés, J.B.; Olivares, C.; Vera, M.; Balocchi, F.; Pérez, F.; Vallejos, C.; Fuentes, R.; et al. Water governance in Chile: Availability, management and climate change. J. Hydrol. 2014, 519, 2538–2567. [Google Scholar] [CrossRef]
- Mudryk, L.R.; Derksen, C.; Howell, S.; Laliberté, F.; Thackeray, C.; Sospedra-Alfonso, R.; Vionnet, V.; Kushner, P.J.; Brown, R. Canadian snow and sea ice: Historical trends and projections. Cryosphere 2018, 12, 1157–1176. [Google Scholar] [CrossRef]
- Demaria, E.M.C.; Maurer, E.P.; Thrasher, B.; Vicuña, S.; Meza, F.J. Climate changes impacts on an alpine watershed in Chile: Do new model projections change the story? J. Hydrol. 2013, 502, 128–138. [Google Scholar] [CrossRef]
- Sun, F.; Hall, A.; Schwartz, M.; Walton, D.B.; Berg, N. Twenty-First-Century Snowfall and Snowpack Changes over the Southern California Mountains. J. Clim. 2016, 29, 91–110. [Google Scholar] [CrossRef]
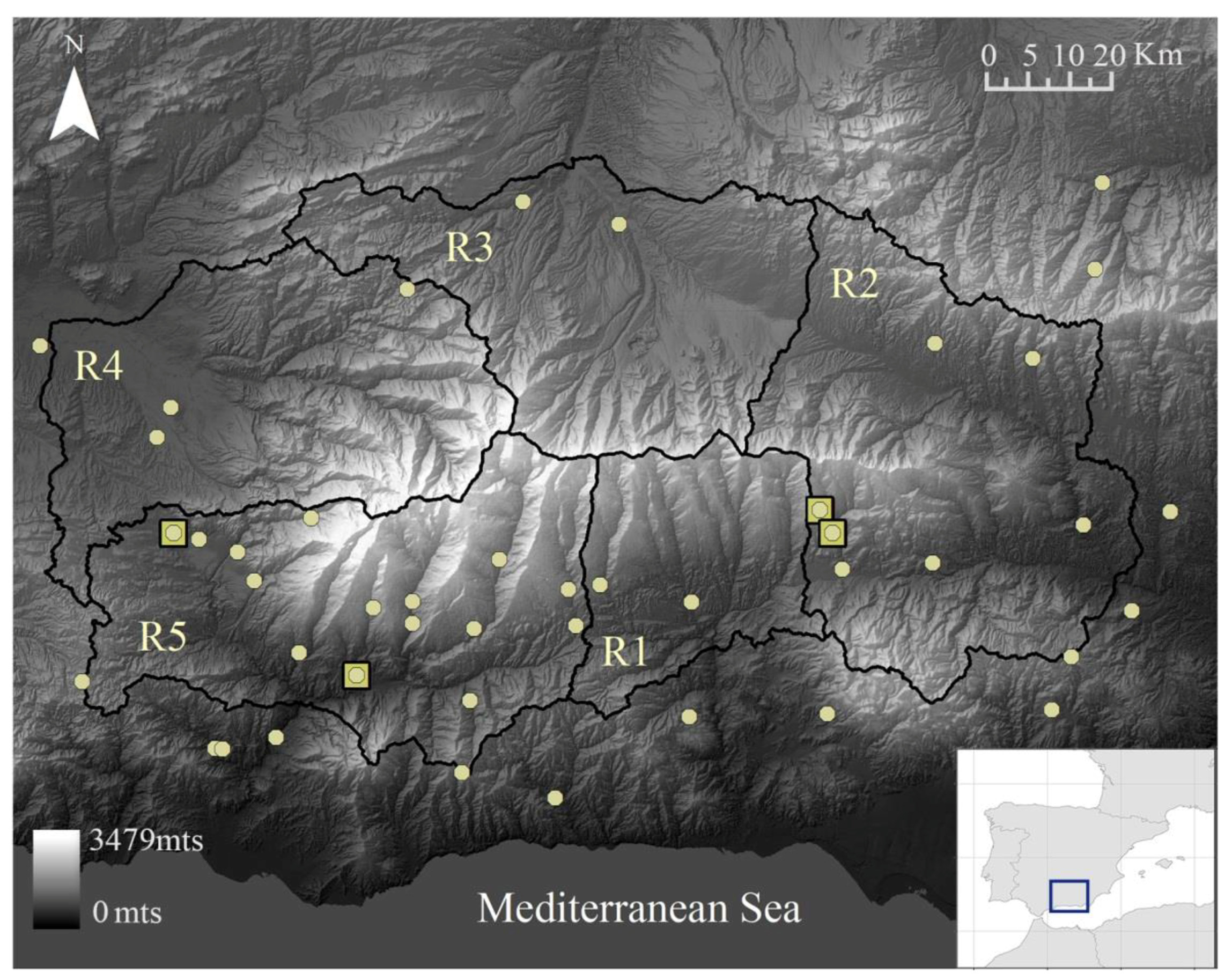
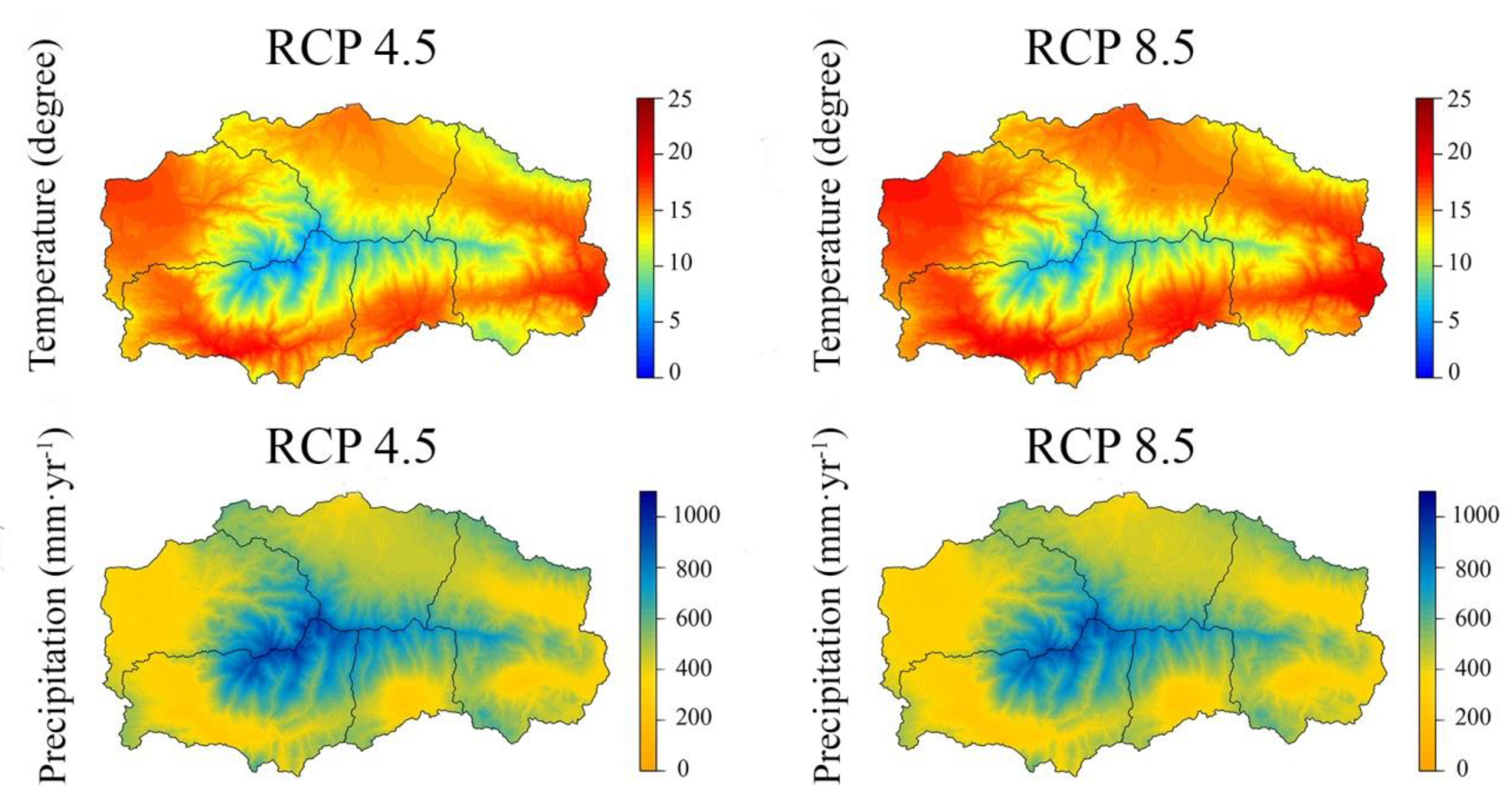
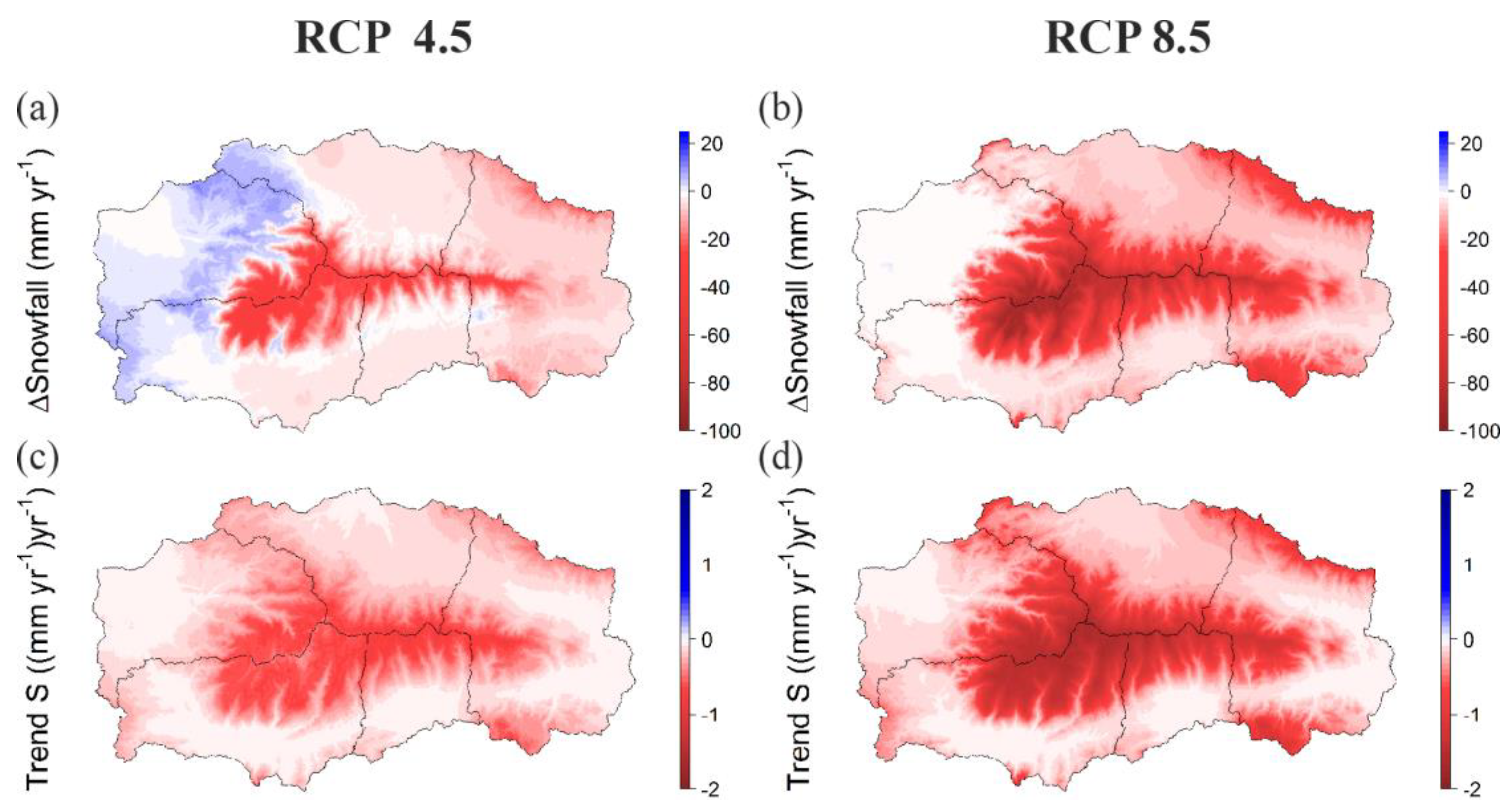

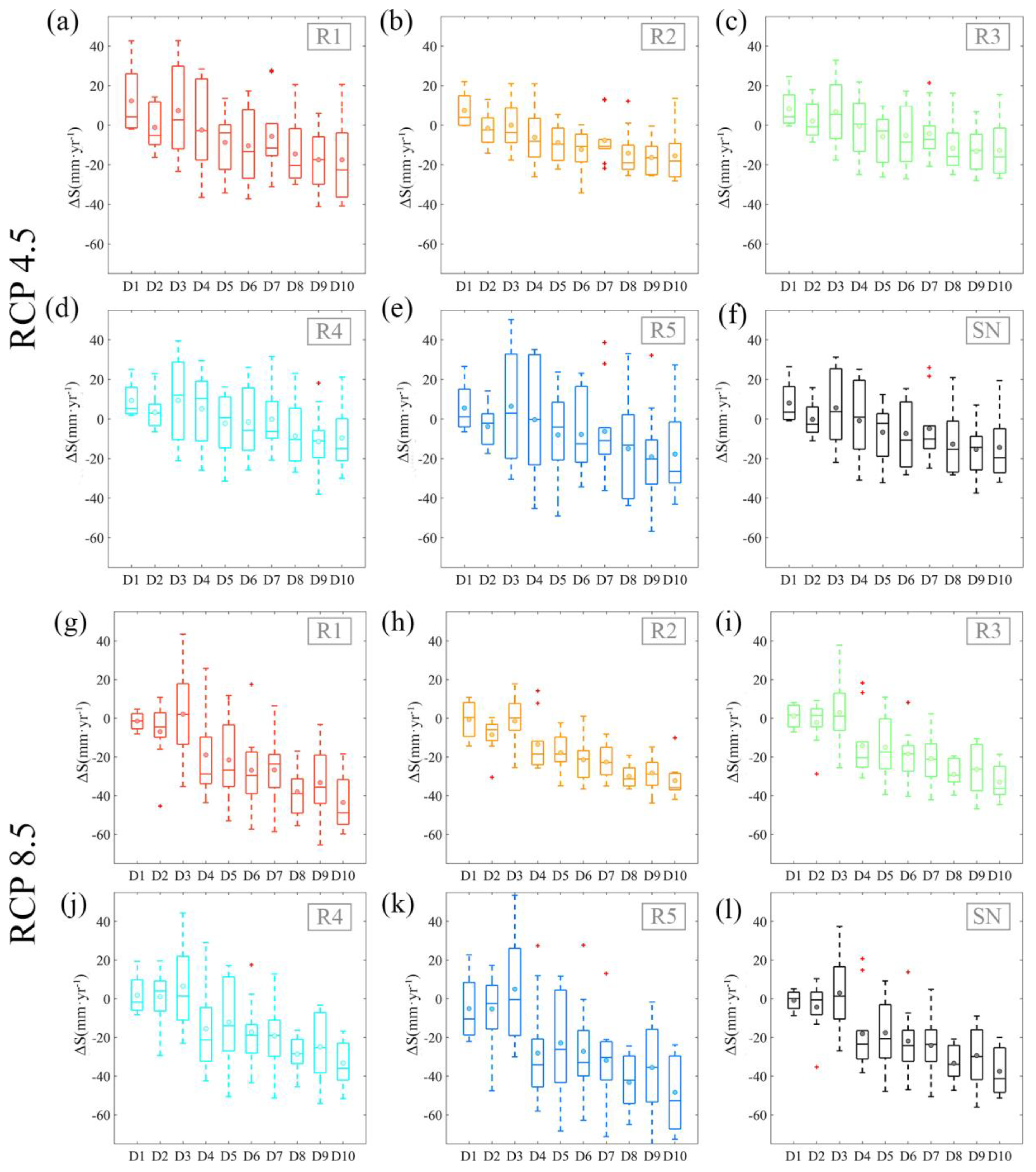
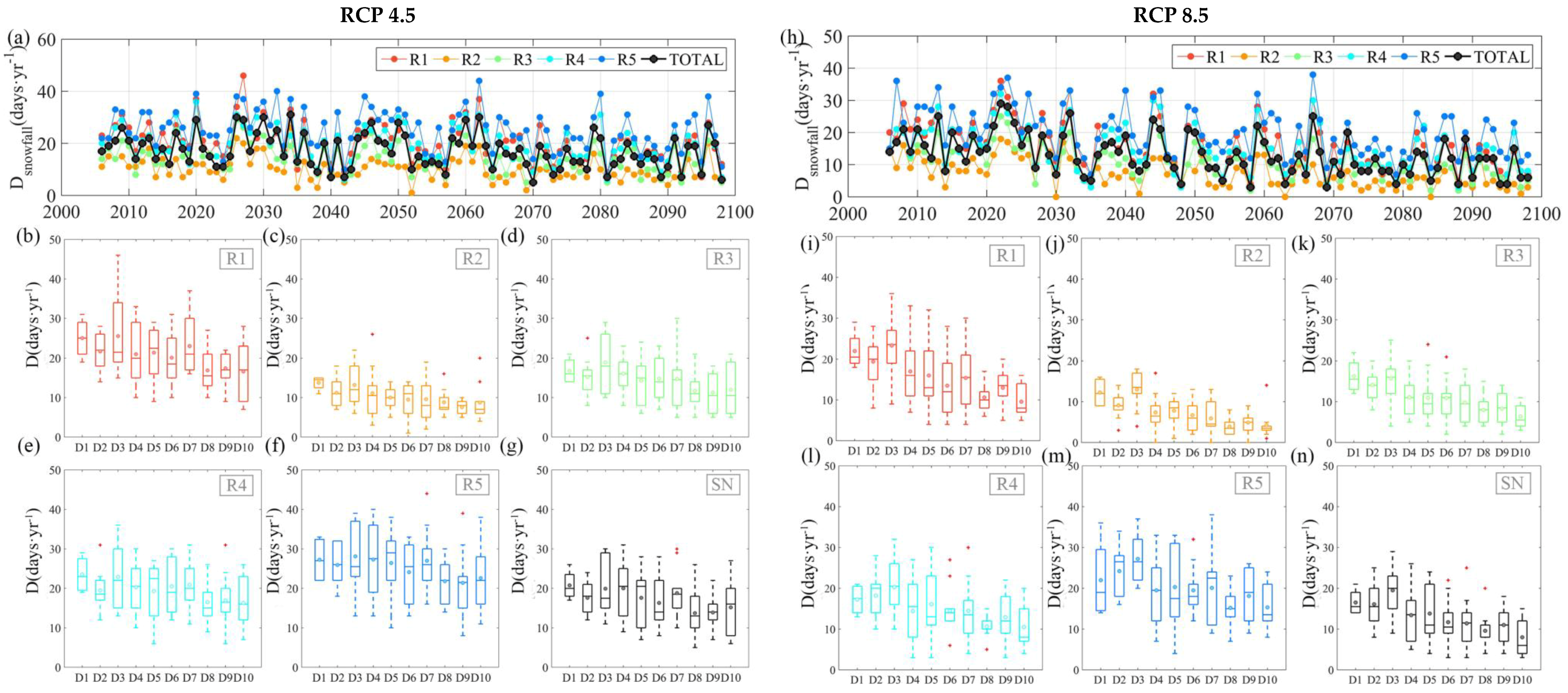
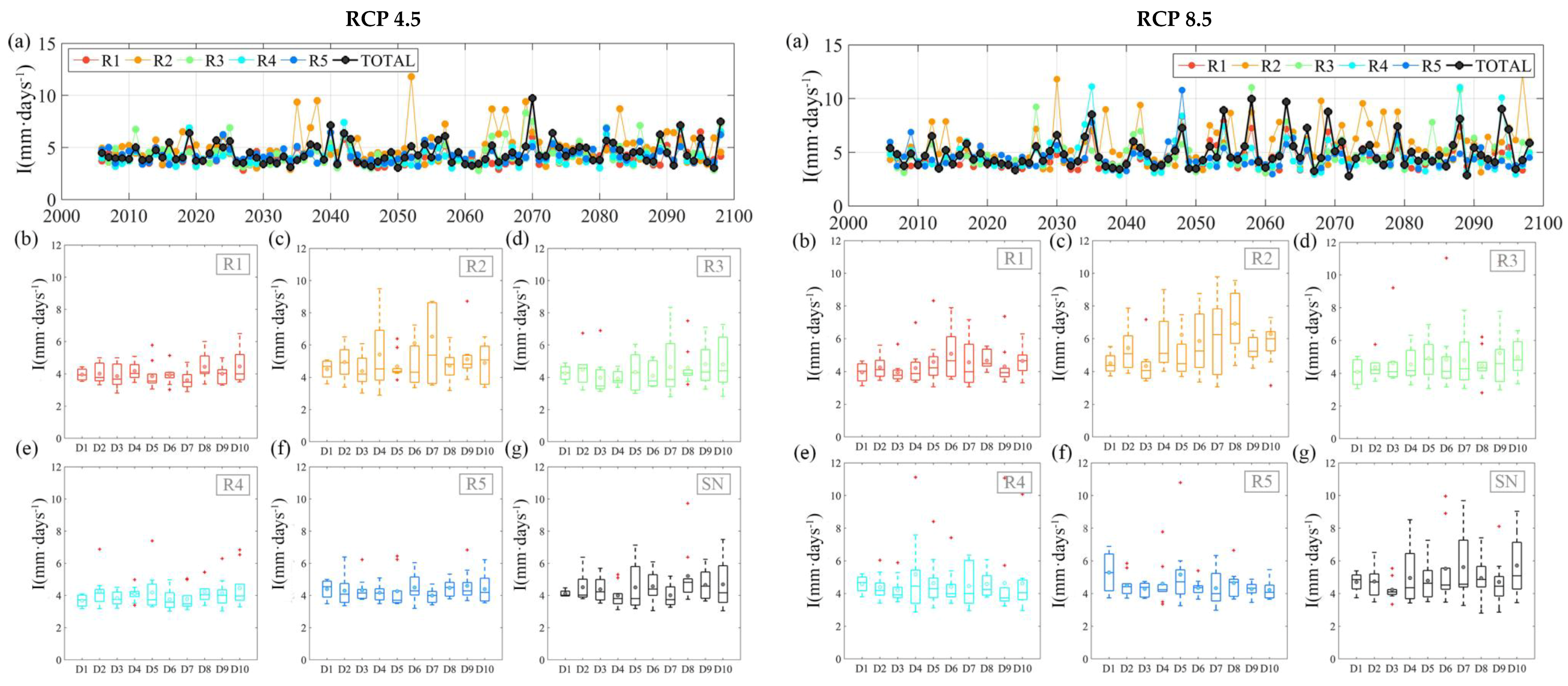
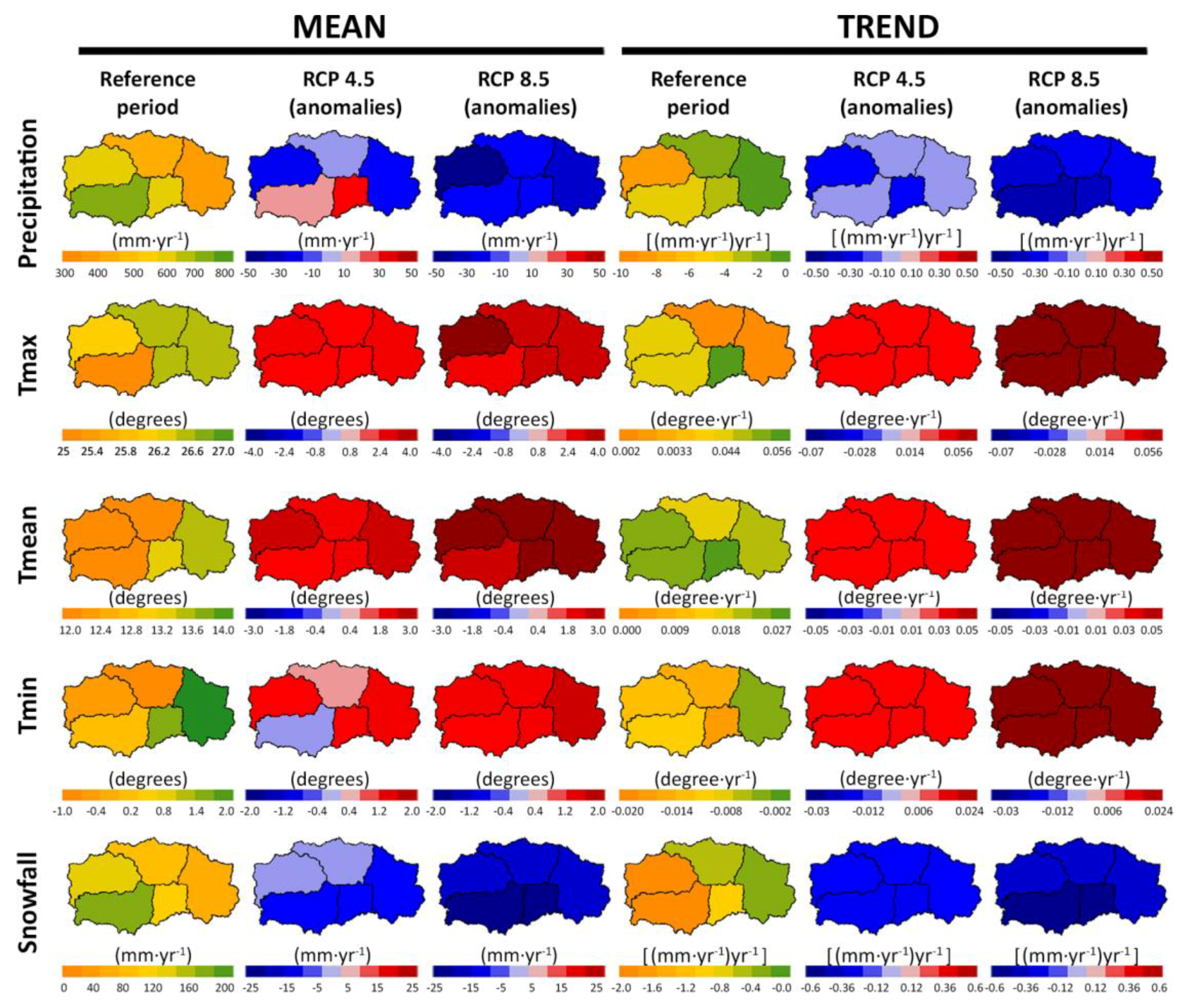
| R1 | R2 | R3 | R4 | R5 | Total SN | |
|---|---|---|---|---|---|---|
| Area (km2) | 459.13 | 1169.00 | 914.43 | 983.16 | 1058.00 | 4583.72 |
| Average altitude (m) | 1330.6 | 1235.0 | 1350.0 | 1270.6 | 1418.5 | 1320.9 |
| Tmean (°C) | 13.2 | 13.4 | 12.2 | 12.1 | 12.0 | 12.6 |
| Tmax (°C) | 26.3 | 26.4 | 26.3 | 26.0 | 25.1 | 26.0 |
| Tmin (°C) | 1.4 | 1.8 | −0.7 | −0.6 | 0.0 | 0.4 |
| P (mm·year−1) | 579 | 373 | 427 | 557 | 658 | 510 |
| S (mm·year−1) | 85 | 44 | 68 | 107 | 160 | 93 |
| E (events·year−1) | 30 | 32 | 32 | 30 | 29 | 31 |
| De (days·year−1) | 3 | 3 | 4 | 3 | 4 | 4 |
| Trend Tmean (°C·year−1) | 0.052 (**) | 0.022 (+) | 0.023 (+) | 0.043 (**) | 0.044 (**) | 0.034 (*) |
| Trend Tmax (°C·year−1) | 0.053 (**) | 0.022 (+) | 0.024 (+) | 0.043 (**) | 0.044 (**) | 0.035 (*) |
| Trend Tmin (°C·year−1) | −0.017 (+) | −0.004 (+) | −0.015 (+) | −0.012 (+) | −0.011 (+) | −0.010 (+) |
| Trend P ((mm·year−1)·year−1) | −3.099 (*) | −1.832 (*) | −2.946 (+) | −8.043 (***) | −4.529 (**) | −4.135 (**) |
| Trend S ((mm·year−1)·year−1) | −1.107 (**) | −0.427 (+) | −0.684 (**) | −1.923 (***) | −2.085 (***) | −1.250 (***) |
| Trend E ((nºev·year−1)·year−1 | −0.116 (+) | −0.061 (+) | −0.001 (+) | 0.038 (+) | −0.047 (+) | 0.012 (+) |
| Trend D((day·year−1)·year−1) | −0.025 (+) | −0.025 (+) | −0.157 (+) | −0.194 (+) | −0.074 (+) | −0.039 (+) |
| DecTrend Tmean (°C·dec−1) | 0.2604 (+) | 0.2109 (+) | 0.1989 (+) | 0.2381 (+) | 0.2403 (+) | 0.2261 (+) |
| DecTrend Tmax (°C·dec−1) | 0.5927 (+) | 0.2689 (+) | 0.2698 (+) | 0.4667 (+) | 0.4639 (+) | 0.3847 (+) |
| DecTrend Tmin (°C·dec−1) | −0.1678 (+) | −0.0195 (+) | −0.1139 (+) | −0.0787 (+) | −0.0787 (+) | −0.0665 (+) |
| DecTrend P((mm·year−1)·dec−1) | −35.24 (+) | −19.63 (+) | −30.40 (+) | −80.75 (+) | −50.16 (+) | −43.49 (+) |
| DecTrend S ((mm·year−1)·dec−1) | −11.45 (+) | −4.39 (+) | −6.99 (+) | −19.29 (+) | −21.97 (+) | −12.87 (+) |
| RCP 4.5 | ||||||
| R1 | R2 | R3 | R4 | R5 | TOTAL (SN) | |
| Tmax (°C) | 28.0 | 28.1 | 28.0 | 27.7 | 26.7 | 27.7 |
| Tmin (°C) | −8.6 | −8.2 | −10.7 | −10.8 | −10.0 | −9.7 |
| Tmean (°C) | 25.2 | 25.4 | 24.2 | 24.5 | 24.0 | 24.7 |
| P (mm·year−1) | 573 | 367 | 421 | 549 | 652 | 503 |
| S (mm·year−1) | 78 | 36 | 64 | 106 | 153 | 87 |
| E (nºev.·year−1) | 40 | 32 | 34 | 38 | 48 | 37 |
| D (days·year−1) | 3 | 2 | 3 | 3 | 3 | 3 |
| Trend Tmax (°C·year−1) | 0.024 (***) | 0.024 (***) | 0.024 (***) | 0.025 (***) | 0.023 (***) | 0.024 (***) |
| Trend Tmin (°C·year−1) | 0.010 (***) | 0.010 (***) | 0.010 (***) | 0.011 (***) | 0.010 (***) | 0.010 (***) |
| Trend Tmean (°C·year−1) | 0.019 (***) | 0.019 (***) | 0.019 (***) | 0.019 (***) | 0.019 (***) | 0.019 (***) |
| Trend P ((mm·year−1)·year−1) | −0.109 (+) | −0.060 (+) | −0.068 (+) | −0.119 (+) | −0.070 (+) | −0.081 (+) |
| Trend S ((mm·year−1)·year−1) | −0.289 (***) | −0.215 (***) | −0.236 (***) | −0.232 (***) | −0.271 (***) | 0.243 (***) |
| Trend E ((nºev.·year−1)·year−1) | −0.068 (+) | −0.076 (+) | −0.061 (+) | −0.042 (+) | −0.027 (+) | −0.056 (+) |
| Trend D ((day·year−1)·year−1) | −0.003 (+) | −0.003 (+) | −0.004 (+) | −0.004 (+) | −0.005 (+) | −0.044 (+) |
| DecTrend Tmean (°C·dec−1) | 0.1826 (**) | 0.1820 (**) | 0.1837 (**) | 0.1868 (**) | 0.1838 (**) | 0.1838 (**) |
| DecTrend Tmax (°C·dec−1) | 0.2242 (***) | 0.2246 (***) | 0.2201 (***) | 0.2207 (***) | 0.2104 (***) | 0.2193 (***) |
| DecTrend Tmin (°C·dec−1) | 0.0838 (**) | 0.0859 (**) | 0.0829 (**) | 0.0915 (**) | 0.0808 (**) | 0.0838 (**) |
| DecTrend((mm·year−1)·dec−1) | −1.0118 (+) | −0.6906 (+) | −0.9842 (+) | −1.6084 (+) | −0.8593 (+) | −1.0129 (+) |
| DecTrend ((mm·year−1)·dec−1) | −2.6852 (+) | −1.9920 (+) | −2.3388 (+) | −2.3325 (+) | −2.6641 (+) | −2.3597 (+) |
| RCP 8.5 | ||||||
| R2 | R3 | R4 | R5 | TOTAL(SN) | ||
| Temp max (°C) | 29.2 | 29.3 | 29.2 | 28.9 | 27.9 | 28.8 |
| Tmin (°C) | −7.9 | −7.5 | −10.1 | −10.2 | −9.4 | −9.0 |
| Tmean (°C) | 26.2 | 26.4 | 25.2 | 25.5 | 25.0 | 25.7 |
| P (mm·year−1) | 548 | 352 | 403 | 528 | 625 | 482 |
| S (mm· year−1) | 62 | 25 | 51 | 92 | 135 | 74 |
| E (nºev.·year−1) | 39 | 30 | 32 | 37 | 46 | 36 |
| De(days·year−1) | 2 | 2 | 2 | 2 | 3 | 2 |
| Trend Tmax (°C·year−1) | 0.061 (***) | 0.062 (***) | 0.062 (***) | 0.064 (***) | 0.062 (***) | 0.062 (***) |
| Trend Tmin (°C·year−1) | 0.028 (***) | 0.028 (***) | 0.028 (***) | 0.028 (***) | 0.028 (***) | 0.028 (***) |
| Trend Tmean (°C·year−1) | 0.047 (***) | 0.046 (***) | 0.047 (***) | 0.047 (***) | 0.047 (***) | 0.047 (***) |
| Trend P ((mm·year−1)·year−1) | −0.408 (**) | −0.290 (**) | −0.286 (*) | −0.370 (+) | −0.436 (*) | −0.352 (**) |
| Trend S ((mm·year−1)·year−1) | −0.408 (***) | −0.362 (***) | −0.416 (***) | −0.442 (***) | −0.553 (***) | −0.448 (***) |
| Trend E ((nºev·year−1)·year−1) | −0.161 (+) | −0.151 (+) | −0.148 (+) | −0.135 (+) | −0.142 (+) | −0.124 (+) |
| Trend D ((day·year−1)·year−1) | −0.016 (+) | −0.008 (+) | −0.008 (+) | −0.008 (+) | −0.008 (+) | −0.008 (+) |
| DecTrend Tmean (°C·dec−1) | 0.465 (***) | 0.463 (***) | 0.467 (***) | 0.472 (***) | 0.467 (***) | 0.467 (***) |
| DecTrend Tmax (°C·dec−1) | 0.653 (***) | 0.655 (***) | 0.657 (***) | 0.682 (***) | 0.660 (***) | 0.659 (***) |
| DecTrend Tmin (°C·dec−1) | 0.270 (***) | 0.269 (***) | 0.267 (***) | 0.271 (***) | 0.266 (***) | 0.266 (***) |
| DecTrend P((mm·year−1)·dec−1) | −4.121 (+) | −2.975 (+) | −2.704 (+) | −3.564 (+) | −4.372 (+) | −3.483 (+) |
| DecTrend S ((mm·year−1)·dec−1) | −4.937 (+) | −3.546 (+) | −4.123 (+) | −4.407 (+) | −5.555 (+) | −4.449 (+) |
| Tmax | Tmin | Tmean | P | Smax | Smin | Smean | Strend | |
|---|---|---|---|---|---|---|---|---|
| R1 | 1.045 | 1.619 | 1.081 | 0.924 | 1.005 | 0.462 | 0.800 | 1.724 |
| R2 | 1.044 | 1.413 | 1.078 | 0.948 | 0.944 | 0.516 | 0.775 | 1.681 |
| R3 | 1.046 | 1.709 | 1.082 | 0.944 | 1.052 | 0.453 | 0.790 | 1.760 |
| R4 | 1.049 | 1.480 | 1.080 | 0.928 | 1.042 | 0.576 | 0.814 | 1.908 |
| R5 | 1.045 | 2.051 | 1.084 | 0.919 | 1.020 | 0.666 | 0.827 | 2.042 |
| Total SN | 1.046 | 1.590 | 1.081 | 0.933 | 1.057 | 0.529 | 0.806 | 1.840 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Palazón, M.J.; Pimentel, R.; Polo, M.J. Climate Trends Impact on the Snowfall Regime in Mediterranean Mountain Areas: Future Scenario Assessment in Sierra Nevada (Spain). Water 2018, 10, 720. https://doi.org/10.3390/w10060720
Pérez-Palazón MJ, Pimentel R, Polo MJ. Climate Trends Impact on the Snowfall Regime in Mediterranean Mountain Areas: Future Scenario Assessment in Sierra Nevada (Spain). Water. 2018; 10(6):720. https://doi.org/10.3390/w10060720
Chicago/Turabian StylePérez-Palazón, María José, Rafael Pimentel, and María José Polo. 2018. "Climate Trends Impact on the Snowfall Regime in Mediterranean Mountain Areas: Future Scenario Assessment in Sierra Nevada (Spain)" Water 10, no. 6: 720. https://doi.org/10.3390/w10060720
APA StylePérez-Palazón, M. J., Pimentel, R., & Polo, M. J. (2018). Climate Trends Impact on the Snowfall Regime in Mediterranean Mountain Areas: Future Scenario Assessment in Sierra Nevada (Spain). Water, 10(6), 720. https://doi.org/10.3390/w10060720







