Compound Extremes in Hydroclimatology: A Review
Abstract
1. Introduction
2. Compound Extremes
2.1. Definition of Compound Extremes
“(1) two or more extreme events occurring simultaneously or successively, (2) combinations of extreme events with underlying conditions that amplify the impact of the events, or (3) combinations of events that are not themselves extremes but lead to an extreme event or impact when combined.”
“A compound event is an extreme impact that depends on multiple statistically dependent variables or events.”
2.2. Typical Compound Extremes
3. Statistical Approaches
3.1. Empirical Approach
3.2. Multivariate Distribution
3.2.1. Copula Approach
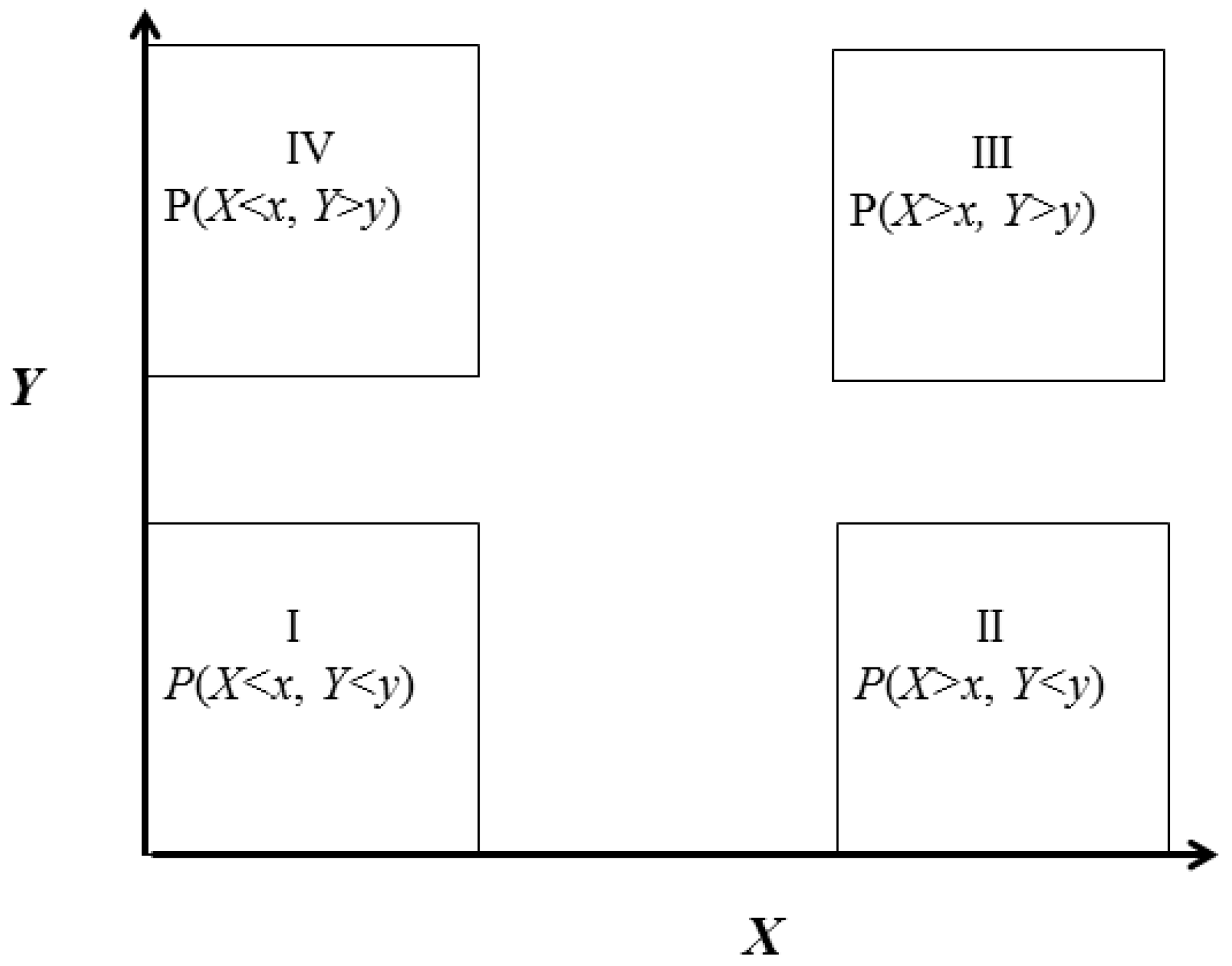
3.2.2. Joint Probability
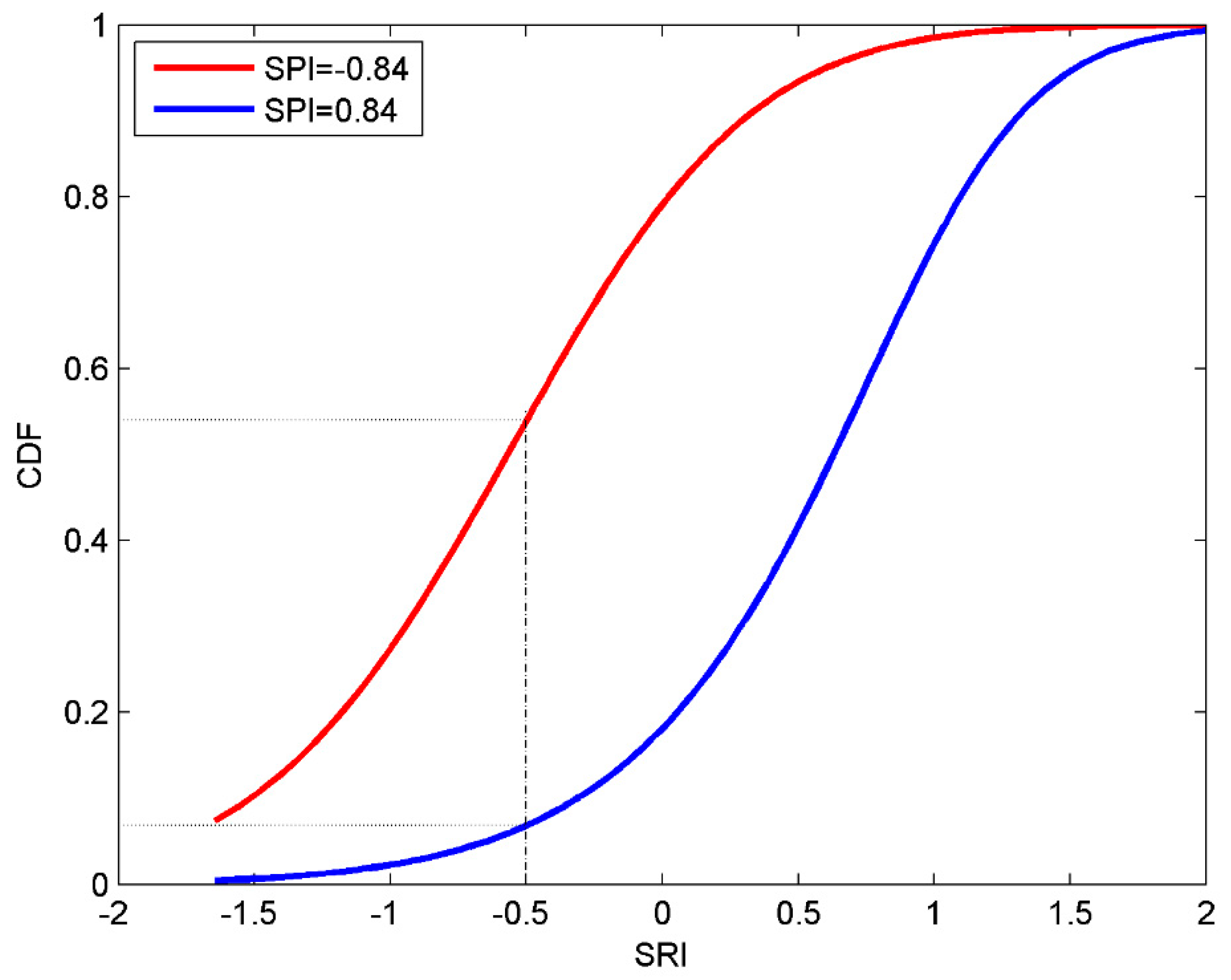
3.2.3. Conditional Probability
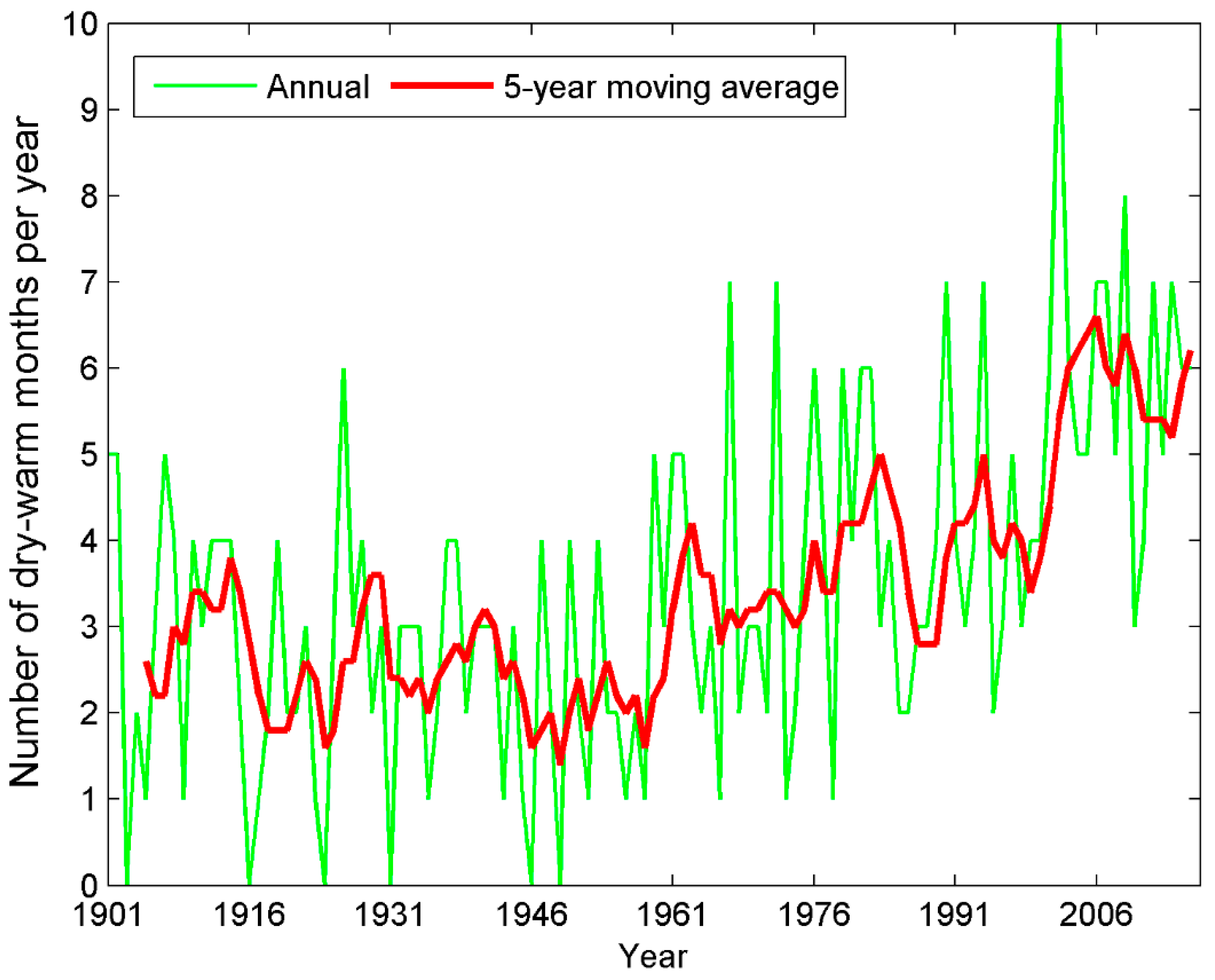
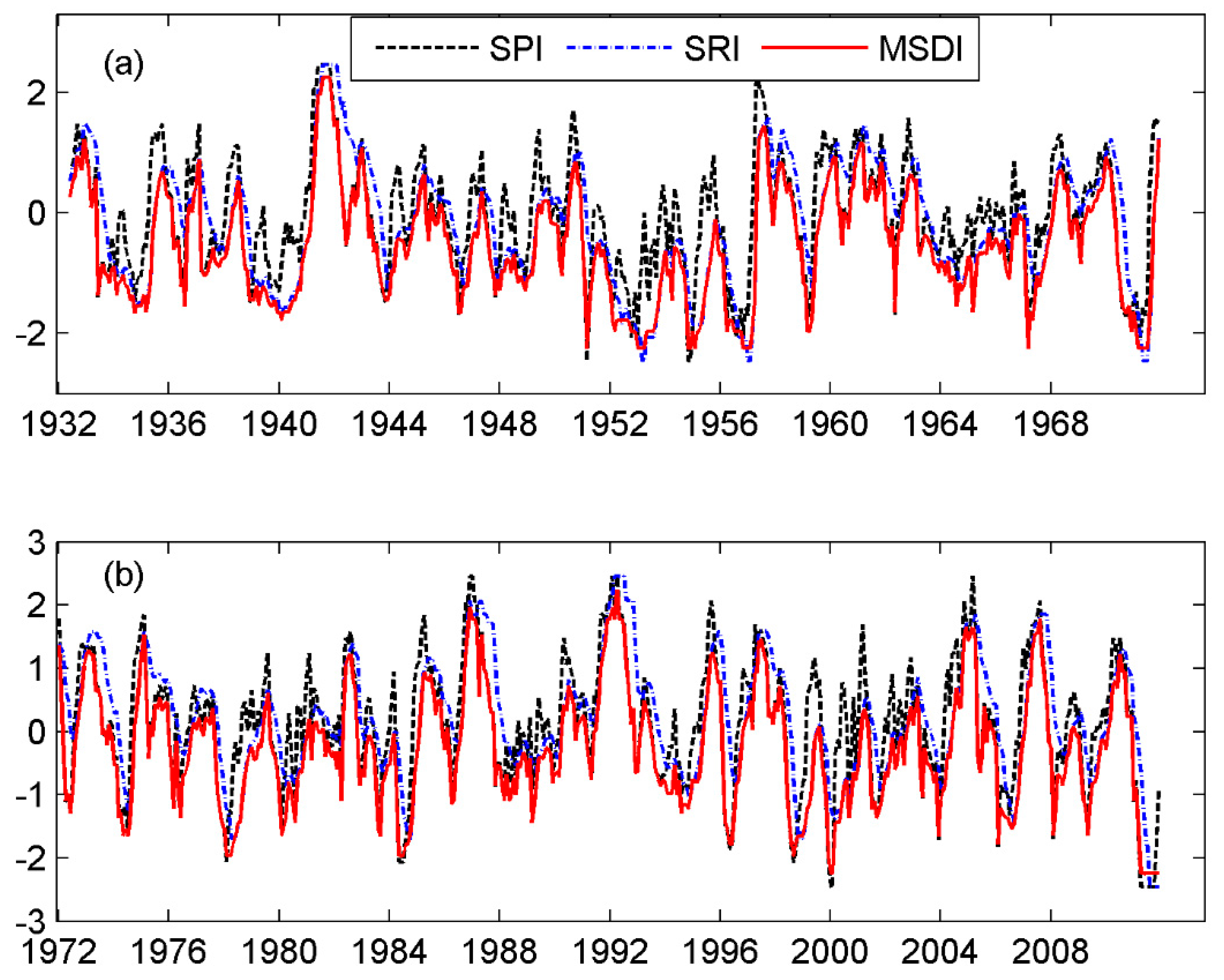
3.3. Indicator Approach
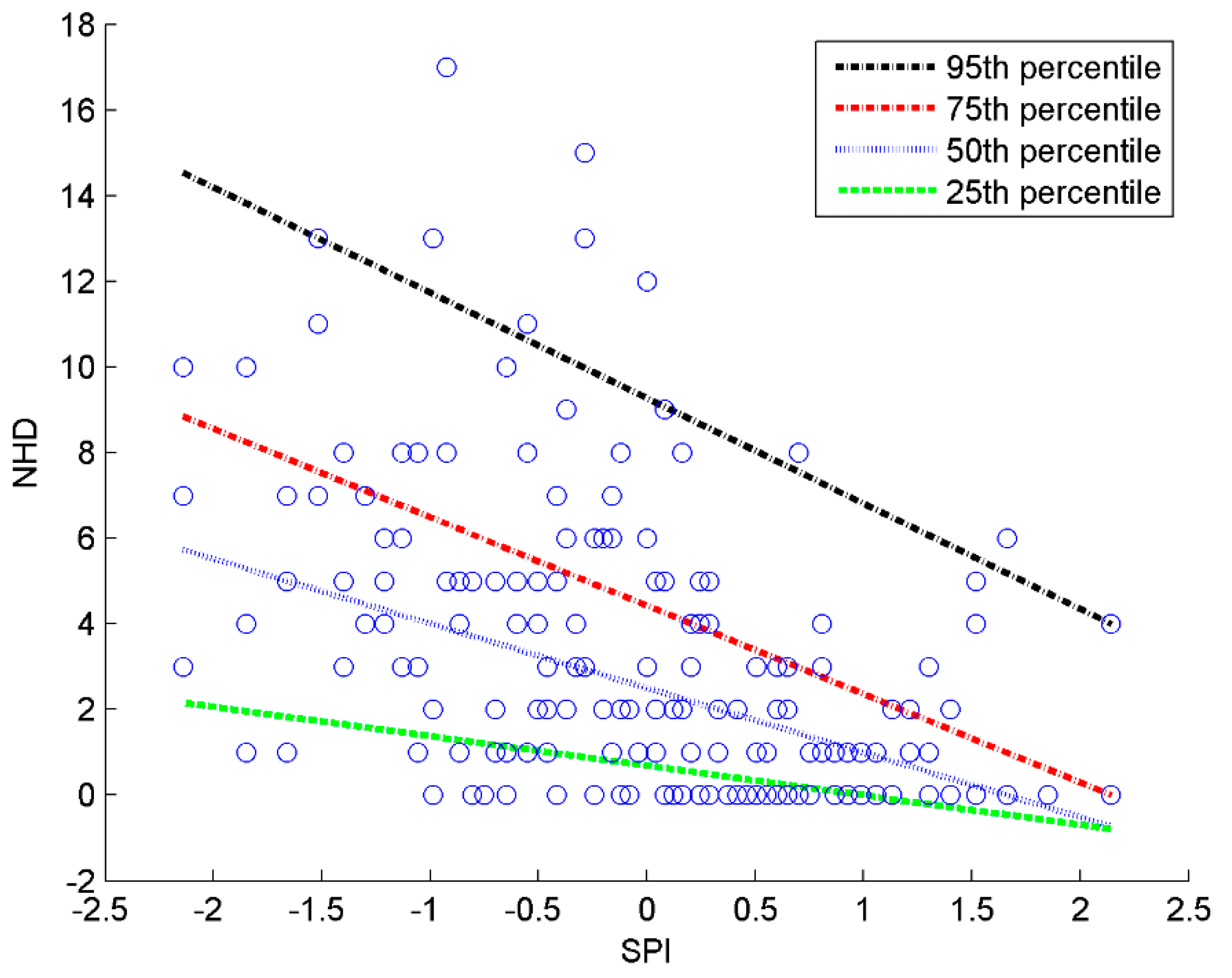
3.4. Quantile Regression
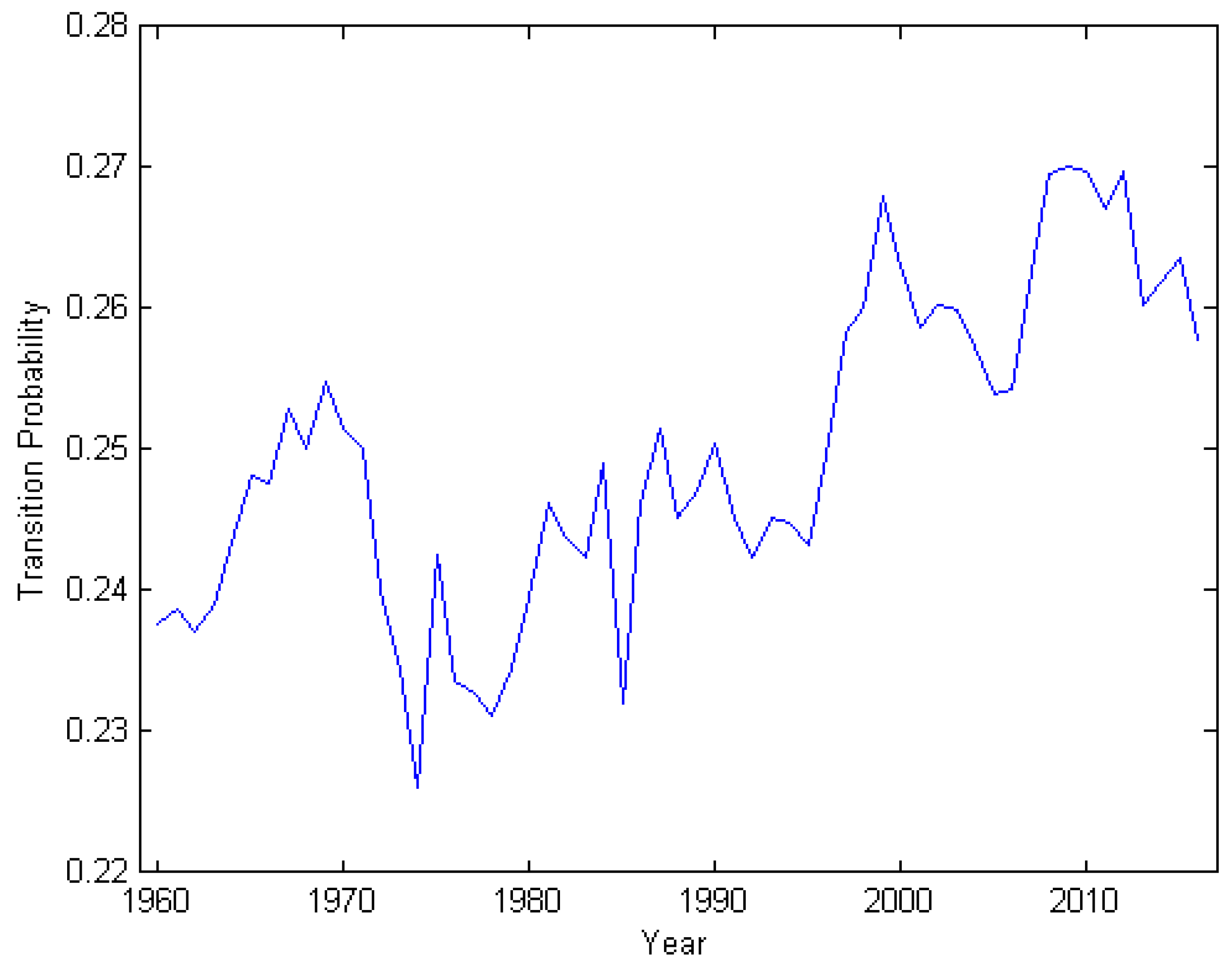
3.5. Markov Chain Model
4. Discussion
4.1. Comparison of Approaches
4.2. High Dimensional Modeling
4.3. Compound Extremes Under Climate Change
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Types of Compound Extremes
| Type of Compound Extremes | Combined Variables/Events/Extremes | Approaches |
|---|---|---|
| Compound drought and hot extreme | Drought and heat wave (hot days or months, high temperature) [37,38,39,65,90,138,156,157,159] | Empirical approach, Quantile regression, Multivariate distribution |
| Compound precipitation and temperature extreme | Heavy precipitation and cold/warm condition [47,87,184,190] | Empirical approach, Markov Chain approach |
| Low precipitation and high temperature [29,179,181,191] | Empirical approach, Multivariate distribution | |
| Dry-warm/dry-cold/wet-warm/wet-cold condition [29,77,80,192] | Empirical approach | |
| Compound flood | Storm surge and high rainfall [35,57,185,193] | Multivariate distribution |
| Storm surge and high discharge/runoff [48,55,56,60,61,136] | Empirical approach, Indicator approach, Multivariate distribution | |
| Storm surge and sea level [73,178] | Empirical approach, Indicator approach | |
| Sea levels and rainfall/river flow [59,97,136,194] | Multivariate distribution | |
| Compound drought | Deficit from precipitation, soil moisture, runoff or other variables [54,153,195] | Indicator approach, Multivariate distribution |
| Combined drought, moisture surplus, precipitation/temperature, and other extremes | Drought indices, precipitation extremes and temperature extremes [146,147,148,196] | Indicator approach |
References
- Reichstein, M.; Bahn, M.; Ciais, P.; Frank, D.; Mahecha, M.D.; Seneviratne, S.I.; Zscheischler, J.; Beer, C.; Buchmann, N.; Frank, D.C. Climate extremes and the carbon cycle. Nature 2013, 500, 287–295. [Google Scholar] [CrossRef] [PubMed]
- Easterling, D.; Groisman, P.Y.; Karl, T.; Evans, J.; Kunkel, K.; Ambenje, P. Observed variability and trends in extreme climate events: A brief review. Bull. Am. Meteorol. Soc. 2000, 81, 417–425. [Google Scholar] [CrossRef]
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation (Srex) a Special Report of Working Groups I And II of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; p. 582. [Google Scholar]
- Horton, R.M.; Mankin, J.S.; Lesk, C.; Coffel, E.; Raymond, C. A review of recent advances in research on extreme heat events. Curr. Clim. Chang. Rep. 2016, 2, 242–259. [Google Scholar] [CrossRef]
- Burt, T.P.; Howden, N.J.K.; Worrall, F. The changing water cycle: Hydroclimatic extremes in the british isles. Wiley Interdiscip. Rev. Water 2016, 3, 854–870. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Changes in extreme precipitation in texas. J. Geophys. Res. Atmos. 2010, 115, D14106. [Google Scholar] [CrossRef]
- Heim, R.R. An overview of weather and climate extremes—Products and trends. Weather Clim. Extrem 2015, 10, 1–9. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; van der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Beniston, M.; Stephenson, D.B.; Christensen, O.B.; Ferro, C.A.T.; Frei, C.; Goyette, S.; Halsnaes, K.; Holt, T.; Jylhä, K.; Koffi, B. Future extreme events in european climate: An exploration of regional climate model projections. Clim. Chang. 2007, 81, 71–95. [Google Scholar] [CrossRef]
- Zisopoulou, K.; Karalis, S.; Koulouri, M.-E.; Pouliasis, G.; Korres, E.; Karousis, A.; Triantafilopoulou, E.; Panagoulia, D. Recasting of the wef nexus as an actor with a new economic platform and management model. Energy Policy 2018, 119, 123–139. [Google Scholar] [CrossRef]
- Dosio, A.; Mentaschi, L.; Fischer, E.M.; Klaus, W. Extreme heat waves under 1.5 °C and 2 °C global warming. Environ. Res. Lett. 2018, 13, 054006. [Google Scholar] [CrossRef]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.A.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global changes in drought conditions under different levels of warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Alfieri, L.; Bisselink, B.; Dottori, F.; Naumann, G.; Roo, A.; Salamon, P.; Wyser, K.; Feyen, L. Global projections of river flood risk in a warmer world. Earth's Future 2016, 5, 171–182. [Google Scholar] [CrossRef]
- Rummukainen, M. Changes in climate and weather extremes in the 21st century. Wiley Interdiscip. Rev. Clim. Chang. 2012, 3, 115–129. [Google Scholar] [CrossRef]
- Stott, P. How climate change affects extreme weather events. Science 2016, 352, 1517–1518. [Google Scholar] [CrossRef] [PubMed]
- Trenberth, K.E.; Fasullo, J.T.; Shepherd, T.G. Attribution of climate extreme events. Nat. Clim. Chang. 2015, 5, 725–730. [Google Scholar] [CrossRef]
- Rahmstorf, S.; Coumou, D. Increase of extreme events in a warming world. Proc. Natl. Acad. Sci. USA 2011, 108, 17905–17909. [Google Scholar] [CrossRef] [PubMed]
- Alexander, L.V. Global observed long-term changes in temperature and precipitation extremes: A review of progress and limitations in ipcc assessments and beyond. Weather Clim. Extrem 2016, 11, 4–16. [Google Scholar] [CrossRef]
- Panagoulia, D.; Vlahogianni, E.I. Nonlinear dynamics and recurrence analysis of extreme precipitation for observed and general circulation model generated climates. Hydrol. Proccess. 2014, 28, 2281–2292. [Google Scholar] [CrossRef]
- Panagoulia, D.; Vlahogianni, E.I. Recurrence quantification analysis of extremes of maximum and minimum temperature patterns for different climate scenarios in the mesochora catchment in central-western greece. Atmos. Res. 2018, 205, 33–47. [Google Scholar] [CrossRef]
- Katz, R.; Parlange, M.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Katz, R.W. Statistics of extremes in climate change. Clim. Chang. 2010, 100, 71–76. [Google Scholar] [CrossRef]
- Leonard, M.; Westra, S.; Phatak, A.; Lambert, M.; van den Hurk, B.; McInnes, K.; Risbey, J.; Schuster, S.; Jakob, D.; Stafford-Smith, M. A compound event framework for understanding extreme impacts. Wiley Interdiscip. Rev. Clim. Chang. 2014, 5, 113–128. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Nicholls, N.; Easterling, D.; Goodess, C.M.; Kanae, S.; Kossin, J.; Luo, Y.; Marengo, J.; McInnes, K.; Rahimi, M. Changes in climate extremes and their impacts on the natural physical environment. In Managing the Risks of Extreme Events and Disasters to Advance climate Change Adaptation; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Allen, S.K., et al., Eds.; A Special Report of Working Groups I And II of the Intergovernmental Panel on Climate Change (IPCC); Cambridge University Press: Cambridge, UK, 2012; pp. 109–230. [Google Scholar]
- McPhillips, L.E.; Chang, H.; Chester, M.V.; Depietri, Y.; Friedman, E.; Grimm, N.B.; Kominoski, J.S.; McPhearson, T.; Méndez-Lázaro, P.; Rosi, E.J.; et al. Defining extreme events: A cross-disciplinary review. Earth’s Future 2018, 6, 441–455. [Google Scholar] [CrossRef]
- Orth, R.; Zscheischler, J.; Seneviratne, S.I. Record dry summer in 2015 challenges precipitation projections in central Europe. Sci. Rep. 2016, 6, 28334. [Google Scholar] [CrossRef] [PubMed]
- Sedlmeier, K.; Feldmann, H.; Schädler, G. Compound summer temperature and precipitation extremes over central Europe. Theor. Appl. Climatol. 2018, 131, 1493–1501. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A.; Phillips, T.J. Changes in concurrent monthly precipitation and temperature extremes. Environ. Res. Lett. 2013, 8, 034014. [Google Scholar] [CrossRef]
- Lyon, B. Southern africa summer drought and heat waves: Observations and coupled model behavior. J. Clim. 2009, 22, 6033–6046. [Google Scholar] [CrossRef]
- Albright, T.P.; Pidgeon, A.M.; Rittenhouse, C.D.; Clayton, M.K.; Wardlow, B.D.; Flather, C.H.; Culbert, P.D.; Radeloff, V.C. Combined effects of heat waves and droughts on avian communities across the conterminous United States. Ecosphere 2010, 1, 1–12. [Google Scholar] [CrossRef]
- Livneh, B.; Hoerling, M.P. The physics of drought in the U.S. Central great plains. J. Clim. 2016, 29, 6783–6804. [Google Scholar] [CrossRef]
- Mazzarella, A.; Rapetti, F. Scale-invariance laws in the recurrence interval of extreme floods: An application to the upper po river valley (Northern Italy). J. Hydrol. 2004, 288, 264–271. [Google Scholar] [CrossRef]
- Merz, B.; Aerts, J.; Arnbjerg-Nielsen, K.; Baldi, M.; Becker, A.; Bichet, A.; Blöschl, G.; Bouwer, L.M.; Brauer, A.; Cioffi, F.; et al. Floods and climate: Emerging perspectives for flood risk assessment and management. Nat. Hazards Earth Syst. Sci. 2014, 14, 1921–1942. [Google Scholar] [CrossRef]
- Van den Hurk, B.; van Meijgaard, E.; de Valk, P.; van Heeringen, K.-J.; Gooijer, J. Analysis of a compounding surge and precipitation event in the Netherlands. Environ. Res. Lett. 2015, 10, 035001. [Google Scholar] [CrossRef]
- Martius, O.; Pfahl, S.; Chevalier, C. A global quantification of compound precipitation and wind extremes. Geophys. Res. Lett. 2016, 43, 7709–7717. [Google Scholar] [CrossRef]
- Mazdiyasni, O.; AghaKouchak, A. Substantial increase in concurrent droughts and heatwaves in the United States. Proc. Natl. Acad. Sci. USA 2015, 112, 11484–11489. [Google Scholar] [CrossRef] [PubMed]
- Mueller, B.; Seneviratne, S.I. Hot days induced by precipitation deficits at the global scale. Proc. Natl. Acad. Sci. USA 2012, 109, 12398–12403. [Google Scholar] [CrossRef] [PubMed]
- Hirschi, M.; Seneviratne, S.I.; Alexandrov, V.; Boberg, F.; Boroneant, C.; Christensen, O.B.; Formayer, H.; Orlowsky, B.; Stepanek, P. Observational evidence for soil-moisture impact on hot extremes in southeastern Europe. Nat. Geosci. 2011, 4, 17–21. [Google Scholar] [CrossRef]
- Wahl, T.; Plant, N.G.; Long, J.W. Probabilistic assessment of erosion and flooding risk in the northern Gulf of Mexico. J. Geophys. Res. Oceans 2016, 121, 3029–3043. [Google Scholar] [CrossRef]
- Serafin, K.A.; Ruggiero, P. Simulating extreme total water levels using a time-dependent, extreme value approach. J. Geophys. Res. Oceans 2014, 119, 6305–6329. [Google Scholar] [CrossRef]
- Li, F.; van Gelder, P.H.A.J.M.; Ranasinghe, R.; Callaghan, D.P.; Jongejan, R.B. Probabilistic modelling of extreme storms along the Dutch coast. Coast. Eng. 2014, 86, 1–13. [Google Scholar] [CrossRef]
- Corbella, S.; Stretch, D.D. Simulating a multivariate sea storm using archimedean copulas. Coast. Eng. 2013, 76, 68–78. [Google Scholar] [CrossRef]
- Svensson, C.; Jones, D.A. Dependence between extreme sea surge, river flow and precipitation in eastern Britain. Int. J. Climatol. 2002, 22, 1149–1168. [Google Scholar] [CrossRef]
- Reed, A.J.; Mann, M.E.; Emanuel, K.A.; Lin, N.; Horton, B.P.; Kemp, A.C.; Donnelly, J.P. Increased threat of tropical cyclones and coastal flooding to new york city during the anthropogenic era. Proc. Natl. Acad. Sci. USA 2015, 112, 12610–12615. [Google Scholar] [CrossRef] [PubMed]
- Hiroaki, I.; Yukiko, H.; Dai, Y.; Sanne, M.; Ward, P.J.; Winsemius, H.C.; Martin, V.; Shinjiro, K. Compound simulation of fluvial floods and storm surges in a global coupled river-coast flood model: Model development and its application to 2007 Cyclone Sidr in Bangladesh. J. Adv. Model. Earth Syst. 2017, 9, 1847–1862. [Google Scholar]
- Benestad, R.E.; Haugen, J.E. On complex extremes: Flood hazards and combined high spring-time precipitation and temperature in Norway. Clim. Chang. 2007, 85, 381–406. [Google Scholar] [CrossRef]
- Bevacqua, E.; Maraun, D.; Hobæk Haff, I.; Widmann, M.; Vrac, M. Multivariate statistical modelling of compound events via pair-copula constructions: Analysis of floods in Ravenna (Italy). Hydrol. Earth Syst. Sci. 2017, 21, 2701–2723. [Google Scholar] [CrossRef]
- Trepanier, J.C.; Yuan, J.; Jagger, T.H. The combined risk of extreme tropical cyclone winds and storm surges along the U.S. Gulf of Mexico Coast. J. Geophys. Res. Atmos. 2017, 122, 3299–3316. [Google Scholar] [CrossRef]
- Petroliagkis, T.I. Estimations of statistical dependence as joint return period modulator of compound events. Part I: Storm surge and wave height. Nat. Hazards Earth Syst. Sci. Discuss. 2017, 2017, 1–46. [Google Scholar] [CrossRef]
- Fischer, E.; Knutti, R. Robust projections of combined humidity and temperature extremes. Nat. Clim. Chang. 2012, 3, 126–130. [Google Scholar] [CrossRef]
- Schnell, J.L.; Prather, M.J. Co-occurrence of extremes in surface ozone, particulate matter, and temperature over eastern north America. Proc. Natl. Acad. Sci. USA 2017, 114, 2854–2859. [Google Scholar] [CrossRef] [PubMed]
- Wilhite, D.; Glantz, M. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Klerk, W.J.; Winsemius, H.C.; van Verseveld, W.J.; Bakker, A.M.R.; Diermanse, F.L.M. The co-incidence of storm surges and extreme discharges within the rhine–meuse delta. Environ. Res. Lett. 2015, 10, 035005. [Google Scholar] [CrossRef]
- Kew, S.F.; Selten, F.M.; Lenderink, G.; Hazeleger, W. The simultaneous occurrence of surge and discharge extremes for the rhine delta. Nat. Hazards Earth Syst. Sci. 2013, 13, 2017–2029. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.D.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Chang. 2015, 5, 1093–1097. [Google Scholar] [CrossRef]
- Muis, S.; Verlaan, M.; Winsemius, H.C.; Aerts, J.C.; Ward, P.J. A global reanalysis of storm surges and extreme sea levels. Nat. Commun. 2016, 7, 11969. [Google Scholar] [CrossRef] [PubMed]
- Bengtsson, L. Probability of combined high sea levels and large rains in Malmö, Sweden, southern Resund. Hydrol. Proccess. 2016, 30, 3172–3183. [Google Scholar] [CrossRef]
- Paprotny, D.; Vousdoukas, M.I.; Morales-Nápoles, O.; Jonkman, S.N.; Feyen, L. Compound flood potential in Europe. Hydrol. Earth Syst. Sci. Discuss. 2018, 2018, 1–34. [Google Scholar] [CrossRef]
- Khanal, S.; Ridder, N.; de Vries, H.; Terink, W.; van den Hurk, B. Storm surge and extreme river discharge: A compound event analysis using ensemble impact modelling. Hydrol. Earth Syst. Sci. Discuss. 2018, 2018, 1–25. [Google Scholar] [CrossRef]
- Svensson, C.; Jones, D.A. Dependence between sea surge, river flow and precipitation in south and west Britain. Hydrol. Earth Syst. Sci. 2004, 8, 973–992. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Swain, D.L.; Touma, D. Anthropogenic warming has increased drought risk in California. Proc. Natl. Acad. Sci. USA 2015, 112, 3931–3936. [Google Scholar] [CrossRef] [PubMed]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Mladenova, I.E.; Basara, J.B.; Svoboda, M. Examining rapid onset drought development using the thermal infrared–based evaporative stress index. J. Hydrometeorol. 2013, 14, 1057–1074. [Google Scholar] [CrossRef]
- Sharma, S.; Mujumdar, P. Increasing frequency and spatial extent of concurrent meteorological droughts and heatwaves in India. Sci. Rep. 2017, 7, 15582. [Google Scholar] [CrossRef] [PubMed]
- Witte, J.C.; Douglass, A.R.; Silva, A.D.; Torres, O.; Levy, R.; Duncan, B.N. Nasa a-train and terra observations of the 2010 Russian Wildfires. Atmos. Chem. Phys. 2011, 11, 19113–19142. [Google Scholar] [CrossRef]
- Rizhsky, L.; Liang, H.; Mittler, R. The combined effect of drought stress and heat shock on gene expression in Tobacco. Plant Physiol. 2002, 130, 1143–1151. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Huang, B. Drought and heat stress injury to two cool-season turfgrasses in relation to antioxidant metabolism and lipid peroxidation. Crop Sci. 2001, 41, 436–442. [Google Scholar] [CrossRef]
- Rammig, A.; Wiedermann, M.; Donges, J.F.; Babst, F.; Von Bloh, W.; Frank, D.; Thonicke, K.; Mahecha, M.D. Coincidences of climate extremes and anomalous vegetation responses: Comparing tree ring patterns to simulated productivity. Biogeosciences 2015, 12, 373–385. [Google Scholar] [CrossRef]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogée, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Cai, W.; Chen, Y.; Liu, S.; Dong, W.; Zhang, H.; Yu, G.; Chen, Z.; He, H.; Guo, W. Severe summer heatwave and drought strongly reduced carbon uptake in Southern China. Sci. Rep. 2016, 6, 18813. [Google Scholar] [CrossRef] [PubMed]
- Koster, R.; Schubert, S.; Suarez, M. Analyzing the concurrence of meteorological droughts and warm periods, with implications for the determination of evaporative regime. J. Clim. 2009, 22, 3331–3341. [Google Scholar] [CrossRef]
- Haigh, I.D.; Wadey, M.P.; Wahl, T.; Ozsoy, O.; Nicholls, R.J.; Brown, J.M.; Horsburgh, K.; Gouldby, B. Spatial and temporal analysis of extreme sea level and storm surge events around the coastline of the UK. Sci. Data 2016, 3, 160107. [Google Scholar] [CrossRef] [PubMed]
- Davison, A.C.; Gholamrezaee, M.M. Geostatistics of extremes. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 581–608. [Google Scholar] [CrossRef]
- Cooley, D.; Cisewski, J.; Erhardt, R.J.; Jeon, S.; Mannshardt, E.; Omolo, B.O.; Sun, Y. A survey of spatial extremes: Measuring spatial dependence and modeling spatial effects. REVSTAT 2012, 10, 135–165. [Google Scholar]
- Hawkes, P.J.; Gonzalez-Marco, D.; Sánchez-Arcilla, A.; Prinos, P. Best practice for the estimation of extremes: A review. J. Hydraul. Res. 2008, 46, 324–332. [Google Scholar] [CrossRef]
- Beniston, M. Trends in joint quantiles of temperature and precipitation in Europe since 1901 and projected for 2100. Geophys. Res. Lett. 2009, 36, L07707. [Google Scholar] [CrossRef]
- Miao, C.; Sun, Q.; Duan, Q.; Wang, Y. Joint analysis of changes in temperature and precipitation on the Loess Plateau during the period 1961–2011. Clim. Dyn. 2016, 47, 3221–3234. [Google Scholar] [CrossRef]
- Leng, G.; Tang, Q.; Huang, S.; Zhang, X.; Cao, J. Assessments of joint hydrological extreme risks in a warming climate in China. Int. J. Climatol. 2016, 36, 1632–1642. [Google Scholar] [CrossRef]
- Morán-Tejeda, E.; Herrera, S.; López-Moreno, J.I.; Revuelto, J.; Lehmann, A.; Beniston, M. Evolution and frequency (1970–2007) of combined temperature–precipitation modes in the Spanish mountains and sensitivity of snow cover. Reg. Environ. Chang. 2013, 13, 873–885. [Google Scholar] [CrossRef]
- Schär, C.; Ban, N.; Fischer, E.M.; Rajczak, J.; Schmidli, J.; Frei, C.; Giorgi, F.; Karl, T.R.; Kendon, E.J.; Tank, A.M.G.K. Percentile indices for assessing changes in heavy precipitation events. Clim. Chang. 2016, 137, 1–16. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Frich, P.L.; Lv, A.; Della-Marta, P.; Gleason, B.; Haylock, M.; Klein, T.A.; Peterson, T.C. Observed coherent changes in climatic extremes during 2nd half of the 20th century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Tank, A.M.G.K.; Wijngaard, J.B.; Können, G.P.; Böhm, R.; Demarée, G.; Gocheva, A.A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C. Daily surface air temperature and precipitation dataset 1901–1999 for European Climate Assessment (ECA). Int. J. Climatol. 2002, 22, 1441–1453. [Google Scholar]
- Alexander, L.; Zhang, X.; Peterson, T.; Caesar, J.; Gleason, B.; Klein Tank, A.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 2006, 111, D05109. [Google Scholar] [CrossRef]
- Sunyer, M.A.; Sørup, H.J.D.; Christensen, O.B.; Madsen, H.; Rosbjerg, D.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K. On the importance of observational data properties when assessing regional climate model performance of extreme precipitation. Hydrol. Earth Syst. Sci. 2013, 17, 4323–4337. [Google Scholar] [CrossRef]
- Sedlmeier, K.; Mieruch, S.; Schädler, G.; Kottmeier, C. Compound extremes in a changing climate-a markov chain approach. Nonlinear Process. Geophys. 2016, 23, 375–390. [Google Scholar] [CrossRef]
- Donat, M.G.; Sillmann, J.; Wild, S.; Alexander, L.V.; Lippmann, T.; Zwiers, F.W. Consistency of temperature and precipitation extremes across various global gridded in situ and reanalysis datasets. J. Clim. 2014, 27, 5019–5035. [Google Scholar] [CrossRef]
- Hofstra, N.; New, M.; McSweeney, C. The influence of interpolation and station network density on the distributions and trends of climate variables in gridded daily data. Clim. Dyn. 2010, 35, 841–858. [Google Scholar] [CrossRef]
- Kirono, D.G.C.; Hennessy, K.J.; Grose, M. Increasing risk of months with low rainfall and high temperature in southeast Australia for the past 150 years. Clim. Risk Manag. 2017, 16, 10–21. [Google Scholar] [CrossRef]
- Trepanier, J.C.; Needham, H.F.; Elsner, J.B.; Jagger, T.H. Combining surge and wind risk from hurricanes using a copula model: An example from Galveston, texas. Prof. Geogr. 2015, 67, 52–61. [Google Scholar] [CrossRef]
- Tebaldi, C.; Sansó, B. Joint projections of temperature and precipitation change from multiple climate models: A hierarchical Bayesian approach. J. R. Stat. Soc. Ser. A 2009, 172, 83–106. [Google Scholar] [CrossRef]
- Sexton, D.M.H.; Murphy, J.M.; Collins, M.; Webb, M.J. Multivariate probabilistic projections using imperfect climate models part I: Outline of methodology. Clim. Dyn. 2011, 38, 1–30. [Google Scholar] [CrossRef]
- Watterson, I. Calculation of joint pdfs for climate change with properties matching recent Australian projections. Aust. Meteorol. Oceanogr. J. 2011, 61, 211–219. [Google Scholar] [CrossRef]
- Estrella, N.; Menzel, A. Recent and future climate extremes arising from changes to the bivariate distribution of temperature and precipitation in Bavaria, Germany. Int. J. Climatol. 2013, 33, 1687–1695. [Google Scholar] [CrossRef]
- Rodrigo, F. On the covariability of seasonal temperature and precipitation in Spain, 1956–2005. Int. J. Climatol. 2015, 35, 3362–3370. [Google Scholar] [CrossRef]
- Hawkes, P.J. Joint probability analysis for estimation of extremes. J. Hydraul. Res. 2008, 46, 246–256. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Review of dependence modeling in hydrology and water resources. Prog. Phys. Geogr. 2016, 40, 549–578. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Dependence Concepts; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Kao, S.C.; Govindaraju, R.S. Trivariate statistical analysis of extreme rainfall events via the Plackett Family of copulas. Water Resour. Res. 2008, 44, W02415. [Google Scholar] [CrossRef]
- Song, S.; Singh, V. Frequency analysis of droughts using the plackett copula and parameter estimation by genetic algorithm. Stoch. Environ. Res. Risk Assess. 2010, 24, 783–805. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T. Multivariate quantiles in hydrological frequency analysis. Environmetrics 2011, 22, 63–78. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ines, A.V.M.; Das, N.N.; Prakash Khedun, C.; Singh, V.P.; Sivakumar, B.; Hansen, J.W. Anatomy of a local-scale drought: Application of assimilated remote sensing products, crop model, and statistical methods to an agricultural drought study. J. Hydrol. 2015, 526, 15–29. [Google Scholar] [CrossRef]
- Schöelzel, C.; Friederichs, P. Multivariate non-normally distributed random variables in climate research–introduction to the copula approach. Nonlinear Process. Geophys. 2008, 15, 761–772. [Google Scholar] [CrossRef]
- Durante, F.; Salvadori, G. On the construction of multivariate extreme value models via copulas. Environmetrics 2010, 21, 143–161. [Google Scholar] [CrossRef]
- Song, S.; Singh, V.P. Meta-elliptical copulas for drought frequency analysis of periodic hydrologic data. Stoch. Environ. Res. Risk Assess. 2010, 24, 425–444. [Google Scholar] [CrossRef]
- Jonathan, P.; Ewans, K. Statistical modelling of extreme ocean environments for marine design: A review. Ocean Eng. 2013, 62, 91–109. [Google Scholar] [CrossRef]
- Renard, B.; Lang, M. Use of a gaussian copula for multivariate extreme value analysis: Some case studies in hydrology. Adv. Water Resour. 2007, 30, 897–912. [Google Scholar] [CrossRef]
- Rueda, A.; Camus, P.; Tomás, A.; Vitousek, S.; Méndez, F.J. A multivariate extreme wave and storm surge climate emulator based on weather patterns. Ocean Model. 2016, 104, 242–251. [Google Scholar] [CrossRef]
- Bardossy, A. Copula-based geostatistical models for groundwater quality parameters. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Bardossy, A.; Li, J. Geostatistical interpolation using copulas. Water Resour. Res. 2008, 44, W07412. [Google Scholar] [CrossRef]
- Kazianka, H.; Pilz, J. Spatial interpolation using copula-based geostatistical models. In geoENV VII—Geostatistics for Environmental Applications; Atkinson, P., Lloyd, C., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 307–319. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Trivedi, P.K.; Zimmer, D.M. Copula modeling: An introduction for practitioners. Found. Trends Econom. 2005, 1, 1–111. [Google Scholar] [CrossRef]
- Serinaldi, F.; Bárdossy, A.; Kilsby, C.G. Upper tail dependence in rainfall extremes: Would we know it if we saw it? Stoch. Environ. Res. Risk Assess. 2015, 29, 1211–1233. [Google Scholar] [CrossRef]
- Genest, C.; Kojadinovic, I.; Nešlehová, J.; Yan, J. A goodness-of-fit test for bivariate extreme-value copulas. Bernoulli 2011, 17, 253–275. [Google Scholar] [CrossRef]
- Salvadori, G.; de Michele, C.; Kottegoda, N.; Rosso, R. Extremes in Nature: An. Approach Using Copulas; Springer: New York, NY, USA, 2007. [Google Scholar]
- Cormier, E.; Genest, C.; Nešlehová, J.G. Using b-splines for nonparametric inference on bivariate extreme-value copulas. Extremes 2014, 17, 633–659. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.-P. A characterization of gumbel’s family of extreme value distributions. Stat. Probab. Lett. 1989, 8, 207–211. [Google Scholar] [CrossRef]
- Singh, V.P.; Jain, S.K.; Tyagi, A. Risk and Reliability Analysis: A Handbook for Civil and Environmental Engineers; ASCE Press: Reston, VA, USA, 2007. [Google Scholar]
- Singh, V.P. Handbook of Applied Hydrology; McGraw Hill Professional: New York, NY, USA, 2016. [Google Scholar]
- Serinaldi, F. An uncertain journey around the tails of multivariate hydrological distributions. Water Resour. Res. 2013, 49, 6527–6547. [Google Scholar] [CrossRef]
- Mazzarella, A. A fractal approach to sea-surge occurrences in the Northern Adriatic Sea. J. Coast. Res. 1998, 14, 1265–1268. [Google Scholar]
- Malamud, B.D.; Turcotte, D.L. The applicability of power-law frequency statistics to floods. J. Hydrol. 2006, 322, 168–180. [Google Scholar] [CrossRef]
- Mazzarella, A.; Diodato, N. The alluvial events in the last two centuries at Sarno, Southern Italy: Their classification and power-law time-occurrence. Theor. Appl. Climatol. 2002, 72, 75–84. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; Michele, C. Multivariate return period calculation via survival functions. Water Resour. Res. 2013, 49, 2308–2311. [Google Scholar] [CrossRef]
- Gräler, B.; Petroselli, A.; Grimaldi, S.; De Baets, B.; Verhoest, N. An update on multivariate return periods in hydrology. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 175–178. [Google Scholar] [CrossRef]
- Serinaldi, F. Dismissing return periods! Stoch. Environ. Res. Risk Assess. 2015, 29, 1179–1189. [Google Scholar] [CrossRef]
- Brunner, M.I.; Seibert, J.; Favre, A.C. Bivariate return periods and their importance for flood peak and volume estimation. Wiley Interdiscip. Rev. Water 2016, 3, 819–833. [Google Scholar] [CrossRef]
- Gräler, B.; van den Berg, M.; Vandenberghe, S.; Petroselli, A.; Grimaldi, S.; De Baets, B.; Verhoest, N. Multivariate return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrol. Earth Syst. Sci. 2013, 17, 1281–1296. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P.; Wei, O.; Cheng, H. An integrated package for drought monitoring, prediction and analysis to aid drought modeling and assessment. Environ. Model. Softw. 2017, 91, 199–209. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; de Michele, C.; Bernardi, M.; Petrella, L. A multivariate copula-based framework for dealing with hazard scenarios and failure probabilities. Water Resour. Res. 2016, 52, 3701–3721. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate standardized drought index: A parametric approach for drought analysis. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
- Moftakhari, H.R.; Salvadori, G.; AghaKouchak, A.; Sanders, B.F.; Matthew, R.A. Compounding effects of sea level rise and fluvial flooding. Proc. Natl. Acad. Sci. USA 2017, 114, 9785–9790. [Google Scholar] [CrossRef] [PubMed]
- Koster, R.D.; Wang, H.; Schubert, S.D.; Suarez, M.J.; Mahanama, S. Drought-induced warming in the continental United States under different SST regimes. J. Clim. 2009, 22, 5385–5400. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P.; Ouyang, W. Quantitative risk assessment of the effects of drought on extreme temperature in Eastern China. J. Geophys. Res. Atmos. 2017, 122, 9050–9059. [Google Scholar] [CrossRef]
- Heffernan, J.E.; Tawn, J.A. A conditional approach for multivariate extreme values (with discussion). J. R. Stat. Soc. B 2004, 66, 497–546. [Google Scholar] [CrossRef]
- Heffernan, J.E.; Resnick, S.I. Limit laws for random vectors with an extreme component. Ann. Appl. Probab. 2007, 17, 537–571. [Google Scholar] [CrossRef]
- Keef, C.; Papastathopoulos, I.; Tawn, J.A. Estimation of the conditional distribution of a multivariate variable given that one of its components is large: Additional constraints for the heffernan and tawn model. J. Multivar. Anal. 2013, 115, 396–404. [Google Scholar] [CrossRef]
- Cheng, L.; Gilleland, E.; Heaton, M.J.; AghaKouchak, A. Empirical bayes estimation for the conditional extreme value model. Stat 2014, 3, 391–406. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall frequency distributions using archimedean copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Yue, S.; Rasmussen, P. Bivariate frequency analysis: Discussion of some useful concepts in hydrological application. Hydrol. Proccess. 2002, 16, 2881–2898. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Gallant, A.J.E.; Karoly, D.J. A combined climate extremes index for the Australian Region. J. Clim. 2010, 23, 6153–6165. [Google Scholar] [CrossRef]
- Gallant, A.J.; Karoly, D.J.; Gleason, K.L. Consistent trends in a modified climate extremes index in the United States, Europe, and Australia. J. Clim. 2014, 27, 1379–1394. [Google Scholar] [CrossRef]
- Karl, T.R.; Knight, R.W.; Easterling, D.R.; Quayle, R.G. Indices of climate change for the United States. Bull. Am. Meteorol. Soc. 1996, 77, 279–292. [Google Scholar] [CrossRef]
- Perkins, S.E.; Alexander, L.V. On the measurement of heat waves. J. Clim. 2013, 26, 4500–4517. [Google Scholar] [CrossRef]
- Brooks, H.E.; Lee, J.W.; Craven, J.P. The spatial distribution of severe thunderstorm and tornado environments from global reanalysis data. Atmos. Res. 2003, 67, 73–94. [Google Scholar] [CrossRef]
- Brooks, H.E. Proximity soundings for severe convection for Europe and the United States from reanalysis data. Atmos. Res. 2009, 93, 546–553. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Kao, S.C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Meng, L.; Shen, Y. On the relationship of soil moisture and extreme temperatures in East China. Earth Interact. 2014, 18, 1–20. [Google Scholar] [CrossRef]
- Ford, T.W.; Quiring, S.M. In situ soil moisture coupled with extreme temperatures: A study based on the Oklahoma mesonet. Geophys. Res. Lett. 2014, 41, 4727–4734. [Google Scholar] [CrossRef]
- Quesada, B.; Vautard, R.; Yiou, P.; Hirschi, M.; Seneviratne, S.I. Asymmetric European summer heat predictability from wet and dry southern winters and springs. Nat. Clim. Chang. 2012, 2, 736–741. [Google Scholar] [CrossRef]
- Herold, N.; Kala, J.; Alexander, L. The influence of soil moisture deficits on Australian heatwaves. Environ. Res. Lett 2016, 11, 064003. [Google Scholar] [CrossRef]
- Zhang, X.-J.; Tang, Q.; Pan, M.; Tang, Y. A long-term land surface hydrologic fluxes and states dataset for China. J. Hydrometeorol. 2014, 15, 2067–2084. [Google Scholar] [CrossRef]
- Steinemann, A. Drought indicators and triggers: A stochastic approach to evaluation. J. Am. Water Resour. Assoc. 2003, 39, 1217–1233. [Google Scholar] [CrossRef]
- Shaby, B.A.; Reich, B.J.; Cooley, D.; Kaufman, C.G. A markov-switching model for heat waves. Ann. Appl. Stat. 2016, 10, 74–93. [Google Scholar] [CrossRef]
- Friederichs, P.; Hense, A. Statistical downscaling of extreme precipitation events using censored quantile regression. Mon. Weather Rev. 2007, 135, 2365–2378. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: San Diego, CA, USA, 2011; Volume 100. [Google Scholar]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Liu, Z.; Törnros, T.; Menzel, L. A probabilistic prediction network for hydrological drought identification and environmental flow assessment. Water Resour. Res. 2016, 52, 6243–6262. [Google Scholar] [CrossRef]
- Brechmann, E.C.; Schepsmeier, U. Modeling dependence with C-and D-vine copulas: The R-package cdvine. J. Stat. Softw. 2013, 52, 1–27. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, X.; Guan, Y. A multivariate conditional model for streamflow prediction and spatial precipitation refinement. J. Geophys. Res. Atmos. 2015, 120, 10116–10129. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J.; Dettinger, M.D.; Krysanova, V. On critiques of “stationarity is dead: Whither water management?”. Water Resour. Res. 2015, 51, 7785–7789. [Google Scholar] [CrossRef]
- Milly, P.; Betancourt, J.; Falkenmark, M.; Hirsch, R.; Kundzewicz, Z.; Lettenmaier, D.; Stouffer, R. Climate change. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Chebana, F.; Ouarda, T.B.; Duong, T.C. Testing for multivariate trends in hydrologic frequency analysis. J. Hydrol. 2013, 486, 519–530. [Google Scholar] [CrossRef]
- Sarhadi, A.; Ausín, M.C.; Wiper, M.P. A new time-varying concept of risk in a changing climate. Sci. Rep. 2016, 6, 35755. [Google Scholar] [CrossRef] [PubMed]
- Bender, J.; Wahl, T.; Jensen, J. Multivariate design in the presence of non-stationarity. J. Hydrol. 2014, 514, 123–130. [Google Scholar] [CrossRef]
- Jonathan, P.; Ewans, K.; Randell, D. Non-stationary conditional extremes of northern North Sea storm characteristics. Environmetrics 2014, 25, 172–188. [Google Scholar] [CrossRef]
- Jonathan, P.; Randell, D.; Wu, Y.; Ewans, K. Return level estimation from non-stationary spatial data exhibiting multidimensional covariate effects. Ocean Eng. 2014, 88, 520–532. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Xu, C.Y.; Guo, S. Bivariate frequency analysis of nonstationary low-flow series based on the time-varying copula. Hydrol. Proccess. 2015, 29, 1521–1534. [Google Scholar] [CrossRef]
- Sarhadi, A.; Burn, D.H.; Concepción Ausín, M.; Wiper, M.P. Time-varying nonstationary multivariate risk analysis using a dynamic bayesian copula. Water Resour. Res. 2016, 52, 2327–2349. [Google Scholar] [CrossRef]
- Little, C.M.; Horton, R.M.; Kopp, R.E.; Oppenheimer, M.; Vecchi, G.A.; Villarini, G. Joint projections of us east coast sea level and storm surge. Nat. Clim. Chang. 2015, 5, 1114–1120. [Google Scholar] [CrossRef]
- Zscheischler, J.; Seneviratne, S.I. Dependence of drivers affects risks associated with compound events. Sci. Adv. 2017, 3, e1700263. [Google Scholar] [CrossRef] [PubMed]
- Hao, Z.; Singh, V.P. Integrating entropy and copula theories for hydrologic modeling and analysis. Entropy 2015, 17, 2253–2280. [Google Scholar] [CrossRef]
- Serinaldi, F. Can we tell more than we can know? The limits of bivariate drought analyses in the United States. Stoch. Environ. Res. Risk Assess. 2016, 30, 1691–1704. [Google Scholar] [CrossRef]
- Whan, K.; Zscheischler, J.; Orth, R.; Shongwe, M.; Rahimi, M.; Asare, E.O.; Seneviratne, S.I. Impact of soil moisture on extreme maximum temperatures in Europe. Weather Clim. Extrem 2015, 9, 57–67. [Google Scholar] [CrossRef]
- Sun, A.Y.; Xia, Y.; Caldwell, T.G.; Hao, Z. Patterns of precipitation and soil moisture extremes in Texas, US: A complex network analysis. Adv. Water Resour. 2018, 112, 203–213. [Google Scholar] [CrossRef]
- Tencer, B.; Bettolli, M.L.; Rusticucci, M. Compound temperature and precipitation extreme events in southern South America: Associated atmospheric circulation, and simulations by a multi-rcm ensemble. Clim. Res. 2016, 68, 183–199. [Google Scholar] [CrossRef]
- Zheng, F.; Westra, S.; Sisson, S.A. Quantifying the dependence between extreme rainfall and storm surge in the coastal zone. J. Hydrol. 2013, 505, 172–187. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Martinez, F.; Kalantari, Z.; Viglione, A. Drought and flood in the anthropocene: Feedback mechanisms in reservoir operation. Earth Syst. Dyn. 2017, 8, 225–233. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Stahl, K.; Di Baldassarre, G.; Clark, J.; Rangecroft, S.; Wanders, N.; Gleeson, T.; Van Dijk, A.I.J.M.; Tallaksen, L.M.; Hannaford, J.; et al. Drought in a human-modified world: Reframing drought definitions, understanding, and analysis approaches. Hydrol. Earth Syst. Sci. 2016, 20, 3631–3650. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Viglione, A.; Carr, G.; Kuil, L.; Yan, K.; Brandimarte, L.; Blöschl, G. Debates—Perspectives on socio-hydrology: Capturing feedbacks between physical and social processes. Water Resour. Res. 2015, 51, 4770–4781. [Google Scholar] [CrossRef]
- Dijk, A.I.; Beck, H.E.; Crosbie, R.S.; Jeu, R.A.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The millennium drought in southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Tencer, B.; Weaver, A.; Zwiers, F. Joint occurrence of daily temperature and precipitation extreme events over Canada. J. Appl. Meteorol. Climatol. 2014, 53, 2148–2162. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef]
- Arsenović, P.; Tošić, I.; Unkašević, M. Trends in combined climate indices in Serbia from 1961 to 2010. Meteorol. Atmos. Phys. 2015, 127, 489–498. [Google Scholar] [CrossRef]
- Zheng, F.; Westra, S.; Leonard, M.; Sisson, S.A. Modeling dependence between extreme rainfall and storm surge to estimate coastal flooding risk. Water Resour. Res. 2014, 50, 2050–2071. [Google Scholar] [CrossRef]
- Lian, J.J.; Xu, K.; Ma, C. Joint impact of rainfall and tidal level on flood risk in a coastal city with a complex river network: A case study of Fuzhou city, China. Hydrol. Earth Syst. Sci. 2013, 17, 679–689. [Google Scholar] [CrossRef]
- Beersma, J.J.; Buishand, T.A. Joint probability of precipitation and discharge deficits in the Netherlands. Water Resour. Res. 2004, 40, W12508. [Google Scholar] [CrossRef]
- Gleason, K.L.; Lawrimore, J.H.; Levinson, D.H.; Karl, T.R.; Karoly, D.J. A revised us climate extremes index. J. Clim. 2008, 21, 2124–2137. [Google Scholar] [CrossRef]
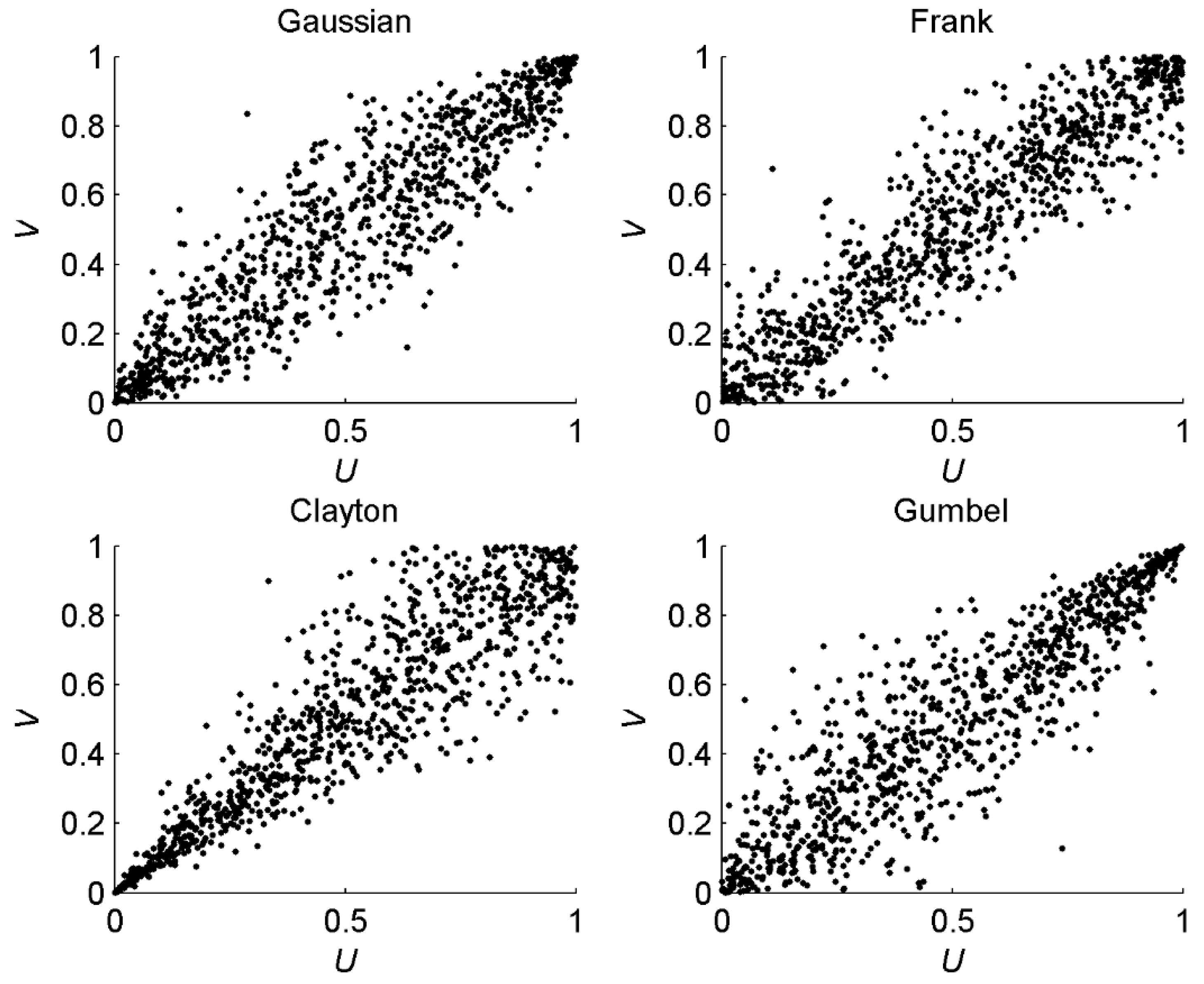

| Copulas | C(u,v) | Parameter |
|---|---|---|
| Gaussian | * | |
| Clayton | ||
| Frank | ||
| Gumbel |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Z.; Singh, V.P.; Hao, F. Compound Extremes in Hydroclimatology: A Review. Water 2018, 10, 718. https://doi.org/10.3390/w10060718
Hao Z, Singh VP, Hao F. Compound Extremes in Hydroclimatology: A Review. Water. 2018; 10(6):718. https://doi.org/10.3390/w10060718
Chicago/Turabian StyleHao, Zengchao, Vijay P. Singh, and Fanghua Hao. 2018. "Compound Extremes in Hydroclimatology: A Review" Water 10, no. 6: 718. https://doi.org/10.3390/w10060718
APA StyleHao, Z., Singh, V. P., & Hao, F. (2018). Compound Extremes in Hydroclimatology: A Review. Water, 10(6), 718. https://doi.org/10.3390/w10060718





