Assessing the Influence of the Three Gorges Dam on Hydrological Drought Using GRACE Data
Abstract
1. Introduction
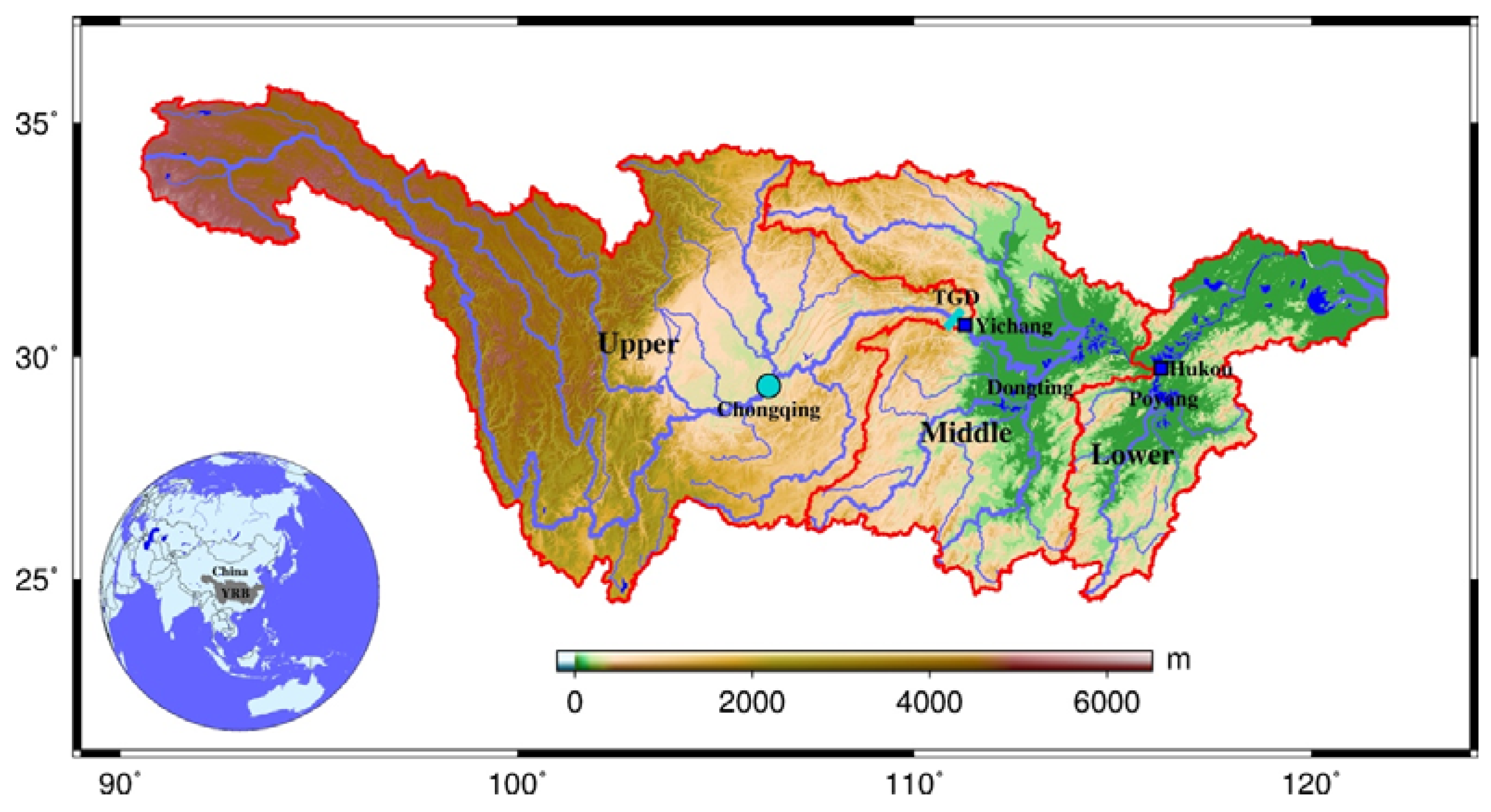
2. Study Area
3. Data and Methods
3.1. GRACE
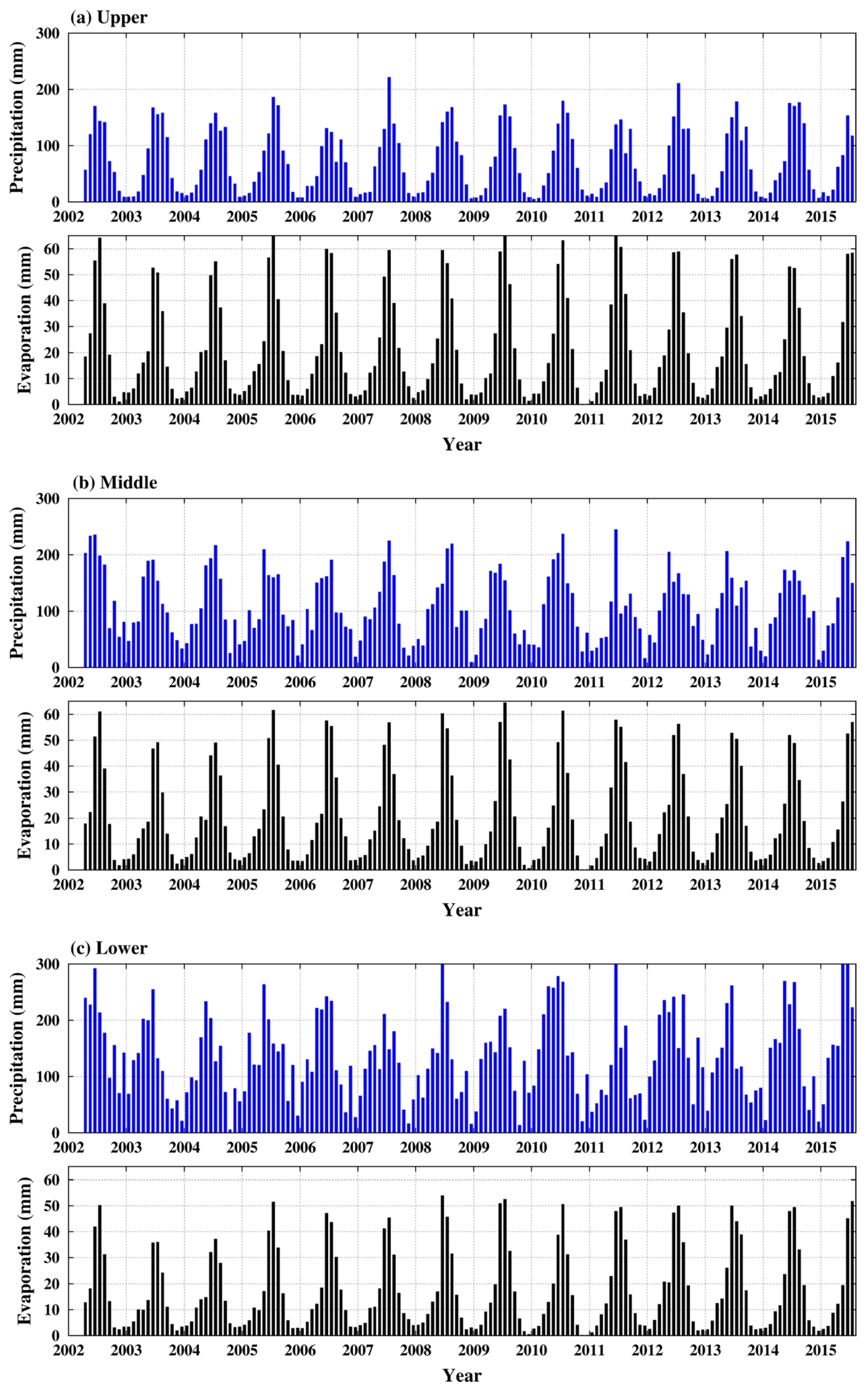
3.2. GLDAS and TRMM
3.3. ANN Approach
3.4. DII Based on TTWS and NTWS
4. Results
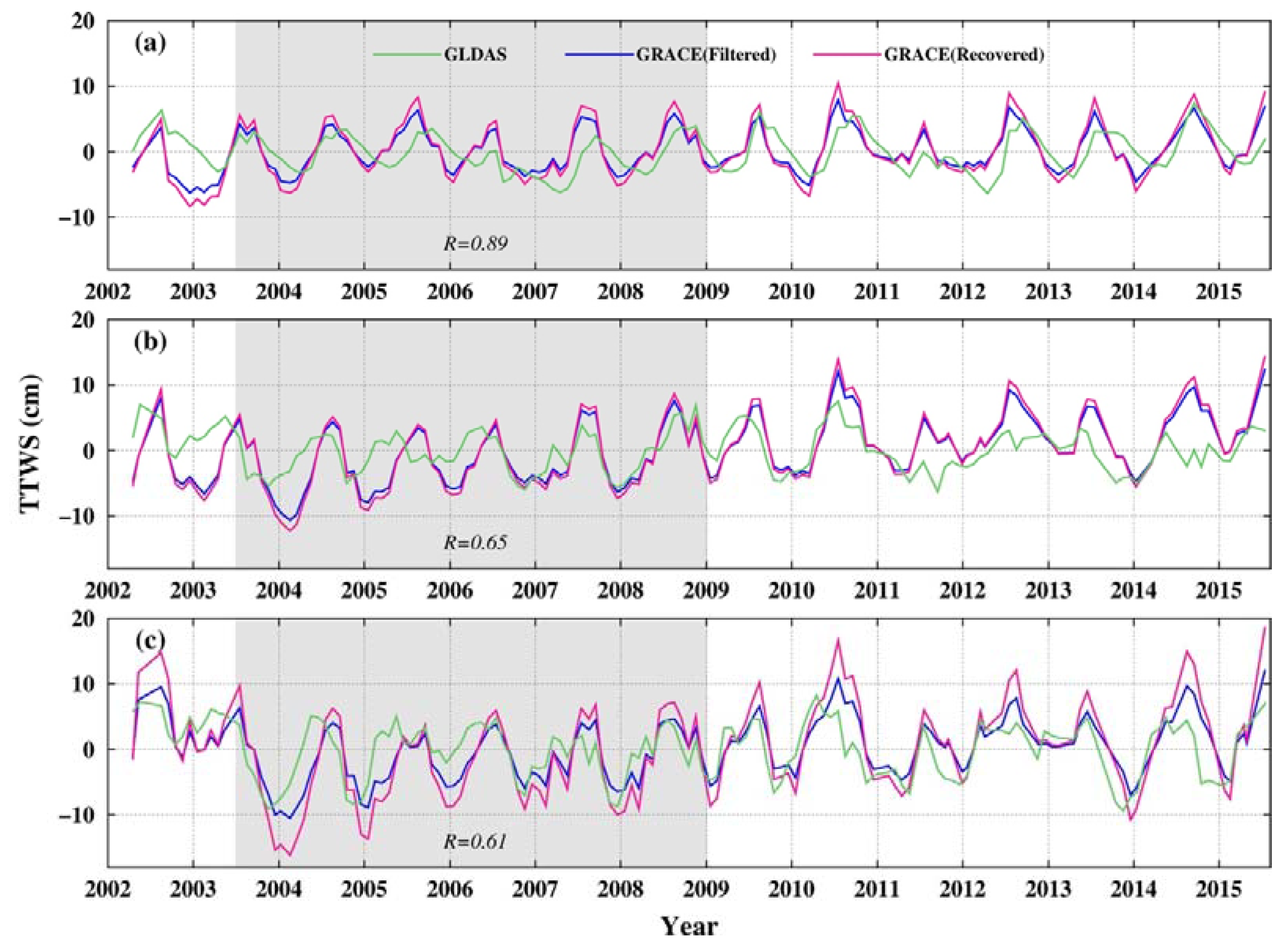
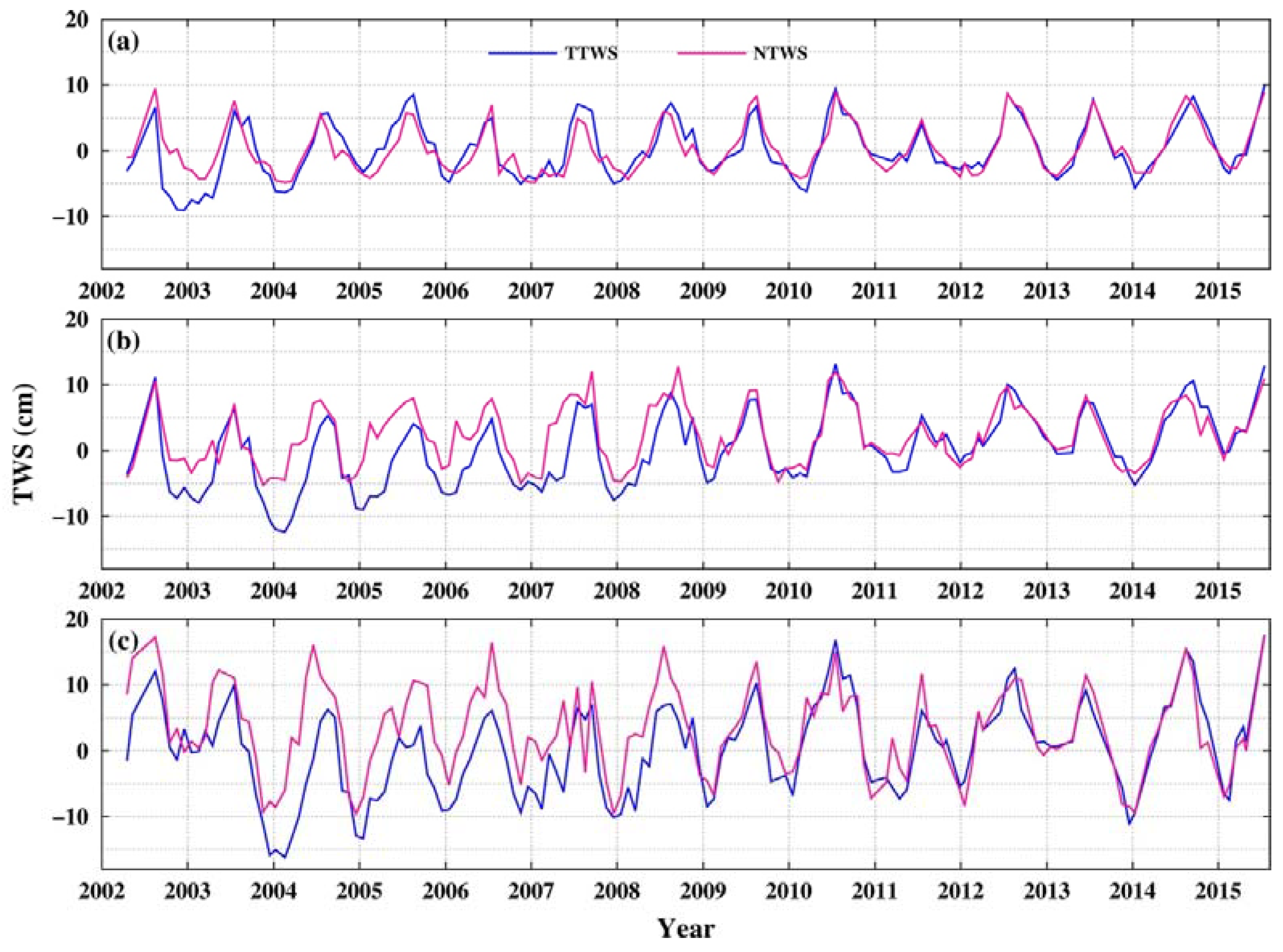
4.1. Recovered TTWS in the YRB
4.2. NTWS in the YRB
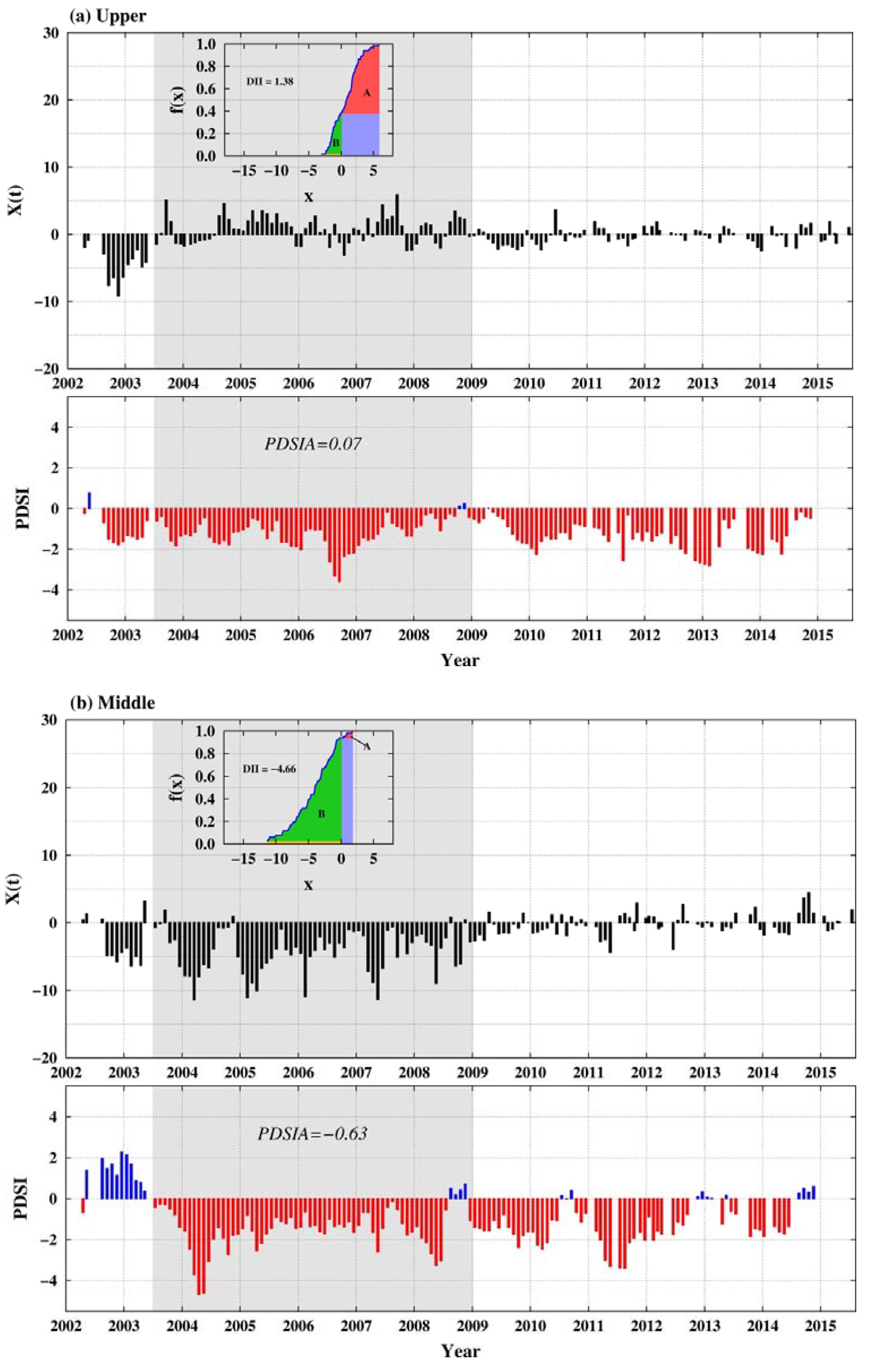
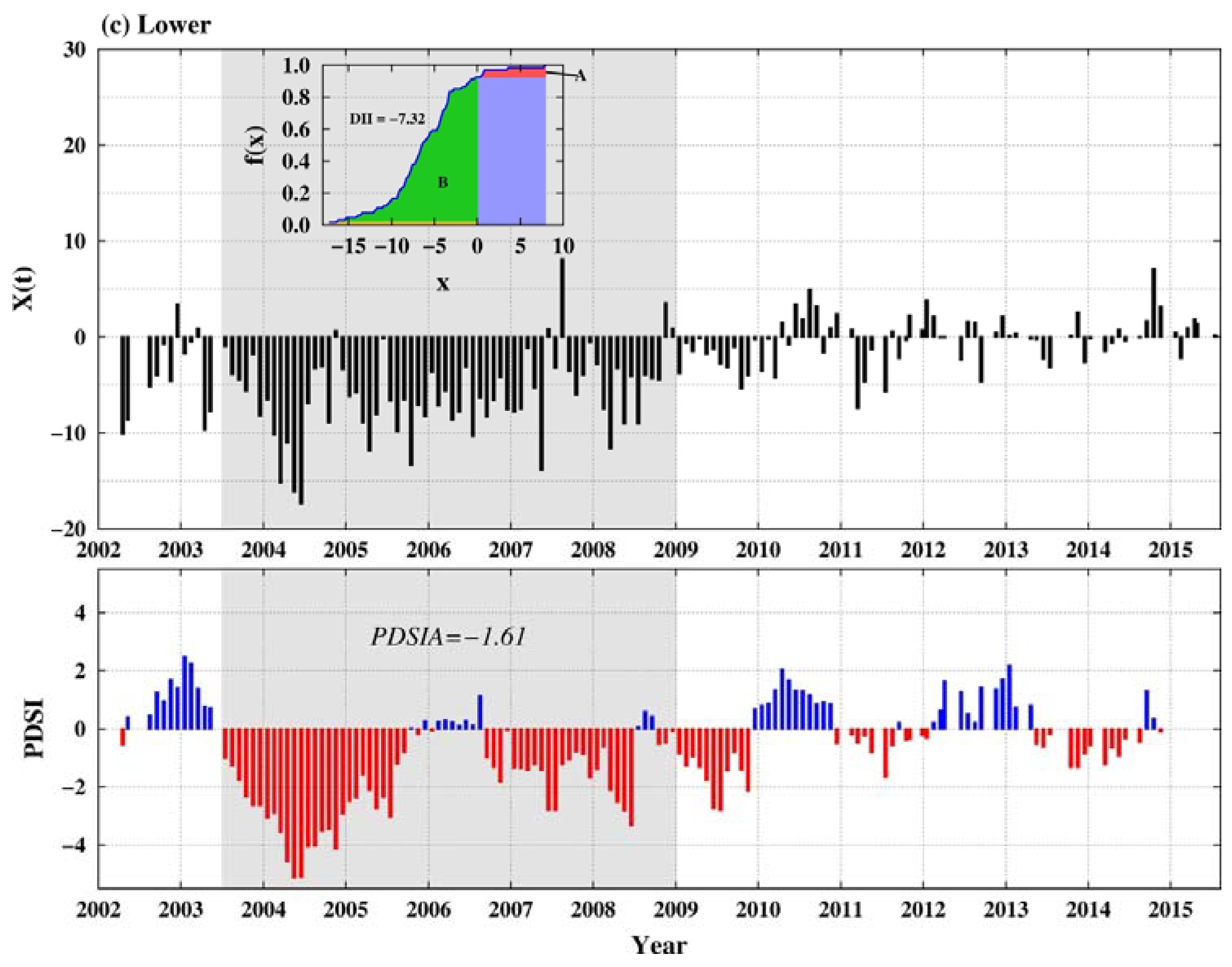
4.3. DII of the YRB
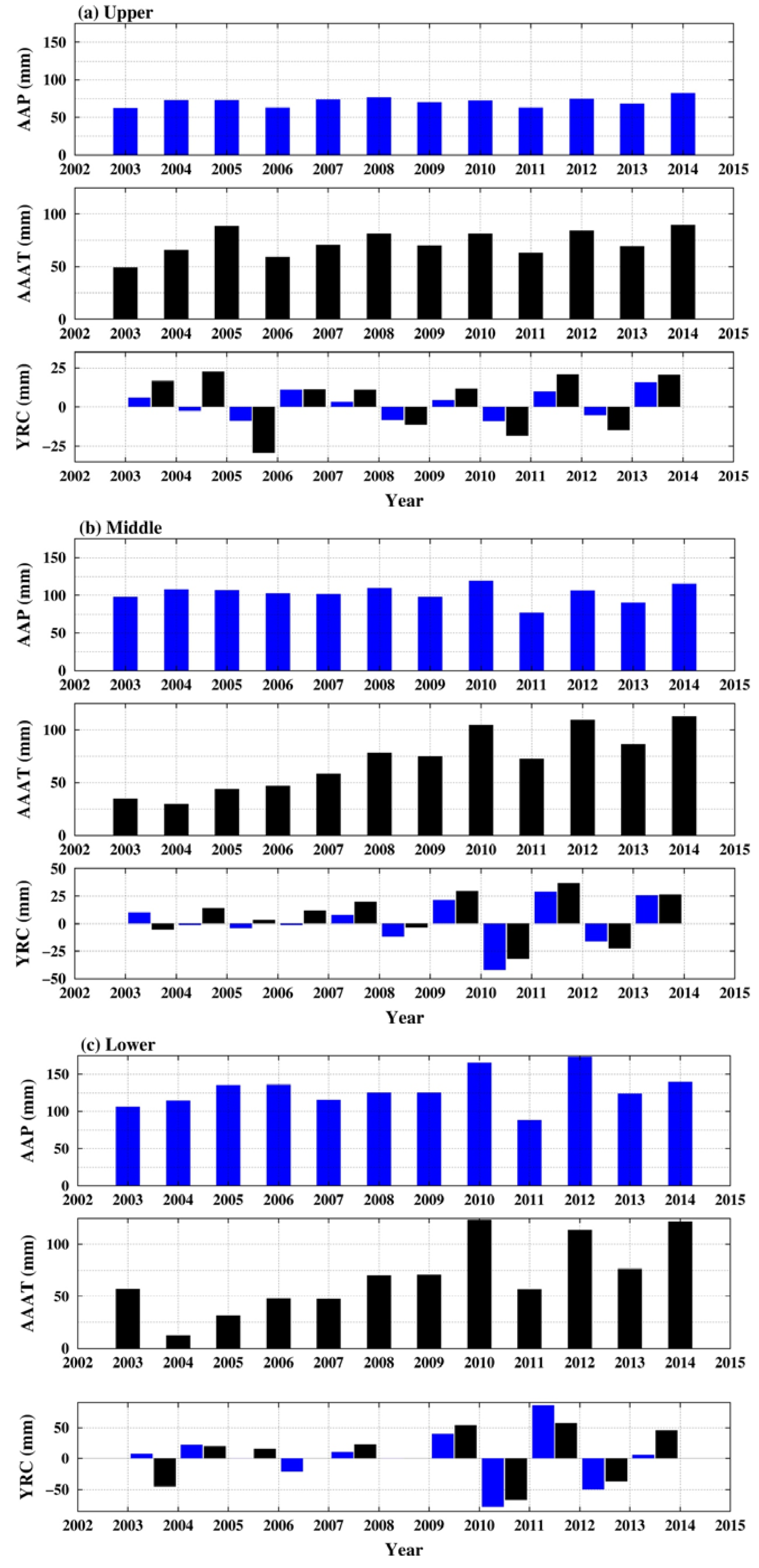
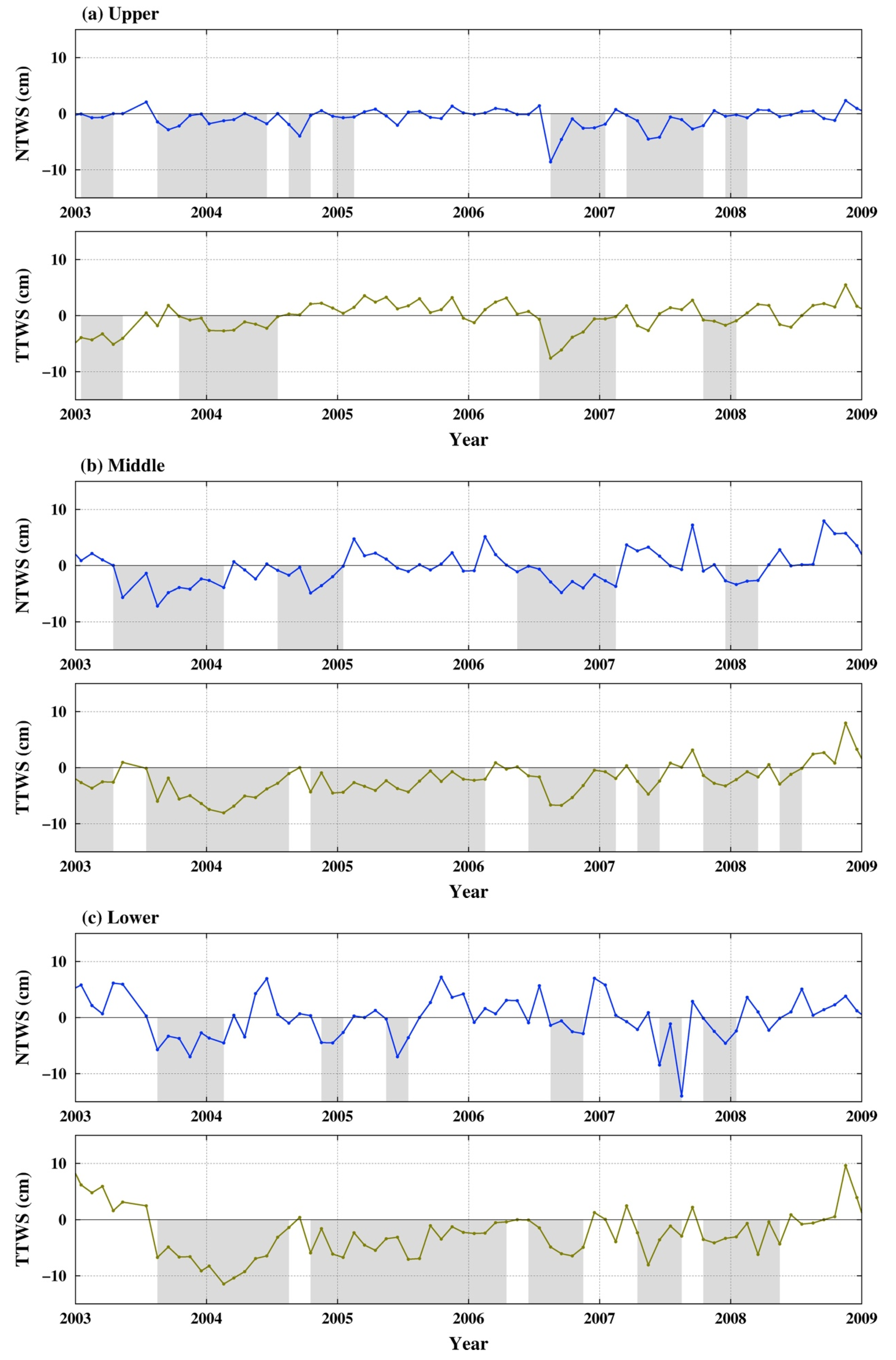
4.4. Characterization of the Hydrological Drought Events
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilhite, D.A.; Glantz, M.H. Understanding the drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Leblanc, M.J.; Tregoning, P.; Ramillien, G.; Tweed, S.O.; Fakes, A. Basin-scale, integrated observations of the early 21st century multiyear drought in Southeast Australia. Water Resour. Res. 2009, 45, 546–550. [Google Scholar] [CrossRef]
- Hisdal, H.; Tallaksen, L.M. Estimation of regional meteorological and hydrological drought characteristics: A case study for Denmark. J. Hydrol. 2003, 281, 230–247. [Google Scholar] [CrossRef]
- Akyuz, D.E.; Bayazit, M.; Onoz, B. Markov Chain Models for Hydrological Drought Characteristics. J. Hydrometeorol. 2012, 13, 298–309. [Google Scholar] [CrossRef]
- Dai, Z.; Du, J.; Li, J.; Li, W.; Chen, J. Runoff characteristics of the Changjiang River during 2006: Effect of extreme drought and the impounding of the Three Gorges Dam. Geophys. Res. Lett. 2008, 35, 521–539. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, L.; Wang, Y.G.; Werner, A.D.; Xin, P.; Jiang, T.; Barry, D.A. Has the Three-Gorges Dam made the Poyang Lake wetlands wetter and drier? Geophys. Res. Lett. 2012, 39, L20402.1–L20402.7. [Google Scholar] [CrossRef]
- Graf, W.L. Dam Nation: A Geographic Census of American Dams and Their Large-Scale Hydrologic Impacts. Water Resour. Res. 1999, 35, 1305–1311. [Google Scholar] [CrossRef]
- Kittinger, J.N.; Coontz, K.M.; Yuan, Z.; Han, D.; Zhao, X.; Wilcox, B.A. Toward holistic evaluation and assessment: Linking ecosystems and human well-being for the Three Gorges Dam. EcoHealth 2009, 6, 601–613. [Google Scholar] [CrossRef] [PubMed]
- Mccartney, M. Living with dams: Managing the environmental impacts. Water Policy 2009, 11, 121–139. [Google Scholar] [CrossRef]
- Bai, Y.; Xie, J.; Wang, X.; Li, C. Model fusion approach for monthly reservoir inflow forecasting. J. Hydroinform. 2016, 18, 634–650. [Google Scholar] [CrossRef]
- Lai, X.; Liang, Q.; Huang, Q.; Jiang, J.; Lu, X.X. Numerical evaluation of flow regime changes induced by the Three Gorges Dam in the Middle Yangtze. Hydrol. Res. 2016, 47, 149–160. [Google Scholar] [CrossRef]
- Li, R.; Chen, Q.; Ye, F. Modelling the impacts of reservoir operations on the downstream riparian vegetation and fish habitats in the Lijiang River. J. Hydroinform. 2011, 13, 229–244. [Google Scholar] [CrossRef]
- Li, S.; Xiong, L.; Dong, L.; Zhang, J. Effects of the Three Gorges Reservoir on the hydrological droughts at the downstream Yichang station during 2003–2011. Hydrol. Process. 2013, 27, 3981–3993. [Google Scholar] [CrossRef]
- Lai, X.; Jiang, J.; Yang, G.; Lu, X.X. Should the Three Gorges Dam be blamed for the extremely low water levels in the middle–lower Yangtze River? Hydrol. Process. 2014, 28, 150–160. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, G.; Guo, R.; Wan, R. Changing landscapes by damming: The Three Gorges Dam causes downstream lake shrinkage and severe droughts. Landsc. Ecol. 2016, 31, 1883–1890. [Google Scholar] [CrossRef]
- Lai, X.; Jiang, J.; Liang, Q.; Huang, Q. Large-scale hydrodynamic modeling of the middle Yangtze River Basin with complex river–lake interactions. J. Hydrol. 2013, 492, 228–243. [Google Scholar] [CrossRef]
- Cai, X.; Feng, L.; Wang, Y.; Chen, X. Influence of the Three Gorges Project on the Water Resource Components of Poyang Lake Watershed: Observations from TRMM and GRACE. Adv. Meteorol. 2015, 1–7. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Yirdaw, S.Z.; Snelgrove, K.R.; Agboma, C.O. GRACE satellite observations of terrestrial moisture changes for drought characterization in the Canadian Prairie. J. Hydrol. 2008, 356, 84–92. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res. Atmos. 2009, 114, B05404. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; da Silva, J.S.; Ramillien, G.; Prigent, C.; Seyler, F.; Calmant, S. Surface freshwater storage and dynamics in the Amazon basin during the 2005 exceptional drought. Environ. Res. Lett. 2012, 7, 44010–44017. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Chao, N.; Wang, Z.; Jiang, W.; Chao, D. A quantitative approach for hydrological drought characterization in Southwestern China using GRACE. Hydrogeol. J. 2016, 24, 1–11. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.Y.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman–Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) Basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Hu, X.; Chen, J.; Zhou, Y.; Huang, C.; Liao, X. Seasonal water storage change of the Yangtze River Basin detected by GRACE. Sci. China Earth Sci. 2006, 49, 483–491. [Google Scholar] [CrossRef]
- Long, D.; Yang, Y.; Wada, Y.; Hong, Y.; Liang, W.; Chen, Y.; Yong, B.; Hou, Z.; Wei, J.; Chen, L. Deriving scaling factors using a global hydrological model to restore GRACE total water storage changes for China’s Yangtze River Basin. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Zhang, Z.; Chao, B.F.; Chen, J.; Wilson, C.R. Terrestrial water storage anomalies of Yangtze River Basin droughts observed by GRACE and connections with ENSO. Glob. Planet. Chang. 2015, 126, 35–45. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113, B08410. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]
- Peltier, W.R. global glacial isostasy and the surface of the ice-age earth: The ICE-5G (VM2) model and GRACE. Annu. Rev. Earth Planet. Sci. 2004, 20, 111–149. [Google Scholar] [CrossRef]
- Wahr, A.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30230. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J.; Milly, P.C.D. Estimated accuracies of regional water storage variations inferred from the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2003, 39, 375–384. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, 2006. [Google Scholar] [CrossRef]
- Swenson, S.C.; Wahr, J.M. Estimating signal loss in regularized GRACE gravity field solutions. Geophys. J. Int. 2011, 185, 693–702. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Multi-sensor analysis of water storage variations in the Caspian Sea. Geophys. Res. Lett. 2007, 34, L16401. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Chen, J.; Seneviratne, S.I.; Viterbo, P.; Holl, S.; Wilson, C.R. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophys. Res. Lett. 2004, 31, 183–213. [Google Scholar] [CrossRef]
- Klees, R.; Zapreeva, E.A.; Winsemius, H.C.; Savenije, H.H.G. The bias in GRACE estimates of continental water storage variations. Hydrol. Earth Syst. Sci. 2007, 11, 1227–1241. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Rodell, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Wang, W.; Cui, W.; Wang, X.; Chen, X. Evaluation of GLDAS-1 and GLDAS-2 forcing data and Noah model simulations over China at monthly scale. J. Hydrometeorol. 2016, 17, 2815–2833. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G. Improving the global precipitation record: GPCP Version 2.1. Geophys. Res. Lett. 2009, 36, 153–159. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Huang, Y.; Salama, M.S.; Krol, M.S.; van der Velde, R.; Hoekstra, A.Y.; Zhou, Y.; Su, Z. Analysis of long-term terrestrial water storage variations in the Yangtze River basin. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 11487–11520. [Google Scholar] [CrossRef]
- Sun, Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Q.; Werner, A.D.; Liu, X. GRACE-Based Hydrological Drought Evaluation of the Yangtze River Basin, China. J. Hydrometeorol. 2016, 17, 811–828. [Google Scholar] [CrossRef]
- Huang, Y.; Salama, M.S.; Krol, M.S.; Su, Z.; Hoekstra, A.Y.; Zeng, Y.; Zhou, Y. Estimation of human-induced changes in terrestrial water storage through integration of GRACE satellite detection and hydrological modeling: A case study of the Yangtze River Basin. Water Resour. Res. 2015, 51, 8494–8516. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33, 178–196. [Google Scholar] [CrossRef]
- Hossein, S.Z.; Han, M.S.; Gyewoon, C. Evaluation of Regional Droughts Using Monthly Gridded Precipitation for Korea. J. Hydroinform. 2012, 14, 1036–1050. [Google Scholar] [CrossRef]
- Zhang, N.; Xia, Z.; Zhang, S.; Jiang, H. Temporal and spatial characteristics of precipitation and droughts in the upper reaches of the Yangtze River basin (China) in recent five decades. J. Hydroinform. 2012, 14, 221–235. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Rana, A.; Moradkhani, H.; Sharma, A. Multi-criteria evaluation of CMIP5 GCMs for climate change impact analysis. Theor. Appl. Climatol. 2015, 1–17. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Qian, T. A Global Dataset of Palmer Drought Severity Index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
| Sub-Basin | Upper (cm) | Middle (cm) | Lower (cm) |
|---|---|---|---|
| Measurement error | 1.66 | 2.28 | 2.94 |
| Leakage error | 2.03 | 2.77 | 2.69 |
| Date | Start Level (m) | End Level (m) | Change (m) |
|---|---|---|---|
| June 2003 | 66.0 | 135.0 | 69.0 |
| October 2006 | 135.0 | 156.0 | 21.0 |
| November 2008 | 145.0 | 172.3 | 27.3 |
| Sub-Basin | Area (km2) | NSE | R2 | MAE (cm) | Uncertainty (cm) |
|---|---|---|---|---|---|
| Upper | 983,118 | 0.92 | 0.96 | 0.93 | 2.78 |
| Middle | 512,733 | 0.87 | 0.93 | 1.29 | 3.76 |
| Lower | 288,205 | 0.85 | 0.92 | 1.89 | 4.41 |
| Sub-Basin | Data | Time Span of Each Event | Duration (Months) | Severity (km3 Months) | No. of Total Months | Total Severity (km3 Months) |
|---|---|---|---|---|---|---|
| Upper Area: 983,118 km2 | NTWS | Jan. 2003 to Apr. 2003 | 4 | −134.39 | 38 | −616.21 |
| Aug. 2003 to Jun. 2004 | 11 | −62.14 | ||||
| Aug. 2004 to Oct. 2004 | 3 | −17.61 | ||||
| Dec. 2004 to Feb. 2005 | 3 | −207.58 | ||||
| Aug. 2006 to Jan. 2007 | 6 | −165.79 | ||||
| Mar. 2007 to Oct. 2007 | 8 | −14.07 | ||||
| Dec. 2007 to Feb. 2008 | 3 | −134.39 | ||||
| TTWS | Jan. 2003 to May 2003 | 5 | −203.39 | 26 | −612.88 | |
| Oct. 2003 to Jul. 2004 | 10 | −142.92 | ||||
| Jul. 2006 to Feb. 2007 | 8 | −222.61 | ||||
| Oct. 2007 to Jan. 2008 | 4 | −43.80 | ||||
| Middle Area: 512,733 km2 | NTWS | Apr. 2003 to Feb. 2004 | 11 | −185.43 | 32 | −440.97 |
| Jul. 2004 to Jan. 2005 | 7 | −69.22 | ||||
| May 2006 to Feb. 2007 | 10 | −126.87 | ||||
| Dec. 2007 to Mar. 2008 | 4 | −59.45 | ||||
| TTWS | Jan. 2003 to Apr. 2003 | 4 | −58.92 | 57 | −914.13 | |
| Jun. 2003 to Aug. 2004 | 15 | −335.13 | ||||
| Oct. 2004 to Feb. 2006 | 17 | −242.72 | ||||
| Jun. 2006 to Feb. 2007 | 9 | −145.17 | ||||
| Apr. 2007 to Jun. 2007 | 3 | −49.41 | ||||
| Oct. 2007 to Mar. 2008 | 6 | −60.99 | ||||
| May 2008 to Jul. 2008 | 3 | −21.78 | ||||
| Lower Area: 288,205 km2 | NTWS | Aug. 2003 to Feb. 2004 | 7 | −88.60 | 24 | −270.40 |
| Nov. 2004 to Jan. 2005 | 3 | −33.66 | ||||
| May 2005 to Jul. 2005 | 3 | −31.30 | ||||
| Aug. 2006 to Nov. 2006 | 4 | −21.41 | ||||
| Jun. 2007 to Aug. 2007 | 3 | −67.86 | ||||
| Oct. 2007 to Jan. 2008 | 4 | −27.58 | ||||
| TTWS | Aug. 2003 to Aug. 2004 | 13 | −263.31 | 51 | −651.64 | |
| Oct. 2004 to Apr. 2006 | 19 | −193.32 | ||||
| Jun. 2006 to Nov. 2006 | 6 | −68.57 | ||||
| Apr. 2007 to Aug. 2007 | 5 | −52.27 | ||||
| Oct. 2007 to May 2008 | 8 | −74.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Wang, Z.; Chao, N.; Song, Q. Assessing the Influence of the Three Gorges Dam on Hydrological Drought Using GRACE Data. Water 2018, 10, 669. https://doi.org/10.3390/w10050669
Li F, Wang Z, Chao N, Song Q. Assessing the Influence of the Three Gorges Dam on Hydrological Drought Using GRACE Data. Water. 2018; 10(5):669. https://doi.org/10.3390/w10050669
Chicago/Turabian StyleLi, Fupeng, Zhengtao Wang, Nengfang Chao, and Qingyi Song. 2018. "Assessing the Influence of the Three Gorges Dam on Hydrological Drought Using GRACE Data" Water 10, no. 5: 669. https://doi.org/10.3390/w10050669
APA StyleLi, F., Wang, Z., Chao, N., & Song, Q. (2018). Assessing the Influence of the Three Gorges Dam on Hydrological Drought Using GRACE Data. Water, 10(5), 669. https://doi.org/10.3390/w10050669





