Abstract
Decision tables have been used for many years in data processing and business applications to simulate complex rule sets. Several computer languages have been developed based on rule systems and they are easily programmed in several current languages. Land management and river–reservoir models simulate complex land management operations and reservoir management in highly regulated river systems. Decision tables are a precise yet compact way to model the rule sets and corresponding actions found in these models. In this study, we discuss the suitability of decision tables to simulate management in the river basin scale Soil and Water Assessment Tool (SWAT+) model. Decision tables are developed to simulate automated irrigation and reservoir releases. A simple auto irrigation application of decision tables was developed using plant water stress as a condition for irrigating corn in Texas. Sensitivity of the water stress trigger and irrigation application amounts were shown on soil moisture and corn yields. In addition, the Grapevine Reservoir near Dallas, Texas was used to illustrate the use of decision tables to simulate reservoir releases. The releases were conditioned on reservoir volumes and flood season. The release rules as implemented by the decision table realistically simulated flood releases as evidenced by a daily Nash–Sutcliffe Efficiency (NSE) of 0.52 and a percent bias of −1.1%. Using decision tables to simulate management in land, river, and reservoir models was shown to have several advantages over current approaches, including: (1) mature technology with considerable literature and applications; (2) ability to accurately represent complex, real world decision-making; (3) code that is efficient, modular, and easy to maintain; and (4) tables that are easy to maintain, support, and modify.
1. Introduction
1.1. Land Management Models
Land management models are used to determine the impact of agricultural and urban management on water quantity, quality, and agricultural productivity. Most agricultural land management models have an operations file to schedule planting, harvest, tillage, irrigation, and fertilizer and pesticide application by month and date. In some models, including EPIC (Erosion Productivity Impact Calculator; [1]), APEX (Agricultural Policy Extender; [2,3]), and SWAT+ (Soil and Water Assessment Tool; [4,5]), land management operations can be “automatically” scheduled based on accumulated heat units. However, current algorithms in these models do not use modern rule-based coding and do not use structured decision tables to input the conditions and action. For example, EPIC, APEX, and SWAT+ currently have automated irrigation scheduling that is based solely on a plant stress or water deficit trigger. Decision tables will allow us to easily add complex conditions for scheduling the irrigation application (e.g., crop type, phenological stage, or water availability in reservoirs) which is not possible in the current models.
1.2. River and Reservoir Management Models
River–reservoir models are designed to simulate the distribution of water within a highly regulated river system with multiple objectives. Hydrologists use river–reservoir models to understand the impact of operational changes to the system that result in changes in water deliveries, reservoir storage, in-stream flows, and power production [6,7]. Operational changes include water transfers and changes in reservoir operation rules. Some of the more commonly used models for river basin management include MODSIM [8], RiverWare [9], MIKEBASIN [10], RIBASIM [11], and WEAP [12]. All of these models have been successfully applied around the world and have proven to be useful in water resources planning. However, each lacks an effective customization capability, which limits their applicability to unique river basin conditions and complex rules and policy [8]. RiverWare is customized using the RiverWare Policy Language (RPL) for developing operational policy. A rule editor allows users to enter expressions in RPL and relationships between river basin objects. RPL is computationally inefficient and unable to adequately simulate conjunctive use of surface and groundwater resources [8]. MODSIM contains a Custom Code Editor that can interface with MODSIM and access all public variables and object classes. This allows for specific operating rules to be customized for specific river basins. As with RiverWare, the language has to be easily understandable and computational efficiency is sacrificed.
1.3. Decision Table Theory
Decision tables are a precise yet compact way to model complex rule sets and their corresponding actions. Decision tables were originally used in business to represent conditional logic by creating a list of tasks depicting business-level rules. They are widely used in data processing applications and have an extensively developed literature [13]. Several computer languages have been developed based on rule systems that use decision trees that can be derived from decision tables. CLIPS (C Language Integrated Production System) was developed at NASA in the 1980s as a tool to define expert systems [14,15]. CLIPS is a non-procedural declarative and rule-based programming language. FORTAB is a decision table language designed to be embedded in FORTRAN, which was developed by the RAND Corporation in the 1980s [16]. Many of the capabilities of CLIPS and FORTAB are now easily programmable in the current C and FORTAN languages.
1.4. Objectives
The aim of this study is to develop a robust and efficient methodology to simulate land and water management in ecohydrologic models. Specific objectives are: (1) to discuss the suitability of decision tables to simulate management in the river basin scale Soil and Water Assessment Tool [4,17] model; and (2) to describe an enhanced SWAT+ framework which incorporates decision tables for management and reservoir operations.
2. Materials and Methods
2.1. Decision Table Structure
Decision tables, like flowcharts and if-then-else and switch-case statements, associate conditions with actions to perform, but can do so in a more compact and intuitive way. They are divided into four quadrants: I. Conditions, II. Condition Alternatives, III. Action Entries or Outcomes, and IV. Actions (Table 1).

Table 1.
The four quadrants of a decision table.
Quadrant I: Conditions. For application of the decision table to SWAT+ management, quadrant I contains condition variables and condition limits. A listing of current SWAT+ variables coded for use in the decision table is given in Table 2. The variables relate to time of year, soil and plant status, reservoir volumes, and flow in channels. In addition to the conditional variable, the model must also know its associated watershed object. For example, if reservoir volume is used as the conditional variable, the reservoir number in the current simulation must be defined. The model would read the conditional variable as “vol res 1”. This example uses the volume of reservoir 1. To develop more generic rules that can be used by multiple reservoirs, res 0 is used to designate the current reservoir being simulated. For reservoirs in series, the outflow from res 1 could be conditioned on volumes of res 2, 3, etc. The condition limits are defined using a limit variable, limit operator, and limit constant. If reservoir volume is again used as the conditional variable, the principle and emergency volumes may be used as limit variables for setting condition limits for reservoir volume. An example input would be “evol × 0.8”, thus setting the limits when determining alternatives. For soil water, there are currently three limit variables, wilting point (wp), field capacity (fc), and total porosity (ul). In the example, the user could input “fc × 0.7”. The alternatives are compared to this limit threshold. Other variables do not have operators and limit variables. For example, using month as the conditional variable, a potential limit could be “5-null” and the alternatives are based on comparing the current month to 5.

Table 2.
Conditional variables currently coded in the Soil and Water Assessment Tool (SWAT+) for use in the decision tables.
Quadrant II: Alternatives. There are four possible alternative operators: >, <, =, and -. The alternative is the final piece to construct the “if” statement needed to implement the associated rule.
| Condition | Alternative |
| “soil_water hru 1 fc × 0.7” | > |
The model will determine if the soil water in hru (hydrologic response unit) 1 is greater than 0.7 × fc. The “-” symbol is used if the condition is not relevant for a specific alternative.
Quadrant III: Action Entries. Action entries or outcomes are either yes or no and specify whether or not an action is triggered. Each condition within an alternative must be true. If all conditions specified by an alternative are true, and the outcome is “y”, then the associated action will be performed. The only options for action entries are “y” and “n”.
Quadrant IV: Actions. The action type and associated information needed to perform the action are input in quadrant IV. The actions currently coded in SWAT+ are listed in Table 3. Most of the actions are related to land management, including planting, harvesting, tillage, fertilizer applications, and drainage water management. There are also currently actions for reservoir release and land use change. For some actions, there are multiple options to execute the action. For the reservoir release action, the user can input a release rate, a weir equation, or drawdown days. The decision table contains a constant and file pointer for all the management actions. The file pointer corresponds to the application type in the associated data file. The plant action points to plant growth parameters, the harvest operation points to data for the method of harvest, and the tillage action points to the tillage implement. Fertilizer and irrigation use the constant to specify the amount of fertilizer or water applied and the file pointer corresponds to the data needed for the application method (e.g., sprinkler irrigation or broadcast fertilizer). For the land-use change actions, the file pointer corresponds to the updated land use.

Table 3.
Actions currently coded in SWAT+ for use in the decision tables.
2.2. Integration of Decision Table Code with SWAT+
SWAT+ is written in FORTRAN using F90 constructs and currently compiled using Visual Studio 2015. The decision table code consists of three subroutines and is relatively simple and robust.
Dtable_read Subroutine. This subroutine reads from an input file containing all decision tables. The decision table consists of three objects (types in FORTRAN): (1) conditional variables; (2) action variables; and (3) decision table variables. The decision table variables include the conditional and action objects and also the alternative and outcome (action entries) variables. All variables needed for each quadrant are included in the decision table variables and are defined in Table 4.

Table 4.
Decision table variables as coded in the SWAT+ model.
Conditions Subroutine. This subroutine loops through all conditions and checks all alternatives for each condition. Since all conditions must be met for an alternative to be positive, we start with the alternative being positive and set it to negative if any condition is not met. Inside the conditions loop, a case statement is used to identify the appropriate conditional variable. Then, appropriate SWAT+ variables are used relative to each conditional variable.
Actions Subroutine. This subroutine loops through all actions and if one (or more) of the alternatives is “y” the action will be performed. SWAT+ variables are updated for each action using the constant and file pointer. When the variables are set for the specified action, the corresponding SWAT+ subroutine is called as shown in Table 3.
3. Results
3.1. Application of Decision Tables
Two examples of decision tables are presented: (1) automated (auto) irrigation; and (2) reservoir release. Both are kept relatively simple to illustrate the concept. However, additional conditions and actions can easily be added to perform more complex rule sets.
3.1.1. Auto Irrigation
The EPIC, APEX, and SWAT+ models [18] include provisions for automatic irrigation. In many agricultural areas, it is known that certain fields are irrigated; however, the timing and amount of irrigation of each application is not readily available. In this case, algorithms were developed to automatically trigger an irrigation application based on water stress on the plant or by soil water deficit. This simplest form of a decision table for irrigation is shown in Table 5.

Table 5.
Decision table for automated irrigation based on plant stress.
The name of the decision table is “auto_irr” and it contains one condition, one alternative, and one action. The logic flows clockwise from quadrant I to IV. In quadrant I, the conditional variable (w_stress) for hru 0 is defined (0 specifies the current hru and thus can be used for any hru in the simulation). The conditional limit is a constant (0.8). A limit variable and operator are not needed in this case. Next, we use the alternative in quadrant II and determine if w_stress <0.8. If the outcome is yes (“y” in quadrant III), we move clockwise to the action in quadrant IV. The action is to irrigate 25 mm using a sprinkler application (found in the irrigation data file).
This is the simplest case and could be input and coded without the use of a decision table. However, users typically need to add additional conditions, i.e., only irrigate a certain crop in the rotation, only irrigate during a certain growth stage, or only irrigate when reservoirs or aquifers are at a specified level. The decision table allows for the addition of conditions and actions in a simple and robust structure.
3.1.2. Auto Irrigation Application
The SWAT+ model was parameterized to simulate continuous corn with the Houston Black soil series from 2007 to 2016. Daily precipitation and maximum and minimum temperatures were input from the USDA-Agricultural Research Service station in Temple, Texas. The auto irrigation decision table as shown in Table 5 was used in this example, with a stress trigger of 0.8 and 25 mm applied at each irrigation. Figure 1 shows the soil moisture, precipitation, and irrigation applications from 2014 to 2016. In 2014 and 2015, typical dry spring and summer periods triggered 11 and 10 irrigation applications, respectively. In 2016, adequate rainfall during critical growing periods only triggered one irrigation application. Irrigation increased corn yields by 3.1, 5.1, and 0.1 t/ha in 2014, 2015, and 2016, respectively. To assess the sensitivity of the decision table parameters, we increased the irrigation amount per application to 50 mm and lowered the plant stress trigger to 0.6 (Figure 1). This resulted in fewer applications, more total water applied each year (25 mm), and slightly higher corn yields (0.1 t/ha).
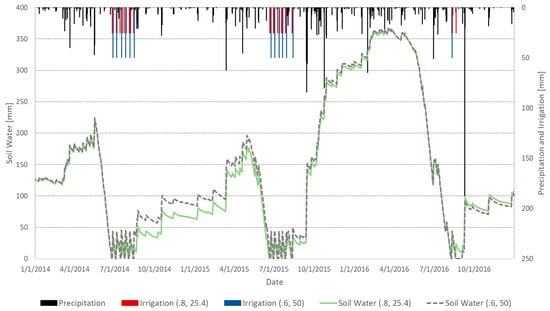
Figure 1.
Soil moisture, precipitation, and irrigation of continuous corn at Temple, Texas using: (1) a plant stress trigger of 0.8 and application of 25 mm; and (2) a plant stress trigger of 0.6 and application of 50 mm.
3.1.3. Reservoir Release
Large reservoirs are managed for multiple uses, including irrigation, power generation, flood control, recreation, and municipal use [19]. Operating rules can be extremely complex and in this example, we focus on flood control as the primary use. The first step in developing the decision table is deciding on the number of actions or release rates. We chose to divide releases based on three storage volumes: (1) principal volume; (2) emergency volume; and (3) 1.3 × principal. The release rate is also a function of flood and non-flood season, resulting in five alternatives and five outcomes. The five conditions are used to determine the storage class and the flood season class. Alternative 1 only checks one condition: if the volume is less than that of the principal volume. If the outcome is yes, the corresponding action is to release at the “below_principal” rate of 2 m3/s. Alternatives 2 and 3 are in the non-flood season with reservoir volumes between principal and 1.3 × principal volumes. Alternative 4 is during flood season at any volume between principal and emergency, while Alternative 5 is for volumes above emergency, regardless of the season.
3.1.4. Reservoir Release Application
Grapevine Reservoir is a 2674 hectare impoundment constructed on Denton Creek near Dallas, a tributary of the Trinity River by the U.S. Army Corps of Engineers in 1952 to provide flood control, municipal and industrial water, and recreation. The reservoir contains 22,626 ha-m of water at conservation elevation and was used to illustrate the reservoir release rules. The decision table is shown in Table 6.

Table 6.
Decision table for reservoir release focusing on flood control.
The release rules as implemented by the decision table realistically simulated flood releases as evidenced by a daily Nash–Sutcliffe Efficiency (NSE) of 0.52 and a percent bias of −1.1% [20]. Measured and simulated daily flows are shown in Figure 2. However, low flow releases were difficult to simulate accurately due to uncertainty in specific local conditions and without understanding of reservoir-specific release rules. We are developing simple generic rules that can be applied to reservoirs across the U.S. for national policy simulations. With local knowledge of individual reservoir release rules, the decision table could be modified to simulate very specific rules and test and optimize alternative rule set parameters.
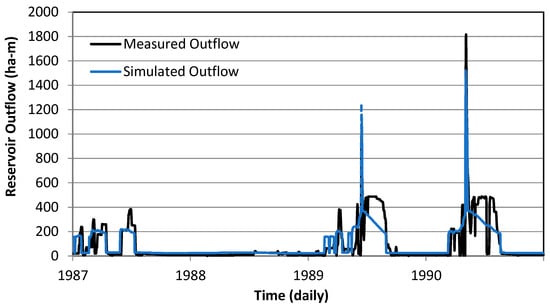
Figure 2.
Measured and simulated daily reservoir releases for Grapevine Reservoir near Dallas, Texas.
This is a relatively simple example focusing on flood control. More complex rules can easily be added to simulate reservoirs managed in series by including conditions for other reservoirs and river flows. Watershed conditions including irrigation demand, plant conditions, and soil water can be added to the conditions. Also, weir outflow as a function of storage can replace the constant outflow shown in this example.
3.2. Management Optimization
The use of a decision table as an external control on SWAT+ model runs also makes it possible to find decision tables that optimize certain SWAT+ model outputs. Some choices of condition variable limits and the actions they trigger will result in more favorable outcomes from the SWAT+ model, such as increased crop yield or reductions in contaminant outputs. Other choices of decision table parameters will produce less favorable outcomes. Finding a set of decision parameters that optimize the output of SWAT+ in a specified way has the form of a non-linear optimization problem. In optimization problems, one formulates an objective function to be minimized that consists of a combination of model outputs, with assigned weights to specify the relative importance placed on the different outputs. For example, it would be possible to define an objective function that decreases in amplitude as predicted crop yields increase and contaminant outputs decrease, with the two competing factors weighted according to their relative importance. The solution of the optimization problem is the set of free variables that produce the smallest possible objective function. In this case, the free variables would be the decision table condition limits and their associated actions, such as conditions under which crops are irrigated and fertilized and how much water and fertilizer are applied. Non-linear optimization problems such as this, in which the derivatives of the objective function with respect to the free variables are not easily computed, are commonly solved by the method of simulated annealing, which requires only repeated calculation of the objective function for different sets of free variables [21]. Combining simulated annealing with decision table controlled SWAT+ simulations could be used to optimize management practices to fit different competing performance criteria.
4. Summary and Conclusions
Decision table theory was developed in the 1960s for data processing and business level rules. CLIPS and FORTAB were computer languages developed in C and FORTRAN, respectively, to define expert systems using a decision table structure. Land, river, and reservoir management models often use embedded expert systems to determine land management and operations (such as plant/harvest, tillage, and fertilization), reservoir releases, and water transfer in canals. In this study, we incorporated decision table data and algorithms into a river basin scale ecohydrologic model (SWAT+). Using decision tables to simulate management in land, river, and reservoir models has several advantages over current approaches, including:
- (1)
- The structure of a decision table can be easily understood by model users. Decision tables were developed over 50 years ago, and there is considerable literature and tutorials available on-line related to developing decision tables.
- (2)
- Decision tables accurately represent complex, real world decision-making.
- (3)
- The code is more modular and easier to maintain than code to simulate management in existing land management models.
- (4)
- The code to implement decision tables is more efficient than languages developed for specific river and reservoir models.
- (5)
- Decision tables can be easily maintained and supported.
- (6)
- It is relatively simple to add the decision tables approach to legacy land, river, and reservoir models.
As incorporated into SWAT+, the decision table is a robust and efficient method to simulate complex, rule-based management. Examples of automated irrigation and reservoir release were shown and other management operations simulated with decision tables were listed. In addition, decision tables have the potential for use in water rights and water transfers, states and transition of natural ecosystems, and the management of animal herds.
Author Contributions
Conceptualization, J.G.A. and P.M.A.; Data curation, M.J.W.; Formal analysis, R.S.; Investigation, J.G.A. and M.J.W.; Methodology, J.A.D.; Validation, K.B.; Writing (original draft), J.G.A.; Writing (review and editing), K.B., M.J.W., R.S., J.A.D., and P.M.A.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Williams, J.R.; Jones, C.A.; Dyke, P.T. A modeling approach to determining the relationship between erosion and soil productivity. Trans. ASAE 1984, 27, 129–144. [Google Scholar] [CrossRef]
- Williams, J.R.; Izaurralde, R.C.; Williams, C.; Steglich, E.M. Agricultural Policy/Environmental Extender Model—Theoretical Documentation Version 0806. Texas A&M AgriLife Research. Available online: http://epicapex.tamu.edu/files/2017/03/THE-APEX0806-theoretical-documentation-Oct-2015.pdf (accessed on 15 May 2015).
- Tuppad, P.; Winchell, P.M.; Wang, X.; Srinivasan, R.; Williams, J.R. ArcAPEX: ArcGIS interface for agricultural policy environmental extender (APEX) hydrology/water quality model. Int. Agric. Eng. J. 2009, 18, 59–71. [Google Scholar]
- Bieger, K.; Arnold, J.G.; Rathjens, H.; White, M.J.; Bosch, D.D.; Allen, P.M.; Volk, M.; Srinivasan, R. Introduction to SWAT+, a completely revised version of the Soil and Water Assessment Tool. J. Am. Water Resour. Assoc. 2017, 53, 115–130. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Wurbs, R.A. Reservoir/river systems management models. Texas Water J. 2012, 3, 26–41. [Google Scholar]
- Wurbs, R.A. Modeling and Analysis of Reservoir System Operations; Prentice-Hall: Upper Saddle River, NJ, USA, 1996; ISBN 0-13-605924-4. [Google Scholar]
- Labadie, J.W. MODSIM: Decision support system for integrated river basin management. In Proceedings of the iEMS International Congress on Environmental Modelling and Software, Burlington, VT, USA, 24-28 June 2006. [Google Scholar]
- Zagona, E.A.; Fulp, T.J.; Shane, R.; Magee, T.; Goranflo, H.M. RiverWare: A generalized tool for complex reservoir system modeling. J. Am. Water Resour. Assoc. 2001, 37, 913–929. [Google Scholar] [CrossRef]
- DHI. MIKE BASIN User’s Manual; DHI Water and Environment: Copenhagen, Denmark, 2006. [Google Scholar]
- Sulis, A.; Sechi, G.M. Comparison of generic simulation models for water resource systems. Environ. Model. Softw. 2013, 40, 214–225. [Google Scholar] [CrossRef]
- Yates, D.; Sieber, J.; Purkey, D.; Huber-Lee, A. WEAP21—A demand-, priority-, and preference-driven water planning model. Water Int. 2005, 30, 487–500. [Google Scholar] [CrossRef]
- Gildersleeve, T.R. Decision Tables and Their Practical Application in Data Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1970; ISBN-13: 978-0131973763. [Google Scholar]
- Giarratano, J.C.; Riley, G. Expert Systems, 3rd ed.; PWS Publishing Co.: Boston, MA, USA, 1998; ISBN 0534950531. [Google Scholar]
- Giarratano, J.C. CLIPS User’s Guide: Volume 1, Rules, CLIPS version 5.0; Software Technology Branch, Lyndon B. Johnson Space Center: Houston, TX, USA, 1991. [Google Scholar]
- Amerding, G.W. FORTAB: A Decision Table Language for Scientific Computing Applications; TR RM-3306-PR; RAND Corporation: Pittsburgh, PA, USA, 1962. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Williams, J.R.; Arnold, J.G.; Kiniry, J.R.; Gassman, P.W.; Green, G.J. History of model development at Temple, Texas. Hydrol. Sci. 2008, 53, 948–960. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. Developing Seasonal and Long-Term Reservoir System Operation Plans Using HEC-PRM; Report RD-40; Hydrologic Engineering Center: Davis, CA, USA, 1996; 445p.
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy of watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Sen, M.K.; Stoffa, P.L. Nonlinear one-dimensional seismic waveform inversion using simulated annealing. Geophysics 1991, 56, 1624–1638. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).