Effects of Water Depth and Ice Thickness on Ice Cover Blasting for Ice Jam Flood Prevention: A Case Study on the Heilong River, China
Abstract
:1. Introduction
2. Methods
2.1. Selection of Explosive Type, Amount, and Timing
2.2. Selection of Blasting Locations
2.3. Challenges to the Study of Blasting Craters
2.4. Regression Analysis for Ice-Blasting Variables
3. Results
3.1. Behavior and Characteristics of Blasting Craters
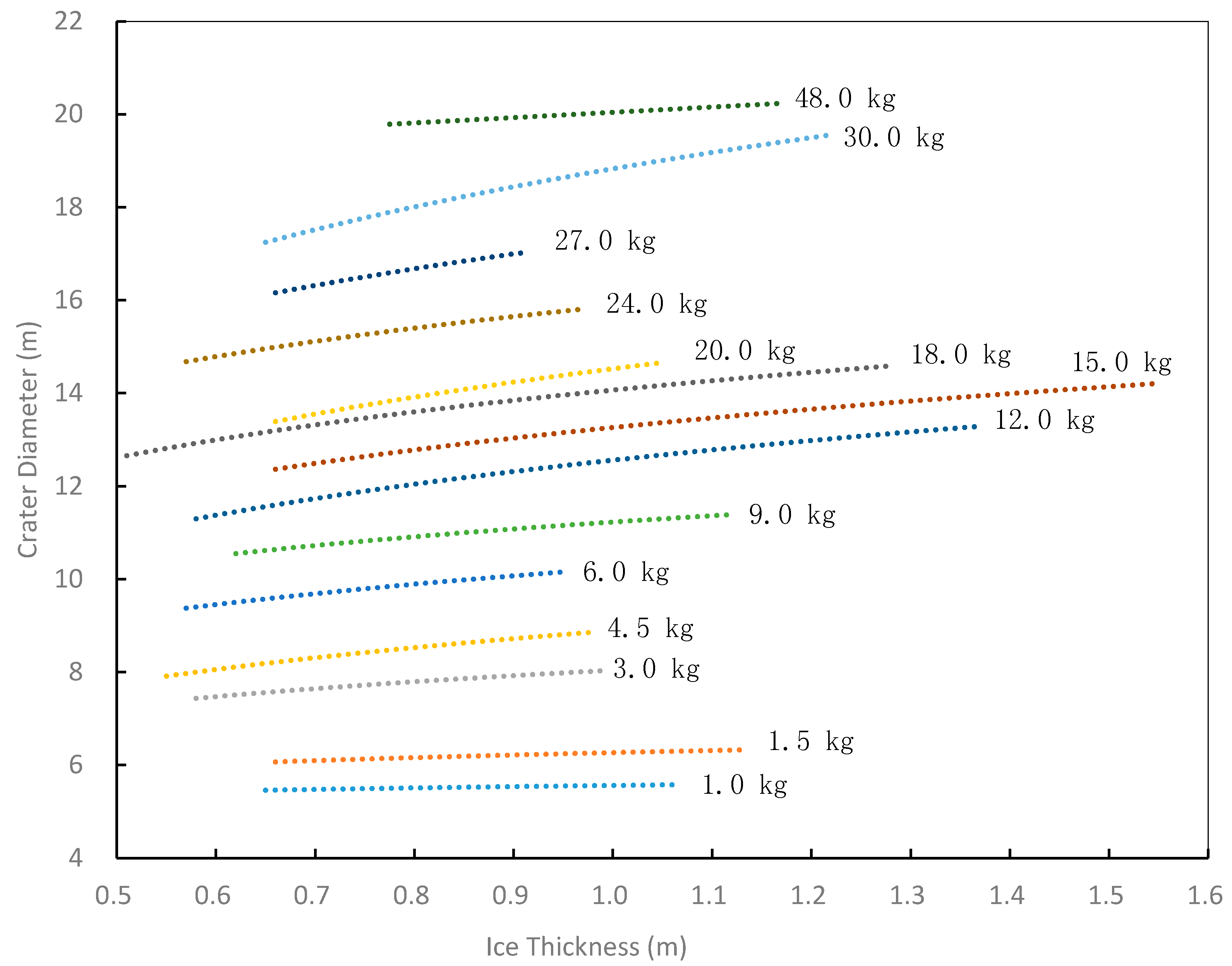
3.2. Relationship between Blasting Crater Radius and Ice Cover Thickness
3.3. Relationship between Water Depth, Blasting Crater Radius, and Ice Cover Thickness
3.4. Proposed Formula and Analysis of Experiment Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Beltaos, S. River Ice Jams; Water Resources Publications: Littleton, CO, USA, 1995. [Google Scholar]
- Beltaos, S. River Ice Breakup; Water Resource Publication: Littleton, CO, USA, 2008. [Google Scholar]
- Shen, H.T. Research on River Ice Processes, Progress and Missing Links. J. Cold Reg. Eng. 2003, 17, 135–142. [Google Scholar] [CrossRef]
- Zhang, F.; Mosaffa, M.; Chu, T.; Lindenschmidt, K.-E. Using remote sensing data to parameterize ice jam modeling for a Northern Inland Delta. Water 2017, 9, 306. [Google Scholar] [CrossRef]
- Mellor, M. Derivation of guidelines for blasting floating ice. Cold Reg. Sci. Technol. 1987, 13, 193–206. [Google Scholar] [CrossRef]
- Mellor, M. Breaking Ice with Explosives; Cold Regions Research & Engineering Laboratory, US Army Corps of Engineers: Hanover, NH, USA, 1982; p. 3. [Google Scholar]
- Ding, L.Q.; He, B.S.; Yan, X.G. New technology of breaking ice to ice prevention. China Flood Drought Manag. 2010, 2, 19–24. (In Chinese) [Google Scholar]
- Liang, X.Q.; He, B.S.; Xie, W.H. Experiment study on the blasting upon thick ice. Eng. Blast. 2012, 18, 83–85. (In Chinese) [Google Scholar]
- Tong, Z.; Yang, X.S.; Xue, P.X. Ice-Broken Explosion Mechanism of Yellow River/New Blasting Technology in China III; Metallurgical Industry Press: Beijing, China, 2012; pp. 57–66. (In Chinese) [Google Scholar]
- Duan, Y.S.; Wang, X.H.; Liu, S.B. Application of blasting technique to against ice jam. J. Glaciol. Geocryol. 2003, 220–226. Available online: http://caod.oriprobe.com/articles/32266117/Application_of_Blasting_Technique_to_Against_Ice_Jam.htm (accessed on 22 May 2018). (In Chinese).
- Yin, H.T.; Yang, X.H.; Jiang, M.; Jin, J.L. Experimental research on ice breaking by extended blasting cartridge under ice. Eng. Blast. 2010, 16, 12–15. (In Chinese) [Google Scholar]
- Wang, T.; Yang, K.L.; Guo, Y.X. Application of artificial neural networks to forecasting ice conditions of the Yellow River in the Inner Mongolia Reach. J. Hydrol. Eng. 2008, 13, 811–816. [Google Scholar]
- Wang, T.; Liu, Z.P.; Guo, X.L.; Fu, H.; Liu, W. Prediction of breakup ice jam with artificial neural networks. J. Hydraul. Eng. 2017, 48, 1355–1362. (In Chinese) [Google Scholar]
- Xia, L.F. Research and practice of underwater ice jam breaking by manual-operated blasting. Blasting 2014, 31, 126–130. (In Chinese) [Google Scholar]
- Shi, R.; Xu, G.G.; Liu, D.R.; Qin, J. Underwater test and analysis for explosion energy of explosives. Chin. J. Explos. Propellants 2008, 31, 1–5. (In Chinese) [Google Scholar]
- Liang, X.Q.; Xiong, F.; Lu, X.L. Experimental research on underwater shock wave characteristic of ice blasting at Yellow River. Blasting 2014, 4, 1–4. (In Chinese) [Google Scholar]
- Dai, C.L.; Yu, C.G.; Liao, H.C.; Zhang, B.S. Survey and Forecast of River Ice; China Water & Power Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Yu, T.C.; Wang, X.F.; Wang, J.L. Underwater shockwave performance of explosives. Energ. Mater. 2003, 11, 182–186. (In Chinese) [Google Scholar]
- Liu, Z.P.; Fu, H.; Guo, X.L.; Wang, T.; Cui, H. Double frequency radar system for ice thickness and water depth measurement. J. Hydraul. Eng. 2017, 48, 1341–1347. (In Chinese) [Google Scholar]
- Bonanno, R.; Loglisci, N.; Cavalletto, S.; Cassardo, C. Analysis of different freezing/thawing parameterizations using the UTOPIA Model. Water 2010, 2, 468–483. [Google Scholar] [CrossRef]
- Wang, J.; Sui, J.Y.; Zhang, H.Y.; Chen, P.; Hirshfield, F. Mechanisms of ice accumulation in a river bend—An experimental study. Int. J. Sediment Res. 2012, 27, 521–537. [Google Scholar] [CrossRef]
- Guo, X.L.; Yang, K.L.; Fu, H.; Xia, Q.; Wang, T.; Yang, S. Ice processes modeling during reverse water transfer of open canals: A case study. J. Hydro-Environ. Res. 2017, 17, 56–67. [Google Scholar] [CrossRef]
- Shen, H.T.; Gao, L.; Kolerski, T.; Liu, L. Dynamics of ice jam formation and release. J. Coast. Res. 2008, 24, 25–32. [Google Scholar] [CrossRef]
- Kolerski, T.; Shen, H.T. Possible effects of the 1984 St. Clair River ice jam on bed changes. Can. J. Civ. Eng. 2015, 42, 696–703. [Google Scholar] [CrossRef]

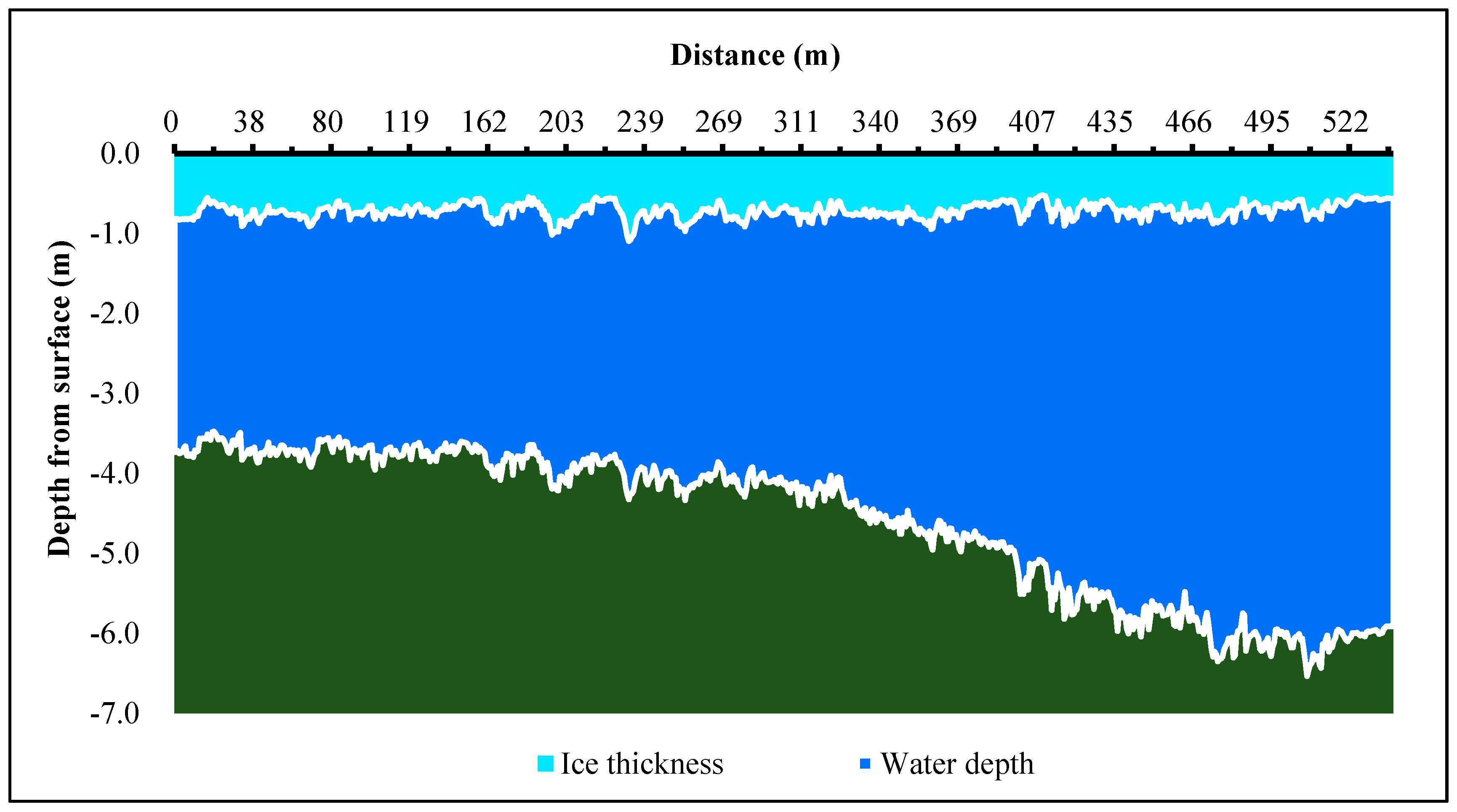





| Year | Breakup Date (Month-Day) | Central Location of Ice Jam | Maximum Head Increase (m) | Period of Ice Jam (Month-Day) |
|---|---|---|---|---|
| 1950 | / | Oupu in Huma reach | 9.40 | 05-09 to 05-11 |
| 1953 | / | Luoguhe in Mohe reach | 7.46 | 05-05 to 05-08 |
| 1956 | / | Luoguhe in Mohe reach | 7.39 | 05-08 to 05-10 |
| 1958 | 05-01 | Malun in Mohe reach | 10.14 | 05-05 to 05-10 |
| 1960 | 04-26 | Jialinda/Lianyin in Mohe reach | 13.56 | 04-27 to 05-10 |
| 1961 | 04-27 | Lianyin in Mohe reach | 8.03 | / |
| 1964 | 04-30 | Guchen Island in Mohe reach | 8.00 | 05-02 to 05-14 |
| 1970 | 04-27 | Huma in Huma reach | 5.22 | / |
| 1971 | 04-23 | Luoguhe in Mohe reach | 9.90 | 04-23 to 05-04 |
| 1973 | 05-05 | Guchen Island in Mohe reach | 8.20 | 05-06 to 06-01 |
| 1977 | 05-03 | Mohe City in Mohe reach | 6.65 | / |
| 1981 | 04-23 | Luoguhe in Mohe reach | 7.46 | 04-28 to 04-30 |
| 1985 | 04-18 | Jialinda/Lianyin in Mohe reach | 12.60 | 04-17 to 05-29 |
| 1986 | 05-04 | Jialinda/Mohe City in Mohe reach | 9.25 | 05-04 to 05-08 |
| 1987 | 05-08 | Oupu in Huma reach | 6.17 | / |
| 1988 | 04-22 | Kaikukang in Tahe reach | 5.11 | / |
| 1991 | 05-01 | Luoguhe in Mohe reach | 8.80 | 04-28 to 05-04 |
| 1994 | 04-29 | Luoguhe in Mohe reach | 10.93 | 04-29 to 05-10 |
| 1995 | 05-03 | Luoguhe in Mohe reach | 10.10 | 05-05 to 05-09 |
| 2000 | 04-28 | Jinshan in Muma reach | 9.23 | 04-29 to 05-01 |
| 2009 | 04-14 | Hongqiling in Mohe reach | / | 04-16 to 04-21 |
| 2010 | 04-25 | Xingan in Mohe reach | 8.34 | 05-03 to 05-09 |
| 2013 | 05-01 | Mohe City in Mohe reach | / | 05-02 to 05-07 |
| Conditions | Type of Regression Equation | Evaluation Method | |
|---|---|---|---|
| Root Mean Square Error (RMSE) | Correlation Coefficient (r) | ||
| Relation between scaled blasting crater radius and scaled ice cover thickness | Pure binomial Equation (6) | 0.8686 | 0.9087 |
| Pure binomial Equation (7) | 0.8745 | 0.9073 | |
| Relation between scaled blasting crater radius, ice scaled thickness, and scaled water depth | Cross trinomial Equation (8) | 0.7577 | 0.9371 |
| Pure trinomial Equation (9) | 0.7621 | 0.9311 | |
| Cross binomial Equation (10) | 0.8294 | 0.9184 | |
| Pure binomial Equation (11) | 0.8308 | 0.9180 | |
| Relative Error | Trinomial Equations | Binomial Equations | ||
|---|---|---|---|---|
| Cross Trinomial Equation (8) | Pure Trinomial Equation (9) | Cross Binomial Equation (10) | Pure Binomial Equation (11) | |
| Average relative error | 7.4 | 7.5 | 8.4 | 8.5 |
| Max relative error | 24.6 | 24.7 | 25.9 | 26.2 |
| Min relative error | 0.0 | 0.1 | 0.1 | 0.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Guo, X.; Fu, H.; Guo, Y.; Peng, X.; Wu, Y.; Li, J.; Xia, Y. Effects of Water Depth and Ice Thickness on Ice Cover Blasting for Ice Jam Flood Prevention: A Case Study on the Heilong River, China. Water 2018, 10, 700. https://doi.org/10.3390/w10060700
Wang T, Guo X, Fu H, Guo Y, Peng X, Wu Y, Li J, Xia Y. Effects of Water Depth and Ice Thickness on Ice Cover Blasting for Ice Jam Flood Prevention: A Case Study on the Heilong River, China. Water. 2018; 10(6):700. https://doi.org/10.3390/w10060700
Chicago/Turabian StyleWang, Tao, Xinlei Guo, Hui Fu, Yongxin Guo, Xuming Peng, Yunan Wu, Jiazhen Li, and Yinyin Xia. 2018. "Effects of Water Depth and Ice Thickness on Ice Cover Blasting for Ice Jam Flood Prevention: A Case Study on the Heilong River, China" Water 10, no. 6: 700. https://doi.org/10.3390/w10060700
APA StyleWang, T., Guo, X., Fu, H., Guo, Y., Peng, X., Wu, Y., Li, J., & Xia, Y. (2018). Effects of Water Depth and Ice Thickness on Ice Cover Blasting for Ice Jam Flood Prevention: A Case Study on the Heilong River, China. Water, 10(6), 700. https://doi.org/10.3390/w10060700





