Analysis of the Erosion Law of Karst Groundwater Using Hydrogeochemical Theory in Liulin Spring Area, North China
Abstract
:1. Introduction
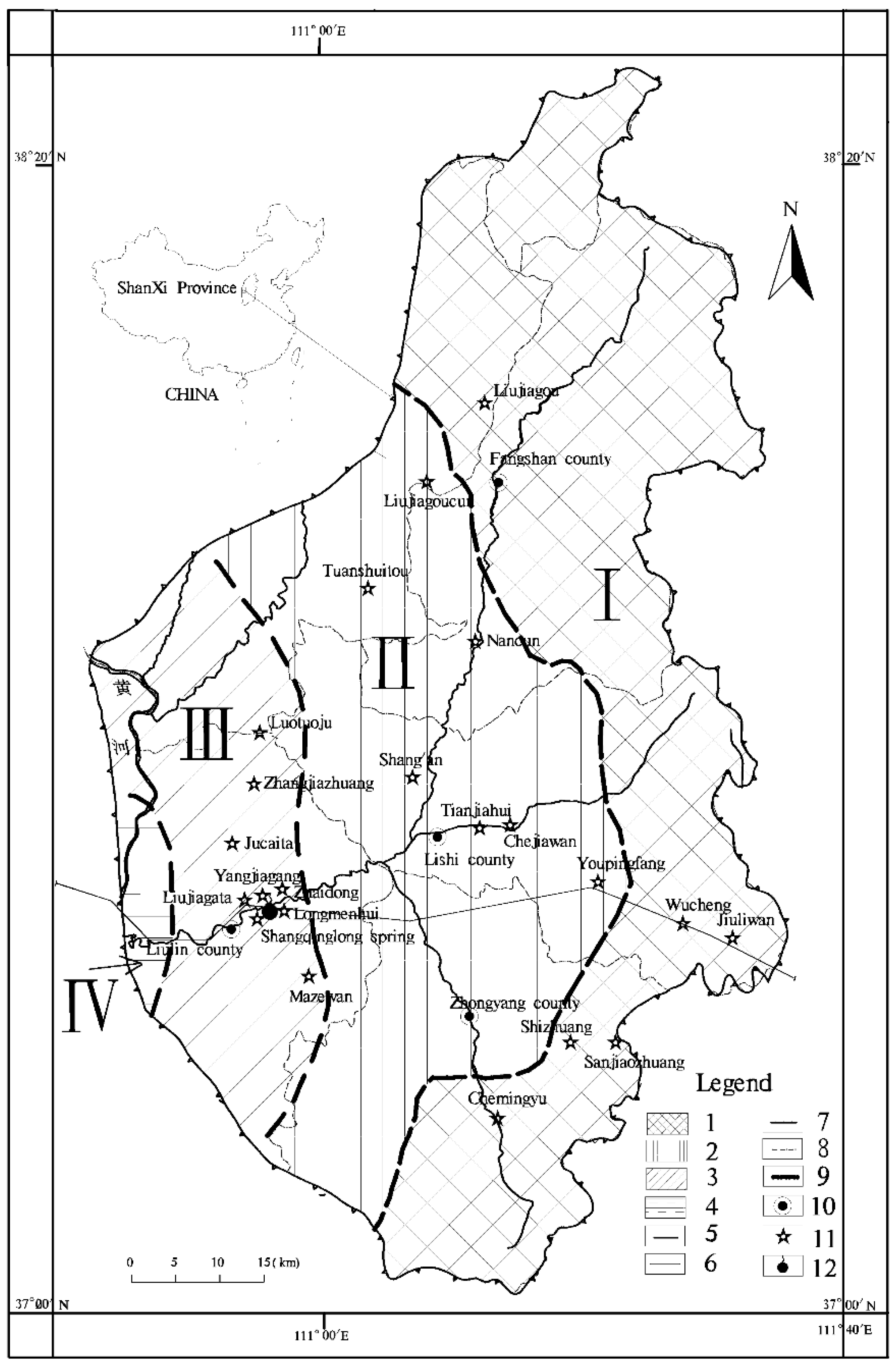
2. Liulin Spring Area
2.1. Physical Geography
2.2. Geology and Hydrogeology
2.3. Sampling and Analysis
3. Model Building and Feature Analysis of Hydrogeochemistry
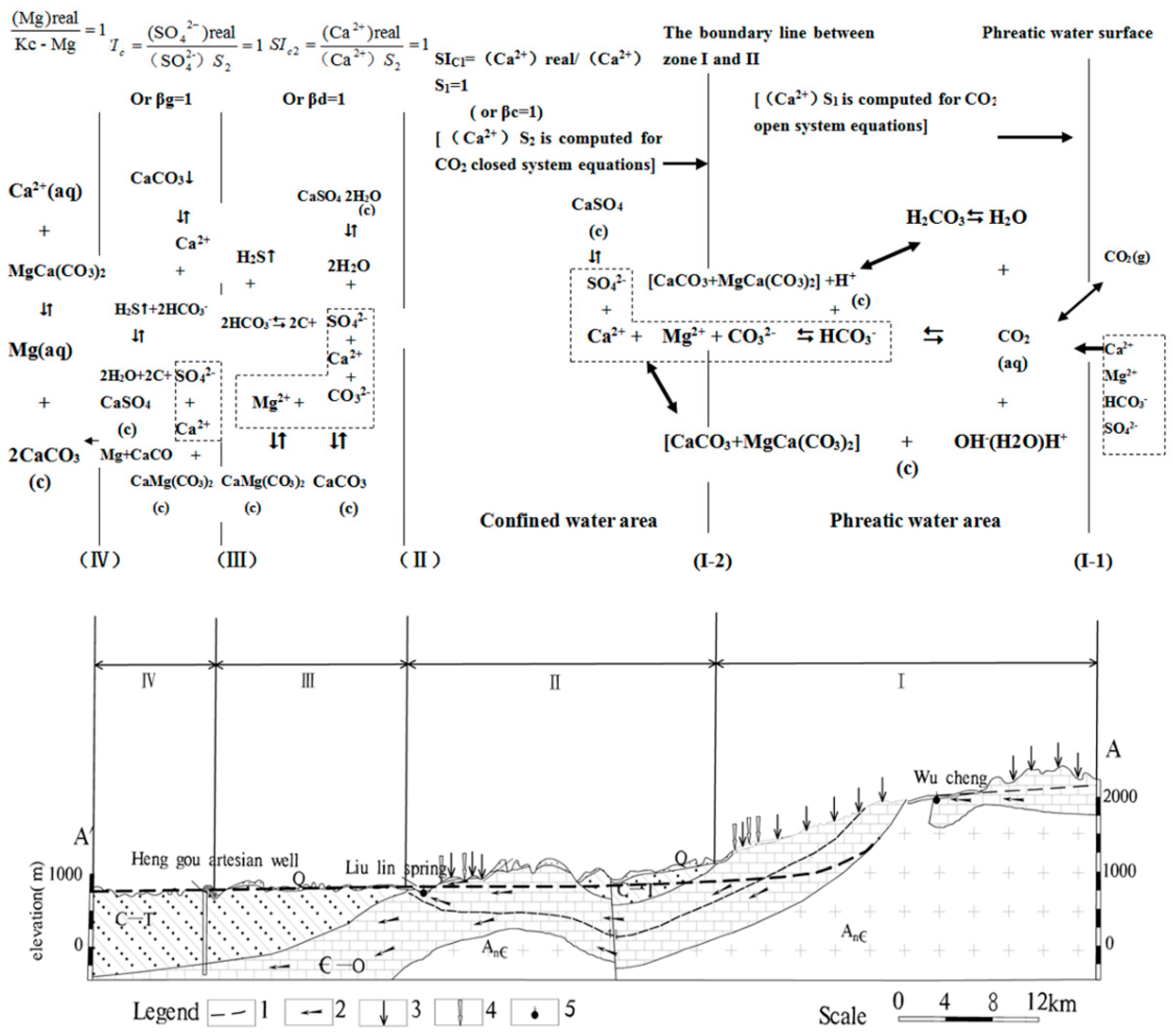
3.1. Hydrogeochemical Partition and the Construction of Its Model
3.2. Geochemical Characteristics Analysis
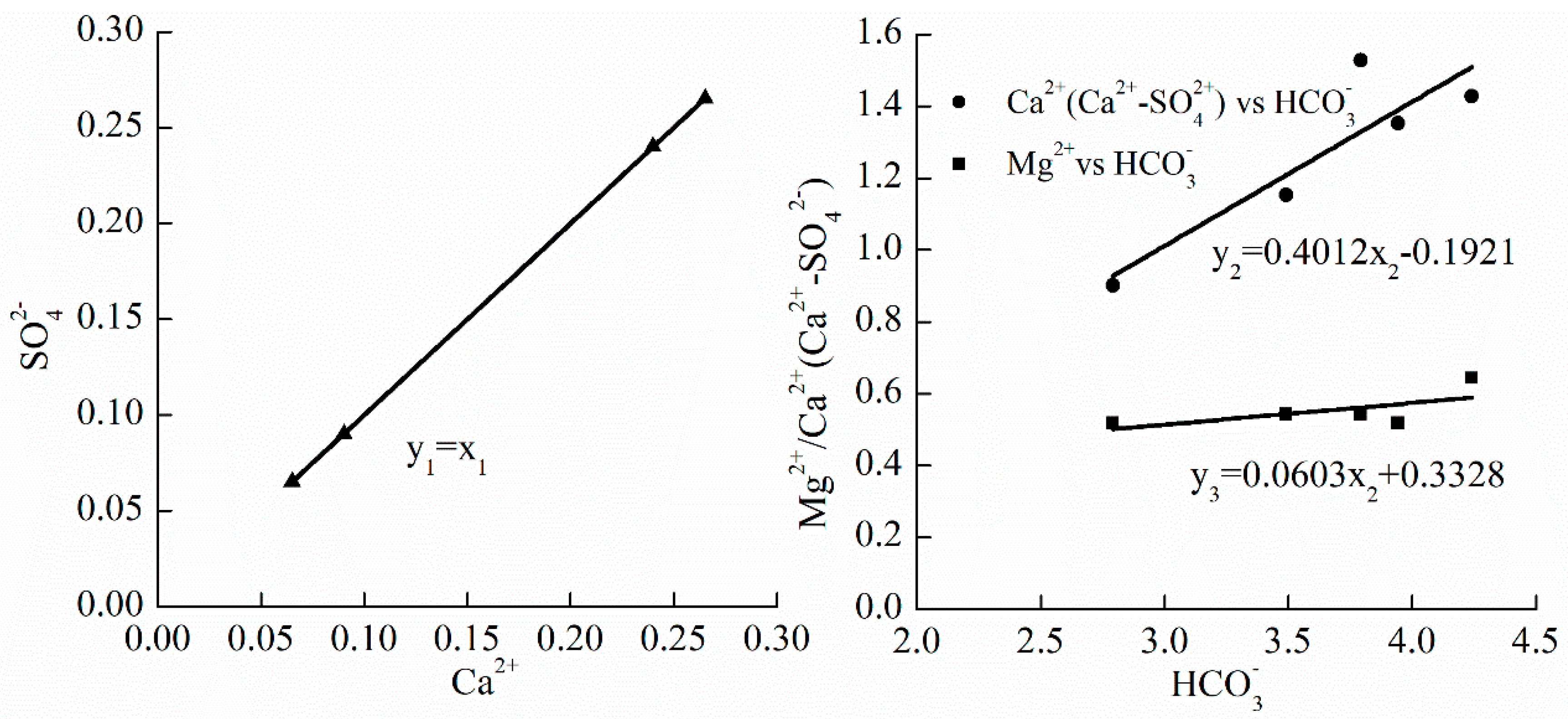
3.2.1. βc ≤ 1 (Zone I)
3.2.2. βc > 1 ~ βd ≤ 1 (Zone II)
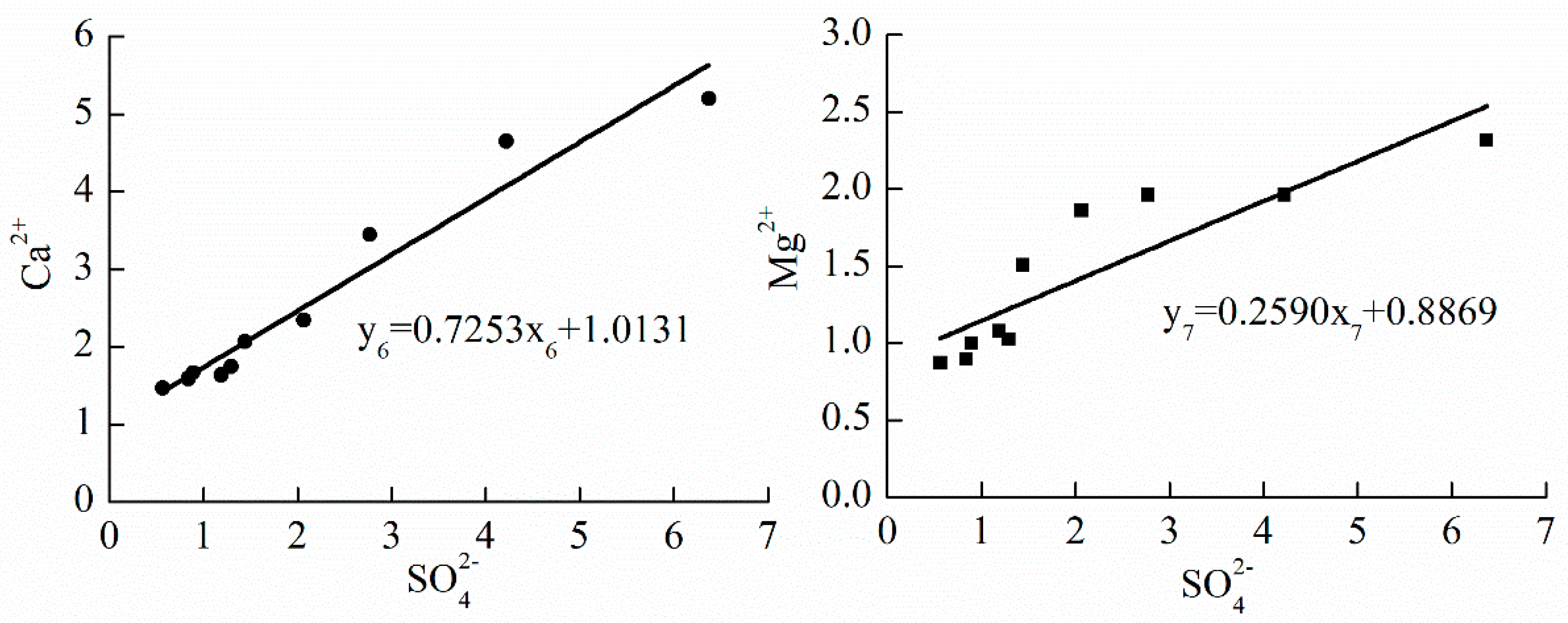
3.2.3. βd > 1 ~ βg ≤ 1 (Zone III)
3.2.4. βg > 1 (Zone IV)
4. Calculation and Discussion of Corrosion Modulus
4.1. βc ≤ 1 (Zone I)
=(m1 + m2 + m3)Ca2+ + m1SO42− + m3Mg2+ + (2m2 + 4m3)HCO3− + 2m1H2O
4.2. βc >1 ~ βd ≤ 1 (Zone II)
4.3. βd >1 ~ βg ≤ 1 (Zone III)
5. Conclusions
- (1)
- In zone I where βc ≤ 1, three kinds of minerals (viz. calcite, dolomite and gypsum) are in the dissolved state. The corrosion modulus of calcite is maximum and the second is that of dolomite, and the value of corrosion modulus of gypsum is minimum; in zone II where βc ~ 1 > βd ≤ 1, the value of corrosion modulus of calcite is negative, which indicates that the reaction of calcite transforms dissolution to precipitation. The corrosion modulus of dolomite and gypsum increased, and the corrosion reaction was dominated by carbonate rocks dissolution; in the third zone where βd > 1 ~ βg ≤ 1, calcite and dolomite achieved a supersaturated state and the corrosion modulus of gypsum increased remarkably.
- (2)
- From zone I to zone III, the corrosion modulus of calcite decreased gradually along the direction of groundwater flow, however, the corrosion modulus of dolomite increased at first then decreased, and the corrosion modulus of gypsum was augmented with the increase in aquifer depth. The dissolution law of karst groundwater in the Liulin spring area shows that the hydrogeochemical environment plays an important role in mineral corrosion. However, there is less work in the hydrodynamic analysis of the spring system, and more efforts in this regard should be made in the future.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cao, Y.Q.; Hu, K.R. Karst Chemistry Environment Hydrogeology; Jilin University Press: Changchun, China, 1994. (In Chinese) [Google Scholar]
- Sappa, G.; Ferranti, F.; De Filippi, F.M.; Cardillo, G. Mg2+-based method for the Pertuso spring discharge evaluation. Water 2017, 9, 67. [Google Scholar] [CrossRef]
- Xie, Y.H.; Yang, M.D. Human Activity and Karst Environment; Beijing Science and Technology Press: Beijing, China, 1994. (In Chinese) [Google Scholar]
- Dreybrodt, W. Processes in Karst Systems: Physics, Chemistry, and Geology; Springer: New York, NY, USA, 1988. [Google Scholar]
- Appelo, C.A.J.; Postma, D. Geochemistry, Groundwater and Pollution; A.A. Balkema Publishers: Avereest, The Netherlands, 1993. [Google Scholar]
- Allred, K. Some carbonate erosion rates of Southeast Alaska. J. Cave Karst Stud. 2004, 66, 89–97. [Google Scholar]
- Gil-Márquez, M.; Barberá, J.A.; Andreo, B.; Mudarra, M. Hydrological and geochemical processes constraining groundwater salinity in wetland areas related to evaporitic (karst) systems. A case study from Southern Spain. J. Hydrol. 2017, 544, 538–554. [Google Scholar] [CrossRef]
- Barbieri, M.; Nigro, A.; Petitta, M. Groundwater mixing in the discharge area of San Vittorino Plain (Central Italy): Geochemical characterization and implication for drinking uses. Environ. Earth Sci. 2017, 76, 393. [Google Scholar] [CrossRef]
- Mottershead, D.N. Rates and patterns of bedrock denudation by coastal salt spray weathering: A seven year record. Earth Surf. Proc. Land. 1989, 14, 383–398. [Google Scholar] [CrossRef]
- Stephenson, W.J.; Kirk, R.M. Measuring erosion rates using the micro-erosion meter: 20 years of data from shore platforms, Kaikoura Peninsula, South Island, New Zealand. Mar. Geol. 1996, 131, 209–218. [Google Scholar] [CrossRef]
- Liu, Z.H. Field experimental research on the corrosion kinetics of limestone and dolomite in allogenic water—Case from Yaoshan Mt. Carsol. Sin. 2000, 19, 1–4. (In Chinese) [Google Scholar]
- Plan, L. Factors controlling carbonate dissolution rates quantified in a field test in the Austrian alps. Geomorphology 2005, 68, 201–212. [Google Scholar] [CrossRef]
- Webb, A.H.; Bawden, R.J.; Busby, A.K.; Hopkins, J.N. Studies on the effects of air pollution on limestone degradation in Great Britain. Atmos. Environ. 1992, 26, 165–181. [Google Scholar] [CrossRef]
- Pulina, M.; Sauro, U. Modello dell’ erosione chimica potenziale di rocce carbonatiche in Italia. Memorie della Soc. Geol. Italiana 1993, 49, 313–323. [Google Scholar]
- Gombert, P. Role of karstic dissolution in global carbon cycle. Glob. Planet. Chang. 2002, 33, 177–184. [Google Scholar] [CrossRef]
- Li, J.Z.; Lin, J.S.; Fang, J.F. Karst corrosion strength analysis and estimation. Geogr. Res. 1994, 13, 90–97. (In Chinese) [Google Scholar]
- Cao, Y.Q.; Hu, K.R. A preliminary study on karst hydrochemical field modeling and quantitative evaluation of erosion of carbonate-sulfate formation. J. Changchun Univ. Earth Sci. 1988, 18, 53–62. (In Chinese) [Google Scholar]
- Mercado, A.; Billings, G.K. Kinetics of mineral dissolution in carbonate aquifers as a tool for hydrological invertigations, I. concentration-time relationships. J. Hydrol. 1975, 24, 303–331. [Google Scholar] [CrossRef]
- Mercado, A.; Billings, G.K. Kinetics of mineral dissolution in carbonate aquifers as a tool for hydrological invertigations, II. hydrogeochemcal models. J. Hydrol. 1975, 24, 365–384. [Google Scholar] [CrossRef]
- Hu, K.R.; Cao, Y.Q. The study of water quality and chemical dynamics model in carbonate area. Hydrogeol. Eng. Geol. 1993, 3, 8–14. (In Chinese) [Google Scholar]

| Zone | Water Sample | Mineral ion Concentration (mmol/L) | Mineral ion Dissolved Quantity (mmol/L) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| HCO3− | SO42− | Ca2+ | Mg2+ | HCO3− | SO42− | Ca2+ | Mg2+ | ||
| βc ≤ 1 | Jiuliwan | 3.20 | 0.20 | 1.15 | 0.61 | 2.79 | 0.09 | 0.99 | 0.52 |
| Liujiagou | 4.35 | 0.18 | 1.58 | 0.61 | 3.94 | 0.07 | 1.42 | 0.52 | |
| Sanjiaozhuang | 4.20 | 0.18 | 1.75 | 0.63 | 3.79 | 0.07 | 1.59 | 0.54 | |
| Shizhuang | 3.90 | 0.38 | 1.58 | 0.63 | 3.49 | 0.27 | 1.42 | 0.54 | |
| Chemingyu | 4.65 | 0.35 | 1.83 | 0.73 | 4.24 | 0.24 | 1.67 | 0.64 | |
| βc > 1 ~ βd ≤ 1 | Youpingfang | 4.45 | 0.45 | 1.55 | 0.96 | 4.04 | 0.34 | 1.39 | 0.87 |
| Chejiawan | 3.95 | 0.12 | 1.40 | 0.61 | 3.54 | 0.01 | 1.24 | 0.52 | |
| Tianjiahui | 3.85 | 0.30 | 1.63 | 0.73 | 3.44 | 0.19 | 1.47 | 0.64 | |
| Nancun | 4.15 | 0.15 | 1.58 | 0.58 | 3.74 | 0.04 | 1.42 | 0.49 | |
| Liujiagou | 4.00 | 0.25 | 1.25 | 0.71 | 3.59 | 0.14 | 1.09 | 0.62 | |
| Shang’an | 4.49 | 0.86 | 1.61 | 1.07 | 4.08 | 0.75 | 1.45 | 0.98 | |
| Tuanshuitou | 4.90 | 2.25 | 2.46 | 1.42 | 4.49 | 2.14 | 2.30 | 1.33 | |
| βd > 1 ~ βg ≤ 1 | Mazewan | 5.35 | 1.30 | 1.80 | 1.17 | 4.94 | 1.19 | 1.64 | 1.08 |
| Loumenhui | 4.05 | 0.68 | 1.63 | 0.96 | 3.64 | 0.57 | 1.47 | 0.87 | |
| Shangqinglong | 4.10 | 1.00 | 1.83 | 1.09 | 3.69 | 0.89 | 1.67 | 1.00 | |
| Zhaidong | 4.35 | 1.40 | 1.91 | 1.12 | 3.94 | 1.29 | 1.75 | 1.03 | |
| Yangjiagang | 4.40 | 0.95 | 1.75 | 0.99 | 3.99 | 0.84 | 1.59 | 0.90 | |
| Liujiagata | 3.75 | 2.18 | 2.51 | 1.95 | 3.34 | 2.07 | 2.35 | 1.86 | |
| Yangjiagang | 3.60 | 6.48 | 5.36 | 2.41 | 3.19 | 6.37 | 5.20 | 2.32 | |
| Zhangjiazhuang | 4.10 | 1.55 | 2.23 | 1.60 | 3.69 | 1.44 | 2.07 | 1.51 | |
| Luotuoju | 4.35 | 4.33 | 4.81 | 2.05 | 3.94 | 4.22 | 4.65 | 1.96 | |
| Jucaita | 4.85 | 2.88 | 3.61 | 2.05 | 4.44 | 2.77 | 3.45 | 1.96 | |
| ion quantity in rainfall | 0.41 | 0.11 | 0.16 | 0.09 | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Wang, K.; Zhang, F.; Chen, J.; Li, A.; Chen, Y. Analysis of the Erosion Law of Karst Groundwater Using Hydrogeochemical Theory in Liulin Spring Area, North China. Water 2018, 10, 674. https://doi.org/10.3390/w10060674
Zheng X, Wang K, Zhang F, Chen J, Li A, Chen Y. Analysis of the Erosion Law of Karst Groundwater Using Hydrogeochemical Theory in Liulin Spring Area, North China. Water. 2018; 10(6):674. https://doi.org/10.3390/w10060674
Chicago/Turabian StyleZheng, Xiuqing, Kai Wang, Fei Zhang, Junfeng Chen, Aimin Li, and Yanping Chen. 2018. "Analysis of the Erosion Law of Karst Groundwater Using Hydrogeochemical Theory in Liulin Spring Area, North China" Water 10, no. 6: 674. https://doi.org/10.3390/w10060674
APA StyleZheng, X., Wang, K., Zhang, F., Chen, J., Li, A., & Chen, Y. (2018). Analysis of the Erosion Law of Karst Groundwater Using Hydrogeochemical Theory in Liulin Spring Area, North China. Water, 10(6), 674. https://doi.org/10.3390/w10060674






