1. Introduction
With urbanization and rapid economic growth, water pollution in China has become increasingly serious. The solution to regional water pollution problems relies upon the consultation and cooperation for water environment conservation of various companies or groups in the region. However, since reducing pollution discharge, scientific and reasonable allocation of amount of pollutant discharge, and other environmental management policies involving the vested interests of various local governments, regional companies, or groups, this has caused the problem of water environmental pollution control and management to become complex. To effectively solve this problem, many researchers have used game theory, which is a powerful tool to analyse and solve contradictory conflicts. Game theory is used in research to analyse and solve reduction and allocation of discharge amount and other water environmental management conflicts.
Pollution discharge rights research started in the 1960s when American researcher Dales first proposed this concept and defined these rights to be ‘rights of right holders to discharge pollutants into the environment in compliance with legal requirements’. The focus of pollution discharge rights research is on how to fairly and reasonably allocate limited environmental capacity usage rights to each polluter in practice.
The equity principle and the optimization models are widely used when study on this issue. Mostafavi et al. [
1] created an allocation model of waste load using a non-dominated archiving multi-colony ant algorithm. Gao Zhu et al. [
2] used a single-objective decision making model which carried out research on the initial allocation of pollutant discharge based on water function regionalization. Ge Min et al. [
3] proposed a provincial initial water rights incentive allocation model with total pollutant discharge constraint, and made a feasible model of the incentive allocation to the provincial initial water rights. Pu Zhengning et al. [
4] developed a multi-objective primary distribution model that optimizes economic efficiency and environmental contribution in Tai Lake. Liu Yong et al. [
5] developed an inexact chance-constrained linear programming (ICCLP) model for optimal water pollution management at the watershed scale and applied to Lake Qionghai watershed in China for water quality improvement with the goal of achieving a minimum total cost. Minciardi et al. [
6] considered two main kinds of decision problems including control problems and planning problems, presented the sustainable planning and control of groundwater resources. Yu Sen et al. [
7] presented a new environmental-fairness-based optimization model (EFOM) for the decision-support of water resources management and water pollution control at the watershed scale, which is capable of optimizing the total discharge quantity in the whole basin and controlling units both spatially and temporally. Xu Jiuping et al. [
8] presented a bi-level optimization waste load allocation programming model under a fuzzy random environment to assist integrated river pollution control. Zhao Laijun et al. [
9] explored cooperative pollution reduction strategies from a macro level, targeting multiple jurisdictional regions.
Game theory is another significant tool to solve the problem of allocating pollution discharge rights. Petrosjan et al. [
10] proposed a multistage supergame model for the management of downstream pollution. Krawczyk et al. [
11] utilized coupled constraint game models to study the discharge and profitability status of three participants in the same river basin. He proved that the Nash equilibrium exists in this game model and provided solutions for it at the same time. Yeung [
12] constructed a differential game model to describe the differential games between polluting enterprises that maximize their own benefits and those of the government, which collects a pollution discharge tax. Polluting enterprises obtain maximum benefits by increasing yield whereas governments collect a pollution discharge tax to reduce pollution. He obtained the feedback equilibrium solution for this model and expanded this model from the case of a single company to that of N companies. Mahjouri et al. [
13] developed a methodology for inter-basin water resources allocation utilizing some crisp cooperative games including Separable Costs Remaining Benefits (SCRB), Maximum Costs Remaining Savings (MCRS), and Shapley Value. Niksokhan et al. [
14] proposed a cooperative game theoretic methodology for trading pollutant discharge permits in rivers. van der Veeren et al. [
15] presented reduction strategies to analyze nitrate in the Rhine River basin. The results showed that the nitrate load in the North Sea will increase environmental damage if some players do not completely cooperate. List et al. [
16] analysed whether local or central regulation is better for controlling environmental pollution under the assumption of asymmetric behaviour using dynamic game theory. Fernandez [
17,
18] studied the effects of wastewater discharge during free trade at the USA–Mexico border, and he obtained results from cooperative and non-cooperative game analysis in order to analyse the reduction of pollutants in upstream and downstream countries. Subsequently, this model was used in the empirical analysis of the Tijuana River upstream of Mexico and downstream of USA. Results showed that if free trade is implemented, both countries will cooperate to reduce wastewater discharge and the employment rates of both countries will reach their highest levels. Bayramoglu [
19] studied the problems caused by eutrophic agriculture activities in the Black Sea in Ukraine and Romania. Shi Guangming et al. [
20] developed a game model to analyse the cost benefits of reducing pollutant discharge in four regions in the Jialu River Basin in China under the premise of stability and fairness considerations.
The aforementioned studies mainly focused on games between various local governments, regional companies, or groups for reducing amount of pollutant discharge, decreasing water environmental pollution control costs, and obtaining maximum self benefits. In this study, Aubin’s [
21] definition of fuzzy coalitions was used to construct a fuzzy cooperative game mathematical model between companies in a region and proposed a pollution discharge rights allocation method based on fuzzy cooperative games. The fuzzy Shapley value was used for allocation of benefits in the fuzzy coalition so that individuals participating in the coalition can all obtain benefits, which will ensure the fairness and sustainability of this cooperative coalition. Lastly, the proposed method was used for analysis on an example. Results showed that this method can increase the overall regional benefits and increase the benefits of various participating bodies.
There has been a widespread phenomenon during the economic development process of China: the fact that local environmental conservation departments will give relatively relaxed pollution discharge rights to industrial enterprises that entered a region at an early stage. This reflects the encouragement and support given by local governments to these companies in order to attract other industrial companies to enter the region. The pollution discharge rights of companies that enter that region later will be gradually and strictly limited. Once the water environmental capacity of that region approaches saturation, the regional permissible pollution discharge will be forbidden to increase further. This is the initial allocation of pollution discharge rights. In recent years, many economically developed regions in China have promoted an industrial transformation to accelerate the growth and development of a high-quality local economy, and the allocation of pollution discharge rights is an important aspect of this process. The initial allocation method for pollution discharge rights to manufacturing industries has exhibited significant stagnation and deficiencies. This has obstructed the industrial transformation and economic development of regions to some extent. Therefore, research on the use of game theory for secondary allocation of pollution discharge rights and provision of relevant environmental management methods is necessary and has important practical application significance.
2. Methods and models
2.1. Crisp Cooperative Games and Fuzzy Cooperative Games
The basis of cooperative games is that all participants in the coalition must comply with an enforceable and binding agreement. Compared with non-cooperative games, cooperative games emphasize efficiency and fairness and are a form of group rationality. In general, there is a hidden assumption in cooperative games; the profits between participants can freely flow through some exchange medium (such as currency), that is, cooperative games with side payments. The results of a cooperative game must satisfy Pareto optimality, thereby preventing the game results from sliding into a Nash equilibrium that is not the best overall result.
Coalition and allocation are the core concepts in cooperative games. Let the number of all the participants in the game be set to
N; then, the crisp coalition
K is a subset of
N, and the set of all crisp coalitions is defined as
P(
K). Then, the characteristic function
v of the crisp coalition can be written as:
v(K) is the value of the coalition K and represents the maximum benefit that can be achieved by coordination of strategies between coalition members (regardless of the measures adopted by other participants). In a crisp coalition, all participants clearly know which coalition they will join and understand the resources they have to contribute when they join the coalition and the benefits obtained. Crisp coalitions require participants to bring all their resources when joining a coalition. According to the definition by Shapley, the benefits obtained by a party in the coalition are determined by its contributions to the coalition.
According to the definition proposed by Aubin [
21], in a fuzzy coalition, a participant is only required to contribute some of his resources to join the coalition and his benefits are the sum of the benefits obtained from joining various coalitions in the game. The definition of a fuzzy coalition is similar to that of a crisp coalition: let the number of all the participants in the game be set to
N;
ki in the set
represents the degree of participation by participant
i in coalition
K, and
L(
N) is the set of all possible fuzzy coalitions.
is the empty set. Then, the characteristic function
v of this fuzzy coalition is:
Specifically, in a fuzzy cooperative game, the participant does not know how many resources he can contribute to join a coalition from the start, and the specific participation status may be one of the many fuzzy solutions. However, the participant can obtain an expected benefit by joining a coalition according to his degree of participation, which is the fuzzy Shapley value. This means that, differently from a crisp coalition, a fuzzy coalition does not require the participant to contribute all his resources to join a specific coalition but the participant is permitted to contribute part of his resources and can simultaneously join many different coalitions. In the model for the amount of pollutant discharge, each company first carries a certain amount of pollution discharge rights to participate in different fuzzy coalitions so that the benefits for the entire regional system are the largest possible, and the total amount of pollutant discharge is controlled within permissible ranges. Following that, maximized benefits are allocated to each company that joined the coalition according to a specific method. At the same time, the amount of pollutant discharge of various companies will be reallocated in different fuzzy coalitions. There is no clear definition in the fuzzy coalition on how to allocate the resources in the coalition to the various participants in the coalition and only the distribution status of a resource among the members in a coalition is provided. On the contrary, fuzzy coalition research focuses on the allocation of increased benefits among the participants, provides the degree of participation of various participants in various coalitions, and determines the benefits that each participant can obtain through coalitions. In actual problems, each participant is restricted by their actual situation and cooperation is usually complex and incomplete and is determined at the same time, largely by the decision-makers themselves. Therefore, it is difficult to achieve the theoretical optimal state. However, theories can be used to determine an optimizable space in which each participant can increase their benefits and ensure the feasibility of cooperation through different degrees of participation in various coalitions and by negotiation and compromise. This can be more rationally used in the actual cooperative environment compared with general optimized results. In addition, the uncertainty of the environment can encourage coalition members to cooperate. This is also the significance of fuzzy cooperative games in solving actual problems.
2.2. Fuzzy Cooperative Game Models for Allocation of Pollution Discharge Rights
In order for participants that cooperate to obtain maximum benefits, that is, maximized yield of various companies in the region, we need to determine the degree of participation of various companies in various fuzzy coalitions. The degree of participation here refers to a company contributing a certain proportion of pollution discharge permits obtained in one allocation to join a certain fuzzy coalition. We set
n to be the number of participants that can form
k coalitions, and the degree of participation of participant
i in coalition
k to be
. During independent production by each participant, the corresponding output per unit pollutant discharge amount is
, which is the rate of return on the amount of pollutant discharge. After the formation of coalitions, each coalition is viewed as a new entity with its own rate of return from pollutant discharge amounts
and upper limit of pollutant discharge amounts
that the coalition can accommodate. These parameters are associated with the upper and lower limits of production capacity of the producers in that coalition. Thus, the objective function and constraints are as follows:
represents the total benefits of coalition k,
represents the total pollutant discharge amounts when joining coalition k,
represents the degree of participation of participant i in coalition k,
represents the pollutant discharge amounts that can be allocated to participant i,
represents the corresponding rate of return from pollutants discharged when joining coalition k,
represents the rate of return when participant i independently exercises its pollution discharge permit,
represents the upper limit for pollutants discharged when joining coalition k, and
represents the benefits obtained when participant i independently exercises his pollutant discharge amounts after joining coalition k.
Constraint (6) means that the pollutant discharge amounts after joining the coalition cannot exceed the upper limit. Constraint (8) means that the total benefits in every coalition must be larger than the benefits when each corresponding participant produces its resources independently; otherwise, a motive for joining the coalition does not exist. Constraint (9) means that the sum of the degrees of participation of every participant in various coalitions is 1. Constraint (10) means that the degree of participation lies between 0 and 1. Planning algorithms or genetic algorithms can be used to obtain the degree of participation by participant i in coalition k, thereby calculating the fuzzy Shapley values of every participant.
2.3. Fuzzy Shapley Values
After the above model is estimated, the degree of participation of different participants in different fuzzy coalitions can be obtained. We can further use different benefit allocation methods to allocate the total net benefits of the system to various production bases. These methods mainly include fuzzy Shapley values, fuzzy kernel minimum, and weak fuzzy kernel minimum methods. This paper employed fuzzy Shapley values for the allocation of benefits.
The fuzzy Shapley value method was developed from the crisp Shapley value method generally used to solve crisp coalitions. Shapley value methods have only one solution. In fact, the Shapley value method examines the possible contribution rate of every participant in a given game coalition on possible sub-coalitions and the size of its probability to confirm the contribution rate of that participant towards the entire coalition, and allocates resources to the participant in the coalition game based on that contribution rate. In earlier studies, Li et al. [
22] obtained a fuzzy Shapley equation with no limitations on eigenfunctions. According to the definition, if
v is a fuzzy characteristic equation,
v(
k) is the benefit generated by all participants that joined the fuzzy coalition
k. Therefore,
v(
k) should be fairly and rationally allocated to all the participants participating in the fuzzy coalition
k. An intuitive method is to introduce the degree of participation
so that the fuzzy game is converted into a crisp game. The corresponding crisp game of that fuzzy game can thus be defined as:
where
can take the values 0 or 1, which represent participation or non-participation in that fuzzy coalition, respectively. For
, the Shapley value of participant
i is:
According to the above equation, we can further obtain the corresponding fuzzy Shapley values for fuzzy game
v and fuzzy coalition
k as follows:
represents the fuzzy Shapley value of participant i,
represents the number of participants in coalition k,
represents the total number of participants, and
represents the degree of participation of participant j in coalition k.
After obtaining , we can obtain the fuzzy Shapley values of every participant in the fuzzy coalition, that is, the final benefit of every production base. It is worth noting that this benefit reflects the degree of contribution by various participants in the coalition and their corresponding returns, and ensures that all participants can receive benefits, thereby ensuring the feasibility of the coalition.
3. Case Analysis
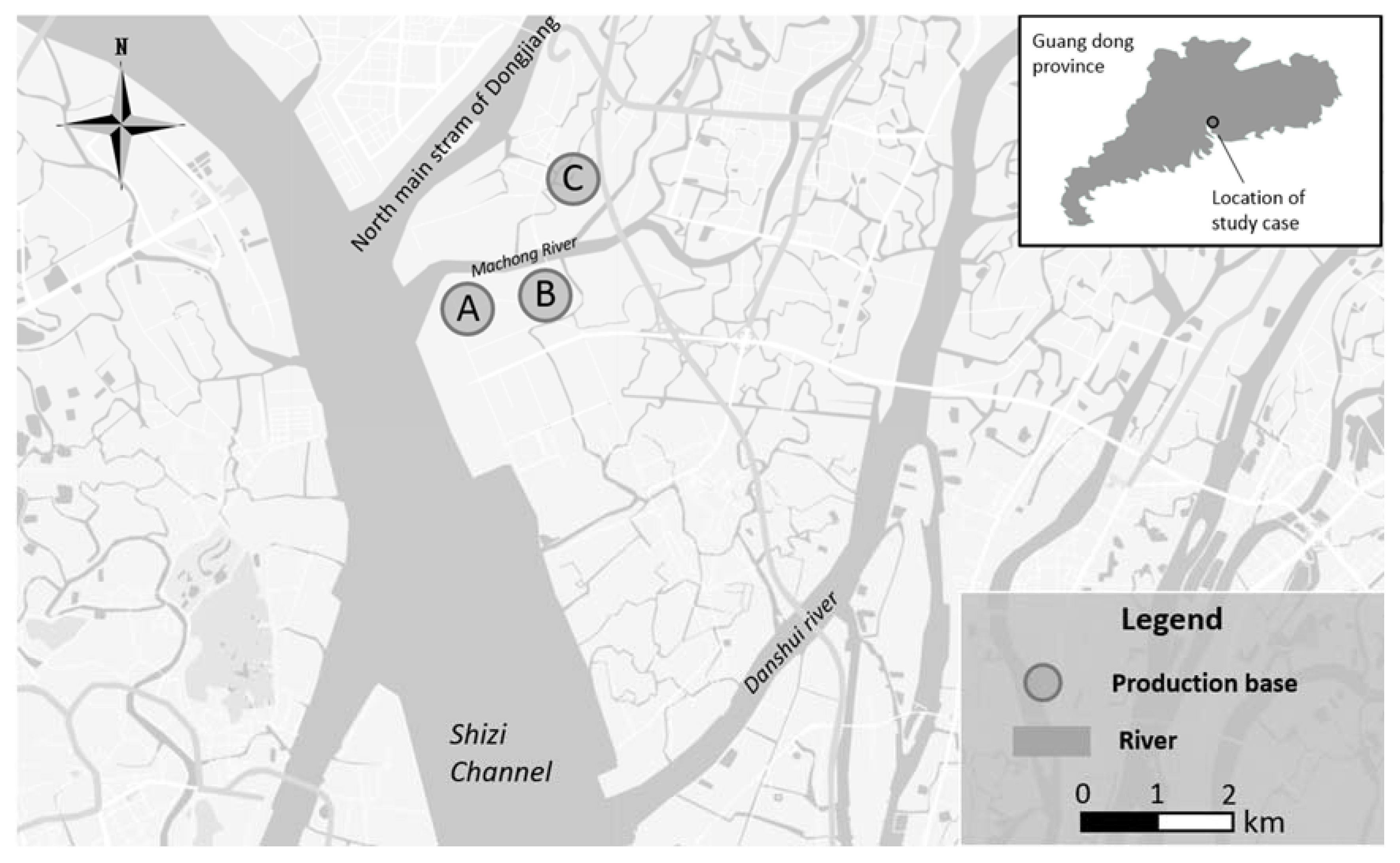
Dongguan City in Guangdong province is a region that is undergoing rapid urbanization and economic development. There are three production bases (A, B, and C) in a region in Dongguan City, and
Figure 1 shows their geographical positions. A is the base for the paper industry and has the largest total annual output and largest amount of COD (Chemical Oxygen Demand) emitted. B and C are the bases for the textile industry and electronic device manufacturing industry, respectively. Their total annual output and amount of COD emitted were comparatively less but their output per unit pollutant discharge amounts are higher than that of A. The wastewater of these three industrial bases is all discharged into the Shizi channel by discharge pipes after undergoing wastewater treatment to meet standards. The amount of water pollutants discharged by the three industrial bases account for 98% of the total pollutant discharge amounts in that town.
The electronic device manufacturing industry and textile industry are development industries focused on by the Dongguan municipal government. However, the water quality standards of the water body receiving pollutants (Shizi channel) have approached the water environmental control standards. Therefore, the environmental protection bureau cannot promote the development of local companies by increasing the amount of water pollutants discharged in this region. An effective method is to use trading of pollution discharge rights in this region to promote the expansion of the scale of production of the electronic device manufacturing industry and textile industry and increase the total output of industries in this region.
The following section uses the trading of COD discharge rights as an example. We employed the fuzzy cooperative game models for the allocation of pollution discharge rights proposed by this study to calculate the transferable COD discharge amount between different production bases, that is, the formation of fuzzy coalitions for trading of pollution discharge rights. Finally, the fuzzy Shapley value method was used to fairly and reasonably allocate the overall benefits to the various production bases obtained by cooperation.
In this model, the three dischargers will trade part of their discharge rights. Then the three dischargers, which are also the players participating this trade, will form the fuzzy coalitions for negotiations and cooperation. In the same way that dischargers A and B form coalition {A,B}, A, B and C form a big coalition {A,B,C}, just like bilateral and multilateral agreement. According to the definition of the fuzzy game, the fuzzy coalitions do not clearly define the specific resource allocation status between players, because it will change by the result of negotiations or additional objective conditions. Nevertheless, the fuzzy game can determine the resource allocation status between different coalitions, and the degree of participation of each player in fuzzy coalitions. Under the framework of the fuzzy cooperative game, we can obtain a kind of expected return of each player, which is the fuzzy Shapley value. Generally speaking, a production base with a higher benefit coefficient will obtain more pollution discharge rights from those with smaller benefit coefficients to increase the overall output of the entire region. However, the production base must carry a payment transfer through other means to the participants that contribute to this pollution discharge right, such as a cash flow or technology transfer. This is to compensate for the benefits it received and achieve the aim of the coalition.
We can obtain the detailed information regarding unit pollutant discharge amount benefit according to the daily operations, output, and pollutant discharge status of the production base. Considering that the trading of pollution discharge rights cannot overly affect the basic operations of production in the companies, each production base uses 40% of its pollutant discharge amounts for trading (
Table 1). At the same time, there are upper limits for the production capacity and amount of pollution discharge rights that can be accepted when coalitions are formed in various production bases.
Table 2 shows the upper limits for the benefit parameters and pollutant discharge amounts for each fuzzy coalition.
According to the data from
Table 1 and
Table 2 as input and reallocation of pollution discharge rights by forming the four fuzzy coalitions of {A,B}, {A,C}, {B,C}, and {A,B,C}, each participant contributes some of their pollution discharge rights as a resource to participate in possible coalitions. Equations (3)–(10) are a linear model and MATLAB was used for the estimation, using planning algorithms to obtain the degree of participation of various production bases in various fuzzy coalitions. We further obtained the results of secondary allocation of pollutant discharge permits by various fuzzy coalitions, as shown in
Table 3 and
Table 4. At this stage, the distribution of the usage status of pollutant discharge amounts by various participants is shown in
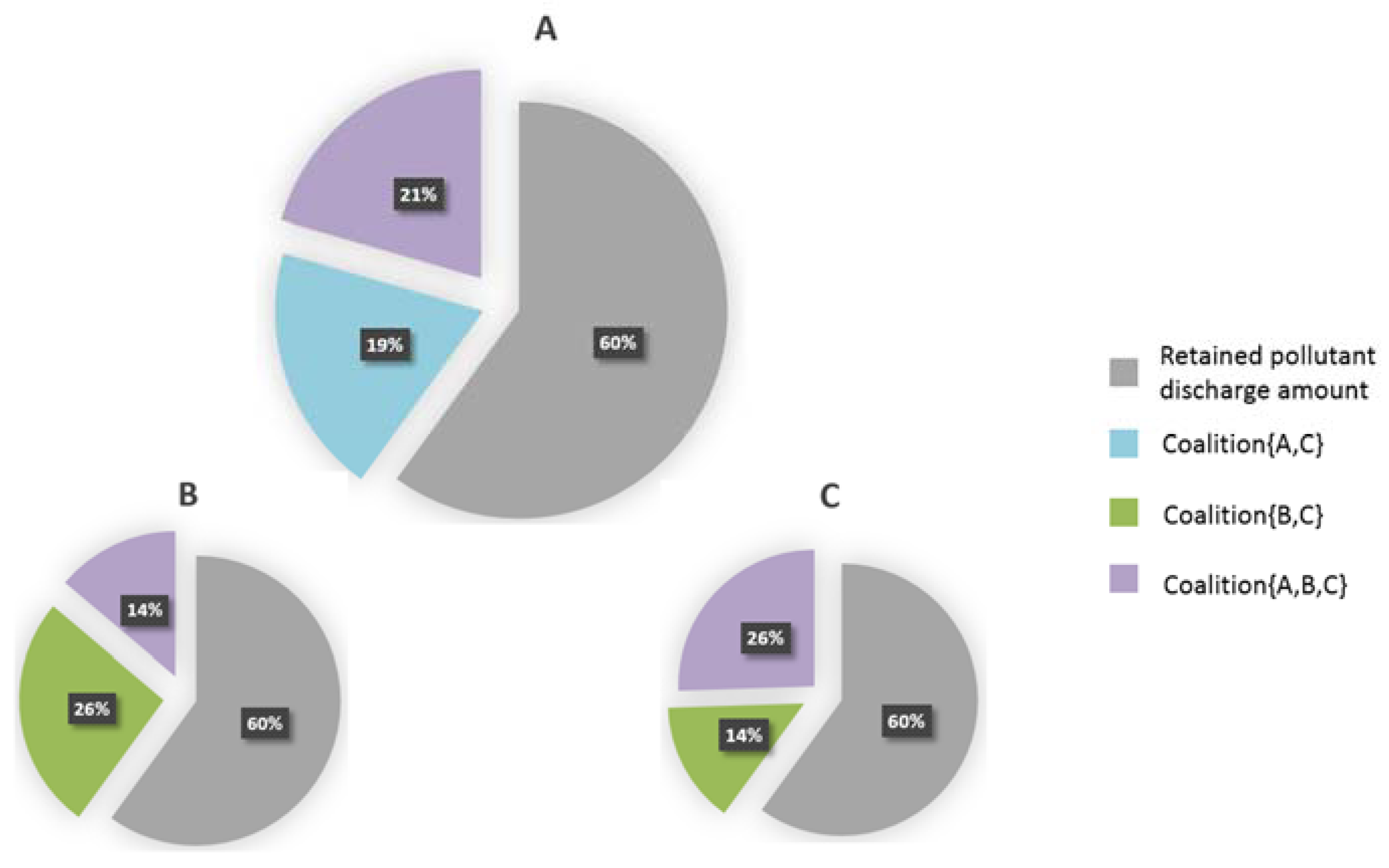
Figure 2.
From
Table 3, we can obtain the degree of participation of each players in fuzzy coalitions. The degree of participation represents the distribution of each player’s resources among their possible coalitions, it also reflects the willingness of each player to participate in the coalition. If the degree of participation is 0, it means the player will not participate in this coalition, due to the low benefits or even negative benefits. After we obtain the degree of participation, we can get secondary allocation results of each fuzzy coalition’s pollutant discharge amounts, which is
Table 4. From
Table 4, we can see that the fuzzy coalitions {A,B,C} and {B,C} have the highest benefit coefficients. Therefore, these models tend to fully satisfy the required pollution discharge rights. It should be noted that the fuzzy coalitions do not clearly define the specific resource allocation status between participants. However, under the framework of these fuzzy coalitions, various participants can determine resource allocation within the fuzzy coalition by negotiations depending on the actual situation.
For reference, here comes one of the feasible scenario of the allocation of the pollution discharge rights between each dischargers. For example, if the negotiation results in that the resources within the coalition are equally distributed to all participants, and the participants can at most increase their production capacity by 1-fold (i.e., expansion of pollutant discharge amount by 1-fold), the allocation status of pollutant discharge amounts under this scenario will be: A has 1763.33 tonnes COD, B has 822.67 tonnes COD, and C has 692 tonnes COD. As shown in
Table 5.
After obtaining the degree of participation of the various participants in the fuzzy coalition, the Shapley value of each participant can be obtained through Equation (16). This can be further used to derive the coalition benefits of the various production bases, as shown in
Table 6. Results showed that the total benefits of the various production bases were increased after joining the coalition, as compared with the case of not joining any coalition. At the same time, this did not harm the benefits of other participants and guaranteed the feasibility of cooperation. The total output of this region also increased compared with the sum of the individual outputs of various production bases before cooperation, that is, individual rationality and group rationality were simultaneously satisfied, and the Pareto optimality was achieved.
Compared to the traditional optimization methods, the fuzzy cooperation game highlights the “negotiation”. Because the traditional optimization methods consider all players as a whole to optimize, the result will be rationally optimal. However, the individuals of each player are not be taken into account during this process. On the other side, fuzzy cooperative game defines a clear expected benefit to ensure the feasibility of the cooperation, and it also provides a value benchmark for resource trading among players. At the same time, the cooperative leave a space of negotiation to the players, which means the allocation result of cooperation may not be the optimal result, but it will be more realistic.
4. Conclusions
China has started paying more and more attention to the importance of the environment during its current phase of development. However, due to historical reasons, companies that have high pollutant discharge amounts and low output usually hold large amounts of pollution discharge rights. This is undoubtedly a form of resource wastage when considered today. Therefore, driving an industrial transformation by establishing means of cooperation between different industries and promoting the reallocation of pollution discharge rights have important significance. This study established a pollution discharge rights–profit allocation model based on fuzzy coalition game theory. Formation of fuzzy coalitions between many producers in a region and reallocation of pollution discharge rights in the region through these coalitions was used to increase the total production value of the region while total pollution discharge amount is constant. At the same time, the fuzzy Shapley value method was used to allocate benefits obtained from the cooperation to the participants in various coalitions, based on the principles of fairness and rationality. This ensured the feasibility and long-term stability of the coalition. Under the framework of these fuzzy coalitions, each participant can conduct negotiations and compromise according to the actual situation and their own requirements to determine the specific allocation status of resources and payments. This model was validated by its application in the case of three production bases near the Shizi channel in Dongguan city, which were the paper industry base, textile industry base, and electronic equipment manufacturing base, for reallocation of pollution discharge rights. Results showed that this model could increase the coalition benefits of the three production bases in this region, which observed increases of 4.28%, 7.74%, and 13.98%, respectively. This provides a theoretical basis for promoting the formation of coalitions to allocate pollution discharge rights in this region and a reference for bargaining and negotiating these rights. At the same time, these rights also tend to be more likely to be pursued by production bases with high output, and this provided a basis for an industrial transformation in this region.