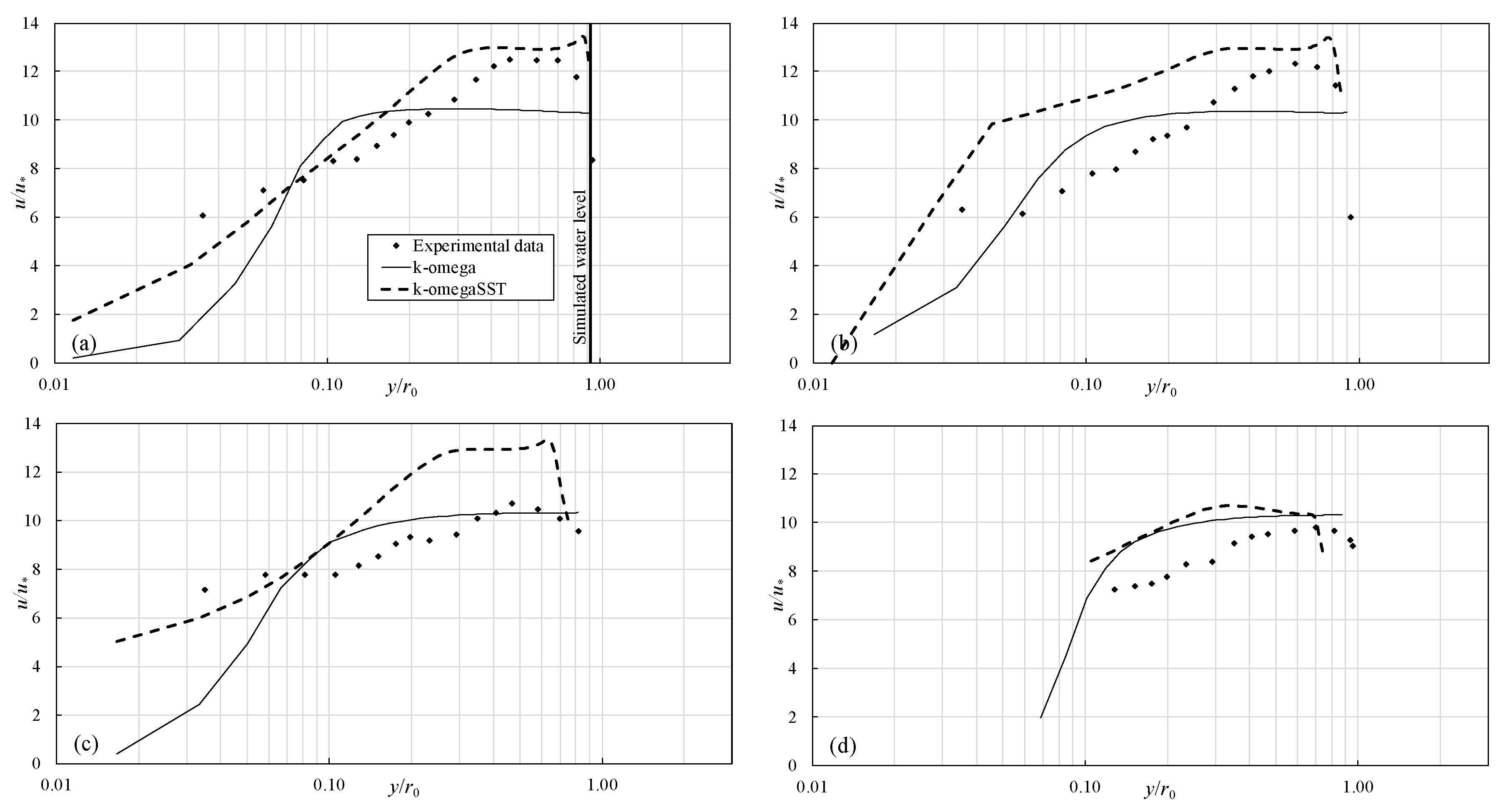
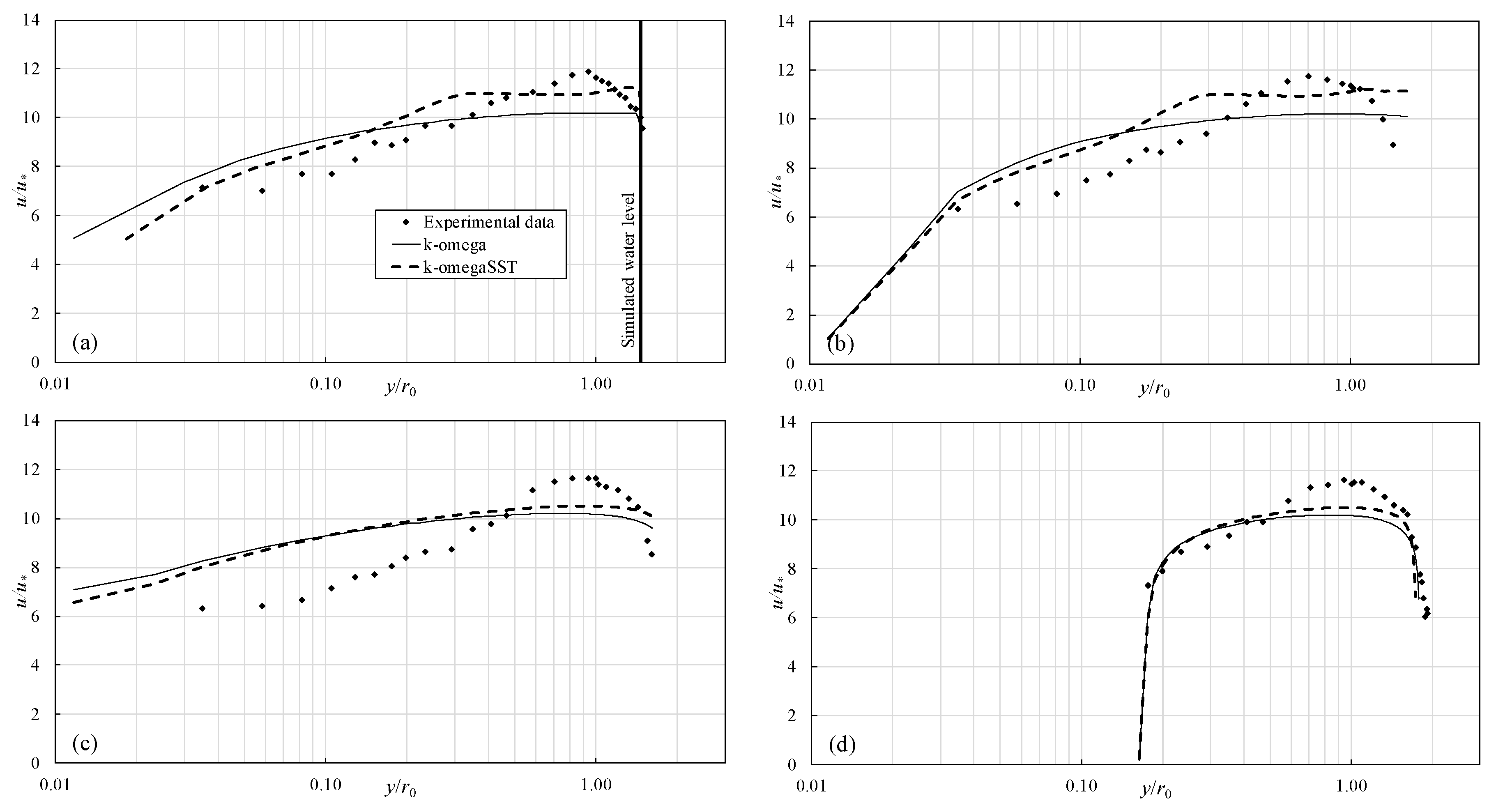
Recently, the researchers’ interest includes experimental observations as well as a numerical simulation of flow in corrugated pipes. A review of numerical techniques used in this field is given in Reference [
4]. Those Authors also presented the details of the numerical simulation of the pressurised pipe flow by means of Large Eddy Simulation (LES) for the 171 mm diameter pipe. In contrast, the simulation of the free-surface flow in corrugated pipes is rare in the literature, especially when the channel slope must be taken into consideration.
In the present study, the flow field is simulated by solving the three-dimensional Reynolds-Averaged Navier-Stokes (RANS) equations (Reference [
10], among others) in conservative form as written here in Cartesian coordinates (the fluid is assumed as incompressible and viscous, and the Einstein summation convention is applied to repeated indexes:
i,
j = 1, 2, 3):
where
is the fluid density,
the water dynamic viscosity, and
the mean fluid pressure,
(
i = 1, 2, 3) stand for the Cartesian coordinates,
denote the mean components of the velocity, and
t and
are, respectively, the time and the mean strain-rate tensor defined by
The quantity
is the Reynolds-stress tensor. The Reynolds-stresses are components of a symmetric second-order tensor. The diagonal components are normal stresses, whereas the off-diagonal elements are shear stresses. Hence, the Reynolds averaging formulation introduces six new unknown quantities that are the six independent components of the symmetric tensor
without additional equations. This means that the defined system is undetermined. To close the system, the Boussinesq approximation was used [
11]. The kinematic eddy-viscosity has been expressed as a function of the turbulent kinetic energy
k and the dissipation rate
ω (Equation (9)), leading to a ‘two-equation’ turbulence model.
2.3.1. Two-Equation Turbulence Models
Two-equation models [
10] provide one equation to compute the turbulent kinetic energy per unit mass
k and one more equation to calculate a specific dissipation rate
ω. In fact, two-equation models are complete to predict properties of a given turbulent flow without prior knowledge of the turbulence structure [
11]. In the present study, in order to constitute a relationship between the Reynolds stresses and the mean flow field and solve the closure problem, the k-ω model proposed by Wilcox [
11] and k-ω SST model developed by Menter [
12] were used.
In the k-ω model, the viscosity term
is defined as
while the turbulence kinetic energy per unit mass
k and the dissipation rate
ω obey the following:
In the above equation,
;
;
, whereas,
and
are computed through auxiliary functions as presented in Wilcox [
11].
The second selected turbulence model, the k-ω SST [
12], has several relatively minor variations from the original SST version [
13,
14]. The turbulence kinetic energy and the dissipation rate are computed using
where
represents a production limiter used in the model to prevent the build-up of turbulence in stagnation regions [
12],
represents the blending function, defined as [
13,
14] follows:
with
and
y represents the distance to the nearest wall. The turbulent eddy viscosity is
where
[
15],
S is defined as the second invariant of the deviatoric stress tensor and
. is a second blending function [
13,
14] expressed as
All the constants are predicted through a blend from the corresponding constants. For example,
is calculated as
. This model contains the following closure coefficients:
;
;
;
;
;
;
[
12].
It is to be noted here that the choice of two k-ω type of turbulence models for this work is due to their generally superior performance with respect to the more classical two-equation k-ε model in wall-bounded flows and, in particular, to their suitability in complex boundary layer flows under adverse pressure gradient and separation, as reported in Menter et al. [
12].
2.3.2. Numerical Solution
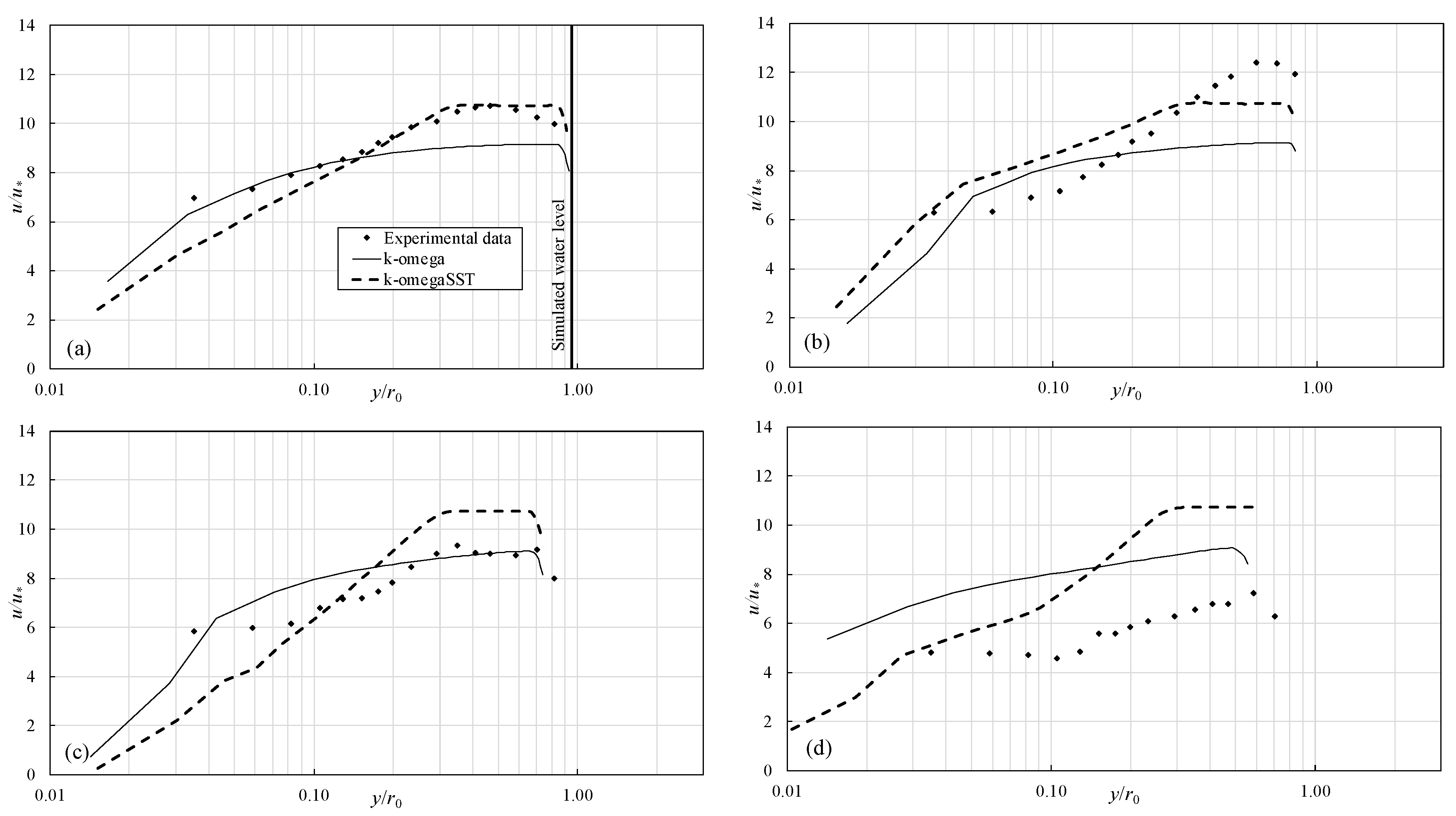
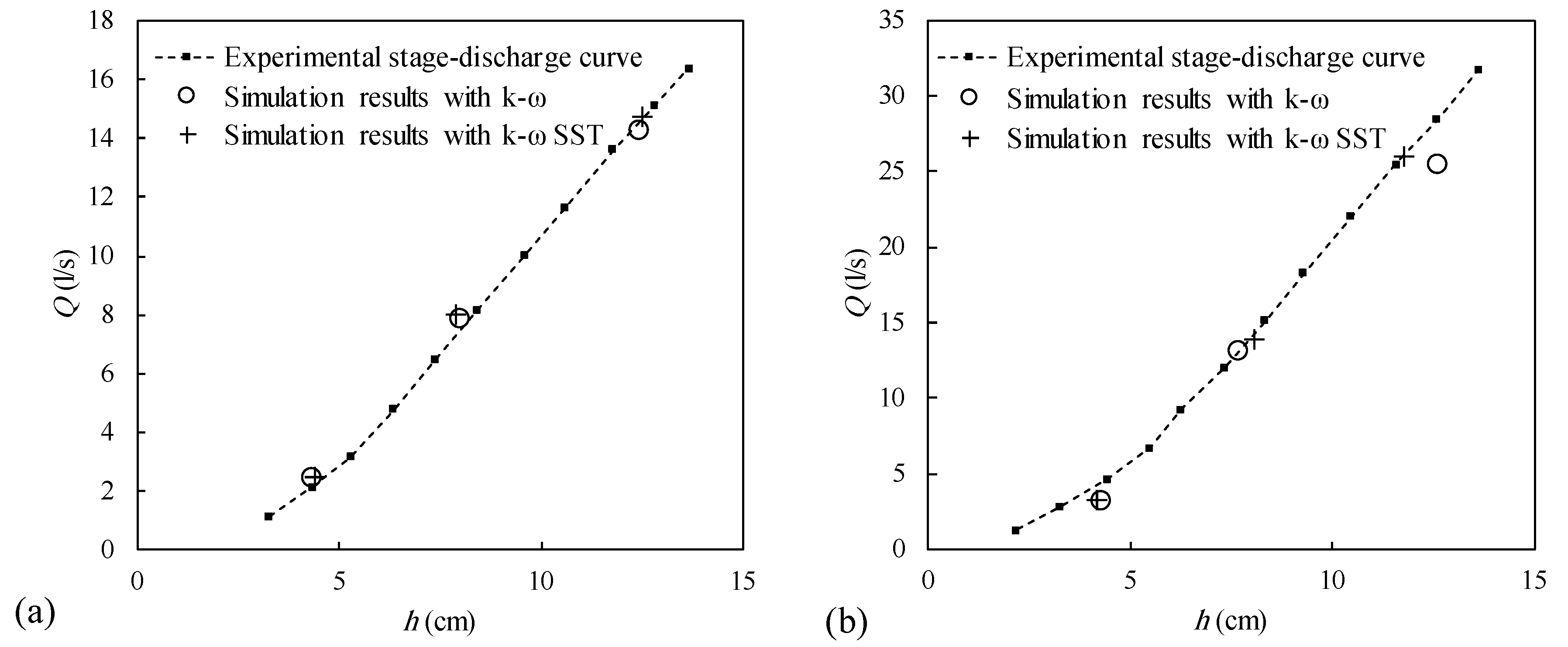
In the four open-channel experimental tests where the velocity was measured, the flow field was simulated by solving the RANS equations with both the k-ω and k-ω SST closure models. The governing Equations (6) and (7), together with the equations of turbulence models, were solved numerically by means of the interFoam solver that is embedded in the OpenFoam
® C++ libraries. The interFoam solver has been designed for incompressible, isothermal, immiscible fluids using the VoF (Volume of Fluid) phase -fraction based interface capturing approach [
16]. The VoF method was used in many investigations (see References [
17,
18,
19,
20], among others). The VoF method, proposed by Hirt and Nichols [
17], locates and tracks the free surface flow. In this method, each fluid phase (herein air and water) has an individual fraction of the volume. If a cell is totally void of water but full of air, the magnitude of volume fraction function is assigned to 0; however, when the cell is completely full of water, the aforementioned magnitude is equal to 1. Note that, if the interface intercepts the cell, the function will have a value between 0 and 1. Then, the indicator function,
, is expressed as
The two-phase flow can be assumed as a mixed fluid; hence, the density and dynamic viscosity are defined as
in which the subscripts 1 and 2 stand for the two selected fluids [
21].
The volume fraction function can be calculated by solving an advection equation for the velocity vector field,
V, as follows [
17,
21]:
The governing equations are discretised with the Finite Volumes (FVM) (see References [
21,
22,
23], among others). As to the discretisation of the solution domain, a ‘structured’ mesh was built where the dependent variables are stored at the cell centre of each cell space domain in a ‘co-located’ arrangement.
In the present study, the PISO (Pressure Implicit with Split Operator) technique suggested by Issa [
24] was employed to couple the pressure–velocity in transient computations. The PISO procedure adopts the ‘Segregated Approach’ and the system of equations is solved sequentially [
24]. Further details of the transient solution procedure can be found in Reference [
23]. The stability of the solution procedure was ensured utilizing an adaptive time step with an initial value of 10
−6 s in conjunction with a mean Courant-Friedrichs-Lewy (CFL) number limit set to 0.5.
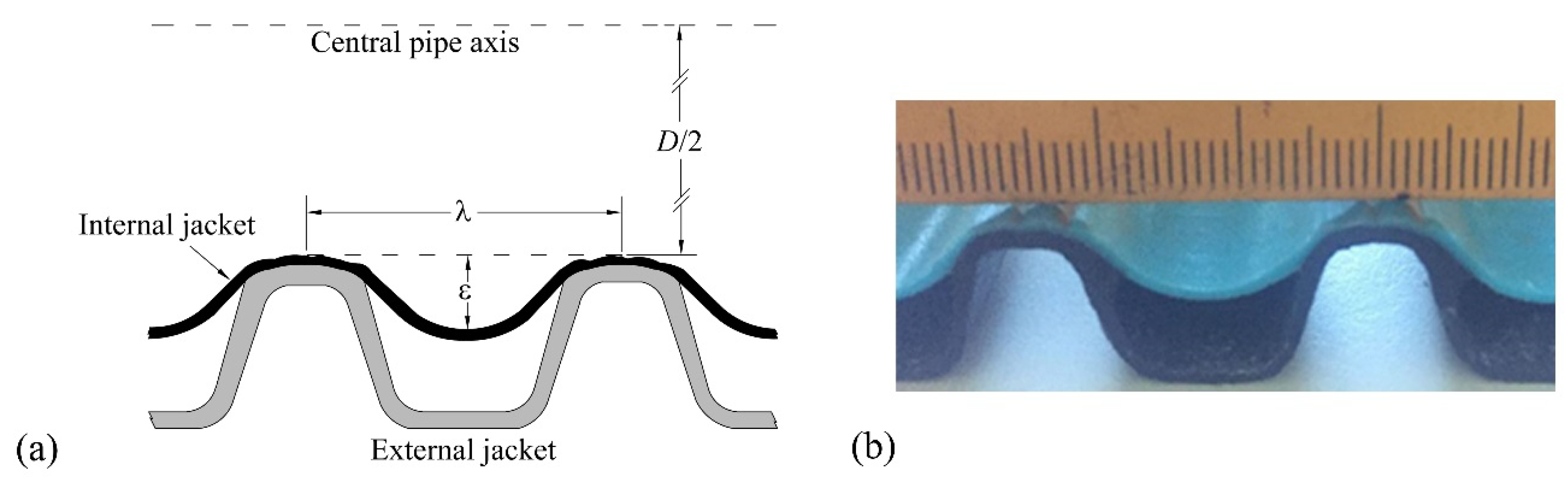
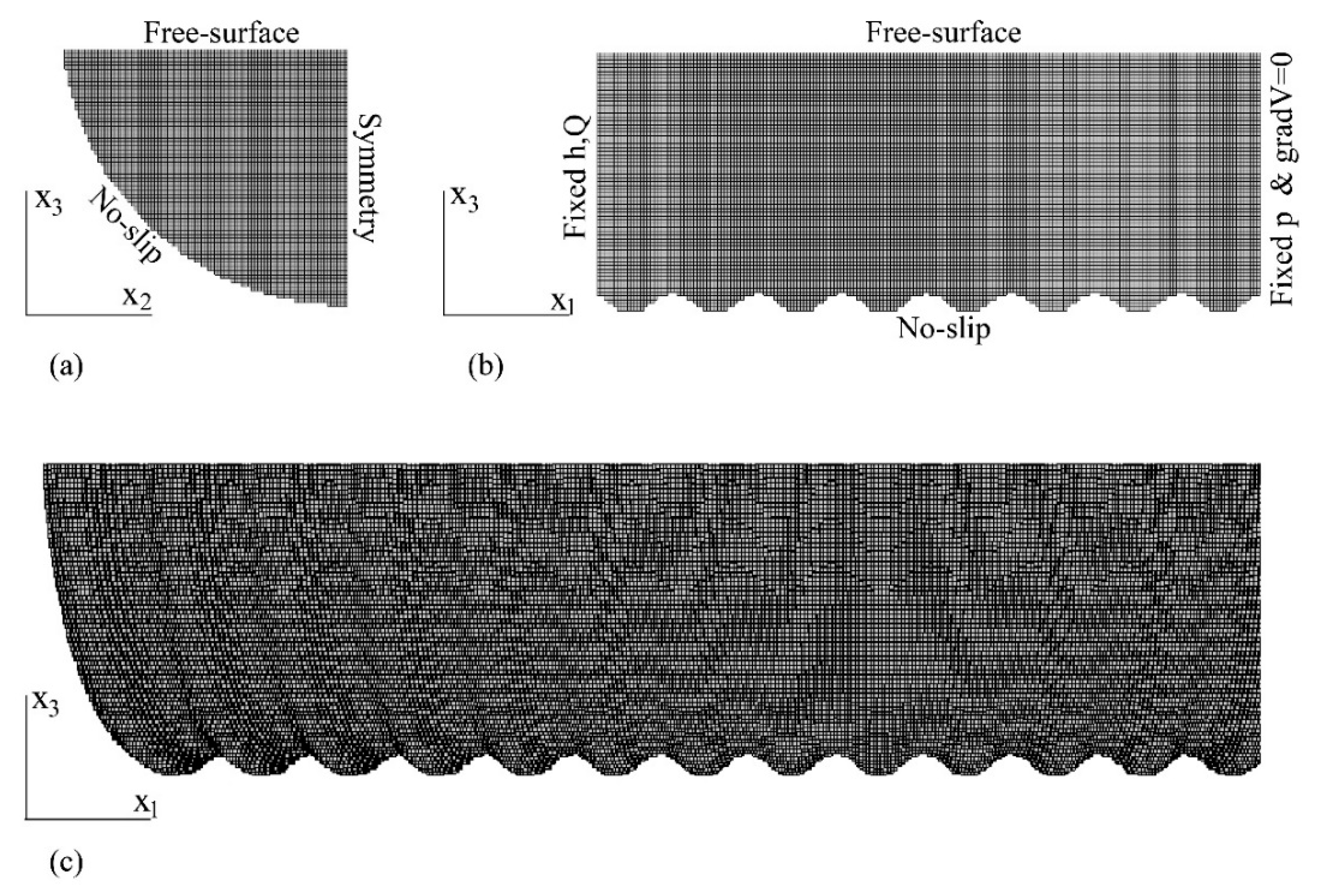
As shown in
Figure 4, a three-dimensional computational grid was generated with an internal diameter
D = 0.171 m, a length
L = 4 m, a roughness height
ε = 0.006 m, and a longitudinal spacing of the roughness elements
λ = 0.0254 m. Experimental conditions and fluids properties used in the simulations are presented in
Table 1 and
Table 2, respectively.
A number of preliminary simulations were performed before selecting the final configuration of the grids. The features of these simulations (that is, A, B, and C) are outlined in
Table 3: Δ
xi are the approximated grid spacing in
xi direction, whereas
Ntotal is the total number of grid points.
The final three-dimensional finite-volume computational domain includes about 27.5 × 10
6 grid points, with a grid spacing of approximately 1 mm. The computational domain has been rotated around the
x2 axis in order to obtain the longitudinal pipe slope of each test with the rotation matrix:
where
is the relevant angle of rotation.
For each simulation, the boundary conditions of no-slip and zero wall-normal velocity at the pipe wall were imposed. On the
x1-
x3 lateral boundary plane that represents the longitudinal section of the halfpipe, a symmetry boundary condition was set [
25]. At the
x2-
x3 inlet section, the flow depth and discharge values corresponding to the simulated test were applied. As for the
x2-
x3 outlet cross-section, the gradient of flow velocity was set to zero in the direction perpendicular to the boundary and a fixed value was imposed to pressure, while the free-surface condition was enforced at the flow free surface.
At the beginning of each simulation, the pipe was initially empty and the flow was entered through the pipe inlet. Simulations were run until a steady-state uniform flow condition was achieved.
A CPU based computational system was used to carry out the computations of the present study. The system included 3 Worker Nodes, each one equipped with 4 CPU type E5-2640 (total 96 cores/16 threads @ 2.0 GHz), 128 GB RAM, 1899 MHz, and 1 TB disk space. The simulations were conducted using 16 processors through the public domain openMPI implementation of the standard Message Passing Interface (MPI) for the parallel running. The technique of parallel computing has been adopted as domain decomposition to split the geometry and the associated fields into segments. In this study, the ‘simple geometric decomposition’ technique was used, in which the domain is broken into segments by direction. The computational time was about 240 h CPU time for each simulation.