Integrated Evaluation of Hybrid Water Supply Systems Using a PROMETHEE–GAIA Approach
Abstract
:1. Introduction
2. MCDA Methodology
- Multiple attribute utility theory essentially combines multiple objectives into a one-dimensional “multi-attribute” function, which can be a value function that is deterministic or a utility function that includes a measure of risk [21].
- Interactive techniques consist of alternating computation steps and dialogue in the decision making, where the decision maker brings a direct contribution towards the elaboration of a solution by intervening in the process and not just in the definition of the problem [20].
- Preference Measures (PM) evaluations,
- Weights, and
- Preference functions.
2.1. PROMETHEE Rankings
2.2. GAIA Plane
2.3. Sensitivity Analysis
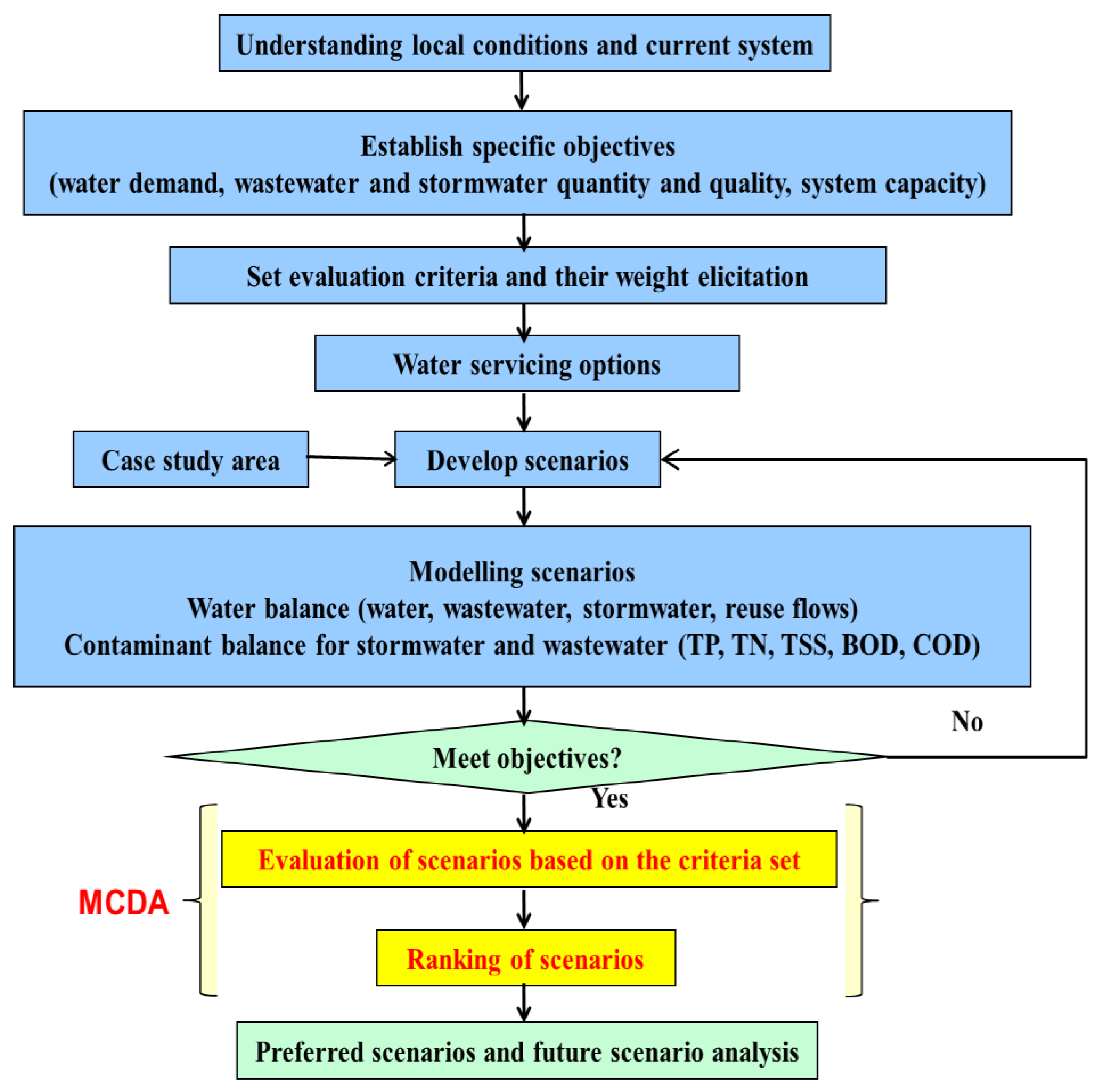
3. Application of Methodology
3.1. Case Study
- Scenario 1: Centralized only—It represents the conventional water supply system based exclusively on supplying a treated potable supply using fresh water resources and is used as a reference to compare with the selected hybrid water supply scenarios evaluated in this study.
- Scenario 2: Centralized along with recycled water via third (separate) pipe—This scenario represents the present condition in the area. In this scenario, wastewater is collected at the development level and distributed through a dual reticulation system for toilet flushing and garden irrigation after treatment. The remaining water demand is met from the potable water supply.
- Scenario 3: Centralized supply combined with treated greywater—In this scenario, greywater is collected from bathroom and laundry use and used for garden irrigation and toilet flushing. Other demands are met via potable supply.
- Scenario 4: Centralized supply combined with rainwater harvesting—In this scenario, rain water is provided for the toilet, garden irrigation, and laundry use. Potable water is supplied for bathroom and kitchen use.
- Scenario 5: Centralized supply combined with stormwater harvesting—In this scenario, stormwater is provided for toilet and garden irrigation. Potable water is supplied for bathroom, laundry, and kitchen use.
- Scenario 6: Centralized supply combined with stormwater harvesting and treated grey water—In this scenario, both stormwater and greywater are provided for garden irrigation and toilet use. However, priority is given to greywater over stormwater as greywater occurs at the unit-block scale compared to stormwater, which occurs at precinct scale. Potable water is supplied for bathroom, laundry, and kitchen use.
- Scenario 7: Centralized supply combined with rainwater harvesting and recycled water via 3rd pipe—In this scenario, rainwater is provided for laundry use, garden irrigation, and toilet use, while recycled water is also used for garden irrigation and toilet use, and potable water is supplied for bathroom and kitchen use.
3.2. Evaluation Criteria
- Reduction in potable water demand from centralized WSS,
- Reduction of wastewater generation,
- Reduction of contaminant (Total Suspended Solids (TSS), Total Phosphorous (TP), Total Nitrogen (TN), Biochemical Oxygen Demand (BOD), and Chemical Oxygen Demand (COD)) concentration in wastewater,
- Reduction in stormwater flow,
- Reduction in contaminant (TSS, TP, TN, BOD, and COD) load in stormwater,
- Increased supply reliability of fit-for-purpose water. Supply reliability is defined as the percentage of average demand met from the combination of alternative water supply storages over the modeling period.
3.3. Data Input
- Evaluation matrix: This matrix includes m number of alternatives, n number of PMs, and (m × n) number of PM evaluations. Table 1 shows the evaluation matrix formulated. This table is based on the water and contaminant balance analysis output reported in Sapkota, Arora, Malano, Moglia, Sharma and Pamminger [15].
- Weights of PMs: Weights required were evaluated by conducting a questionnaire survey among 37 water professionals which included personnel from water utilities, private water consultancies, CSIRO, universities, environmental agencies, and the Australian Water Association. [46]. Table 2 below presents the weight distribution between different subcriteria for various criteria. For internal consistency reliability of the calculated weights of different subcriteria, Cronbach’s alpha [47] was calculated and found to be within the acceptable range of 0.5–0.9 [46]. Further, a weight sensitivity analysis was conducted in MCDA, as suggested by the study.
- Preference functions of PMs: Preference functions were determined by conducting a questionnaire survey among experts, representing water professionals from Victorian water utilities to determine the preference function [46]. Usual preference function as shown in Figure 2 was used for this study. For this type of function, the decision maker has a strict preference for the alternative having the greatest value [48]. This means that even if there is a very small difference in criterion value, an alternative with a higher value is selected.
4. Results
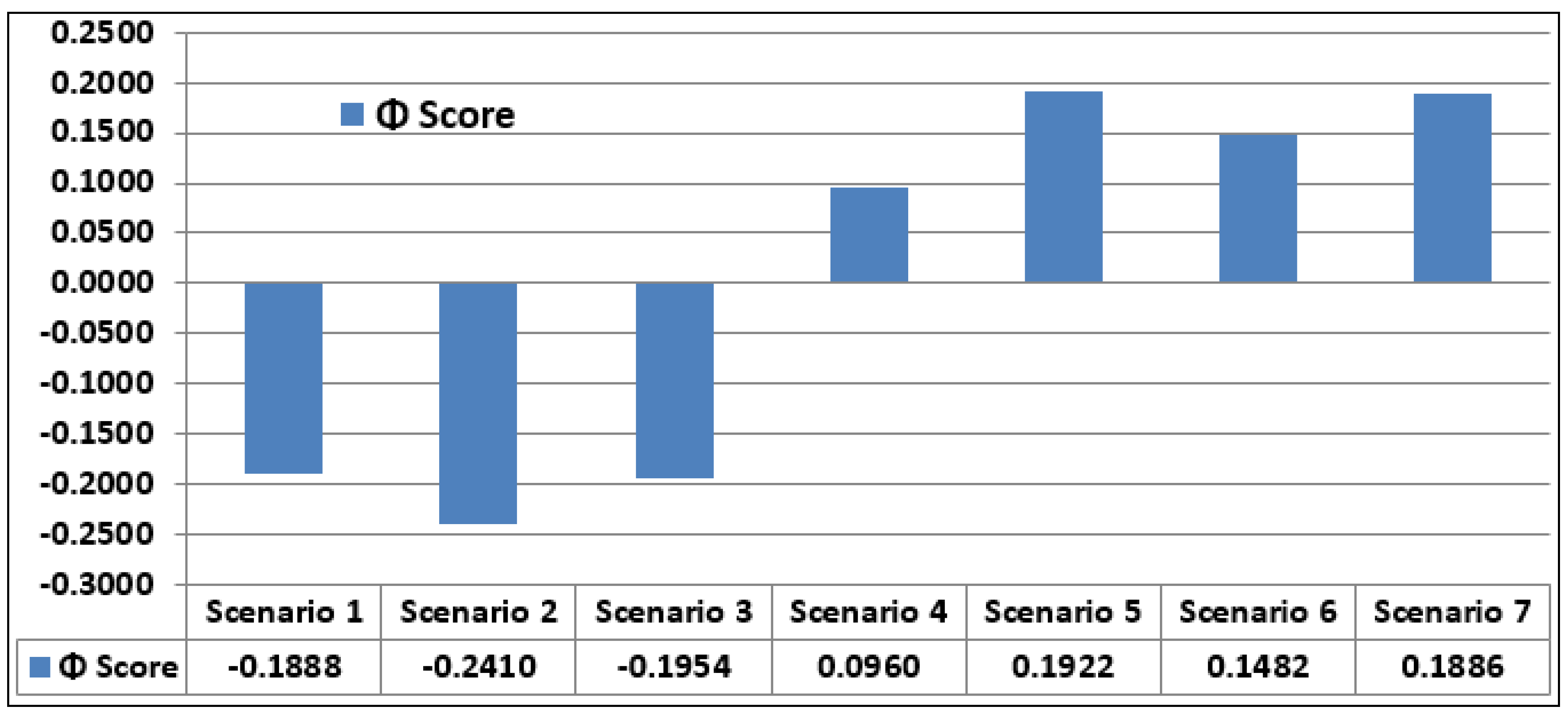
4.1. PROMETHEE Rankings
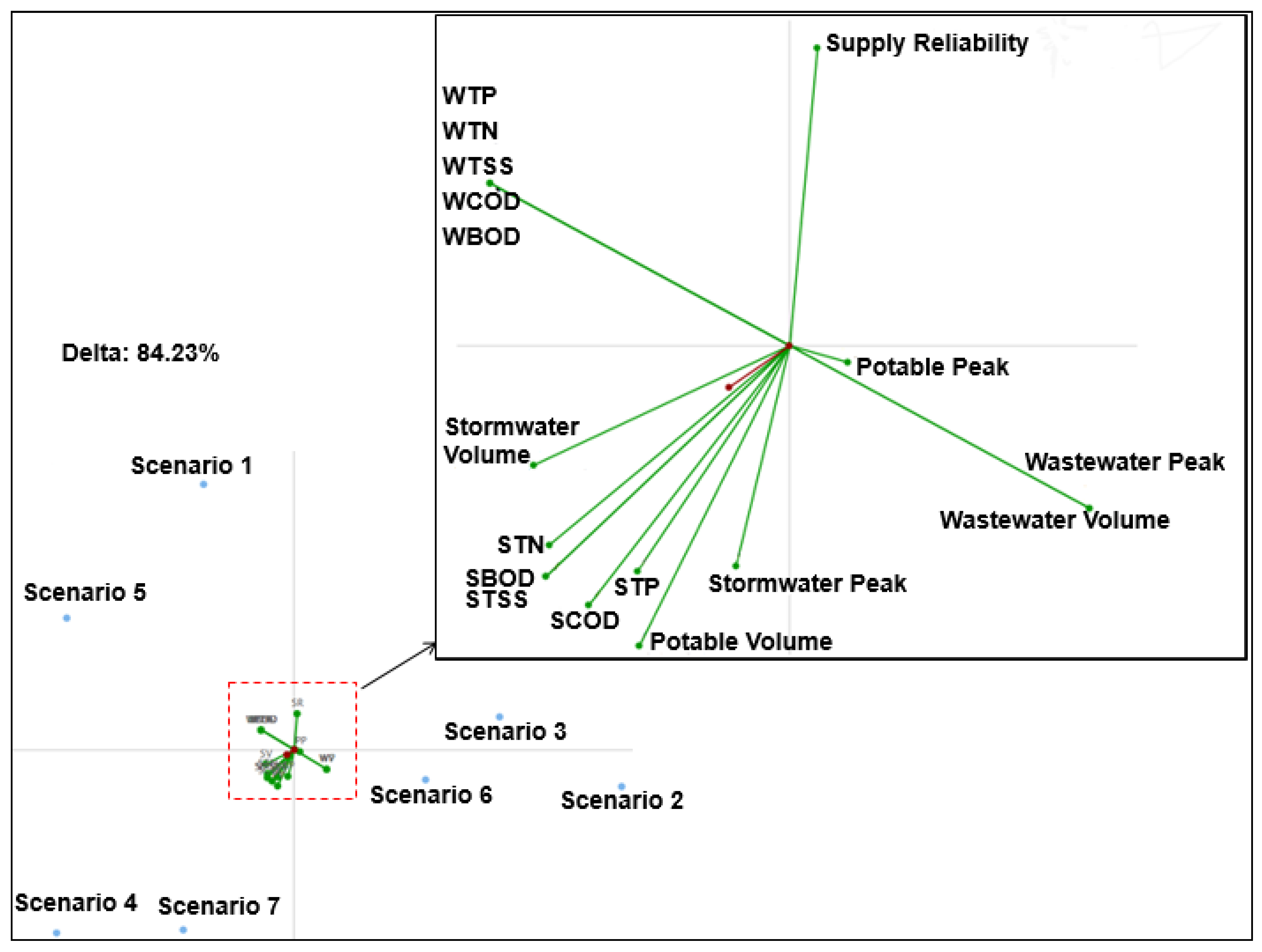
4.2. GAIA Analysis
4.3. Sensitivity Analysis
5. Discussion
6. Conclusions
- MCDA analysis shows that Scenario 5 (centralized system along with stormwater harvesting) is the most preferred scenario, with Scenario 7 (centralized system along with treated wastewater and rainwater tanks) is the second preference.
- The same analysis shows that Scenario 2 (centralized with treated waste water) is presented as the worst scenario in the study.
- GAIA analysis shows that Scenario 5 (centralized water supply system along with stormwater harvesting) is the best and Scenario 2 (centralized water supply system along with treated wastewater) is the worst
- Thus, MCDA and GAIA analyses provide similar results in terms of scenario ranking
- Potable water supply peak flow, stormwater peak flow, and wastewater contaminant concentration are found to be the most robust criteria in ranking the hybrid water supply scenarios
- Stormwater contaminant load is found to be the unstable criterion in ranking the scenarios.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Tsoukalas, I.K.; Makropoulos, C.K.; Michas, S.N. Identification of potential sewer mining locations: A monte-carlo based approach. Water Sci. Technol. 2017, 76, 3351–3357. [Google Scholar] [CrossRef] [PubMed]
- Cook, S.; Sharma, A.K.; Gurung, T.R. Evaluation of alternative water sources for commercial buildings: A case study in Brisbane, Australia. Resour. Conserv. Recycl. 2014, 89, 86–93. [Google Scholar] [CrossRef]
- Ashbolt, S.C.; Perera, B.J.C. Multicriteria analysis to select an optimal operating option for a water grid. Water Resour. Plan. Manag. 2017, 143, 05017005. [Google Scholar] [CrossRef]
- Sharma, A.K.; Pezzaniti, D.; Myers, B.; Cook, S.; Tjandraatmadja, G.; Chacko, P.; Chavoshi, S.; Kemp, D.; Leonard, R.; Koth, B. Water sensitive urban design: An investigation of current systems, implementation drivers, community perceptions and potential to supplement urban water services. Water 2016, 8, 272. [Google Scholar] [CrossRef]
- Sapkota, M.; Arora, M.; Malano, H.; George, B.; Nawarathna, B.; Sharma, A.; Moglia, M. Development of a framework to evaluate the hybrid water supply systems. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013; pp. 2387–2393. [Google Scholar]
- Sapkota, M.; Arora, M.; Malano, H.; Moglia, M.; Sharma, A.; George, B.; Pamminger, F. An overview of hybrid water supply systems in the context of urban water management: Challenges and opportunities. Water 2015, 7, 153–174. [Google Scholar] [CrossRef]
- Marleni, N.; Gray, S.; Sharma, A.; Burn, S.; Muttil, N. Impact of water management practice scenarios on wastewater flow and contaminant concentration. J. Environ. Manag. 2015, 151, 461–471. [Google Scholar] [CrossRef] [PubMed]
- Marlow, D.R.; Moglia, M.; Cook, S.; Beale, D.J. Towards sustainable urban water management: A critical reassessment. Water Res. 2013, 47, 7150–7161. [Google Scholar] [CrossRef] [PubMed]
- Sapkota, M.; Arora, M.; Malano, H.; Moglia, M.; Sharma, A.; George, B.; Pamminger, F. An integrated framework for assessment of hybrid water supply systems. Water 2016, 8, 4. [Google Scholar] [CrossRef]
- Sharma, A.; Burn, S.; Gardner, T.; Gregory, A. Role of decentralised systems in the transition of urban water systems. Water Sci. Technol. 2010, 10, 577–583. [Google Scholar] [CrossRef]
- Weber, B.; Cornel, P.; Wagner, M. Semi-centralised supply and treatment systems for (fast growing) urban areas. Water Sci. Technol. 2007, 55, 349–356. [Google Scholar] [CrossRef] [PubMed]
- Poustie, M.S.; Deletic, A.; Brown, R.R.; Wong, T.; de Haana, F.J.; Skinner, R. Sustainable urban water futures in developing countries: The centralised, decentralised or hybrid dilemma. Urban Water J. 2015, 12, 543–558. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; Zischg, J.; Sitzmann, M.; Bach, P.M. Impact of hybrid water supply on the centralised water system. Water 2017, 9, 855. [Google Scholar] [CrossRef]
- Sharma, A.; Grant, A.L.; Grant, T.; Pamminger, F.; Opray, L. Environmental and economic assessment of urban water services for a greenfield development. Environ. Eng. Sci. 2009, 26, 921–934. [Google Scholar] [CrossRef]
- Sapkota, M.; Arora, M.; Malano, H.; Moglia, M.; Sharma, A.; Pamminger, F. Understanding the impact of decentralised water supply scenarios on wastewater and stormwater flows. Resour. Conserv. Recycl. 2018, 130, 82–94. [Google Scholar] [CrossRef]
- Abrishamchi, A.; Ebrahimian, A.; Tajrishi, M.; Mariño, M.A. Case study: Application of multicriteria decision making to urban water supply. J. Water Resour. Plan. Manag. 2005, 131, 326–335. [Google Scholar] [CrossRef]
- Al-Shemmeri, T.; Al-Kloub, B.; Pearman, A. Model choice in multicriteria decision aid. Eur. J. Oper. Res. 1997, 97, 550–560. [Google Scholar] [CrossRef]
- Hajkowicz, S.; Collins, K. A review of multiple criteria analysis for water resource planning and management. Water Resour. Manag. 2007, 21, 1553–1566. [Google Scholar] [CrossRef]
- Moglia, M.; Sharma, A.K.; Maheepala, S. Multi-criteria decision assessments using subjective logic: Methodology and the case of urban water strategies. J. Hydrol. 2012, 452–453, 180–189. [Google Scholar] [CrossRef]
- Vincke, P. Multicriteria Decision-Aid; Wiley: West Sussex, UK, 1992. [Google Scholar]
- Ganoulis, J. Evaluating alternative strategies for wastewater recycling and reuse in the mediterranean area. Water Sci. Technol. Water Supply 2003, 3, 11–19. [Google Scholar]
- Braune, I.; Pinkwart, A.; Reeg, M. Application of multi-criteria analysis for the evaluation of sustainable energy systems—A review of recent literature. In Proceedings of the 5th Dubrovnic Conference on Sustainable Development of Energy, Water and Environment Systems, Dubrovnik, Croatia, 30 September–3 October 2009. [Google Scholar]
- Al-Kloub, B.; Al-Shemmeri, T.; Pearman, A. Theory and methodology—The role of weights in multi-criteria decision aid, and the ranking of water projects in jordan. Eur. J. Oper. Res. 1997, 99, 278–288. [Google Scholar] [CrossRef]
- Butler, D.; Jowitt, P.; Ashley, R.; Blackwood, D.; Davies, J.; Oltean-Dumbrava, C.; McIlkenny, G.; Foxon, T.; Gilmour, D.; Smith, H.; et al. Sward: Decision support processes for the UK water industry. Manag. Environ. Qual. An Int. J. 2003, 14, 444–459. [Google Scholar] [CrossRef]
- Van Moeffaert, D. Multi Criteria Decision Aid in Sustainable Urban Water Management. Master’s Thesis, Deptartment of Industrial Ecology, Royal Institute of Technology (KTH), Stockholm, Sweden, 2003. [Google Scholar]
- Brans, J.P.; Vincke, P.; Mareschal, B. How to select and how to rank projects: The promethee method. Eu. J. Oper. Res. 1986, 24, 228–238. [Google Scholar] [CrossRef]
- Brans, J.-P.; Mareschal, B. The PROMCALC & GAIA decision support system for multicriteria decision aid. Decis. Support Syst. 1994, 12, 297–310. [Google Scholar]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. Promethee: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Brans, J.P.; Mareschal, B. Promethee methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Eds.; Springer Science + Business Media, Inc.: New York, NY, USA, 2005; pp. 163–195. [Google Scholar]
- De Smet, Y.; Lidouh, K. An introduction to multicriteria decision aid: The PROMETHEE and GAIA methods. In Business Intelligence; Aufaure, M.-A., Zimányi, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 150–176. [Google Scholar]
- Hayez, Q.; De Smet, Y.; Bonney, J. D-Sight: A New Decision Support System to Address Multi-Criteria Problems; Technical Report number TR/SMG/2011-004; Universite Libre de Bruxelles: Brussels, Belgium, 2011. [Google Scholar]
- Mustajoki, J.; Marttunen, M. Comparison of Multi-Criteria Decision Analytical Software; Report on IMPERA Project; Finish Environmental Institute: Helsinki, Finland, 2013. [Google Scholar]
- Mutikanga, H.E.; Sharma, S.K.; Vairavamoorthy, K. Multi-criteria decision analysis: A strategic planning tool for water loss management. Water Resour. Manag. 2011, 25, 3947–3969. [Google Scholar] [CrossRef]
- Zardari, N.H.; Yusop, Z.; Shirazi, S.M.; Roslan, N.A.B. Prioritization of farmlands in a multicriteria irrigation water allocation: PROMETHEE and GAIA applications. Trans. ASABE 2015, 58, 73–82. [Google Scholar]
- Peng, Y.; Zhang, Y.; Kou, G.; Shi, Y. A multicriteria decision making approach for estimating the number of clusters in a data set. PLoS ONE 2012, 7, e41713. [Google Scholar] [CrossRef] [PubMed]
- Hayez, Q.; De Smet, Y.; Bonney, J. D-sight: A new decision making software to address multi-criteria problems. Int. J. Decis. Support Syst. Technol. IJDSST 2012, 4, 1–23. [Google Scholar] [CrossRef]
- Hayez, Q.; Mareschal, B.; De Smet, Y. New GAIA visualization methods. In Proceedings of the IEEE 13th International Conference on Information Visualisation, Barcelona, Spain, 15–17 July 2009; pp. 247–251. [Google Scholar]
- Nemery, P.; Mareschal, B.; Ishizaka, A. Unification of problem formulation with promethee: Keynote paper. In Proceedings of the 52th Operational Research Society Conference, London, UK, 7–9 September 2010; Volume 1. [Google Scholar]
- Kodikara, P.N. Multi-Objective Optimal Operation of Urban Water Supply Systems. Ph.D. Thesis, Victoria University, Victoria, Australia, 2008. [Google Scholar]
- Mareschal, B.; De Smet, Y. Visual promethee: Developments of the PROMETHEE & GAIA multicriteria decision aid methods. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management (IEEM 2009), Hong Kong, China, 8–11 December 2009; pp. 1646–1649. [Google Scholar]
- Mousseau, V. Eliciting information concerning the relative importance of criteria. In Advances in Multicriteria Analysis; Pardalos, P.M., Siskos, Y., Zopounidis, C., Eds.; Springer: New York, NY, USA, 1995; pp. 17–43. [Google Scholar]
- Stewart, T.J. Dealing with uncertainties in mcda. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: New York, NY, USA, 2005; pp. 445–466. [Google Scholar]
- Inamdar, P.M. Selection and Evaluation of Potential Stormwater Harvesting Sites in Urban Areas. Ph.D. Thesis, Victoria University, Victoria, Australia, 2014. [Google Scholar]
- Mitchell, V.G.; Diaper, C. Simulating the urban water and contaminant cycle. Environ. Model. Softw. 2006, 21, 129–134. [Google Scholar] [CrossRef]
- Mitchell, V.G.; Diaper, C.; Gray, S.R.; Rahilly, M.; Technolgy, C.M.A.I. Uvq: Modelling the movement of water and contaminants through the total urban water cycle. In Proceedings of the 28th International Hydrology and Water Resources Symposium, Wollongong, Australia, 10–14 November 2003; p. 8. [Google Scholar]
- Sapkota, M.; Arora, M.; Malano, H. Multi-criteria decision analysis for hybrid water supply systems. In Proceedings of the 22nd International Congress on Modelling and Simulation (MODSIM), Hobart, Australia, 3–8 December 2017; pp. 1794–1800. [Google Scholar]
- Gliem, J.A.; Gliem, R.R. Calculating, interpreting, and reporting cronbach’s alpha reliability coefficient for likert-type scales. In Proceedings of the Midwest Research-to-Practice Conference in Adult, Continuing, and Community Education, Columbus, OH, USA, 8–10 October 2003; pp. 82–88. [Google Scholar]
- Brans, J.P.; Vincke, P. A preference ranking organisation method: (The promethee method for multiple criteria decision-making). Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Ranjan, R.; Chatterjee, P.; Chakraborty, S. Performance evaluation of Indian states in tourism using an integrated PROMETHEE-GAIA approach. Opsearch 2015, 53, 63–84. [Google Scholar] [CrossRef]
- Fernández, N.G. The Management of Missing Values in PROMETHEE Methods. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2013. [Google Scholar]
- Pietrucha-Urbanik, K. Assessing the costs of losses incurred as a result of failure. In Dependability Engineering and Complex Systems; Zamojski, W., Mazurkiewicz, J., Sugier, J., Walkowiak, T., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2016; Volume 470, pp. 355–362. [Google Scholar]
- Pietrucha-Urbanik, K.; Żelazko, A. Approaches to assess water distribution failure. Period. Polytech. Civ. Eng. 2017, 61, 632. [Google Scholar] [CrossRef]
- Tchorzewska-Cieslak, B. Risk management in water safety plans. Ochr. Srod. 2009, 31, 57–60. [Google Scholar]

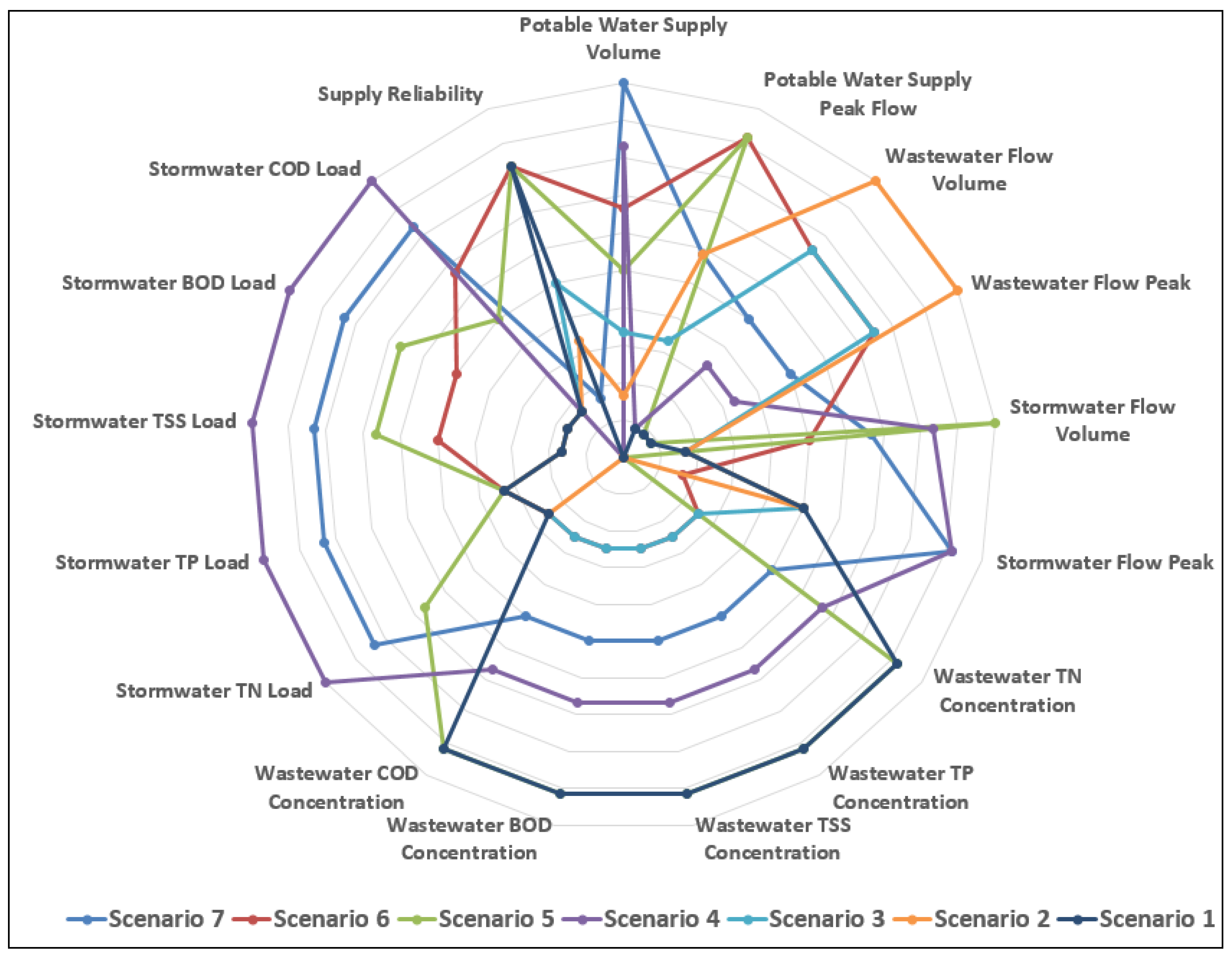
| Criteria | Sub Criteria | Sce 1 | Sce 2 | Sce 3 | Sce 4 | Sce 5 | Sce 6 | Sce 7 |
|---|---|---|---|---|---|---|---|---|
| Potable water supply | Volume(ML/year) | 1036 | 860 | 859 | 787 | 856 | 856 | 761 |
| Peak(ML/day) | 6.11 | 5.05 | 5.18 | 6.11 | 4.94 | 4.94 | 5.05 | |
| Sewage flow | Volume(ML/year) | 678 | 511 | 526 | 674 | 678 | 526 | 630 |
| Peak(ML/day) | 31.7 | 31.5 | 31.5 | 31.7 | 31.7 | 31.5 | 31.7 | |
| Stormwater flow | Volume(ML/year) | 2490 | 2490 | 2490 | 2257 | 2069 | 2477 | 2277 |
| Peak(ML/day) | 1808 | 1808 | 1808 | 1808 | 1860 | 1810 | 1808 | |
| Sewage contaminants | TN (mg/L) | 59.1 | 78.1 | 74.3 | 59.6 | 59.1 | 74.3 | 62.7 |
| TP(mg/L) | 15.5 | 20.6 | 19.5 | 15.6 | 15.5 | 19.5 | 16.6 | |
| TSS(mg/L) | 259.3 | 343.7 | 338.6 | 261.7 | 259.3 | 338.6 | 279.2 | |
| BOD(mg/L) | 207.5 | 275.1 | 274.2 | 209.4 | 207.5 | 274.2 | 223.3 | |
| COD(mg/L) | 459.2 | 608.7 | 595.1 | 465.4 | 459.2 | 595.1 | 496.3 | |
| Stormwater contaminants | TN(Kg/year) | 4856 | 4856 | 4856 | 4630 | 4846 | 4856 | 4693 |
| TP(Kg/year) | 375 | 375 | 375 | 365 | 375 | 375 | 367 | |
| TSS(Kg/year) | 101,349 | 101,349 | 101,349 | 99,876 | 101,250 | 101,347 | 100,568 | |
| BOD(Kg/year) | 14,951 | 14,951 | 14,951 | 14,144 | 14,936 | 14,950 | 14,325 | |
| COD(Kg/year) | 69,995 | 69,995 | 69,995 | 65,553 | 69,926 | 69,993 | 66,548 | |
| Supply Reliability | % | 99.9 | 96 | 98 | 91 | 99.9 | 99.9 | 95 |
| Criteria | Subcriteria | Weight |
|---|---|---|
| Potable water supply | Volume | 0.47 |
| Peak | 0.53 | |
| Sewage flow | Volume | 0.48 |
| Peak | 0.52 | |
| Stormwater flow | Volume | 0.52 |
| Peak | 0.48 | |
| Sewage contaminants | TN | 0.21 |
| TP | 0.21 | |
| TSS | 0.20 | |
| BOD | 0.19 | |
| COD | 0.19 | |
| Stormwater contaminants | TN | 0.21 |
| TP | 0.20 | |
| TSS | 0.19 | |
| BOD | 0.20 | |
| COD | 0.20 |
| Criteria | Best Alternative |
|---|---|
| Wastewater contaminants | Scenario 5 |
| Potable water peak | Scenario 6 |
| Wastewater volume | Scenario 6 |
| Wastewater peak | Scenario 6 |
| Supply reliability | Scenario 1 |
| Potable water volume | Scenario 7 |
| Stormwater peak | Scenario 7 |
| Stormwater volume | Scenario 4 |
| Preference Measures | Current Weight (%) | Minimum Weight (%) | Maximum Weight (%) | Range Difference (%) |
|---|---|---|---|---|
| Potable Water Supply Volume | 9.09 | 0 | 9.42 | 9.42 |
| Potable Water Supply Peak Flow | 7.95 | 7.44 | 100 | 92.56 |
| Wastewater Flow Volume | 8.82 | 0 | 9.23 | 9.23 |
| Wastewater Flow Peak | 8.02 | 0 | 8.43 | 8.43 |
| Stormwater Flow Volume | 8.18 | 0 | 8.36 | 8.36 |
| Stormwater Flow Peak | 7.41 | 6.89 | 100 | 93.11 |
| Wastewater TN Concentration | 3.31 | 2.87 | 100 | 97.13 |
| Wastewater TP Concentration | 3.18 | 2.75 | 100 | 97.25 |
| Wastewater TSS Concentration | 2.99 | 2.55 | 100 | 97.45 |
| Wastewater BOD Concentration | 3.24 | 2.8 | 100 | 97.2 |
| Wastewater COD Concentration | 3.17 | 2.74 | 100 | 97.26 |
| Stormwater TN Load | 3.46 | 0 | 4.53 | 4.53 |
| Stormwater TP Load | 3.47 | 0 | 3.83 | 3.83 |
| Stormwater TSS Load | 3.35 | 0 | 4.42 | 4.42 |
| Stormwater BOD Load | 3.22 | 0 | 4.3 | 4.3 |
| Stormwater COD Load | 3.18 | 0 | 3.72 | 3.72 |
| Supply Reliability | 17.95 | 17.72 | 100 | 82.28 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapkota, M.; Arora, M.; Malano, H.; Sharma, A.; Moglia, M. Integrated Evaluation of Hybrid Water Supply Systems Using a PROMETHEE–GAIA Approach. Water 2018, 10, 610. https://doi.org/10.3390/w10050610
Sapkota M, Arora M, Malano H, Sharma A, Moglia M. Integrated Evaluation of Hybrid Water Supply Systems Using a PROMETHEE–GAIA Approach. Water. 2018; 10(5):610. https://doi.org/10.3390/w10050610
Chicago/Turabian StyleSapkota, Mukta, Meenakshi Arora, Hector Malano, Ashok Sharma, and Magnus Moglia. 2018. "Integrated Evaluation of Hybrid Water Supply Systems Using a PROMETHEE–GAIA Approach" Water 10, no. 5: 610. https://doi.org/10.3390/w10050610
APA StyleSapkota, M., Arora, M., Malano, H., Sharma, A., & Moglia, M. (2018). Integrated Evaluation of Hybrid Water Supply Systems Using a PROMETHEE–GAIA Approach. Water, 10(5), 610. https://doi.org/10.3390/w10050610








