Simulation of Soil Wetting Pattern of Vertical Moistube-Irrigation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specific Discharge Calculation
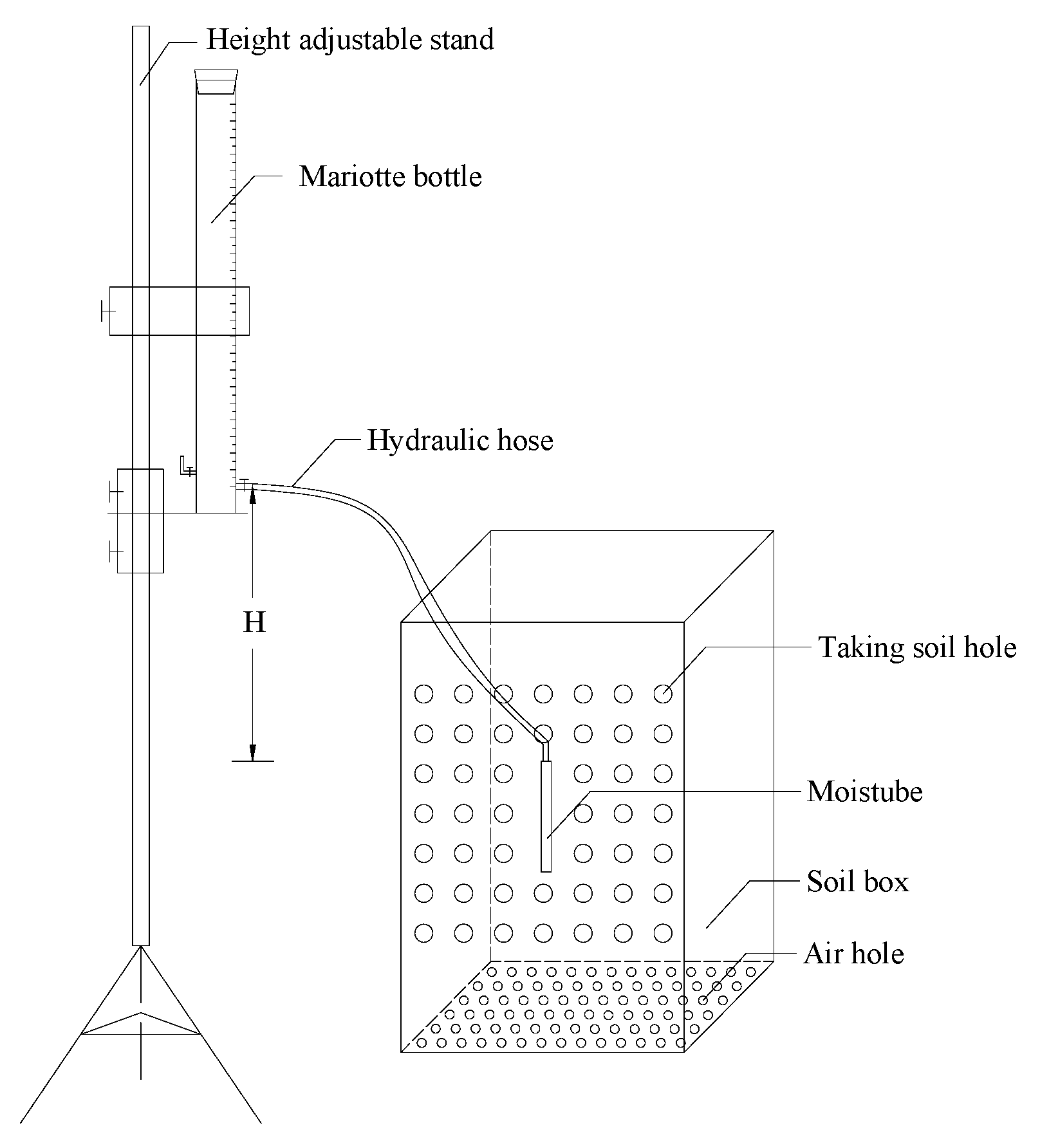
2.2. Laboratory Experiments
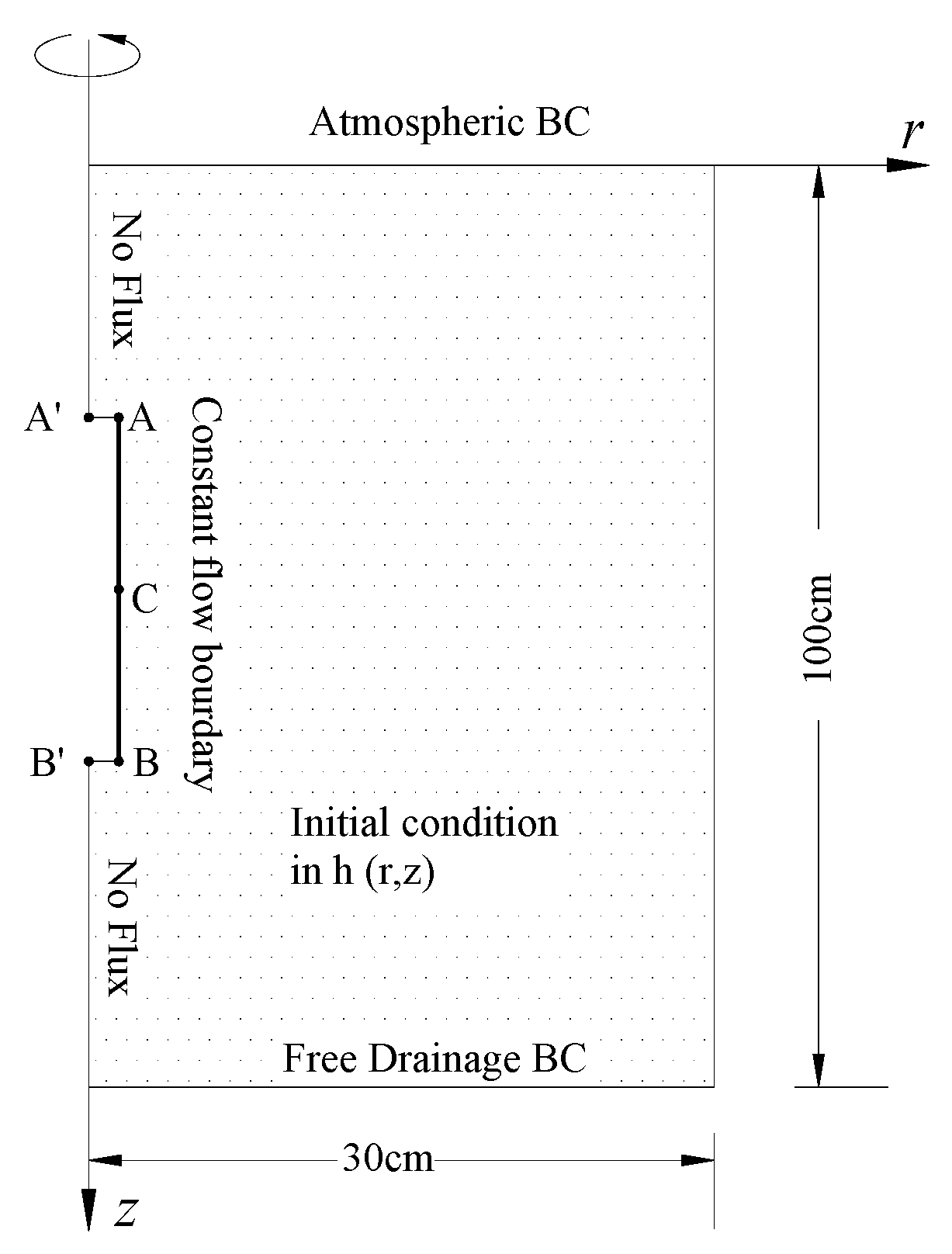
2.3. Numerical Model
2.4. Statistical Analysis
3. Results and Discussion
3.1. Comprehensive Permeability Coefficient
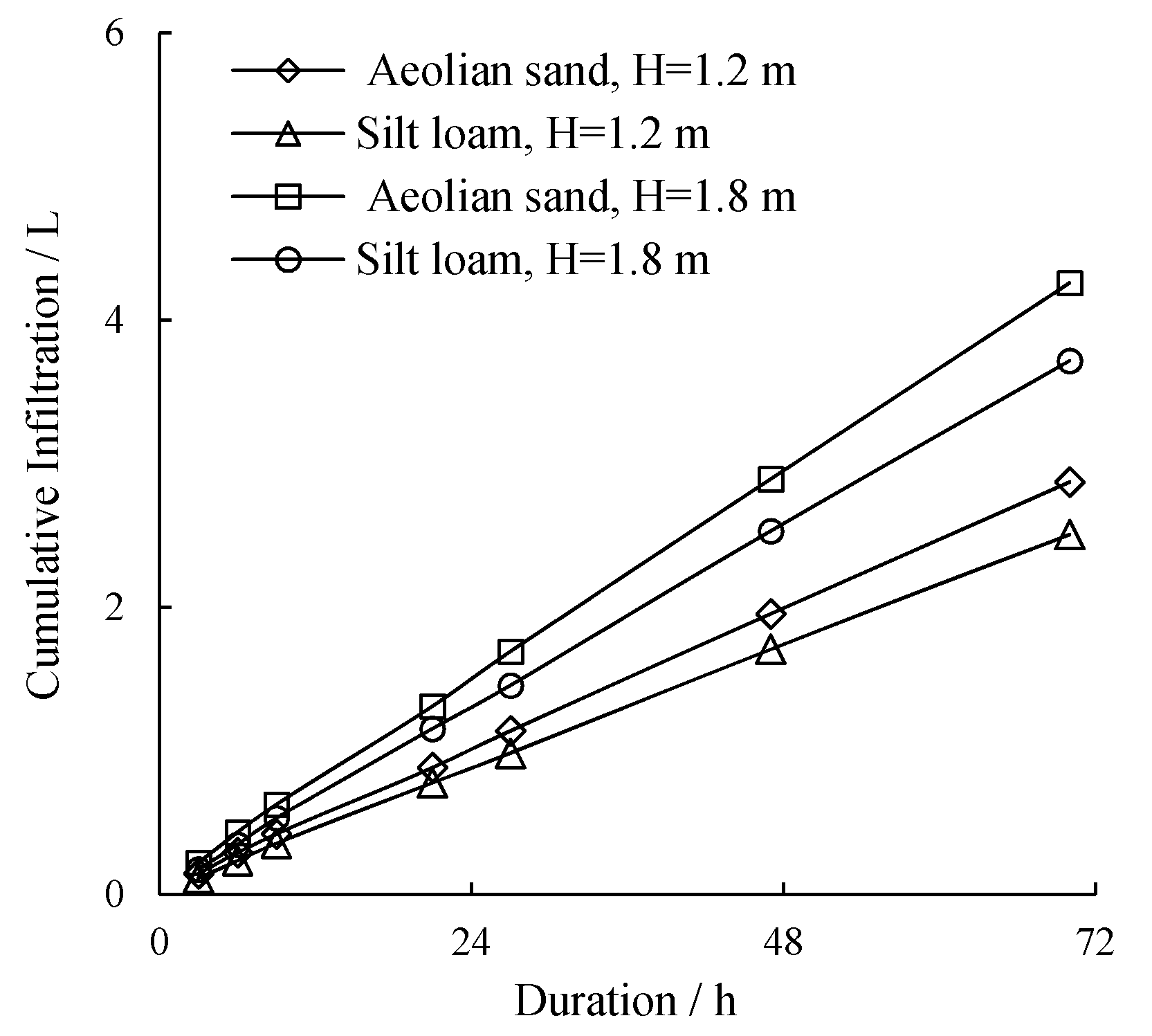
3.2. Specific Discharge Determination
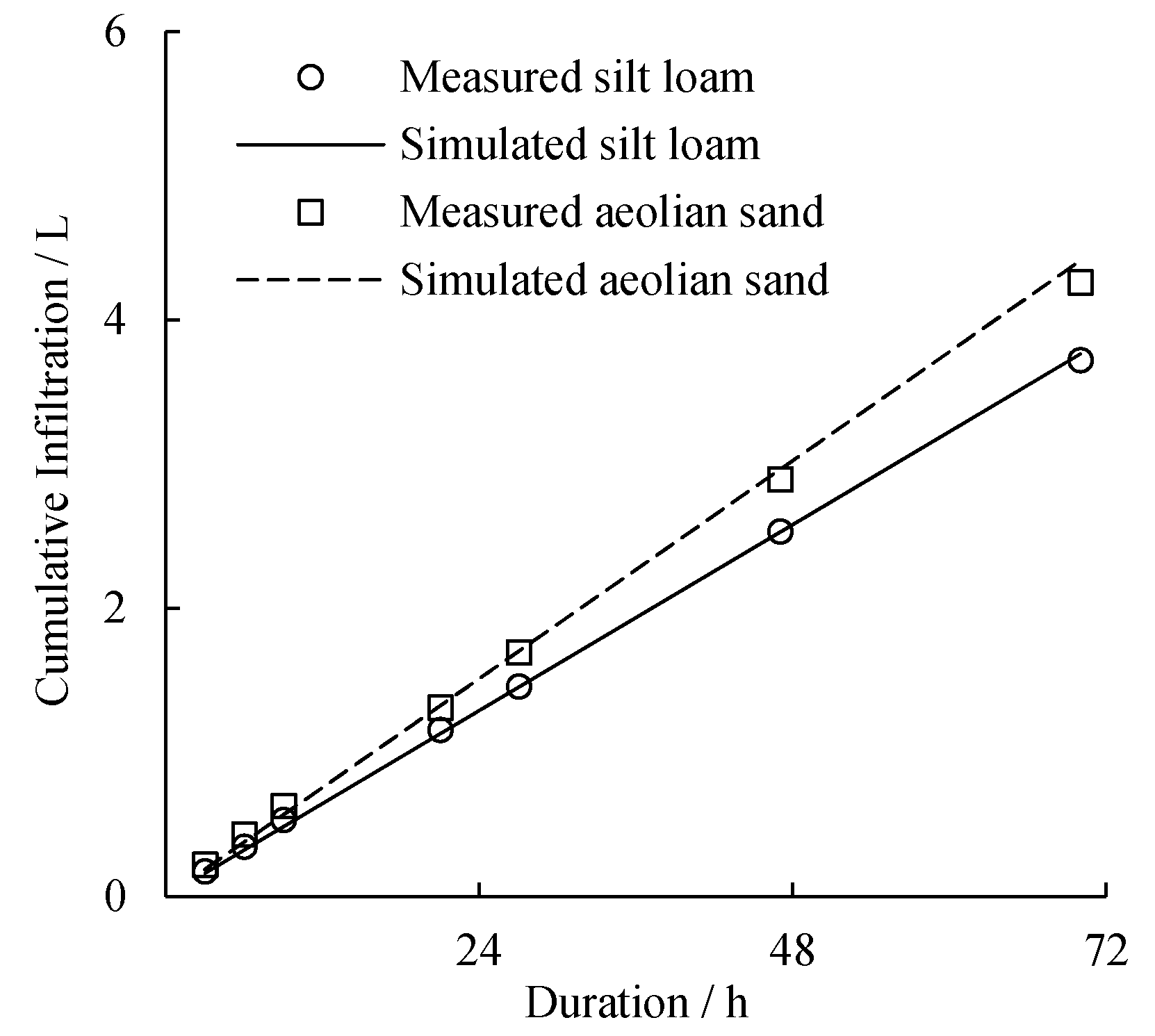
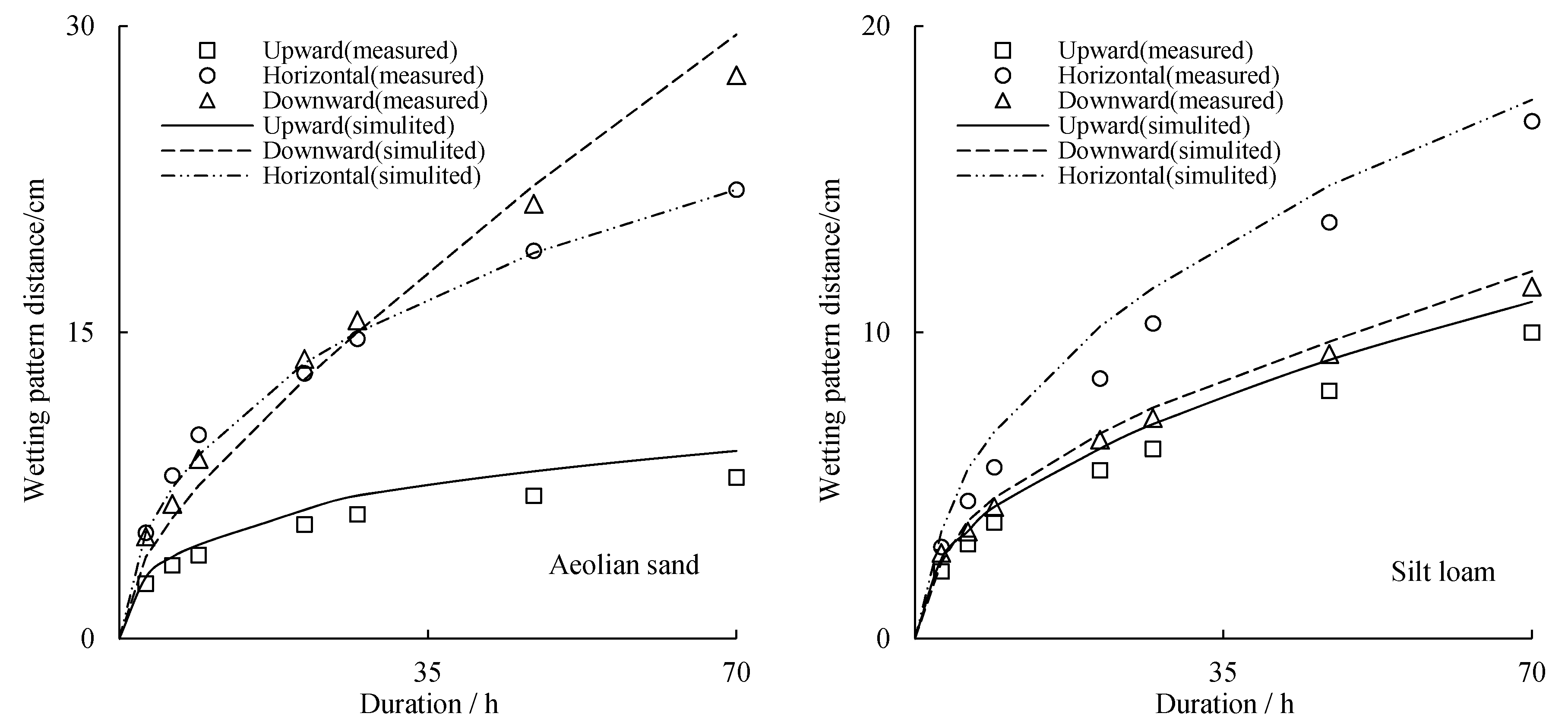
3.3. Simulation Verification
3.4. Different Factors Affecting Wetting Patterns of Moistube-Irrigation
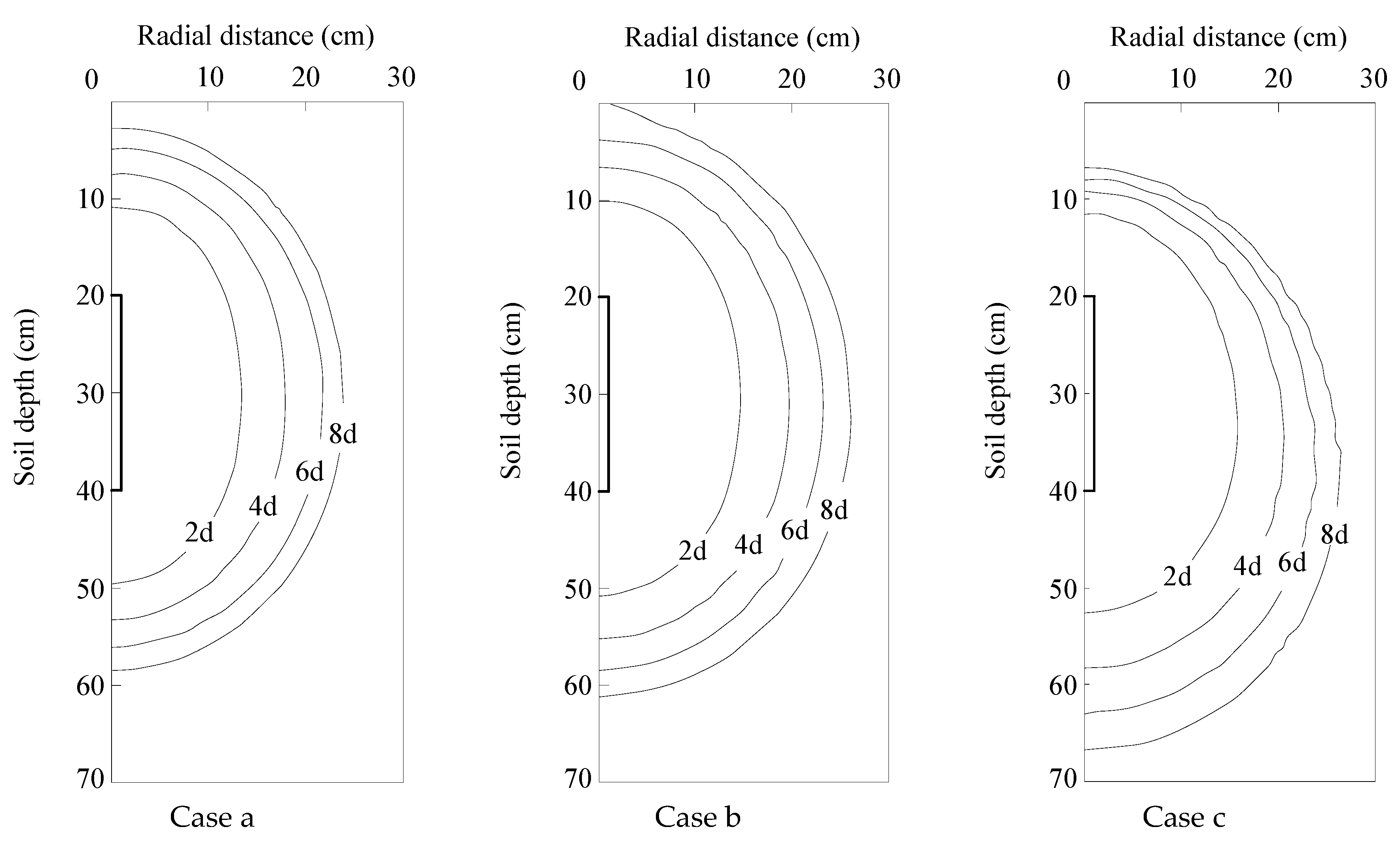
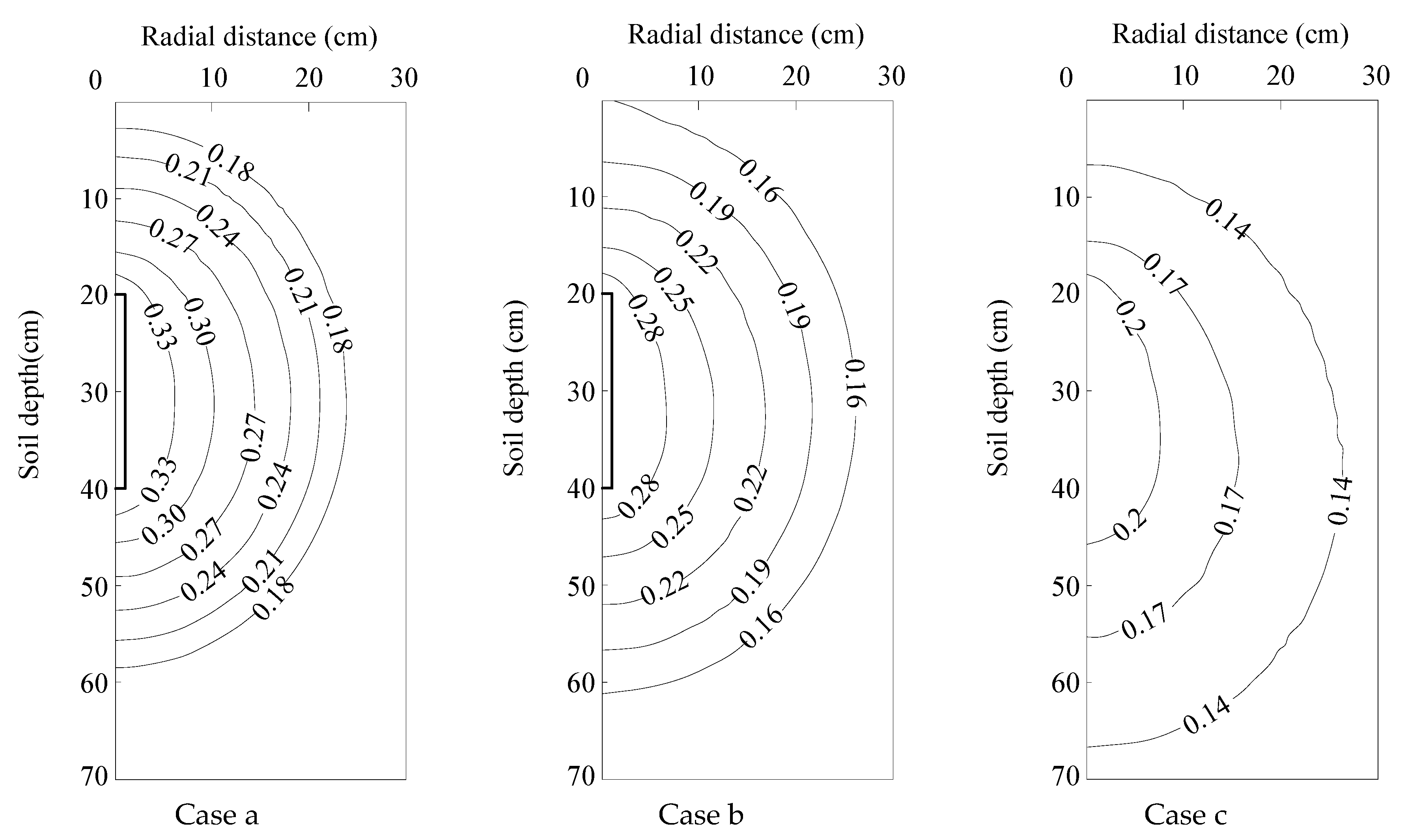
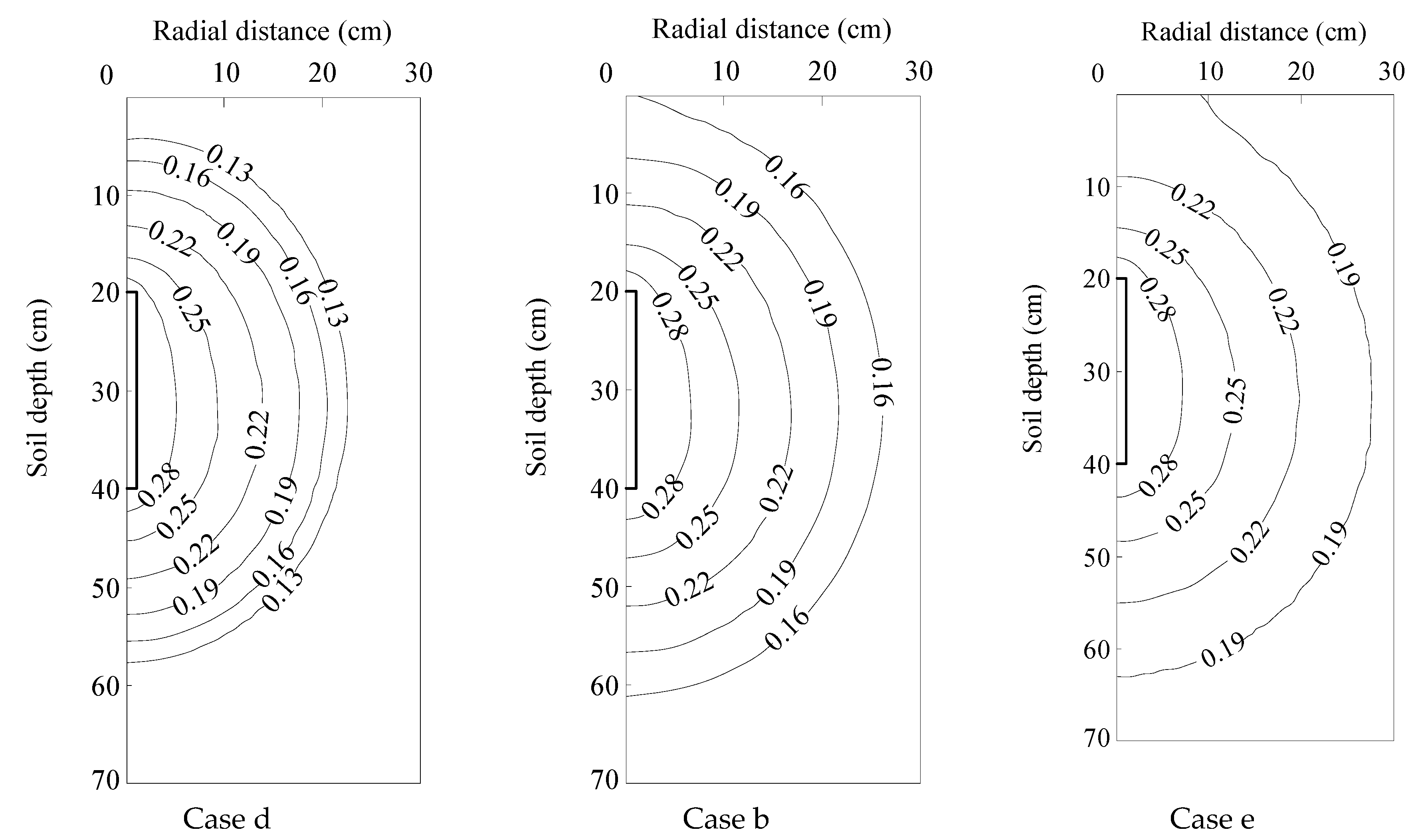
3.4.1. Influence of Soil Texture
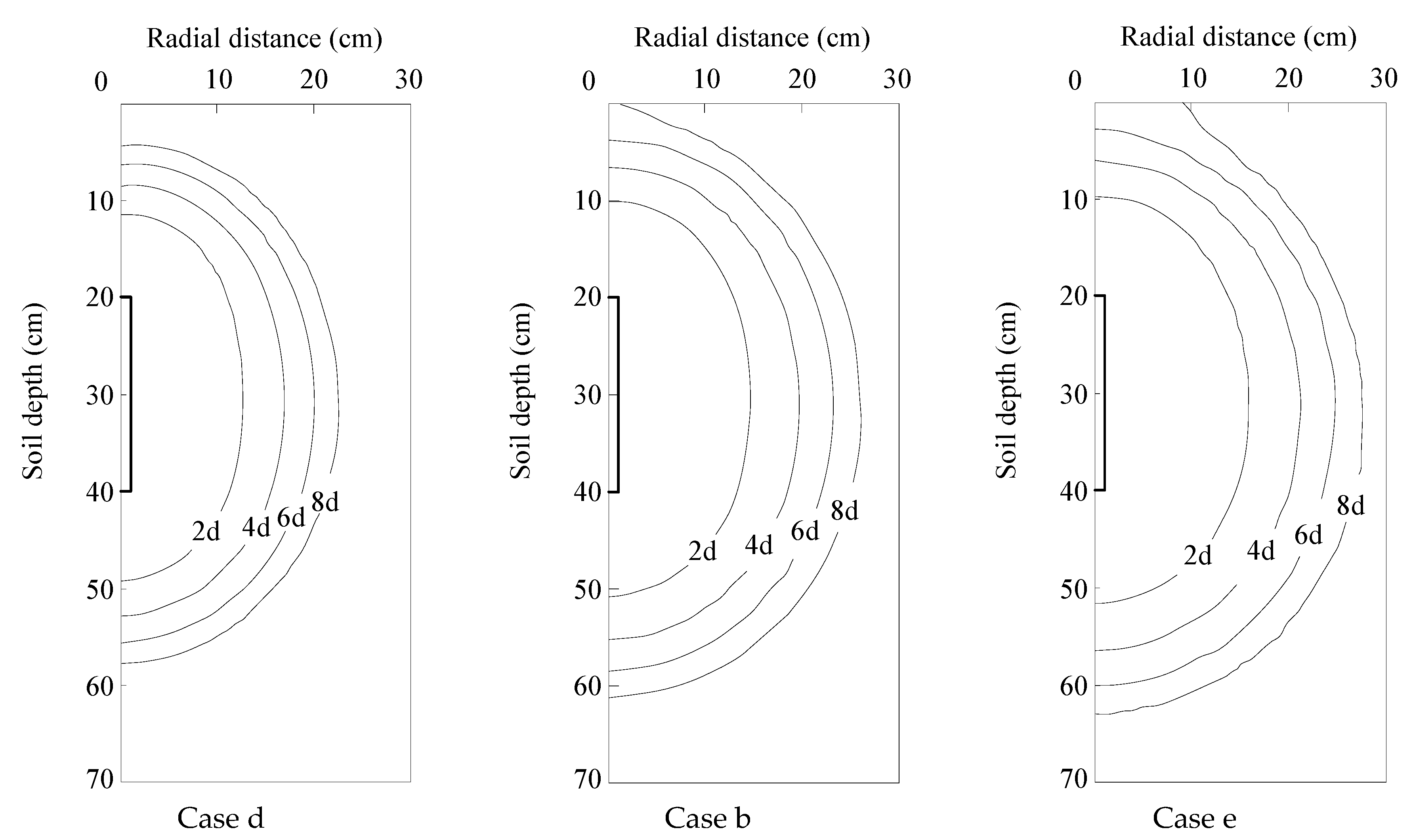
3.4.2. Influence of Soil Initial Water Content
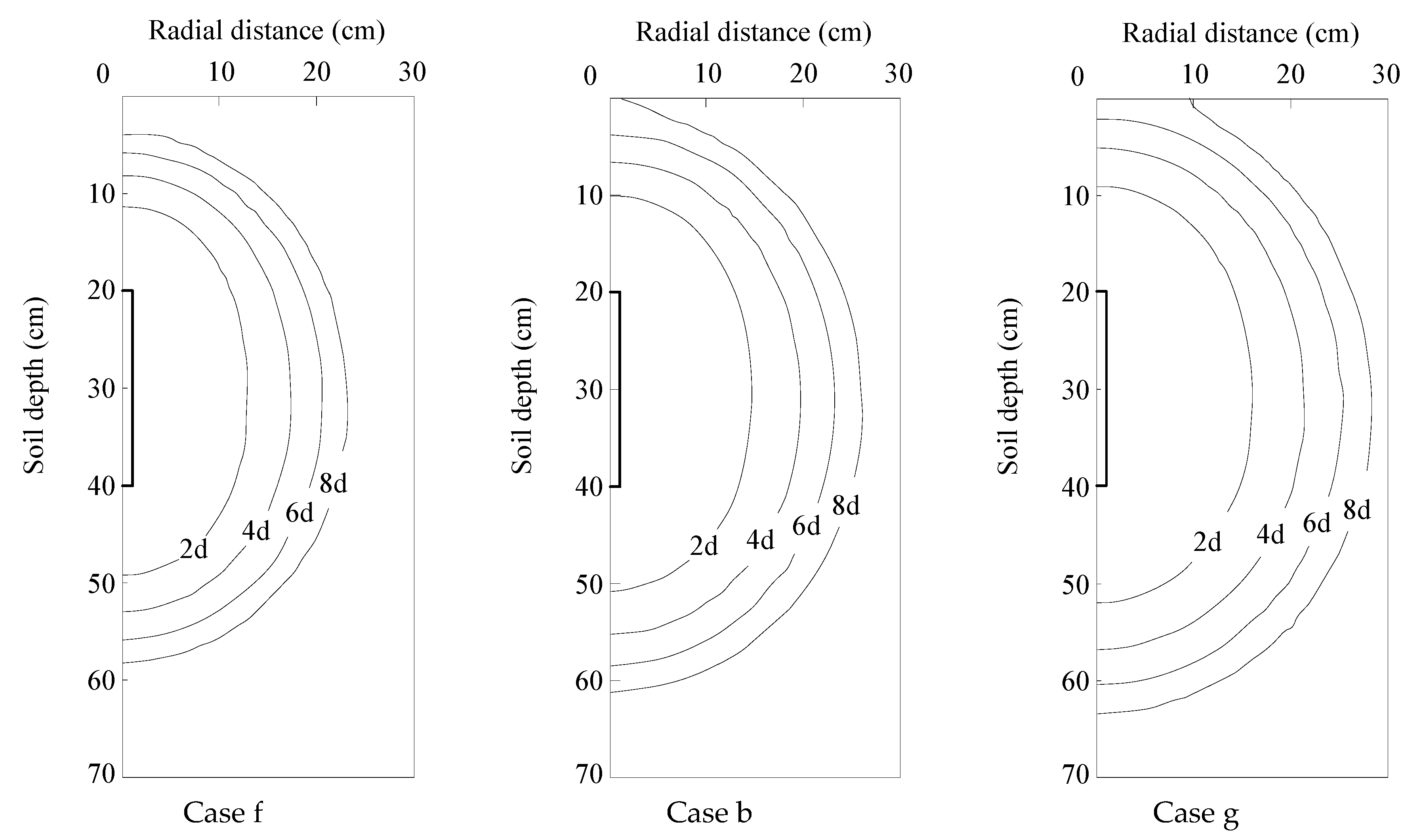
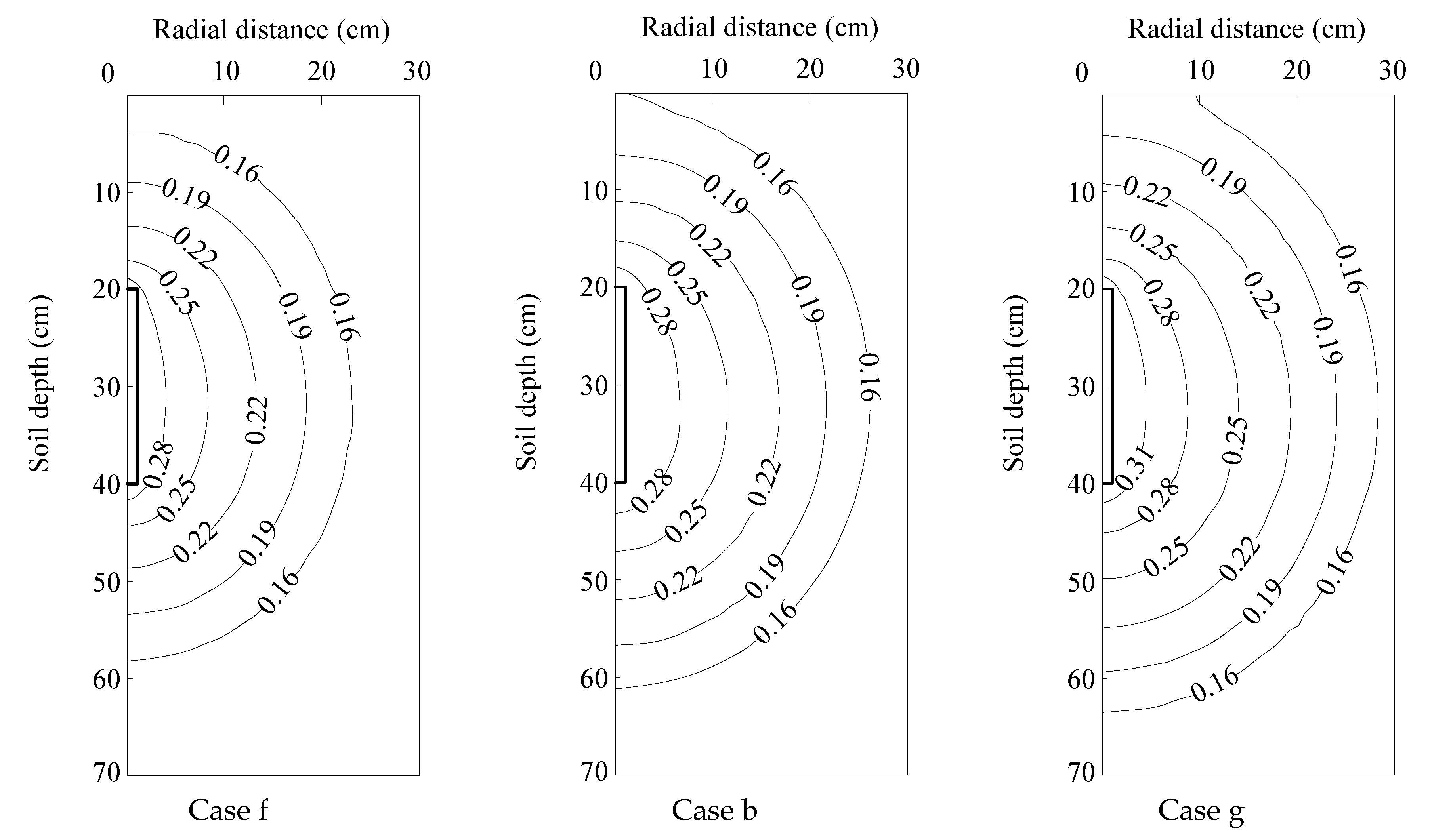
3.4.3. Influence of Pressure Head
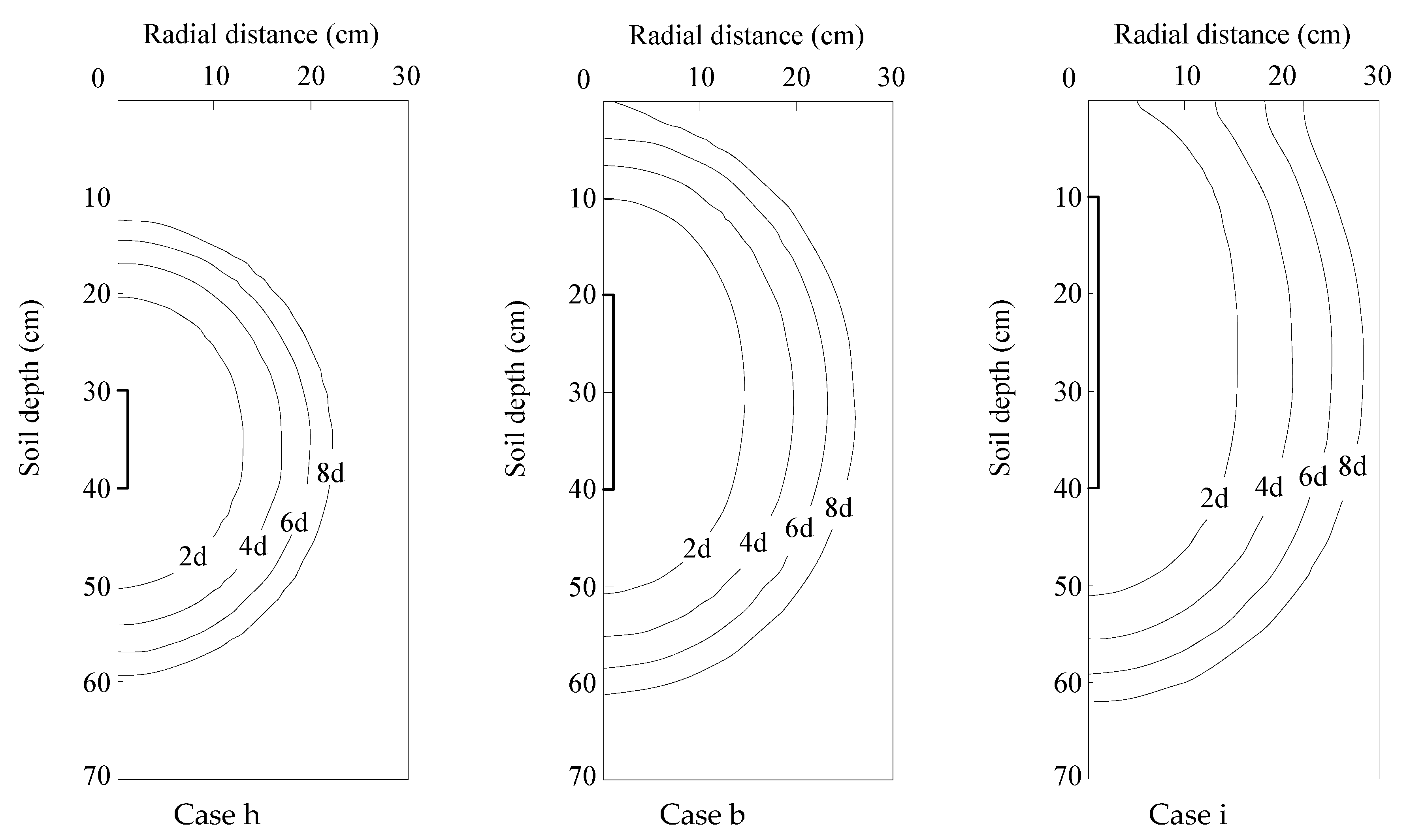
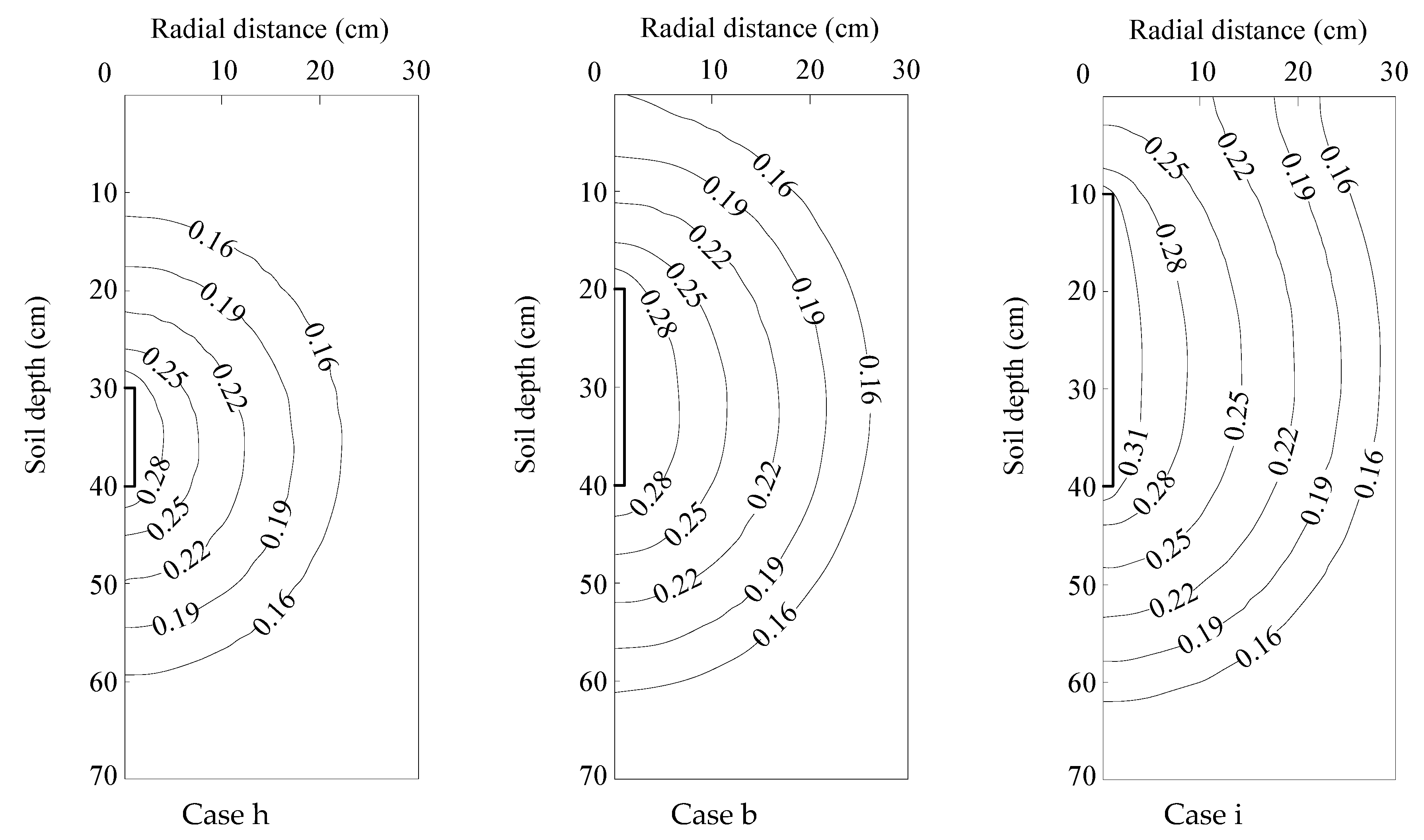
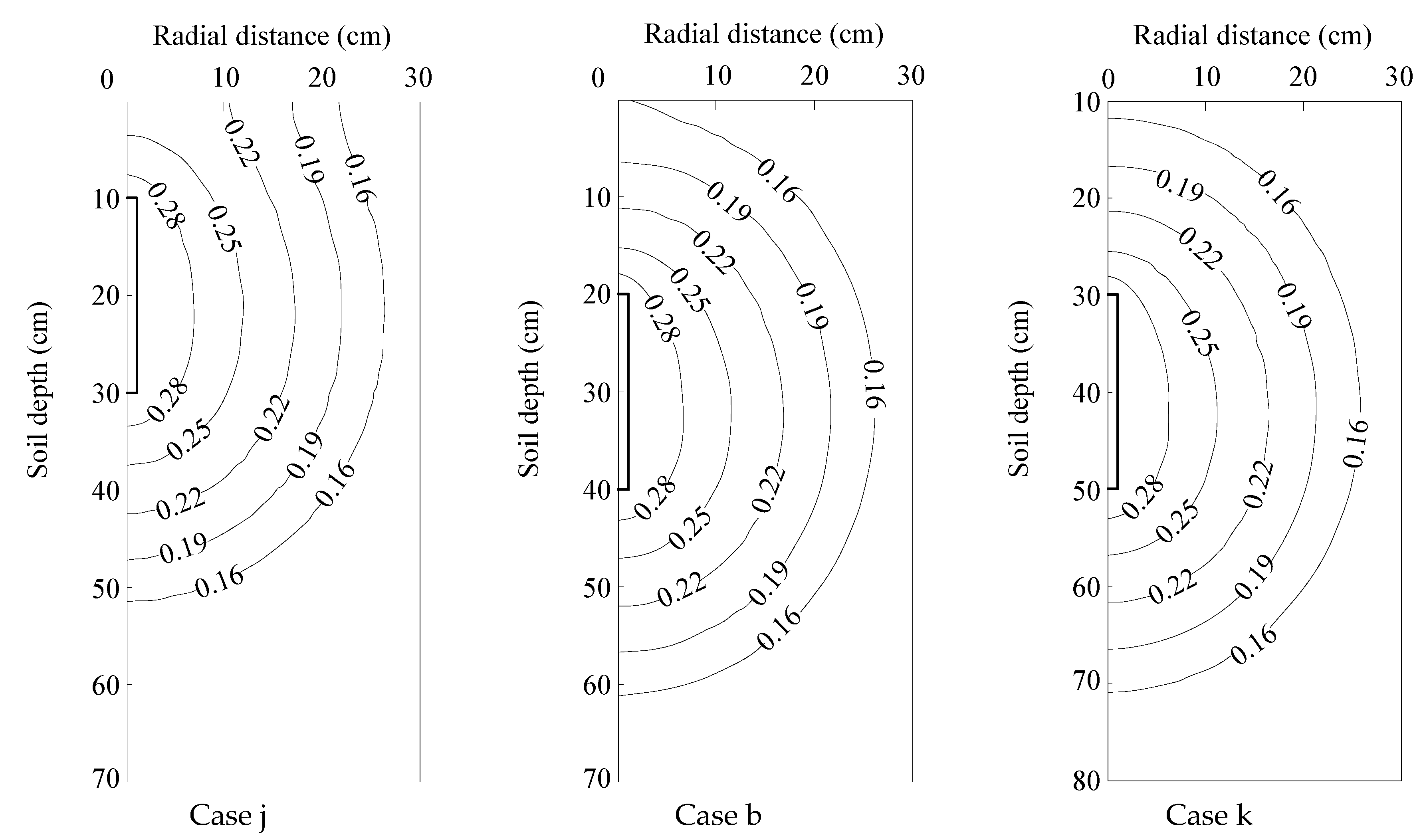
3.4.4. Influence of Moistube Length
3.4.5. Influence of Moistube Buried Depth
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Fan, Y.W.; Huang, N.; Gong, J.G.; Shao, X.X.; Zhang, J.; Zhao, T. A simplified infiltration model for predicting cumulative infiltration during vertical line source irrigation. Water 2018, 10, 89. [Google Scholar] [CrossRef]
- Du, S.Q.; Kang, S.Z.; Li, F.S.; Du, T.S. Water use efficiency is improved by alternate partial root-zone irrigation of apple in arid northwest China. Agric. Water Manag. 2017, 179, 184–192. [Google Scholar] [CrossRef]
- Li, Y.B.; Fan, Y.W.; Liu, Y.; Ma, X.Y. Influencing factors and simplified model of film hole irrigation. Water 2017, 9, 543. [Google Scholar] [CrossRef]
- Kang, S.Z.; Hu, X.T.; Jerie, P.; Zhang, J.H. The effects of partial rootzone drying on root, trunk sap flow and water balance in an irrigated pear (Pyrus communis, L.) orchard. J. Hydrol. 2003, 280, 192–206. [Google Scholar] [CrossRef]
- Petty, J.D.; Huckins, J.N.; Martin, D.B.; Adornato, T.G. Use of semipermeable membrane devices (SPMDS) to determine bioavailable organochlorine pesticide residues in streams receiving irrigation drainwater. Chemosphere 1995, 30, 1891–1903. [Google Scholar] [CrossRef]
- Yang, Q. Irrigation Method with Semi Permeable Membrane, Irrigation Container and Irrigation System Made of Semi Permeable Membrane and Their Application. EP2153714, 17 February 2010. [Google Scholar]
- Niu, W.Q.; Zhang, J.; Zhang, L.L.; Xue, W.L.; Zhang, L.T. Effects of buried depth and pressure head on water movement of wetted soil during moistube-irrigation. Trans. Chin. Soc. Agric. Mach. 2013, 44, 128–134. (In Chinese) [Google Scholar]
- Yu, X.D.; Liu, X.G.; Zhu, Y.F.; Qi, Y.T.; Yang, Q.L.; Tang, J.K. Effects of soil texture and water pressure on moistube infiltration in vertical inserting mode. J. Drain. Irrig. Mach. Eng. 2017, 35, 71–79. (In Chinese) [Google Scholar]
- Kandelous, M.M.; Šimůnek, J.; Van Genuchten, M.T.; Malek, K. Soil water content distributions between two emitters of a subsurface drip irrigation system. Soil Sci. Soc. Am. J. 2011, 75, 488–497. [Google Scholar] [CrossRef]
- Skaggs, T.H.; Trout, T.J.; Rothfuss, Y. Drip irrigation water distribution patterns: Effects of emitter rate, pulsing, and antecedent water. Soil Sci. Soc. Am. J. 2010, 74, 1886. [Google Scholar] [CrossRef]
- Subbaiah, R. A review of models for predicting soil water dynamics during trickle irrigation. Irrig. Sci. 2013, 31, 225–258. [Google Scholar] [CrossRef]
- El-Nesr, M.N.; Alazba, A.A.; Šimůnek, J. Hydrus simulations of the effects of dual-drip subsurface irrigation and a physical barrier on water movement and solute transport in soils. Irrig. Sci. 2014, 32, 111–125. [Google Scholar] [CrossRef]
- Naglič, B.; Kechavarzi, C.; Coulon, F.; Pintar, M. Numerical investigation of the influence of texture, surface drip emitter discharge rate and initial soil moisture condition on wetting pattern size. Irrig. Sci. 2014, 32, 421–436. [Google Scholar] [CrossRef]
- Patel, N.; Rajput, T.B.S. Effect of subsurface drip irrigation on onion yield. Irrig. Sci. 2009, 27, 97. [Google Scholar] [CrossRef]
- Khoshravesh-Miangoleh, M.; Kiani, A. Effect of magnetized water on infiltration capacity of different soil textures. Soil Use Manag. 2015, 30, 588–594. [Google Scholar] [CrossRef]
- Gumbs, F.A.; Warkentin, B.P. The effect of bulk density and initial water content on infiltration in clay soil samples. Soil Sci. Soc. Am. Proc. 1972, 36, 720–724. [Google Scholar] [CrossRef]
- Sharda, A.K. Influence of soil bulk density on horizontal water infiltration. Soil Res. 1977, 15, 83–86. [Google Scholar] [CrossRef]
- Yang, J.L.; Zhang, G.L. Water infiltration in urban soils and its effects on the quantity and quality of runoff. J. Soils Sediments 2011, 11, 751–761. [Google Scholar] [CrossRef]
- Dao, T.H. Tillage and winter wheat residue management effects on water infiltration and storage. Soil Sci. Soc. Am. J. 2016, 57, 1586–1595. [Google Scholar] [CrossRef]
- Liu, H.; Lei, T.W.; Zhao, J.; Yuan, C.P.; Fan, Y.T.; Qu, L.Q. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the run off-on-out method. J. Hydrol. 2011, 396, 24–32. [Google Scholar] [CrossRef]
- Bresler, E.; Heller, J.; Diner, N.; Ben-Asher, J.; Brandt, A.; Goldberg, D. Infiltration from a trickle source: II. Experimental data and theoretical predictions. Soil Sci. Soc. Am. J. 1971, 35, 683–689. [Google Scholar] [CrossRef]
- Ah Koon, P.D.; Gregory, P.J.; Bell, J.P. Influence of drip irrigation emission rate on distribution and drainage of water beneath a sugarcane and a fallow plot. Agric Water Manag. 1990, 17, 267–282. [Google Scholar] [CrossRef]
- Khan, A.A.; Yitayew, M.; Warrick, A.W. Field evaluation of water and solute distribution from a point source. Irrig Drain Eng. 1996, 22, 221–227. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Ren, L. Water and nitrogen distribution as affected by fertigation of ammonium nitrate from a point source. Irrig Sci. 2003, 22, 12–30. [Google Scholar]
- Ismail, S.M.; El-Abedin, T.K.Z.; Wassif, M.M.; Nesr, M.N.E. Physical and hydraulic barriers under surface and subsurface drip irrigation systems. Misr. J. Agric. Eng. Res. MSAE 2006, 23, 1001–1016. [Google Scholar]
- Patel, N.; Rajput, T.B.S. Effect of drip tape placement depth and irrigation level on yield of potato. Agric. Water Manag. 2007, 88, 209–223. [Google Scholar] [CrossRef]
- Brandt, A.; Bresler, E.; Diner, N.; Ben-Asher, I.; Heller, J.; Goldberg, D. Infiltration from a trickle source: I. mathematical model. Soil Sci. Soc. Am. J. Proc. 1971, 35, 675–682. [Google Scholar] [CrossRef]
- Warrick, A.W. Point and line infiltration calculation of the wetted soil surface. Soil Sci. Soc. Am. J. 1985, 49, 1581–1583. [Google Scholar] [CrossRef]
- Revol, P.B.; Clothier, E.; Mailhol, J.C.; Vachaud, G.; Vauclin, M. Infiltration from a surface point source and drip irrigation: 2. An approximate time-dependent solution for wet front position. Water Resour. Res. 1997, 33, 1869–1874. [Google Scholar] [CrossRef]
- Singh, D.K.; Rajput, T.B.S.; Singh, D.K.; Sikarwar, H.S.; Sahoo, R.N.; Ahmad, T. Simulation of soil wetting pattern with subsurface drip irrigation from line source. Agric. Water Manag. 2006, 83, 130–134. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Kang, S.Z.; Zhang, L. Comparison of APRI and HYDRUS-2D models to simulate soil water dynamics in a vineyard under alternate partial root zone drip irrigation. Plant Soil. 2007, 291, 211–223. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef]
- Skaggs, T.H.; Trout, T.J.; Šimůnek, J.; Shouse, P.J. Comparison of HYDRUS-2D simulations of drip irrigation with experimental observations. J. Irrig. Drain. Eng. 2004, 130, 304–310. [Google Scholar] [CrossRef]
- Provenzano, G. Using HYDRUS -2D simulation model to evaluate wetted soil volume in subsurface drip irrigation systems. J. Irrig. Drain. Eng. 2007, 133, 342–349. [Google Scholar] [CrossRef]
- Stewart, R.D.; Rupp, D.E.; Najm, M.R.A.; Selker, J.S. Modeling effect of initial soil moisture on sorptivity and infiltration. Water Resour. Res. 2013, 49, 7037–7047. [Google Scholar] [CrossRef]
- Karandish, F.; Šimůnek, J. Two-dimensional modeling of nitrogen and water dynamics for various N-managed water-saving irrigation strategies using HYDRUS. Agric. Water Manag. 2017, 193, 174–190. [Google Scholar] [CrossRef]
- Tuller, M.; Or, D. Hydraulic conductivity of variably saturated porous media: Film and corner flow in angular pore space. Water Resour. Res. 2001, 37, 1257–1276. [Google Scholar] [CrossRef]
- Zhang, S.H.; Lei, T.W.; Ding, Y.Y.; Xu, C.P. Finite element modeling of soil water movement under subsurface irrigation with porous pipe and its application. Trans. Chin. Soc. Agric. Eng. 2002, 18, 1–5. (In Chinese) [Google Scholar]
- Niu, W.Q.; Zhang, M.Z.; Xu, J.; Zou, X.Y.; Zhang, R.C.; Li, Y. Prediction Methods and Characteristics of Flow for Moistube. Trans. Chin. Soc. Agric. Mach. 2017, 48, 217–224. (In Chinese) [Google Scholar]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. The HYDRUS Software Package for Simulating the Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Technical Manual, Version 1.0; PC Progress: Prague, Czech Republic, 2006; p. 241. [Google Scholar]
- Xing, X.; Kang, D.; Ma, X. Differences in loam water retention and shrinkage behavior: Effects of various. types and concentrations of salt ions. Soil Till. Res. 2017, 167, 61–72. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Leij, F.J.; Yates, S.R. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; Research Report No. EPA/600/2-91/065; US Salinity Laboratory, US Department of Agriculture, Agricultural Research Service: Riverside, CA, USA, 1991. Available online: http://www.pc-progress.com/documents/programs/retc.pdf (accessed on 1 December 1991).
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Jiang, P.F.; Lei, T.W.; Liu, X.H.; Wu, Y.; Li, X.; Wang, Q.J. Principles and experimental verification of capillary suction method for fast measurement of field capacity. Trans. Chin. Soc. Agric. Eng. 2006, 22, 1–5. (In Chinese) [Google Scholar]




| Soil Type | Particle Size/mm | Bulk Density (g/cm3) | Saturated Soil Water Content (cm3/cm3) | Field Capacity (cm3/cm3) | Wilting Coefficient (%) | ||
|---|---|---|---|---|---|---|---|
| 0.02~2.00 | 0.002~0.02 | 0~0.002 | |||||
| Aeolian sand | 97.69 | 2.31 | 0.00 | 1.60 | 0.43 | 0.051 | 1.8 |
| Silt loam | 24.35 | 65.55 | 10.10 | 1.30 | 0.50 | 0.286 | 6.7 |
| Soil Type | Residual Soil Water Content (cm3/cm3) | Saturated Soil Water Content (cm3/cm3) | Parameter α in the Soil Water Retention Function (1/cm) | Parameter n in the Soil Water Retention Function (-) | Saturated Hydraulic Conductivity (cm/min) |
|---|---|---|---|---|---|
| Aeolian sand | 0.02 | 0.43 | 0.162 | 2.24 | 0.4210 |
| Silt loam | 0.02 | 0.50 | 0.014 | 1.51 | 0.0143 |
| Case | Soil Texture | Initial Water Content * | Pressure Head ** | Moistube Length | Buried Depth*** |
|---|---|---|---|---|---|
| a | Silt loam | 50% | 1.5 | 20 | 40 |
| b | Loam | 50% | 1.5 | 20 | 40 |
| c | Sandy loam | 50% | 1.5 | 20 | 40 |
| d | Loam | 40% | 1.5 | 20 | 40 |
| e | Loam | 60% | 1.5 | 20 | 40 |
| f | Loam | 50% | 1.0 | 20 | 40 |
| g | Loam | 50% | 2.0 | 20 | 40 |
| h | Loam | 50% | 1.5 | 10 | 40 |
| i | Loam | 50% | 1.5 | 30 | 40 |
| j | Loam | 50% | 1.5 | 20 | 30 |
| k | Loam | 50% | 1.5 | 20 | 50 |
| Soil Texture | Residual Soil Water Content (cm3·cm−3) | Saturated Soil Water Content (cm3·cm−3) | Parameter α in the Soil Water Retention Function (cm−1) | Parameter n in the Soil Water Retention Function (-) | Saturated Hydraulic Conductivity (cm·min−1) |
|---|---|---|---|---|---|
| Silt loam | 0.067 | 0.450 | 0.020 | 1.41 | 0.0075 |
| Loam | 0.078 | 0.430 | 0.036 | 1.56 | 0.0173 |
| Sandy loam | 0.065 | 0.410 | 0.075 | 1.89 | 0.0737 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.-W.; Huang, N.; Zhang, J.; Zhao, T. Simulation of Soil Wetting Pattern of Vertical Moistube-Irrigation. Water 2018, 10, 601. https://doi.org/10.3390/w10050601
Fan Y-W, Huang N, Zhang J, Zhao T. Simulation of Soil Wetting Pattern of Vertical Moistube-Irrigation. Water. 2018; 10(5):601. https://doi.org/10.3390/w10050601
Chicago/Turabian StyleFan, Yan-Wei, Ning Huang, Jie Zhang, and Tong Zhao. 2018. "Simulation of Soil Wetting Pattern of Vertical Moistube-Irrigation" Water 10, no. 5: 601. https://doi.org/10.3390/w10050601
APA StyleFan, Y.-W., Huang, N., Zhang, J., & Zhao, T. (2018). Simulation of Soil Wetting Pattern of Vertical Moistube-Irrigation. Water, 10(5), 601. https://doi.org/10.3390/w10050601






