1. Introduction
The landscape of southern Brazil is characterized by the Pampa biome, which occupies 63% of the State of Rio Grande do Sul. Grassland is the dominant vegetation and livestock production is a main economic activity in the area, but large areas have been converted into cropland, mainly for soybean production, thus suppressing the native grass vegetation [
1]. Therefore, the sustainability of this biome for livestock production requires the planting of new and highly productive grasses such as the Tifton 85 bermudagrass [
2,
3], recently introduced in the region. Assessing grass evapotranspiration and water requirements as influenced by the frequency of cuttings is required to support an upgraded management of those grasslands. An innovative approach used is to relate the frequency of cuttings with the density coefficient (K
d) and then estimate the basal crop coefficient from K
d following the Allen and Pereira approach [
4].
Studies on evapotranspiration (ET) of grasslands are numerous. Research has commonly been devoted to assessing the dynamics and abiotic driving factors of ET, mainly relative to climate influences on the processes of energy partition into latent and sensible heat. Such studies often use eddy covariance and/or Bowen ratio energy balance (BREB) observations, data which are commonly used in analysis performed with the Penman–Monteith (PM) combination equation [
5] and/or the Priestley–Taylor (PT) equation [
6], thus using the canopy resistance or the PT parameter α as behavioral indicators [
7,
8,
9]. As an alternative to those measurement techniques, scintillometer measurements [
10] and satellite images [
11,
12,
13] were also used. Adopting similar research approaches, other studies compared the ET of grasslands with ET of forests or shrublands [
14,
15,
16]. In addition to the available energy for evaporation, soil water availability and crop ground cover or the leaf area index (LAI) were often identified as main driving factors influencing grass ET [
14,
15,
16,
17].
Studies such as those referred to above are likely of great importance for understanding the variability of grass ET when focusing on the Pampa biome but different, operational research approaches are required when aiming at knowing grassland water requirements and/or grassland water management issues. Related operational studies are also numerous and refer to various climates, grass species and diverse herbage uses for hay or for grazing with different frequency of cuttings. However, such ET studies are lacking in southern Brazil and for Tifton 85 bermudagrass. ET research aiming at improved farm water management generally uses the grass reference ET (ET
o) proposed in the Food and Agriculture Organization guidelines for computing crop water requirements (FAO56) [
17]; nevertheless, recent studies [
3,
18] relative to irrigated bermudagrass yields used the climatic potential ET equation of Thornthwaite [
19], developed in 1948.
The reference ET
o was defined after parameterizing the PM combination equation [
5] for a cool season grass, thus resulting that ET
o is defined as the rate of evapotranspiration from a hypothetical reference crop with an assumed crop height h = 0.12 m, a fixed daily canopy resistance r
s = 70 s m
−1, and an albedo of 0.23, closely resembling the evapotranspiration from an extensive surface of green grass of uniform height, actively growing, completely shading the ground and not short of water [
17]. This definition is described by the daily PM-ET
o equation [
17], which represents the climatic demand of the atmosphere. Thus, following FAO56 [
17], the ET
o is to be used with a crop coefficient (K
c) when estimating or predicting the ET of a given surface, that is, the K
c-ET
o approach. K
c is the ratio between the crop ET and ET
o and varies with the crop surface characteristics and the crop growth stage, and is influenced by the climate and management. Single and dual K
c may be used [
17]. The dual K
c consists of the sum K
e + K
cb of the soil evaporation coefficient (K
e) and the basal crop coefficient (K
cb), and thus with consideration of both processes included in evapotranspiration. The K
c values are standard or potential when the crop is not stressed, while actual K
c values (K
c act or K
cb act) are often smaller than the standard K
c or K
cb when water, salt, disease or management stresses affect crop transpiration. These effects may be considered using a stress coefficient applied to K
c or K
cb. Tabulated values of standard K
c and K
cb are provided by Allen et al. [
17] for a variety of crops, including grasses and pastures. The standard K
c and K
cb values are transferable to other sites considering adjustments for climate described by Allen et al. [
17]. The time variation of the K
c and K
cb values are described by K
c curves [
17] that describe in a simplified way the dynamics of LAI and vegetation ET. The form of these curves varies from one crop to another; for grasses with cuttings, several successive K
c curves should be considered, each representing the dynamics of ET during each crop growth cycle between cuttings [
17].
The operational use of the ET
o equation implies, therefore, the use of crop coefficients and the build-up of K
c curves to describe the respective time variation. It could be observed that several papers reporting on the use of the grass reference ET
o did not follow the concepts described above. A few authors directly compared ET obtained with eddy covariance, BREB, or a soil water balance with ET
o but not searching for a K
c value [
20], or even assumed equality between grass ET and ET
o [
21]. Other authors just computed daily K
c act values (often using different designations for that parameter) but did not search for a K
c curve that would describe their seasonal variation [
22,
23], or just identified a mean seasonal K
c act [
24]. The lack of search for a K
c curve led some authors to consider the K
c-ET
o approach as non-useful [
25]. By contrast, Pronger et al. [
26] did not clearly assume the concepts behind actual vs. potential K
c and, in addition to K
s, adopted a correction factor to ET
o for highly stressed grass. This is theoretically not appropriate because it contradicts the concepts of reference ET, which depends solely upon the climate and not the crop under study, and of the K
c act that has to be derived from the standard K
c when adapting to the management and environmental conditions [
17]. The approaches referred to above, like other research quoted before, may support an improved understanding of the dynamic behaviour of grass ET but are likely not appropriate for operational use in irrigation water management.
The FAO56 K
c-ET
o method [
17] was first applied by Cancela et al. [
27] to grass using the single K
c act with successive four-stage curves relative to four cuttings using the ISAREG soil water balance model [
28]. Single K
c act four stage curves were defined for remote-sensed grazed grasslands [
29,
30]. By contrast, other authors preferred replacing the typical four stages curve by average monthly K
c act values [
31]. The FAO dual K
c approach [
32] was successfully used by Greenwood et al. [
33], who reported on a large number of K
cb act curves to represent numerous grass cuttings using the FAO56 spreadsheet [
17]. The FAO dual K
c approach was adopted by Wu et al. [
34] to represent a natural groundwater dependent grassland, then using a seasonal four-growth stages K
cb act curve using the SIMDualKc model [
35]. Krauß et al. [
36] also used the dual K
c method to estimate the footprint of milk production but did not report about the K
c curves used.
The dual K
c approach has the advantage of partitioning ET into crop transpiration (T
c) and soil evaporation (E
s). Knowing T
c and E
s provides for a more detailed water balance and a better approach to understanding the functioning of the ecosystems. In addition, partitioning ET allows estimating T
c and therefore better calculating yields [
37] since it directly relates to biomass production. Moreover, good results were obtained with the soil water balance SIMDualKc model [
35] for the partition of ET using the FAO dual Kc approach, namely when applied to crops that nearly fully cover the ground, such as wheat, barley and soybean [
38,
39,
40] whose E
s estimated values compared well with E
s observations using microlysimeters. T
c simulated also compared well with sap flow observations in tree crops [
41,
42], thus confirming the goodness of ET partitioning.
The application of various ET partition methods to grass is often reported, namely using the two source Shuttelworth and Wallace [
43] model (SW). It is very precise when an appropriate parameterization is achieved, which is a quite demanding task that limits the operational use of SW in agricultural water management practice; various examples of the application of SW to grass are reported in the literature [
44,
45]. Other double source models were applied to grass, such as the one reported by Huang et al. [
46], which is based upon the estimation of gross ecosystem productivity using CO
2 fluxes observed with the eddy covariance method, and that proposed by Wang and Yamanaka [
47], which consists of a modification of the SW model. Empirical ET partitioning approaches include the use of time series of soil surface temperature [
15], and the adoption of a radiation extinction coefficient (k
rad) combined with a ground cover index [
20] or with LAI when using the PT equation [
48]. These approaches using k
rad are comparable with the FAO dual K
c approach [
17,
32]. Partitioning ET fluxes using stable isotopes is another proved alternative [
49,
50].
The dual K
c approach has been shown to be appropriate to partitioning grass ET, as reported above [
33,
34], and has shown to be less demanding in terms of parameterization and field and laboratory instrumentation than other ET partition methods. In addition, it is easily implemented using the referred SIMDualKc model, which has been extensively tested as reported above. Therefore, the objectives of this study consist of (a) assessing and partitioning evapotranspiration of Tyfton 85 bermudagrass in southern Brazil as influenced by the frequency of cuttings using the model SIMDualKc applied to two years of field data; and (b) deriving crop coefficient curves adapted to grass cuttings of various frequencies. Moreover, the study aims to contribute to the sustainability of grass uses in the Pampa biome, and to create the knowledge required to cope further with climate change in the region.
4. Conclusions
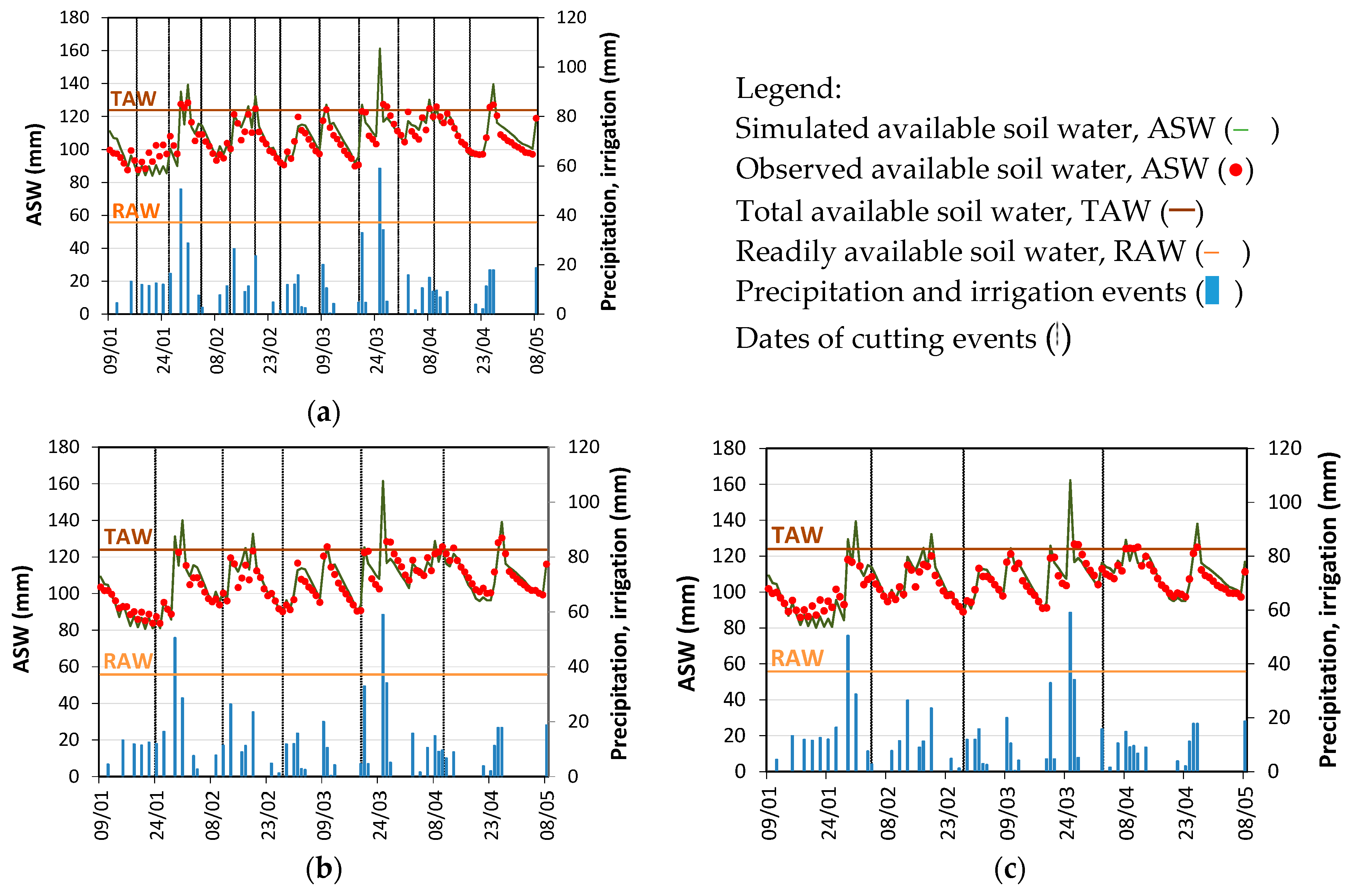
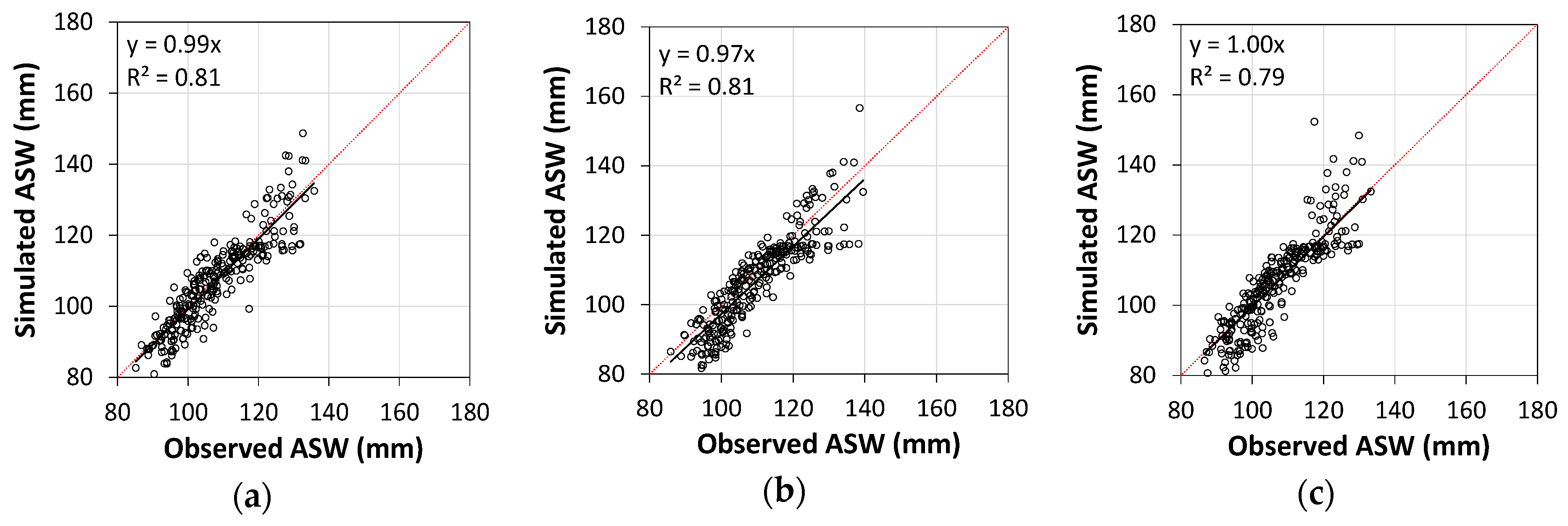
The current study is a first application of the FAO dual crop coefficient approach to assess evapotranspiration and water use of a bermudagrass, more precisely the Tifton 85. It was performed using two years of field data relative to three cutting treatments where intervals between cuttings were defined by CGDD of 124 °C, 248 °C and 372 °C. These independent data sets were used to calibrate and validate the water balance model SIMDualKc, which allowed the K
cb and K
e curves for Tifton 85 to be obtained when managed with those three cutting intervals. Data of Summer and Autumn of 2016 were used for calibration and data for Spring 2015 and 2016, and Summer and Autumn of 2017 were used for validation. The procedure used led to quite small errors of estimation of the available soil water throughout both years, which allowed us to assume that the calibrated K
cb values were accurately estimated and may be considered as standard for the three cutting frequencies studied after adjustments with Equation (7). It is important to note that the estimation of the initial K
cb values from the crop cover and height has shown quite small differences to the calibrated values. Moreover, the Allen and Pereira [
4] Equation (4) was revealed to be very accurate in estimating K
cb from h and f
c provided that K
cb full is well estimated. The operational use of this Equation (4) is therefore recommended.
The K
cb curves consist of a series of K
cb curves relative to each cutting cycle, each one constructed with three linear segments. This approach follows the one proposed by the FAO56 guidelines [
17] and differs from the commonly used single K
c curve. It was revealed to be accurate in describing crop transpiration and providing for the accuracy of soil water dynamics computed through the calibration and validation processes. However, for the case of very frequent cuttings (CGDD of 124 °C) there was no advantage over a single, averaged K
cb.
The Ke curve reflects the abundant and stormy rains that occurred in both years of field experiments, which made the soil evaporation layer wet most of the time. Thus, the Ke curve varied little throughout the periods under analysis. However, the soil water evaporation was mitigated due the organic mulch effect of the plant litter covering the ground, which reduced the energy available at the soil surface, thus reducing Ke and Es. Comparing Ke for the three cutting treatments, this resulted in a larger value for that with very frequent cuttings (CGDD of 124 °C) because the ground cover was smaller than for cuttings with large intervals, thus giving more time for the crop to grow and crop density to increase during each cutting cycle. Due to the nearly flat form of the Ke curve, the Kc curve and the sum of the Ke and Kcb curves do not reflect the aggregation of individual Kc curves relative to each cycle of cutting. Therefore, by contrast with the Kcb curves, a single Kc value is appropriate, however specific for each cutting treatment.
Results for the soil water balance are marked by the enormous amount of rain observed during these two years, likely due to the impacts of ENSO. Thus, the amount of runoff and, mainly, deep percolation exceeded crop ET. Thus, the option of irrigating to avoid any water stress was shown to be inappropriate despite not being prejudicial to the experiments. However, the large number of rainy days and the large amount of rain were likely associated with reduced solar radiation and temperature, which could have contributed to reduce transpiration and the Kcb values. However, the latter, as well as the Kc values, are larger than most of Kcb and Kc values reported in literature, which support the assumption that Kcb values may be considered standard and transferable to other locations after appropriate adjustments.
The soil evaporation fraction (Es/ETc) for all cases was small, near 13% in the case of frequent cuttings and about 9% when cuttings were less frequent. These values could slightly decrease if soil wettings were less frequent. These results indicate that beneficial consumptive water use by the crop is high, with the transpiration ratio near 90%. These results agree well with those reported in literature relative to well-managed grasslands, particularly tropical ones. This may indicate that the Tifton 85 bermudagrass has the potential to contribute to the sustainability of the Pampa biome in southern Brazil. Adopting a median cuttings frequency (CGDD of 248 °C) is likely the most favorable. However, more studies are required, mainly relative to herbage production and water productivity, which are expected to be undertaken based upon the field data used in the current study.
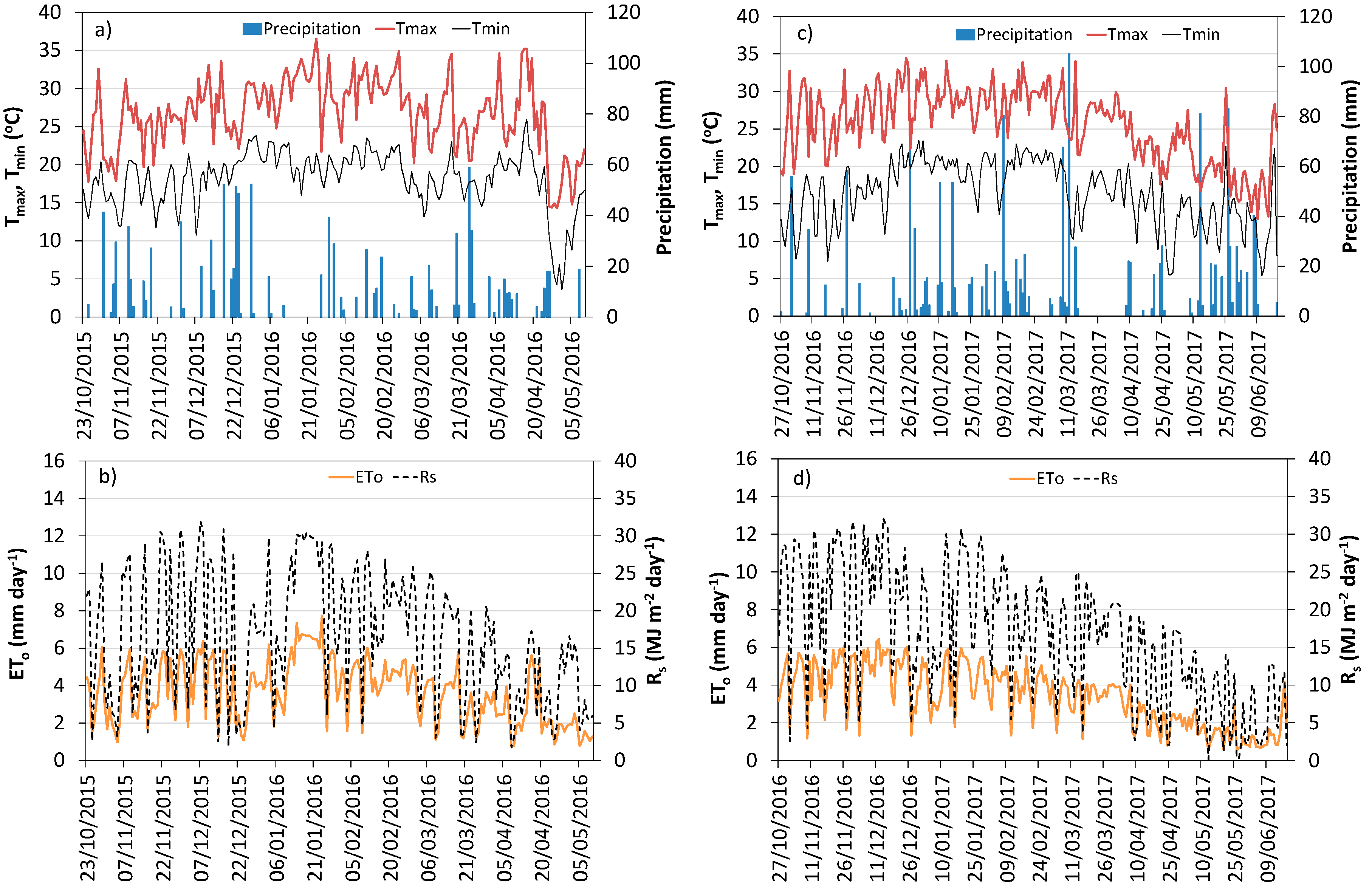
 ) and minimum (
) and minimum ( ) temperatures, and rainfall (
) temperatures, and rainfall ( ); (b,d) solar radiation (
); (b,d) solar radiation ( ) and reference evapotranspiration (
) and reference evapotranspiration ( ).
).
 ) and minimum (
) and minimum ( ) temperatures, and rainfall (
) temperatures, and rainfall ( ); (b,d) solar radiation (
); (b,d) solar radiation ( ) and reference evapotranspiration (
) and reference evapotranspiration ( ).
).
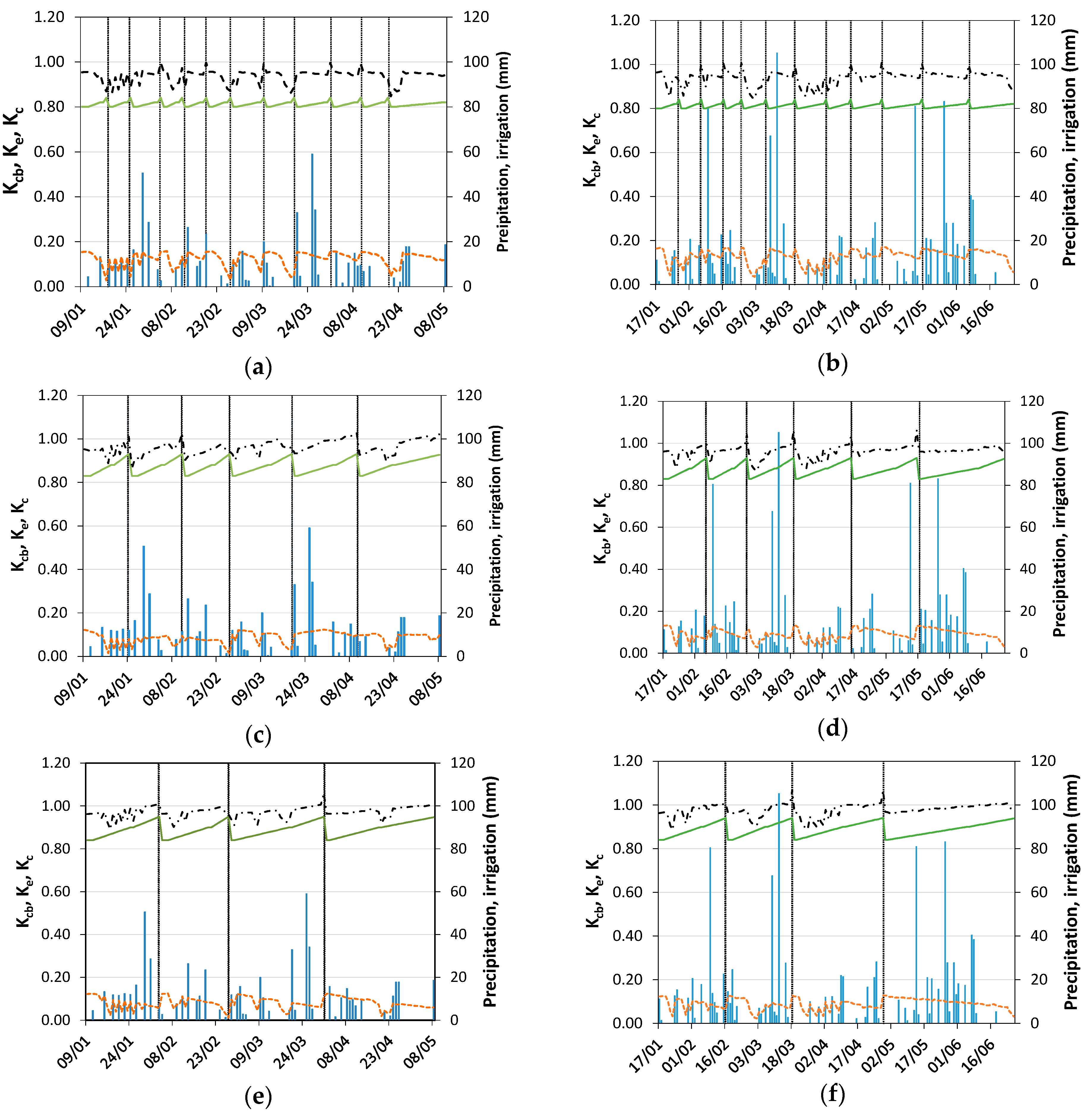
 ), soil evaporation coefficient (Ke,
), soil evaporation coefficient (Ke,  ) and average crop coefficient (Kc,
) and average crop coefficient (Kc,  ) curves of Tifton 85 bermudagrass and all cutting treatments with CGDD of 124 °C (a,b), 248 °C (c,d) and 372 °C (e,f) relative to the Summer–Autumn periods of 2016 (a,c,e) and 2017 (b,d,f).
) curves of Tifton 85 bermudagrass and all cutting treatments with CGDD of 124 °C (a,b), 248 °C (c,d) and 372 °C (e,f) relative to the Summer–Autumn periods of 2016 (a,c,e) and 2017 (b,d,f).
 ), soil evaporation coefficient (Ke,
), soil evaporation coefficient (Ke,  ) and average crop coefficient (Kc,
) and average crop coefficient (Kc,  ) curves of Tifton 85 bermudagrass and all cutting treatments with CGDD of 124 °C (a,b), 248 °C (c,d) and 372 °C (e,f) relative to the Summer–Autumn periods of 2016 (a,c,e) and 2017 (b,d,f).
) curves of Tifton 85 bermudagrass and all cutting treatments with CGDD of 124 °C (a,b), 248 °C (c,d) and 372 °C (e,f) relative to the Summer–Autumn periods of 2016 (a,c,e) and 2017 (b,d,f).