On the Relationship between Aquatic Plant Stem Characteristics and Drag Force: Is a Modeling Application Possible?
Abstract
:1. Introduction
2. Materials and Methods
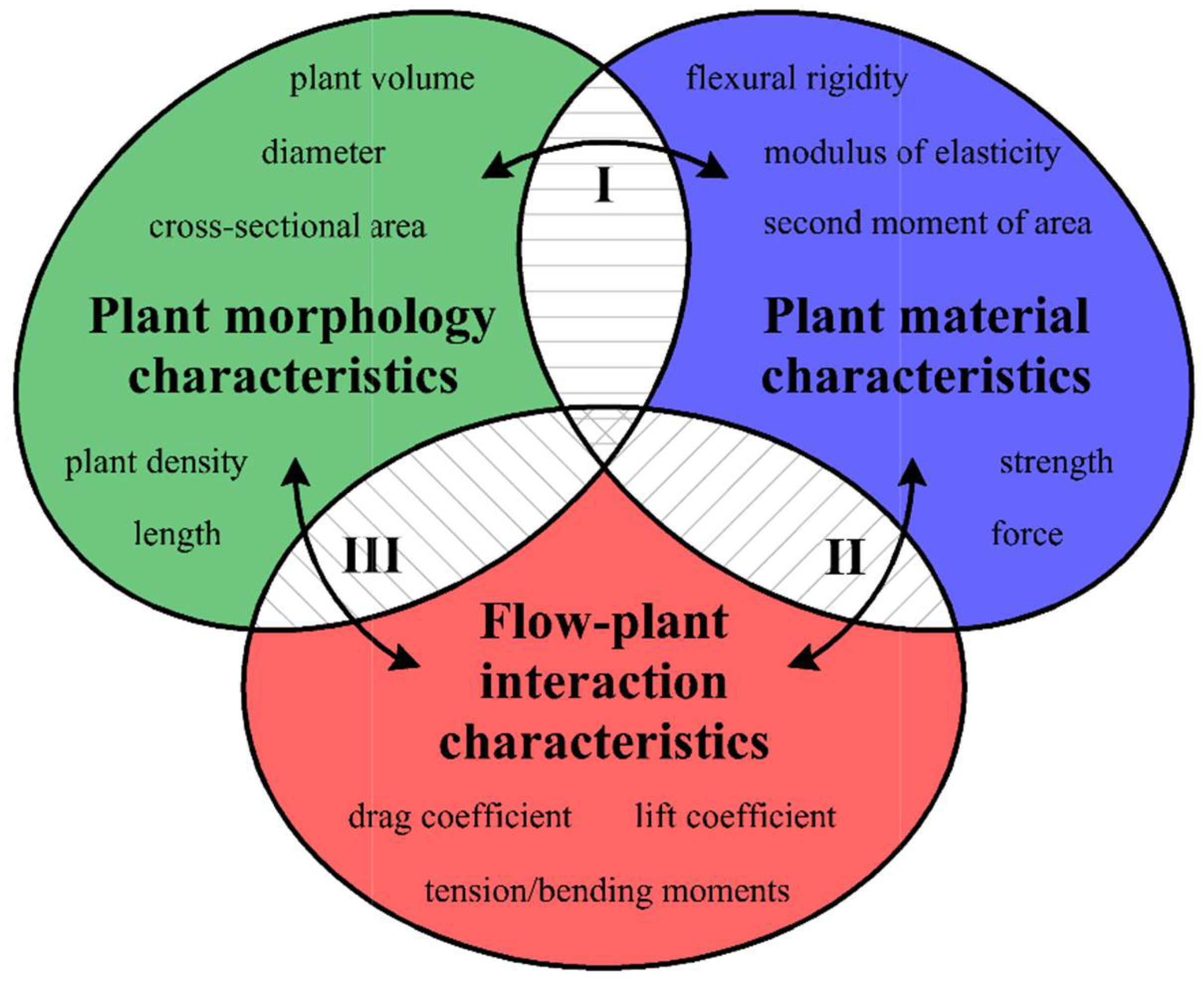
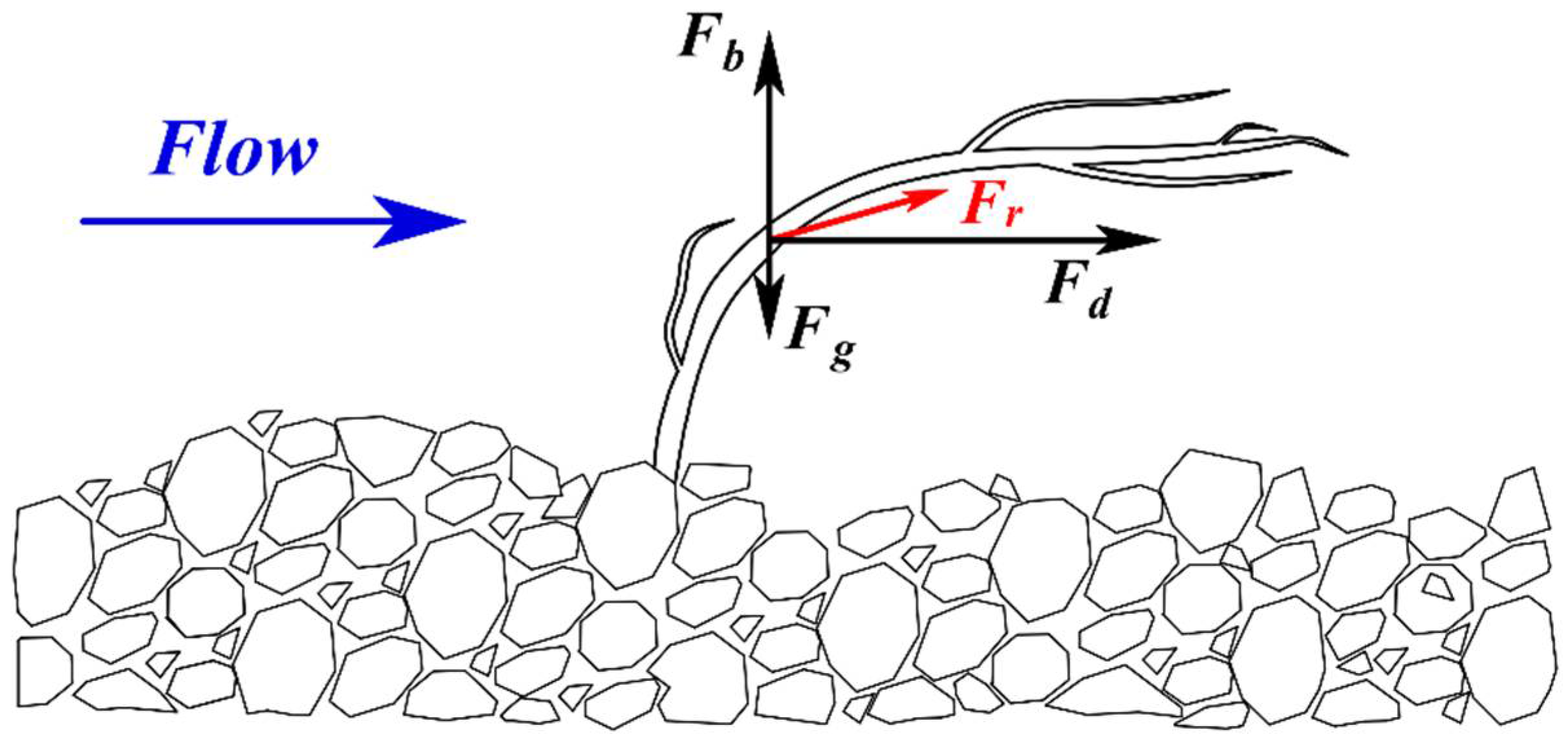
2.1. Theoretical Assumptions
- The flexural rigidity EI, which has a constant modulus of elasticity E [MPa] for solid materials with a circular cross-sectional shape, is expressed as [53]where IC is the second moment of area for the circular cross-section and is defined as , [mm4], and d is the stem diameter [mm].
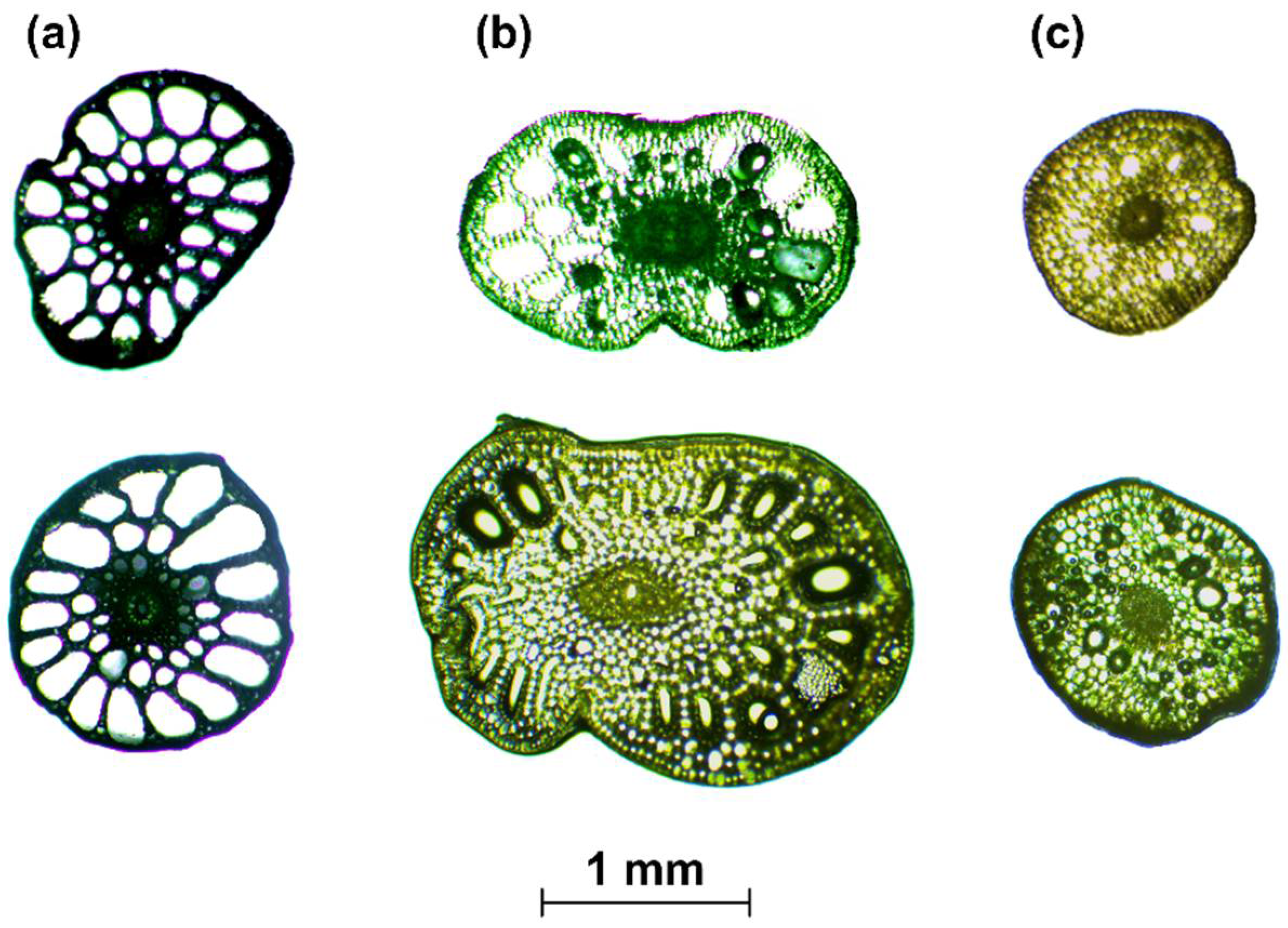
- When the cross-section of the stem plant has a circular shape (the ideal situation), the second moment of area I depends on the plant diameter d to the fourth power, i.e., I ~ d4. This condition is true even in the case when the shape scales with the increase in diameter—that is, when the cross-sections are similar (in the sense of the similarity of the figures). On the other hand, stems of aquatic plants do not have uniform cross-sections or perfect circular shapes (Figure 3). To simplify the biomechanical measurements, the cross-sectional area of the stem is usually compared to a specific shape with a solid structure [35,36]. However, a plant stem is not a solid material. The internal structure of a plant is more complex and it is not uniform for the plant’s entire lifecycle. In addition, a cross-sectional area does not change proportionally with the increase in diameter. Hence, the assumption of diameter to the fourth power as described by Equation (3) that is used for solid materials is not correct for biological systems. Therefore, in our nonideal situation, the second moment of area is approximately I ~ F(d) d4, where F(d) is a function of the shape, which, in turn, is a function of time d(t), as hydrophytes change their dimensions throughout the growing season. In addition, we assume here that the shapes of cross-sections of plants with the same diameters are (roughly) the same.
- In the ideal situation, flexural modulus E does not depend on the plant diameter. E is the property of the material from which the plant was “built”. However, our situation is not ideal, and when the plant grows, the material from which it was built changes. Thus, again, E ~ H(d, t).
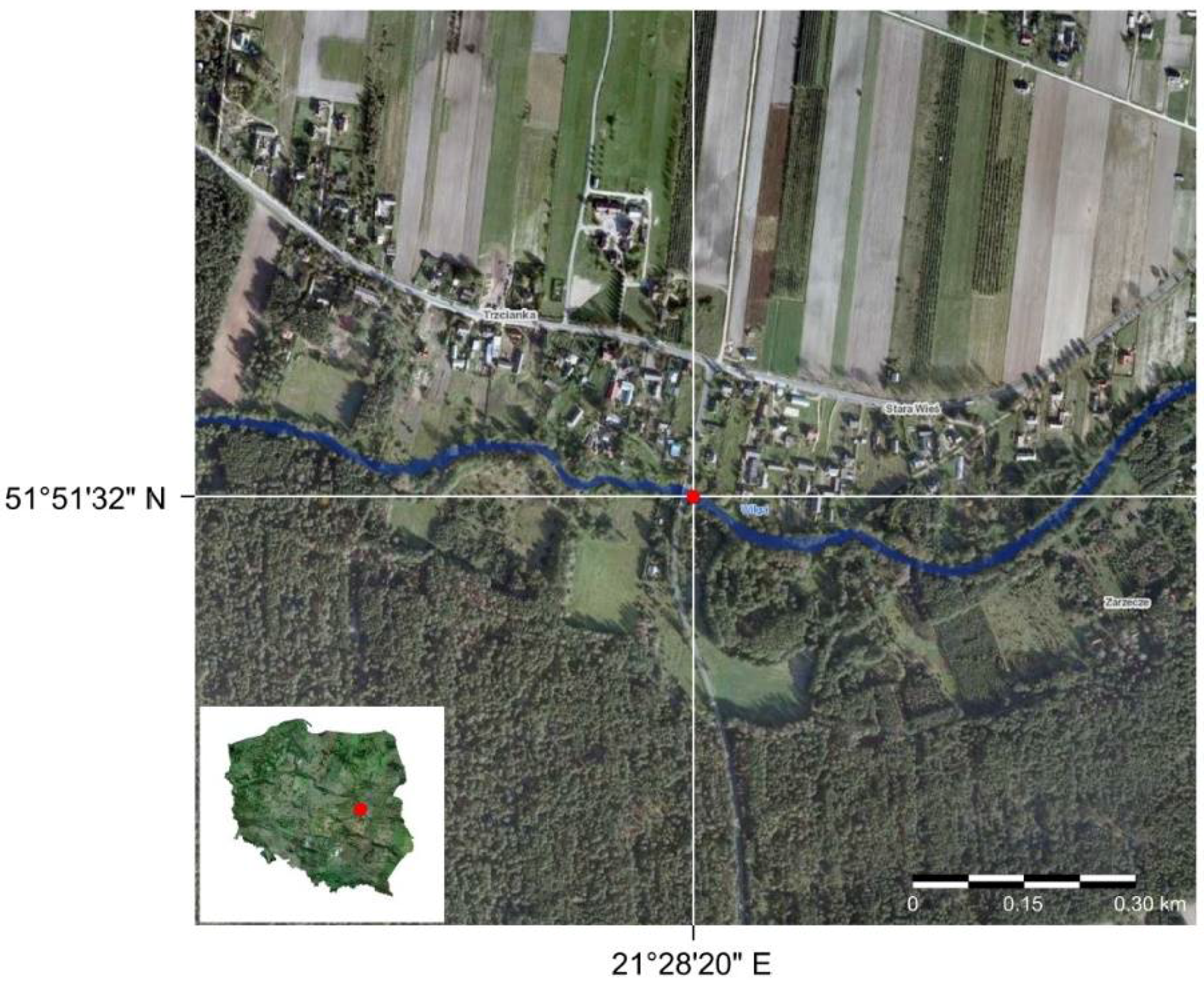
2.2. Data
2.3. Regression Calculations
3. Results
3.1. Regression Analysis
3.1.1. Case 1
3.1.2. Case 2
3.1.3. Cases Comparison
3.2. Data Analysis
4. Discussion
5. Conclusions
- (1)
- The relationship between flexural rigidity of aquatic plant stem and drag has the following form: EI = adb.
- (2)
- Our work showed that two approaches may be used for estimating plant stiffness based on plant morphology in a detailed (case 1) or general way (case 2), which is needed to obtain drag forces (Equation (1)).
- (3)
- With a constant coefficient b, the increase in the diameter of the plant stem may cause monotonous changes in the ratio of the drag and bending forces.
- (4)
- The model may be applied in many laboratory measurements of flow–biota interactions as well as in widely understood aquatic plant management.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nikora, V. Hydrodynamics of aquatic ecosystems: An interface between ecology, biomechanics and environmental fluid mechanics. River Res. Appl. 2010, 26, 367–384. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Tymiński, T.; Kałuża, T. Investigation of Mechanical Properties and Flow Resistance of Flexible Riverbank Vegetation. Pol. J. Environ. Stud. 2012, 21, 201–207. [Google Scholar]
- Aberle, J.; Järvelä, J. Flow resistance of emergent rigid and flexible floodplain vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- Aberle, J.; Järvelä, J. Hydrodynamics of vegetated channels. In Rivers—Physical, Fluvial and Environmental Processes; Rowiński, P., Radecki-Pawlik, A., Eds.; GeoPlanet: Earth and Planetary Sciences; Springer: Berlin, Germany, 2015. [Google Scholar]
- Nikora, V.; Larned, S.; Nikora, N.; Debnath, K.; Cooper, G.; Reid, M. Hydraulic resistance due to aquatic vegetation in small streams: Field study. J. Hydraul. Eng. 2008, 134, 1326–1332. [Google Scholar] [CrossRef]
- Stephan, U.; Gutknecht, D. Hydraulic resistance of submerged flexible vegetation. J. Hydrol. 2002, 269, 27–43. [Google Scholar] [CrossRef]
- Rood, S.B.; Samuelson, G.M.; Braatne, J.H.; Gourley, C.R.; Hughes, F.M.; Mahoney, J.M. Managing river flows to restore floodplain forests. Front. Ecol. Environ. 2005, 3, 193–201. [Google Scholar] [CrossRef]
- Stromberg, J.C.; Beauchamp, V.B.; Dixon, M.D.; Lite, S.J.; Paradzick, C. Importance of low-flow and high-flow characteristics to restoration of riparian vegetation along rivers in arid south-western United States. Freshw. Biol. 2007, 52, 651–679. [Google Scholar] [CrossRef]
- Jelinek, S.; Te, T.; Gehrig, S.L.; Stewarth, H.; Nicol, J.M. Facilitating the restoration of aquatic plant communities in a Ramsar wetland. Restor. Ecol. 2016, 24, 528–537. [Google Scholar] [CrossRef]
- Moody, M.L.; Les, D.H.; Ditomaso, J.M. The role of plant systematic in invasive aquatic plant management. J. Aquat. Plant Manag. 2008, 46, 7–15. [Google Scholar]
- Hussner, A.; Stiers, I.; Verhofstad, M.J.J.M.; Bakker, E.S.; Grutters, B.M.C.; Haury, J.; Van Valkenburg, J.L.C.H.; Brundu, G.; Newman, J.; Clayton, J.S.; et al. Management and control methods of invasive alien freshwater aquatic plants: A review. Aquat. Bot. 2017, 136, 112–137. [Google Scholar] [CrossRef]
- Marion, A.; Nikora, V.; Puijalon, S.; Bouma, T.; Koll, K.; Ballio, F.; Tait, S.; Zaramella, M.; Sukhodolov, A.; O’Hare, M.; et al. Aquatic interfaces: A hydrodynamic and ecological perspective. J. Hydraul. Res. 2014, 52, 744–758. [Google Scholar] [CrossRef]
- Siniscalchi, F.; Nikora, V.I. Flow-plant interactions in open-channel flows: A comparative analysis of five freshwater plant species. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Nikora, V.I.; Goring, D.G.; Biggs, B.J.F. A simple model of stream periphyton-flow interactions. Oikos 1998, 81, 607–611. [Google Scholar] [CrossRef]
- Nikora, V.I.; Larned, S.; Biggs, B.J.F. Hydrodynamic effects in aquatic ecosystems with a focus on periphyton. Recent Res. Dev. Fluid Dyn. 2003, 4, 41–70. [Google Scholar]
- Larned, S.T.; Nikora, V.I.; Biggs, B.J. Mass-transfer-limited nitrogen and phosphorus uptake by stream periphyton: A conceptual model and experimental evidence. Limnol. Oceanogr. 2004, 49, 1992–2000. [Google Scholar] [CrossRef]
- Kouwen, N.; Unny, T.E. Flexible roughness in open channels. J. Hydraul. Div. 1973, 99, 713–728. [Google Scholar]
- Usherwood, J.R.; Ennos, A.R.; Ball, D.J. Mechanical and anatomical adaptations in terrestrial and aquatic buttercups to their respective environments. J. Exp. Bot. 1997, 48, 1469–1475. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H.M. Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res.-Ocean. 2002, 107. [Google Scholar] [CrossRef]
- Zhu, G.; Yuan, C.; Di, G.; Zhang, M.; Ni, L.; Cao, T.; Fang, R.; Wu, G. Morphological and biomechanical response to eutrophication and hydrodynamic stresses. Sci. Total Environ. 2018, 622, 421–435. [Google Scholar] [CrossRef] [PubMed]
- Miler, O.; Albayrak, I.; Nikora, V.; O’Hare, M. Biomechanical properties of aquatic plants and their effects on plant-flow interactions in streams and rivers. Aquat. Sci. 2012, 74, 31–44. [Google Scholar] [CrossRef]
- Łoboda, A.M.; Przyborowski, Ł.; Karpiński, M.; Bialik, R.J.; Nikora, V.I. Biomechanical properties of aquatic plants: The effect of test conditions. Limnol. Oceanogr. Meth. 2018. [Google Scholar] [CrossRef]
- Patterson, M.R.; Harwell, M.C.; Orth, L.M.; Orth, R.J. Biomechanical properties of the reproductive shoots of eelgrass. Aquat. Bot. 2001, 69, 27–40. [Google Scholar] [CrossRef]
- Koch, E.W.; Ackerman, J.; van Keulen, M.; Verduin, J. Fluid dynamics in seagrass ecology: From molecules to ecosystems. In Seagrasses: Biology, Ecology and Conservation; Larkum, A.W.D., Orth, R.J., Duarte, C.M., Eds.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Davies, P.; Morvan, C.; Sire, O.; Baley, C. Structure and properties of fibres from sea-grass (Zostera marina). J. Mater. Sci. 2007, 42, 4850–4857. [Google Scholar] [CrossRef]
- Fonseca, M.S.; Koehl, M.A.R.; Kopp, B.S. Biomechanical factors contributing to self-organization in seagrass landscapes. J. Exp. Mar. Biol. Ecol. 2007, 340, 227–246. [Google Scholar] [CrossRef]
- Gaylord, B.; Denny, M.W. Flow and flexibility: I. Effects of size, shape and stiffness in determining wave forces on the stipitate kelps Eisenia arborea and Pterygophora californica. J. Exp. Biol. 1997, 200, 3141–3164. [Google Scholar] [PubMed]
- Denny, M.W.; Gaylord, B. The mechanics of wave-swept algae. J. Exp. Biol. 2002, 205, 1355–1362. [Google Scholar] [PubMed]
- Harder, D.L.; Hurd, C.L.; Speck, T. Comparison of mechanical properties of four large, wave-exposed seaweeds. Am. J. Bot. 2006, 93, 1426–1432. [Google Scholar] [CrossRef] [PubMed]
- Mach, K.J.; Hale, B.B.; Denny, M.W.; Nelson, D.V. Death by small forces: A fracture and fatigue analysis of wave-swept macroalgae. J. Exp. Biol. 2007, 210, 2231–2243. [Google Scholar] [CrossRef] [PubMed]
- Brewer, C.A.; Parker, M. Adaptations of macrophytes to life in moving water: Upslope limits and mechanical properties of stems. Hydrobiologia 1990, 194, 133–142. [Google Scholar] [CrossRef]
- Bociąg, K.; Gałka, A.; Łazarewicz, T.; Szmeja, J. Mechanical strenght of stems in aquatic macrophytes. Acta Soc. Bot. Pol. 2009, 78, 181–187. [Google Scholar] [CrossRef]
- Miler, O.; Albayrak, I.; Nikora, V.; O’Hare, M. Biomechanical properties and morphological characteristics of lake and river plants: Implications for adaptations to flow conditions. Aquat. Sci. 2014, 76, 465–481. [Google Scholar] [CrossRef]
- Łoboda, A.M.; Bialik, R.J.; Karpiński, M.; Przyborowski, Ł. Seasonal changes in the biomechanical properties of Elodea canadensis Michx. Aquat. Bot. 2018, 147, 43–51. [Google Scholar] [CrossRef]
- Łoboda, A.M.; Bialik, R.J.; Karpiński, M.; Przyborowski, Ł. Two simultaneously occurring Potamogeton species: Similarities and differences in seasonal changes of biomechanical properties. Pol. J. Environ. Stud. 2019. accepted. [Google Scholar] [CrossRef]
- Schutten, J.; Dainty, J.; Davy, A.J. Root anchorage and its significance for submerged plants in shallow lakes. J. Ecol. 2005, 93, 556–571. [Google Scholar] [CrossRef]
- Sand-Jensen, K. Drag and reconfiguration of freshwater macrophytes. Freshw. Biol. 2003, 48, 271–283. [Google Scholar] [CrossRef]
- Nepf, H.; Ghisalberti, M. Flow and transport in channels with submerged vegetation. Acta Geophys. 2008, 56, 753–777. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. From the blade scale to the reach scale: A characterization of aquatic vegetative drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Rowiński, P.M. Vertical velocity distributions through and above submerged, flexible vegetation. Hydrol. Sci. J. 2008, 53, 905–920. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Rowiński, P.M. Influence of a method of evaluation of the curvature of flexible vegetation elements on vertical distributions of flow velocities. Acta Geophys. 2012, 60, 1098–1119. [Google Scholar] [CrossRef]
- Hui, E.Q.; Hu, X.E.; Jiang, C.B.; Zhu, Z.D. A study of drag coefficient related with vegetation based on the flume experiment. J. Hydrodyn. 2010, 22, 329–337. [Google Scholar] [CrossRef]
- Albayrak, I.; Nikora, V.; Miler, O.; O’Hare, M.T. Flow–plant interactions at leaf, stem and shoot scales: Drag, turbulence, and biomechanics. Aquat. Sci. 2014, 76, 269–294. [Google Scholar] [CrossRef]
- Liu, X.; Zeng, Y. Drag coefficient for rigid vegetation in subcritical open-channel flow. Environ. Fluid Mech. 2017, 17, 1035–1050. [Google Scholar] [CrossRef]
- Albayrak, I.; Nikora, V.; Miler, O.; O’Hare, M. Flow-plant interactions at a leaf scale: Effects of leaf shape, serration, roughness and flexural rigidity. Aquat. Sci. 2012, 74, 267–286. [Google Scholar] [CrossRef]
- Rominger, J.T.; Nepf, H.M. Effects of blade flexural rigidity on drag force and mass transfer rates in model blades. Limnol. Oceanogr. 2014, 59, 2028–2041. [Google Scholar] [CrossRef]
- Tsujimoto, T. Fluvial processes in streams with vegetation. J. Hydraul. Res. 1999, 37, 789–803. [Google Scholar] [CrossRef]
- Tanaka, N. Vegetation bioshields for tsunami mitigation: Review of effectiveness, limitations, construction, and sustainable management. Landsc. Ecol. Eng. 2009, 5, 71–79. [Google Scholar] [CrossRef]
- Shih, S.S.; Hong, S.S.; Chang, T.J. Flume Experiments for Optimizing the Hydraulic Performance of a Deep-Water Wetland Utilizing Emergent Vegetation and Obstructions. Water 2016, 8, 265. [Google Scholar] [CrossRef]
- Westlake, D.F.; Dawson, F.H. The effects of autumnal weed cuts in a lowland stream on water levels and flooding in the following spring. Verh. Int. Ver. Limnol. 1988, 23, 1273–1277. [Google Scholar] [CrossRef]
- Dawson, F.H. Ecology and Management of Water Plants in Lowland Streams; Report of the Freshwater Biological Association; Freshwater Biological Association: Ambleside, UK, 1989; Volume 57, pp. 43–60. [Google Scholar]
- ASTM D790-03. In Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials; ASTM International: West Conshohocken, PA, USA, 2003.
- Bialik, R.J.; Karpiński, M.; Rajwa, A.; Luks, B.; Rowiński, P.M. Bedform characteristics in natural and regulated channels: A comparative field study on the Wilga River, Poland. Acta Geophys. 2014, 62, 1413–1434. [Google Scholar] [CrossRef]
- Fukushima, T.; Sato, K. Lodging of cabbage seedling due to its own weight. Biosyst. Eng. 2009, 103, 438–444. [Google Scholar] [CrossRef]
- Falk, S.; Hertz, C.H.; Virgin, H.I. On the relation between turgor pressure and tissue rigidity. I. Physiol. Plant. 1958, 11, 802–817. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant Biomechanics. An Engineering Approach to Plant Form and Function; University of Chicago Press: Chicago, IL, USA, 1992; ISBN 0-226-58641-6. [Google Scholar]
- Chambers, P.A.; Kalff, J. Light and nutrients in the control of aquatic plant community structure. I. In situ experiments. J. Ecol. 1987, 75, 611–619. [Google Scholar] [CrossRef]
- Chambers, P.A. Light and nutrients in the control of aquatic plant community structure. II. In situ observations. J. Ecol. 1987, 75, 621–628. [Google Scholar] [CrossRef]
- Zalewska-Gałosz, J. Occurrence and distribution of Potamogeton hybrids (Potamogetonaceae) in Poland. Feddes Repert. 2002, 113, 380–393. [Google Scholar] [CrossRef]
- Nepf, H.M.; Koch, E.W.K. Vertical secondary flows in submersed plant-like arrays. Limnol. Oceanogr. 1999, 44, 1072–1080. [Google Scholar] [CrossRef]
- Järvelä, J. Effect of submerged flexible vegetation on flow structure and resistance. J. Hydrol. 2005, 307, 233–241. [Google Scholar] [CrossRef]
- Righetti, M. Flow analysis in a channel with flexible vegetation using double-averaging method. Acta Geophys. 2008, 56, 801–823. [Google Scholar] [CrossRef]
- Kałuża, T.; Tymiński, T. Analysis of the flow resistance in zones with flexible vegetation. Infrastruct. Ecol. Rural Areas 2010, 8, 79–91. (In Polish) [Google Scholar]
- Baptist, M.J. A flume experiment on sediment transport with flexible, submerged vegetation. In Proceedings of the International Workshop on RIParian FORest Vegetated Channels: Hydraulic, Morphological and Ecological Aspects, RIPFOR, Trento, Italy, 20–22 February 2003. [Google Scholar]
- Velasco, D.; Bateman, A.; Redondo, J.M.; DeMedina, V. An open channel flow experimental and theoretical study of resistance and turbulent characterization over flexible vegetated linings. Flow Turbul. Combust. 2003, 70, 69–88. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G.G.; Albertson, J.D. Momentum transfer and turbulent kinetic energy budgets within a dense model canopy. Bound.-Layer Meteorol. 2004, 111, 589–614. [Google Scholar] [CrossRef]
- Huai, W.X.; Zeng, Y.H.; Xu, Z.G.; Yang, Z.H. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation. Adv. Water Resour. 2009, 32, 487–492. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Rowiński, P.M. Application of one-dimensional model to calculate water velocity distributions over elastic elements simulating Canadian waterweed plants (Elodea Canadensis). Acta Geophys. 2013, 61, 194–210. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Kiczko, A. Experimental Investigation of Kinetic Energy and Momentum Coefficients in Regular Channels with Stiff and Flexible Elements Simulating Submerged Vegetation. Acta Geophys. 2015, 63, 1405–1422. [Google Scholar] [CrossRef]
- Ortiz, A.C.; Ashton, A.; Nepf, H. Mean and turbulent velocity fields near rigid and flexible plants and the implications for deposition. J. Geophys. Res.-Earth 2013, 118, 2585–2599. [Google Scholar] [CrossRef]
 represents case 1, and the blue line
represents case 1, and the blue line  represents case 2.
represents case 2.
 represents case 1, and the blue line
represents case 1, and the blue line  represents case 2.
represents case 2.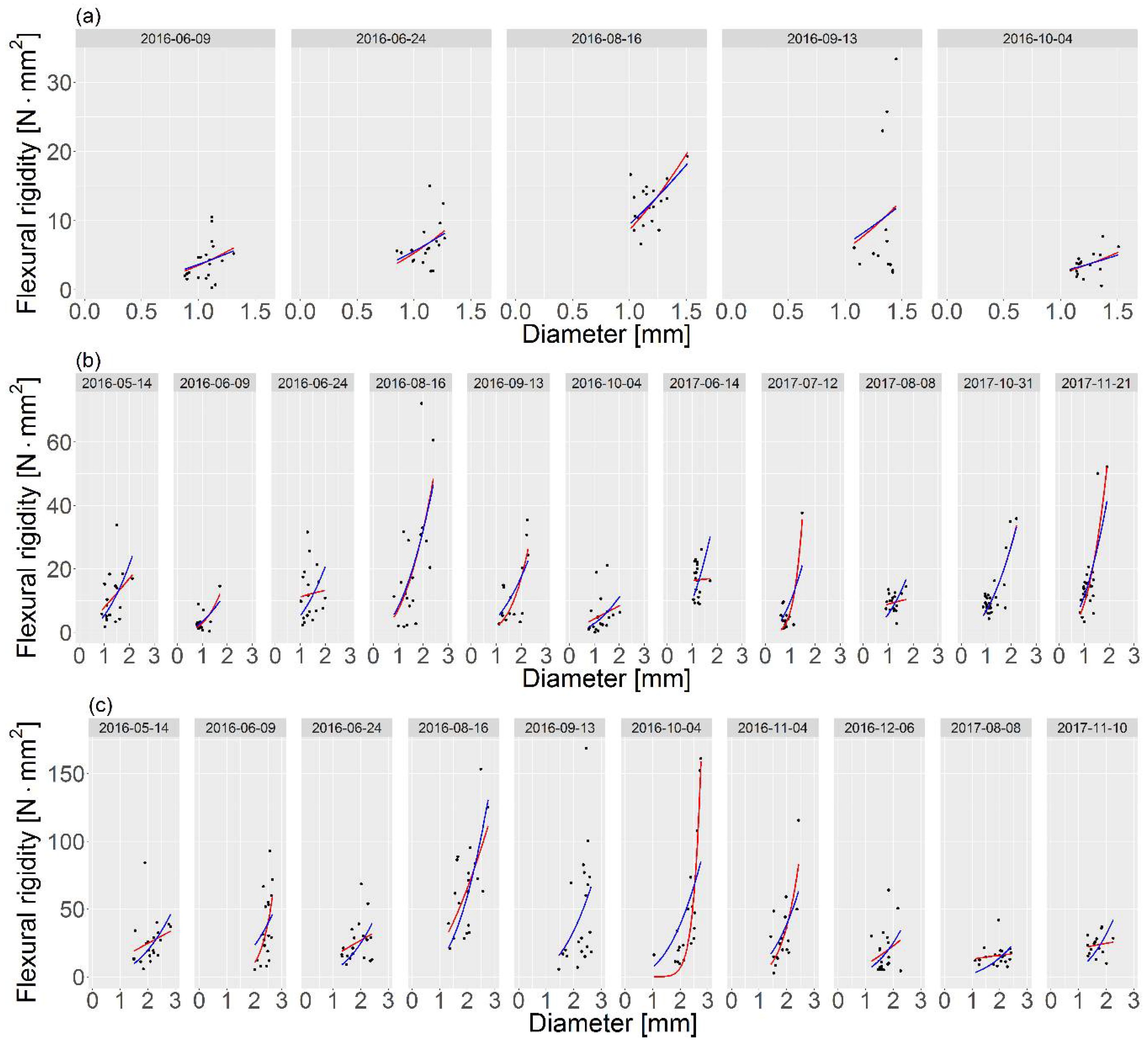
| E. canadensis | |||||||||
| Date of Collection | Mean Stem Diameter * | Mean Flexural Modulus * | Case 1 | Case 2 | MSE Relative Diff. | ||||
| [mm] | [MPa] | a | b | MSE | a | b | MSE | [%] | |
| 2016-06-09 | 1.07 | 62.54 | 3.47 | 2.20 | 6.51 | 3.67 |  | 6.58 | 1.08 |
| 2016-06-24 | 1.10 | 95.32 | 3.36 | 1.93 | 8.19 | 5.59 | 8.23 | 0.49 | |
| 2016-08-16 | 1.18 | 141.20 | 10.32 | 1.14 | 7.64 | 9.47 | 1.60 | 7.97 | 4.32 |
| 2016-09-13 | 1.37 | 60.07 | 5.49 | 2.03 | 75.86 | 6.36 |  | 76.09 | 0.30 |
| 2016-10-04 | 1.24 | 32.31 | 2.22 | 2.31 | 2.27 | 2.63 | 2.33 | 2.64 | |
| P. pectinatus | |||||||||
| Date of Collection | Mean stem Diameter ** | Mean Flexural Modulus ** | Case 1 | Case 2 | MSE Relative Diff. | ||||
| [mm] | [MPa] | a | b | MSE | a | b | MSE | [%] | |
| 2016-05-14 | 1.30 | 94.51 | 7.93 | 1.10 | 49.70 | 5.41 |  | 55.99 | 12.66 |
| 2016-06-09 | 0.97 | 86.59 | 2.93 | 2.66 | 6.39 | 3.45 | 6.75 | 5.63 | |
| 2016-06-24 | 1.37 | 90.18 | 11.16 | 0.24 | 62.14 | 5.26 | 81.85 | 31.72 | |
| 2016-08-16 | 1.56 | 94.09 | 7.26 | 2.17 | 212.51 | 8.20 | 213.32 | 0.38 | |
| 2016-09-13 | 1.68 | 36.66 | 1.74 | 3.31 | 49.88 | 4.44 | 54.80 | 9.86 | |
| 2016-10-04 | 1.26 | 55.08 | 4.26 | 0.98 | 30.49 | 2.91 | 1.98 | 32.43 | 6.36 |
| 2017-06-14 | 1.22 | 168.50 | 16.32 | 0.07 | 26.49 | 10.35 |  | 43.03 | 62.44 |
| 2017-07-12 | 0.84 | 252.97 | 6.55 | 4.32 | 14.71 | 9.70 | 31.96 | 117.27 | |
| 2017-08-08 | 1.21 | 109.72 | 8.89 | 0.28 | 8.04 | 5.75 | 13.19 | 64.05 | |
| 2017-10-31 | 1.24 | 117.56 | 6.77 | 2.02 | 18.15 | 6.90 | 18.17 | 0.11 | |
| 2017-11-21 | 1.17 | 174.56 | 9.18 | 2.69 | 43.26 | 11.49 | 50.22 | 16.09 | |
| P. crispus | |||||||||
| Date of Collection | Mean Stem Diameter ** | Mean Flexural Modulus ** | Case 1 | Case 2 | MSE Relative Diff. | ||||
| [mm] | [MPa] | a | b | MSE | a | b | MSE | [%] | |
| 2016-05-14 | 2.10 | 33.54 | 13.28 | 0.89 | 261.59 | 3.57 |  | 299.24 | 14.37 |
| 2016-06-09 | 2.43 | 19.78 | 0.12 | 6.29 | 395.53 | 4.16 | 451.57 | 14.18 | |
| 2016-06-24 | 1.87 | 51.59 | 14.99 | 0.84 | 194.40 | 4.53 | 247.34 | 27.28 | |
| 2016-08-16 | 1.97 | 105.21 | 20.86 | 1.65 | 706.28 | 10.82 | 781.83 | 10.69 | |
| 2016-09-13 | 2.23 | 36.38 | 6.23 | 2.45 | 1329.52 | 6.17 | 2.46 | 1329.53 | 0 |
| 2016-10-04 | 2.21 | 43.17 | 0.01 | 9.90 | 349.31 | 7.06 |  | 1062.55 | 204.18 |
| 2016-11-04 | 1.84 | 55.22 | 2.17 | 4.10 | 275.05 | 7.09 | 323.51 | 17.64 | |
| 2016-12-06 | 1.70 | 52.71 | 8.64 | 1.35 | 239.71 | 4.57 | 248.21 | 3.55 | |
| 2017-08-08 | 1.90 | 38.50 | 12.93 | 0.29 | 51.47 | 2.56 | 81.82 | 59.14 | |
| 2017-11-10 | 1.65 | 77.41 | 20.40 | 0.27 | 54.41 | 5.72 | 114.66 | 110.85 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łoboda, A.M.; Karpiński, M.; Bialik, R.J. On the Relationship between Aquatic Plant Stem Characteristics and Drag Force: Is a Modeling Application Possible? Water 2018, 10, 540. https://doi.org/10.3390/w10050540
Łoboda AM, Karpiński M, Bialik RJ. On the Relationship between Aquatic Plant Stem Characteristics and Drag Force: Is a Modeling Application Possible? Water. 2018; 10(5):540. https://doi.org/10.3390/w10050540
Chicago/Turabian StyleŁoboda, Anna Maria, Mikołaj Karpiński, and Robert Józef Bialik. 2018. "On the Relationship between Aquatic Plant Stem Characteristics and Drag Force: Is a Modeling Application Possible?" Water 10, no. 5: 540. https://doi.org/10.3390/w10050540
APA StyleŁoboda, A. M., Karpiński, M., & Bialik, R. J. (2018). On the Relationship between Aquatic Plant Stem Characteristics and Drag Force: Is a Modeling Application Possible? Water, 10(5), 540. https://doi.org/10.3390/w10050540






