Evaluation and Hydrological Simulation of CMADS and CFSR Reanalysis Datasets in the Qinghai-Tibet Plateau
Abstract
1. Introduction
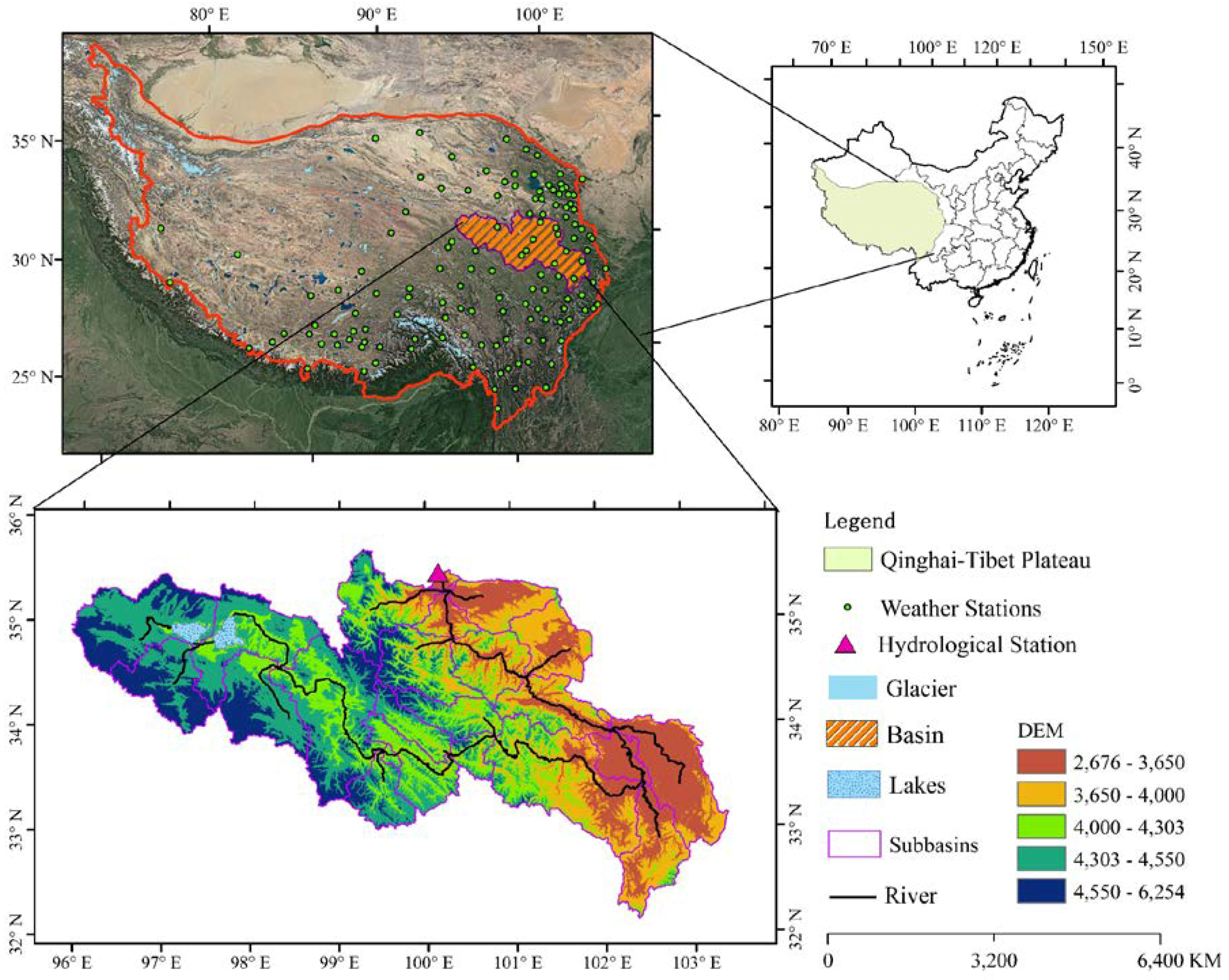
2. Study Area
3. Data and Methods
3.1. Data
3.2. Hydrological Models
3.3. Spatial Analysis Methods
3.4. Evaluation Index
4. Results
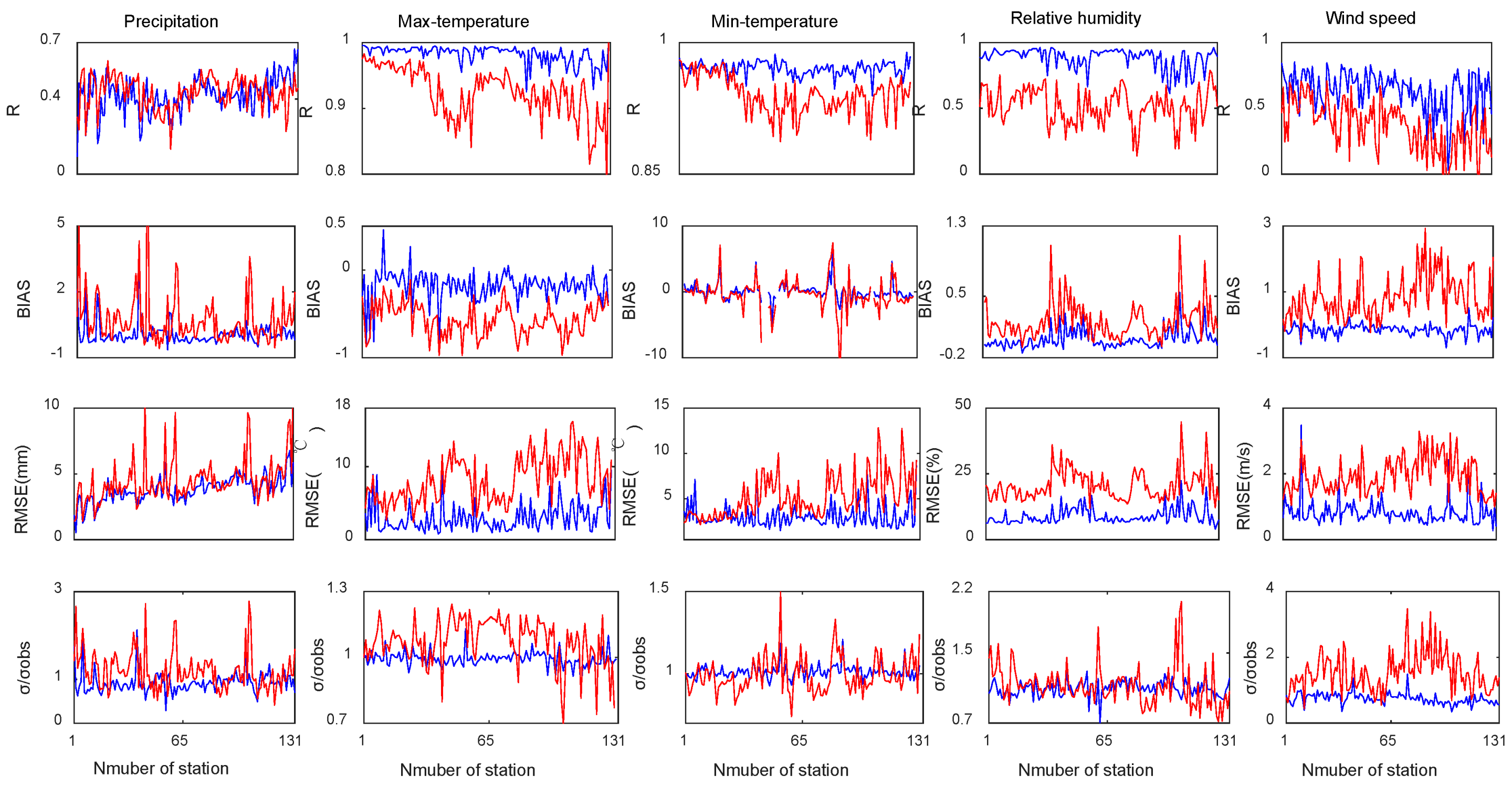
4.1. Comparison of CMADS and CFSR with Observation Data
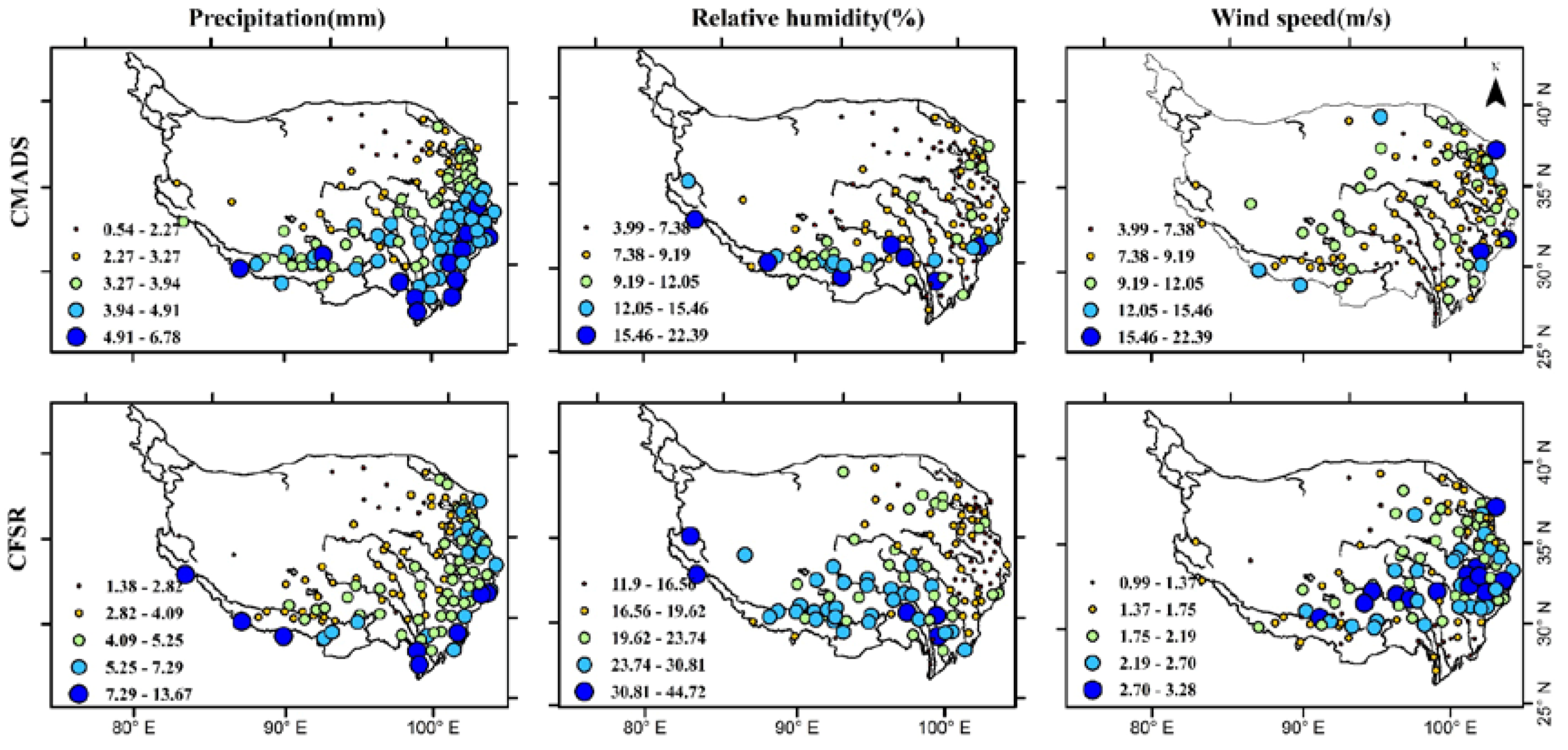
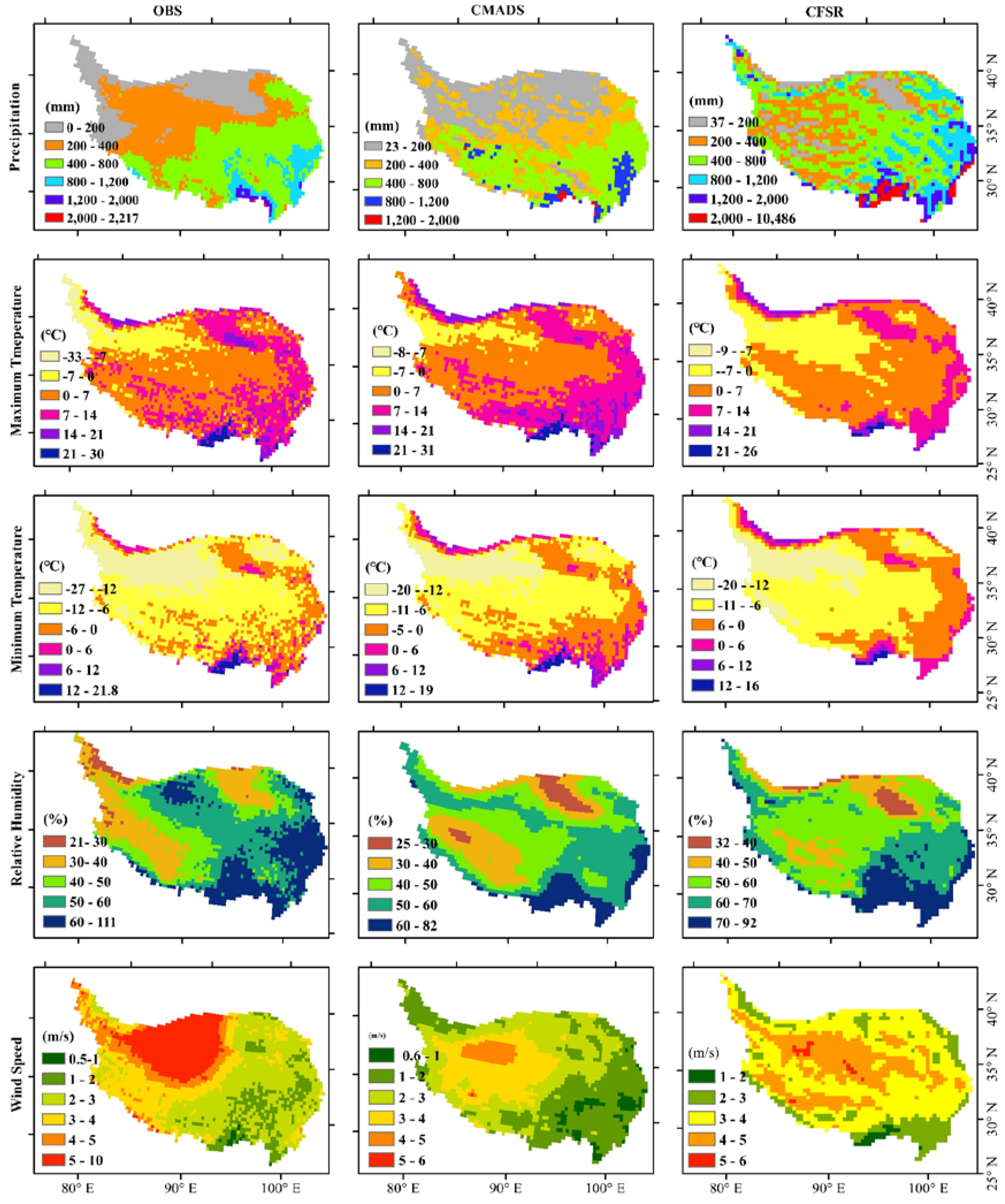
4.2. Distribution of Observed Data, CMADS and CFSR
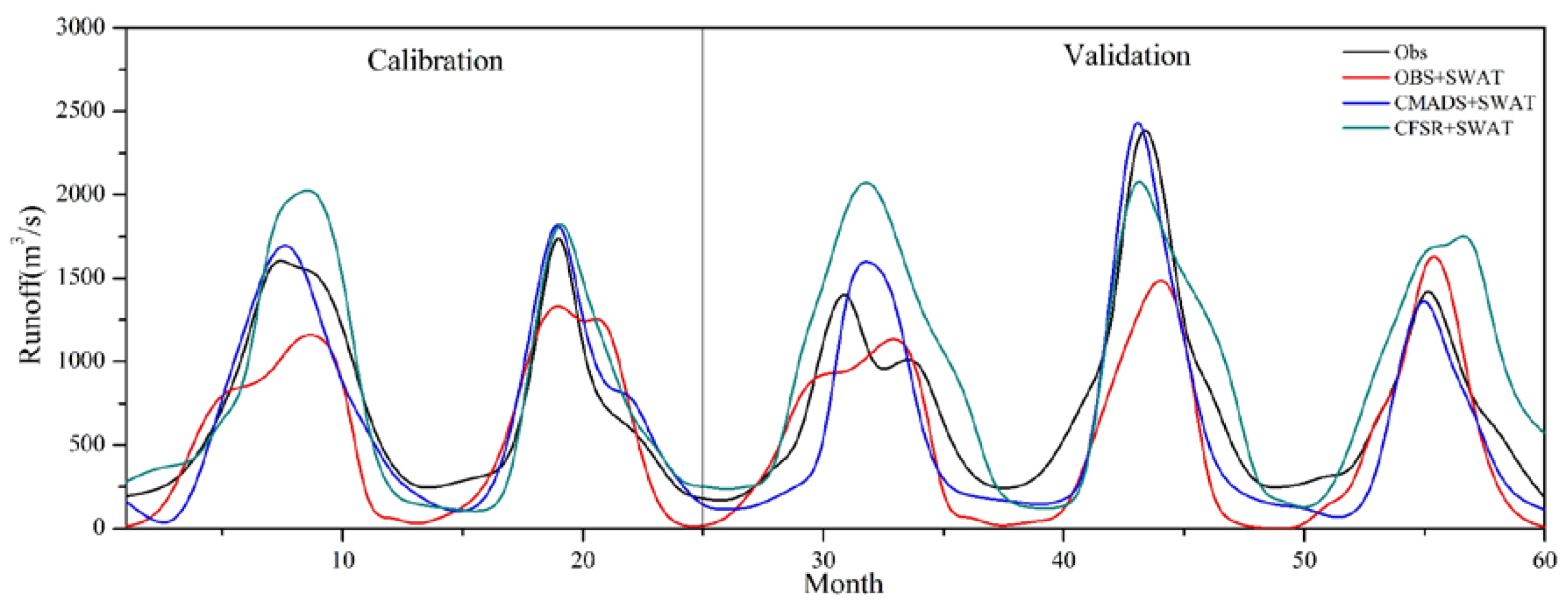
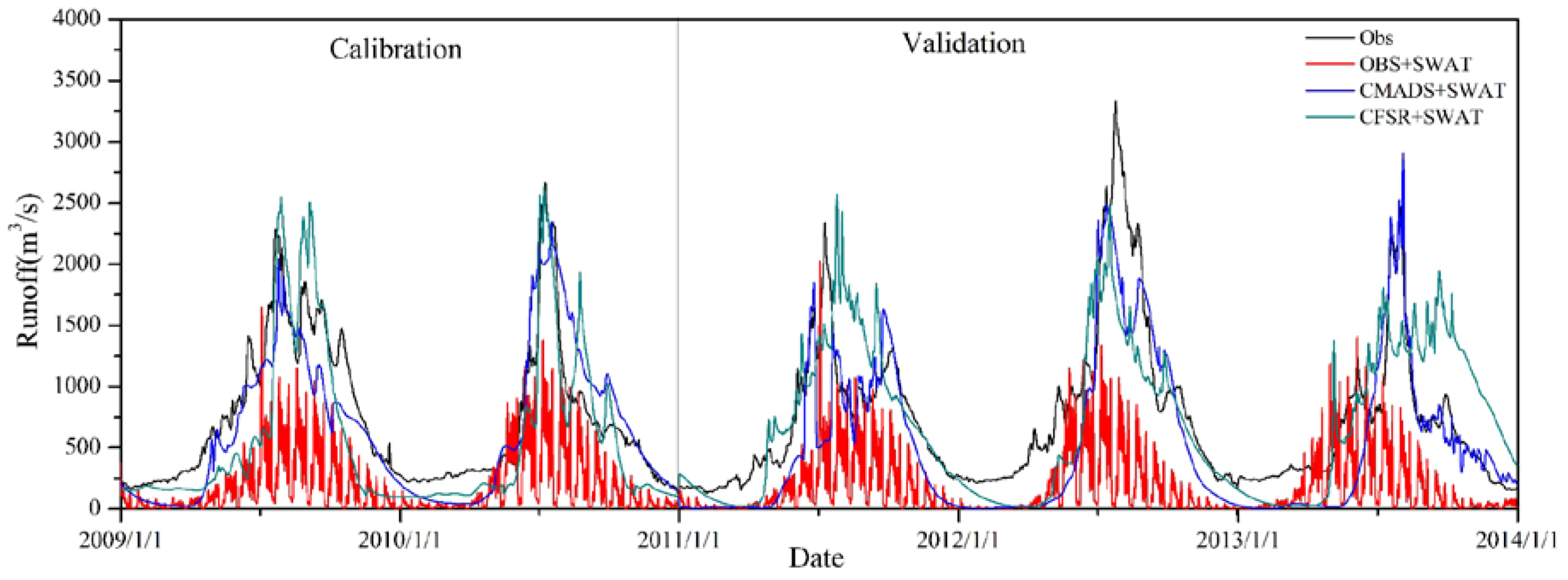
4.3. Runoff Simulation in the Yellow River Source Basin
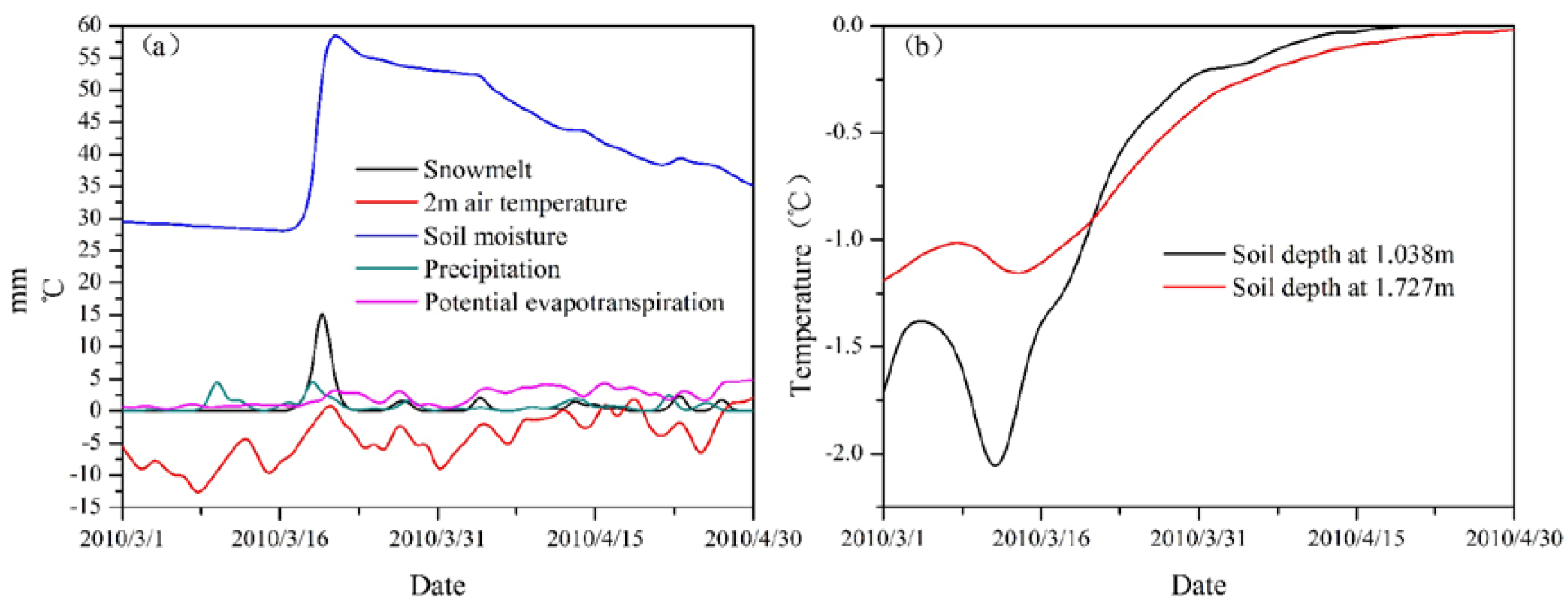
4.4. Analysis of Snowmelt and Related variables
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qiu, J. The Third Pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Kong, D.; Shi, P.; Singh, V.P.; Sun, P. Vegetation phenology on the Qinghai-Tibetan Plateau and its response to climate change (1982–2013). Agric. For. Meteorol. 2018, 248, 408–417. [Google Scholar] [CrossRef]
- Zhou, J.; Pomeroy, J.W.; Zhang, W.; Cheng, G.; Wang, G.; Chen, C. Simulating cold regions hydrological processes using a modular model in the west of China. J. Hydrol. 2014, 509, 13–24. [Google Scholar] [CrossRef]
- Silberstein, R.P. Hydrological models are so good, do we still need data? Environ. Model. Softw. 2006, 21, 1340–1352. [Google Scholar] [CrossRef]
- Sun, W.; Ishidaira, H.; Bastola, S.; Yu, J. Estimating daily time series of streamflow using hydrological model calibrated based on satellite observations of river water surface width: Toward real world applications. Environ. Res. 2015, 139, 36–45. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Yang, Y.; Han, Z.; Tang, G.; Maguire, L.; Chu, Z.; Hong, Y. Comprehensive evaluation of Ensemble Multi-Satellite Precipitation Dataset using the Dynamic Bayesian Model Averaging scheme over the Tibetan plateau. J. Hydrol. 2018, 556, 634–644. [Google Scholar] [CrossRef]
- Huang, D.; Gao, S. Impact of different reanalysis data on WRF dynamical downscaling over China. Atmos. Res. 2018, 200, 25–35. [Google Scholar] [CrossRef]
- Agutu, N.O.; Awange, J.L.; Zerihun, A.; Ndehedehe, C.E.; Kuhn, M.; Fukuda, Y. Assessing multi-satellite remote sensing, reanalysis, and land surface models’ products in characterizing agricultural drought in East Africa. Remote Sens. Environ. 2017, 194, 287–302. [Google Scholar] [CrossRef]
- Moalafhi, D.B.; Sharma, A.; Evans, J.P. Reconstructing hydro-climatological data using dynamical downscaling of reanalysis products in data-sparse regions—Application to the Limpopo catchment in southern Africa. J. Hydrol. Reg. Stud. 2017, 12, 378–395. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Sharp, E.; Dodds, P.; Barrett, M.; Spataru, C. Evaluating the accuracy of CFSR reanalysis hourly wind speed forecasts for the UK, using in situ measurements and geographical information. Renew. Energy 2015, 77, 527–538. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Chen, Q.; Bi, H.; Qiu, J.; Zou, P. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.-Y.; Chen, S.; Chen, H. Similarity and difference of global reanalysis datasets (WFD and APHRODITE) in driving lumped and distributed hydrological models in a humid region of China. J. Hydrol. 2016, 542, 343–356. [Google Scholar] [CrossRef]
- Tomy, T.; Sumam, K.S. Determining the Adequacy of CFSR Data for Rainfall-Runoff Modeling Using SWAT. Procedia Technol. 2016, 24, 309–316. [Google Scholar] [CrossRef]
- Wang, X.; Pang, G.; Yang, M.; Zhao, G. Evaluation of climate on the Tibetan Plateau using ERA-Interim reanalysis and gridded observations during the period 1979–2012. Quat. Int. 2017, 444, 76–86. [Google Scholar] [CrossRef]
- Gao, L.; Hao, L.; Chen, X.-W. Evaluation of ERA-interim monthly temperature data over the Tibetan Plateau. J. Mt. Sci. 2014, 11, 1154–1168. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L.; Ye, Q. Precipitation variability in High Mountain Asia from multiple datasets and implication for water balance analysis in large lake basins. Glob. Planet. Chang. 2016, 145, 20–29. [Google Scholar] [CrossRef]
- You, Q.; Min, J.; Zhang, W.; Pepin, N.; Kang, S. Comparison of multiple datasets with gridded precipitation observations over the Tibetan Plateau. Clim. Dyn. 2014, 45, 791–806. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X. Evaluation of multireanalysis products with in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Poméon, T.; Jackisch, D.; Diekkrüger, B. Evaluating the performance of remotely sensed and reanalysed precipitation data over West Africa using HBV light. J. Hydrol. 2017, 547, 222–235. [Google Scholar] [CrossRef]
- Essou, G.R.C.; Brissette, F.; Lucas-Picher, P. Impacts of combining reanalyses and weather station data on the accuracy of discharge modelling. J. Hydrol. 2017, 545, 120–131. [Google Scholar] [CrossRef]
- Kan, B.Y.; Su, F.G.; Tong, K.; Zhang, L.L. Analysis of the Applicability of Four Precipitation Datasets in the Upper Reaches of the Yarkant River, the Karakorum. J. Glaciol. Geocryol. 2013, 35, 710–722. [Google Scholar]
- Guo, Y.; Wang, Z.; Wu, Y. Comparison of applications of different reanalyzed precipitation data in the Lhasa River Basin based on HIMS model. Prog. Geogr. 2017, 36, 1033–1039. [Google Scholar]
- Gao, R.; Mu, Z.; Peng, L.; Z, Y.; Yin, Z.; Tang, R. Application of CFSR and ERA-Interim Reanalysis Data in Runoff Simulation in High Cold Alpine Area. Water Resour. Power 2017, 35, 8–12. [Google Scholar]
- Malago, A.; Bouraoui, F.; Vigiak, O.; Grizzetti, B.; Pastori, M. Modelling water and nutrient fluxes in the Danube River Basin with SWAT. Sci. Total Environ. 2017, 603–604, 196–218. [Google Scholar] [CrossRef] [PubMed]
- Patil, A.; Ramsankaran, R. Improving streamflow simulations and forecasting performance of SWAT model by assimilating remotely sensed soil moisture observations. J. Hydrol. 2017, 555, 683–696. [Google Scholar] [CrossRef]
- Vellei, M.; Herrera, M.; Fosas, D.; Natarajan, S. The influence of relative humidity on adaptive thermal comfort. Build. Environ. 2017, 124, 171–185. [Google Scholar] [CrossRef]
- Xiong, Y.; Meng, Q.-S.; Gao, J.; Tang, X.-F.; Zhang, H.-F. Effects of relative humidity on animal health and welfare. J. Integr. Agric. 2017, 16, 1653–1658. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, H.; Wang, D.; Wang, G.; Wu, J.; Bian, J.; Liu, J. A new method for wind speed forecasting based on copula theory. Environ. Res. 2018, 160, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Sedaghat, A.; Hassanzadeh, A.; Jamali, J.; Mostafaeipour, A.; Chen, W.-H. Determination of rated wind speed for maximum annual energy production of variable speed wind turbines. Appl. Energy 2017, 205, 781–789. [Google Scholar] [CrossRef]
- Li, T.; Li, J. A 564-year annual minimum temperature reconstruction for the east central Tibetan Plateau from tree rings. Glob. Planet. Chang. 2017, 157, 165–173. [Google Scholar] [CrossRef]
- Villarini, G.; Khouakhi, A.; Cunningham, E. On the impacts of computing daily temperatures as the average of the daily minimum and maximum temperatures. Atmos. Res. 2017, 198, 145–150. [Google Scholar] [CrossRef]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: An application in the Blue Nile River Basin. JAWRA J. Am. Water Resour. Assoc. 2014, 50, 1226–1241. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Yen, H.; Collick, A.S.; Tilahun, S.A.; Langan, S.; Steenhuis, T.S. Evaluation of CFSR, TMPA 3B42 and ground-based rainfall data as input for hydrological models, in data-scarce regions: The upper Blue Nile Basin, Ethiopia. Catena 2017, 152, 242–251. [Google Scholar] [CrossRef]
- Hu, S.; Qiu, H.; Yang, D.; Cao, M.; Song, J.; Wu, J.; Huang, C.; Gao, Y. Evaluation of the applicability of climate forecast system reanalysis weather data for hydrologic simulation: A case study in the Bahe River Basin of the Qinling Mountains, China. J. Geogr. Sci. 2017, 27, 546–564. [Google Scholar] [CrossRef]
- Tian, L.; Liu, T.; Bao, A.M.; Huang, Y. Application of CFSR Precipitation Dataset inHydrological model for Arid Mountains Area: A Case Study in the Kaidu River Basin. Arid Zone Res. 2017, 34, 755–761. [Google Scholar]
- Meng, X.Y.; Dan, L.Y.; Liu, Z.-H. Energy balance-based SWAT model to simulate the mountain snowmelt and runoff—Taking the application in Juntanghu watershed (China) as an example. J. Mt. Sci. 2015, 12, 368–381. [Google Scholar] [CrossRef]
- Wang, Y.J.; Meng, X.Y.; Liu, Z.H.; Ji, X.N. Snowmelt Runoff Analysis under Generated Climate Change Scenarios for the Juntanghu River Basin, in Xinjiang, China. Tecnología y Ciencias del Agua 2016, 7, 41–54. [Google Scholar]
- Meng, X.Y. Spring Flood Forecasting Based on the WRF-TSRM Mode. Tehnički Vjesnik 2018, 25, 141–151. [Google Scholar]
- Meng, X.; Wang, H.; Lei, X.; Cai, S.; Wu, H.; Ji, X.; Wang, J. Hydrological Modeling in the Manas River Basin Using Soil and Water Assessment Tool Driven by CMADS. Tehnički Vjesnik 2017, 24, 525–534. [Google Scholar]
- Zhu, X.; Wu, T.; Li, R.; Wang, S.; Hu, G.; Wang, W.; Qin, Y.; Yang, S. Characteristics of the ratios of snow, rain and sleet to precipitation on the Qinghai-Tibet Plateau during 1961–2014. Quat. Int. 2017, 444, 137–150. [Google Scholar] [CrossRef]
- Qin, Y.; Yang, D.; Gao, B.; Wang, T.; Chen, J.; Chen, Y.; Wang, Y.; Zheng, G. Impacts of climate warming on the frozen ground and eco-hydrology in the Yellow River source region, China. Sci. Total Environ. 2017, 605–606, 830–841. [Google Scholar] [CrossRef] [PubMed]
- Nicoll, T.; Brierley, G.; Yu, G.A. A broad overview of landscape diversity of the Yellow River source zone. J. Geogr. Sci. 2013, 23, 793–816. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H. Significance of the China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS) of East Asia. Water 2017, 9, 765. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Wu, Y.; Long, A.; Wang, J.; Shi, C.; Ji, X. Investigating spatiotemporal changes of the land-surface processes in Xinjiang using high-resolution CLM3.5 and CLDAS: Soil temperature. Sci. Rep. 2017, 7, 13286. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.X.; Xie, Z.H.; Qian, H.; Liang, M.L.; Yang, X.C. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as weather input data for watershed models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Grusson, Y.; Anctil, F.; Sauvage, S.; Sánchez Pérez, J. Testing the SWAT Model with Gridded Weather Data of Different Spatial Resolutions. Water 2017, 9, 54. [Google Scholar] [CrossRef]
- Hutchinson, M.F.; Gessler, P.E. Splines—More than just a smooth interpolator. Geoderma 1994, 62, 45–67. [Google Scholar] [CrossRef]
- McKenney, D.W.; Pedlar, J.H.; Papadopol, P.; Hutchinson, M.F. The development of 1901–2000 historical monthly climate models for Canada and the United States. Agric. For. Meteorol. 2006, 138, 69–81. [Google Scholar] [CrossRef]
- Liu, Z.H.; Li, L.T.; McVicar, T.R.; Van Niel, T.G.; Yang, Q.K.; Li, R. Introduction of the Professional Interpolation Software for Meteorology Data: ANUSPLINN. Meteorol. Mon. 2008, 34, 92–100. [Google Scholar]
- Wang, J.F.; Li, X.H.; Christakos, G.; Liao, Y.L.; Zhang, T.; Gu, X.; Zheng, X.Y. Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, Q.; Lin, Q.; Cai, C. Quantitative analysis of the impacts of terrestrial environmental factors on precipitation variation over the Beibu Gulf Economic Zone in Coastal Southwest China. Sci. Rep. 2017, 7, 44412. [Google Scholar] [CrossRef] [PubMed]
- Golkar, F.; Sabziparvar, A.A.; Khanbilvardi, R.; Nazemosadat, M.J.; Parsa, S.Z.; Rezaei, Y. Estimation of instantaneous air temperature using remote sensing data. Int. J. Remote Sens. 2018, 39, 258–275. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25°global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Sheng, H.U.; Cao, M.; Qiu, H.; Song, J.; Jiang, W.U.; Yu, G.; Jingzhong, L.I.; Sun, K. Applicability evaluation of CFSR climate data for hydrologic simulation: A case study in the Bahe River Basin. Acta Geogr. Sin. 2016, 71, 1571–1587. [Google Scholar]
- Zeng-Yun, H.U.; Yong-Yong, N.I.; Shao, H.; Yin, G.; Yan, Y.; Jia, C.J. Applicability study of CFSR, ERA-Interim and MERRA precipitation estimates in Central Asia. Arid Land Geogr. 2013, 36, 700–708. [Google Scholar]
- Wang, J.Z.; Liu, Z.H.; Tiyip, T.; Wang, L.; Zhang, B. Thawing Process of Seasonal Frozen Soil on Northern Slope of the Tianshan Mountains During Snowmelt Period. Arid Zone Res. 2017, 34, 282–291. [Google Scholar]
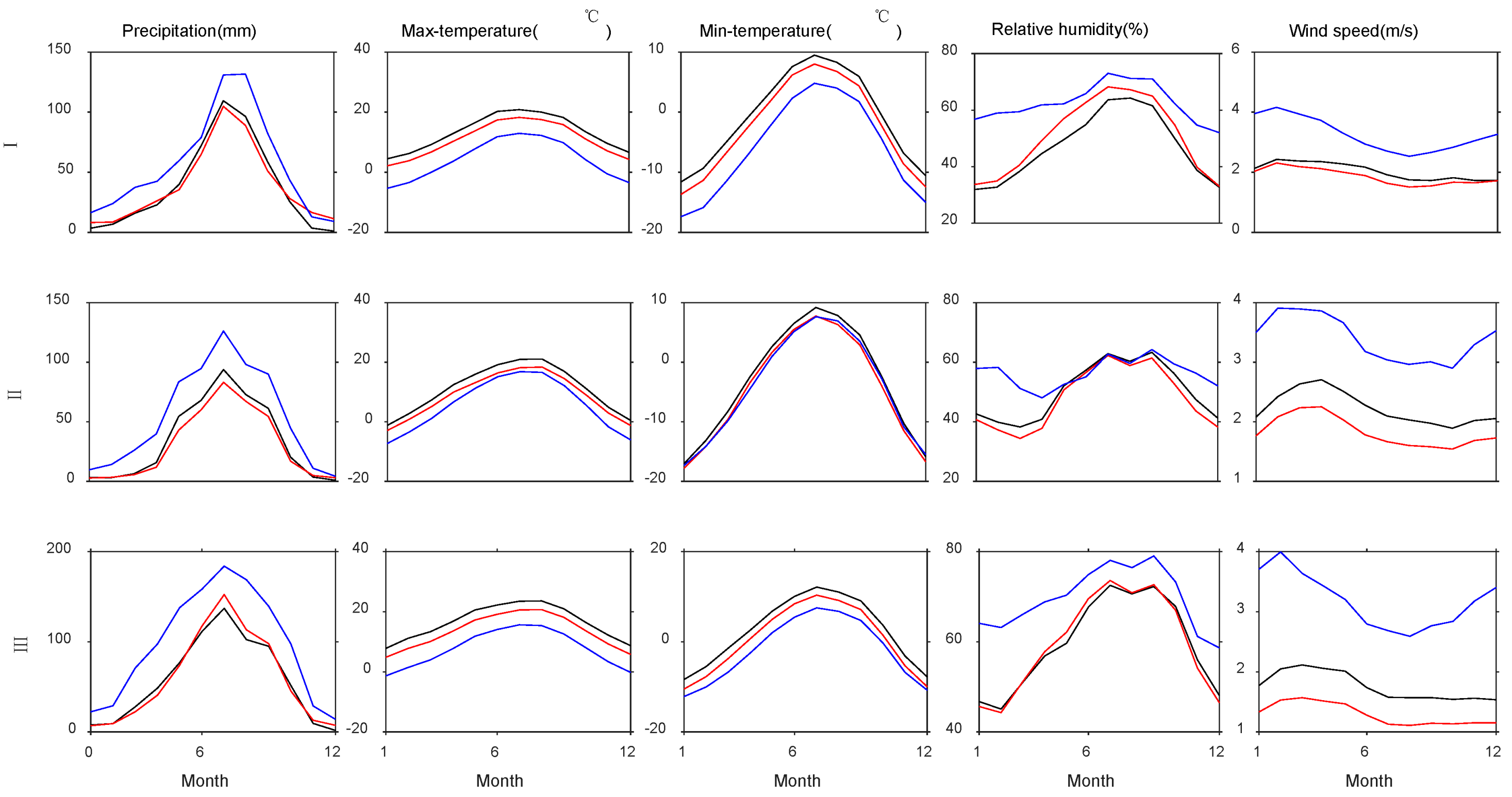
| Datasets | Elements | R | BIAS | RMSE | σ/σobs |
|---|---|---|---|---|---|
| CMADS | Precipitation | 0.46 | 0.08 | 3.77 | 0.92 |
| Max-temperature | 0.98 | −0.18 | 2.99 | 0.99 | |
| Min-temperature | 0.97 | −0.26 | 3.06 | 1.01 | |
| Humidity | 0.88 | 0.01 | 8.92 | 1.09 | |
| Wind speed | 0.64 | −0.15 | 0.83 | 0.74 | |
| CFSR | Precipitation | 0.43 | 0.76 | 4.50 | 1.19 |
| Max-temperature | 0.93 | −0.56 | 8.22 | 1.07 | |
| Min-temperature | 0.94 | −0.95 | 5.21 | 0.99 | |
| Humidity | 0.52 | 0.22 | 20.63 | 1.13 | |
| Wind speed | 0.37 | 0.83 | 1.93 | 1.53 |
| Forcing Data | Monthly | Daily | ||||||
|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | |||||
| R2 | NSE | R2 | NSE | R2 | NSE | R2 | NSE | |
| OBS+SWAT | 0.56 | −0.8 | 0.49 | −0.72 | 0.46 | −0.72 | 0.43 | −0.91 |
| CMADS+SWAT | 0.91 | 0.78 | 0.86 | 0.68 | 0.83 | 0.63 | 0.71 | 0.59 |
| CFSR+SWAT | 0.89 | 0.69 | 0.75 | 0.52 | 0.65 | 0.42 | 0.58 | 0.47 |
| Factors | Pre | Tem | Wind | Solar | PET | SW | Ele | Slope | ST1 |
|---|---|---|---|---|---|---|---|---|---|
| q statistic | 0.32 | 0.72 | 0.24 | 0.57 | 0.34 | 0.63 | 0.04 | 0.04 | 0.49 |
| Factors | ST2 | ST3 | ST4 | ST5 | ST6 | ST7 | ST8 | ST9 | ST10 |
| q statistic | 0.63 | 0.66 | 0.42 | 0.47 | 0.47 | 0.50 | 0.75 | 0.65 | 0.27 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Shanguan, D.; Liu, S.; Ding, Y. Evaluation and Hydrological Simulation of CMADS and CFSR Reanalysis Datasets in the Qinghai-Tibet Plateau. Water 2018, 10, 513. https://doi.org/10.3390/w10040513
Liu J, Shanguan D, Liu S, Ding Y. Evaluation and Hydrological Simulation of CMADS and CFSR Reanalysis Datasets in the Qinghai-Tibet Plateau. Water. 2018; 10(4):513. https://doi.org/10.3390/w10040513
Chicago/Turabian StyleLiu, Jun, Donghui Shanguan, Shiyin Liu, and Yongjian Ding. 2018. "Evaluation and Hydrological Simulation of CMADS and CFSR Reanalysis Datasets in the Qinghai-Tibet Plateau" Water 10, no. 4: 513. https://doi.org/10.3390/w10040513
APA StyleLiu, J., Shanguan, D., Liu, S., & Ding, Y. (2018). Evaluation and Hydrological Simulation of CMADS and CFSR Reanalysis Datasets in the Qinghai-Tibet Plateau. Water, 10(4), 513. https://doi.org/10.3390/w10040513






