The Risk Assessment of River Water Pollution Based on a Modified Non-Linear Model
Abstract
:1. Introduction
2. Materials and Methods
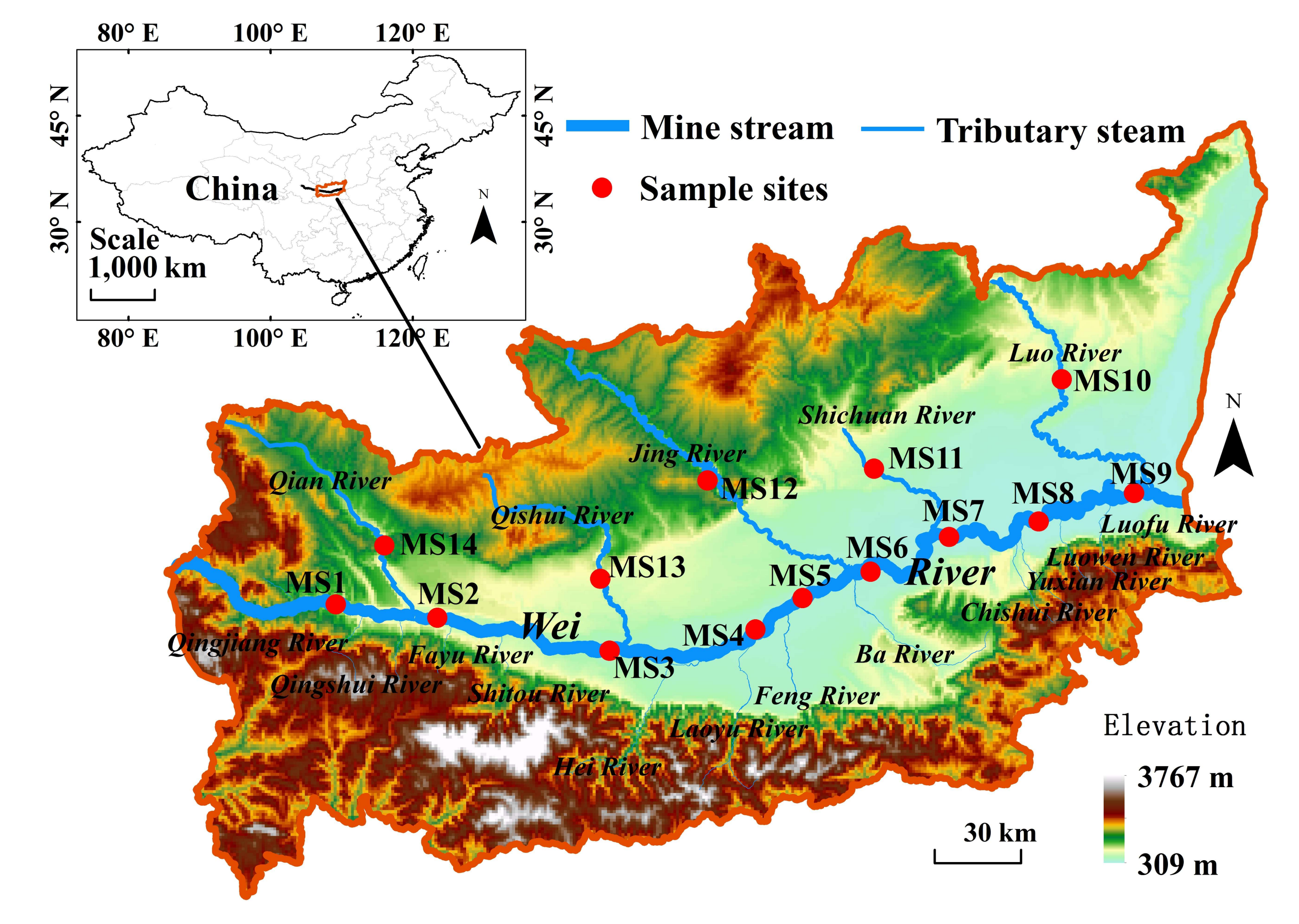
2.1. Study Area and Data
2.2. Assessment Model
3. Results and Discussion
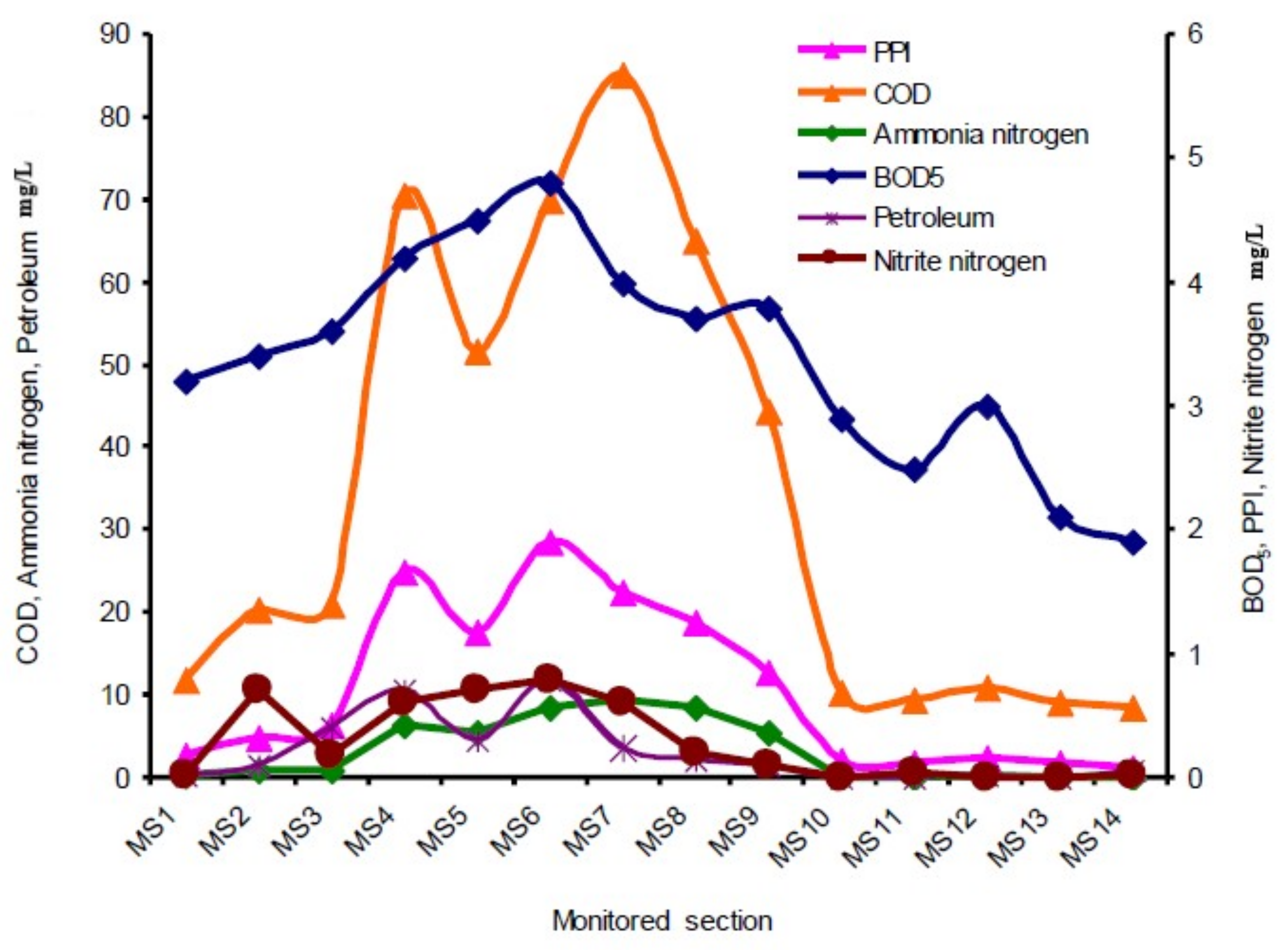
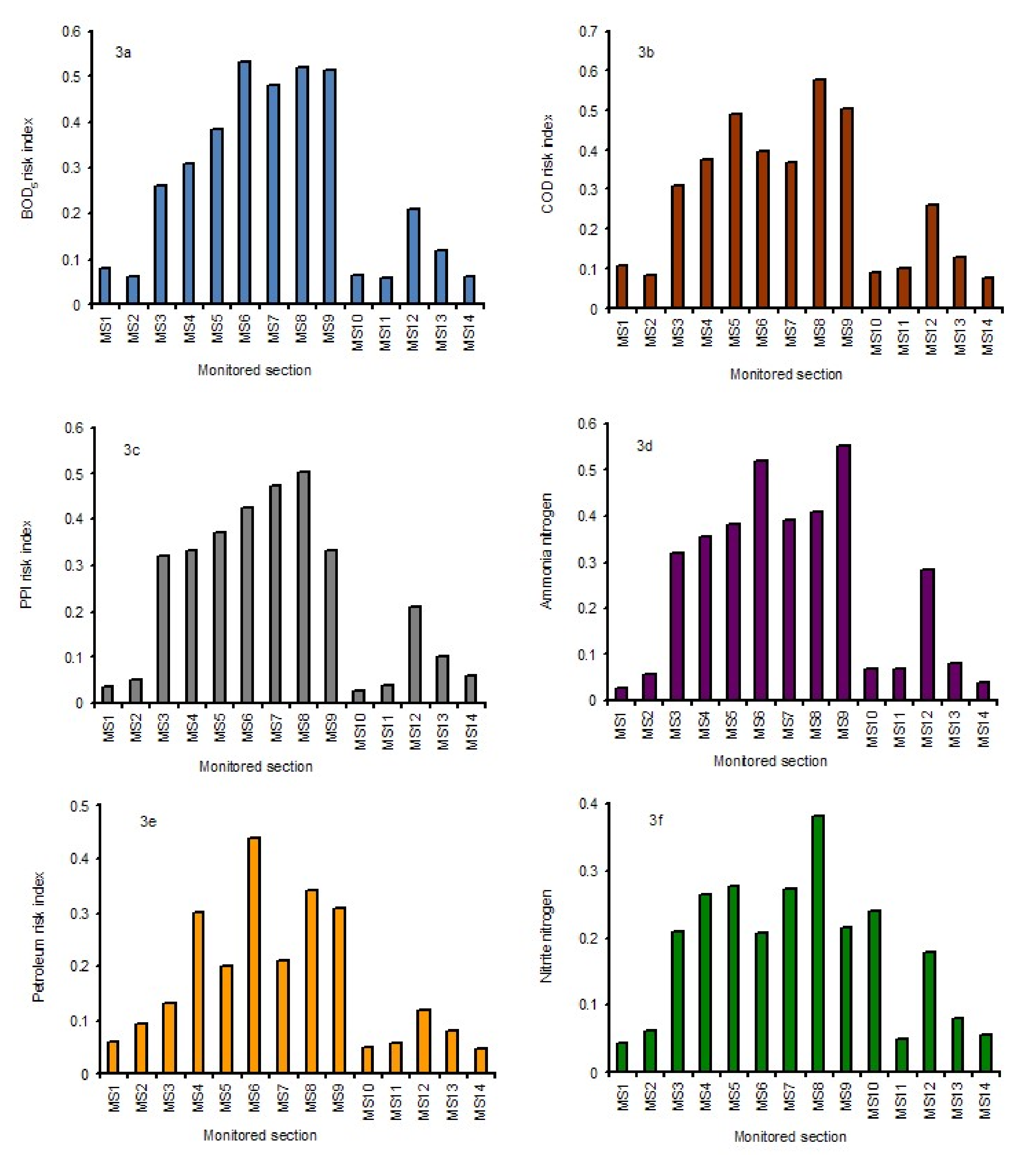
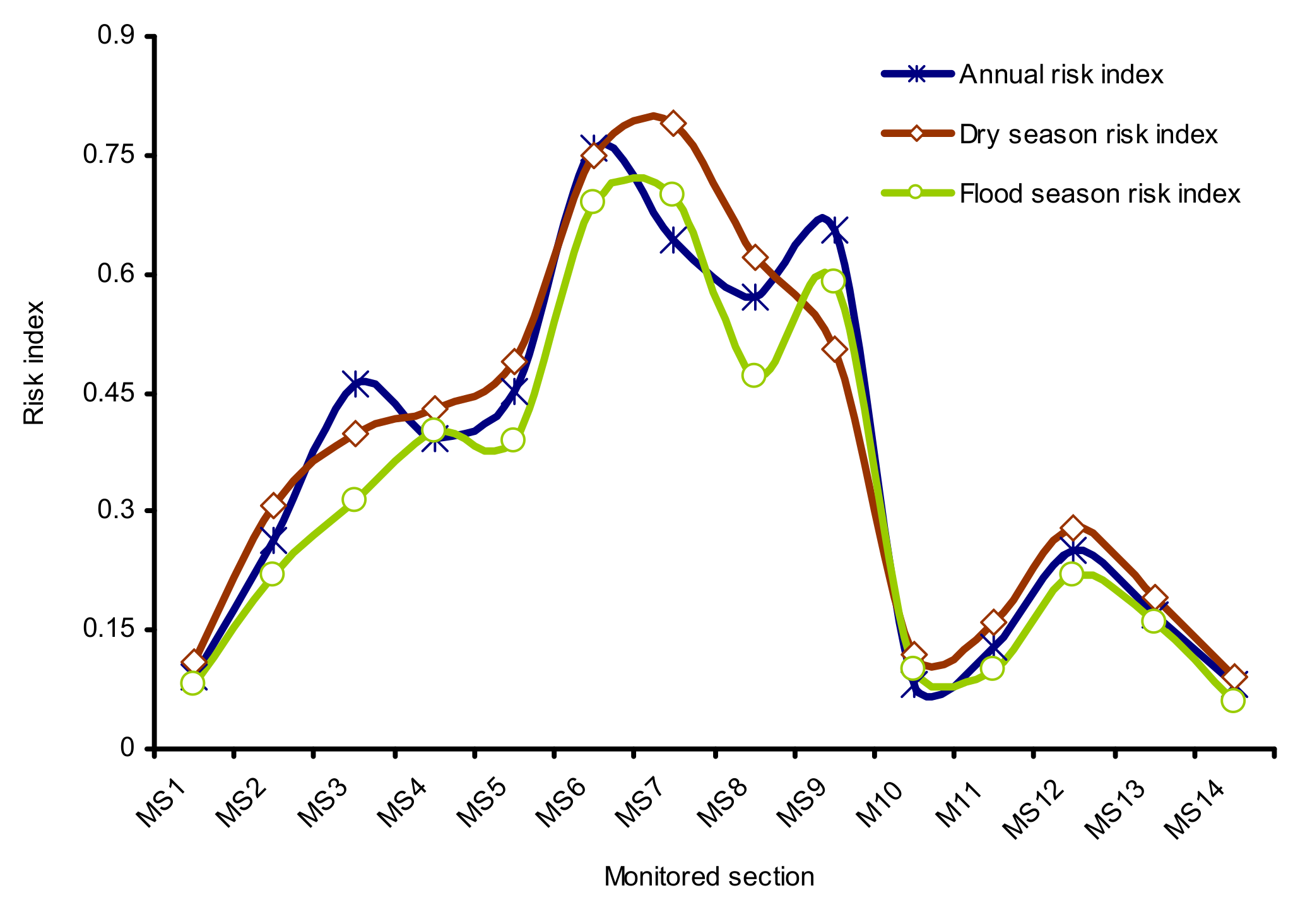
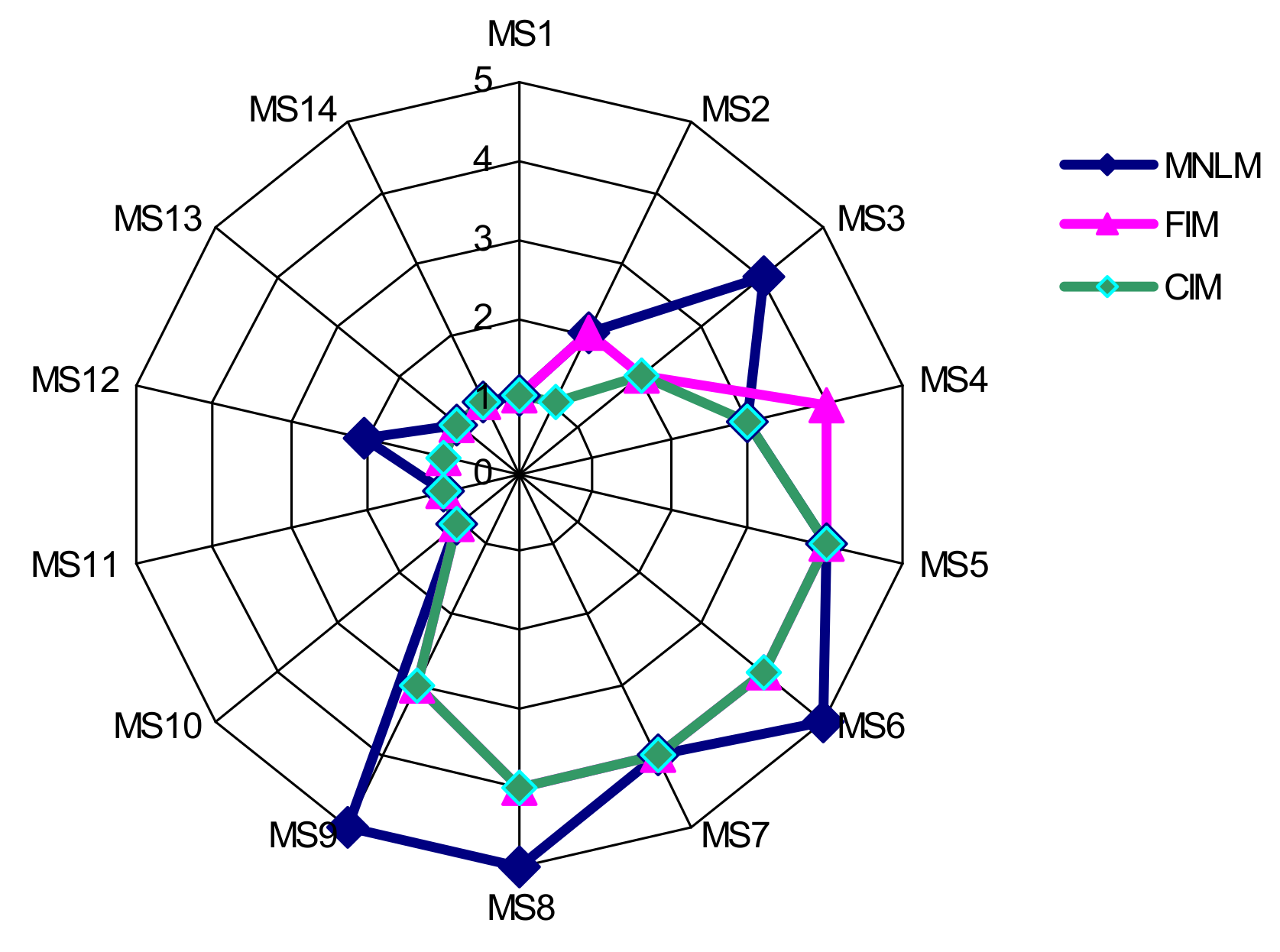
3.1. Results
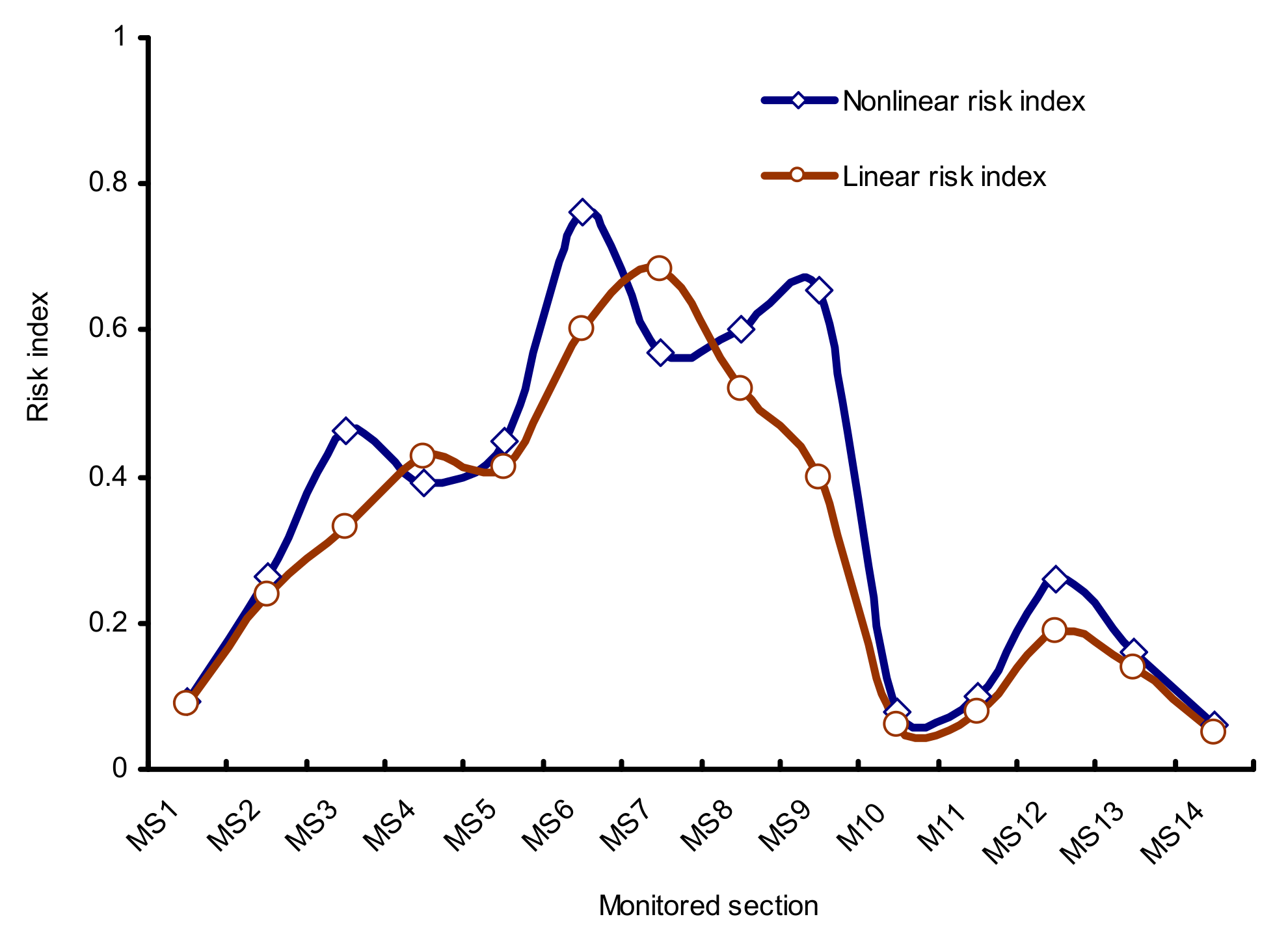
3.2. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Landis, W.G.; Thomas, J.F. Regional risk assessment as a part of the long-term receiving water study. Integr. Environ. Assess. Manag. 2009, 5, 234–247. [Google Scholar] [CrossRef] [PubMed]
- Aouissi, J.; Benabdallah, S.; Chabaâne, Z.L.; Cudennec, C. Modeling Water Quality to Improve Agricultural Practices and Land Management in a Tunisian Catchment Using the Soil and Water Assessment Tool. J. Environ. Qual. 2014, 43, 18–25. [Google Scholar] [CrossRef] [PubMed]
- Koch, M.; Missimer, M.T. Water Resources Assessment and Management in Drylands. Water 2016, 8, 239. [Google Scholar] [CrossRef]
- Goonetilleke, A.; Vithanage, M. Water Resources Management: Innovation and Challenges in a Changing World. Water 2017, 9, 281. [Google Scholar] [CrossRef]
- Shakhawat, C.; Tahir, H.; Neil, B. Fuzzy rule based modeling from human health risk from naturally occurring radioactive material sing produced water. J. Environ Radioact. 2006, 89, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Dahiya, S.; Singh, B.; Gaur, S.; Garg, V.K.; Kushwaha, H.S. Analysis of groundwater quality using fuzzy synthetic evaluation. J. Hazard. Mater. 2007, 147, 938–946. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.J.; He, J.T.; Chen, H.H. Assessment of groundwater contamination risk using hazard quantification, a modified drastic model and groundwater value. Beijing Plain, China. Sci. Total Environ. 2012, 432, 216–226. [Google Scholar] [CrossRef] [PubMed]
- Zou, B.; Zeng, Y.N.; Benjamin, F.Z.; Yang, L.B.; Zang, H.H. Spatial and Temporal Health Risk Assessment of Water Environment in Urban Area. Geogr. Geo-Inf. Sci. 2009, 25, 94–98. [Google Scholar]
- Guo, Q.C.; He, Z.F.; Li, L.; Kou, L.Q. Application of BP Neural Network on Water Environmental Quality Evaluation of Weihe River. Bull. Soil Water Conserv. 2011, 31, 112–115. [Google Scholar]
- Li, J.K.; Li, H.E.; Shen, B.; Qin, Y.M.; Dong, W. Monitoring and estimating non-point source pollution on typical sections along the Weihe River. Adv. Water Sci. 2011, 22, 818–828. [Google Scholar] [CrossRef]
- Wang, T.R.; Sun, G.N.; Liu, S.Y. Relationship between Spatiotemporal Variation of Water Pollution and Runoff Volume of Mainstream Section of the Weihe River in Shaanxi Province. Arid Zone Res. 2011, 28, 599–615. [Google Scholar] [CrossRef]
- Guan, J.L.; Wang, L.; Pei, X.L.; Yang, Y.Z.; Xing, Y.; Liu, Y. Trends of Major Pollutants Found in Weihe Rive in Shaanxi Provicnce. Bull. Soil Water Conserv. 2012, 32, 51–60. [Google Scholar] [CrossRef]
- Liu, Y.G.; Wang, N.L.; Wang, L.G.; Zhao, Y.Q.; Wu, X.B. Application of GIS in regional ecological risk assessment of water resources. Environ. Eng. Manag. J. 2013, 12, 1465–1474. [Google Scholar]
- Wang, Y.; He, B.; Duan, W.L.; Li, W.H.; Lou, P.P.; Razafindrabe, N.H.B. Source Apportionment of Annual Water Pollution Loads in River Basins by Remote-Sensed Land Cover Classification. Water 2016, 8, 361. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, J.; Ho, K.C.; Yang, Z. Development of a relative risk model for evaluating ecological risk of water environment in the Haihe River Basin estuary area. Sci. Total Environ. 2012, 420, 79–89. [Google Scholar] [CrossRef] [PubMed]
- Ding, A.W.; Chong, X.; Bao, Z.F.; Xue, X.; Zhang, S.H. Fuzzy Comprehensive Assessment Method Based on the Entropy Weight Method and Its Application in the Water Environmental Safety Evaluation of the Heshangshan Drinking Water Source Area, Three Gorges Reservoir Area, China. Water 2017, 9, 329. [Google Scholar] [CrossRef]
- Lermontov, A.; Yokoyama, L.; Lermontov, M.; Machado, M.A. River quality analysis using fuzzy water quality index: Ribeira do Iguape river watershed, Brazil. Ecol. Indic. 2009, 9, 1188–1197. [Google Scholar] [CrossRef]
- Geng, Y.N.; Zhang, J.; Zhou, Q.; Xu, C.D.; Zhao, Y.Q. Fuzzy synthetic evaluation of Weihe water quality. Environ. Eng. Manag. J. 2011, 10, 1477–1484. [Google Scholar]
- Peng, Y.; Xu, Q.X. Source Water Pollution Risk Discrimination Technique and its Application. Environ. Monit. Forewarn. 2009, 10, 1–4. [Google Scholar]
- VonderOhe, P.C.; Dulio, V.; Slobodnik, J.; Deckere, E.; Kühne, R.; Ebert, R.U.; Ginebreda, A.; Cooman, W.D.; Schüürmann, G.; Brack, W. A new risk assessment approach for the prioritization of 500 classical and emerging organic microcontaminants as potential river basin specific pollutants under the European Water Framework Directive. Sci. Total Environ. 2011, 409, 2064–2077. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.P.; Huang, G.H.; Fan, Y.R. A Semi-Infinite Interval-Stochastic Risk Management Model for River Water Pollution Control under Uncertainty. Water 2017, 9, 351. [Google Scholar] [CrossRef]
- Noori, R.; Sabahi, M.S.; Karbassi, A.R.; Baghvand, A.; Zadeh, H.T. Multivariate statistical analysis of surface water quality based on correlations and variations in the data set. Desalination 2010, 260, 129–136. [Google Scholar] [CrossRef]
- Hall, K.K.; Evanshen, B.G.; Maier, K.J.; Scheuerman, P.R. Application of Multivariate Statistical Methodology to Model Factors Influencing Fate and Transport of Fecal Pollution in Surface Waters. J. Environ. Qual. 2014, 43, 358–370. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.X.; Xu, S.G.; Liu, J.W. Dynamic Assessment of Comprehensive Water Quality Considering the Release of Sediment Pollution. Water 2017, 9, 375. [Google Scholar] [CrossRef]
- Santhi, C.; Kannan, N.; White, M.; Luzio, M.D.; Arnold, J.G.; Wang, X.; Williams, J.R. An Integrated Modeling Approach for Estimating the Water Quality Benefits of Conservation Practices at the River Basin Scale. J. Environ. Qual. 2014, 43, 177–198. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.N.; Yuan, X.Z.; Jang, J.L.; Zeng, G.M.; Jiang, H.W. An integrated model for assessing the risk of water environmental pollution based on fuzziness. China Environ. Sci. 2011, 31, 516–521. [Google Scholar]
- Xue, Y.; Song, J.X.; Zhang, Y.; Kong, F.H.; Wen, M.; Zhang, G.T. Nitrate Pollution and Preliminary Source Identification of Surface Water in a Semi-Arid River Basin, Using Isotopic and Hydrochemical Approaches. Water 2016, 8, 328. [Google Scholar] [CrossRef]
- Liu, Y.G.; Fu, Z.J. Ecological risk integrated assessment and driving factors for water resources in Shaanxi province. Bull. Soil Water Conserv. 2012, 32, 273–278. [Google Scholar] [CrossRef]
- Hoang, L.; Griensven, A.; Keur, P.; Refsgaard, J.C.; Troldborg, L.; Nilsson, B.; Mynett, A. Comparison and Evaluation of Model Structures for the Simulation of Pollution Fluxes in a Tile-Drained River Basin. J. Environ. Qual. 2014, 43, 86–99. [Google Scholar] [CrossRef] [PubMed]
- Environmental Monitoring Division of Ministry of Environmental Protection. Twelfth Five-Year Environment Monitoring Workbook; Environmental Monitoring Division of Ministry of Environmental Protection: Beijing, China, 2012.
- Liu, Y.G.; Yang, Y.X.; Xu, C.D. Risk evaluation of water pollution in the middle catchment of Weihe River. J. Residuals Sci. Technol. 2015, 12, 133–136. [Google Scholar] [CrossRef]
| Monitoring Site | BOD5 | COD | Potassium Permanganate | Ammonia Nitrogen | Petroleum | Nitrite Nitrogen |
|---|---|---|---|---|---|---|
| MS1 | 0.178 | 0.217 | 0.169 | 0.196 | 0.143 | 0.088 |
| MS2 | 0.152 | 0.192 | 0.165 | 0.182 | 0.173 | 0.136 |
| MS3 | 0.148 | 0.181 | 0.151 | 0.213 | 0.167 | 0.14 |
| MS4 | 0.185 | 0.176 | 0.132 | 0.187 | 0.164 | 0.156 |
| MS5 | 0.151 | 0.188 | 0.184 | 0.213 | 0.163 | 0.101 |
| MS6 | 0.146 | 0.198 | 0.183 | 0.175 | 0.191 | 0.107 |
| MS7 | 0.171 | 0.19 | 0.165 | 0.189 | 0.183 | 0.102 |
| MS8 | 0.169 | 0.177 | 0.173 | 0.214 | 0.15 | 0.117 |
| MS9 | 0.173 | 0.164 | 0.184 | 0.187 | 0.171 | 0.121 |
| MS10 | 0.168 | 0.178 | 0.167 | 0.203 | 0.166 | 0.118 |
| MS11 | 0.153 | 0.157 | 0.178 | 0.218 | 0.165 | 0.129 |
| MS12 | 0.157 | 0.162 | 0.178 | 0.198 | 0.189 | 0.116 |
| MS13 | 0.167 | 0.169 | 0.173 | 0.194 | 0.175 | 0.122 |
| MS14 | 0.175 | 0.164 | 0.188 | 0.186 | 0.169 | 0.118 |
| Pollution Parameters | Water Pollution Risk Assessment Gradesand Index | ||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| Negligible Risk | Acceptable Risk | Marginal Risk | Unacceptable Risk | Catastrophic Risk | |
| BOD5 | 0.115 | 0.116–0.135 | 0.135–0.154 | 0.155–0.231 | 0.332–0.634 |
| COD | 0.125 | 0.126–0.255 | 0.256–0.367 | 0.368–0.450 | 0.451–0.783 |
| Petroleum | 0.03 | 0.031–0.213 | 0.214–0.301 | 0.302–0.423 | 0.424–0.598 |
| Nitrite nitrogen | 0.036 | 0.037–0.143 | 0.144–0.234 | 0.235–0.416 | 0.417–0.524 |
| Potassium permanganate | 0.084 | 0.085–0.138 | 0.139–0.286 | 0.287–0.371 | 0.372–0.605 |
| Ammonia nitrogen | 0.049 | 0.050–0.186 | 0.187–0.283 | 0.284–0.391 | 0.392–0.421 |
| Comprehensive level | <0.25 | 0.25–0.35 | 0.35–0.45 | 0.45–0.65 | >0.65 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, J.; Zhao, Y. The Risk Assessment of River Water Pollution Based on a Modified Non-Linear Model. Water 2018, 10, 362. https://doi.org/10.3390/w10040362
Liu Y, Zhang J, Zhao Y. The Risk Assessment of River Water Pollution Based on a Modified Non-Linear Model. Water. 2018; 10(4):362. https://doi.org/10.3390/w10040362
Chicago/Turabian StyleLiu, Yinge, Junhui Zhang, and Yaqian Zhao. 2018. "The Risk Assessment of River Water Pollution Based on a Modified Non-Linear Model" Water 10, no. 4: 362. https://doi.org/10.3390/w10040362
APA StyleLiu, Y., Zhang, J., & Zhao, Y. (2018). The Risk Assessment of River Water Pollution Based on a Modified Non-Linear Model. Water, 10(4), 362. https://doi.org/10.3390/w10040362






