Identification of Hydrological Drought in Eastern China Using a Time-Dependent Drought Index
Abstract
:1. Introduction
2. Methodology
2.1. Traditional Standardized Streamflow Index (SSI)
2.2. Change Point and Trend Analysis
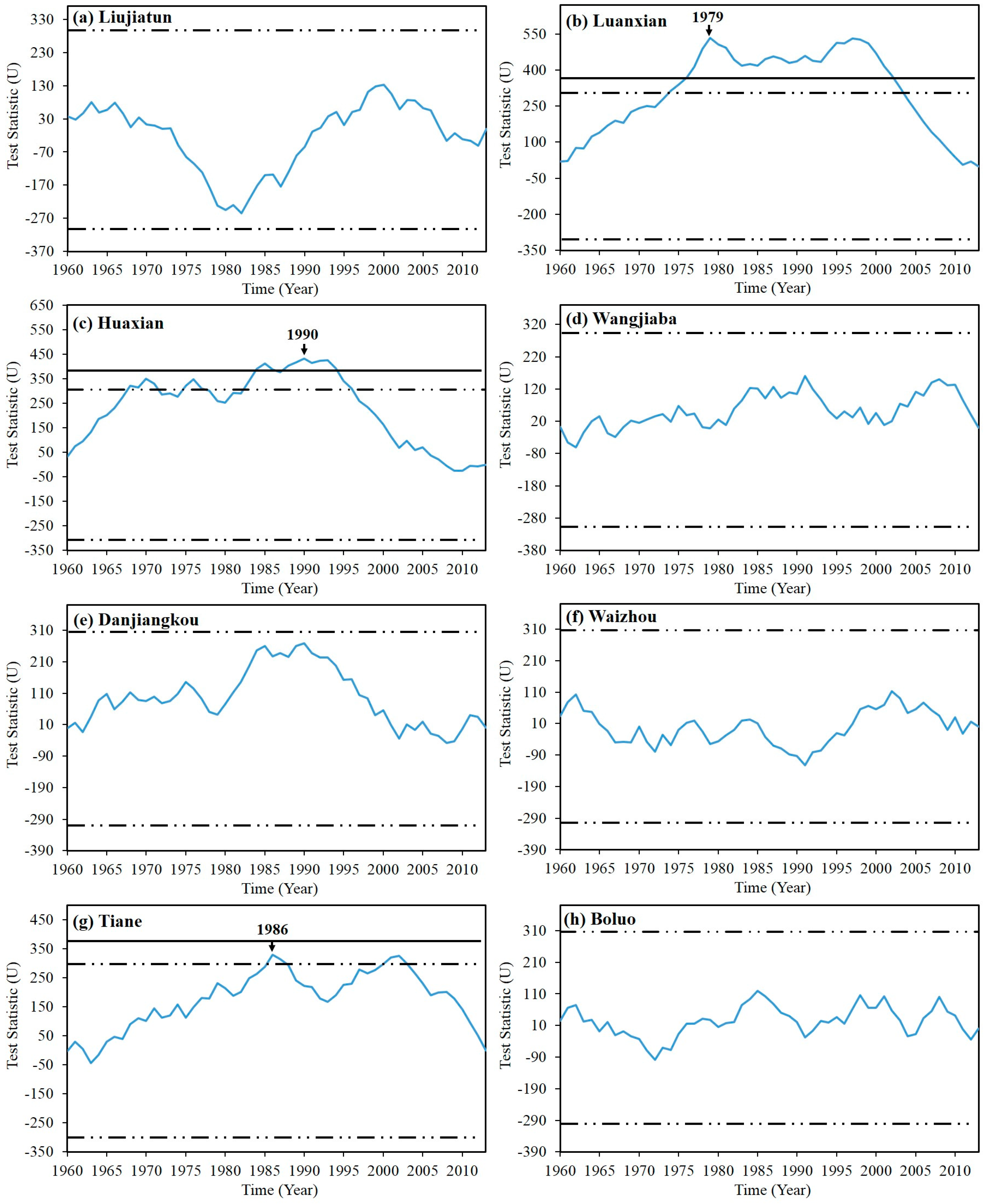
2.2.1. Change Point Analysis
2.2.2. Temporal Trend Analysis
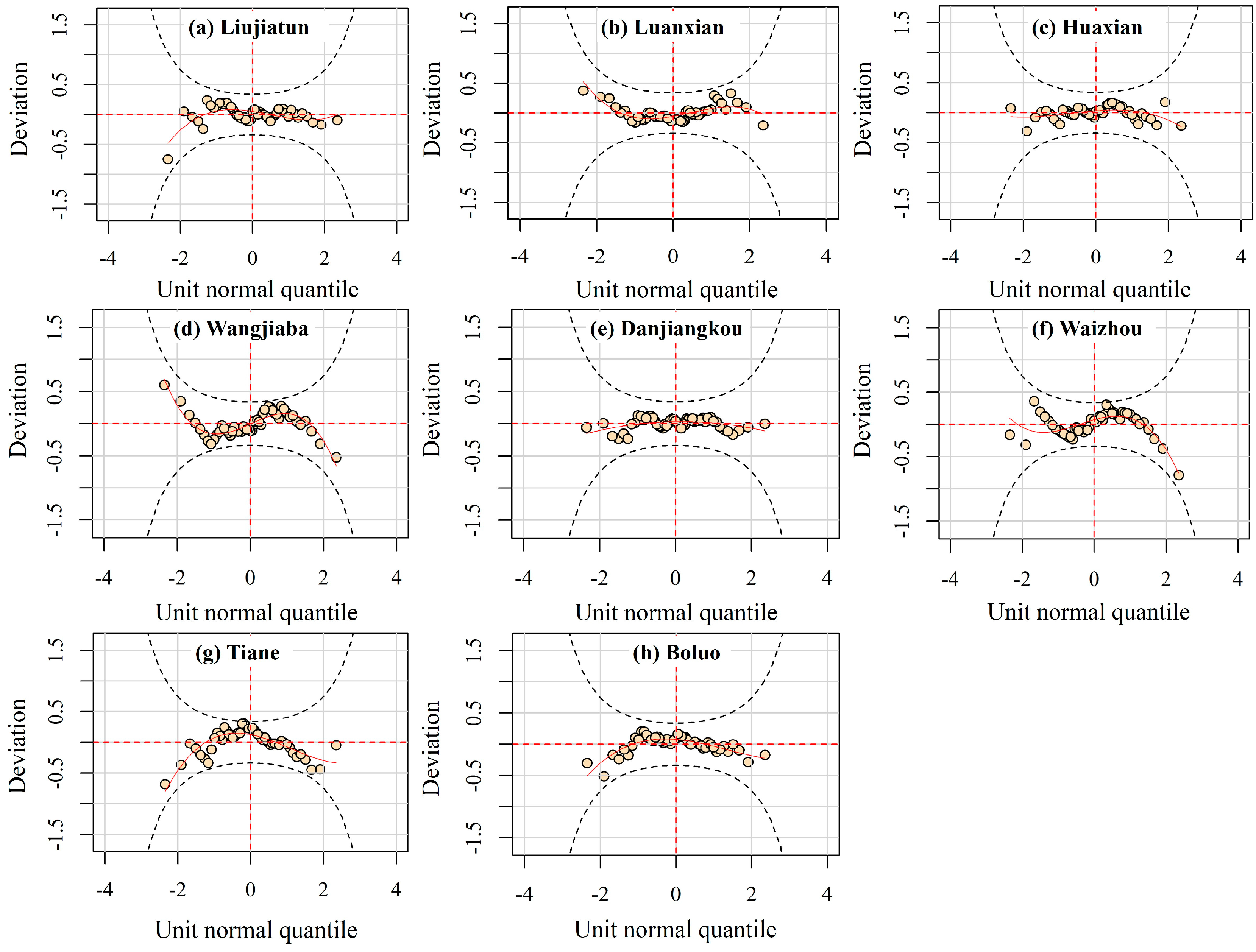
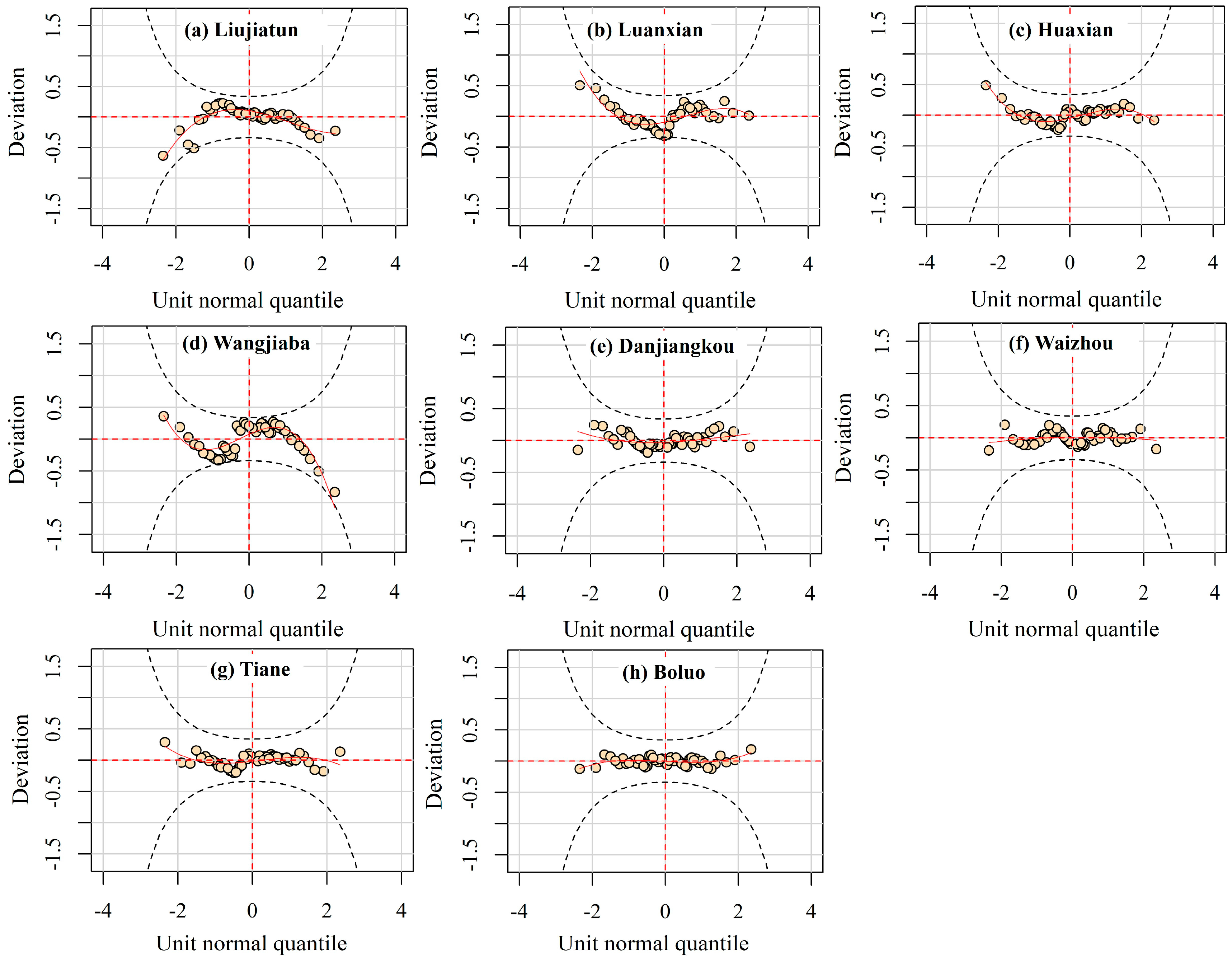
2.3. GAMLSS Model
2.4. Construction of the Time-Dependent Standardized Streamflow Index (SSIvar)
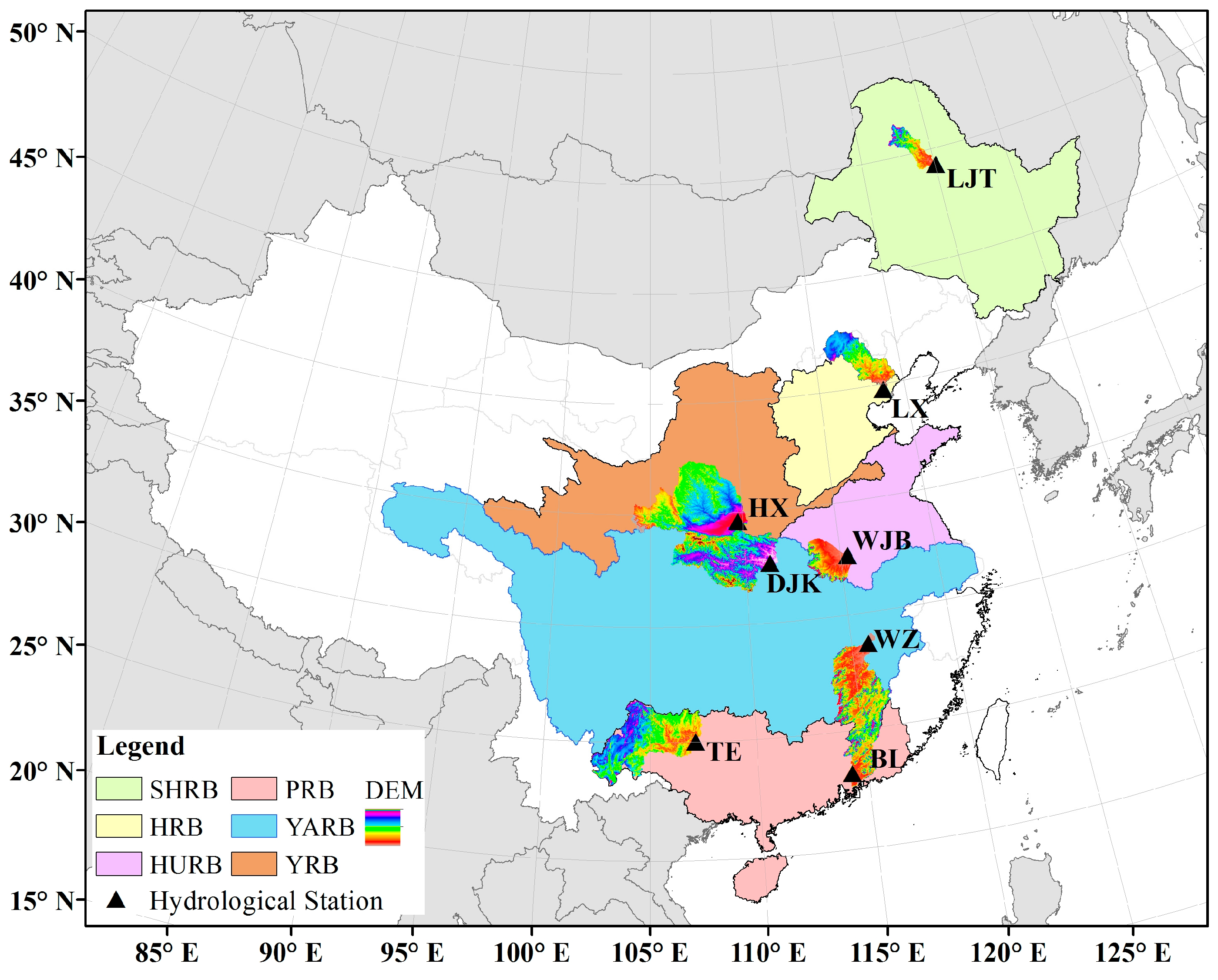
3. Study Area and Dataset
4. Results and Discussion
4.1. Change Point Analysis
4.2. Trend Analysis
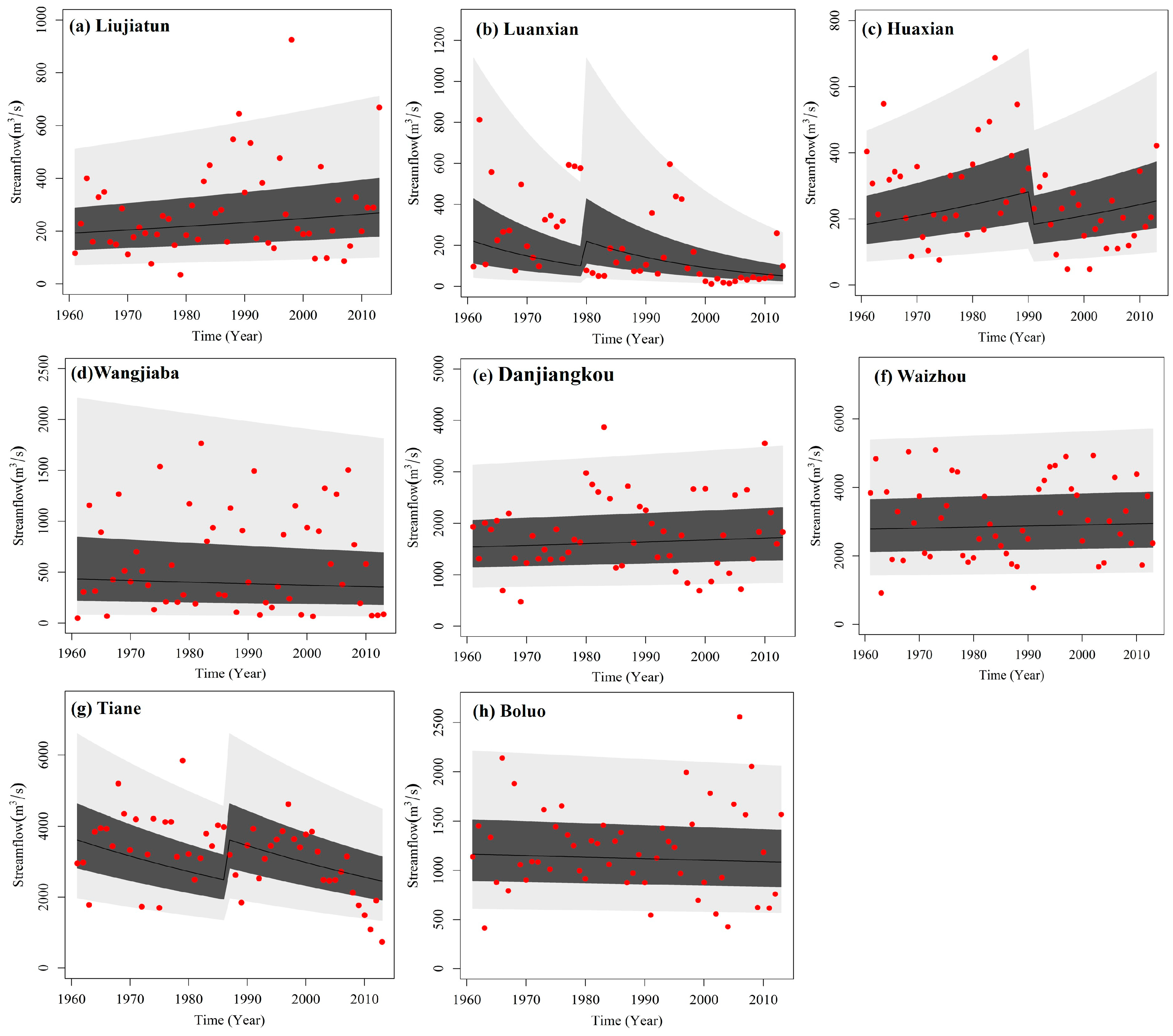
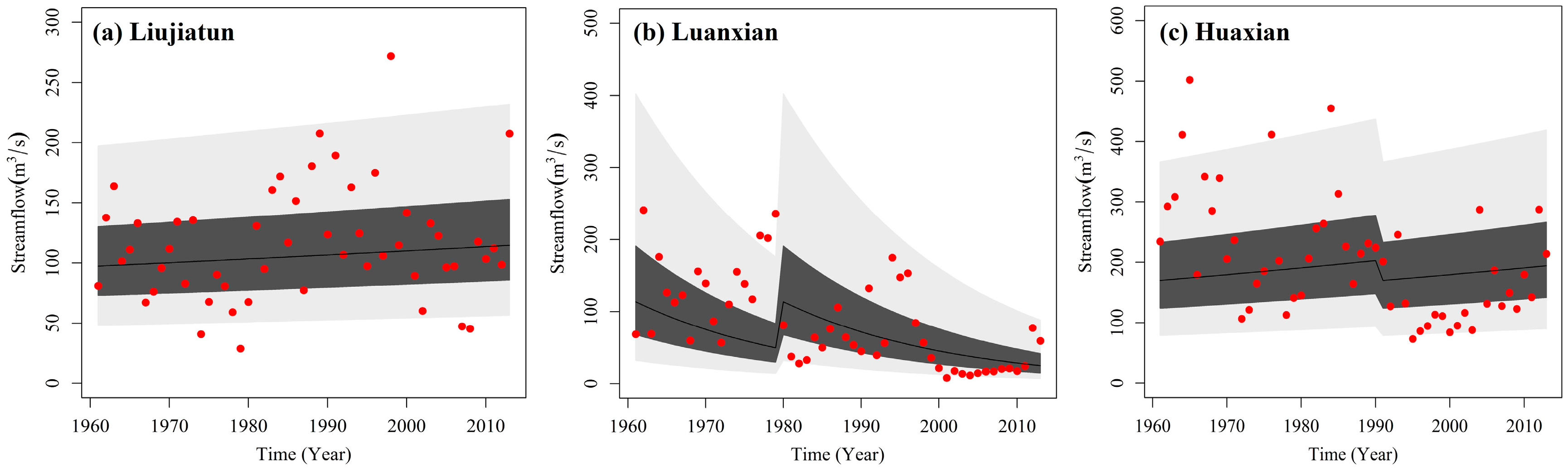
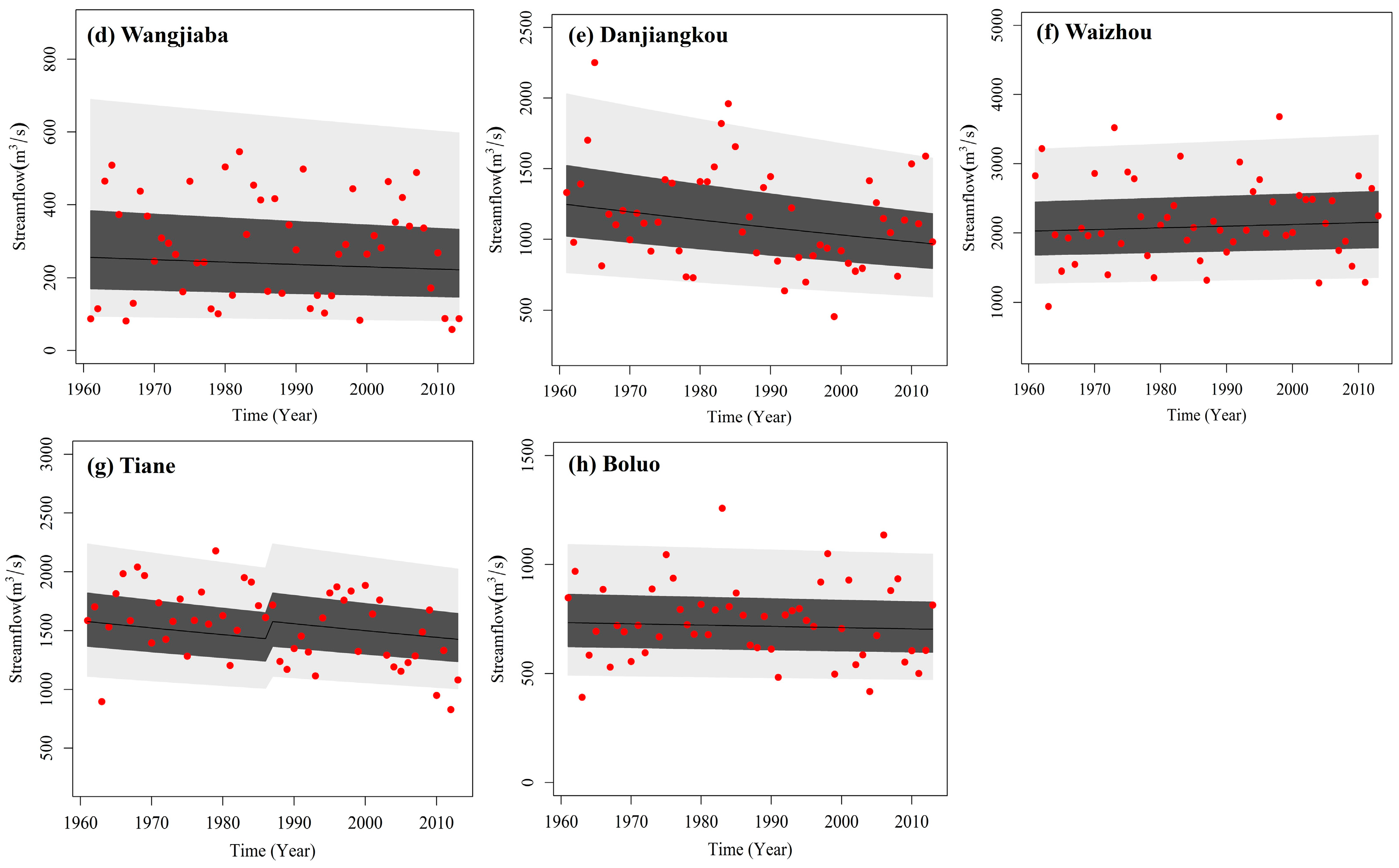
4.3. Modeling with GAMLSS
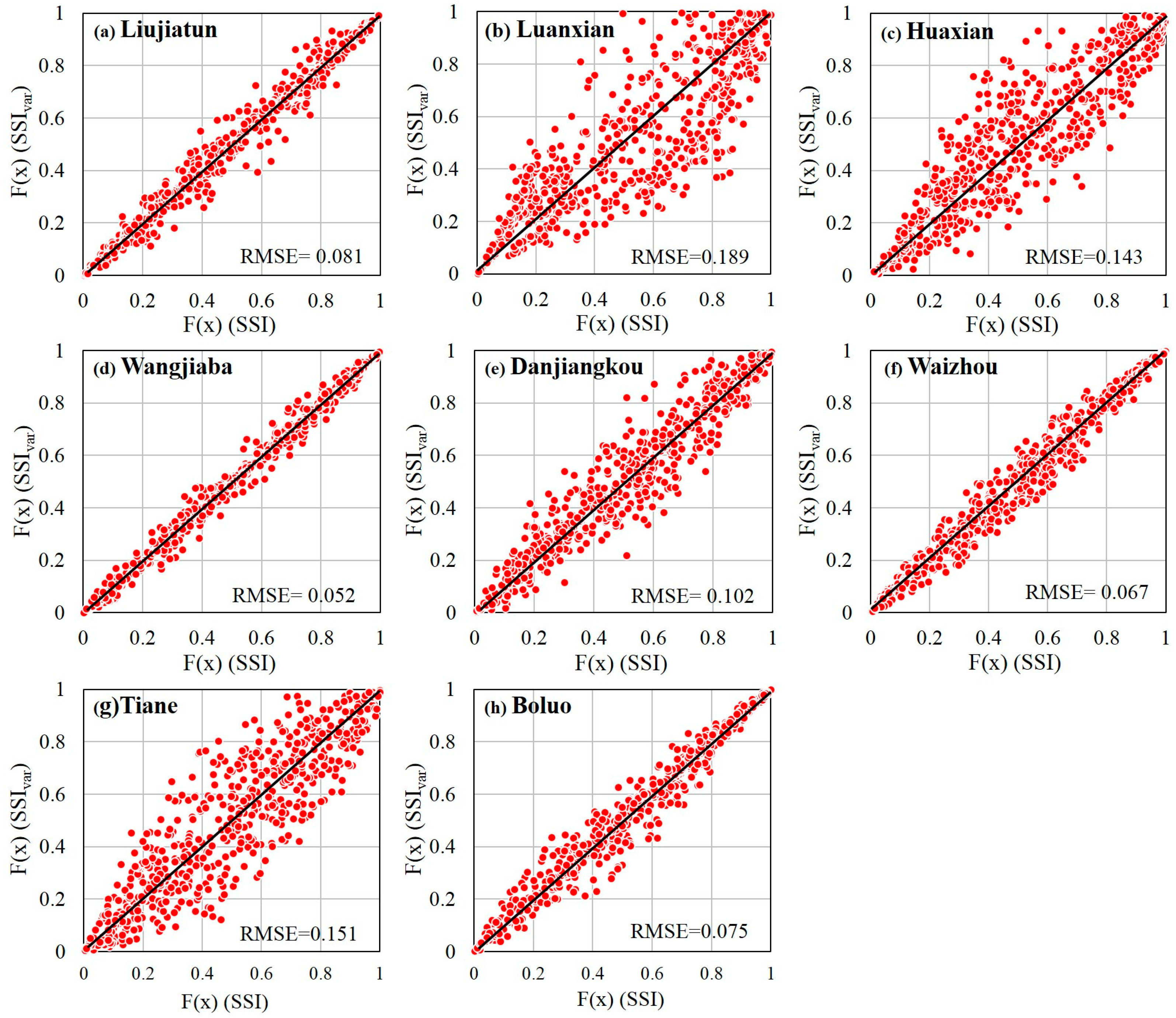
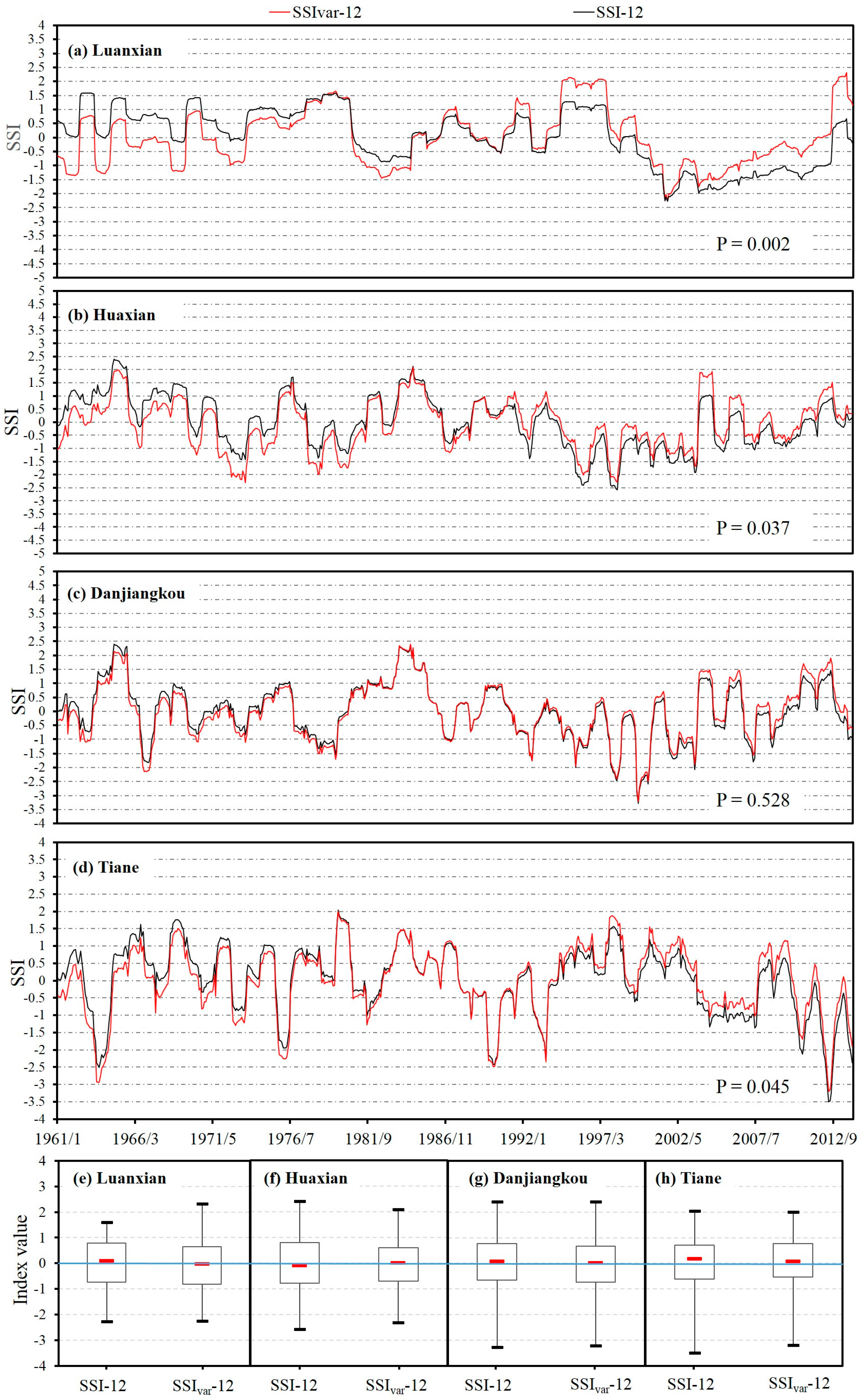
4.4. Construction of the SSIvar
5. Conclusions
- (1)
- Generalized Additive Models in Location, Scale and Shape (GAMLSS) provide a flexible and useful framework for modeling distributions of streamflow series considering both trend and change point. In particular, they provide the capability for modeling the non-stationarities in streamflow records.
- (2)
- Based on the selected optimal distribution, the developed SSIvar is capable of taking the nonstationarity of streamflow series into account; thus, it is likely to be more reliable and suitable than the traditional SSI for drought assessment in a changing environment. The differences between the SSIvar and SSI indicate that the presence of nonstationarity should be considered in regional drought assessment. The SSIvar is proven to be a feasible alternative for drought forecast and water resource management under changing environment.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wilhite, D.A. Drought: A Global Assessment; Routledge: New York, NY, USA, 2000. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Wen, L.; Rogers, K.; Ling, J.; Saintilan, N. The impacts of river regulation and water diversion on the hydrological drought characteristics in the lower murrumbidgee river, Australia. J. Hydrol. 2011, 405, 382–391. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, W.; Singh, V.P.; Liu, Y. Combined use of meteorological drought indices at multi-time scales for improving hydrological drought detection. Sci. Total Environ. 2016, 571, 1058–1068. [Google Scholar] [CrossRef] [PubMed]
- Doell, P.; Fiedler, K.; Zhang, J. Global-scale analysis of river flow alterations due to water withdrawals and reservoirs. Hydrol. Earth Syst. Sci. 2009, 13, 2413–2432. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January; 1993; pp. 179–184. [Google Scholar]
- Vicente-Serrano, S.M.; Lopez-Moreno, J.I.; Begueria, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Moran-Tejeda, E. Accurate computation of a streamflow drought index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef]
- Villarini, G.; Serinaldi, F.; Smith, J.A.; Krajewski, W.F. On the stationarity of annual flood peaks in the continental united states during the 20th century. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.H.; Singh, V.P.; Xiao, M.Z.; Xu, C.Y. Stationarity of annual flood peaks during 1951–2010 in the pearl river basin, China. J. Hydrol. 2014, 519, 3263–3274. [Google Scholar] [CrossRef]
- Villarini, G.; James, A.S.; Napolitano, F. Nonstationarity modeling of a long record of rainfall and temperature over Rome. Adv. Water Resour. 2010, 33, 1256–1267. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Lopez-Moreno, J.I. Nonstationarity influence of the North Atlantic Oscillation on European precipitation. J. Geophys. Res.-Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Climate change—Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Chang, N.-B.; Vasquez, M.V.; Chen, C.-F.; Imen, S.; Mullon, L. Global nonlinear and nonstationarity climate change effects on regional precipitation and forest phenology in Panama, Central America. Hydrol. Processes 2015, 29, 339–355. [Google Scholar] [CrossRef]
- Coulibaly, P.; Baldwin, C.K. Nonstationarity hydrological time series forecasting using nonlinear dynamic methods. J. Hydrol. 2005, 307, 164–174. [Google Scholar] [CrossRef]
- Verdon, D.C.; Wyatt, A.M.; Kiem, A.S.; Franks, S.W. Multidecadal variability of rainfall and streamflow: Eastern Australia. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Xu, X.; Yang, D.; Yang, H.; Lei, H. Attribution analysis based on the budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Ishak, E.H.; Rahman, A.; Westra, S.; Sharma, A.; Kuczera, G. Evaluating the nonstationarity of Australian annual maximum flood. J. Hydrol. 2013, 494, 134–145. [Google Scholar] [CrossRef]
- Russo, S.; Dosio, A.; Sterl, A.; Barbosa, P.; Vogt, J. Projection of occurrence of extreme dry-wet years and seasons in Europe with stationary and nonstationarity standardized precipitation indices. J. Geophys. Res. Atmos. 2013, 118, 7628–7639. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Feng, P.; Hu, R. A time-dependent drought index for nonstationarity precipitation series. Water Resour. Manag. 2015, 29, 5631–5647. [Google Scholar] [CrossRef]
- El Adlouni, S.; Ouarda, T.B.M.J.; Zhang, X.; Roy, R.; Bobee, B. Generalized maximum likelihood estimators for the nonstationarity generalized extreme value model. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Underwood, F.M. Describing long-term trends in precipitation using generalized additive models. J. Hydrol. 2009, 364, 285–297. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C 2005, 54, 507–544. [Google Scholar] [CrossRef]
- Slater, L.J.; Villarini, G. Evaluating the drivers of seasonal streamflow in the US Midwest. Water 2017, 9, 695. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1965. [Google Scholar]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Alan, D.Z.; Justin, S.; Edwin, P.M.; Bart, N.; Eric, F.W.; Dennis, P.L. Detection of intensification in global- and continental-scale hydrological cycles: Temporal scale of evaluation. J. Clim. 2003, 16, 535–547. [Google Scholar]
- Zhang, X.B.; Harvey, K.D.; Hogg, W.D.; Yuzyk, T.R. Trends in Canadian streamflow. Water Resour. Res. 2001, 37, 987–998. [Google Scholar] [CrossRef]
- Stasinopoulos, D.M.; Rigby, R.A. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 2007, 23. [Google Scholar] [CrossRef]
- Lopez, J.; Frances, F. Nonstationarity flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Filliben, J.J. The probability plot correlation coefficient test for normality. Technometrics 1975, 17, 111–117. [Google Scholar] [CrossRef]
- Buuren, S.V.; Fredriks, M. Worm plot: A simple diagnostic device for modelling growth reference curves. Stat. Med. 2001, 20, 1259–1277. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
| State | Categories | SSI Values |
|---|---|---|
| D0 | Extreme Drought | (−∞, −2) |
| D1 | Severe Drought | [−2, −1.5) |
| D2 | Moderate Drought | [−1.5, −1] |
| D3 | Slight Drought | [−1, 0) |
| D4 | Normal | [0, +∞) |
| Distribution | Probability Density Function | Distribution Moments | Link Functions |
|---|---|---|---|
| Gamma | |||
| Lognormal | |||
| Gumbel | |||
| Weibull | |||
| Logistic |
| River Basin | Station | Drainage Area (km2) | Longitude | Latitude | Climatic Zone | Mean (m3/s) |
|---|---|---|---|---|---|---|
| SHRB | Liujiatun (LJT) | 19,665 | 125.08 | 49.25 | Humid and semi-humid | 115.09 |
| HRB | Luanxian (LX) | 44,100 | 118.75 | 39.73 | Semi-arid and semi-humid | 83.73 |
| YRB | Huaxian (HX) | 106,498 | 109.76 | 34.58 | Arid and semi-arid | 204.90 |
| HURB | Wangjiaba (WJB) | 30,630 | 115.60 | 32.43 | Humid and semi-humid | 282.62 |
| YARB | Danjiangkou (DJK) | 159,000 | 111.51 | 32.58 | Humid | 1141.64 |
| Waizhou (WZ) | 80,948 | 115.84 | 28.63 | Humid | 2164.33 | |
| PRB | Tiane (TE) | 105,535 | 107.16 | 24.99 | Humid | 1528.32 |
| Boluo (BL) | 25,325 | 114.30 | 23.17 | Humid | 737.71 |
| Stations | MK | |
|---|---|---|
| Liujiatun (LJT) | 0.198 | 0.142 |
| Luanxian (LX) | 0.475 | −2.352 |
| Huaxian (HX) | 0.397 | −1.992 |
| Wangjiaba (WJB) | −0.137 | −0.691 |
| Danjiangkou (DJK) | 0.272 | −1.155 |
| Waizhou (WZ) | −0.073 | 0.093 |
| Tiane (TE) | 0.202 | −2.553 |
| Boluo (BL) | 0.066 | −0.351 |
| Stations | Optimal CDF | Stationary | Nonstationarity in (Mean) | Nonstationarity in (Variance) | Nonstationarity in both and |
|---|---|---|---|---|---|
| Monthly averaged AIC values and for stationary and optimal nonstationarity models (3-month scale) AIC/ | |||||
| Liujiatun (LJT) | LOGNO | 506.34/0.988 | 503.17/0.991 (Y) | — | — |
| Luanxian (LX) | WEI | 530.36/0.981 | 509.67/0.986 (Y) | — | — |
| Huaxian (HX) | GA | 636.00/0.985 | 627.37/0.989 (Y) | — | — |
| Wangjiaba (WJB) | GA | 676.77/0.980 | 675.63/0.981 (Y) | — | — |
| Danjiangkou (DJK) | GA | 783.77/0.992 | 780.92/0.994 (Y) | — | — |
| Waizhou (WZ) | LOGNO | 853.29/0.982 | 849.13/0.983 (Y) | — | — |
| Tiane (TE) | GA | 796.66/0.983 | 787.23/0.985 (Y) | — | — |
| Boluo (BL) | LOGNO | 727.17/0.991 | — | 725.74/0.992 (Y) | — |
| Monthly averaged AIC values for stationary and optimal nonstationarity models (12-month scale) AIC/ | |||||
| Liujiatun (LJT) | GA | 558.34/0.992 | 553.36/0.993 (Y) | — | — |
| Luanxian (LX) | GA | 573.77/0.983 | 553.55/0.983 (Y) | — | — |
| Huaxian (HX) | LOGNO | 632.70/0.982 | 622.24/0.983 (Y) | — | — |
| Wangjiaba (WJB) | WEI | 683.71/0.975 | — | 680.13/0.979 (Y) | — |
| Danjiangkou (DJK) | LOGNO | 781.23/0.989 | 778.44/0.991 (Y) | — | — |
| Waizhou (WZ) | GA | 828.92/0.991 | — | 825.65/0.993 (Y) | — |
| Tiane (TE) | WEI | 770.24/0.985 | 763.67/0.988 (Y) | — | — |
| Boluo (BL) | GA | 707.72/0.987 | — | 702.34/0.991 (Y) | — |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, L.; Xia, J.; Ning, L.; She, D.; Zhan, C. Identification of Hydrological Drought in Eastern China Using a Time-Dependent Drought Index. Water 2018, 10, 315. https://doi.org/10.3390/w10030315
Zou L, Xia J, Ning L, She D, Zhan C. Identification of Hydrological Drought in Eastern China Using a Time-Dependent Drought Index. Water. 2018; 10(3):315. https://doi.org/10.3390/w10030315
Chicago/Turabian StyleZou, Lei, Jun Xia, Like Ning, Dunxian She, and Chesheng Zhan. 2018. "Identification of Hydrological Drought in Eastern China Using a Time-Dependent Drought Index" Water 10, no. 3: 315. https://doi.org/10.3390/w10030315
APA StyleZou, L., Xia, J., Ning, L., She, D., & Zhan, C. (2018). Identification of Hydrological Drought in Eastern China Using a Time-Dependent Drought Index. Water, 10(3), 315. https://doi.org/10.3390/w10030315







