A Simulation-Optimization Model for Seawater Intrusion Management at Pingtung Coastal Area, Taiwan
Abstract
:1. Introduction
2. Methodology
2.1. SEAWAT
2.2 Artificial Neural Networks
2.3. Management Model Formulation
2.4. Differential Evolution
3. Study Area
3.1. General Background
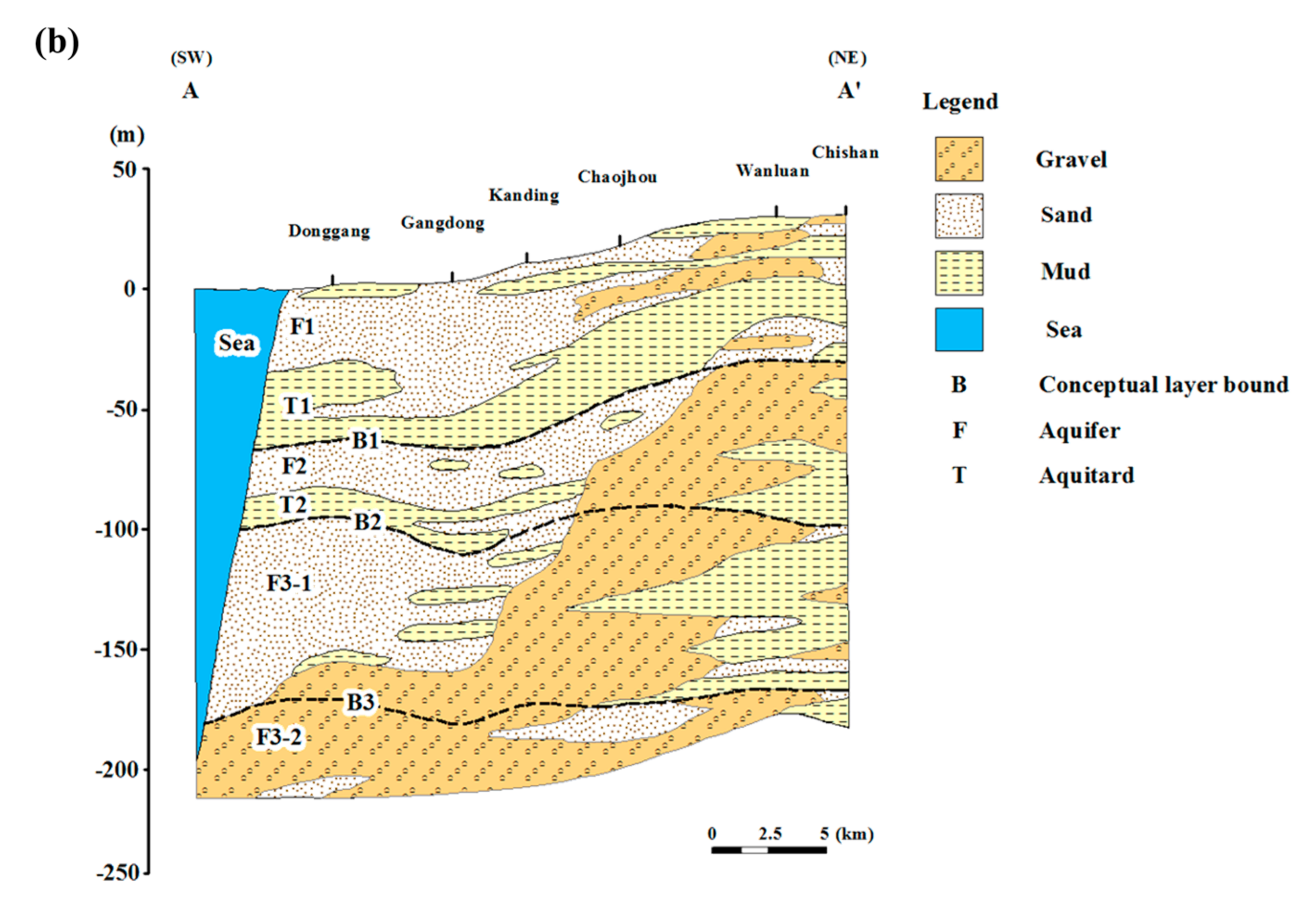
3.2. Hydrogeology
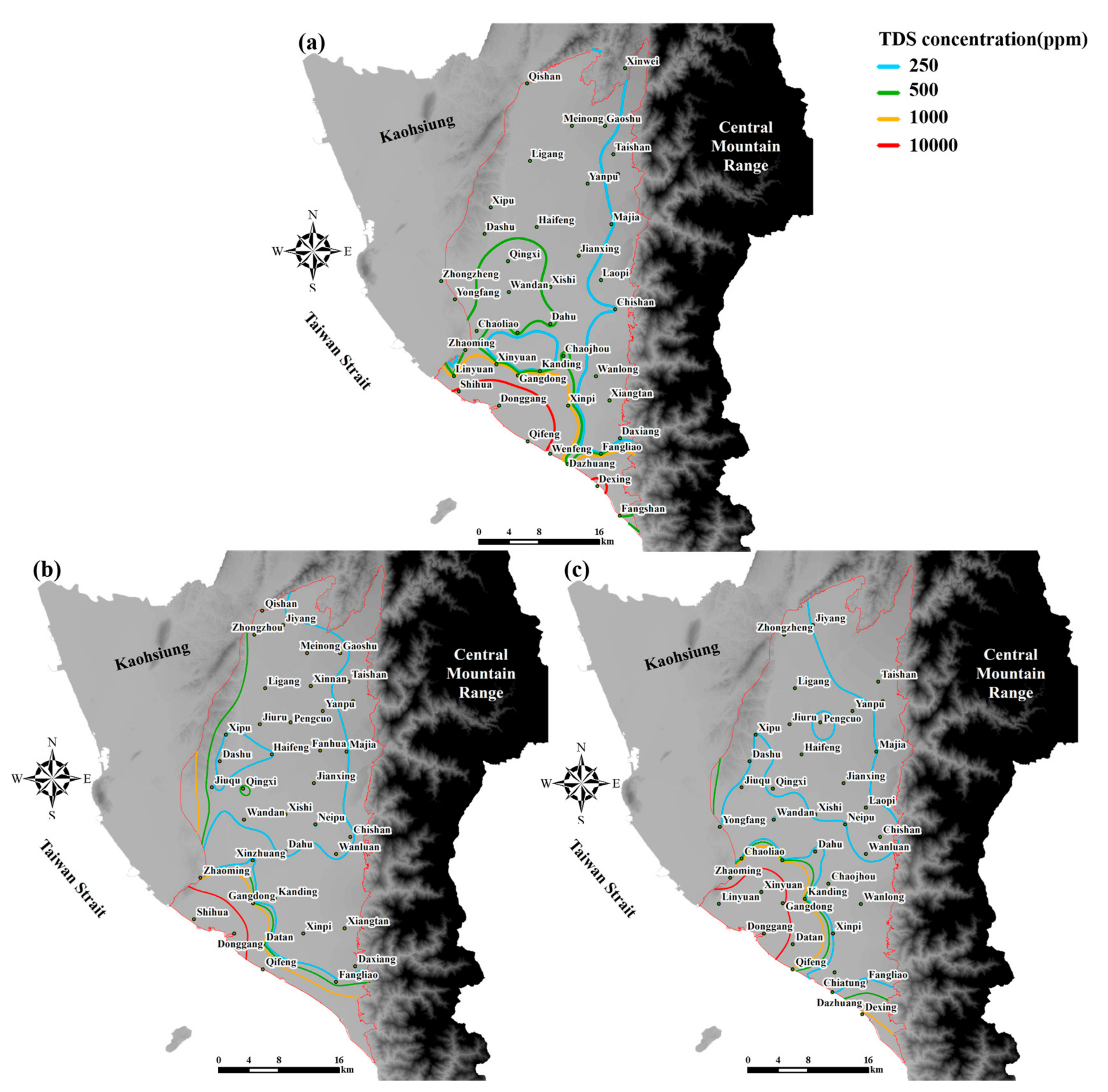
3.3. Seawater Intrusion in Pingtung Plain
3.4. Regional Groundwater Flow Model
4. Results
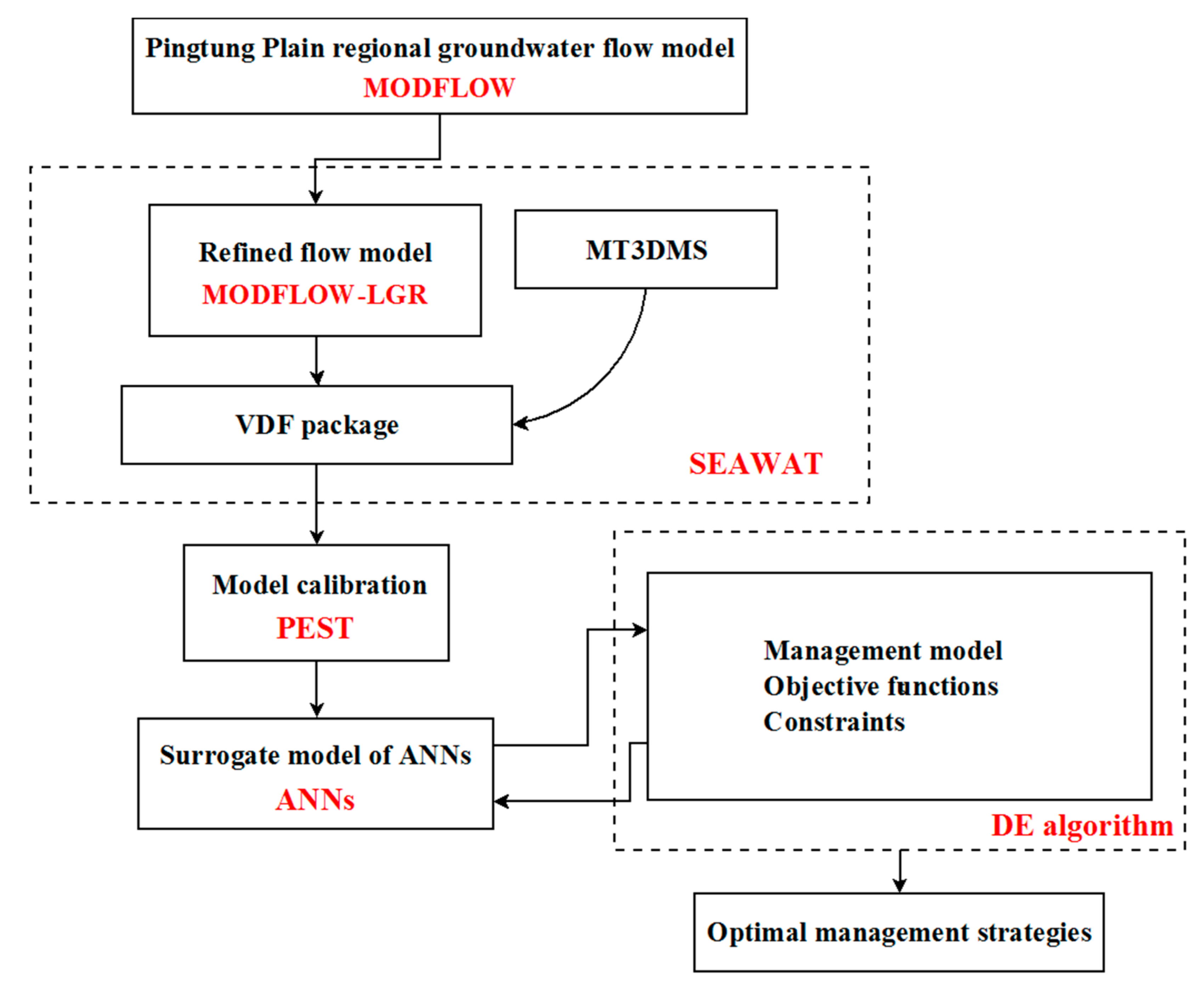
4.1. Development of the SWI Model
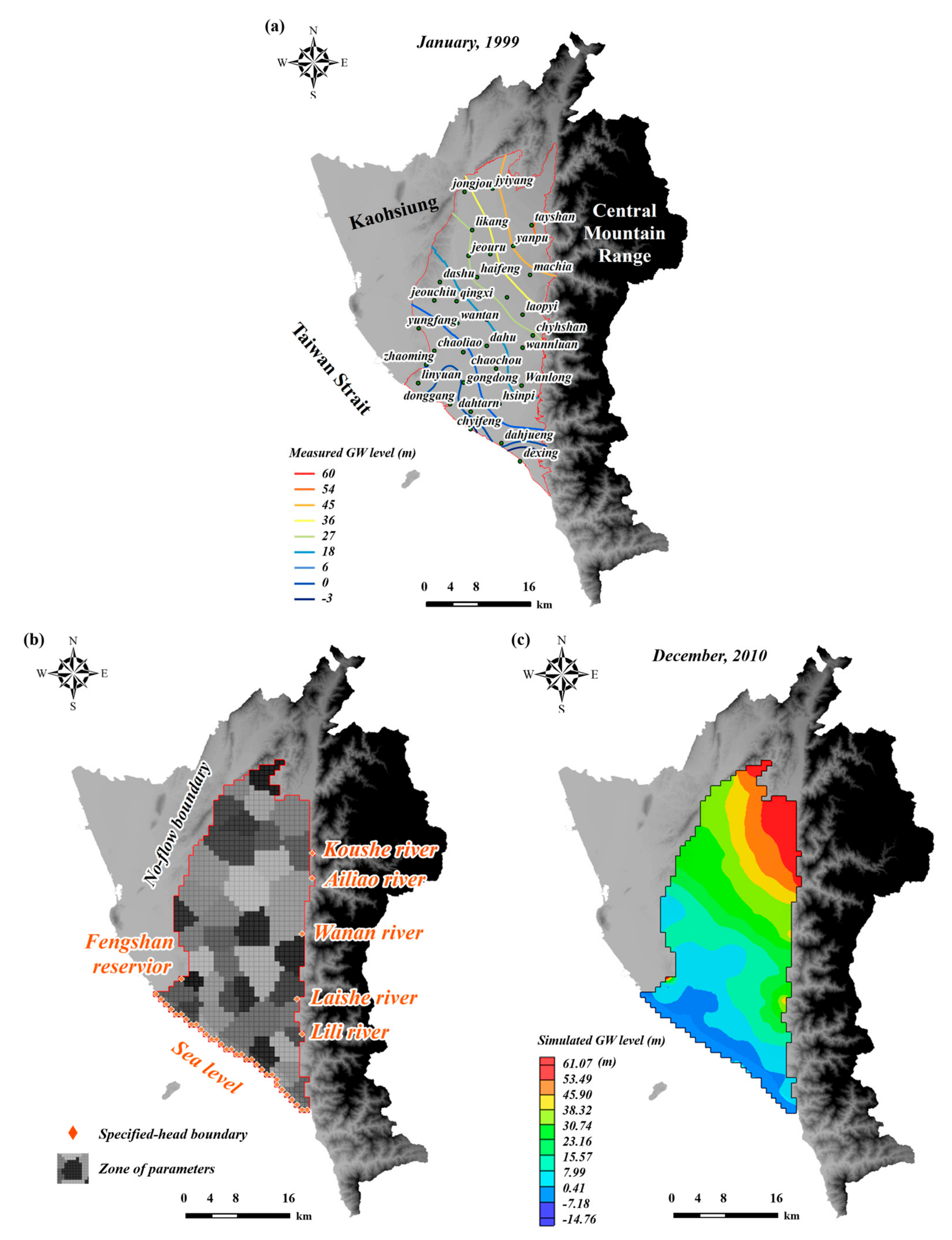
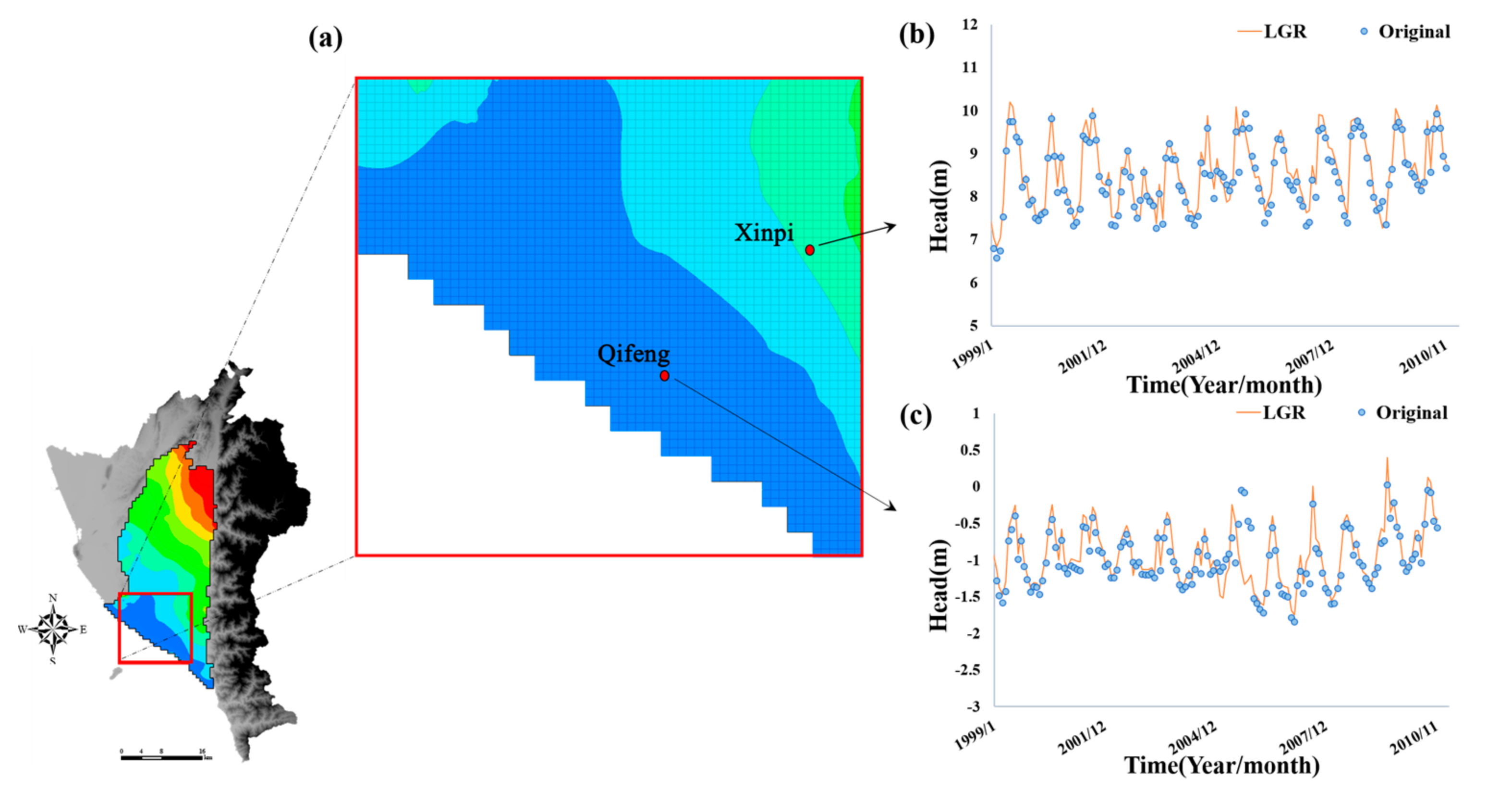
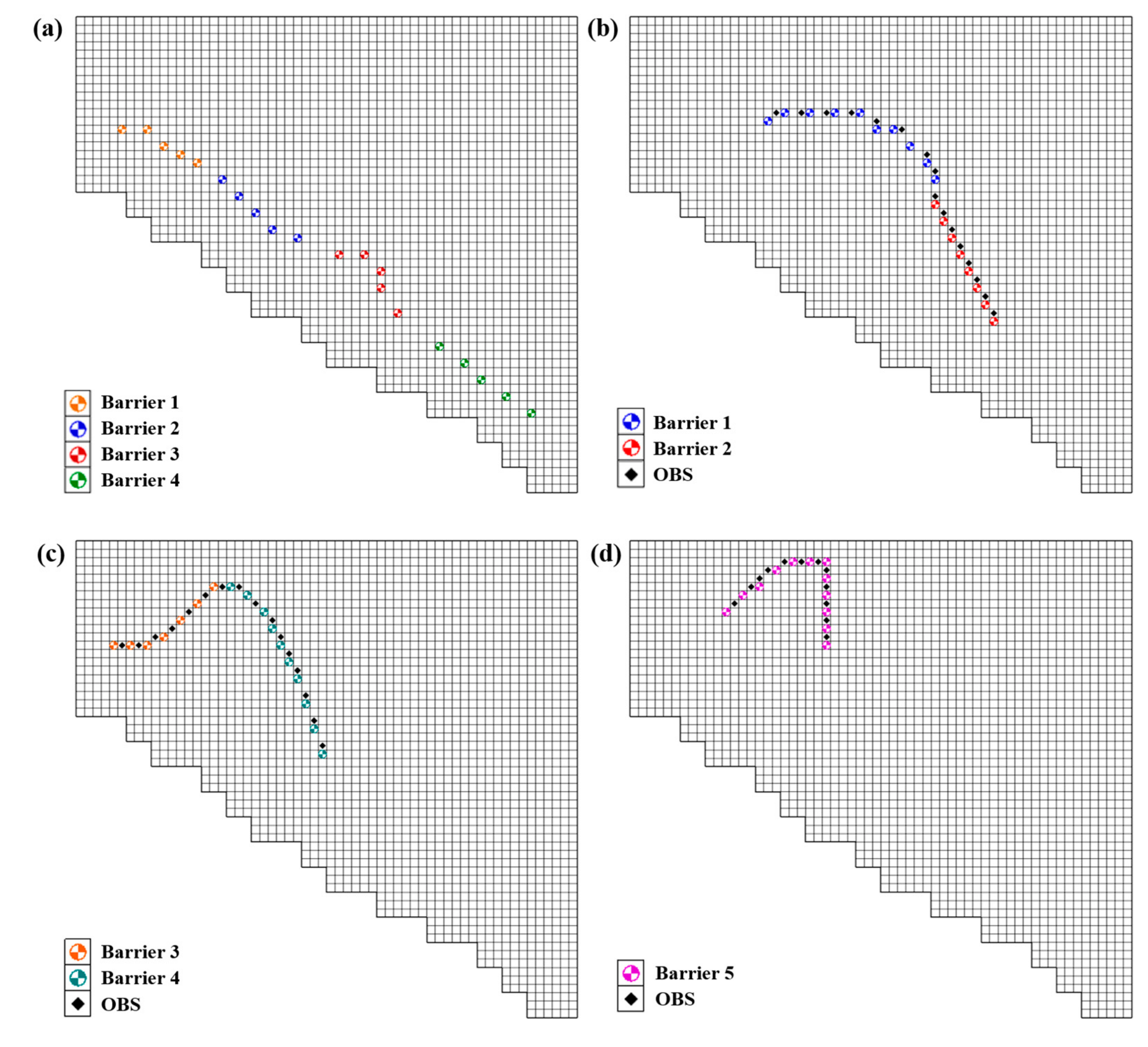
4.1.1. Refinement of Regional Groundwater Flow Model
4.1.2. SWI Model of Pingtung Plain
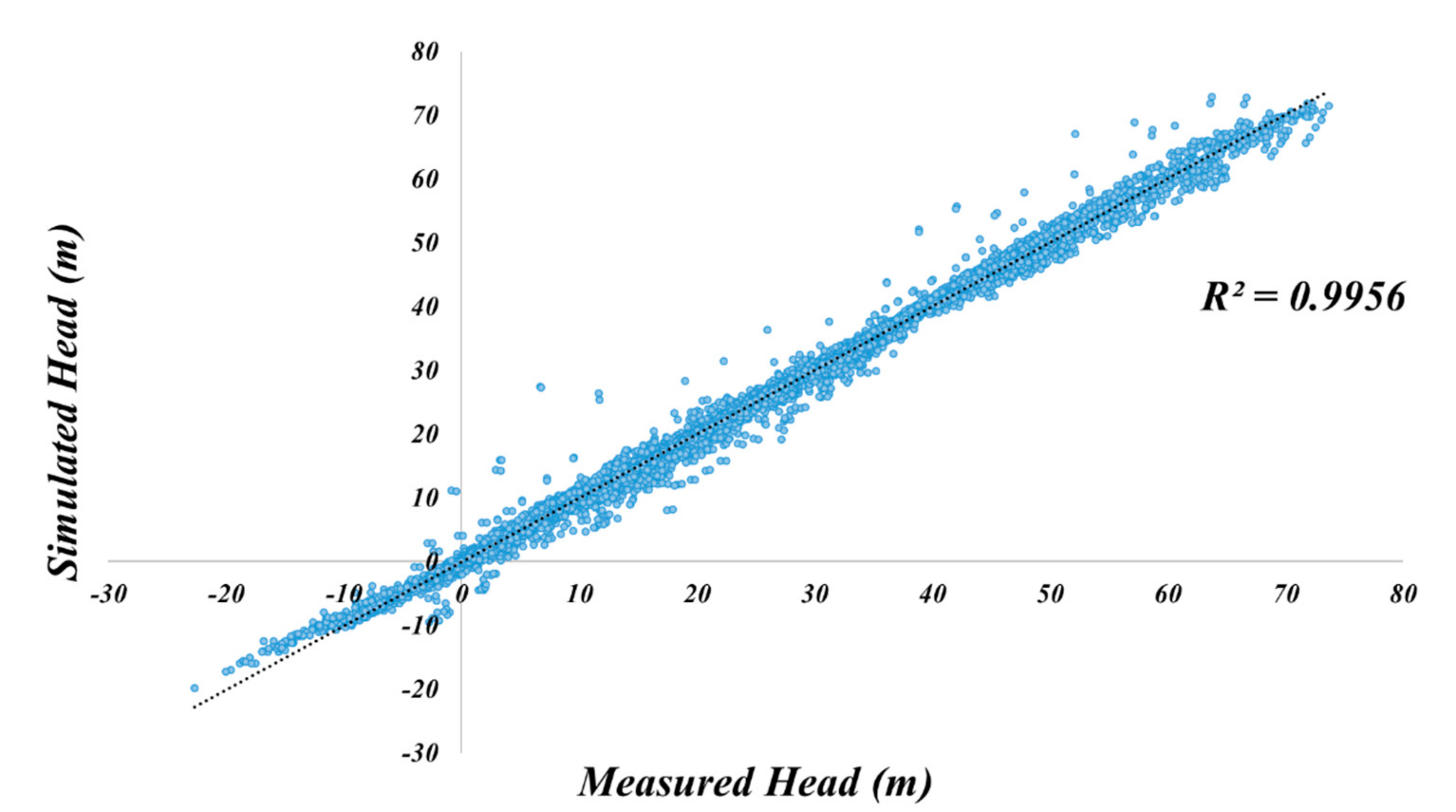
4.1.3. Calibration of SWI Model
4.2. The Surrogate Model of ANNs
4.2.1. Management Scenario #1
4.2.2. Management Scenario #2
4.3. Results of SWI Management
4.3.1. The Setting of DE Algorithm
4.3.2. The Results of Status Quo
4.3.3. The Management Results of Scenario #1
4.3.4. The Management Results of Scenario #2
5. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Chiang, C.-Y.; Wang, C.-H. Seawater Intrusion in the Groundwater Area of Pingtung Plain. Groundwater and Hydrogeological in the Pingtung Plain, Taiwan; Water Resources Agency MOEA: Taichung, Taiwan, 1998. (In Chinese) [Google Scholar]
- Chang, L.-C. Hydrogeological Survey and Groundwater Resource Estimation in Taiwan—Potential Estimation of Groundwater Recharge and Groundwater Flow Model (3/4); Bulletin of the Central Geological Survey MOEA: Taipei, Taiwan, 2011. (In Chinese) [Google Scholar]
- Werner, A.D. A review of seawater intrusion and its management in Australia. Hydrogeol. J. 2010, 18, 281–285. [Google Scholar] [CrossRef]
- Werner, A.D.; Bakker, M.; Post, V.E.; Vandenbohede, A.; Lu, C.; Ataie-Ashtiani, B.; Simmons, C.T.; Barry, D.A. Seawater intrusion processes, investigation and management: Recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Shi, L.; Jiao, J.J. Seawater intrusion and coastal aquifer management in china: A review. Environ. Earth Sci. 2014, 72, 2811–2819. [Google Scholar] [CrossRef]
- Cheng, A.D.; Halhal, D.; Naji, A.; Ouazar, D. Pumping optimization in saltwater-intruded coastal aquifers. Water Resour. Res. 2000, 36, 2155–2165. [Google Scholar] [CrossRef]
- Mantoglou, A. Pumping management of coastal aquifers using analytical models of saltwater intrusion. Water Resour. Res. 2003, 39, 183. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Ketabchi, H. Elitist continuous ant colony optimization algorithm for optimal management of coastal aquifers. Water Resour. Manag. 2011, 25, 165–190. [Google Scholar] [CrossRef]
- Lu, C.; Shi, W.; Xin, P.; Wu, J.; Werner, A.D. Replenishing an unconfined coastal aquifer to control seawater intrusion: Injection or infiltration? Water Resour. Res. 2017, 53. [Google Scholar] [CrossRef]
- Mahesha, A. Control of seawater intrusion through injection-extraction well system. J. Irrig. Drain. Eng. 1996, 122, 314–317. [Google Scholar] [CrossRef]
- Rastogi, A.; Choi, G.W.; Ukarande, S. Diffused interface model to prevent ingress of sea water in multi-layer coastal aquifers. J. Spatial Hydrol. 2004, 4, 1–31. [Google Scholar]
- Mantoglou, A.; Papantoniou, M.; Giannoulopoulos, P. Management of coastal aquifers based on nonlinear optimization and evolutionary algorithms. J. Hydrol. 2004, 297, 209–228. [Google Scholar] [CrossRef]
- Shamir, U.; Bear, J.; Gamliel, A. Optimal annual operation of a coastal aquifer. Water Resour. Res. 1984, 20, 435–444. [Google Scholar] [CrossRef]
- Finney, B.A.; Samsuhadi, A.; Willis, R. Quasi-three-dimensional optimization model of Jakarta basin. J. Water Resour. Plan. Manag. 1992, 118, 18–31. [Google Scholar] [CrossRef]
- Zheng, C.; Bennett, G. Applied Contaminant Transport Modeling; John Wiley & Sons. Inc.: New York, NY, USA, 2002; p. 621. [Google Scholar]
- Abarca, E.; Vázquez-Suñé, E.; Carrera, J.; Capino, B.; Gámez, D.; Batlle, F. Optimal design of measures to correct seawater intrusion. Water Resour. Res. 2006, 42, 203–206. [Google Scholar] [CrossRef]
- Bear, J.; Cheng, A.H.-D.; Sorek, S.; Ouazar, D.; Herrera, I. Seawater Intrusion in Coastal Aquifers: Concepts, Methods and Practices; Springer Science & Business Media: Berlin, Germany, 1999; Volume 14. [Google Scholar]
- Badon-Ghyben, W. Nota in Verband Met de Voorgenomen Putboring Nabil Amsterdam’tijdschr; Kononkl. Inst. Ing.: The Hague, The Netherlands, 1888; Volume 27, pp. 1888–1889. [Google Scholar]
- Herzberg, D. Die Wasserversorgung Einiger Nordseebäder. J. Gasbeleucht. Wasserversorg. 1901, 44, 815–844. [Google Scholar]
- Singh, A. Simulation and optimization modeling for the management of groundwater resources. I: Distinct applications. J. Irrig. Drain. Eng. 2013, 140, 04013021. [Google Scholar] [CrossRef]
- Voss, C.I.; Provost, A.M. Sutra; US Geological Survey Water Resource Investigation Reports: Reston, VA, USA, 1984; pp. 84–4369. [Google Scholar]
- Lin, H.-C.J.; Richards, D.R.; Yeh, G.-T.; Cheng, J.-R.; Cheng, H.-P. Femwater: A Three-Dimensional Finite Element Computer Model for Simulating Density-Dependent Flow and Transport in Variably Saturated Media; DTIC Document; DTIC: Fort Belvoir, VA, USA, 1997. [Google Scholar]
- Guo, W.; Bennett, G. Seawat Version 1.1—A Computer Program for Simulations of Ground Water Flow of Variable Density; Missimer International Inc.: Fort Myers, FL, USA, 1998. [Google Scholar]
- Willis, R.; Finney, B.A. Planning model for optimal control of saltwater intrusion. J. Water Resour. Plan. Manag. 1988, 114, 163–178. [Google Scholar] [CrossRef]
- Das, A.; Datta, B. Development of multiobjective management models for coastal aquifers. J. Water Resour. Plan. Manag. 1999, 125, 76–87. [Google Scholar] [CrossRef]
- Javadi, A.; Abd-Elhamid, H.; Farmani, R. A simulation-optimization model to control seawater intrusion in coastal aquifers using abstraction/recharge wells. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 1757–1779. [Google Scholar] [CrossRef]
- Ahlfeld, D.P.; Mulligan, A.E. Optimal Management of Flow in Groundwater Systems; Academic Press: San Diego, CA, USA, 2000; Volume 1. [Google Scholar]
- Wanakule, N.; Mays, L.W.; Lasdon, L.S. Optimal management of large-scale aquifers: Methodology and applications. Water Resour. Res. 1986, 22, 447–465. [Google Scholar] [CrossRef]
- Culver, T.B.; Shoemaker, C.A. Optimal control for groundwater remediation by differential dynamic programming with quasi-newton approximations. Water Resour. Res. 1993, 29, 823–831. [Google Scholar] [CrossRef]
- Culver, T.B.; Shoemaker, C.A. Dynamic optimal ground-water reclamation with treatment capital costs. J. Water Resour. Plan. Manag. 1997, 123, 23–29. [Google Scholar] [CrossRef]
- Singh, A. Simulation and optimization modeling for the management of groundwater resources. II: Combined applications. J. Irrig. Drain. Eng. 2014, 140, 04014002. [Google Scholar] [CrossRef]
- Ketabchi, H.; Ataie-Ashtiani, B. Coastal groundwater optimization—Advances, challenges, and practical solutions. Hydrogeol. J. 2015, 23, 1129–1154. [Google Scholar] [CrossRef]
- Singh, A. Optimization modelling for seawater intrusion management. J. Hydrol. 2014, 508, 43–52. [Google Scholar] [CrossRef]
- Aguado, E.; Remson, I. Ground-water hydraulics in aquifer management. J. Hydraul. Div. 1974, 100, 103–118. [Google Scholar]
- Gorelick, S.M. A review of distributed parameter groundwater management modeling methods. Water Resour. Res. 1983, 19, 305–319. [Google Scholar] [CrossRef]
- Ndambuki, J.; Otieno, F.; Stroet, C.; Veling, E. Groundwater management under uncertainty: A multi-objective approach. Water SA 2000, 26, 35–42. [Google Scholar]
- Deininger, R.A. Systems Analysis of Water Supply Systems; Wiley: Hoboken, NJ, USA, 1970. [Google Scholar]
- Maddock, T. Ground-water planning model—A basic for a data collection network. In Proceedings of the International Symposium on Uncertainties in Hydrologic and Water Resource Systems, Tuscon, AZ, USA, 11–14 December 1972. [Google Scholar]
- Maddock, T. The operation of a stream-aquifer system under stochastic demands. Water Resour. Res. 1974, 10, 1–10. [Google Scholar] [CrossRef]
- Rosenwald, G.W.; Green, D.W. A method for determining the optimum location of wells in a reservoir using mixed-integer programming. Soc. Pet. Eng. J. 1974, 14, 44–54. [Google Scholar] [CrossRef]
- Heidari, M. Application of Linear System's Theory and Linear Programming to Ground Water Management in Kansas; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar]
- Hallaji, K.; Yazicigil, H. Optimal management of a coastal aquifer in southern turkey. J. Water Resour. Plan. Manag. 1996, 122, 233–244. [Google Scholar] [CrossRef]
- Johnson, V.M.; Rogers, L.L. Accuracy of neural network approximators in simulation-optimization. J. Water Resour. Plan. Manag. 2000, 126, 48–56. [Google Scholar] [CrossRef]
- Bhattacharjya, R.K.; Datta, B. Optimal management of coastal aquifers using linked simulation optimization approach. Water Resour. Manag. 2005, 19, 295–320. [Google Scholar] [CrossRef]
- Bhattacharjya, R.; Datta, B. Ann-ga-based model for multiple objective management of coastal aquifers. J. Water Resour. Plan. Manag. 2009, 135, 314–322. [Google Scholar] [CrossRef]
- Kourakos, G.; Mantoglou, A. Pumping optimization of coastal aquifers based on evolutionary algorithms and surrogate modular neural network models. Adv. Water Resour. 2009, 32, 507–521. [Google Scholar] [CrossRef]
- Dhar, A.; Datta, B. Saltwater intrusion management of coastal aquifers. I: Linked simulation-optimization. J. Hydrol. Eng. 2009, 14, 1263–1272. [Google Scholar] [CrossRef]
- Rao, S.; Sreenivasulu, V.; Bhallamudi, S.M.; Thandaveswara, B.; Sudheer, K. Planning groundwater development in coastal aquifers/planification du développement de la ressource en eau souterraine des aquifères côtiers. Hydrol. Sci. J. 2004, 49, 155–170. [Google Scholar] [CrossRef]
- Christelis, V.; Mantoglou, A. Pumping optimization of coastal aquifers assisted by adaptive metamodelling methods and radial basis functions. Water Resour. Manag. 2016, 30, 5845–5859. [Google Scholar] [CrossRef]
- Nikolos, I.K.; Stergiadi, M.; Papadopoulou, M.P.; Karatzas, G.P. Artificial neural networks as an alternative approach to groundwater numerical modelling and environmental design. Hydrol. Process. 2008, 22, 3337–3348. [Google Scholar] [CrossRef]
- Papadopoulou, M.P.; Nikolos, I.K.; Karatzas, G.P. Computational benefit using artificial intelligent methodologies for the solution of an environmental design problem: Saltwater intrusion. Water Sci. Technol. 2010, 62, 1479–1490. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Langevin, C.D. User’s Guide to Seawat: A Computer Program for Simulation of Three-Dimensional Variable-Density Ground-Water Flow; USGS: Tallahassee, FL, USA, 2002. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. Modflow-2000, the U.S. Geological Survey Modular Ground-Water Model-User Guide to Modularization Concepts and the Ground-Water Flow Process; Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2000. [Google Scholar]
- Zheng, C.; Wang, P.P. Mt3dms: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems: Documentation and User’s Guide; DTIC Document; DTIC: Fort Belvoir, VA, USA, 1999. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning Internal Representations by Error Propagation, Parallel Distributed Processing; MIT Press: Cambridge, UK, 1986; Volume 1, pp. 318–362. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Vesterstrom, J.; Thomsen, R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In Proceedings of the IEEE Congress on Evolutionary Computation, CEC2004, Portland, OR, USA, 19–23 June 2004; pp. 1980–1987. [Google Scholar]
- Karterakis, S.M.; Karatzas, G.P.; Nikolos, I.K.; Papadopoulou, M.P. Application of linear programming and differential evolutionary optimization methodologies for the solution of coastal subsurface water management problems subject to environmental criteria. J. Hydrol. 2007, 342, 270–282. [Google Scholar] [CrossRef]
- Chiu, Y.-C. Application of differential evolutionary optimization methodology for parameter structure identification in groundwater modeling. Hydrogeol. J. 2014, 22, 1731–1748. [Google Scholar] [CrossRef]
- Chiang, C.-Y. Hydrogeological Survey of Pingtung Plain with the Project of Groundwater Observation Network in Taiwan; Bulletin of the Central Geological Survey MOEA: Taipei, Taiwan, 2002; pp. 1012–6821. (In Chinese) [Google Scholar]
- Peng, T.-R.; Liu, T.-S.; Guo, H.-Y. Groundwaters Salinization in Chemical Compositions of Coastal Area in Pingtung Plain; The Chinese Society of Soil and Fertilizer Sciences: Taipei, Taiwan, 2000; pp. 353–362. (In Chinese) [Google Scholar]
- Chiang, C.-Y. Seawater Intrusion in the Pingtung Plain; Bulletin of the Central Geological Survey MOEA: Taipei, Taiwan, 6821 2000; pp. 1012–6821. (In Chinese) [Google Scholar]
- Cheng, Y. An Optimal Water Allocation for the Ailiao Irrigation District in Pingtung County, Taiwan. Ph.D. Thesis, National Cheng Kung University, Tainan, Taiwan, 2008. (In Chinese). [Google Scholar]
- Central Geological Survey. MOEA Report of Hydrogeologic Investigation for Pingtung Plain; Central Geological Survey: Taipei, Taiwan, 1997. (In Chinese) [Google Scholar]
- Mehl, S.W.; Hill, M.C. Modflow–LGR—Documentation of Ghost Node Local Grid Refinement (Lgr2) for Multiple Areas and the Boundary Flow and Head (Bfh2) Package; US Geological Survey Techniques and Methods: Reston, VA, USA, 2013. [Google Scholar]
- Hydrological Year Book of Taiwan. Taiwan Water Resources Agency MOEA: Taipei, Taiwan, 1997. (In Chinese)
- Hydrological Year Book of Taiwan. Taiwan Water Resources Agency MOEA: Taipei, Taiwan, 1998.
- Water Resource Bureau. Hydrological Year Book of Taiwan; Taiwan Water Resources Agency MOEA: Taipei, Taiwan, 1999. (In Chinese) [Google Scholar]
- Doherty, J.; Brebber, L.; Whyte, P. Pest: Model-Independent Parameter Estimation; Watermark Computing: Corinda, Australia, 1994; pp. 551–554. [Google Scholar]
- Hill, M.C.; Banta, E.R.; Harbaugh, A.W.; Anderman, E.R. Modflow-2000, the US Geological Survey Modular Ground-Water Model; User Guide to the Observation Sensitivity and Parameter-Estimation Processes and Three Post-Processing Programs; 2331-1258; US Geological Survey: Denver, CO, USA, 2000. [Google Scholar]

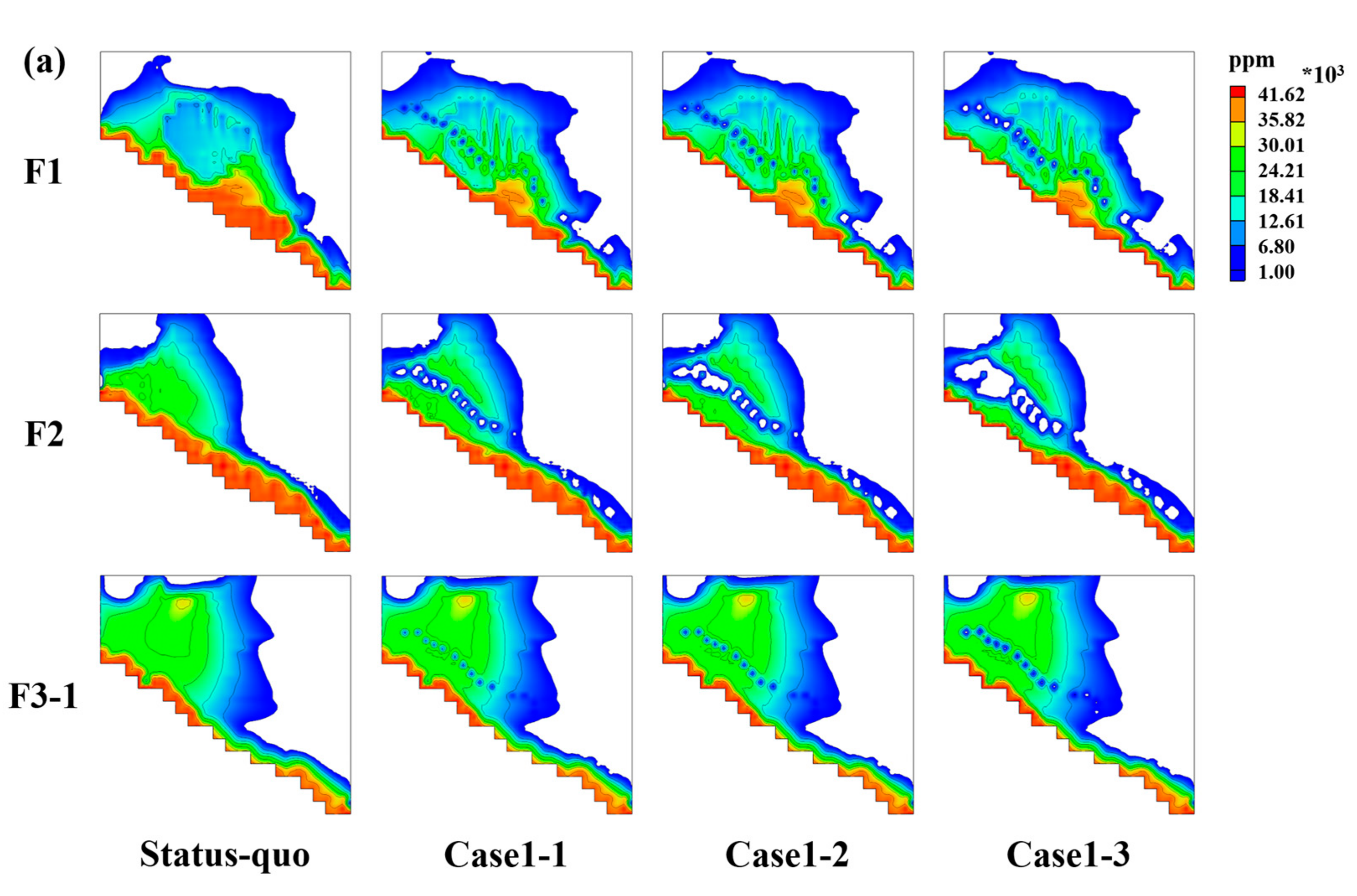
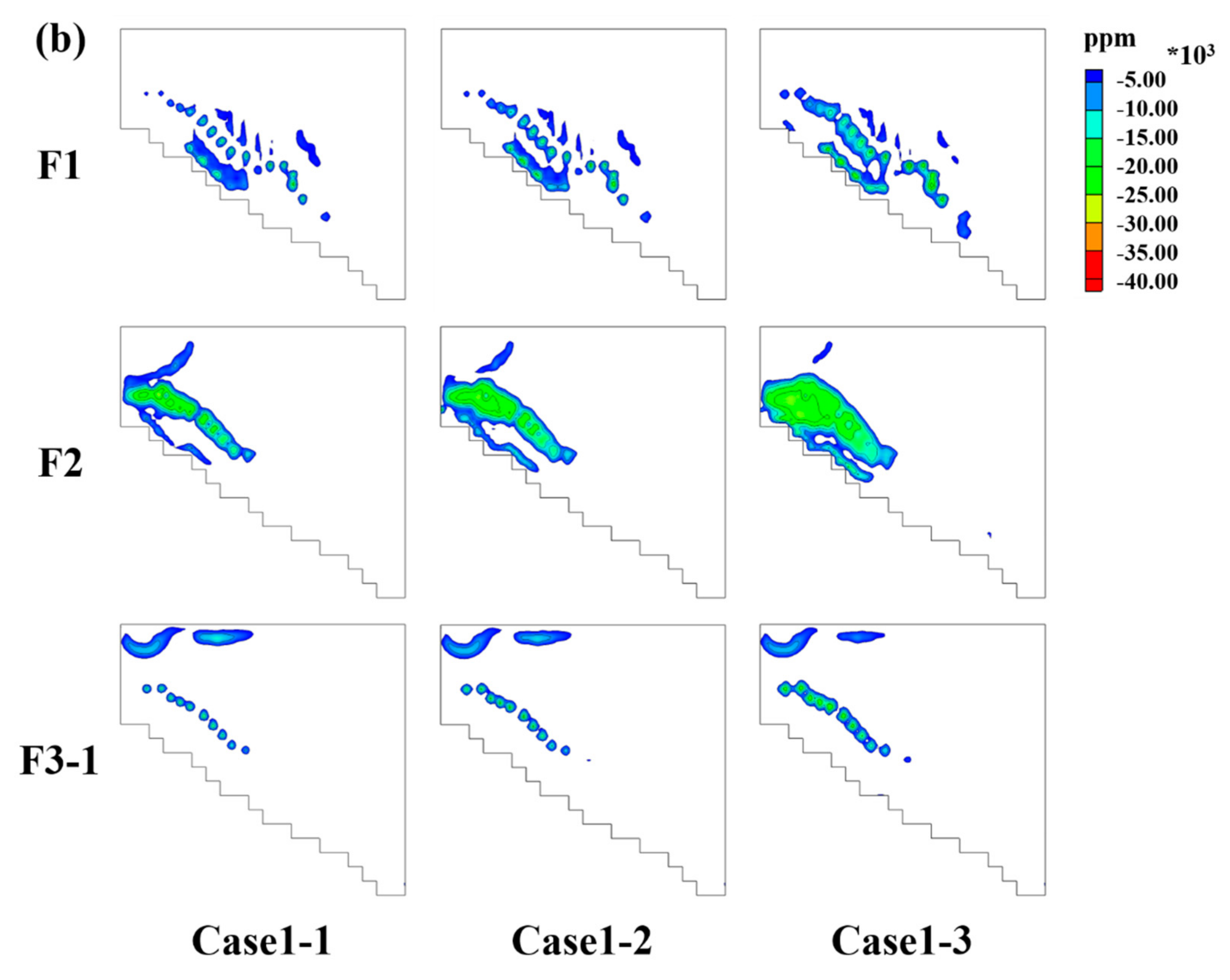


| Model Parameter | Regional Flow Model (Calibrated by Chang [2]) | SWI Model(Calibrate Based on Historical TDS Data) | ||||
|---|---|---|---|---|---|---|
| Aquifer F1 | Aquifer F2 | Aquifer F3-1 | Aquifer F1 | Aquifer F2 | Aquifer F3-1 | |
| Grid cell size in x and y-directions (m) | 1000 × 1000 | 333 × 333 | ||||
| Grid cell size in z-direction (m) | 9–85 | 4–93 | 5–100 | 4.3–17.67 | 1.6–20 | 10.3–27.7 |
| Horizontal hydraulic conductivity (m·day−1) | 0.15–231.55 | 0.03–200.30 | 0.61–230.00 | 0.15–100.00 | 17.12–200.30 | 1.98–230.00 |
| Vertical hydraulic conductivity (m·day−1) | 0.003–4.63 | 0.0006–4.00 | 0.01–4.60 | 0.003–2.00 | 0.34–4.00 | 0.04–4.60 |
| Specific storage (m−1) | 6 × 10−6–6 × 10−5 | 6.8 × 10−6–5 × 10−5 | 6 × 10−6–4 × 10−5 | 6 × 10−6–4 × 10−5 | 1 × 10−5–2 × 10−5 | 6.75 × 10−6–1.8 × 10−5 |
| Specific yield (-) | 0.06–0.30 | --- | --- | 0.06–0.21 | --- | --- |
| Dispersivity (m) | --- | --- | --- | 0.01–400.00 | 0.01–300.00 | 0.001–500.00 |
| Number of Neurons | Mean Square Error (MSE) |
|---|---|
| 3 | 4.6813 |
| 5 | 0.72893 |
| 7 | 0.2347 |
| 9 | 0.14783 |
| Data Set | Correlation Coefficient (R) | |
|---|---|---|
| Scenario #1 | Scenario #2 | |
| Training | 0.99785 | 0.96787 |
| Validation | 0.99787 | 0.96741 |
| Testing | 0.99779 | 0.96516 |
| All | 0.99784 | 0.9674 |
| Mechanism of Vector Selection | Random (Uniform Distribution) |
|---|---|
| Number of decision variables | 4 in Scenario #1 and 5 in Scenario #2 |
| Lower bound of decision variables | 0 |
| Upper bound of decision variables | 1000 |
| Population size | 30, 50, 100 |
| Max iterations | 200 |
| Scale factor F | 0.85 |
| Crossover probability | 1 |
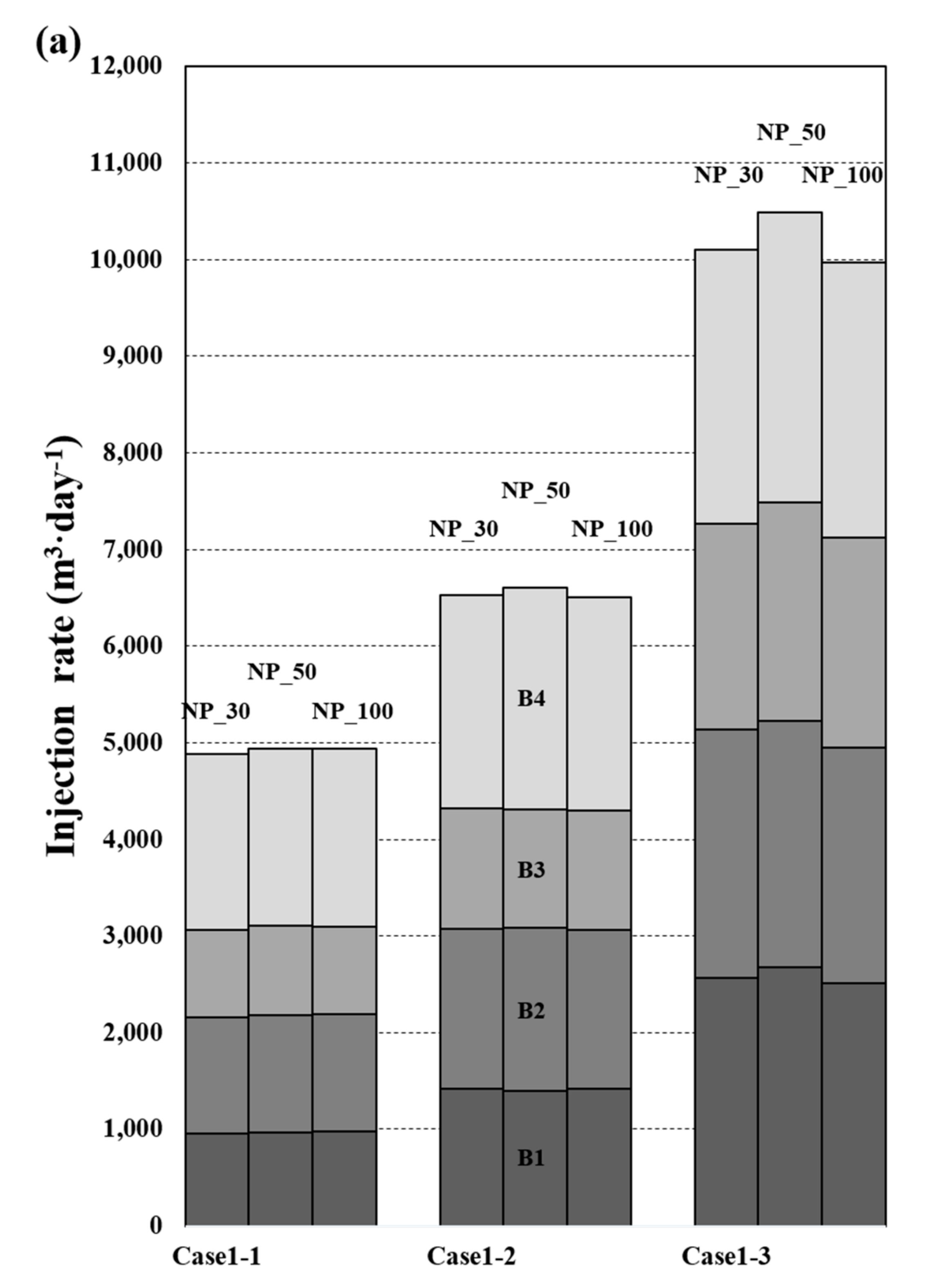
| Cases | Objective Function | Injection Rate #1 | Injection Rate #2 | Injection Rate #3 | Injection Rate #4 | Injection Rate #5 |
|---|---|---|---|---|---|---|
| Scenario #1 | ||||||
| Case 1-1 | 4840.15 | 944.85 | 1193.85 | 893.45 | 1808.00 | --- |
| Case 1-2 | 6415.30 | 1429.75 | 1619.85 | 1178.00 | 2187.70 | --- |
| Case 1-3 | 9825.00 | 2633.50 | 2436.65 | 1991.65 | 2763.20 | --- |
| Scenario #2 | ||||||
| Case 2-1 | 5446.64 | 2505.50 | 0.64 | 0.028 | 1833.60 | 1106.88 |
| Case 2-2 | 12964.55 | 2694.70 | 1069.84 | 1040.41 | 5010.80 | 3148.80 |
| Case 2-3 | 26076.50 | 6766.50 | 7253.52 | 1277.22 | 5341.10 | 5438.16 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, P.-S.; Chiu, Y.-C. A Simulation-Optimization Model for Seawater Intrusion Management at Pingtung Coastal Area, Taiwan. Water 2018, 10, 251. https://doi.org/10.3390/w10030251
Huang P-S, Chiu Y-C. A Simulation-Optimization Model for Seawater Intrusion Management at Pingtung Coastal Area, Taiwan. Water. 2018; 10(3):251. https://doi.org/10.3390/w10030251
Chicago/Turabian StyleHuang, Po-Syun, and Yung-Chia Chiu. 2018. "A Simulation-Optimization Model for Seawater Intrusion Management at Pingtung Coastal Area, Taiwan" Water 10, no. 3: 251. https://doi.org/10.3390/w10030251
APA StyleHuang, P.-S., & Chiu, Y.-C. (2018). A Simulation-Optimization Model for Seawater Intrusion Management at Pingtung Coastal Area, Taiwan. Water, 10(3), 251. https://doi.org/10.3390/w10030251





