Forecasting Quarterly Inflow to Reservoirs Combining a Copula-Based Bayesian Network Method with Drought Forecasting
Abstract
:1. Introduction
2. Methodology
2.1. Procedures of Quarterly Inflow Forecasting
2.2. Copula-Based Bayesian Network
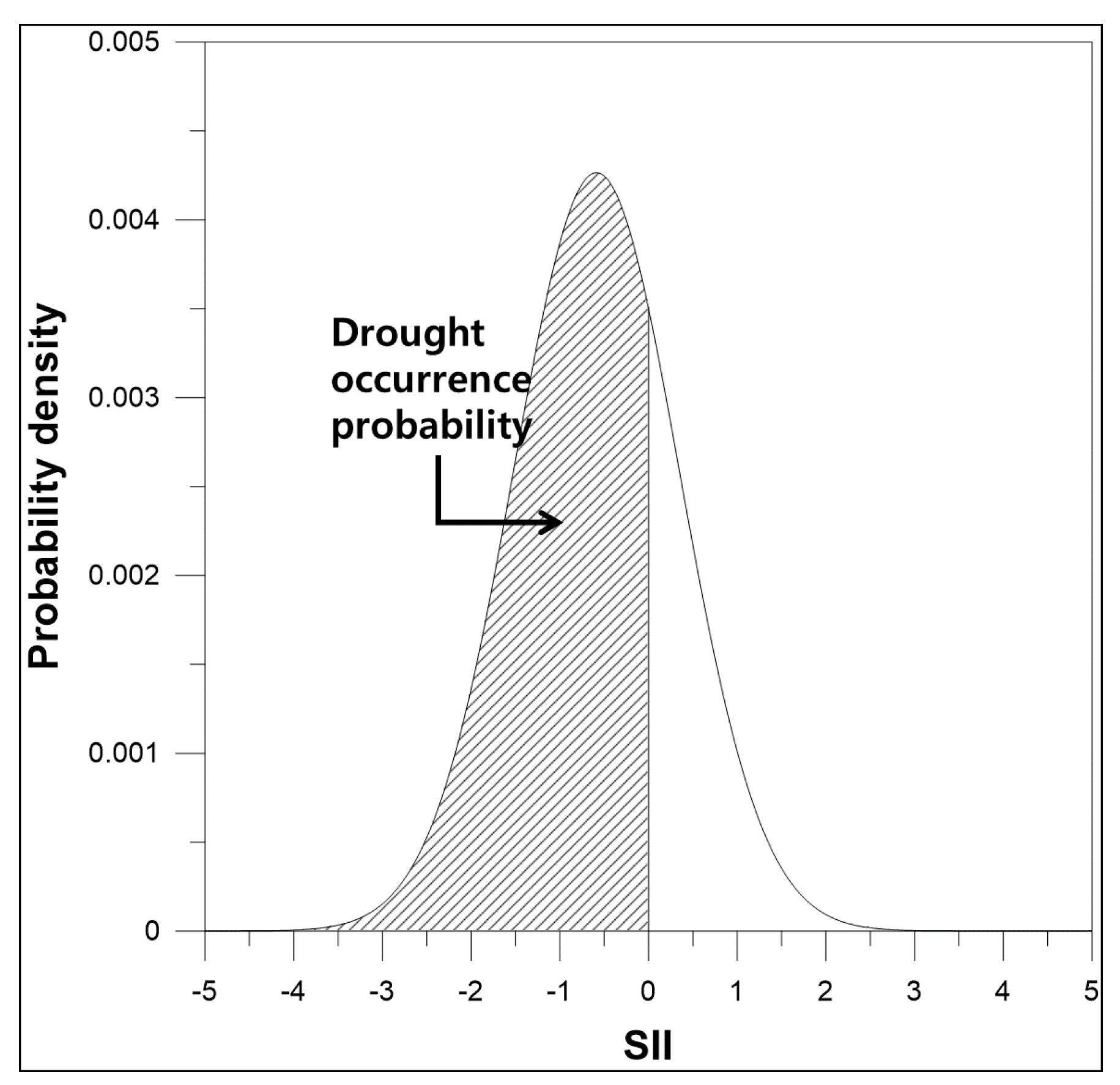
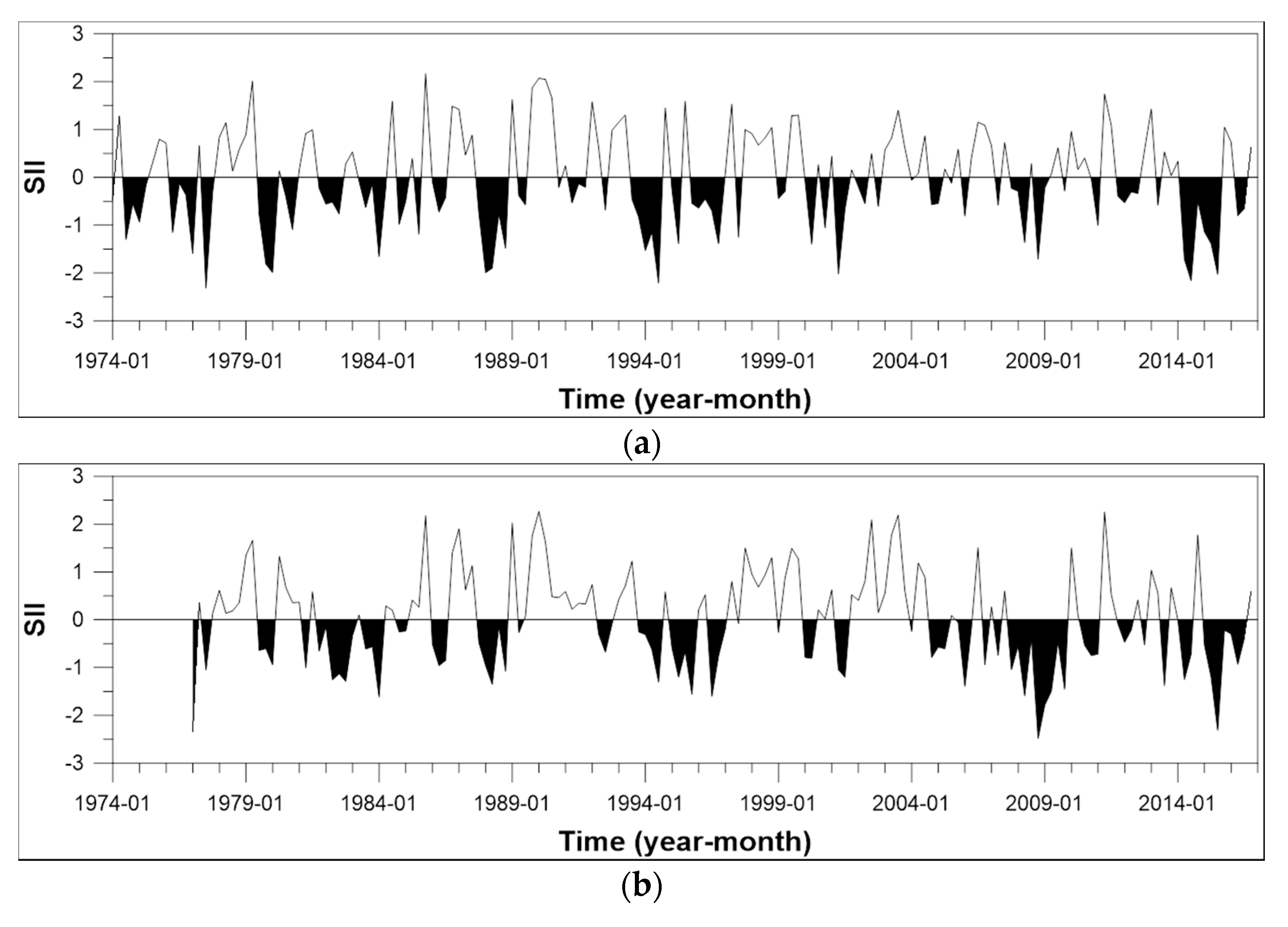
2.3. Drought Forecasting Using Drought Index
2.4. Quarterly Inflow Forecasting Combined with Drought Forecasting
- (1)
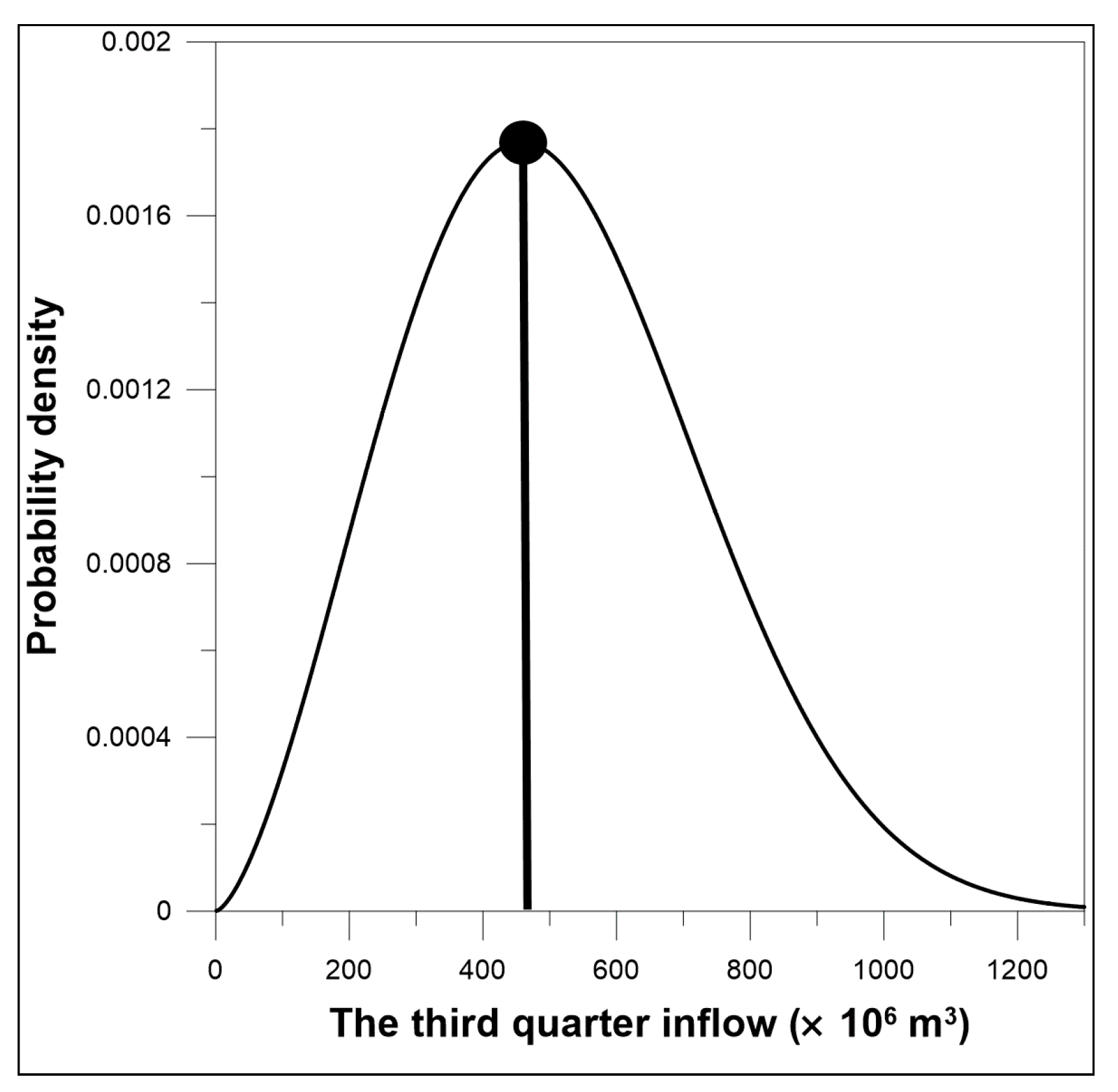
- Use the probability distribution of the next quarter inflow (like that in Figure 3) to calculate the cumulative probability that corresponds to a specific inflow of the next quarter.
- (2)
- Use the cumulative probability to calculate the SII.
- (3)
- When the calculated SII is the same as the lower bound value of each drought stage, set the corresponding quarterly inflow as the quarterly inflow that represents that drought stage (for D4, the inflow where the SII is −2.5).
- (4)
- Repeat Steps (1) to (3) for all quarters and quarterly inflows.
3. Results
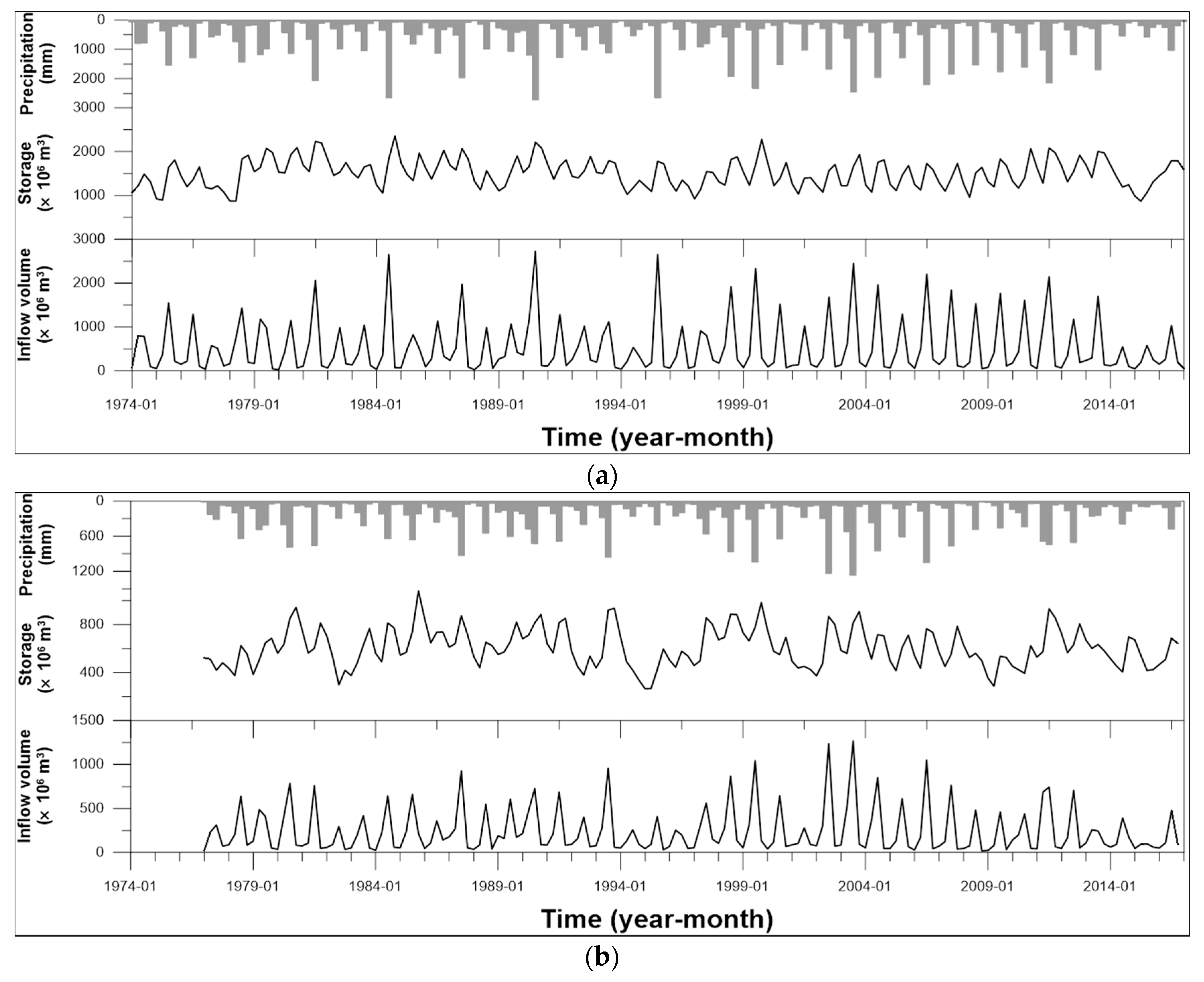
3.1. Two Selected Dams in This Study
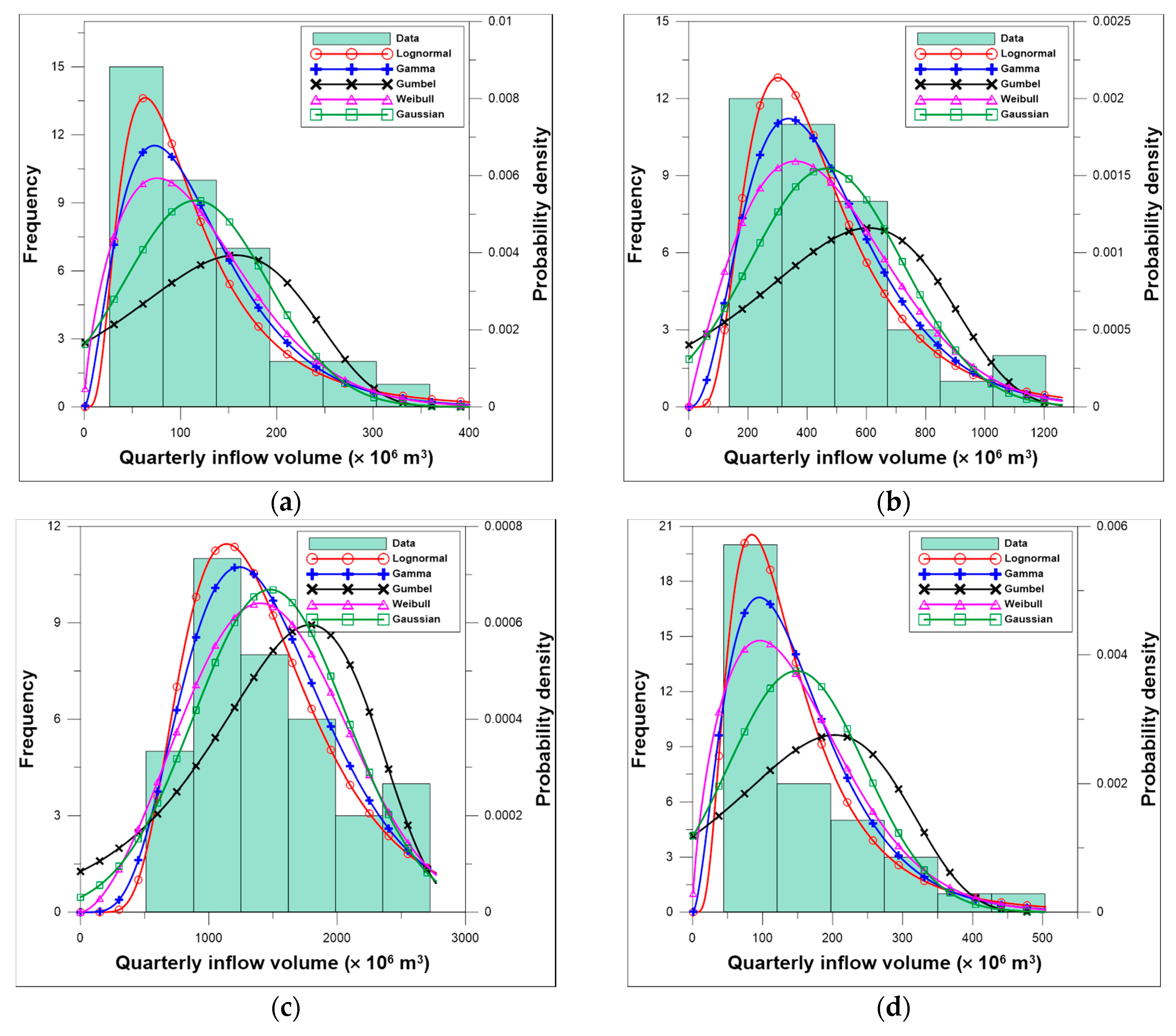
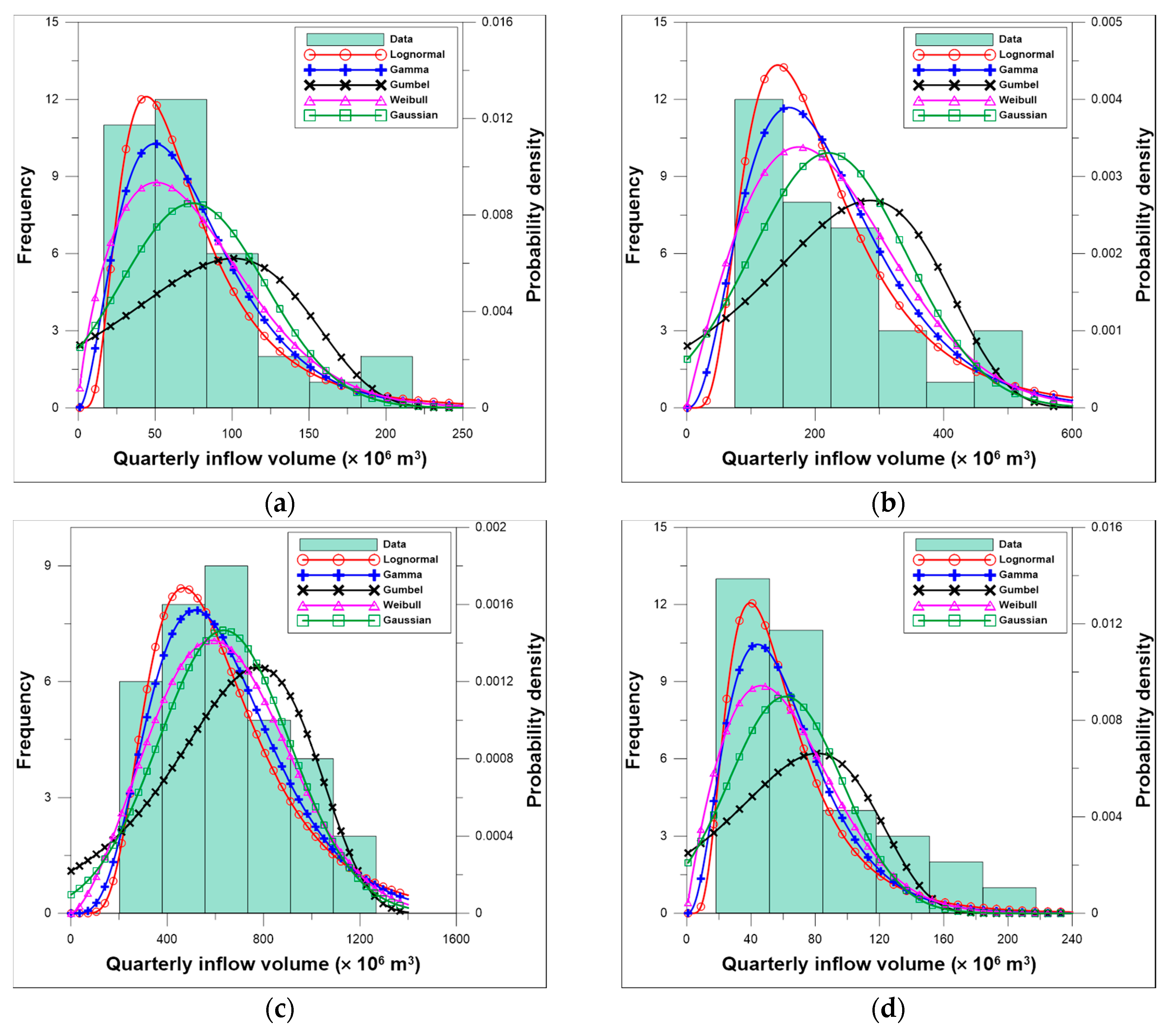
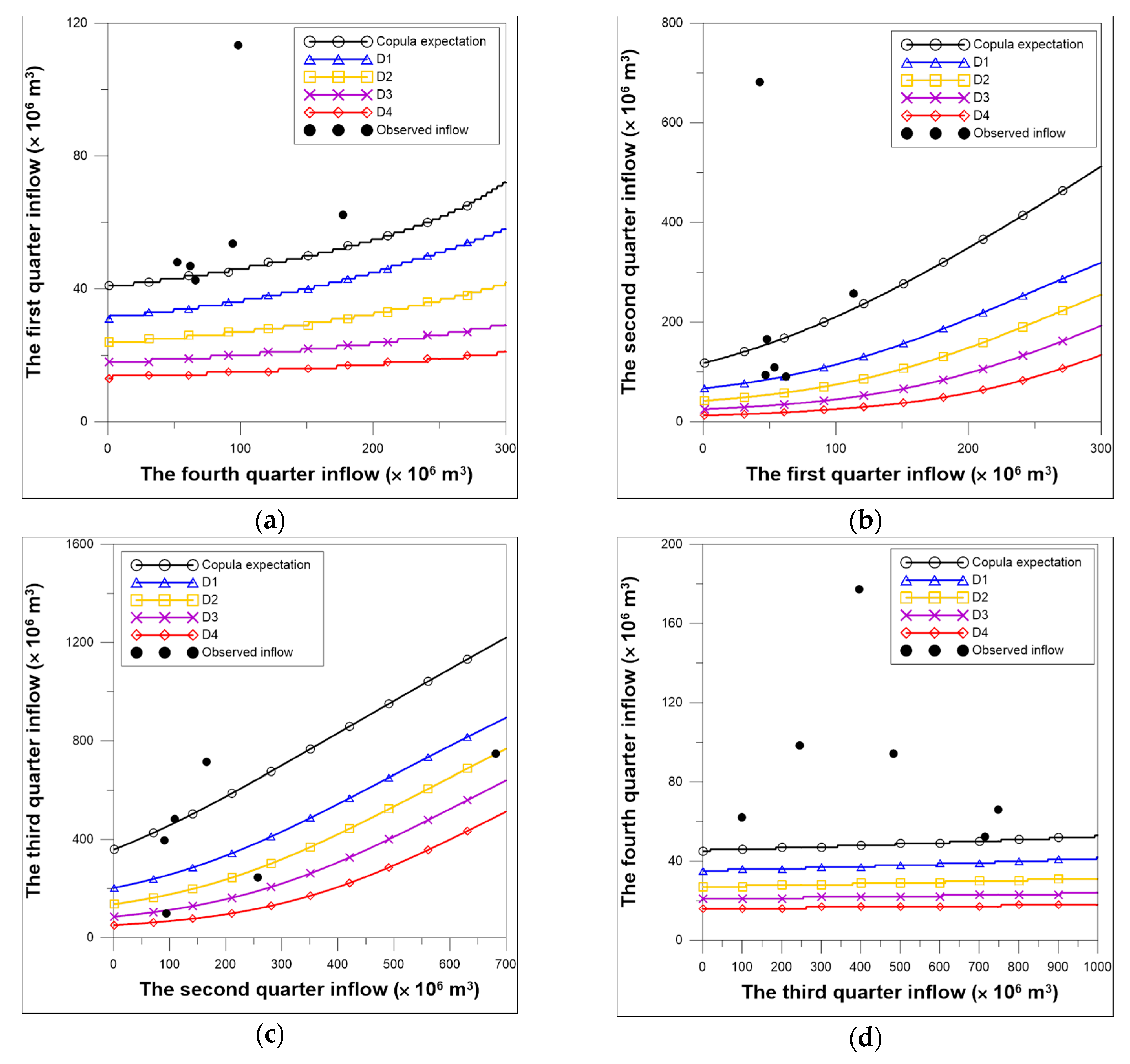
3.2. Quarterly Inflow Forecasting Curves Conforming to Drought Stages
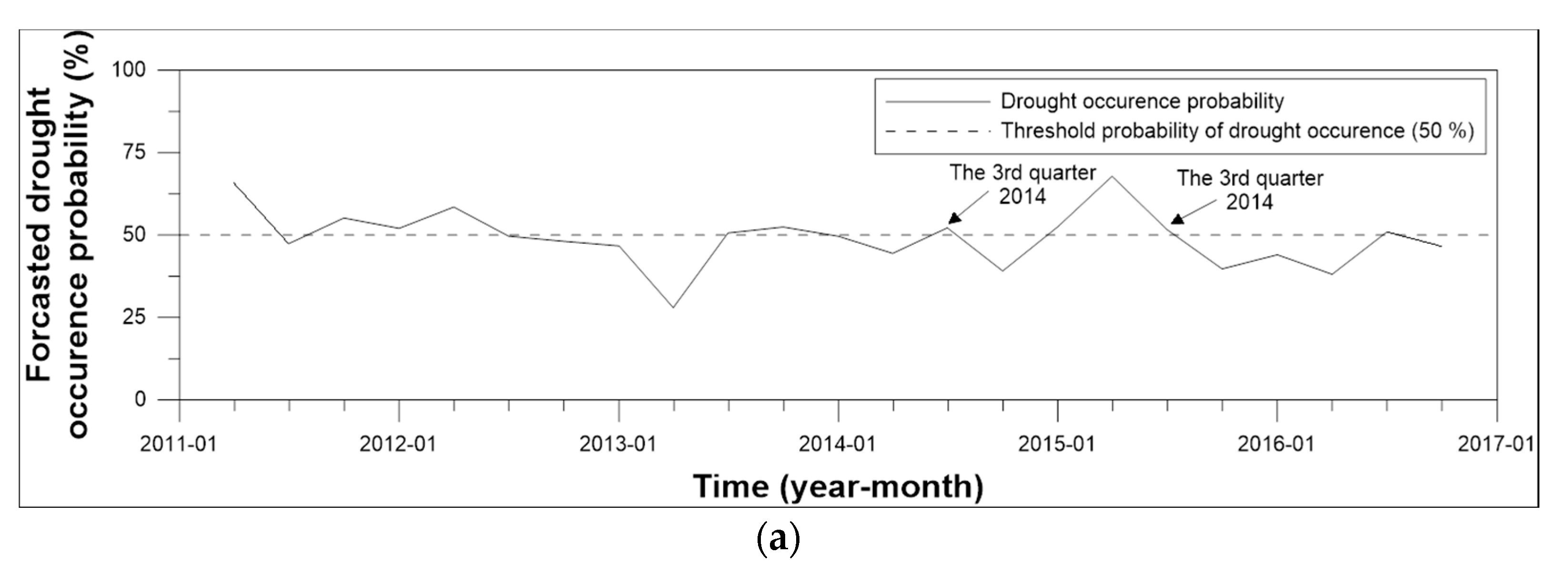
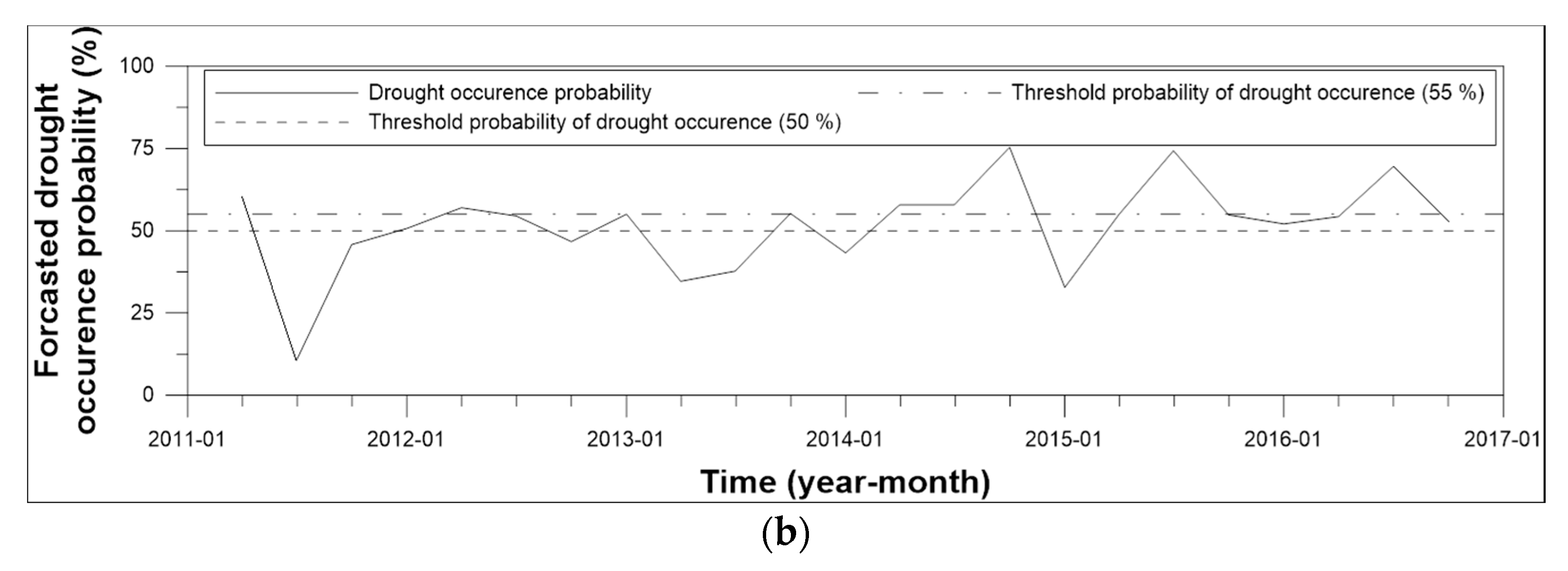
3.3. Quarterly Drought Forecast Results
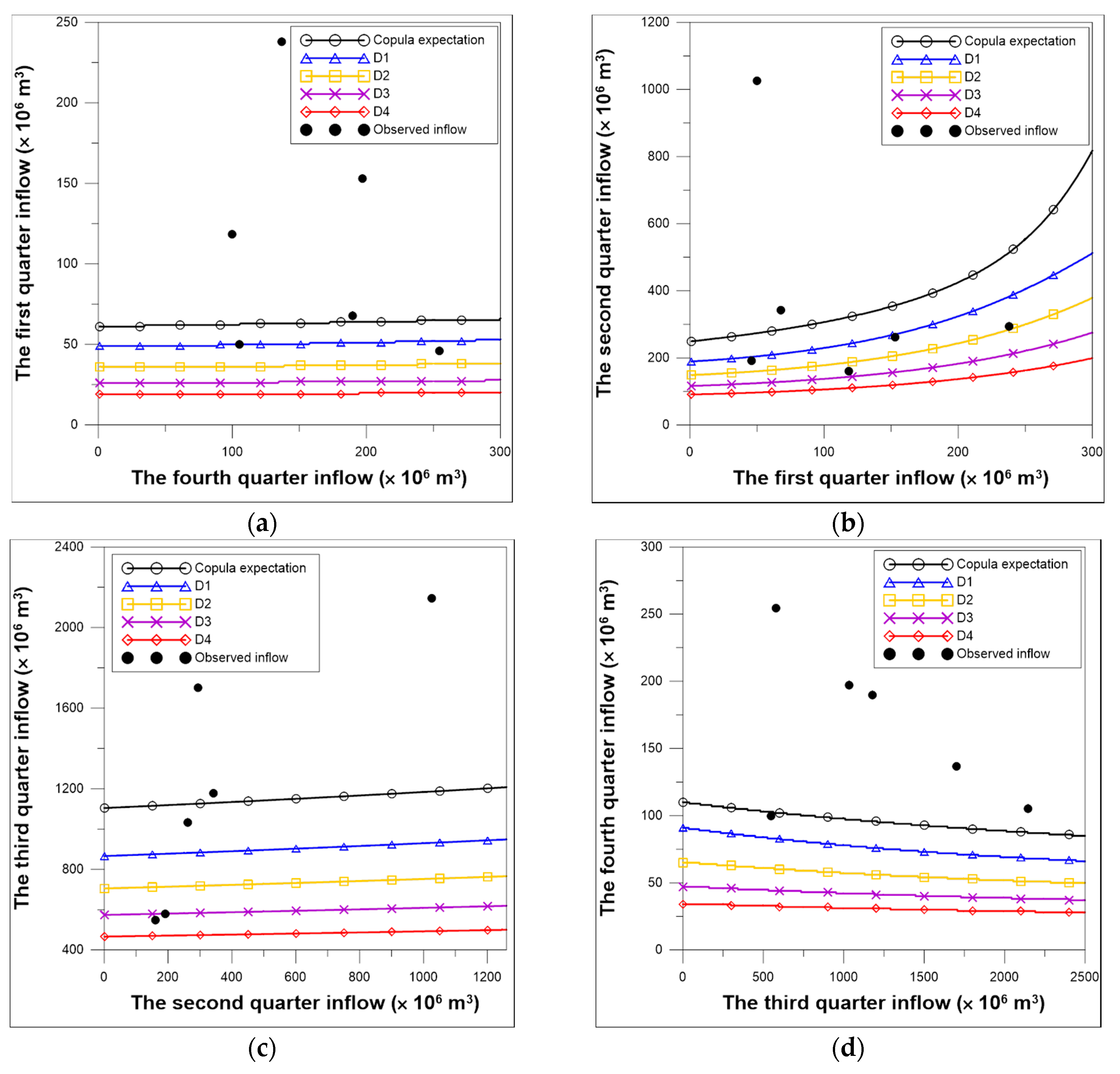
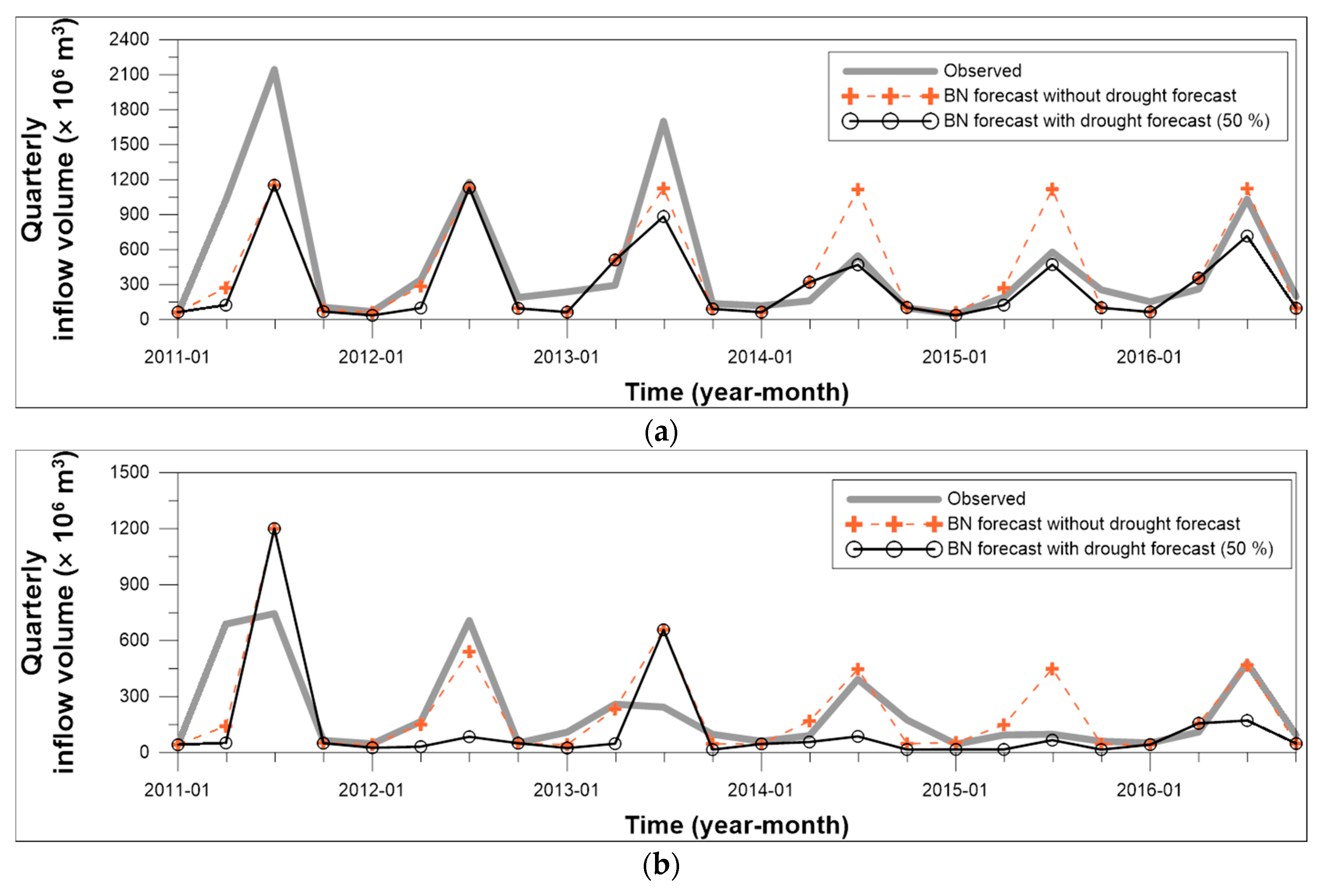
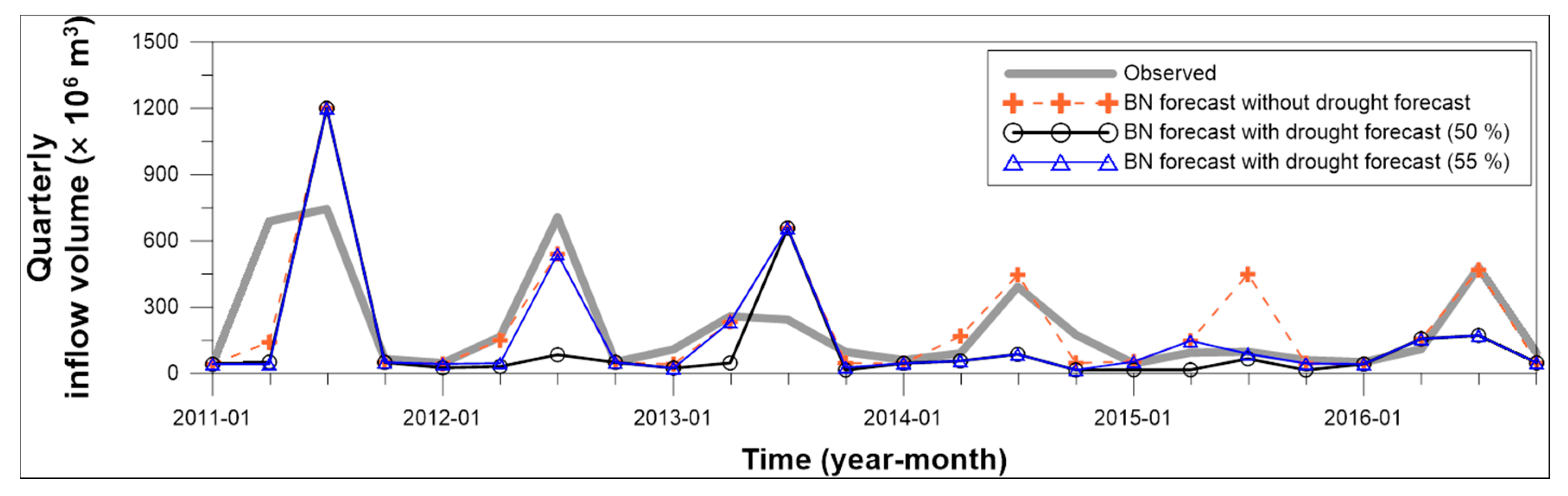
3.4. Quarterly Inflow Forecast Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jeong, D.I.; Kim, Y.O. Forecasting monthly inflow to Chungju dam using ensemble streamflow prediction. KSCE J. Civ. Eng. 2002, 22, 321–331. [Google Scholar]
- Croley, T.E. Using Meteorology Probability Forecasts in Operational Hydrology; ASCE Press: Reston, VA, USA, 2000; ISBN 978-0-7844-0459-1. [Google Scholar]
- Croley, T.E. Climate-biased storm-frequency estimation. J. Hydrol. Eng. 2001, 6, 275–283. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Kim, Y.O. Updating ensemble probabilities based on climate forecasts. In Proceedings of the Conference on Water Resources Planning and Management and Symposium on Managing the Extremes Floods and Drought, Roanoke, VA, USA, 19–22 May 2002. [Google Scholar]
- Jeong, D.I.; Kim, Y.O.; Cho, S.Z.; Shin, H.J. A study on rainfall-runoff models for improving ensemble streamflow prediction—I. Rainfall-runoff models using artificial neural networks. KSCE J. Civ. Eng. 2002, 23, 521–530. [Google Scholar]
- Jee, Y.G.; Kim, S.J.; Kim, P.S. Forecasting monthly inflow for the storage management of small dams. In Proceedings of the Korea Water Resources Association Conference, Iksan, Korea, 11–16 September 2005. [Google Scholar]
- Jin, Y. Reservoir Operations Applying a Discrete Hedging Rule with Ensemble Streamflow Prediction to Cope with Droughts. Master’s Thesis, Pukyong National University, Busan, Korea, February 2016. [Google Scholar]
- Pearl, J. Fusion, propagation, and structuring in Belief networks. J. Artif. Intell. Res. 1986, 29, 241–288. [Google Scholar] [CrossRef]
- Jensen, F. Introduction to Bayesian Networks; Springer: Secaucus, NJ, USA, 1996; ISBN 0387915028. [Google Scholar]
- Reckhow, K.H. Water quality prediction and probability networks models. Can. J. Fish. Aquat. Sci. 1999, 56, 1150–1158. [Google Scholar] [CrossRef]
- Borsuk, M.E.; Stow, C.A.; Reckhow, K.H. Integrated approach to total maximum daily load development for the Neuse River estuary using a Bayesian probability network model (Neu-BERN). J. Water Res. Plan. Manag. 2003, 129, 271–282. [Google Scholar] [CrossRef]
- Bromley, J.; Jackson, N.A.; Clymer, O.J.; Giacomello, A.M.; Jensen, F.V. The use of Hugin® to develop Bayesian networks as an aid to integrated water resource planning. Environ. Model. Softw. 2005, 20, 231–242. [Google Scholar] [CrossRef]
- Castelletti, A.; Soncini-Sessa, R. Bayesian networks in water resource modelling and management. Environ. Model. Softw. 2007, 22, 1073–1074. [Google Scholar] [CrossRef]
- Ticehurst, J.L.; Newham, L.T.H.; Rissik, D.; Letcher, R.A.; Jakeman, A.J. A Bayesian network approach for assessing the sustainability of coastal lakes in New South Wales, Australia. Environ. Model. Softw. 2007, 22, 1129–1139. [Google Scholar] [CrossRef]
- Barton, D.N.; Saloranta, T.; Moe, S.J.; Eggestad, H.O.; Kuikka, S. Bayesian belief networks as a meta-modelling tool in integrated river basin management-Pros and cons in evaluation nutrient abatement decisions under uncertainty in a Norwegian river basin. Ecol. Econ. 2008, 66, 91–104. [Google Scholar] [CrossRef]
- Henriksen, H.J.; Barlebo, H.C. Reflections on the use of Bayesian belief networks for adaptive management. J. Environ. Manag. 2008, 88, 1025–1036. [Google Scholar] [CrossRef] [PubMed]
- Elidan, G. Copula Bayesian networks. In Proceedings of the Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010. [Google Scholar]
- Fevre, A.C.; Adlouni, S.E.; Perreault, L.; Thiémonge, N.; Bobée, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40, W01101. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Canossi, M.; Petaccia, A.; Rosso, R. Bivariate statistical approach to check adequacy of dam spillway. J. Hydrol. Eng. 2005, 10, 50–57. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Gumbel-Hougaard copula for trivariate rainfall frequency analysis. J. Hydrol. Eng. 2007, 12, 409–419. [Google Scholar] [CrossRef]
- Gebremichael, M.; Krajewski, W.F. Application of copulas to modeling temporal sampling errors in statelite-derived rainfall estimates. J. Hydrol. Eng. 2007, 12, 404–408. [Google Scholar] [CrossRef]
- Wong, G.; Lambert, M.F.; Leonard, M.; Metcalfe, A.V. Drought analysis using trivariate copulas conditional on climatic states. J. Hydrol. Eng. 2010, 15, 129–141. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. Drought analysis under climate change using copula. J. Hydrol. Eng. 2013, 18, 746–759. [Google Scholar] [CrossRef]
- Shin, J.Y.; Ajmal, M.; Yoo, J.Y.; Kim, T.W. A Bayesian network-based probabilistic framework for drought forecasting and outlook. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. A Bayesian framework for probabilistic seasonal drought forecasting. J. Hydrometeorol. 2013, 14, 1685–1705. [Google Scholar] [CrossRef]
- Russel, S.J.; Peter, N. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2009; ISBN 978-0136042594. [Google Scholar]
- Yoo, J.Y.; Shin, J.Y.; Kim, D.; Kim, T.W. Drought risk analysis using stochastic rainfall generation model and copula functions. J. Korea Water Resour. Assoc. 2013, 46, 425–437. [Google Scholar] [CrossRef]
- Zezula, I. On multivariate Gaussian copula. J. Stat. Plan. 2009, 139, 3942–3946. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of standardized runoff index for characterizing hydrological drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2008, 23, 881–897. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Lopez-Moreno, I.; Vicente-Serrano, S. Investigation of scaling properties in monthly streamflow and Standardized Streamflow Index (SSI) time series in the Ebro Basin (Spain). Physica A 2012, 391, 1662–1678. [Google Scholar] [CrossRef]
- Gusyev, M.A.; Hasegawa, A.; Magome, J.; Kuribayashi, D.; Sawano, H.; Lee, S. Drought assessment in the Pampanga River basin, the Philippines-Part1: Characterizing a role of dams in historical droughts with standardized indices. In Proceedings of the Conference on Modelling and Simulation, Broadbeach, Australia, 29 November–4 December 2015. [Google Scholar]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, American Meteorological Society, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Son, K.H.; Bae, D.H.; Chung, J.S. Drought analysis and assessment by using land surface model on South Korea. J. Korea Water Resour. Assoc. 2011, 44, 667–681. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Hasegawa, A.; Gusyev, M.; Iwami, Y. Meteorological drought and flood assessment using the comparative SPI approach in Asia under climate change. J. Disas. Res. 2016, 11, 1082–1090. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Function with Formulas, Graphs, and Mathematical Tables; U.S. Department of Commerce: Washington, DC, USA, 1964; ISBN 9781591242178.
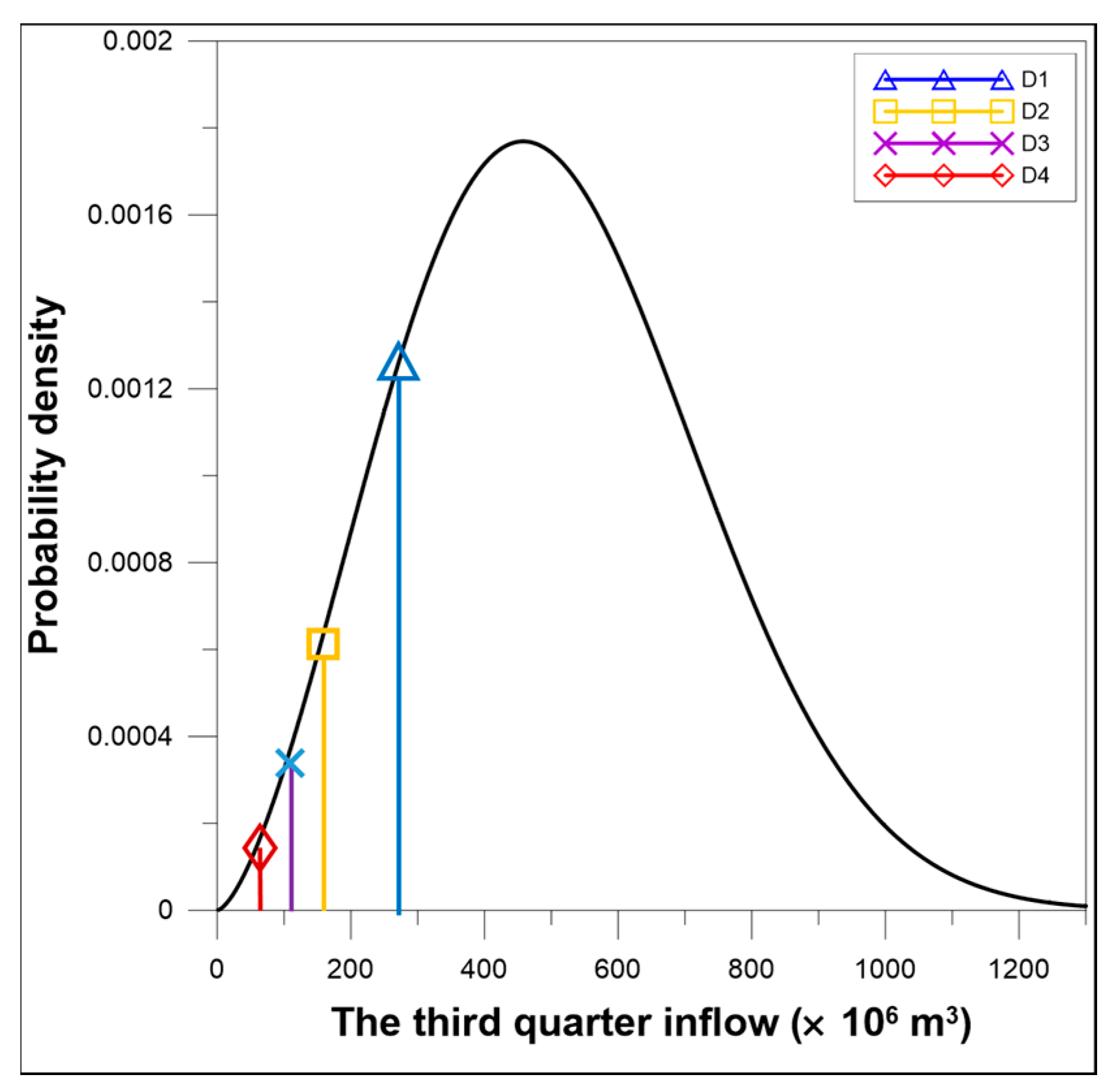

| SII Range | Drought Category |
|---|---|
| 2.00 ≤ SII | Extreme wet |
| 1.50 ≤ SII < 2.00 | Very wet |
| 1.00 ≤ SII < 1.50 | Moderately wet |
| 0.00 ≤ SII < 1.00 | Near normal |
| −1.00 ≤ SII < 0.00 | Mild drought (D1) |
| −1.50 ≤ SII < −1.00 | Moderate drought (D2) |
| −2.00 ≤ SII < −1.50 | Severe drought (D3) |
| SII < −2.00 | Extreme drought (D4) |
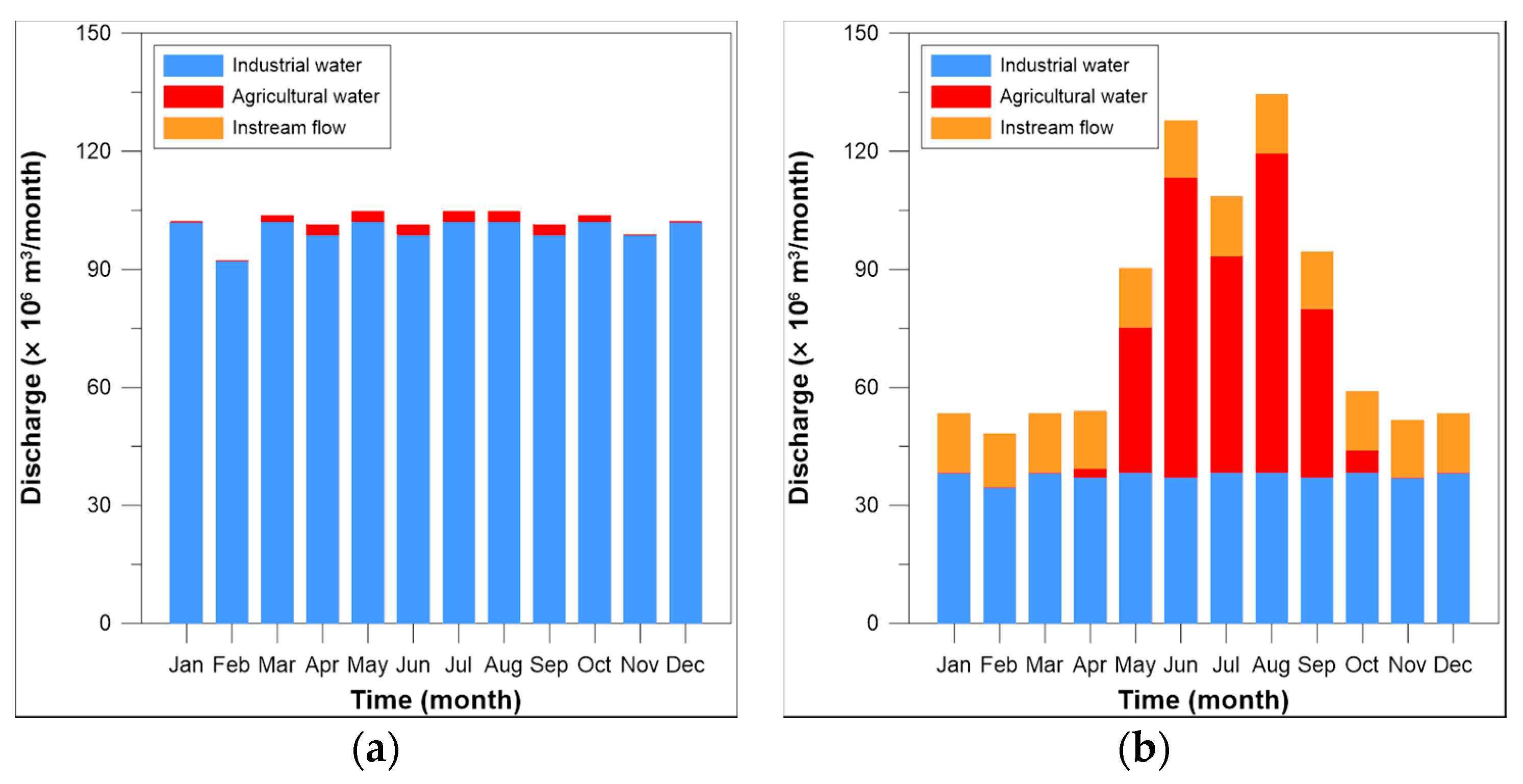
| Engineering Data | Soyanggang Dam | Andong Dam |
|---|---|---|
| Basin area (km2) | 2703 | 1584 |
| Year completed | 1973 | 1976 |
| Total storage capacity (× 106 m3) | 2900 | 1248 |
| Average yearly inflow (× 106 m3) | 1750 | 940 |
| Yearly water supply (× 106 m3) | 1213 | 926 |
| industrial water | 1200 | 450 |
| agricultural water | 13 | 300 |
| instream flow | - | 176 |
| Dam | Distribution | Quarter | Threshold Value | |||
|---|---|---|---|---|---|---|
| First | Second | Third | Fourth | |||
| Soyanggang | Lognormal | 0.0724 | 0.0636 | 0.0898 | 0.1242 | 0.219 |
| Gamma | 0.1062 | 0.0898 | 0.1110 | 0.1583 | ||
| Gumbel | 0.2189 | 0.2029 | 0.1534 | 0.2334 | ||
| Weibull | 0.1169 | 0.1127 | 0.1261 | 0.1601 | ||
| Gaussian | 0.1691 | 0.1570 | 0.1438 | 0.2082 | ||
| Andong | Lognormal | 0.0915 | 0.1001 | 0.1057 | 0.0813 | 0.232 |
| Gamma | 0.1267 | 0.1123 | 0.0771 | 0.1072 | ||
| Gumbel | 0.2457 | 0.1930 | 0.1288 | 0.2396 | ||
| Weibull | 0.1394 | 0.1038 | 0.0736 | 0.1380 | ||
| Gaussian | 0.1871 | 0.1205 | 0.0932 | 0.1713 | ||
| Dam | First and Second Quarters | Second and Third Quarters | Third and Fourth Quarters | Fourth and First Quarters |
|---|---|---|---|---|
| Soyanggang | 0.4781 | 0.0543 | –0.1770 | 0.0739 |
| Andong | 0.3767 | 0.4828 | 0.1281 | 0.1831 |
| Cases | Absolute Error for the Third Quarter 2014 (%) | Absolute Error for the Third Quarter 2015 (%) | Range of Absolute Error for the Third Quarter (%) | Range of Absolute Error for All Quarters (%) |
|---|---|---|---|---|
| BN forecast without drought forecast | 103.6 | 93.3 | 4.1–103.6 | 3.2–103.6 |
| BN forecast with drought forecast by 50% criteria | 14.2 | 18.6 | 4.1–48.0 | 3.2–100.1 |
| Cases | Absolute Error for the Third Quarter 2013 (%) | Absolute Error for the Third Quarter 2015 (%) | Range of Absolute Error for the Third Quarter (%) | Range of Absolute Error for All Quarters (%) |
|---|---|---|---|---|
| BN forecast without drought forecast | 169.7 | 355.6 | 2.2–355.6 | 1.2–355.6 |
| BN forecast with drought forecast by 50% criteria | 169.7 | 32.1 | 32.1–169.7 | 1.2–169.7 |
| BN forecast with drought forecast by 55% criteria | 169.7 | 9.4 | 9.4–169.7 | 1.2–169.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Lee, S.; Jin, Y. Forecasting Quarterly Inflow to Reservoirs Combining a Copula-Based Bayesian Network Method with Drought Forecasting. Water 2018, 10, 233. https://doi.org/10.3390/w10020233
Kim K, Lee S, Jin Y. Forecasting Quarterly Inflow to Reservoirs Combining a Copula-Based Bayesian Network Method with Drought Forecasting. Water. 2018; 10(2):233. https://doi.org/10.3390/w10020233
Chicago/Turabian StyleKim, Kwanghoon, Sangho Lee, and Youngkyu Jin. 2018. "Forecasting Quarterly Inflow to Reservoirs Combining a Copula-Based Bayesian Network Method with Drought Forecasting" Water 10, no. 2: 233. https://doi.org/10.3390/w10020233
APA StyleKim, K., Lee, S., & Jin, Y. (2018). Forecasting Quarterly Inflow to Reservoirs Combining a Copula-Based Bayesian Network Method with Drought Forecasting. Water, 10(2), 233. https://doi.org/10.3390/w10020233





