Assessment of Irrigated Agriculture Vulnerability under Climate Change in Southern Italy
Abstract
1. Introduction
2. Materials and Methods
2.1. Selected Reservoirs
2.2. Climate Data
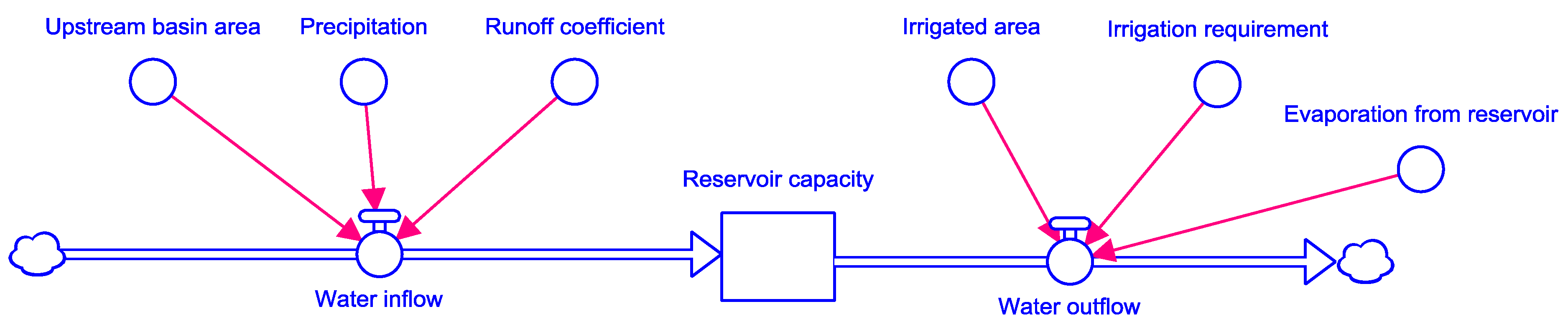
2.3. Total Water Inflow
2.3.1. Reservoir Upstream Basin Area
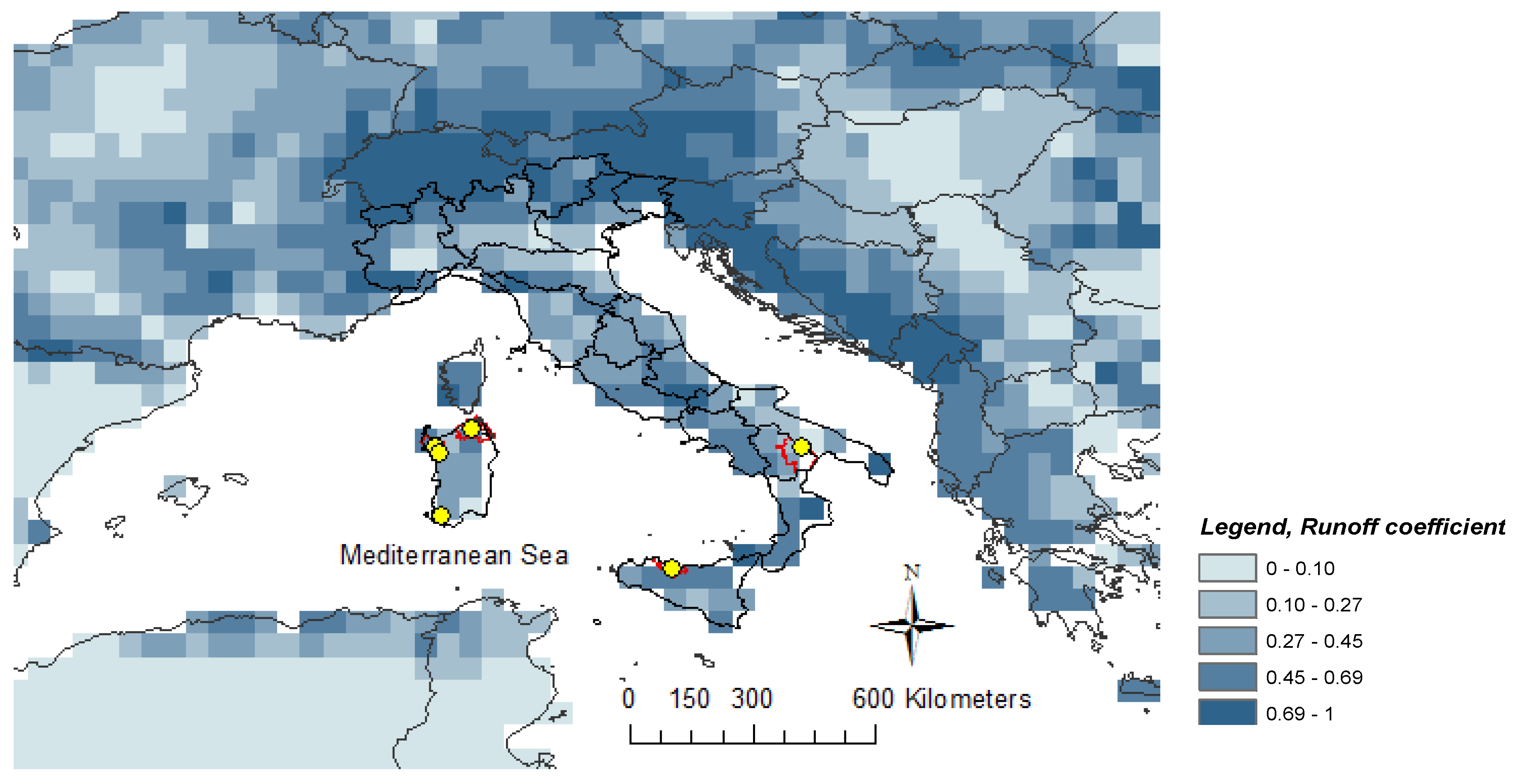
2.3.2. Runoff Coefficient
2.4. Evaporation from Open Water
2.5. Total Water Distribution
2.5.1. Crop Irrigation Requirements and Applications-SIMETAW_GIS Platform
2.5.2. Total District Irrigation
2.6. Irrigation System Resilience and Vulnerability
Classes of Resilience and Vulnerability
2.7. Temporal Self-Sufficiency in Demand Capacity (TSSDC)
2.8. Allowable Water Losses for Irrigation (AWLI)
3. Results
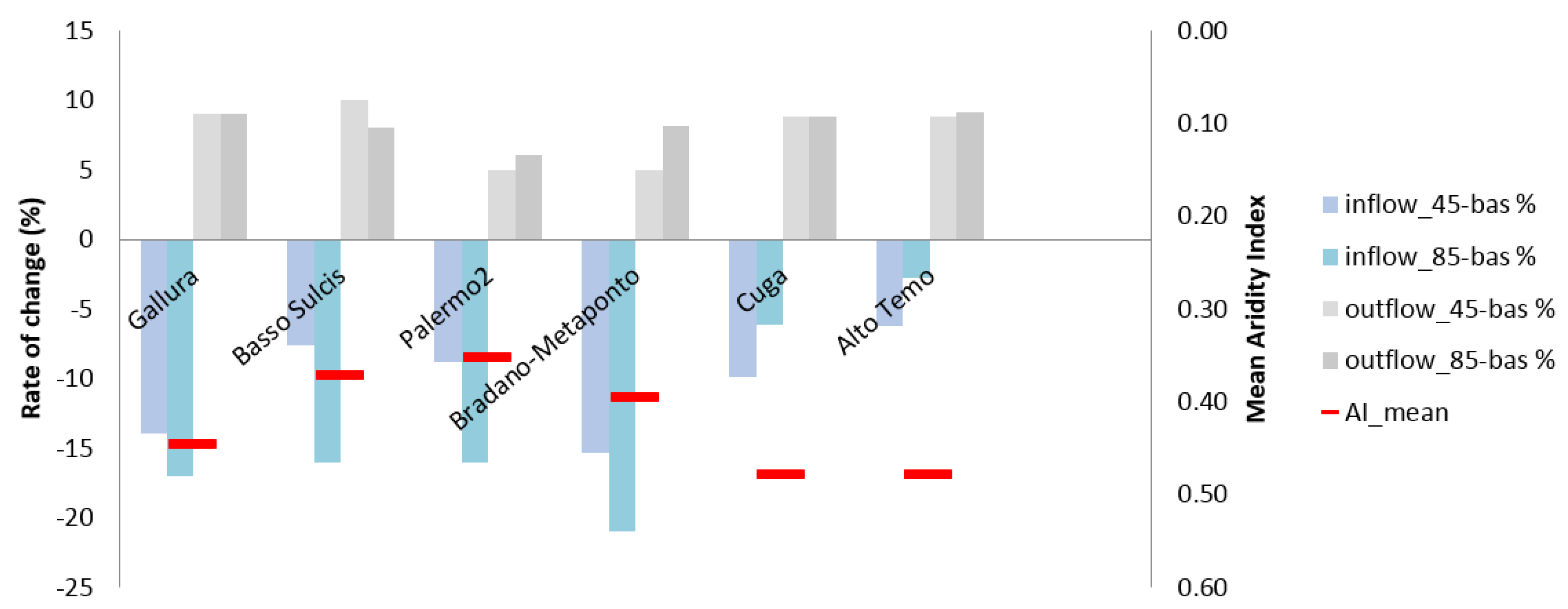
3.1. Reservoir Water Inflow
3.2. Reservoir Water Outflow: Irrigation Requirement
3.3. Evaporation from Reservoirs Surface
3.4. Resilience and Vulnerability of the Irrigated Agriculture
3.5. Temporal Reservoir Self-Sufficiency in Prolonged Drought Conditions
3.6. Water Losses and Improvement of System Efficiency
4. Discussion
Limitation and Constrains of the Work
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.L.; Itenfisu, D.; Steduto, P.; Berengena, J.; Yrisarry, J.B.; et al. Recommendation on standardized surface resistance for hourly calculation of reference ETo by the FAO56 Penman–Monteith method. Agric. Water Manag. 2006, 81, 1–22. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Allen, S.K., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; p. 582. [Google Scholar]
- Bates, B.C.; Kundzewicz, Z.W.; Wu, S.; Palutikof, J.P. Climate Change and Water; Technical Paper of the Intergovernmental Panel on Climate Change; IPCC Secretariat: Geneva, Switzerland, 2008; p. 210. [Google Scholar]
- McDonald, R.I.; Green, P.; Balk, D.; Fekete, B.M.; Revenga, C.; Todd, M.; Montgomery, M. Urban growth, climate change, and freshwater availability. Proc. Natl. Acad. Sci. USA 2011, 108, 6312–6317. [Google Scholar] [CrossRef] [PubMed]
- Harrison, P.A.; Dunford, R.; Savin, C.; Rounsevell, M.D.A.; Holman, I.P.; Kebede, A.S.; Stuch, B. Cross-sectoral impacts of climate change and socioeconomic change for multiple, European land-and water-based sectors. Clim. Chang. 2014. [Google Scholar] [CrossRef]
- McDonald, R.I.; Weber, K.; Padowski, J.; Florke, M.; Schneider, C.; Green, P.A.; Gleeson, T.; Eckmann, S.; Lehner, B.; Balk, D.; et al. Water on an urban planet: Urbanization and the reach of urban water infrastructure. Glob. Environ. Chang. 2014, 27, 96–105. [Google Scholar] [CrossRef]
- Ferragina, E.; Canitano, G. Geopolitical Implications of Water and Food Security in Southern and Eastern Mediterranean Countries. In Building Sustainable Agriculture for Food Security in the Euro Mediterranean Area: Challenges and Policy Options; Paciello, M.C., Ed.; Edizioni Nuova Cultura for Istituto Affari Internazionali (IAI): Roma, Italy, 2014; pp. 33–56. ISBN 9788868125080. [Google Scholar]
- Godfray, H.C.J.; Garnett, T. Food security and sustainable intensification. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014, 369. [Google Scholar] [CrossRef] [PubMed]
- Alexandratos, N.; Bruinsma, J. World Agriculture towards 2030/2050: The 2012 Revision; ESA 2012. Working Paper 12-03; FAO: Rome, Italy, 2012. [Google Scholar]
- Brooks, J. (Ed.) Agricultural Policies for Poverty Reduction; OECD Publishing: Paris, France, 2012. [Google Scholar]
- ISRI. Le Risorse Idriche in Sardegna. In Programma Operativo Della Regione Autonoma Della Sardegna 2000–2006; Aggiornamento Della Valutazione Intermedia, V. 1.1; ISRI: Cagliari, Italy, 2008. [Google Scholar]
- Food and Agriculture Organization of the United Nations (FAO). AQUASTAT Main Database, Food and Agriculture Organization of the United Nations (FAO). Available online: http://www.fao.org/nr/water/aquastat/data/query/index.html?lang=en (accessed on 1 September 2017).
- EUROSTAT. Available online: http://ec.europa.eu/eurostat/statistics-explained/index.php/File:Figure_6_Irrigated_area_by_type_of_crops_Italy_2010.PNG (accessed on 8 September 2017).
- Tubiello, F.N.; Donatelli, M.; Rosenzweig, C.; Stockle, C.O. Effects of climate change and elevated CO2 on cropping systems: Model predictions at two Italian locations. Eur. J. Agron. 2000, 13, 179–189. [Google Scholar] [CrossRef]
- Kapur, B.; Steduto, P.; Todorovic, M. Prediction of climatic change for the next 100 years in the Apulia region, Southern Italy. Ital. J. Agron. 2007, 4, 365–371. [Google Scholar] [CrossRef]
- Rodriguez-Diaz, J.A.; Weatherhead, E.K.; Knox, J.W.; Camacho, E. Climate change impacts on irrigation water requirements in the Guadalquivir river basin in Spain. Reg. Environ. Chang. 2007, 7, 149–159. [Google Scholar] [CrossRef]
- Yano, T.; Aydin, M.; Haraguchi, T. Impact of climate change on irrigation demand and crop growth in a Mediterranean environment of Turkey. Sensors 2007, 7, 2297–2315. [Google Scholar] [CrossRef] [PubMed]
- Mancosu, N. Agricultural Water Demand Assessment Using the SIMETAW# Model. Ph.D. Thesis, University of Sassari, Sassari, Italy, 2013. [Google Scholar]
- Riediger, J.; Breckling, B.; Nuske, R.S.; Schröder, W. Will climate change increase irrigation requirements in agriculture of Central Europe? A simulation study for Northern Germany. Environ. Sci. Eur. 2014, 26, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Saadi, S.; Todorovic, M.; Tanasijevic, L.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Climate change and Mediterranean agriculture: Impacts on winter wheat and tomato crop evapotranspiration, irrigation requirements and yield. Agric. Water Manag. 2014, 147, 103–115. [Google Scholar] [CrossRef]
- Tanasijevic, L.; Todorovic, M.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Impacts of climate change on olive crop evapotranspiration and irrigation requirements in the Mediterranean region. Agric. Water Manag. 2014, 144, 54–68. [Google Scholar] [CrossRef]
- Gallo, A. Assessment of the Climate Change Impact and Adaptation Strategies on Italian Cereal Production Using High Resolution Climate Data. Ph.D. Thesis, University of Sassari, Sassari, Italy, 2015. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Nam, W.H.; Choi, J.Y. Development of an irrigation vulnerability assessment model in agricultural reservoirs utilizing probability theory and reliability analysis. Agric. Water Manag. 2014, 142, 115–126. [Google Scholar] [CrossRef]
- Nam, W.H.; Choi, J.N.; Hong, E.M. Irrigation vulnerability assessment on agricultural water supply riskfor adaptive management of climate change in South Korea. Agric. Water Manag. 2015, 152, 173–187. [Google Scholar] [CrossRef]
- Mereu, S.; Sušnik, J.; Trabucco, A.; Daccache, A.; Vamvakeridou-Lyroudia, L.; Renoldi, S.; Virdis, A.; Savić, D.; Assimacopoulos, D. Operational resilience of reservoirs to climate change, agricultural demand, and tourism: A case study from Sardinia. Sci. Total Environ. 2016, 543, 1028–1038. [Google Scholar] [CrossRef] [PubMed]
- Yamba, F.D.; Walimwipi, H.; Jain, S.; Zhou, P.; Cuamba, B.; Mzezewa, C. Climate change/variability implications on hydroelectricity generation in the Zambezi River Basin. Mitig. Adapt. Strateg. Glob. Chang. 2011, 16, 617–628. [Google Scholar] [CrossRef]
- Meza, F.J.; Wilks, D.S.; Gurovich, L.; Bambach, N. Impacts of Climate Change on Irrigated Agriculture in the Maipo Basin, Chile: Reliability of Water Rights and Changes in the Demand for Irrigation. J. Water Resour. Plan. Manag. 2012, 138, 421–430. [Google Scholar] [CrossRef]
- Kling, H.; Stanzel, P.; Preishuber, M. Impact modelling of water resources development and climate scenarios on Zambezi River discharge. J. Hydrol. Reg. Stud. 2014, 1, 17–43. [Google Scholar] [CrossRef]
- European Environmental Agency (EEA). Water Quantity, River Floods and Droughts in Impacts of Europe’s Changing Climate—2008 Indicator-Based Assessment; Joint EEA-JRC-WHO Report, EEA Report No 4/2008; European Environmental Agency, European Communities: Copenhagen, Denmark, 2008; ISBN 978-92-9167-372-8. [Google Scholar]
- Stagl, J.; Mayr, E.; Koch, H.; Hattermann, F.F.; Huang, S. Effects of Climate Change on the Hydrological Cycle in Central and Eastern Europe. Chapter 3. In Managing Protected Areas in Central and Eastern Europe under Climate Change; Rannow, S., Neubert, M., Eds.; Advances in Global Change Research; Springer: Dordrecht, The Netherlands, 2014; Volume 58. [Google Scholar]
- Hargreaves, G.H.; Riley, J.P.; Sikka, A. Influence of climate on irrigation, Canadian. Water Resour. J. 1993, 18, 53–59. [Google Scholar] [CrossRef]
- Cancelliere, A.; Rossi, G. Drought and water scarcity risk in the Mediterranean. In Proceedings of the EC Expert Group on Water Scarcity and Drought, FEM, Venice, Italy, 13–14 October 2011. [Google Scholar]
- Garrote, L.; Iglesias, A.; Granados, A.; Mediero, L.; Carrasco, F.M. Quantitative Assessment of Climate Change Vulnerability of Irrigation Demands in Mediterranean Europe. Water Resour. Manag. 2015, 29, 325–338. [Google Scholar] [CrossRef]
- Lehner, B.; Reidy Liermann, C.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High resolution mapping of the world’s reservoirs and dams for sustainable river flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos 2008, 89, 93–94. [Google Scholar] [CrossRef]
- CBGallura. Consorzio di Bonifica Della Gallura. Available online: http://www.cbgallura.it/index.php?option=com_content&view=article&id=47&Itemid=54 (accessed on 25 October 2017).
- CBNurra. Consorzio di Bonifica Della Nurra. Available online: http://www.bonificanurra.it/index.php/comprensorio/24-tavole.html (accessed on 25 October 2017).
- CBBasso-Sulcis. Consorzio di Bonifica del Basso Sulcis. Available online: http://www.consorziobassosulcis.it/servizioirr.asp (accessed on 25 October 2017).
- CBPalermo2. Available online: http://adpaloha.altervista.org/wpcontent/uploads/2012/10/ROSAMARINA.pdf (accessed on 3 November 2017).
- CBStornara and Tara. Available online: http://lnx.bonificastornaratara.it/page-una-colonna-php/ (accessed on 16 November 2017).
- CBBradano-Metaponto. Available online: http://www.bradanometaponto.it/PianoClassifica.html (accessed on 16 November 2017).
- Gualdi, S.; Somot, S.; Li, L.; Artale, V.; Adani, M.; Bellucci, A.; Braun, A.; Calmanti, S.; Carillo, A.; Dell’Aquila, A.; et al. The CIRCE simulations: Regional Climate Change Projections with Realistic Representation of the Mediterranean Sea. Bull. Amer. Meteor. Soc. 2013, 94, 65–81. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Sanna, A.; Fogli, P.G.; Manzini, E.; Vichi, M.; Oddo, P.; Navarra, A. Effects of tropical cyclones on ocean heat transport in a high resolution coupled general circulation model. J. Clim. 2011, 24, 4368–4384. [Google Scholar] [CrossRef]
- Rockel, B.; Will, A.; Hense, A. The regional Climate Model COSMO-CLM (CCLM). Meteorol. Z. 2008, 17, 347–348. [Google Scholar] [CrossRef]
- IPCC. Annex II: Glossary. In Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Mach, K.J., Planton, S., von Stechow, C., Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; pp. 117–130. [Google Scholar]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. The CGIAR-CSI SRTM 90 m Database. 2008. Available online: http://srtm.csi.cgiar.org (accessed on 5 December 2017).
- ESRI. ArcGIS Desktop: Release 10.5, Environmental Systems Research Institute: Redlands, CA, USA, 2013.
- Fekete, B.M.; Vӧrӧsmarty, C.J.; Grabs, W. Global, Composite Runoff Fields Based on Observed River Discharge and Simulated Water Balances; Report No. 22; Global Runoff Data Centre (GRDC), Federal Institute of Hydrology (BFG): Koblenz, Germany, 2000. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Terrestrial Air Temperature and Precipitation: Monthly and Annual Time Series (1950–1999). 2001. Available online: http://climate.geog.udel.edu/~climate/html_pages/README.ghcn_ts2.html (accessed on 19 September 2017).
- Florida Department of Transportation (FDOT). Drainage Handbook Hydrology; Florida Department of Transportation: Tallahassee, FL, USA, 2012.
- RAS. Campagna di Sensibilizzazione per un Uso Consapevole e Amorevole Dell’acqua; Scheda No. 8. Progetto Altriponti, Osservatorio Mediterraneo: Un Ponte Dacqua; Regione Autonoma della Sardegna: Sassari, Italy, 2002. [Google Scholar]
- Brandis, P. La Disponibilità idrica e la politica del territorio in Sardegna. In La Sardegna nel Mondo Mediterraneo: 1° Convegno Internazionale di Studi Geografico-Storici, 7–9, 1979; Gallizzi: Sassari, Italy, 1981; p. 96. [Google Scholar]
- CBBradano-Metaponto. Available online: www.bradanometaponto.it/SANGIULIANO.html (accessed on 16 November 2017).
- Jensen, M.E. Estimating Evaporation from Water Surfaces. In Proceedings of the CSU/ARS Evapotranspiration Workshop, Fort Collins, CO, USA, 15 March 2010; pp. 1–27. [Google Scholar]
- Masia, S. A Modeling Tool to Assess Local and Regional Impact of Climate Change on Crop Water Requirement in Euro-Mediterranean Countries, and Assessment of Mediterranean Irrigated Agriculture Vulnerability. Ph.D. Thesis, University of Sassari, Sassari, Italy, 2017. [Google Scholar]
- Snyder, R.L.; Geng, S.; Orang, M.N.; Matyac, J.S.; Sarreshteh, S. A simulation model for ET of applied water. Acta Hortic. 2004, 664, 623–629. [Google Scholar] [CrossRef]
- Snyder, R.L.; Geng, S.; Orang, M.; Sarreshteh, S. Calculation and Simulation of Evapotranspiration of Applied Water. J. Integr. Agric. 2012, 11, 489–501. [Google Scholar] [CrossRef]
- Mancosu, N.; Spano, D.; Orang, M.; Sarreshteh, S.; Snyder, R.L. SIMETAW#—A Model for Agricultural Water Demand Planning. Water Resour. Manag. 2016, 30, 541–557. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- Allen, R.G.; Walter, I.A.; Elliott, R.L.; Howell, T.A.; Itenfisu, D.; Jensen, M.E. The ASCE Standardized Reference Evapotranspiration Equation; American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- ISTAT. Censimento Agricoltura. 2010. Available online: http://daticensimentoagricoltura.istat.it/Index.aspx?lang=it# (accessed on 23 November 2017).
- ADB Basilicata. Available online: http://www.adb.basilicata.it/adb/risorseidriche/invaso.asp?invaso=SGiuliano (accessed on 23 November 2017).
- Ministero Delle Infrastrutture e dei Trasporti (MIT). Puglia: Il Sistema Idrico, a Cura di Guido Viceconte; MIT: Roma, Italy, 2003. [Google Scholar]
- United Nations Environment Programme (UNEP). World Atlas of Desertification; Middleton, N., Thomas, D.S.G., Eds.; Edward Arnold: London, UK, 1992; p. 69. ISBN 0340555122. [Google Scholar]
- Villani, G.; Tomei, F.; Tomozeiu, R.; Marletto, V. Climatic scenarios and their impacts on irrigated agriculture in Emilia-Romagna, Italy. Ital. J. Agrometeorol. 2011, 16, 5–17. [Google Scholar]
- Ventrella, D.; Charfeddine, M.; Moriondo, M.; Rinaldi, M.; Bindi, M. Agronomic adaptation strategies under climate change for winter durum wheat and tomato in southern Italy: Irrigation and nitrogen fertilization. Reg. Environ. Chang. 2012, 12, 407–419. [Google Scholar] [CrossRef]
- Campi, P.; Navarro, A.; Giglio, L.; Palumbo, A.D.; Mastrorilli, M. Modelling for water supply of irrigated cropping systems on climate change. Ital. J. Agron. 2012, 7, 259–265. [Google Scholar] [CrossRef]
- Auci, S.; Vignani, D. Climate Change Effects and Agriculture in Italy: A Stochastic Frontier Analysis at Regional Level; MPRA 2014; Paper 53500; University Library of Munich: Munich, Germany, 2014; Available online: https://mpra.ub.uni-muenchen.de/53500/ (accessed on 23 November 2017).
- Water Framework Directive (WFD). EC Directive 2000/60/EC of the European Parliament and of the Council, Establishing a Framework for Community Action in the Field of Water Policy; FAO: Rome, Italy, 2000. [Google Scholar]
- Water Information System Europe (WISE). Water Note 10. Climate Change: Addresssing Floods, Drought and Changing Aquatic Ecosystems. Water Notes on the Implementation of the Water Framework Directive; European Commission (DG Environment): Brussels, Belgium, 2008; ISBN 978-92-79-11039-9. [Google Scholar]
- WWF/CMCC Report Scenari Per L’italia. II Paradosso Climatico Degli Estremi Opposti Nel Futuro Dell’Italia; Elaborazione WWF Italia su Testi a Cura del Gruppo di Lavoro Coordinato da Paola Mercogliano (CMCC); EARTH HOUR: Gland, Switzerland, 2016. [Google Scholar]
- Zollo, A.L.; Rillo, V.; Bucchignani, E.; Montesarchio, M.; Mercogliano, P. Extreme temperature and precipitation events over Italy: Assessment of high-resolution simulations with COSMO-CLM and future scenarios. Int. J. Climatol. 2016, 36, 987–1004. [Google Scholar] [CrossRef]
- Longobardi, A.; Mautone, M.; De Luca, C. Reservoirs performances under climate variability: A case study. In Evolving Water Resources Systems: Understanding, Predicting and Managing Water–Society Interactions, Proceedings of the ICWRS 2014, Bologna, Italy, 4–6 June 2014; IAHS Publication: Oxford, UK, 2014; Volume 364. [Google Scholar]
- Preziosi, E.; Del Bon, A.; Romano, E.; Petrangeli, A.B.; Casadei, S. Vulnerability to drought of a complex water supply system. The upper Tiber basin case study (Central Italy). Water Resour. Manag. 2013, 27, 4655–4678. [Google Scholar] [CrossRef]
- Stakhiv, V.; Stewart, B. Needs for Climate Information in Support of Decision-Making in the Water Sector. Procedia Environ. Sci. 2010, 1, 102–119. [Google Scholar] [CrossRef]
- ISTAT. Andamento Meteo-Climatico in Italia Anni 2000–2009; Statistiche in Breve: Rome, Italy, 2010. [Google Scholar]
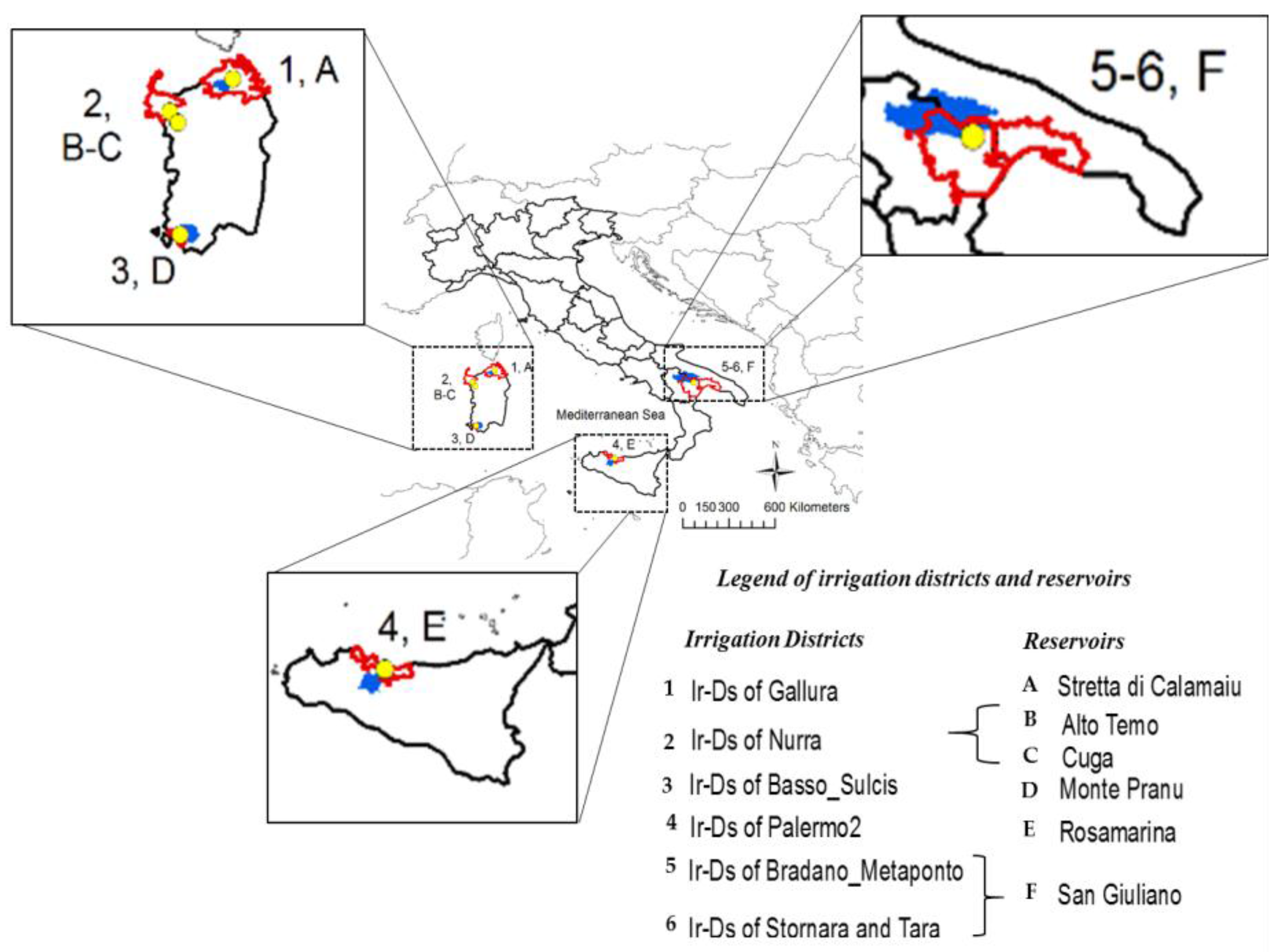
| Reservoir | Irrigation District | Municipalities (N°) | Administrative Unit | Reservoir Maximum Capacity (Mm3) | Reservoir Surface Area (km2) | Elevation (m.a.s.l.) | Lon (° E) | Lat (° N) |
|---|---|---|---|---|---|---|---|---|
| Stretta di Calamaiu | Gallura | 17 [39] | Sardinia | 105.2 | 5.70 | 170 | 9.27 | 41.01 |
| Cuga | Nurra | 5 [40] | Sardinia | 31.7 | 3.00 | 101 | 8.45 | 40.61 |
| Alto Temo | Nurra | 5 [40] | Sardinia | 95.7 | 4.99 | 242 | 8.56 | 40.47 |
| Monte Pranu | Basso Sulcis | 6 [41] | Sardinia | 62 | 6.98 | 42 | 8.59 | 39.09 |
| Rosamarina | Palermo 2 | 16 [42] | Sicily | 100 | 5.41 | 153 | 13.64 | 37.95 |
| San Giuliano | Stornara and Tara; Bradano Metaponto | 24 [43] + 31 [44] | Apulia and Basilicata | 107 | 10.14 | 100 | 16.53 | 40.6 |
| Reservoir | Country | Lat ° N | Lon ° E | Rc_Obs | Rc_Sim | Literature |
|---|---|---|---|---|---|---|
| Pedra’E Othoni | Italy | 40.32 | 9.54 | 0.40 | 0.46 | [28] |
| Coghinas | Italy | 40.93 | 8.80 | 0.25 | 0.26 | [54] |
| Flumendosa | Italy | 39.43 | 9.61 | 0.32 | 0.34 | [54] |
| Temo | Italy | 40.47 | 8.56 | 0.45 | 0.42 | [55] |
| Cuga | Italy | 40.61 | 8.45 | 0.36 | 0.42 | [55] |
| Stretta di Calamaiu | Italy | 41.01 | 9.27 | 0.35 | 0.45 | [55] |
| San Giuliano | Italy | 40.6 | 16.53 | 0.22 | 0.35 | [56] |
| Irrigated Crops | Irrigation District | |||||
|---|---|---|---|---|---|---|
| Gallura | Nurra | Basso Sulcis | Palermo 2 | Bradano-Metaponto | Stornara and Tara | |
| Maize | 25 | 466 | 12 | 0.05 | 392 | 129 |
| Grape | 327 | 1160 | 97 | 49 | 1368 | 7156 |
| Fruit trees | 12 | 66 | 6 | 130 | 8075 | 47 |
| Vegetables | 84 | 697 | 912 | 910 | 2704 | 1673 |
| Wheat | 53 | 202 | 105 | 35 | 1649 | 0 |
| Most relevant crops (i.e., sum of the above) | 501 | 2591 | 1131 | 1125 | 14,188 | 9005 |
| All crops | 1402 | 4704 | 1382 | 3826 | 25,202 | 13,203 |
| Class of Resilience | Definition | Value |
|---|---|---|
| A | Highly resilient | RI > 1 |
| B | Resilient | 0.50 ≤ RI ≤ 1 |
| C | Moderately resilient | 0.20 ≤ RI ≤ 0.50 |
| D | Slightly resilient | 0 ≤ RI ≤ 0.20 |
| E | No resilient | RI < 0 |
| Class of Vulnerability | Definition | Value |
|---|---|---|
| A | Highly vulnerable | VI < −1 |
| B | Vulnerable | −1 ≤ VI ≤ −0.5 |
| C | Moderately vulnerable | −0.50 ≤ VI ≤ −0.20 |
| D | Slightly vulnerable | −0.20 ≤ VI ≤ 0 |
| E | Not vulnerable | VI > 0 |
| Reservoirs | Basin Annual Precipitation | Basin Area | Runoff Coefficient | Reservoir Water Inflow | ||||
|---|---|---|---|---|---|---|---|---|
| baseline | RCP 45 | RCP 85 | Baseline | RCP 45 | RCP 85 | |||
| mm | mm | mm | km2 | Mm3 year−1 | Mm3 year−1 | Mm3 year−1 | ||
| Stretta di Calamaiu | 492 | 423 | 407 | 339 | 0.45 | 75 | 65 | 62 |
| Cuga | 436 | 393 | 412 | 73 | 0.42 | 13 | 12 | 13 |
| Alto Temo | 476 | 447 | 464 | 124 | 0.42 | 25 | 23 | 24 |
| Monte Pranu | 378 | 349 | 318 | 420 | 0.32 | 51 | 47 | 43 |
| Rosamarina | 386 | 350 | 324 | 529 | 0.50 | 102 | 93 | 86 |
| San Giuliano | 448 | 379 | 352 | 1634 | 0.35 | 256 | 217 | 201 |
| Irrigation District | Reservoir | Baseline | RCP 4.5 | RCP 8.5 | |||
|---|---|---|---|---|---|---|---|
| WD | E | WD | E | WD | E | ||
| Mm3 | Mm3 | Mm3 | |||||
| Gallura | Stretta di Calamaiu | 5.77 | 5.15 | 6.30 | 5.66 | 6.28 | 5.84 |
| Nurra | Cuga-Alto Temo | 20.07 | 7.54 | 21.84 | 8.22 | 21.80 | 8.38 |
| Basso Sulcis | Monte Pranu | 5.62 | 7.11 | 6.18 | 7.67 | 6.05 | 7.86 |
| Palermo 2 | Rosamarina | 16.79 | 5.46 | 17.67 | 5.75 | 17.73 | 5.98 |
| Bradano Metaponto | San Giuliano | 37.1 | 11.82 | 38.9 | 11.91 | 40.2 | 13.39 |
| Ir-Ds | Gallura | Nurra | Basso Sulcis | Palermo 2 | Bradano Metaponto Stornara and Tara | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Reservoir | Stretta di Calamaiu | Cuga-Alto Temo | Monte Pranu | Rosamarina | San Giuliano | |||||
| 4.5-b | 8.5-b | 4.5-b | 8.5-b | 4.5-b | 8.5-b | 4.5-b | 8.5-b | 4.5-b | 8.5-b | |
| Maximum Capacity (Mm3) | 105.2 | 127.4 | 62 | 100 | 107 | |||||
| WI (Mm3) | −10 | −13 | −3 | −1 | −4 | −8 | −9 | −16 | −39 | −55 |
| WD (Mm3) | 0.53 | 0.51 | 1.77 | 1.73 | 0.56 | 0.43 | 0.88 | 0.94 | 1.8 | 3 |
| E (Mm3) | 0.51 | 0.69 | 0.68 | 0.84 | 0.56 | 0.75 | 0.29 | 0.52 | 0.09 | 1.57 |
| CWS (Mm3) | −11.04 | −14.20 | −7.08 | −5.69 | −5.02 | −9.25 | −10.26 | −17.55 | −40.89 | −59.57 |
| VI (fraction) | −0.17 | −0.23 | −0.53 | −0.35 | −0.13 | −0.24 | −0.13 | −0.22 | −0.20 | −0.29 |
| TSSDC-VI (fraction) | −0.24 | −0.30 | −0.56 | −0.40 | −0.20 | −0.30 | −0.17 | −0.27 | −0.04 | −0.09 |
| AWLI-VI (%) | −2.57 | −3.18 | −45.92 | −30.14 | −3.34 | −5.06 | −3.46 | −5.77 | −3.16 | −6.49 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masia, S.; Sušnik, J.; Marras, S.; Mereu, S.; Spano, D.; Trabucco, A. Assessment of Irrigated Agriculture Vulnerability under Climate Change in Southern Italy. Water 2018, 10, 209. https://doi.org/10.3390/w10020209
Masia S, Sušnik J, Marras S, Mereu S, Spano D, Trabucco A. Assessment of Irrigated Agriculture Vulnerability under Climate Change in Southern Italy. Water. 2018; 10(2):209. https://doi.org/10.3390/w10020209
Chicago/Turabian StyleMasia, Sara, Janez Sušnik, Serena Marras, Simone Mereu, Donatella Spano, and Antonio Trabucco. 2018. "Assessment of Irrigated Agriculture Vulnerability under Climate Change in Southern Italy" Water 10, no. 2: 209. https://doi.org/10.3390/w10020209
APA StyleMasia, S., Sušnik, J., Marras, S., Mereu, S., Spano, D., & Trabucco, A. (2018). Assessment of Irrigated Agriculture Vulnerability under Climate Change in Southern Italy. Water, 10(2), 209. https://doi.org/10.3390/w10020209







