On the Role of Minor Branches, Energy Dissipation, and Small Defects in the Transient Response of Transmission Mains
Abstract
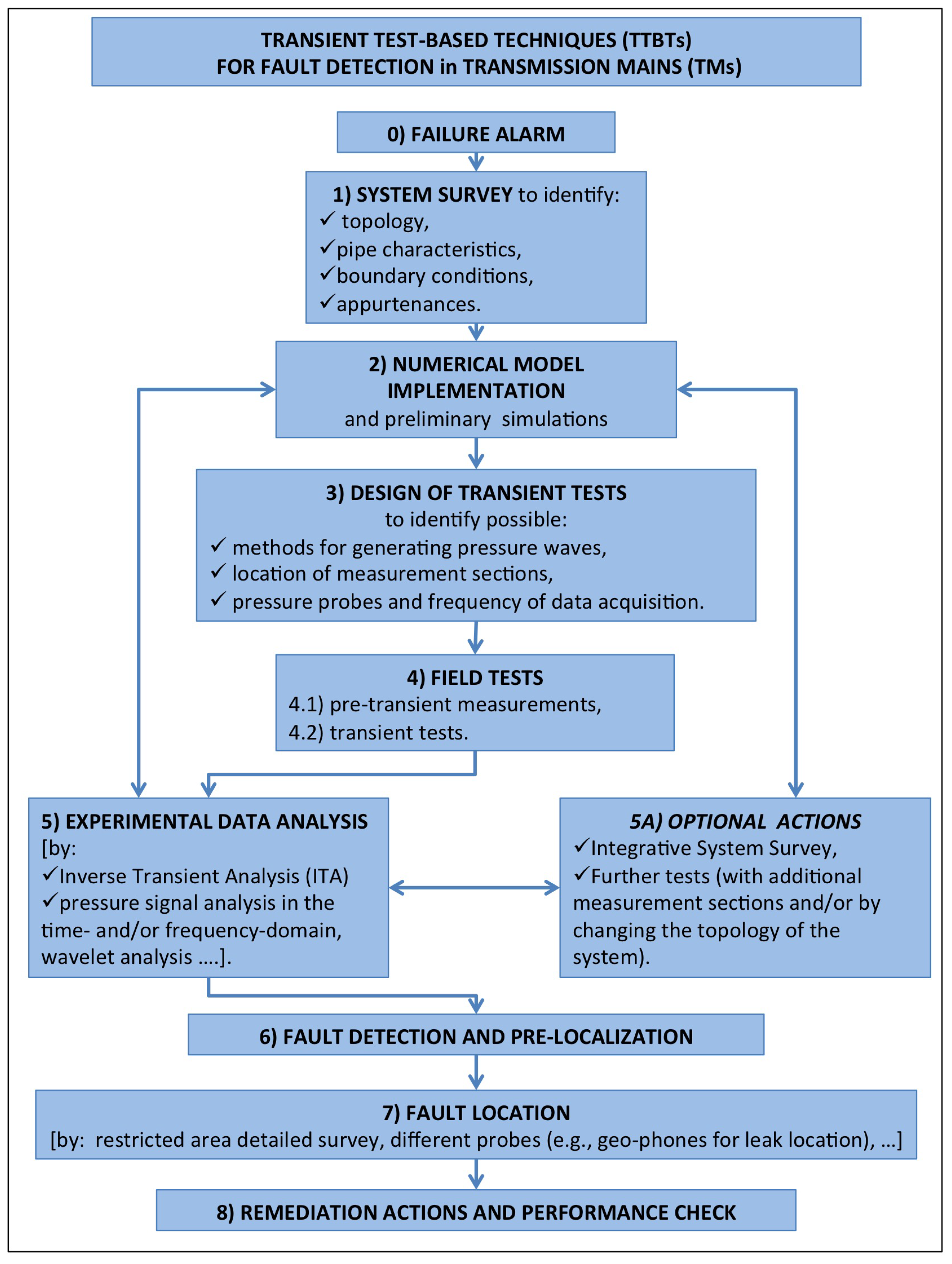
1. Introduction
2. The Investigated Transmission Main and Transient Tests
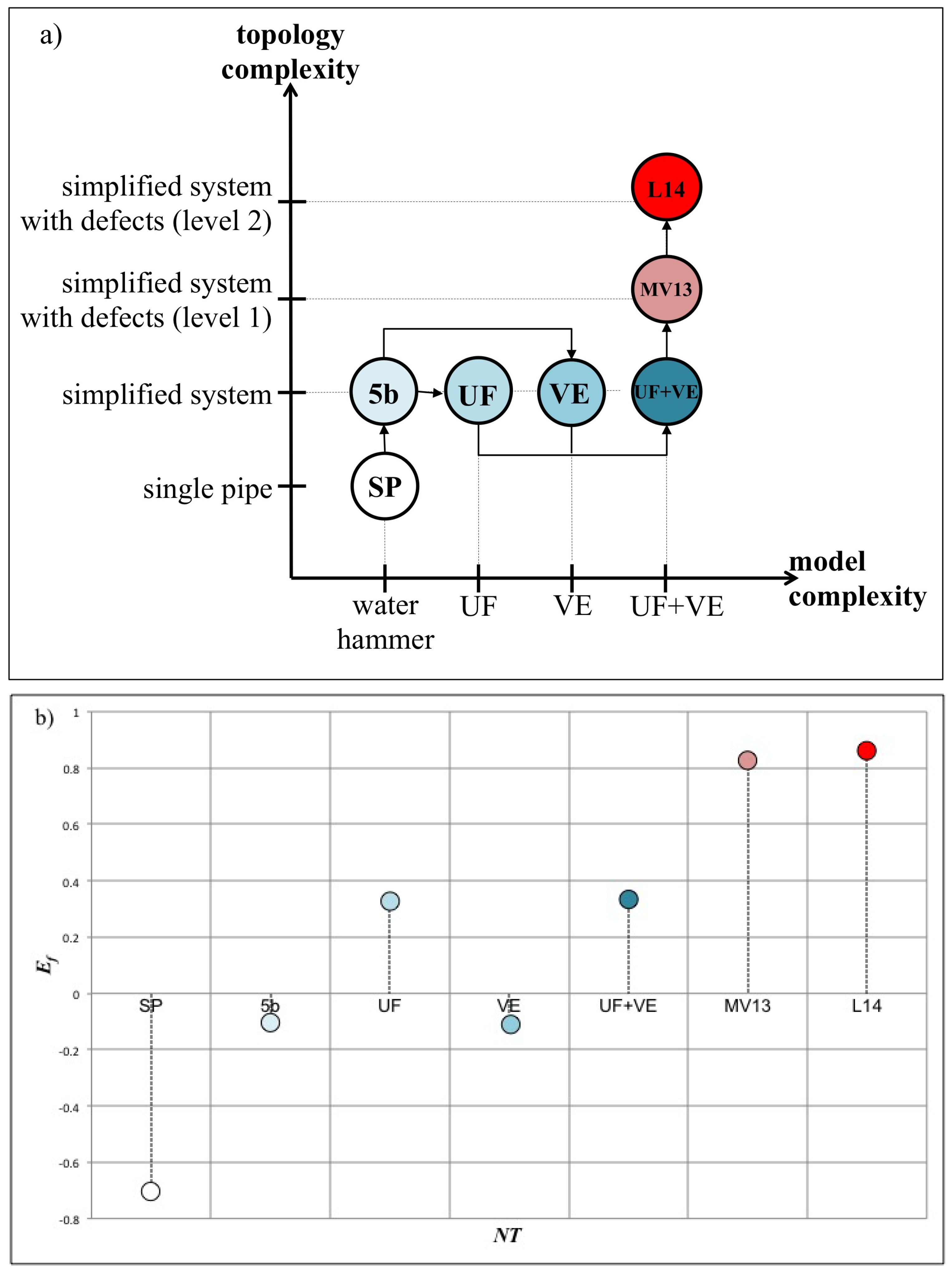
3. Numerical Tests for Transient Simulation
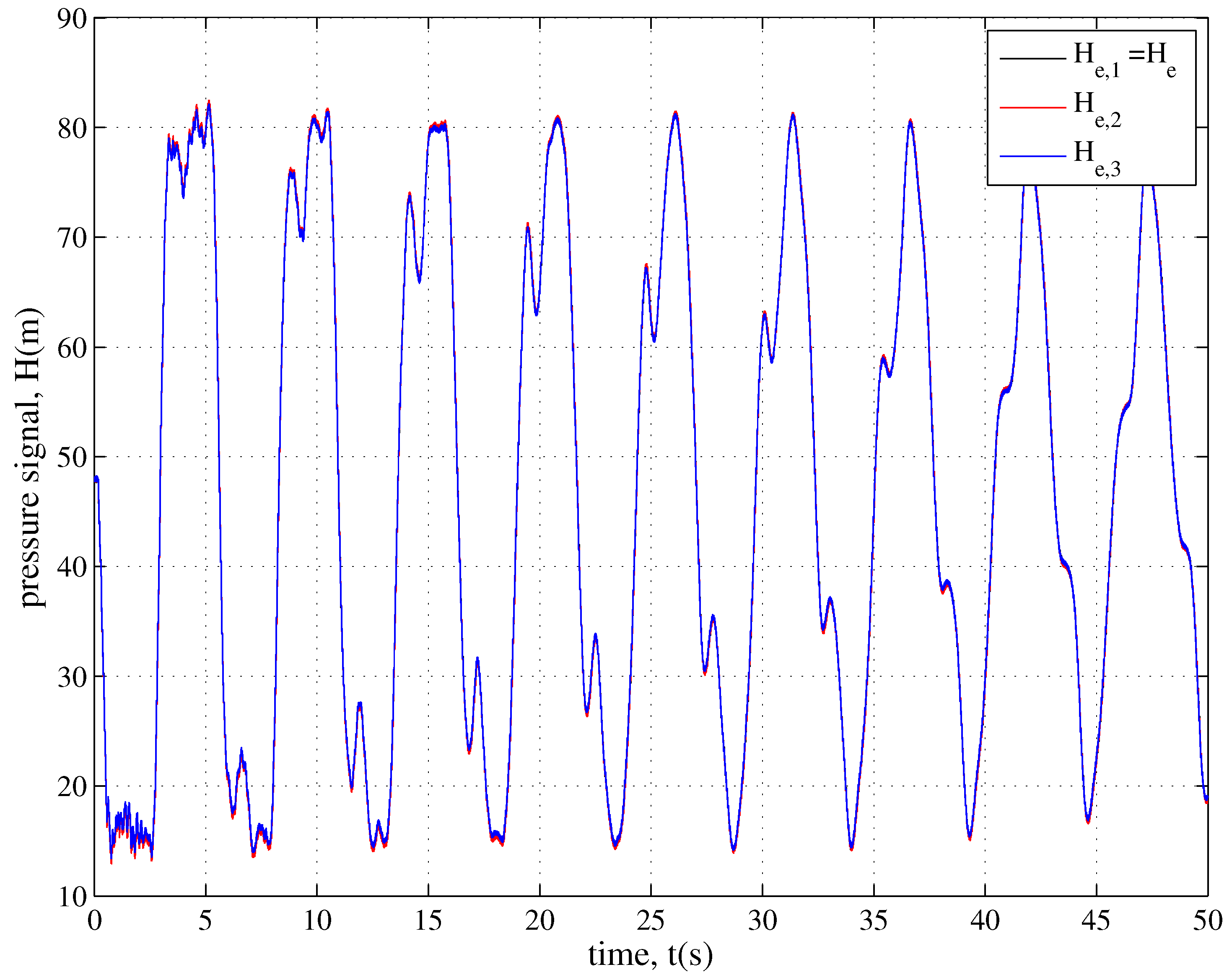
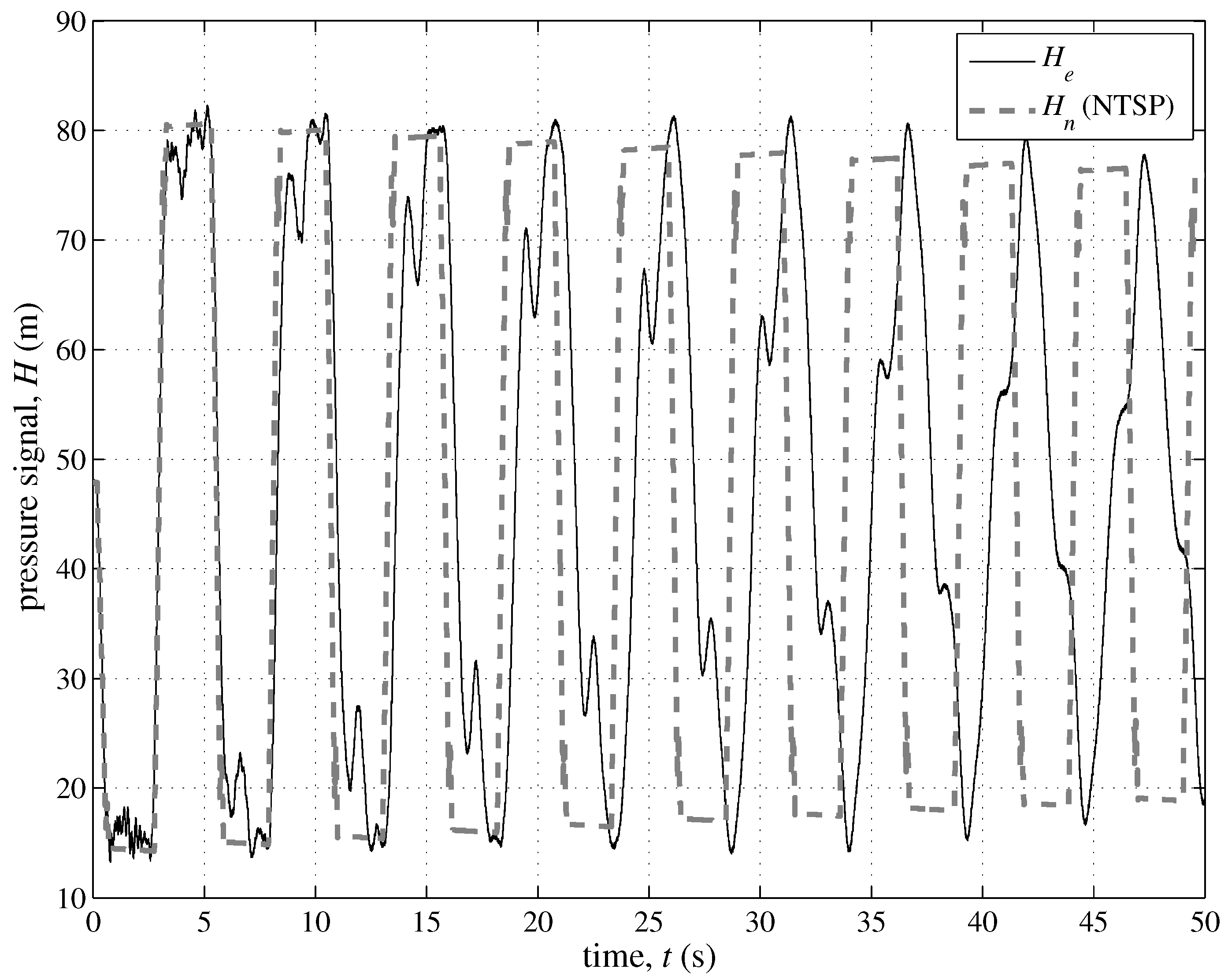
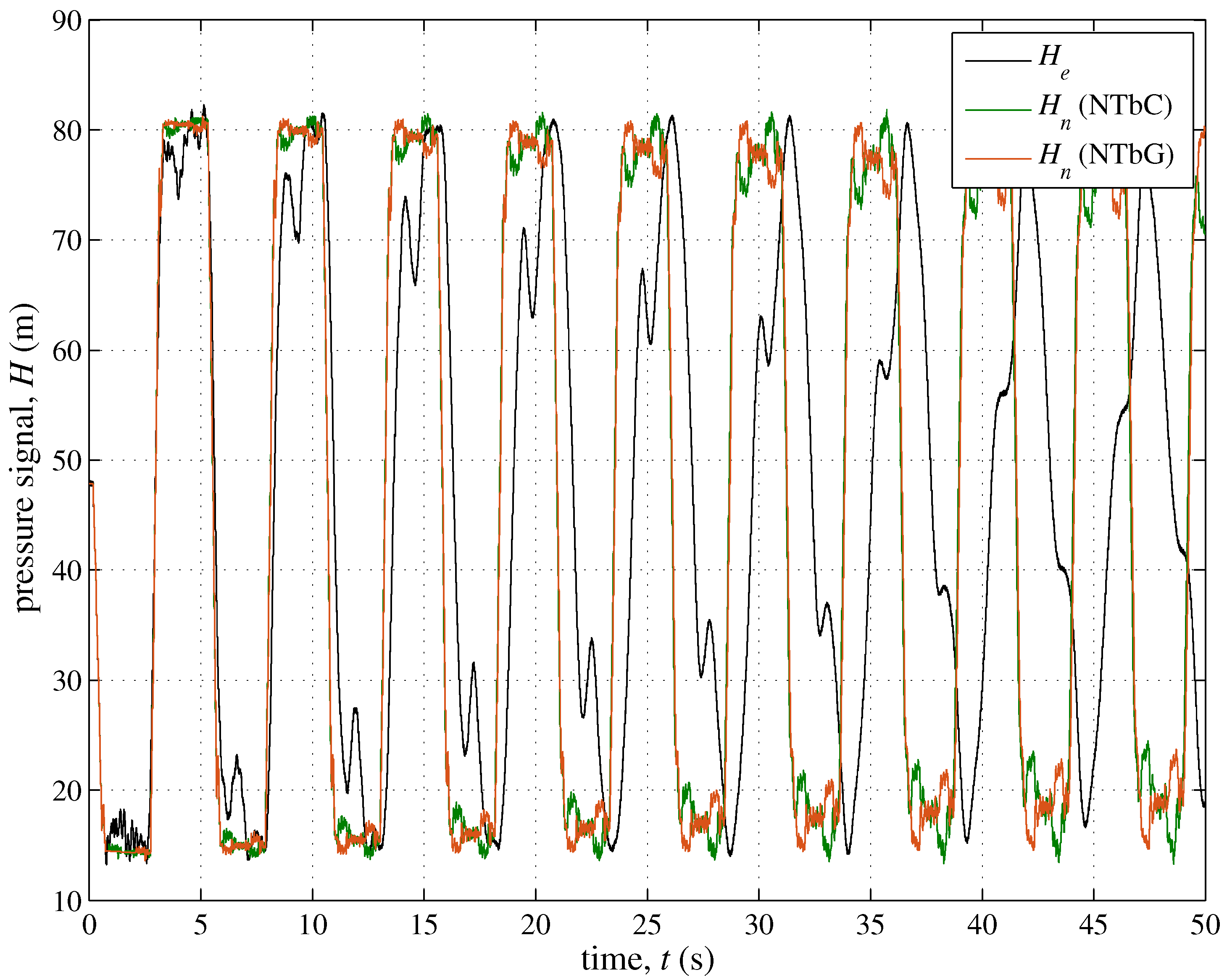
3.1. The Role of the Minor Branches
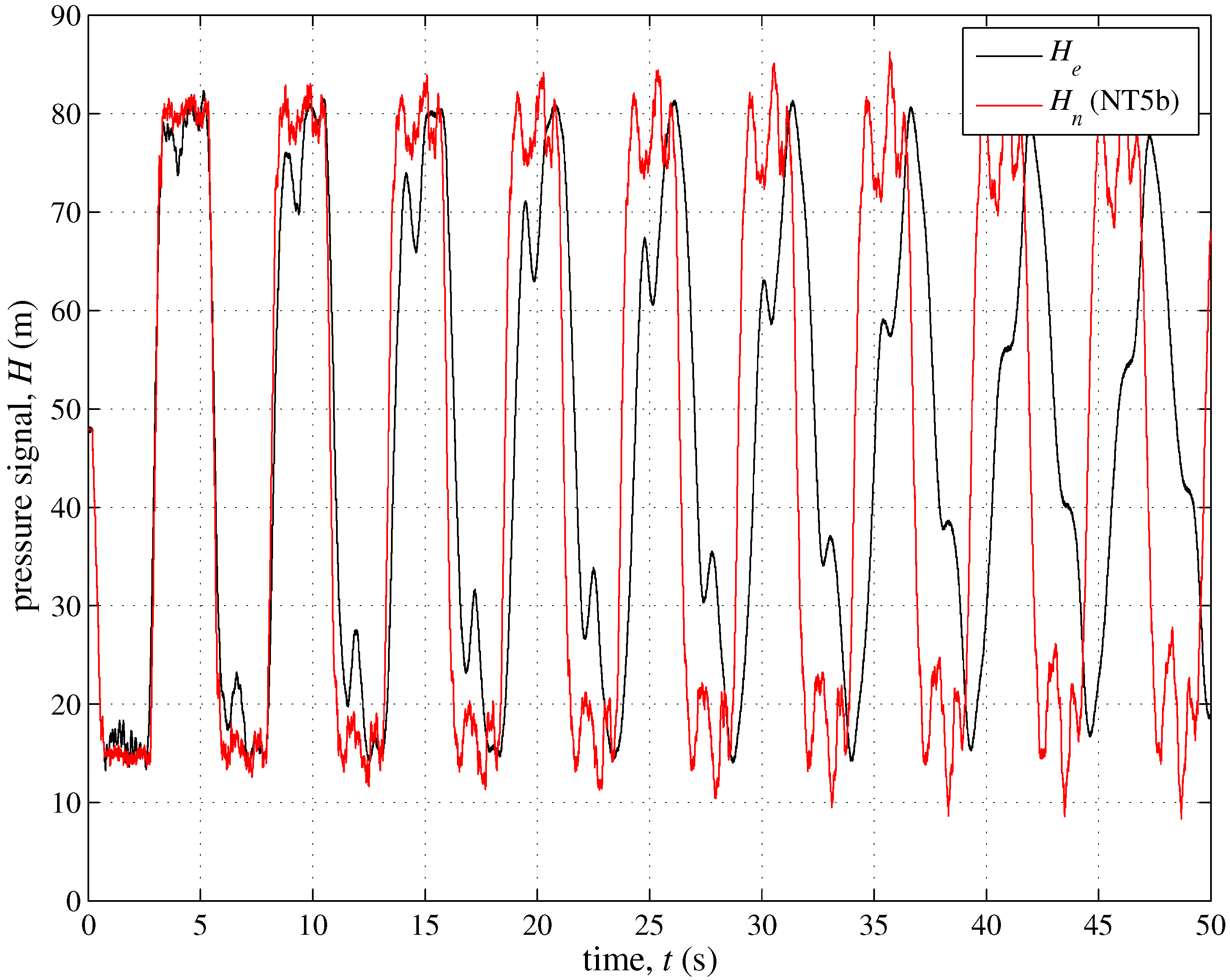
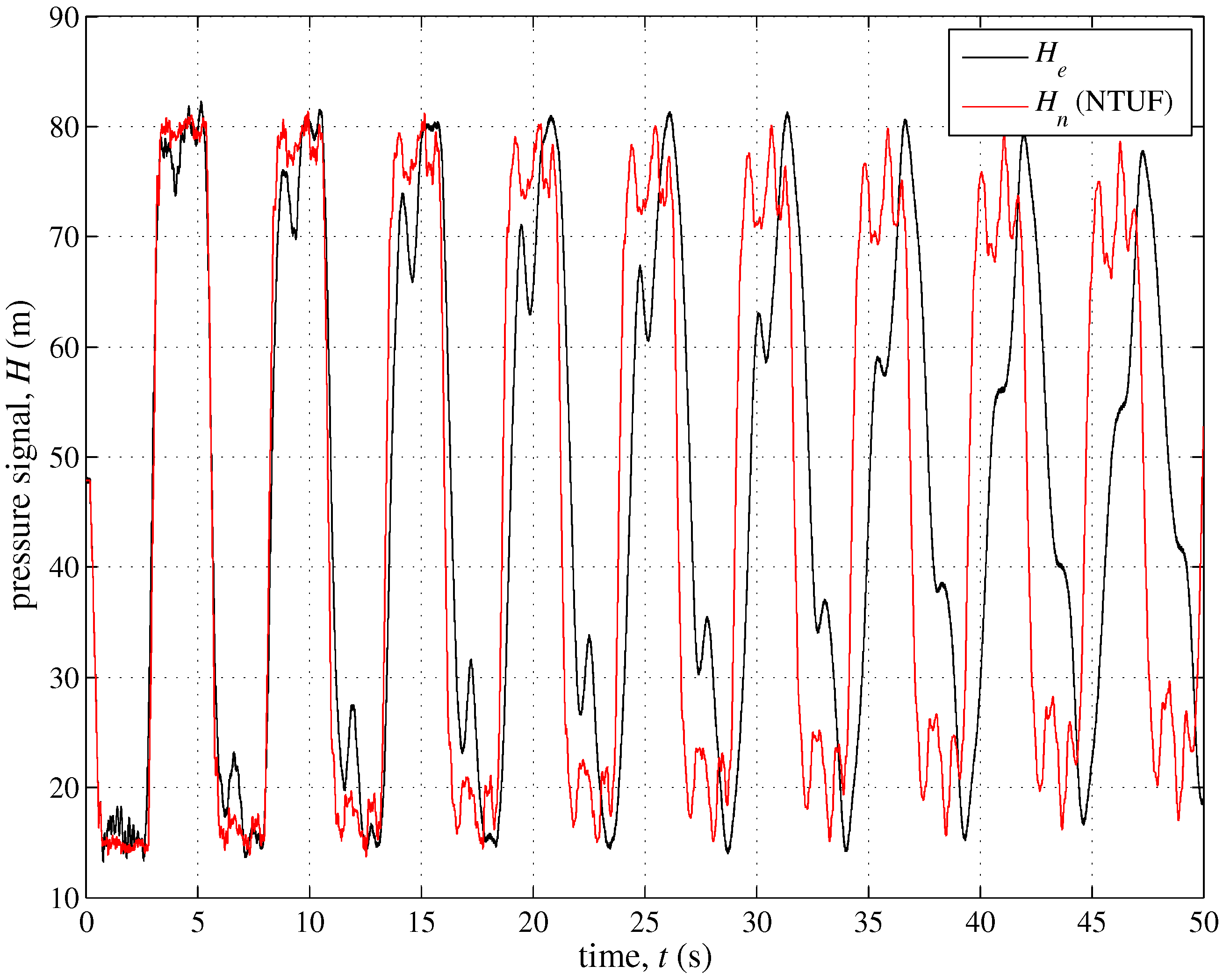
3.2. The Role of the Unsteady Friction and Viscoelasticity
3.3. The Role of Small Defects
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Single Element Kelvin-Voigt (1 K-V) Models
References
- Laven, L.; Lambert, A.O. What do we know about real losses on transmission mains? In Proceedings of the IWA Specialised Conference “Water Loss 2012”, Manila, Philippines, 26–29 February 2012. [Google Scholar]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Capponi, C.; Carrettini, C.A.; Chiesa, C.; Segalini, D.; Lanfranchi, E.A. Anomaly pre-localization in distribution-transmission mains by pump trip: Preliminary field tests in the Milan pipe system. J. Hydroinform. 2015, 17, 377–389. [Google Scholar] [CrossRef]
- Liggett, J.A.; Chen, L.C. Inverse transient analysis in pipe networks. J. Hydraul. Eng. 1994, 120, 934–955. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Vibroacoustic measurements for detecting water leaks in buried small-diameter plastic pipes. J. Pipeline Syst. Eng. Pract. 2017, 8, 04017022. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Leak detection in water-filled small-diameter polyethylene pipes by means of acoustic emission measurements. Appl. Sci. 2017, 7. [Google Scholar] [CrossRef]
- Stephens, M.; Lambert, M.F.; Simpson, A.R. Determining the internal wall condition of a water pipeline in the field using an inverse transient. J. Hydraul. Eng. 2013, 139, 310–324. [Google Scholar] [CrossRef]
- Taghvaei, M.; Beck, S.B.M.; Boxall, J.B. Leak detection in pipes using induced water hammer pulses and cepstrum analysis. Int. J. COMADEM 2010, 13, 19–25. [Google Scholar]
- Brunone, B.; Ferrante, M.; Meniconi, S. Portable pressure wave-maker for leak detection and pipe system characterization. J. Am. Water Works Assoc. 2008, 100, 108–116. [Google Scholar]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Massari, C. Small amplitude sharp pressure waves to diagnose pipe systems. Water Resour. Manag. 2011, 25, 79–96. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Frisinghelli, M.; Mazzetti, E.; Larentis, M.; Costisella, C. Safe transients for pipe survey in a real transmission main by means of a portable device: The case study of the Trento (I) supply system. Procedia Eng. 2017, 186, 228–235. [Google Scholar] [CrossRef]
- Mazzocchi, E.; Pachoud, A.J.; Farhat, M.; Hachem, F.E.; Cesare, G.D. Signal analysis of an actively cavitation bubble in pressurized pipes for detection of wall stiffness drops. J. Fluids Struct. 2016, 65, 60–75. [Google Scholar] [CrossRef]
- Gong, J.; Lambert, M.F.; Nguyen, S.T.N.; Zecchin, A.C.; Simpson, A.R. Detecting thinner-walled pipe sections using a spark transient pressure wave generator. J. Hydraul. Eng. 2018, 144, 06017027. [Google Scholar] [CrossRef]
- Covas, D.; Ramos, H. Case studies of leak detection and location in water pipe systems by inverse transient analysis. J. Wat. Res. Plan. Man. 2010, 136, 248–257. [Google Scholar] [CrossRef]
- Duan, H.; Lee, P.; Ghidaoui, M.; Tuck, J. Transient wave-blockage interaction and extended blockage detection in elastic water pipelines. J. Fluids Struct. 2014, 46, 2–16. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Capponi, C. Mechanism of interaction of pressure waves at a discrete partial blockage. J. Fluids Struct. 2016, 62, 33–45. [Google Scholar] [CrossRef]
- Contractor, D.N. The reflection of waterhammer pressure waves from minor losses. J. Basic Eng. 1965, 87, 445–451. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Ferrante, M. In-line pipe device checking by short period analysis of transient tests. J. Hydraul. Eng. 2011, 137, 713–722. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Massari, C. Transient tests for locating and sizing illegal branches in pipe systems. J. Hydroinform. 2011, 13, 334–345. [Google Scholar] [CrossRef]
- Louati, M.; Ghidaoui, M.S. High frequency acoustic wave properties in a water-filled pipe. Part 1: Dispersion and multi-path behavior. J. Hydraul. Res. 2017, 55, 613–631. [Google Scholar] [CrossRef]
- Louati, M.; Ghidaoui, M.S. High frequency acoustic wave properties in a water-filled pipe. Part 2: Range of propagation. J. Hydraul. Res. 2017, 55, 632–646. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Massari, C. Potential of transient tests to diagnose real supply pipe systems: What can be done with a single extemporary test. J. Water Resour. Plan. Manag. 2010, 137, 238–241. [Google Scholar] [CrossRef]
- Meniconi, S.; Duan, H.; Brunone, B.; Ghidaoui, M.; Lee, P.; Ferrante, M. Further developments in rapidly decelerating turbulent pipe flow modeling. J. Hydraul. Eng. 2014, 140, 04014028. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. Experimental examination of unsteady friction models for transient pipe flow simulation. J. Fluids Eng. Trans. ASME 2006, 128, 1351–1363. [Google Scholar] [CrossRef]
- Liou, J.C.P. Understanding line packing in frictional water hammer. J. Fluids Eng. Trans. ASME 2016, 138, 081303. [Google Scholar] [CrossRef]
- Wylie, E.; Streeter, V. Fluid Transients in Systems; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1993; p. 463. [Google Scholar]
- Larock, B.E.; Jeppson, R.W.; Watters, G.Z. Hydraulics of Pipeline Systems; CRC Press: Boca Raton, FL, USA, 1999; p. 552. [Google Scholar]
- Bergant, A.; Simpson, A.R.; Vitkovsky, J. Developments in unsteady pipe flow friction modelling. J. Hydraul. Res. 2001, 39, 249–257. [Google Scholar] [CrossRef]
- Brunone, B.; Morelli, L. Automatic control valve induced transients in an operative pipe system. J. Hydraul. Eng. 1999, 125, 534–542. [Google Scholar] [CrossRef]
- Brunone, B.; Golia, U.M. Discussion of “Systematic evaluation of one-dimensional unsteady friction models in simple pipelines” by J.P. Vitkovsky, A. Bergant, A.R. Simpson, and M. F. Lambert. J. Hydraul. Eng. 2008, 134, 282–284. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A review of water hammer theory and practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Pezzinga, G. Evaluation of unsteady flow resistances by quasi-2D or 1D models. J. Hydraul. Eng. 2000, 126, 778–785. [Google Scholar] [CrossRef]
- Pezzinga, G.; Brunone, B.; Meniconi, S. Relevance of pipe period on Kelvin-Voigt viscoelastic parameters: 1D and 2D inverse transient analysis. J. Hydraul. Eng. 2016, 142, 04016063. [Google Scholar] [CrossRef]
- Pezzinga, G.; Scandura, P. Unsteady flow in installations with polymeric additional pipe. J. Hydraul. Eng. 1995, 121, 802–811. [Google Scholar] [CrossRef]
- Pezzinga, G. Unsteady flow in hydraulic networks with polymeric additional pipe. J. Hydraul. Eng. 2002, 128, 238–244. [Google Scholar] [CrossRef]
- Covas, D.; Stoianov, I.; Mano, J.F.; Ramos, H.; Graham, N.; Maksimovic, C. The dynamic effect of pipe-wall viscoelasticity in hydraulic transients. Part II—Model development, calibration and verification. J. Hydraul. Res. 2005, 43, 56–70. [Google Scholar] [CrossRef]
- Franke, P.G.; Seyler, F. Computation of unsteady pipe flow with respect to visco-elastic material properties. J. Hydraul. Res. 1983, 21, 345–353. [Google Scholar] [CrossRef]
- Keramat, A.; Tijsseling, A.S.; Hou, Q.; Ahmadi, A. Fluid-structure interaction with pipe-wall viscoelasticity during water hammer. J. Fluids Struct. 2012, 28, 434–455. [Google Scholar] [CrossRef]
- Keramat, A.; Kolahi, A.G.; Ahmadi, A. Water hammer modeling of viscoelastic pipes with a time-dependent Poisson’s ratio. J. Fluids Struct. 2013, 43, 164–178. [Google Scholar] [CrossRef]
- Soares, A.K.; Covas, D.; Reis, L.F. Analysis of PVC pipe-wall viscoelasticity during water hammer. J. Hydraul. Eng. 2008, 134, 1389–1395. [Google Scholar] [CrossRef]
- Weinerowska-Bords, K. Accuracy and parameter estimation of elastic and viscoelastic models of the water hammer. Task Q. 2007, 11, 383–395. [Google Scholar]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Massari, C. Energy dissipation and pressure decay during transients in viscoelastic pipes with an in-line valve. J. Fluid Struct. 2014, 45, 235–249. [Google Scholar] [CrossRef]
- Pezzinga, G.; Brunone, B.; Cannizzaro, D.; Ferrante, M.; Meniconi, S.; Berni, A. Two-dimensional features of viscoelastic models of pipe transients. J. Hydraul. Eng. 2014, 140, 04014036. [Google Scholar] [CrossRef]
- Hachem, F.E.; Schleiss, A.J. A review of wave celerity in frictionless and axisymmetrical steel-lined pressure tunnels. J. Fluids Struct. 2011, 27, 311–328. [Google Scholar] [CrossRef]
- Parmakian, J. Waterhammer Analysis; Dover: New York, NY, USA, 1963. [Google Scholar]
- Montuori, C. Colpo d’ariete in presenza di resistenze in condotte di notevole spessore. L’Energia Elettrica 1966, XLIII, 1–18. (In Italian) [Google Scholar]

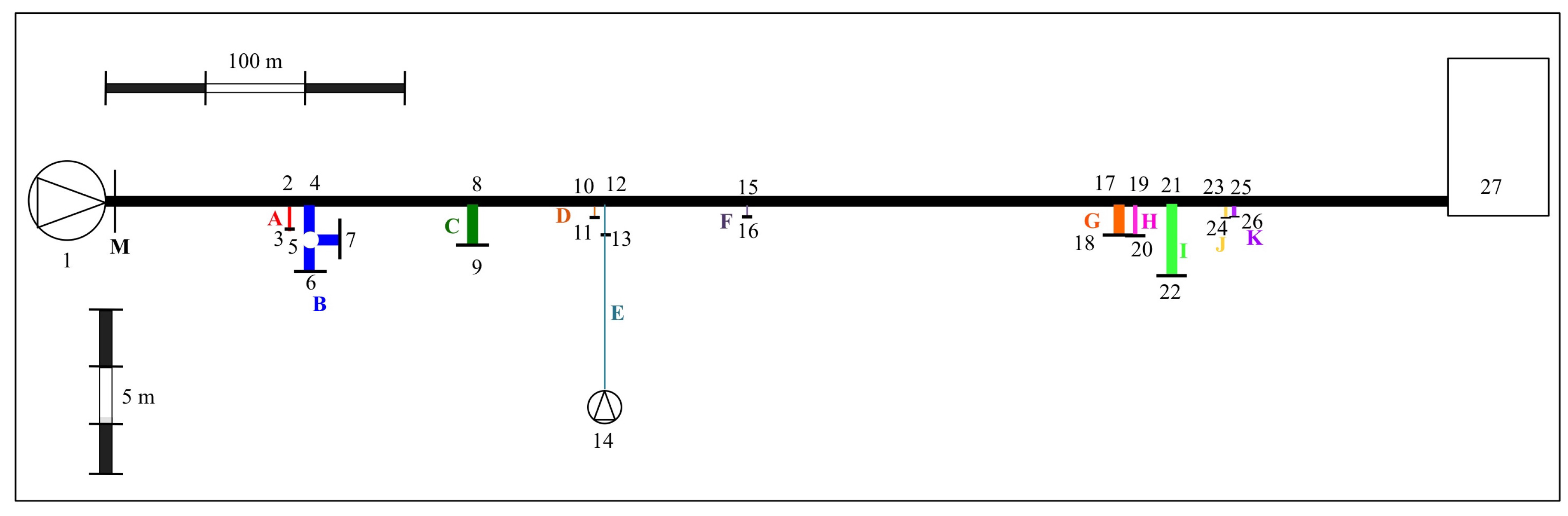
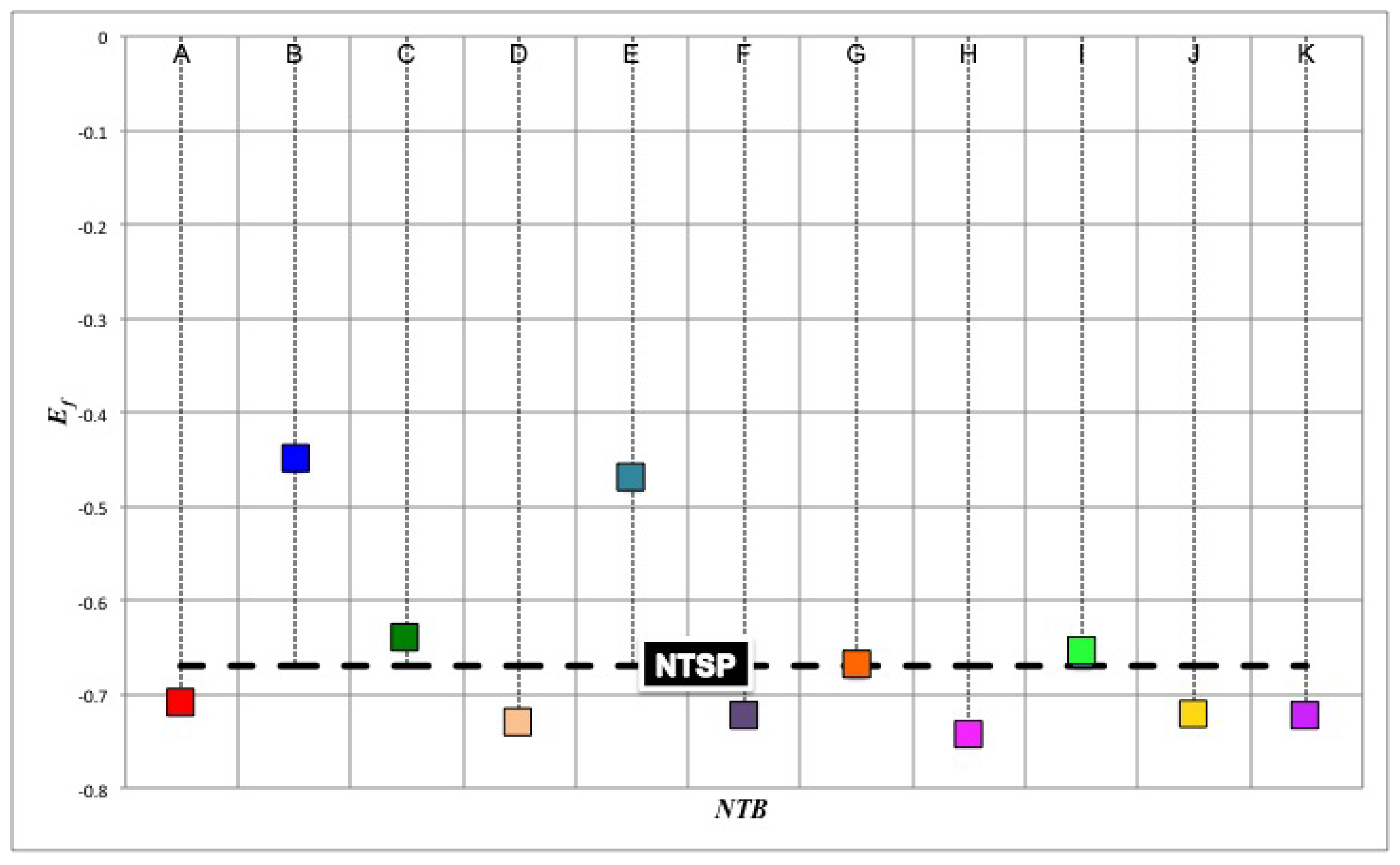
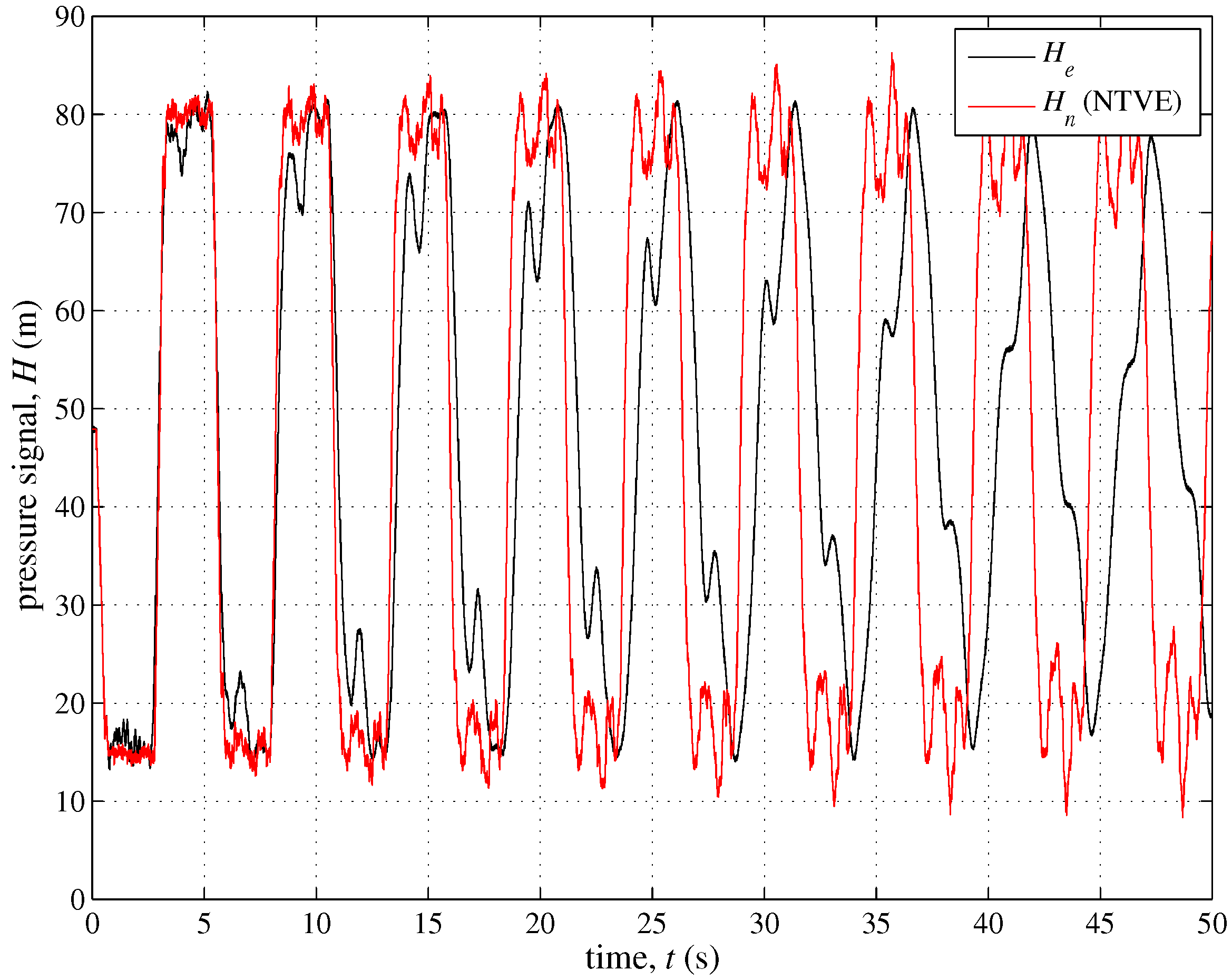
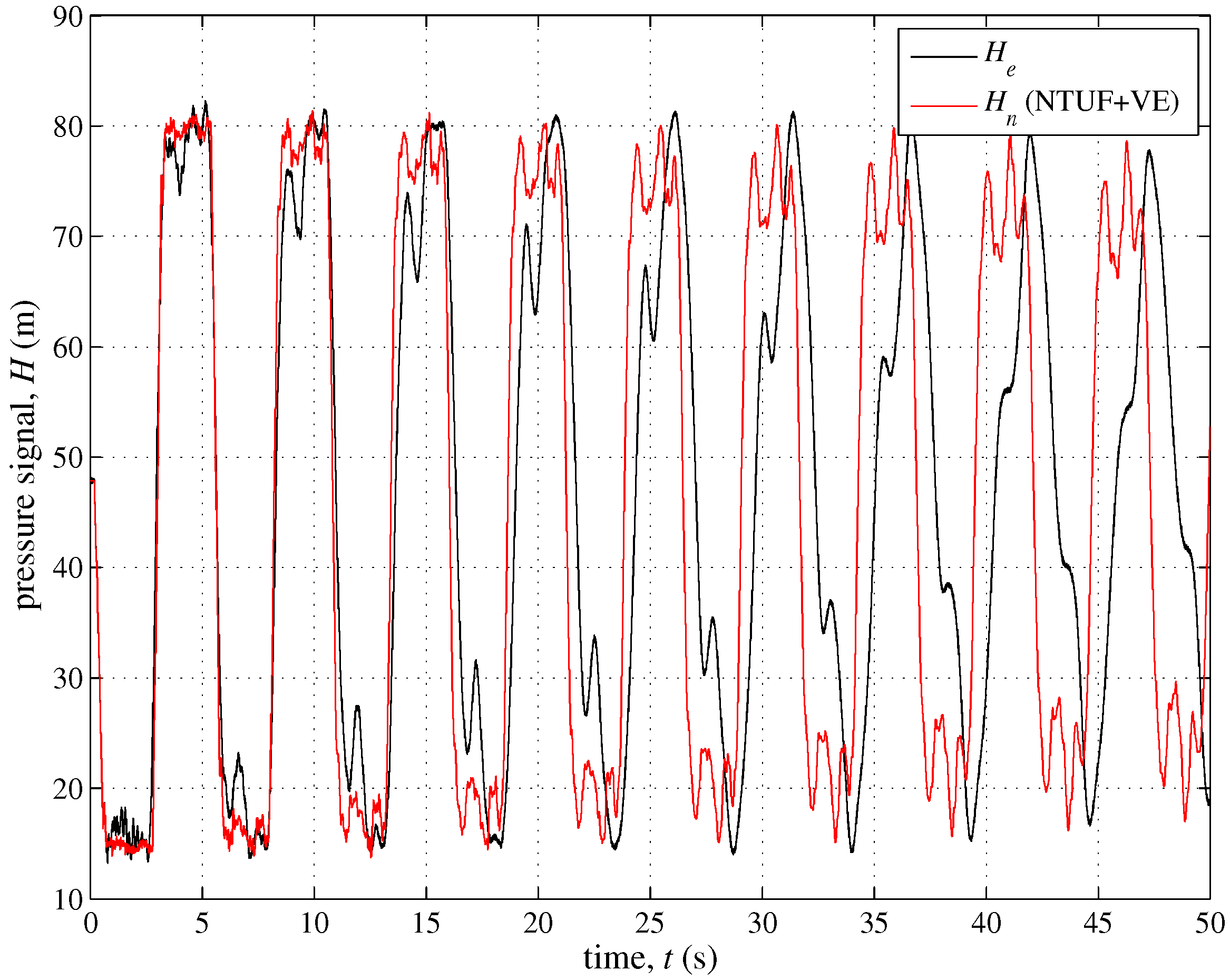
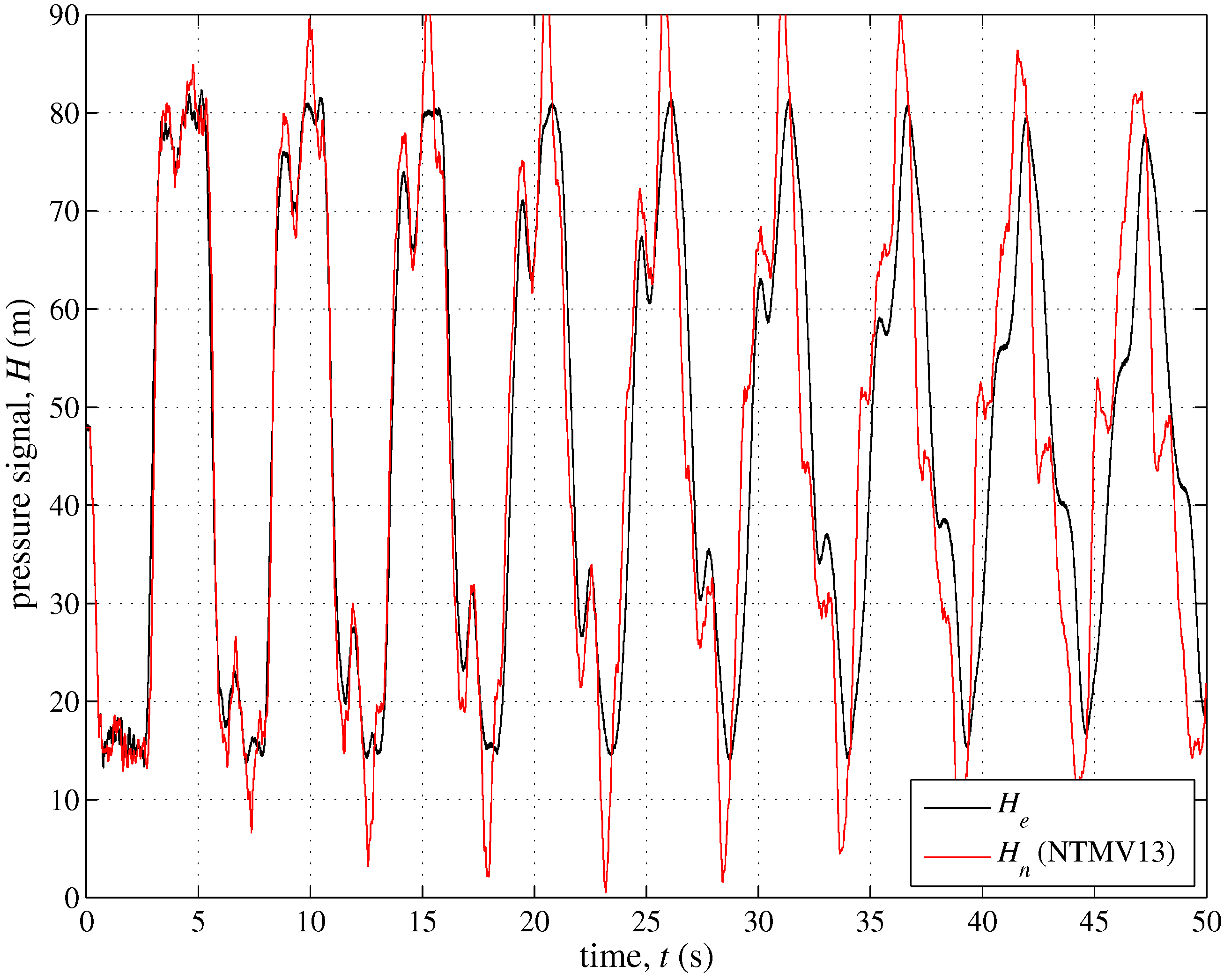
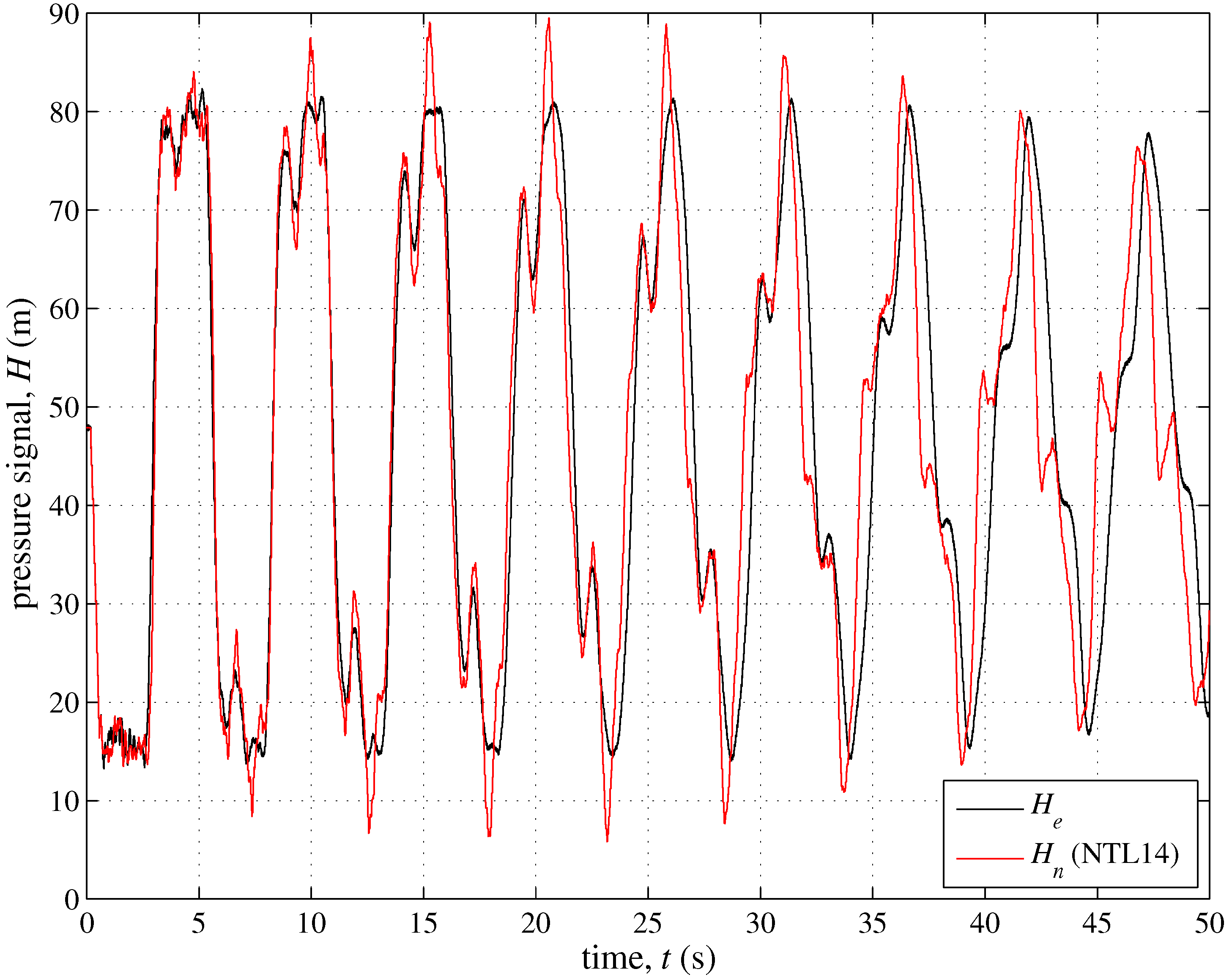
| Branch | Initial Node—End Node | (m) | (mm) | Material (−) | (−) |
|---|---|---|---|---|---|
| A | 2–3 | 1.7 | 150 | steel | |
| B | 4–5 | 3.1 | 506 | steel | |
| 5–6 | 1.8 | 506 | steel | ||
| 5–7 | 2.7 | 200 | steel | ||
| C | 8–9 | 3.5 | 506 | steel | |
| D | 10–11 | 0.7 | 80 | steel | |
| E’ | 12–13 | 3 | 247 | PEAD | |
| F | 15–16 | 1.1 | 100 | steel | |
| G | 17–18 | 3 | 506 | steel | |
| H | 19–20 | 3 | 200 | steel | |
| I | 21–22 | 6.8 | 506 | steel | |
| J | 23–24 | 1 | 150 | steel | |
| K | 25–26 | 0.76 | 200 | steel |
| Numerical | Simulated Topology | Model | |
|---|---|---|---|
| Test (NT#) | and Functioning Conditions | Assumptions | (−) |
| SP | single pipe (i.e., no branches) | Equations (1) and (2) | |
| 5b | only branches B, C, E, G, and I inactive and valve 13 fully closed | “ ” | |
| UF | as 5b | UF included | 0.30 |
| VE | as 5b | VE included | |
| UF + VE | as 5b | UF + VE included | 0.30 |
| MV13 | as 5b but with a malfunctioning valve at node 13 | “ ” | 0.80 |
| L14 | as MV13 but with E branch with a small leak | “ ” | 0.83 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meniconi, S.; Brunone, B.; Frisinghelli, M. On the Role of Minor Branches, Energy Dissipation, and Small Defects in the Transient Response of Transmission Mains. Water 2018, 10, 187. https://doi.org/10.3390/w10020187
Meniconi S, Brunone B, Frisinghelli M. On the Role of Minor Branches, Energy Dissipation, and Small Defects in the Transient Response of Transmission Mains. Water. 2018; 10(2):187. https://doi.org/10.3390/w10020187
Chicago/Turabian StyleMeniconi, Silvia, Bruno Brunone, and Matteo Frisinghelli. 2018. "On the Role of Minor Branches, Energy Dissipation, and Small Defects in the Transient Response of Transmission Mains" Water 10, no. 2: 187. https://doi.org/10.3390/w10020187
APA StyleMeniconi, S., Brunone, B., & Frisinghelli, M. (2018). On the Role of Minor Branches, Energy Dissipation, and Small Defects in the Transient Response of Transmission Mains. Water, 10(2), 187. https://doi.org/10.3390/w10020187






