Abstract
Over the past few decades, the concept of resilience has emerged as an important consideration in the planning and management of water infrastructure systems. Accordingly, various resilience measures have been developed for the quantitative evaluation and decision-making of systems. There are, however, numerous considerations and no clear choice of which measure, if any, provides the most appropriate representation of resilience for a given application. This study provides a critical review of quantitative approaches to measure the resilience of water infrastructure systems, with a focus on water resources and distribution systems. A compilation of 11 criteria evaluating 21 selected resilience measures addressing major features of resilience is developed using the Axiomatic Design process. Existing gaps of resilience measures are identified based on the review criteria. The results show that resilience measures have generally paid less attention to cascading damage to interrelated systems, rapid identification of failure, physical damage of system components, and time variation of resilience. Concluding the paper, improvements to resilience measures are recommended. The findings contribute to our understanding of gaps and provide information to help further improve resilience measures of water infrastructure systems.
1. Introduction
The reliability with risk management has been widely used as the primary criterion in engineering and managing water infrastructure systems [1,2,3,4,5,6,7]. Conventional risk-based strategies have been implemented to guide protection and prevention options that seek to mitigate or avoid the likelihood of expected (targeted) disruptive events and the potential adverse impact from the events [8,9,10,11]. These options can enhance water systems’ reliability to some extent and be helpful to prevent undesirable consequences. However, recent experience from natural and man-made water-related disasters suggests that current water infrastructure systems cannot protect and prevent all disruptive events and may perform unreliably because of high uncertainty of disturbances, complicated interdependency of infrastructure systems, and stochastic failures resulting from unpredictable events [12,13,14,15,16].
Over the past few years, attention is shifting more toward resilience-based strategies such as mitigation and recovery options, which make critical infrastructure systems (including water systems) more adaptively reliable [17,18,19,20]. The term resilience means to “bounce back” from a disruption and has been defined in various disciplines for their own targets [21]. Resilience can be understood as a comprehensive system capacity to withstand and absorb disruptions and quickly recover to the pre-disrupted condition [22]. The resilience concept has also gained greatly increasing prominence in designing and managing water infrastructure systems. Previous researchers, e.g., Moy et al. [23], Wang and Blackmore [24], and Butler et al. [14,25] have discussed the general concepts and definitions of resilience for water infrastructure systems. Several definitions of resilience have been also suggested for target water systems, as described in the following section.
As the resilience concept in water systems has evolved, resilience measures have been recognized as important in the decision-making process for developing strategies for preparedness, response, and recovery of water infrastructure systems against unexpected disruptive events. The quantitative measurement of resilience can provide various benefits such as understanding and comparing system resilience under different environmental, organizational, social, and economic conditions; identifying vulnerable parts that need improvement with resilience strategies; and enhancing transparency in planning an infrastructure system [26].
Unfortunately, despite these benefits, resilience measures and strategies have not yet been widely applied to design and manage water infrastructure systems [15,27]. Furthermore, previous measures typically have one or more of several drawbacks: (1) inconsistent and theoretically deficient approaches to defining resilience; (2) not adaptable for different types of water infrastructures; (3) dependency on parameter estimation assumptions; (4) substantial and intensive computational efforts when applying to complex real systems; and (5) insufficient information to guide decision making [17,18,19,28].
In this regard, the purpose of this paper is to critically review existing resilience measures for water infrastructure systems and provide insights to design improved measures. A number of studies (e.g., [21,26]) provide overviews and suitability assessments of resilience measures in various fields. However, there are few attempts to focus deeply on reviewing resilience measures for water infrastructure systems. Herein, this study focuses on quantitative approaches to measure resilience of water infrastructure systems, especially related to water supply, i.e., water resources systems and water distribution networks. The goal of this study is to identify and recommend improvements to resilience measures and in turn produce synthesized information useful for aiding the choice of resilience measure to use for a particular water infrastructure system analysis.
2. Review Methodology
2.1. Selection of Resilience Measures for Review
To accomplish a broad review of the literature, the authors followed four steps to search and select relevant publications: first, the authors defined a review question, which is “how are the resilience measures for water infrastructure systems defined in a quantitative approach?”. Second, potential relevant publications were identified using standard research databases (e.g., Web of Science, JSTOR, and ScienceDirect) search. The search key words include terms related to resilience/reliability/availability measure for water resources/distribution systems. Third, the identified publications were filtered by examining titles and abstracts to constrain the scope of the review to modeling and quantitative measures of resilience in water infrastructure systems or to be irrelevant to the above-mentioned review question. Fourth, the publications for the review were finally selected by examining full-text of the first filtered publications. Among the selected publications, those citing and re-using a previously developed measure were noted. Using this literature search process, the authors identified 21 resilience measures to consider for this review (see list in Table 1). It is important to note that more than 50% of the selected measures have been introduced in the most recent three years. A brief overview of these measures is described in the following section. In order to understand types and characteristics of the selected measures, the authors broadly classified the measures by a probabilistic approach and a deterministic approach, each of which is also clustered by a dynamic approach and a static approach [21]. The probabilistic approach considers the stochasticity of system functions (or disturbances) and the probability-based formulation of the measures, while the deterministic approach does not consider them. The dynamic approach considers time-dependent functions of a system, while the static approach does not consider them. A critical analysis of these measures was carried out for the evaluation of their performance against the review criteria described below.

Table 1.
Listing of measures selected for review.
2.2. Criteria for Literature Review
The review criteria were defined based on the Axiomatic Design process that has been widely used in engineering and non-engineering fields [46]. Axiomatic Design provides a systematic design process founded on logical thinking at the iterative interplay between “what to achieve” and “how to achieve it” [46,47]. The design sequence consists of four domains as shown in Figure 1: (1) “Customer Domain”, (2) “Functional Domain”, (3) “Physical Domain”, and (4) “Process Domain”. The “Customer Attributes (CAs)” in the “Customer Domain”, which represents customer needs to achieve a design goal, are transformed into the “Functional Requirements (FRs)” and “Constraints (Cs)” in the “Functional Domain”. The “Design Parameters (DPs)” in the “Physical Domain” are defined for satisfying the specified FRs. This interplay between FRs and DPs is mostly considered as the major design process. Finally, the “Process Variables (PVs)” in the “Process Domain” are determined for design satisfying the specified DPs. The former and latter domain in the sequence can be considered as design requirements and the design solution to the requirements, respectively. In this context, the Axiomatic Design is commonly described as a “mapping process” between these domains by “zigzagging” (For more information, see [47]).
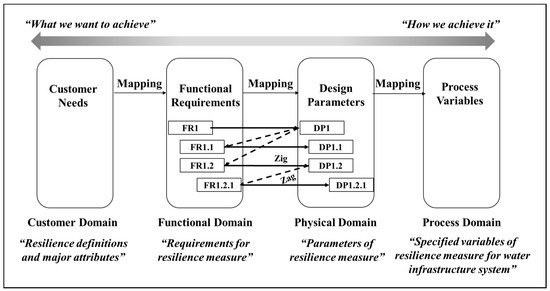
Figure 1.
Axiomatic Design process with four domains (Modified from [48]).
With regard to the Axiomatic Design process, the review criteria in this study are designed as follows: first, for customer needs the major capabilities of resilient systems (i.e., major attributes of resilience) are chosen from resilience definitions in various fields. Second, the FRs are defined as requirements of the resilience measure to evaluate the capabilities. Then, the DPs are defined as parameters of the resilience measure to describe the requirements. The PVs corresponding to each DP can be determined by the specified variables of the resilience measure of water infrastructure systems. Various PVs corresponding to a DP may be defined with dependence on type of water infrastructure and their purpose in water management. Since this study aims to review resilience measures of water infrastructure systems with systematic criteria, rather than design a new resilience measure of a certain water infrastructure, the authors regard DPs as review criteria.
The resilience concept was emerged first in psychology and psychiatry fields and was established by ecologist Holling [49], who defined resilience for ecological systems as “a measure of the persistence of systems and of their ability to absorb change and disturbance and still maintain the same relationships between populations or state variables”. Inspired by this Holling’s definition, various fields have established their own resilience concepts and definitions. Since there has been extensive discussion on the resilience definitions, e.g., [21,50,51,52], related issues are not repeated here. The resilience concepts and definitions for water infrastructure systems have been also discussed [14,23,24,25] and suggested for target water systems: Hashimoto et al. [29] defined resilience for water resources systems as the ability to quickly recover from a system failure. Butler et al. [14] described a system’s ability to minimize consequence and duration of the service failure under disrupted conditions. Liu et al. [36] described resilience as the capacity of water resources systems to undergo unexpected disturbances and sustain its essential performance. Klise et al. [22] referred to resilience of drinking water systems as the ability to manage the systems to mitigate the disruptive impacts of failures and rapidly recover to a normal level of service to supply safe water for the population served. Todini [31] introduced resilience for a water distribution system as the ability to overcome disrupted hydraulic conditions (hydraulic pressure) with satisfying them at the nodes. Chmielewski et al. [45] described resilience as a system’s ability to satisfy its performance for service communities through response (prevention and mitigation) and recovery process. Yazdani et al. [35] viewed resilience as the ability to reduce potential possibility and impact of system failures and minimize the total disrupted service under system disruptions (emergency conditions). Candelieri et al. [53] and Herrera et al. [38] considered resilience as a system’s capability to maintain its performance under failure in some components or abnormal status. However, as noted in Table 1, some of the measures based on the resilience definitions are overlapped with or are used as a surrogate measure for comparable water management concepts such as reliability, robustness, availability, and redundancy (connectivity), which characterize system abilities, performance, or configurations. For example, the Todini [31]’s measure has been used to evaluate resilience as a comparative concept to reliability of a water distribution network.
There is a lack of clarity in the resilience definitions in various fields including water infrastructure systems due to unique insight and inconsistencies; however, it is noted that the major capabilities (attributes) of a resilient system that are commonly described in many of the definitions include the following: (1) withstanding capability—withstanding system disruptions and maintaining normal functionality under the disruptions; (2) absorptive capability—immediately absorbing the disruptions and minimizing system damage; (3) restorative capability—quickly recovering to the normal or acceptable state; and (4) adaptive capability—adapting to the changing conditions and uncertain disruptions. In addition to these capabilities, many definitions include the terms such as “comprehensive ability”, “maintaining performance/functions of a system/entity”, “recovery to original/normal/acceptable state”, and “uncertainty”. In this regard, the authors define a system’s resilience as a comprehensive ability of a system to sustain its performance within an acceptable level by combating disruptions with the fundamental capabilities (i.e., withstanding, absorptive, restorative, and adaptive capabilities) in timely and efficient ways, after failures of the system, for a given uncertain environments. The authors believe that measuring intrinsic resilience of a system based on this definition needs to evaluate the fundamental resilience capabilities (attributes) synthetically. This idea is also supported by Nan and Sansavini [54] and Francis and Bekera [55]. Thus, in this study, these four capabilities are considered as the “customer needs” for the resilience measure.
Withstanding capability is the ability to sustain essential performance of a system at an acceptable level during and after disruptive events or when exposed to long-term disruptions [19,56]. This capability is related to ensuring reliability, durability, and continuity of system functionality. One of the ways to evaluate this capability would be to define system functionality and then compare the functionalities under normal and disrupted conditions. Thus, these two factors, i.e., system functionality and comparison with a baseline, were considered as requirements of the resilience measure to evaluate withstanding capability of a target system.
Absorptive capability is the system strength, which is related to functionality in the immediate aftermath of a disruption, when an infrastructure system failed to withstand a disruption [26]. This capability is demonstrated during a very short period. Though a system is well prepared to withstand disruptions, the potential impacts from unexpected disruptions may cross a functionality threshold of the system. Thus, the system with high absorptive capability can accommodate the initial and sudden disruptions without a significant degradation in the system functionality and minimize the disrupted state or loss of the system functionality [56,57]. In order to evaluate this capability, the functionality threshold needs to be first defined, which is related to the minimum acceptable level or normal state of system functionality. There is also a need to estimate the adverse impacts on a system. The adverse impacts are estimated based on violence of the system from the threshold or residual functionality of the system in the immediate aftermath of disruptions. A water infrastructure system consists of various components such as pipeline, tank, pump, and treatment plants. The system impacts can be evaluated for the conditions of the individual components or the functionality of the whole system. Furthermore, a water infrastructure system is tightly interconnected with other critical infrastructure sectors, such as energy, transportation, and telecommunications. A failure in a water infrastructure system can be cascaded to/from these interconnected infrastructure systems. The cascading impacts of a system failure are important to evaluate total consequence of the system failure. In this regard, the factors, i.e., adverse impacts on whole system and components, cascading impacts on interconnected systems, and the acceptable level of system impacts, were considered as requirements of the resilience measure to evaluate absorptive capability.
Restorative capability is a distinctive attribute of system resilience, comparing to the conventional concepts of vulnerability, risk, and reliability. This is related to recovery ability to quickly reinstate all disrupted system components and performance to normal functionality or acceptable state. The conventional protection and prevention strategies with predictive estimates are concerned with yielding a catastrophic failure in system functionality due to uncertainty of the disruptive events, which may exceed the expected. Thus, this capability is more emphasized in resilience engineering [26]. The effective method to address recovery ability would be to consider recovery speed according to the severity of disruptions [26,57,58]. This would be dependent on rapid identification of system failures and recovery time after disruptions. For example, rapid detection and diagnosis of system failure and immediate emergency actions in a timely and efficient manner can contribute to the avoidance of potential expanded and cascaded impacts in the whole system or interconnected systems by isolation of the disrupted components and rapid implementation of recovery actions [56,59]. Thus, the factors, i.e., rapid identification of system failures and rapid recovery, were considered as requirements of the resilience measure to evaluate restorative capability.
Adaptive capability is related to the ability of keeping variation of system functionality in an acceptable range under changing conditions and uncertain disruptions; thereby maintaining sustained functionality over longer time scales [56,59]. Most internal and external disturbances (e.g., material deterioration, landslides, contamination intrusion, and climate change) on a water infrastructure system are difficult to predict and have inherent temporal and spatial uncertainties. The disturbances can affect system functionality in the compounded form of various disruptions (e.g., internal deterioration of system condition with an earthquake). Thus, the resilience measure needs to address uncertainty of the system disturbances with various scenarios. The changing conditions and disturbances of a system (e.g., aging pipes and climate change) can affect the whole functionality of the system in the future and system resilience over a long time period. Comparison of the resilience at different time periods can help evaluate whether the level of resilience, which the system pursues as a long-term goal, is maintained and examine the dynamic and evolutionary nature of system resilience over time [60]. The system that has high adaptability to changes may maintain its resilience within an acceptable range over a long time period. In this regard, evaluation of this capability needs to be included in the analysis of the long-term variation of the system resilience. System redundancy, which is the capability to satisfy operational requirements of a system by alternative components, can also enhance a system’s adaptive and absorptive capabilities against uncertain disruptions [56,61]. A system with more redundancy can minimize damage from changing disruptive events by partial or complete replacement of failed system components and keep system functionalities within acceptable levels over a longer period. In this regard, the authors considered system redundancy as a requirement to evaluate the adaptive capability.
Based on the acknowledged factors in each resilience capability, the FRs and DPs for a resilience measure can be summarized as shown in Table 2.

Table 2.
FRs and DPs for resilience measure.
The mapping process in Axiomatic Design should fundamentally satisfy the “Independence Axiom—maintaining the independence of FRs” [47]. This axiom indicates that each DP should be satisfied with only the corresponding FR without relating to other FRs. In order to identify whether the mapping process of FRs and DPs in this study satisfies the “Independence Axiom”, Table 3 shows a design matrix that evaluates the relationships between the FRs and DPs. The symbol ‘×’ in Table 3 indicates the non-zero value of the matrix components, i.e., existence of a relationship between the FRs and DPs. For satisfaction of the “Independence Axiom”, the design matrix should be in diagonal or triangular form [62]. The diagonal matrix, called an “uncoupled design”, means the relationship between the FRs and DPs perfectly satisfies the “Independence Axiom”. The upper or lower triangle matrix, called a “decoupled design”, also guarantees the “Independence Axiom” if the DPs are established in an appropriate sequence since the set of DPs with a proper order can minimize the degree of dependence between the FRs [48,62]. In this regard, the authors finally adopted the design parameters as criteria for critical review of the selected resilience measures since the design matrix in Table 3 represents the triangle matrix, a decoupled design. The selected measures are analyzed by whether they have addressed these eleven criteria.

Table 3.
Construction of the design matrix.
3. Overview of the Selected Resilience Measures
This section describes the overview of the selected resilience measures (shown in Table 1) for water infrastructure systems. Many of the resilience measures have been developed as a surrogate measure of water systems’ reliability to evaluate performance.
Hashimoto et al. [29] introduced a resilience measure for water resources systems as the inverse of the expected time periods that the system remains in an unsatisfactory state. The resilience measure, which is quantified in a statistical way, is defined as the probability of recovery (R) to the satisfactory state (S) at time step t + 1 once a failure (F) has occurred at time step t, represented in Equation (1). They described that a system failure is the occurrence of an unsatisfactory state of the system identified when functionality exceeds a threshold. Thus, if a water resource manager defines a system functionality (e.g., the amount of water release in reservoir operation), the system resilience is evaluated by estimation of probabilities related to the satisfactory (or recovered) and unsatisfactory states of the system functionality. The states are determined by a threshold (e.g., a contractual obligation) indicating transition to system failure. By their definition and Equation (1), the lower the probability of remaining in unsatisfactory state after a failure is (i.e., the higher the probability of rapid recovery is), the larger resilience is. In this context, the resilience measure focuses on rapid recovery to a satisfactory functionality after system failure.
Hashimoto’s resilience measure has been widely used and cited, with or without modification. Fowler et al. [63] used this measure to evaluate the resilience of a water resource system during drought events with various climate change scenarios. Srdjevic et al. [64] used this measure to evaluate resilience as one of the multi-criteria for various scenarios of water management based on reservoirs, river flows, and water allocation. Asefa et al. [13] also applied the evaluation of resilience in a water resources system under changing future climatic conditions (e.g., monthly rainfall) and water supply conditions (e.g., future demand, reservoir storage capacity, and surface water withdrawal restriction). Li and Lence [17] extended Hashimoto’s resilience measure for approximation of water resources system resilience (“lag-1 resilience”) with consideration of stochastic hydrological conditions and a nonstationary process of the system functionality. Chanda et al. [65] analyzed spatial and temporal variation of the resilience to characterize long-term drought.
Kjeldsen and Rosbjerg [33] introduced their resilience measure based on Hashimoto’s definition, i.e., the inverse of the mean time duration that the system remains in an unsatisfactory state, as shown in Equation (2).
where, is the time duration over the jth unsatisfactory state of the system and n is the total number of transition events from the satisfactory state to the failure state. The time duration over the unsatisfactory state is considered as the time period when water service cannot satisfy the water demand. The short time duration over the unsatisfactory state implies a rapid recovery time from a system failure. Jain and Bhunya [66] used this measure for measuring resilience of a multipurpose storage reservoir with Monte Carlo simulations to explore statistics of the resilience. Kjeldsen and Rosbjerg [33] also represented the resilience measure (Equation (3)), which is based on pth percentile in the cumulative distribution function (F) fitted to the recurrence time or the time duration of the failure events.
Moy et al. [23] proposed the resilience index as the inverse of the maximum successive time periods under an unsatisfactory state of the system while the Hashimoto’s measure was described as the inverse of the mean value of time periods under a failure.
Vogel and Bolognese [30] adopted the standardized net inflow ([67]) as a resilience measure of a storage reservoir system (Equation (4)).
where is the fraction of annual reservoir yield over the mean annual inflow to the reservoir () and and are the standard deviation and the coefficient of variation, respectively, for the annual inflows. The reservoir system, which has more than unity in value of m, is dominated by “within-year system behavior” in water supply. This reservoir usually refills by the end of each year, while one having the m values between 0 and 1 is dominated by “over-year system behavior”, continuing drawdown over long periods with multiyear, and thereby being vulnerable to continuous drought over several years. Thus, reservoirs with m values closer to zero require more recovery time from a water supply failure comparing to the reservoirs with the m values closer to unity. They also introduced a measure to evaluate over-year system behavior through combining the two-state Markov Model (failure state and no-failure state) and general storage–reliability–yield relationships. The failure state of a reservoir system was defined as the summation of the storage water and annual inflow that cannot satisfy the threshold demand in year t. The measure was described as the conditional probability that the no-failure state in year t + 1 follows the failure state in year t. They recommended use of this measure with preference since it includes probabilistic impact of the inflows, which the m index of Equation (4) does not. The value of the conditional probability near unity (large value of the m) indicates that the reservoir shows the behavior of within-year systems and, therefore, a more resilient system.
Mehran et al. [37] proposed a multivariate approach as a performance measure of a water resources system to socioeconomic drought, termed “Multivariate Standardized Reliability and Resilience Index (MSRRI)”. The MSRRI combines two univariate indicators: “inflow-demand reliability indicator (IDR)”, which considers change of inflow to reservoirs due to climatic and meteorological states, and “water storage resilience indicator (WSR)”, which addresses performance of the engineered infrastructure against climatic and hydrological variability. The WSR indicator provides performance information on the sufficiency of the reservoir storage for meeting water demand over the selected time period, as defined in Equation (5).
where, for time step t (month), is the reservoir storage, is the inflow to the reservoir, is the water demand, is the reservoir storage required for minimum operation, and is the total water demand over the analysis time period. The value of WSR is estimated for every month t and thereby time variation of resilience can be identified over the long-term period. The negative value of the WSR indicates shortage of reservoir storage to supply the demand, i.e., the system damage. The higher positive value of the WSR shows a more resilient reservoir system, since it indicates sufficient reservoir storage to meet demand.
Qi et al. [43] described resilience of a river basin and its time variation based on the concept of “critical slowing down” as a generic leading indicator of low resilience of system, which has been used for description of stability and resilience in ecology fields (For more information, see [68]). A system state of critical slowing down is generally determined by the increasing autocorrelation in time-series of a system state variable. Thus, low autocorrelation of state variables at time t and t + indicates higher resilience of the system. In this sense, the authors defined resilience at time t as the number of points representing large deviation beyond a threshold () from points on perfect autocorrelation (i.e., linear correlation) of a state variable (e.g., annual water discharge) at time t and t +. The time variation of resilience can be investigated by estimation of the resilience in time-series.
Liu et al. [36] proposed a resilience measure, represented in Equation (6), based on Hooke’s law in mechanics. This measure describes the relationship between deformation of an elastic object (e.g., spring) and its bounce-back force from the elastic deformation.
where R0 is the “constant background resilience” related to intrinsic resistance, is the sensitivity representing adaptive learning ability from disruptions, and D is the system stress by external disruptions. The spring coefficient and elastic deformation in Hooke’s law description can be considered as the and D in this measure, respectively. In this sense, the second term of Equation (6) indicates adaptive capacity to the external disruptions. Sensitivity is estimated by various indicators related to human domain (e.g., service population and flood-affected area), support domain (e.g., Gross Domestic Product, investment in water management project, and storage capacity), and natural domain (e.g., annual precipitation and water resources) of the water resources system and weighting factors. They considered drought, flood, and water pollution as the external disruptive events and estimated stresses of the water resources system from them as the inverse of the average available water resources for the minimum threshold; the flood discharge for the design flood discharge; the total river and stream miles for those satisfying water quality standards, respectively. This study did not address measurement of the “constant background resilience” and provide sufficient information. The resultant resilience () is evaluated as the sum of resilience values for the disruptive events considering “Parallelogram rule of force” in physics as shown in Equation (7). The resultant resilience provides integrated evaluation of the system resilience with respect to multiple disruptions during various disruptive events as well as drought (d), flood (f), and water pollution (p).
Amarasinghe et al. [15] dealt with resilience for a water supply system to rainfall variation due to climate change. They referred to resilience as the system’s ability to maintain water service in the presence of rainfall reduction associated with climate change impacts. In this context, their resilience measure considered failure thresholds (e.g., inability to satisfy 50% of the water demand) as the critical conditions of a system, which represent maintaining system functionality (i.e., satisfactory water service) without failure. Thus, they proposed a resilience measure including indicators related to system functionality in water service corresponding to the failure threshold and compared to full service capacity in the water supply, as represented in Equation (8).
where is the indicator characterizing the water service capacity at failure threshold and representing the absorbable level of potential reduction in the water supply, is the indicator representing the absorbable level of disruptions, is the full water service capacity, is the minimum level of water service at the failure threshold, is the level of disruption (e.g., rainfall reduction) corresponding to the failure threshold, and is the level of absorbable disruption. These indicators (, , and ) were estimated with multiple rainfall scenarios considering uncertainty and temporal variability of future rainfall. Larger values of and (i.e., smaller values of ) indicate that the water supply system is more resilient to disruptions since this represents high system ability to absorb disruptions and potential reduction in water use.
Todini [31] proposed a resilience measure for the looped water distribution networks to cope with uncertainties in failures. The physical and hydraulic failures (e.g., pipe breakage and growing demand) in the water distribution network may entail more internal energy dissipation (losses) with variation of the water flow and pressure. He considered that the resilience of a water distribution network depends on sufficient energy surplus to overcome increasing internal energy dissipation in the case of disruptions. The energy surplus represents the available energy storage that can be dissipated under changes in operation conditions by a disruption. In this regard, the proposed resilience measure was defined as the fraction of the available energy surplus at the nodes over the maximum energy surplus in the network, which would be internally dissipated to meet the required demand and head at the nodes (Equation (9)). This measure shows a standardized form by total energy surplus in water networks under normal condition. The system failure state occurs when the available head at the nodes cannot meet the threshold (i.e., required head at the nodes).
where, and are design demand and head required at node i, is the available head at node i, is the flow from jth reservoir, is the total head in jth reservoir, is the energy supplied to the network from kth pump, is the specific weight of water, and n, r, and p are the number of nodes, reservoirs, and pumps, respectively, in the network. This measure is independent of the type of disruptive events and does not need to simulate various failure events and their statistical analysis; thereby it can significantly reduce the computational load.
Similar to Hashimoto’s resilience measure in the water resources systems, several authors have used Todini’s measure to estimate the water distribution system resilience, with or without modification, according to their research purposes. Greco et al. [69] and Tsakiris and Spiliotis [70] considered the failure cases in which minimum design requirements are not satisfied, and thereby values of the resilience can be negative. Greco et al. [69] also considered all the possible failure scenarios such as simultaneous failure of one or multiple pipes in estimation of Todini’s resilience measure. This notes that Todini’s measure can be applied to evaluate resilience with uncertainty scenarios of disruptions, if it is necessary. Creaco et al. [71] generalized Todini’s measure by considering pressure-driven modeling and energy dissipation by pipe leakage and analyzed time variation of resilience with changing pipe leakage and roughness. Liu et al. [72] used hydraulic head surplus for the resilience measure, which estimates available hydraulic head surplus compared to head surplus at previous nodes, instead of hydraulic energy surplus in Todini’s measure.
Prasad and Park [32] extended Todini’s measure, called “Network Resilience Index (NRI)”, incorporating the effects of energy surplus and loop reliability. The loops in a network become more reliable during segment isolations when the connected pipes to a node have less variation in diameters. In order to represent the loop reliability, they defined “uniformity ()” in diameters, as the ratio of average diameter for the maximum diameter of the connected pipes to the demand nodes (Equation (10)). The value of uniformity is unity if the diameters of connected pipes to a node are the same.
where is the number of connected pipes to a node , is the diameter of th pipe connected to the node . To take into account the loop reliability in resilience measure, they incorporated the uniformity as the weighting factor of energy surplus at each node into Todini’s resilience measure (Equation (11)). Creaco et al. [73] introduced “loop diameter uniformity” defined as the average of the diameter uniformity in a loop. However, the loop diameter uniformity was used as one of the resilience parameters to represent the loop’s reliability, rather than being incorporated into the Todini’s measure. Raad et al. [74] compared this measure and Todini’s measure with another surrogate reliability measure (e.g., flow entropy). Bi et al. [75] considered this measure to quantify an objective related to resilience for optimizing water distribution networks with another objective related to cost.
Jayaram and Srinivasan [34] proposed the “Modified Resilience Index (MRI)” to improve Todini’s resilience measure. This measure is more applicable for water distribution networks with multiple reservoirs. When one of the reservoirs, which has higher total head compared with others, delivers a large portion of total demand, this would increase energy surplus feeding to the network (i.e., the denominator in Equation (9)). In addition, this may increase energy surplus at demand nodes (i.e., the numerator in Equation (9)). Thus, the value of the Todini’s resilience measure may not increase, even though there are increases in the energy surplus at the demand nodes. Consequently, they suggested a resilience measure (i.e., MRI) of which value is varied in direct proportion to the total energy surplus at the demand nodes (Equation (12)). The value of the MRI can be greater than unity while Todini’s measure has a maximum value of 1. The larger value of the MRI indicates the larger amount of energy surplus at the demand nodes, and thereby the greater resilience in the water distribution network. They also investigated time variation of resilience with changing system conditions (internal roughness of pipes and water demand) over a long-term period by using the MRI measure.
Wright et al. [39] suggested a resilience measure based on the concept of “reserve capacity”. Reserve capacity is the residual amount of water in a system after supplying the required demand. The reserve capacity is estimated at a critical node where the difference between allowable head and the head at the node shows a minimum value. This measure indicates how closely the water distribution network is operated to a threshold condition, i.e., full capacity. The value of reserve capacity below unity indicates that the water distribution network cannot satisfy water demand without violating the threshold.
Zhuang et al. [18] described the concept of “availability” as system resilience of a water distribution network, which is defined as the fraction of water supplied to demand nodes during disruptions (Equation (13)).
where is the water flow supplied to the ith node at time t, is the water demand required at ith node at time t, T is the total time period under system disruption, and N is the number of the nodes. This measure can also be estimated for individual nodal availability and provide information on the intensity of the system failure. The computational framework for the system resilience was conducted by Monte Carlo simulation considering uncertainties in the nodal demands and pipe breakage occurrence. This framework for resilience evaluation is framed as follows: (1) random sampling of failure scenarios for pipe breaks and water demands; (2) identification of unintended isolated segments with near valve closure; (3) hydraulic simulation with normal and abnormal condition with response actions (e.g., pump operation); (4) estimation of the system and nodal availability. The hydraulic simulation in this framework also considers consecutive breaks of pipes and their restoration as the mean time between failures using the frequency of pipe failures, and mean time to repair pipe breakage using a regression relationship with the pipe diameter, respectively. This framework illustrates the impacts of practical system response and operation such as the location and closure of the nearest valves to pipe burst and adaptive pumps operation on system resilience.
Cimellaro et al. [19] proposed a global resilience measure by combining social, technical, and environmental system performance. The social, technical, and environmental performance was defined as the functionality of each domain under disruptions compared to their functionality under normal operating conditions. The performance is estimated by use of the ratio of the numbers of households satisfying water requirements after disruptions over a total number of households for the social domain, the ratio of the tank water level over the level corresponding to the tank reservoir capacity during a control time period for the technical domain, and the ratio of water quality over the pre- and post-disruptions for the environmental domain. The functionality in the technical domain (i.e., tank water level) can be generalized to the other system components (e.g., pump and valves). In the technical domain, the difference between the disrupted functionality and baseline can be considered as a loss of the system components. The resilience related to each system functionality () for the analysis time frame () is estimated by Equation (14). The integrand is related to the slope of the functionality curve, i.e., recovery rate. The global resilience can be finally evaluated by multiplying the resilience values for the system’s performance in the three domains. They also highlighted that resilience is a dynamic quantity characterized by uncertainty. Thus, in a case study, they considered uncertainty of potential disruptions with pipe breakage probability and various scenarios for failure location according to the pipe importance and spatial districts. Simonovic and Arunkumar [76] defined a similar resilience measure concept to this measure and applied it to a water resource system.
Chmielewski et al. [45] proposed a resilience framework with modeling of physical damage and functionality of a water distribution system in response to natural disasters such as a seismic event. The framework has the following procedures. First, system functionalities: pressure, water flow and quality at demand nodes under normal conditions are analyzed by a functionality model (i.e., hydraulic analysis for assessing system functionalities). Results from the analysis of the normal functionalities are considered as a baseline for comparison to post-disruption conditions. Second, physical damage states of system components (e.g., pipeline, tank, pump, and treatment plants) from disruptive events (e.g., seismic event) are evaluated by a damage model (i.e., analysis of physical damage to system components) such as system components’ fragility curves for the disruptive events. The components that have conditions below damage thresholds are removed from the hydraulic analysis in the functionality model at the following step. Third, each system functionality, pressure, water flow, and quality at each node, is evaluated to reflect the damage state of the system components and their recovery rate. At each time step, recovering functionalities at demand nodes are estimated over the recovery time period. Then, the recovering functionalities at each time step can be compared to the baseline functionalities or acceptable operational thresholds (e.g., at least 90% of baseline functionality) to track the level of system recovery. System resilience is finally measured as a percentage of the functionality level at demand nodes over the level of baseline functionality or an acceptable operational threshold, at time steps.
Structure-based measures have been recently used for evaluation of the water infrastructure system resilience. A water infrastructure system, especially the water distribution network, can be depicted as a spatially organized network of multiple interconnected components [35]. Expansion of the water system network and increase of components’ interconnection provides an opportunity to improve system resilience through strategic network redundancy [35]. For example, if water flow cannot be supplied through a pipe due to the pipe break, it can reach the demand node by alternative routes through looped and connected networks. Therefore, structure-based measures evaluate how the structural network of a water infrastructure system impacts the system resilience, especially network redundancy and connectivity of supply routes. Graph theory (network theory) is used to evaluate structural network features such as redundancy and connectivity by quantifying system networks of multiple nodes (e.g., reservoir, tanks, and consumption nodes) and links (e.g., pipes). Table 4 describes statistical and spectral measurements in graph theory, which are commonly used to evaluate network redundancy and connectivity as resilience features.

Table 4.
Structural network measurements commonly used for resilience measure (Adapted from [35,53]).
Yazdani et al. [35] examined the resilience of water distribution networks in a growing city with expansion options, using the network measurements in Table 4. Candelieri et al. [53] and Soldi et al. [77] suggested that the spectral measurements, i.e., spectral gap and algebraic connectivity, which are useful to identify node or edge cut-set (whose failure and removal entail a structural disconnection) and summarize invariant attributes of the network topology, are the most relevant measure in graph theory to assess the overall resilience of a water distribution network.
Herrera et al. [38] suggested “water-flow closeness” that incorporates energy dissipation related to water flowing along the pipes into the original concept of the closeness centrality, i.e., geodesic distance of link (pipe) between nodes. They also proposed “K-shortest path” to represent connectivity between nodes and water sources (e.g., tanks and reservoirs). The K-shortest path is estimated by the average distance of the routes between a node and its water sources, which are weighted by the hydraulic energy loss in water transportation. The nodes showing a low value of water-flow closeness and K-shortest path require large energy dissipation to supply water and have poor network connectivity to their water sources. Therefore, a water network including the nodes with low value of water-flow closeness and K-shortest path can be considered as a system with low resilience. Herrera et al. [42] extended these resilience measures for large-scale water networks. A water distribution network can be divided into sub-networks using sectorization approaches such as graph clustering, spectral clustering, and multi-level partitioning [78]. Then, they proposed two indices related to the resilience of the sub-network: the trimmed mean (discarding very high or low value of data in estimation of mean value) and variability (standard deviation normalized by the trimmed mean value) of K-shortest Path values in sub-networks nodes. It is noted that the sub-network with high variability includes the nodes with low resilience.
Farahmandfar et al. [44] incorporated pipeline reliability, which is defined as the probability of pipe failure, into the node degree in the water network configuration.
Pandit and Crittenden [41] suggested multi-criteria analysis with the network measurements to assess the resilience of water distribution networks and compare design options of the networks. Each measurement is estimated as a dimensionless value with linear transformations, i.e., difference between the measurement values and the maximum or minimum measurement value among them for the design options of the network over the difference between the maximum and minimum. Then, system resilience can be evaluated as a single value of 0–1 by summation of the dimensionless values of the measurements with weighting factors.
Water resources systems can be natural and man-made such as rivers, aqueducts, canals and groundwater and their connected networks over a wide area. In this regard, Porse and Lund [40] used network measurements to analyze the connectivity of water resources as the resilience of a water resources system with a large-scale network. They also suggested weighted betweenness centrality, which incorporates the monthly capacity of water resources and their annual flow target, to assess the relative importance of sub-networks in a large-scale water resources system. They described the spatial variation of structural connectivity of the sub-networks in the target water resources system.
4. Discussion
4.1. Gaps of Evaluation Criteria in the Selected Measures
Since the 1980s, the concept of resilience and its measure for water infrastructure systems have evolved to develop more adaptive and reliable water systems against expected and unexpected disturbances. It was noted that Hashimoto’s and Todini’s measures have been the most widely used and cited, with or without modification, to evaluate resilience of water resources systems and water distribution networks, respectively. As seen from the Table 1, the structure-based measures (i.e., measures in graph theory) have been recently introduced to evaluate network features of water infrastructure systems and their resilience.
Table 5, with review criteria in the rows and measures in the columns, shows whether the selected measures address the criteria. Resilience measures that were used with or without slight modification from previous measures are excluded in Table 5. It is noted that there are no resilience measures addressing the criteria for the cascading damage and rapid failure detection.

Table 5.
Evaluation across the selected measures against review criteria.
As mentioned earlier, a water infrastructure system is a critical lifeline infrastructure, which is complicatedly interconnected and mutually affected with other critical infrastructure systems. Comprehensive understanding and addressing the interdependency across the infrastructure systems has gained growing prominence in decision making to improve the resilience of urban infrastructure systems [79]. In this context, the interdependency between water and other infrastructure systems and their propagated impacts have recently received substantial attention to evaluate resilience more comprehensively [80]. There has been a lot of research on modeling and assessment (e.g., system dynamics model and dynamic graph model) to analyze the performance and mutual impacts over the interconnected infrastructure systems. It is believed that the cascading damage from/to water infrastructure systems can be considered in the resilience measures by recent efforts described above.
Rapid and accurate failure identification and immediate response can greatly contribute to the mitigation of system damage and rapid recovery, which are considered as major resilience strategies. For example, the late detection of pipe breaks and isolation of segments by valve closure may accumulate water and head loss in a water distribution network and delay the implementation of recovery actions. A resilience measure therefore needs to consider a system capability to detect and identify system failures (or damage) quickly.
It was also found that a small proportion of the selected measures address damage to the components of a water infrastructure system. A water infrastructure system is spatially organized with multiple interconnected components. Enhancement of whole system resilience requires prioritizing investment in system components such as the determination of vulnerable ones to threatening disturbances and their appropriate rehabilitation or replacement schedule. The selected measures need to consider damage or fragility of the various components to inform the process of selecting appropriate resilience-based strategies.
It was also identified that the selected measures, except Hashimoto et al. [29], Mehran et al. [37], Qi et al. [43], Todini [31], and Jayaram and Srinivasan [34], have not addressed long-term variation of system resilience. Many of the selected measures evaluate system resilience as “a snapshot in time [60]”, so they could not reflect the variable nature of resilience. A water infrastructure system with high resilience may fail in the future and may not maintain performance at an acceptable level during the whole time period due to changing disturbances and degraded system conditions (e.g., pipe deterioration and accumulated contaminants in reservoir). It is believed that resilience measures, which address long-term variation of resilience, provide useful information for decision making to help guide investment in infrastructure systems for long-term horizons, develop preparedness plans, and implement resilience-based strategies.
Further improvements of the resilience measures are discussed according to the four major attributes of resilience (described in review methodology section) in the following sections.
4.2. Discussion on System Functionality in Pre- and Post-Disruption
Table 5 shows that many of the selected measures have addressed baseline functionality and comparison with the baseline, except structure-based measures. The majority of the selected measures estimate system functionalities (e.g., energy surplus, storage and water demand). However, the measures, except Cimellaro et al. [19] and Chmielewski et al. [45], have paid less attention to considering multiple functionalities together. The increased resilience to one functionality may decrease resilience to another one (e.g., flood control and water quality) in some situations [81]. For example, increasing the capacity of a tank may contribute to the enhancement of system resilience by storing more water in the tank, yet it may take more time to recover the system once water in the tank is contaminated. Increasing the storage capacity of a dam reservoir may also increase flood risk in the case of unexpected dam collapse. In this regard, the authors believe that resilience measures need to address multiple functionalities for tradeoffs between competing ones, thus improving the comprehensive system capacity of resilience.
Furthermore, considering interdependency of water infrastructure systems with other critical infrastructures, system functionalities that can directly or indirectly reflect interaction with other infrastructures also need to be addressed in resilience measures. It is considered that Todini’s resilience measure can evaluate system resilience with consideration of interrelation between water and power distribution networks since it addresses energy surplus in the measure. The backup power in a water network system can ensure resilience by Todini’s measure. However, the resilience can also be dependent on a transport infrastructure system in terms of constraints on the recovery schedule of the water pipe breakage. It is, therefore, recommended to consider system functionality addressing the performance of the interconnected infrastructure systems together or their integrated functionality.
Meanwhile, resilience capabilities (e.g., withstanding, absorptive, restorative, and adaptive capabilities) can be characterized by functionality transitions following system disruptions [54]. Integrated and balanced improvements of the capabilities are needed to improve system resilience with effective investments [55]. Identifying weak and strong capabilities of a system is required in order for the decision-making process to invest resilience-based infrastructure options. However, most of the existing measures evaluate system resilience considering the capabilities partially or synthetically. It is believed that a resilience measure also needs to provide information on individual resilience capabilities with respect to functionality transition in pre- and post-disrupted conditions.
4.3. Discussion on System Absorptions of Disruptions
From Table 5, it can be seen that the majority of the selected measures, directly and indirectly, include the threshold functionality (e.g., minimum water service, minimum required head, and target demand), except structure-based measures. Thresholds of network redundancy and connectivity in the structure-based measures can also be defined as levels of the redundancy and connectivity of providing minimum required water service under system disruptions. In the real world, it is difficult to maximize network redundancy and connectivity with infrastructure due to economic and spatial constraints. The threshold in the structure-based measure can provide investment criteria of a water infrastructure system for satisfying minimum system redundancy and connectivity. It is believed that there is a need to pay more attention to the development of estimating the thresholds in the structure-based measure.
As described earlier, compared with whole system damage, components damage has received relatively less attention in the selected measures. A water infrastructure system includes many components with linear elements (e.g., pipelines and canals) and nodal elements (e.g., reservoirs, tanks, and treatment plants). For the different components, their damage can be individually varied with different disturbances [45] and give different influences on total damage of a whole system according to their contributions. It is considered that the effective way to address components damage would be to use damage fragility functions, which represent the probability of exceeding a given damage level for a given disturbance intensity [45]. However, the fragility functions that have been developed are limited to several disruptive events (e.g., seismic event) and system components (e.g., pipelines, tanks, and canals). Water infrastructure systems are becoming more complicated with various components (e.g., Information and Communications Technologies) and are increasingly threatened by emerging disruptive events (e.g., cyber attacks). Therefore, the fragility functions need to be improved further, considering the diversity of water system components and multiple disturbances. Furthermore, for a disruptive event, multiple components can be failed successively or simultaneously. A failure in a single component may or may not lead to system damage. There can be a variety of failure routes with multiple components. It is believed that a resilience measure needs to consider information on the various failure routes such as occurrence probability of the routes or joint fragility functions for the components in the failure routes.
Meanwhile, consideration of cascading damage in a resilience measure can be crucial in terms of evaluating rapid recovery of a system (third resilience attribute in the review methodology section) as well as absorption of system disruption (second resilience attribute). A water system component, if it fails, may need more rapid recovery to reduce cumulative damage over the recovery period because its failure can lead to more social and economic damage according to interdependency with other critical infrastructure. For example, failures in pipelines delivering water to hospitals require relatively more rapid recovery, comparing to pipelines delivering water to normal residential areas. Therefore, the authors believe that there is a need to address propagated damage to social, economic, and organizational elements from the failure of a water system in a resilience measure.
4.4. Discussion on Rapid Recovery of Disrupted System
As described earlier, the existing resilience measures have paid less attention to the detection time or detection capability to system failures. With the enormous advancement in cyber technologies such as sensors, meters, and controllers, embedding cyber networks into the water infrastructure systems, called water cyber–physical systems, has recently emerged as a popular option to monitor and control system operational conditions [82,83,84]. In this context, there have recently been many efforts to evaluate and improve the detection capability of water systems. For example, Ostfeld et al. [85] compared sensor network designs, which were optimized by various research groups to improve the detection capability for chemical attacks (e.g., deliberate or accidental contamination intrusion to water distribution systems). They have quantitatively evaluated the detection capability of the water distribution systems with hypothetical sensor networks along with multiple design objectives (e.g., minimization of the expected minimum detection time and maximization of the detection likelihood of the contamination intrusion). Taormina and Galelli [86] also looked at the real-time detection algorithm for cyber–physical attacks using deep learning techniques (e.g., AutoEncoder Neural Networks). In order to evaluate the system’s detection capability, they developed detection performance measures considering detection time, detection accuracy, and false alarms to the cyber–physical attacks. The authors believe that these quantitative approaches to evaluating the detection capability will be helpful to evaluate resilience considering detection time or detection capability to system failure. In addition, elapsed time to identify disrupted components or specified failure location also needs to be considered to evaluate the detection capability of systems because it can affect the time to initiate recovery actions for the disrupted systems.
The resilience measure should also provide information on recovery plans with various potential recovery scenarios to be prepared in advance of system disruptions, while it should suggest effective recovery actions under system disruption. However, the results in Table 5 show that fewer than 50% of the selected measures have addressed rapidity of recovery. Furthermore, the resilience measures that estimate recovery time based on a probabilistic approach such as Hashimoto’s measure may show unreliable results when there are few data, lack of long data series, and large variance of data [66,69]. Some of the selected measures, especially for a water distribution network, have estimated the recovery time based on an assumption with a specific period or simple empirical relationship with a single variable such as pipe diameter. Recovery time including failure identification time and repair time can be dependent on various factors such as severity of system damage, budget, labor, recovery scheduling, accessibility and operation of other infrastructures (e.g., transportation) [60]. Different components in failure routes may require different recovery time and scheduling [87]. In addition, joint restoration strategies of water infrastructure with other interconnected infrastructure can affect recovery time [79]. The authors recommend further development of a more reasonable estimation of recovery time with respect to the various affecting factors and potential recovery scenarios.
Meanwhile, social capacity (i.e., local community’s knowledge, social networks, and active participation) can considerably contribute to water infrastructure system resilience [88,89]. For example, the shared information from social communities can be helpful to compensate for and supplement the information from the physical sensors under cyber-attack to smart water systems. A water utility manager may identify failures in a water distribution network quickly from customers’ appeals and complaints. It is therefore recommended to incorporate social capacity into a resilience measure to evaluate the restorative capability of a water infrastructure system.
4.5. Discussion on Adaptation to Changing Disruptions and Their Uncertainty
As shown in Table 5, it was determined that about 60% of the selected measures have dealt with uncertainty of system disruptions directly or by following research. These measures mostly adopted uncertainty scenarios of disruptive events or iterative approaches (e.g., Monte Carlo sampling) to consider the stochastic nature of disturbances with inherent randomness and variability. A water infrastructure system continuously faces complex disturbances from, e.g., climate change, population, economy, other infrastructure, culture, and policies [90]. These disturbances can cause system failure in a form of compound (multiple) disruptions with successive or simultaneous occurrence of two or more disruptive events [81]. Thus, there is a need to incorporate these multifaceted disturbances and their uncertainty scenarios into a resilience measure. Furthermore, system resilience can be characterized by disturbance properties such as types, likelihoods, and intensities. Two water systems that have the same configurations and performance would have different resilience under the different properties of the disturbances [91]. Therefore, it is recommended to incorporate the disturbance properties into a resilience measure.
The disturbances have spatial variations as well as temporal variations [92]. They can cause different impacts on system functionality spatially, especially in water infrastructure systems with a large and extensive scale; thus, the resilience may be varied within sub-sectors of the system. A water infrastructure system can be spatially divided into several sectors. The large variation of resilience for the divided sectors may lead to an overestimation or underestimation of the overall system resilience (average or minimum/maximum value for the resilience in system sectors) in the decision-making process. Nevertheless, a few measures have addressed spatial variation of disruptions or multi-scale resilience. Hence, it is recommended to incorporate the spatial variation of disturbances and resilience into resilience measures. Visualization techniques, which employ high-dimensional data analysis approaches, such as mapping with colors and shapes, are also helpful to represent sub-sectors with low resilience and prioritize their improvements.
Temporal variation of resilience provides essential information in long-term planning of water infrastructure systems. Considering the variable nature of resilience, some researchers such as Jayaram and Srinivasan [34] evaluated time variation of “the snapshot resilience in time”. However, in general, system resilience needs to be evaluated as a “temporal continuum” [60]. In other words, current resilience of a water infrastructure system has been affected by one in the past and will influence resilience in the future. It is therefore believed that there is a need for further development of a resilience measure integrating temporal variation of the snapshot resilience over a long-term period.
Meanwhile, structure-based measures, which analyze system redundancy and connectivity, have not received much attention in resilience measures for water resources systems. Nowadays, diversified and decentralized water resources systems with, e.g., rainwater harvesting, reclaimed water, and desalinated water have been highlighted to enhance water security and water supply reliability as a way toward achieving water sustainability [93,94]. The distributed water resources that are connected to each other can improve resilience since the failure in one of the water resources can be compensated from the functioning of the others. As shown in Porse and Lund [40], the application of the structure-based measures can be extended to analyze networks of natural and man-made water resources (i.e., analysis of redundancy and connectivity of water resources) for resilience measures of diversified and decentralized systems. In this regard, water infrastructure systems include multiple networks with various nodes and links and constitute “Network of networks” with other interdependent infrastructure systems. Thus, there is a need to quantify the complex networks consisting of heterogeneous nodes and links in the structure-based measures.
5. Conclusions
Over the past decade, the concept of resilience and its strategies have gained prominence among researchers and practitioners. As water-related disasters and their uncertainties advance and propagated risk across critical infrastructure systems is uncovered, there has been a number of efforts to develop resilience measures for design, analysis, and decision making. However, improvement is still required to overcome numerous limitations. There is neither a consistently and entirely approved resilience definition for water infrastructure systems, nor a unique measure to evaluate system resilience. Numerous resilience concepts and measures have been defined and verified with consideration of system targets, however none of them fully address the concerns noted herein about comprehensive assessment of resilience for water infrastructure systems. This paper has provided an overview of quantitative approaches to measure water infrastructure system resilience, described gaps in existing approaches, and finally suggested improvements of resilience measures for water infrastructure systems.
After an extensive literature search, 21 resilience measures were selected and reviewed. In this study, the authors focused on water resources systems and water network systems. For the critical review of the selected measures, eleven review criteria were identified based on key resilience attributes discovered through the Axiomatic Design process. The selected measures were analyzed against the criteria. The Axiomatic Design was useful to identify the review criteria logically considering requirements of resilience measures from the pre-defined customer needs (i.e., major resilience attributes) perspective. It is believed that these criteria can be used as a pool of indicators to develop new resilience measures or assess the suitability of existing resilience measures. Existing resilience measures or newly developed measures cannot consider all these criteria. In particular, the selected resilience measures that pay less attention to some of these criteria cannot be stated to be insufficient for the evaluation of system resilience since they have been developed and verified with dependence on their own purpose. However, the authors recommend considering these criteria to improve the existing resilience measures and provide more comprehensive measures.
The selected measures were reviewed according to how they addressed the eleven criteria and a comparison table (Table 5) was developed to examine the inclusion of the criteria over the selected measures. The result showed that the selected measures have not addressed the cascading damage to/from interconnected infrastructure systems and the rapid detection time of system failures. Furthermore, it was found that the measures have paid less attention to the damage of water infrastructure system components and variation of system resilience over a long time period. The resilience measures should provide guidance or information for the decision-making process in order to enhance the water infrastructure system resilience. The authors strongly believe that further improvement of resilience measures is needed to address these issues. From the overview of the selected measures against the review criteria, more improvements of the resilience measures were discussed according to the pre-described resilient system features.
There have been few attempts to review the research on quantitative resilience measures that are specified for a water infrastructure system. The authors hope that the findings and discussions in this study will be used to encourage water-related research and engineering communities in the development of improved, quantitative, and practical resilience measures of water infrastructure systems. The authors also identify the following challenges as future work. First, a water system includes various components such as water and wastewater treatment plants and distributed small-scale water facilities (e.g., rainwater harvesting) as well as water resources and water distribution networks addressed in this study. They are interconnected to each other in a comprehensive perspective of natural and man-made water cycles. The authors therefore believe that more review studies on resilience measures for the aforementioned water infrastructures are needed to establish more consistency, applicability, and interconnectedness. Second, there have been many developments for resilience measures of infrastructure systems in various fields (e.g., see [21,60]). To improve the resilience measures of water infrastructure systems, the authors believe that it is worth investigating the resilience measures in other fields. Third, investment of water infrastructure systems may not be able to focus on a single performance i.e., resilience. As described earlier, resilience of a water infrastructure system should also consider the resilience of interconnected infrastructure systems and dependent communities. Furthermore, there is a need to compare and interconnect with other performance such as water sustainability and vulnerability. It is therefore believed that interconnected or integrated measures addressing the major multiple performance of a water infrastructure system need to be investigated to identify the tradeoffs between them.
Acknowledgments
This research was supported by the Pacific Northwest National Laboratory (PNNL). PNNL is operated for DOE by Battelle Memorial Institute under contract DE-AC05-76RL01830.
Author Contributions
Sangmin Shin and Seven J. Burian planned the review of resilience measures for water infrastructure systems, analyzed gaps in the measures and wrote the paper. Sangmin Shin and Seungyub Lee developed review criteria to evaluate the resilience measures, collected literature addressing quantitative resilience measures and overviewed them. David R. Judi, Erfan Goharian, and Timothy McPherson contributed to the discussion on identifying gaps and improvements in the resilience measures. Masood Parvania contributed to the discussion on improvements of resilience measures for interdependent infrastructure systems.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gheisi, A.; Forsyth, M.; Naser, G. Water distribution systems reliability: A review of research literature. J. Water Resour. Plan. Manag. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Shafiqul Islam, M.; Sadiq, R.; Rodriguez, M.J.; Najjaran, H.; Hoorfar, M. Reliability assessment for water supply systems under uncertainties. J. Water Resour. Plan. Manag. 2013, 140, 468–479. [Google Scholar] [CrossRef]
- Farmani, R.; Walters, G.; Savic, D. Evolutionary multi-objective optimization of the design and operation of water distribution network: Total cost vs. Reliability vs. Water quality. J. Hydroinform. 2006, 8, 165–179. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S. Water pipe network reliability assessment using the dac method. Desalination Water Treat. 2011, 33, 97–106. [Google Scholar] [CrossRef]
- Tsitsifli, S.; Kanakoudis, V.; Bakouros, I. Pipe networks risk assessment based on survival analysis. Water Resour. Manag. 2011, 25, 3729–3746. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tolikas, D. The role of leaks and breaks in water networks: Technical and economical solutions. J. Water Supply Res. Technol. AQUA 2001, 50, 301–311. [Google Scholar]
- Kanakoudis, V.K.; Tolikas, D.K. Performance Indices of a Water Network—Part I: Theory. In Proceedings of the International Conference “Protection and Restoration of the Environment VI”, Skiathos, Greece, 1–5 July 2002; Center for Environmental Systems at Stevens Institute of Technology: Hoboken, NJ, USA, 2002; pp. 257–266. [Google Scholar]
- Kanakoudis, V. Vulnerability based management of water resources systems. J. Hydroinform. 2004, 6, 133–156. [Google Scholar]
- Kanakoudis, V.; Tolikas, D. Assessing the performance level of a water system. Water Air Soil Pollut. Focus 2004, 4, 307–318. [Google Scholar] [CrossRef]
- Blackmore, J.M.; Plant, R.A. Risk and resilience to enhance sustainability with application to urban water systems. J. Water Resour. Plan. Manag. 2008, 134, 224–233. [Google Scholar] [CrossRef]
- Kanakoudis, V.K.; Tolikas, D.K. Performance Indices of a Water Network—PART III: Risk Analysis. In Proceedings of the International Conference “Protection and Restoration of the Environment VI”, Skiathos, Greece, 1–5 July 2002; Center for Environmental Systems at Stevens Institute of Technology: Hoboken, NJ, USA, 2002; pp. 277–285. [Google Scholar]
- Little, R.G. Controlling cascading failure: Understanding the vulnerabilities of interconnected infrastructures. J. Urban Technol. 2002, 9, 109–123. [Google Scholar] [CrossRef]
- Asefa, T.; Clayton, J.; Adams, A.; Anderson, D. Performance evaluation of a water resources system under varying climatic conditions: Reliability, resilience, vulnerability and beyond. J. Hydrol. 2014, 508, 53–65. [Google Scholar] [CrossRef]
- Butler, D.; Farmani, R.; Fu, G.; Ward, S.; Diao, K.; Astaraie-Imani, M. A new approach to urban water management: Safe and sure. Procedia Eng. 2014, 89, 347–354. [Google Scholar] [CrossRef]
- Amarasinghe, P.; Liu, A.; Egodawatta, P.; Barnes, P.; McGree, J.; Goonetilleke, A. Quantitative assessment of resilience of a water supply system under rainfall reduction due to climate change. J. Hydrol. 2016, 540, 1043–1052. [Google Scholar] [CrossRef]
- Tsitsifli, S.; Kanakoudis, V. Predicting the behavior of a pipe network using the “critical z-score” as its performance indicator. Desalination 2010, 250, 258–265. [Google Scholar] [CrossRef]
- Li, Y.; Lence, B.J. Estimating resilience for water resources systems. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Zhuang, B.; Lansey, K.; Kang, D. Resilience/availability analysis of municipal water distribution system incorporating adaptive pump operation. J. Hydraul. Eng. 2012, 139, 527–537. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Tinebra, A.; Renschler, C.; Fragiadakis, M. New resilience index for urban water distribution networks. J. Struct. Eng. 2015, 142, C4015014. [Google Scholar] [CrossRef]
- Kanakoudis, V.K.; Tolikas, D.K. Managing Water Resources and Supply Systems: Fail-Safe vs. Safe-Fail. In Proceedings of the EWRA 5th International Conference “Water Resources Management in the Era of Transition”, Athens, Greece, 4–8 September 2002; Symetria Publications: Athens, Greece, 2002; pp. 194–204. [Google Scholar]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Klise, K.A.; Murray, R.; Walker, L.T.N. Systems Measures of Water Distribution System Resilience; Sandia National Laboratories (SNL-NM): Albuquerque, NM, USA, 2015.
- Moy, W.S.; Cohon, J.L.; ReVelle, C.S. A programming model for analysis of the reliability, resilience, and vulnerability of a water supply reservoir. Water Resour. Res. 1986, 22, 489–498. [Google Scholar] [CrossRef]
- Wang, C.; Blackmore, J.M. Resilience concepts for water resource systems. J. Water Resour. Plan. Manag. 2009, 135, 528–536. [Google Scholar] [CrossRef]
- Butler, D.; Ward, S.; Sweetapple, C.; Astaraie-Imani, M.; Diao, K.; Farmani, R.; Fu, G. Reliable, resilient and sustainable water management: The safe & sure approach. Glob. Chall. 2016, 1, 63–77. [Google Scholar] [CrossRef]
- Sharifi, A.; Yamagata, Y. On the suitability of assessment tools for guiding communities towards disaster resilience. Int. J. Disaster Risk Reduct. 2016, 18, 115–124. [Google Scholar] [CrossRef]
- Matthews, J.C. Disaster resilience of critical water infrastructure systems. J. Struct. Eng. 2015, 142, C6015001. [Google Scholar] [CrossRef]
- Reca, J.; Martinez, J.; Banos, R.; Gil, C. Optimal design of gravity-fed looped water distribution networks considering the resilience index. J. Water Resour. Plan. Manag. 2008, 134, 234–238. [Google Scholar] [CrossRef]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Vogel, R.M.; Bolognese, R.A. Storage-reliability-resilience-yield relations for over-year water supply systems. Water Resour. Res. 1995, 31, 645–654. [Google Scholar] [CrossRef]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.-S. Multiobjective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Kjeldsen, T.R.; Rosbjerg, D. Choice of reliability, resilience and vulnerability estimators for risk assessments of water resources systems/choix d’estimateurs de fiabilité, de résilience et de vulnérabilité pour les analyses de risque de systèmes de ressources en eau. Hydrol. Sci. J. 2004, 49. [Google Scholar] [CrossRef]
- Jayaram, N.; Srinivasan, K. Performance-based optimal design and rehabilitation of water distribution networks using life cycle costing. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Liu, D.; Chen, X.; Nakato, T. Resilience assessment of water resources system. Water Resour. Manag. 2012, 26, 3743–3755. [Google Scholar] [CrossRef]
- Mehran, A.; Mazdiyasni, O.; AghaKouchak, A. A hybrid framework for assessing socioeconomic drought: Linking climate variability, local resilience, and demand. J. Geophys. Res. Atmos. 2015, 120, 7520–7533. [Google Scholar] [CrossRef]
- Herrera, M.; Abraham, E.; Stoianov, I. Graph-theoretic surrogate measures for analysing the resilience of water distribution networks. Procedia Eng. 2015, 119, 1241–1248. [Google Scholar] [CrossRef]
- Wright, R.; Herrera, M.; Parpas, P.; Stoianov, I. Hydraulic resilience index for the critical link analysis of multi-feed water distribution networks. Procedia Eng. 2015, 119, 1249–1258. [Google Scholar] [CrossRef]
- Porse, E.; Lund, J. Network analysis and visualizations of water resources infrastructure in California: Linking connectivity and resilience. J. Water Resour. Plan. Manag. 2015, 142, 04015041. [Google Scholar] [CrossRef]
- Pandit, A.; Crittenden, J.C. Index of network resilience for urban water distribution systems. Int. J. Crit. Infrastruct. 2016, 12, 120–142. [Google Scholar] [CrossRef]
- Herrera, M.; Abraham, E.; Stoianov, I. A graph-theoretic framework for assessing the resilience of sectorised water distribution networks. Water Resour. Manag. 2016, 30, 1685–1699. [Google Scholar] [CrossRef]
- Qi, M.; Feng, M.; Sun, T.; Yang, W. Resilience changes in watershed systems: A new perspective to quantify long-term hydrological shifts under perturbations. J. Hydrol. 2016, 539, 281–289. [Google Scholar] [CrossRef]
- Farahmandfar, Z.; Piratla, K.R.; Andrus, R.D. Resilience evaluation of water supply networks against seismic hazards. J. Pipeline Syst. Eng. Pract. 2016, 8, 04016014. [Google Scholar] [CrossRef]
- Chmielewski, H.; Guidotti, R.; McAllister, T.; Gardoni, P. Response of Water Systems under Extreme Events: A Comprehensive Approach to Modeling Water System Resilience. In Proceedings of the World Environmental and Water Resources Congress 2016, West Palm Beach, FL, USA, 22–26 May 2016; American Society of Civil Engineers: Reston, VA, USA, 2016; pp. 475–486. [Google Scholar]
- Kulak, O.; Cebi, S.; Kahraman, C. Applications of axiomatic design principles: A literature review. Expert Syst. Appl. 2010, 37, 6705–6717. [Google Scholar] [CrossRef]
- Suh, N.P. Axiomatic Design: Advances and Applications (the Oxford Series on Advanced Manufacturing); Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Guenov, M.D.; Barker, S.G. Application of axiomatic design and design structure matrix to the decomposition of engineering systems. Syst. Eng. 2005, 8, 29–40. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Manyena, S.B. The concept of resilience revisited. Disasters 2006, 30, 434–450. [Google Scholar] [CrossRef] [PubMed]
- Mayunga, J.S. Understanding and Applying the Concept of Community Disaster Resilience: A Capital-Based Approach. Available online: https://www.u-cursos.cl/usuario/3b514b53bcb4025aaf9a6781047e4a66/mi_blog/r/11._Joseph_S._Mayunga.pdf (accessed on 7 February 2018).
- Meerow, S.; Newell, J.P.; Stults, M. Defining urban resilience: A review. Landsc. Urban Plan. 2016, 147, 38–49. [Google Scholar] [CrossRef]
- Candelieri, A.; Soldi, D.; Archetti, F. Network analysis for resilience evaluation in water distribution networks. Environ. Eng. Manag. J. 2015, 14, 1261–1270. [Google Scholar]
- Nan, C.; Sansavini, G. A quantitative method for assessing resilience of interdependent infrastructures. Reliab. Eng. Syst. Saf. 2017, 157, 35–53. [Google Scholar] [CrossRef]
- Francis, R.; Bekera, B. A metric and frameworks for resilience analysis of engineered and infrastructure systems. Reliab. Eng. Syst. Saf. 2014, 121, 90–103. [Google Scholar] [CrossRef]
- Sharifi, A.; Yamagata, Y. Principles and criteria for assessing urban energy resilience: A literature review. Renew. Sustain. Energy Rev. 2016, 60, 1654–1677. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Dinh, L.T.; Pasman, H.; Gao, X.; Mannan, M.S. Resilience engineering of industrial processes: Principles and contributing factors. J. Loss Prev. Process Ind. 2012, 25, 233–241. [Google Scholar] [CrossRef]
- Sharifi, A. A critical review of selected tools for assessing community resilience. Ecol. Indic. 2016, 69, 629–647. [Google Scholar] [CrossRef]
- Kallaos, J.; Mainguy, G.; Wyckmans, A. Considering resilience: Steps towards an assessment framework. TeMA J. Land Use Mobil. Environ. 2014, 7, 5–28. [Google Scholar]
- Suh, N.P. Complexity: Theory and Applications; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Fowler, H.; Kilsby, C.; O’Connell, P. Modeling the impacts of climatic change and variability on the reliability, resilience, and vulnerability of a water resource system. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Srdjevic, B.; Medeiros, Y.; Faria, A. An objective multi-criteria evaluation of water management scenarios. Water Resour. Manag. 2004, 18, 35–54. [Google Scholar] [CrossRef]
- Chanda, K.; Maity, R.; Sharma, A.; Mehrotra, R. Spatiotemporal variation of long-term drought propensity through reliability-resilience-vulnerability based drought management index. Water Resour. Res. 2014, 50, 7662–7676. [Google Scholar] [CrossRef]
- Jain, S.; Bhunya, P. Reliability, resilience and vulnerability of a multipurpose storage reservoir/confiance, résilience et vulnérabilité d’un barrage multi-objectifs. Hydrol. Sci. J. 2008, 53, 434–447. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Dakos, V.; van Nes, E.H.; Donangelo, R.; Fort, H.; Scheffer, M. Spatial correlation as leading indicator of catastrophic shifts. Theor. Ecol. 2010, 3, 163–174. [Google Scholar] [CrossRef]
- Greco, R.; Di Nardo, A.; Santonastaso, G. Resilience and entropy as indices of robustness of water distribution networks. J. Hydroinform. 2012, 14, 761–771. [Google Scholar] [CrossRef]
- Tsakiris, G.; Spiliotis, M. Applying resilience indices for assessing the reliability of water distribution systems. Water Util. J. 2012, 3, 19–27. [Google Scholar]
- Creaco, E.; Franchini, M.; Todini, E. Generalized resilience and failure indices for use with pressure-driven modeling and leakage. J. Water Resour. Plan. Manag. 2016, 142, 04016019. [Google Scholar] [CrossRef]
- Liu, H.; Savić, D.A.; Kapelan, Z.; Creaco, E.; Yuan, Y. Reliability surrogate measures for water distribution system design: Comparative analysis. J. Water Resour. Plan. Manag. 2016, 143, 04016072. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Todini, E. The combined use of resilience and loop diameter uniformity as a good indirect measure of network reliability. Urban Water J. 2016, 13, 167–181. [Google Scholar] [CrossRef]
- Raad, D.; Sinske, A.; Van Vuuren, J. Comparison of four reliability surrogate measures for water distribution systems design. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Bi, W.; Dandy, G.C.; Maier, H.R. Use of domain knowledge to increase the convergence rate of evolutionary algorithms for optimizing the cost and resilience of water distribution systems. J. Water Resour. Plan. Manag. 2016, 142, 04016027. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Arunkumar, R. Quantification of resilience to water scarcity, a dynamic measure in time and space. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 13–17. [Google Scholar] [CrossRef]
- Soldi, D.; Candelieri, A.; Archetti, F. Resilience and vulnerability in urban water distribution networks through network theory and hydraulic simulation. Procedia Eng. 2015, 119, 1259–1268. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Santonastaso, G.F.; Tzatchkov, V.; Varela, J.M.R. Economic and energy criteria for district meter areas design of water distribution networks. Water 2017, 9, 463. [Google Scholar] [CrossRef]
- Ouyang, M.; Wang, Z. Resilience assessment of interdependent infrastructure systems: With a focus on joint restoration modeling and analysis. Reliab. Eng. Syst. Saf. 2015, 141, 74–82. [Google Scholar] [CrossRef]
- Eusgeld, I.; Nan, C.; Dietz, S. “System-of-systems” approach for interdependent critical infrastructures. Reliab. Eng. Syst. Saf. 2011, 96, 679–686. [Google Scholar] [CrossRef]
- Diao, K.; Sweetapple, C.; Farmani, R.; Fu, G.; Ward, S.; Butler, D. Global resilience analysis of water distribution systems. Water Res. 2016, 106, 383–393. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.M.; Panguluri, S.; Nelson, T.D.; Wyman, R.P. Protecting drinking water utilities from cyberthreats. J. Am. Water Works Assoc. 2017, 109, 50–58. [Google Scholar] [CrossRef]
- Taormina, R.; Galelli, S.; Tippenhauer, N.O.; Salomons, E.; Ostfeld, A. Characterizing cyber-physical attacks on water distribution systems. J. Water Resour. Plan. Manag. 2017, 143, 04017009. [Google Scholar] [CrossRef]
- Wang, Z.; Song, H.; Watkins, D.W.; Ong, K.G.; Xue, P.; Yang, Q.; Shi, X. Cyber-physical systems for water sustainability: Challenges and opportunities. IEEE Commun. Mag. 2015, 53, 216–222. [Google Scholar] [CrossRef]
- Ostfeld, A.; Uber, J.G.; Salomons, E.; Berry, J.W.; Hart, W.E.; Phillips, C.A.; Watson, J.-P.; Dorini, G.; Jonkergouw, P.; Kapelan, Z. The battle of the water sensor networks (bwsn): A design challenge for engineers and algorithms. J. Water Resour. Plan. Manag. 2008, 134, 556–568. [Google Scholar] [CrossRef]
- Taormina, R.; Galelli, S. Real-Time Detection of Cyber-Physical Attacks on Water Distribution Systems Using Deep Learning. In Proceedings of the World Environmental and Water Resources Congress 2017, Sacramento, CA, USA, 21–25 May 2017; American Society of Civil Engineers: Reston, VA, USA, 2017; pp. 469–479. [Google Scholar]
- Hu, Z.; Mahadevan, S. Resilience assessment based on time-dependent system reliability analysis. J. Mech. Des. 2016, 138, 111404. [Google Scholar] [CrossRef]
- Pahl-Wostl, C.; Craps, M.; Dewulf, A.; Mostert, E.; Tabara, D.; Taillieu, T. Social learning and water resources management. Ecol. Soc. 2007, 12. [Google Scholar] [CrossRef]
- Ward, S.; Butler, D. Rainwater harvesting and social networks: Visualising interactions for niche governance, resilience and sustainability. Water 2016, 8, 526. [Google Scholar] [CrossRef]
- Gallopín, G.C. Five stylized scenarios. In Global Water Futures 2050; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2012. [Google Scholar]
- Haimes, Y.Y. On the definition of resilience in systems. Risk Anal. 2009, 29, 498–501. [Google Scholar] [CrossRef] [PubMed]
- Amarasinghe, U.; Sharma, B.R.; Aloysius, N.; Scott, C.; Smakhtin, V.; De Fraiture, C. Spatial Variation in Water Supply and Demand Across River Basins of India; IWMI (International Water Management Institute): Colombo, Sri Lanka, 2005; Volume 83. [Google Scholar]
- Sapkota, M.; Arora, M.; Malano, H.; Moglia, M.; Sharma, A.; George, B.; Pamminger, F. An overview of hybrid water supply systems in the context of urban water management: Challenges and opportunities. Water 2014, 7, 153–174. [Google Scholar] [CrossRef]
- Ma, X.C.; Xue, X.; González-Mejía, A.; Garland, J.; Cashdollar, J. Sustainable water systems for the city of tomorrow—A conceptual framework. Sustainability 2015, 7, 12071–12105. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).