Abstract
The concentration (using a lesser amount of water) of domestic slurry promotes resource recovery (nutrients and biomass) while saving water. This article is aimed at developing numerical methods to support engineering processes such as the design and implementation of sewerage for concentrated domestic slurry. The current industrial standard for computational fluid dynamics-based analyses of turbulent flows is Reynolds-averaged Navier–Stokes (RANS) modelling. This is assisted by the wall function approach proposed by Launder and Spalding, which permits the use of under-refined grids near wall boundaries while simulating a wall-bounded flow. Most RANS models combined with wall functions have been successfully validated for turbulent flows of Newtonian fluids. However, our experiments suggest that concentrated domestic slurry shows a Herschel–Bulkley-type non-Newtonian behaviour. Attempts have been made to derive wall functions and turbulence closures for non-Newtonian fluids; however, the resulting laws or equations are either inconsistent across experiments or lack relevant experimental support. Pertinent to this study, laws or equations reported in literature are restricted to a class of non-Newtonian fluids called power law fluids, which, as compared to Herschel–Bulkley fluids, yield at any amount of applied stress. An equivalent law for Herschel–Bulkley fluids that require a minimum-yield stress to flow is yet to be reported in literature. This article presents a theoretically derived (with necessary approximations) law of the wall for Herschel–Bulkley fluids and implements it in a RANS solver using a specified shear approach. This results in a more accurate prediction of the wall shear stress experienced by a circular pipe with a turbulent Herschel–Bulkley fluid flowing through it. The numerical results are compared against data from our experiments and those reported in literature for a range of Reynolds numbers and rheological parameters that are relevant to the prediction of pressure losses in a sewerage transporting non-Newtonian domestic slurry. Nonetheless, the application of this boundary condition could be extended to areas such as chemical and food engineering, wherein turbulent non-Newtonian flows can be found.
1. Introduction
This research is aimed at experimentally and numerically supporting the design of a novel sanitation system for urban areas with emphasis on the reduction of water usage, the improved recovery of nutrients and biomass and the efficient transport of domestic slurry. The experiments provide information on the rheology of the slurry and the pressure losses it brings about (due to wall friction) while flowing (turbulent) through circular pipes and bends. Using our experiments, we wish to develop a suitable simulation methodology to enable industrial studies and applications such as the design of sewerage carrying concentrated domestic slurry. The scope of this article is thus restricted to exploring the potential of the current state-of-the-art in industrial computational fluid dynamics for modelling and not the theoretical study of the turbulent properties of domestic slurry.
We used a clay-based slurry for the experiments, which was confirmed to be rheologically similar to concentrated domestic slurry. Similarly to many industrial slurries (clay, coal, iron oxide, etc.), the experimental slurry also departs from Newtonian behaviour [1]. A Newtonian fluid is a fluid for which the shear stress and the strain rate are related linearly through
In Equation (1), is the molecular viscosity that depends on temperature and pressure but not the flow; is the stress tensor, whereas is the strain rate tensor, defined as
Variables representing tensors are printed in bold, whereas vectors are underlined. Above, is the velocity vector and is the velocity gradient tensor or . In the fields of rheology and non-Newtonian fluid mechanics, it is common practice to replace as follows:
We use from now on to conform with rheological practices.
The stress due to viscosity in any fluid that deviates from Newtonian behaviour can be defined as
where the function is not directly related to but to its second invariant , the shear rate; and are related through
is the Frobenius product of and tr is the trace of a square matrix, which is the sum of its diagonal elements. T is the transpose of a matrix.
In Equation (4), is the apparent viscosity that, unlike the molecular viscosity, depends not only on the fluid’s temperature and pressure but also on the flow conditions such as the shear rate and even the duration of the shear [1].
1.1. Herschel–Bulkley Fluids
For succinctness, this article does not provide a detailed description of non-Newtonian fluids and their properties, for which the reader is referred to Chabbra and Richardson [1]. Nonetheless, a rheogram that plots the relation between the shear stress and the shear rate for various non-Newtonian fluids is shown in Figure 1.
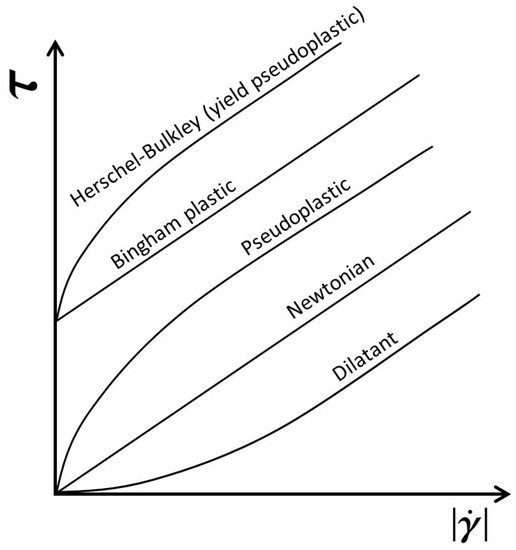
Figure 1.
Rheograms of time-independent flow behaviour (adapted from [1]).
One notices that a Herschel–Bulkley fluid displays shear-thinning (pseudoplastic behaviour), which is the reduction in the apparent viscosity with increasing shear rate. Further, Herschel–Bulkley fluids require a minimum shear stress before they flow as a fluid does. This minimum stress is called the yield stress, and hence such fluids are also called yield pseudoplastic fluids. Herschel and Bulkley [2] introduced a mathematical definition for Herschel–Bulkley fluids:
where is the yield stress, m is the fluid-consistency index and n is the fluid-behaviour index (all are standard terms as used in Chabbra and Richardson [1]). Further, all terms in Equation (7) are scalars, with being the shear rate and being the second invariant of the stress tensor . Equation (7) is only valid when . If , (see Figure 1). In three dimensions with full tensor notation [3], Equation (7) reads
If a Herschel–Bulkley fluid undergoes a laminar flow through a circular pipe, one can simply calculate the velocity profile and shear stress through the balance between the shear stress and the pressure gradient across the pipe. From Figure 2, one can write
where p is the pressure; is the shear stress against the direction of the flow; R and D are the radius and the diameter, respectively; L is the length of the section under consideration; r is the radial distance from the pipe’s centreline; and is the axial velocity at a radial distance r from the centreline. Further, the average flow velocity V is defined as
where the volumetric flow rate Q is
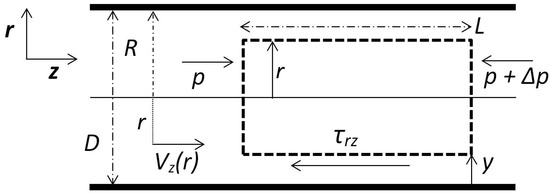
Figure 2.
A schematic of a circular horizontal pipe.
Using Equations (7), (9) and (11), one obtains an implicit relation between , r and the wall shear stress [4]:
where .
(The readers are referred to Chabbra and Richardson [1], Govier and Aziz [5] and Bird et al. [6,7] for details and relevant literature. Heywood and Cheng [8] provide a review of known expressions for the laminar flow of Herschel–Bulkley fluids through circular horizontal pipes.)
Akin to Equation (12), expressions that relate the wall stress to the flow velocity for the turbulent flow of Herschel–Bulkley fluids have also been proposed. Heywood and Cheng [8] mention that such expressions are correlations of experimental data and are not fully theoretical. Two such semi-theoretical expressions were proposed by Torrance [9] and Hanks [10]. Further, Wilson and Thomas [11] proposed a correlation based on the relation between the dissipative small-scale turbulent eddies and the thickness of the viscous boundary layer. This was extended to Herschel–Bulkley fluids [12] and compared against experiments by Slatter [13]. Slatter [13] reported that the correlation by Thomas and Wilson [12] is accurate in the early turbulent regime but diverges when the shear stress (or the flow velocity) increases, leading to more turbulence. It is also noted that semi-theoretical models are sensitive to the rheological properties of the fluids.
1.2. Computational Fluid Dynamics (CFD) and Non-Newtonian Fluids
With the development of computational resources, analyses of many industrial flows are being increasingly made as numerical computations of the Navier–Stokes (NS) equations. However, turbulent flows display a range of length and time scales; resolving all of these is not feasible at high Reynolds numbers [14]. Therefore, these scales are mathematically altered (a process called decomposition) to reduce the range of length and time scales to a manageable quantity while ensuring that the decomposed scales represent the macroscopic properties of the flow under consideration.
One such approach is called Reynolds-averaged Navier–Stokes (RANS) modelling, in which the turbulent scales are ensemble-averaged (an average over many instances of the flow) to obtain a time-independent representation of the flow [15]. It is assumed (with most RANS models) that the flow under consideration is fully turbulent. The following equations in indicial notation result from the Reynolds-decomposition and time-averaging of the NS equations for an incompressible Newtonian fluid in the absence of body forces.
In the above equations, the velocity has been decomposed as : the sum of an ensemble-average, , and a quantity that fluctuates across instances, . One now solves the above equations to obtain an ensemble-averaged velocity and pressure field, and . If the molecular viscosity is not constant but is a function of the shear rate, the Reynolds decomposition of the diffusive term will result in an ensemble-averaged and a fluctuating value of the effective viscosity [16]. Upon including this term, Equation (14) reads
where is the ensemble-averaged effective viscosity of the non-Newtonian fluid under study.
To solve Equation (14), one needs a closure for , known as the Reynolds stress. RANS methods model in terms of the known velocity field (the ensemble-averaged in this case) to close Equations (13) and (14). Wilcox [17] presents a detailed description of RANS models, of which the – [18] and the Reynolds stress model (RSM; see Launder et al. [19] and references therein) are used in this article. For brevity, the readers are requested to refer to Wilcox [17] and the references therein for details.
On the other hand, to solve Equation (15), one also needs a closure for the term mentioned as the fluctuating-viscosity stress tensor in literature [20,21]. Known closures include those proposed by Pinho et al. [21] and Leighton et al. [22]; the latter was based on a priori direct numerical simulation. However, the validation of such closures is restricted to very low Reynolds numbers, as direct numerical simulation is computationally intensive [23]. In fact, higher-Reynolds-number-based experimental (or numerical) studies that could be used to ascertain the contribution of the fluctuating viscosity tensor to RANS dynamics and validate appropriate closures are hitherto unavailable, thus limiting the application of such closures to theoretical studies. Following an appropriate definition of the Reynolds number used by Rudman and Blackburn [23] for their numerical studies, only the lowest Reynolds numbers observed in our experiments are perhaps comparable with studies used to validate the proposed closure.
Further, the closure proposed by Gavrilov and Rudyak [16] assumes that the fluctuations in effective viscosity () are smaller than the ensemble-averaged viscosity. In a turbulent flow, the turbulent viscosity brings about a higher amount of dissipation as compared to the molecular (or effective) viscosity [24]. Under such circumstances, the fluctuations themselves, if considered small, may not affect the dissipation of energy to a great extent and could possibly be ignored.
On the contrary, there is relatively more literature on the usage of RANS models (without a closure for the fluctuating viscosity) for the simulation of various types of non-Newtonian fluids, of which Malin [25,26,27] is amongst the first; – and – [24] were used. Both models were noted to deliver similar results despite different formulations and simulation methodologies. It is fair to mention that the model was not specifically calibrated for non-Newtonian fluids but was used with model constants determined for Newtonian fluids; however, the turbulent viscosity was numerically dampened near the walls with a suitable function. For Herschel–Bulkley fluids, at high Reynolds numbers (∼), the simulated predictions converged onto values determined by a semi-empirical equation proposed by Dodge and Metzner [28] (see Section 1.3).
Similarly, Bartosik [29] numerically modified the eddy viscosity to account for non-Newtonian behaviour (viscous effects) near the walls, where it is more dominant than turbulence. Bartosik [30] used the modifications to simulate experiments conducted by Slatter [13] on Herschel–Bulkley fluids. It was noted that the concerned modification improves the accuracy of the – model even when the yield stresses are high ( Pa or more).
The above-mentioned numerical studies have experimental counterparts that support a mathematical modification of the different behaviour of non-Newtonian fluids near walls [28,31,32] (see Skelland [4] for a detailed overview). However, the modifications these studies suggested are applicable to power-law fluids (see Figure 1).
Other computational fluid dynamics (CFD)-based analyses include those of Singh et al. [33] (and references therein) and Gnambode et al. [34], which are based on more computationally expensive techniques, namely, direct numerical simulation and large eddy simulation, respectively. Apart from these, there is literature relevant to fields such as biofluid mechanics, anaerobic digestors, and so forth, concerning the use of standard RANS models for non-Newtonian fluid flows.
1.3. Wall-Bounded Flows
This work concerns the wall-bounded turbulent flow of Herschel–Bulkley fluids. For any fluid, as the Reynolds number of the flow increases, the effects of viscosity diminish [35]. Nonetheless, in the presence of walls, all flows slow down to zero velocity at the wall (the no-slip condition), and in doing so, even a turbulent flow passes through a laminar region near the wall [36]. Therefore, RANS models such as the – that are meant for the analysis of fully turbulent flows require a correction to model the transition into a laminar regime and ultimately zero velocity.
Such empirical corrections have permitted the use of RANS models for a range of industrial applications. This article examines one possible correction that may enable the application of RANS models for the simulation of Herschel–Bulkley fluids. The effects of the fluctuating viscosity tensor have been ignored in light of the fact that the Reynolds number in this study was relatively high and little experimental support is available to verify this effect. Another alternative would also be a modification for the model constants of various RANS models. However, this would also require detailed experimental data such as velocity fields and their fluctuations in time, for fully turbulent flows of non-Newtonian fluids (at Reynolds numbers higher than those reported in existing literature).
We therefore work on a simple modification of the behaviour near walls, where turbulence diminishes (as done by Malin [27], Bartosik [30] for high Reynolds numbers) as an alternative numerical model. We would like to mention again that our purpose is to explore suitable modelling techniques and not to formulate a theoretical basis for the turbulence of non-Newtonian fluids.
To begin with, Equation (16) defines the wall function developed by Launder and Spalding [18] on the basis of the velocity profile of a turbulent Newtonian fluid in a smooth tube proposed by Prandtl [37,38], which was later extended to the universal law of the wall [39]. For a Newtonian fluid,
where is the von Kármán constant and for a smooth wall. Therefore,
Equation (16) can also be expressed as
by merging the constant in Equation (16) with . is another constant that equals . Equation (16) is not valid in the immediate vicinity of the wall but in the regions close to the wall where the flow is still turbulent. Immediately next to wall (see Figure 3),
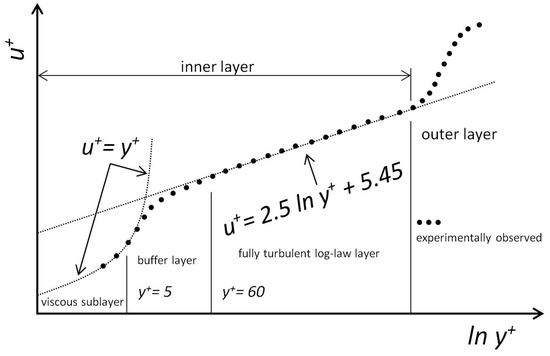
Figure 3.
The law of the wall (adapted from ANSYS [40]).
The terms and are used to non-dimensionalise the distance from a wall (y) and the velocity at that distance parallel to the wall (u).
1.4. Non-Newtonian Wall Functions
Equivalents of Equation (16) for non-Newtonian fluids have also been proposed. Dodge and Metzner [28] used dimensional analysis and experimental data to propose an equation similar to Equation (16) for a power-law fluid () but with different coefficients.
where
and
Clapp [31] (see Skelland [4] for details and more references) used Prandtl’s concept of mixing length [37,38] to derive an expression for the turbulent region of a wall-bounded flow of a power-law fluid. Clapp’s equation has a form similar to that of Equation (23) but with the following experimentally determined constants:
The experimental data reported by Clapp [31] deviated by no more than from Equations (23), (26) and (27) for . It is important to note that the in the above equations is not the same as in Equation (20), but is
Other expressions for the velocity profile of wall-bounded non-Newtonian flows have also been proposed. Skelland [4] provides a detailed summary of such expressions. Additionally, Sawko [32] compares the above-mentioned wall models and a revised wall modelling approach (developed by Sawko [32]) based on analytical and experimental analyses of turbulent boundary layers.
1.5. Approach
The preceding section mentions the few strategies that exist for the modelling of wall-bounded non-Newtonian flows, although only those applicable to power-law fluids that yield to a non-zero stress. In other words, expressions such as Equations (23)–(25) have not yet been proposed or tested for yield viscoplastic and yield pseudoplastic fluids, of which the latter concerns us here.
This section elucidates the derivation and subsequent validation of an expression that could be used for modelling domestic slurries with Herschel–Bulkley rheology in a turbulent flow regime within a circular horizontal pipe. The approach is similar to that followed by Clapp [31], which is based on Prandtl’s concept of mixing length [37,38] but includes the influence of yield stress as well. It is fair to mention that the proposed approach is based on certain approximations and that the intention is not to propose an exact and theoretically correct expression for the turbulent behaviour of Herschel–Bulkley fluids.
This article is divided into the following sections. Section 2 summarises the derivation and describes the NS solver and the related numerical challenges. Section 3 presents an overview of the experimental test cases considered in this article. Section 4 contains the results obtained from numerical analyses on the test cases mentioned in Section 3, and Section 5 reflects the conclusions and recommendations.
2. Methodology
This section provides details on the solver, the RANS models and numerical methods used for this article. This is followed by a derivation for the wall modification for Herschel–Bulkley fluids.
2.1. Solver and Numerics
ANSYS FLUENT [40], which is based on a finite-volume method, has been used to solve the RANS Equations (13) and (14) mentioned in Section 1.2. The spatial discretisation was done with a second-order upwind scheme to ensure numerical stability. The pressure was resolved with second-order accuracy but was decoupled from the velocity field with the semi-implicit method for pressure-linked equations (SIMPLE).
Amongst the RANS models, – was used with the standard model constants, whereas the RSM was used in two different configurations. (Please refer to ANSYS [40] for details. We did not use the – model because of the associated computational costs.)
- The Reynolds stresses in the wall-adjacent cells are calculated explicitly in terms of the wall shear stress. This setting shall be referred to as RSM1.
- A transport equation for is solved to obtain the Reynolds stresses in the cells adjacent to the wall, which shall be quoted as RSM2.
To implement the constitutive relation Equation (7), FLUENT uses a biviscosity model similar to that proposed by Tanner and Milthorpe [41] (see Mitsoulis [42] for a summary of similar approaches) [40]. This approach prevents numerical instability arising from the yield stress at zero strain.
2.2. Wall Modelling: Specified Shear Approach
The following equations describe the wall model implemented in ANSYS FLUENT (from ANSYS [40]), which is based on Launder and Spalding [18]:
where the subscript 1 refers to the first grid point next to a wall; is the turbulence kinetic energy (TKE) and is an empirical constant equal to , as mentioned in Section 1.3; and are similar to and (see Equations (20)–(22)) but with the wall shear expressed in terms of turbulence parameters.
As per ANSYS [40], the quantities and are nearly equal in equilibrium boundary layers (verified through post-processing).
Once a flow field is initialised, Equation (31) is used to obtain , after which is calculated from Equation (29) and then used to obtain from Equation (30). This is used in the RANS equations to obtain a new velocity field, following which the process is repeated until a converged solution is obtained. We consider a solution as converged once the iterative residuals for continuity, velocity, and are below .
2.2.1. An Appropriate Reynolds Number
To categorise the flow analysed in this article, one requires a suitable Reynolds number. Because the viscosity of a non-Newtonian fluid changes with the local flow conditions, one cannot use the standard Reynolds number. Instead, Rudman et al. [43] have proposed a Reynolds number based on the wall effective viscosity defined below. This viscosity can only be determined once the wall shear stress is known, and hence it serves only as a post-experimental (numerical) parameter.
We name this apparent viscosity . Then using Equation (7), replacing with the wall stress and expressing as (see Figure 2 for details), one obtains
Rudman et al. [43] further used this to define a Reynolds number as
where V is the average flow velocity and D is the pipe diameter. Rudman et al. [43] mentioned that this definition of the Reynolds number was more pertinent to the analysis of wall-bounded flows as it reflected the behaviour of Herschel–Bulkley fluids in the near-wall region, as compared to the more commonly used Metzner–Reed Reynolds numbers [44]. is used while presenting the results of the simulations.
2.2.2. Specified Wall Shear Based on Prandtl’s Mixing Length
Following the approach put forth by Launder and Spalding [18], we derive a relation between the wall shear stress and the velocity near a wall for a Herschel–Bulkley fluid. The derivation is based on Prandtl’s theory [37,38]. The comprehensive book by Skelland [4] presents a clear derivation for the original law of the wall for a Newtonian fluid.
Prandtl began by describing the overall shear stress (see Figure 2) at any distance y from the wall as the sum of laminar and turbulent stresses:
Prandtl’s concept of mixing length (proposed originally for a Newtonian fluid) expresses as
The total stress can be written in terms of using Equation (9):
Replacing with Equation (7),
Near the wall, one may make certain assumptions regarding the laminar and turbulent stresses, as is usually done for Newtonian fluids and is done for non-Newtonian fluids by Dodge and Metzner [28] and Clapp [31]. Firstly, . Secondly, immediately near the wall within the laminar sublayer and up to the transition zone, the laminar stress is more than the turbulent stress (as also done by Prandtl). Therefore,
From Equation (39),
Integrating with respect to y and using the boundary condition at , one obtains
If , Equation (41) reduces to that proposed by Clapp [31] for a power-law fluid. A further reduces the equation to that for a Newtonian fluid (law of the wall, Prandtl).
In contrast to the laminar region, within the turbulent core but still near the wall, the turbulence-related stresses outweigh the laminar stresses.
Although the laminar stress is low, in Equation (42) is retained to include in this analysis, which is also present in Equation (33).
Upon integration with respect to y,
where is the constant of integration. Further mathematical modifications to the logarithmic term lead to
In the previous step, the term comprising and is absorbed inside . As illustrated in Skelland [4] for a Newtonian fluid, one may express the constant in terms of other known terms (and the unknown ).
If and , Equation (47) reduces to the law of the wall or Equation (18) with and having their Newtonian definitions. This also implies that one must set in Equation (47) as . Doing so, one finally obtains
Equation (48) is referred to as .
While deriving , it was assumed in the step corresponding to Equation (42) that retaining does not alter the assumption that the laminar stresses are much lower than the turbulent stresses in the core turbulent region. However, this also implies that must itself be low as compared to .
Before discussing the effect of neglecting the magnitude of the yield stress, one must understand the flow regime of a Herschel–Bulkley fluid inside a smooth pipe. Figure 4 depicts the velocity profile of a Herschel–Bulkley fluid in a laminar flow.
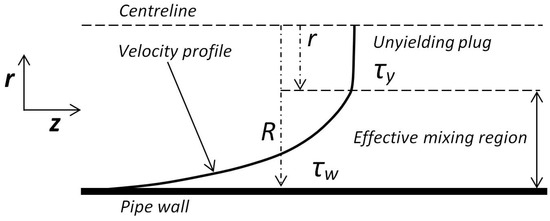
Figure 4.
The effective mixing region in a pipe carrying a Herschel–Bulkley fluid with yield stress . The unyielding plug represents the region wherein .
At the centre of the pipe, the shear stress must reduce to zero, which in the case of a Herschel–Bulkley fluid implies a region that does not yield but flows as a plug, as shown in Figure 4. In the case of a turbulent flow, this plug is not as smooth as is shown in the Figure 4 for a laminar flow. However, direct numerical studies by Rudman and Blackburn [23] (at ) show the existence of a region characterised by a high effective viscosity and a smoother, nearly uniform velocity profile. Further, this region also displays reduction in turbulence and hence turbulent mixing, which possibly could lead to laminar pockets coexisting with unsteady turbulent flow until the wall, followed by a transition to a laminar flow consistent with a wall boundary. As a result, the effective mixing region that could sustain turbulence is reduced to that shown in Figure 4.
The extent of this region is controlled by the value of the yield stress defined by Equation (37). Assuming this region of low (or zero) turbulence is circular is shape (not the case, as shown by direct numerical simulation, but simplifies the explanation provided below), the region will have a stress equal to the yield stress. Therefore,
While deriving Equation (44), we neglected the fact that the turbulent stress term involves a mixing length or that is directly proportional to the distance from the wall [37,38]. This mixing length is an estimate of the distance over which a parcel of fluid retains its properties before mixing with the surrounding fluid. For a Newtonian flow, this implies that the maximum mixing length is R.
However, for a Herschel–Bulkley fluid, at a distance from the pipe’s wall, a parcel of fluid must merge into the unyielding plug; one may hypothesise that the mixing length could be thought as being reduced by a factor that depends on the size (radius) of the plug. One may rewrite y as or .
For clarity, is defined as follows:
Upon introducing this into Equation (42),
thus redefining the mixing length for a wall-bounded Herschel–Bulkley fluid as .
Following the procedure used to derive with Equation (51) as the basis for the turbulent regime, one obtains another equation, , that reads
Further modifications given by [28] to define a suitable for a power-law fluid could also be extended to Herschel–Bulkley fluids as
Equation (53) and its relation with would require experimental verification, which we are unable to perform. Therefore, we shall avoid commenting on the velocity profile of the slurries that this article concerns.
One notices that both and are implicit in terms of for a given value of u in the first cell near a wall boundary. Thus unlike the original wall function described in Section 1.3, and must be implemented as specified shear boundary conditions.
An example of such an approach is the use of the Monin–Obukhov similarity theory [45] to relate the shear stress on the ground to the velocity field at the first computational node, while simulating the atmospheric boundary layer using large-eddy simulation [46,47]. As the simulation progresses in time, the implementation of a theoretical (or semi-empirical) relation between the instantaneous wall shear stress and the instantaneous velocity at the first grid point results in an accurate velocity profile (not instantaneous but time-averaged) of the atmospheric flow near the earth’s surface.
This study aims to do the same but with RANS. As the simulation progresses towards a time-independent ensemble-averaged solution, the implementation of or will impose a theoretical constraint on the velocity field (the iterated values) and the wall shear. Thus, upon beginning the simulation with a uniform velocity field equalling the average flow velocity in the pipe, one expects to converge onto a solution that satisfies or near the wall for a Herschel–Bulkley fluid, which is equivalent to using the original wall function for a Newtonian fluid.
Although the original wall function provided an input to generate an accurate velocity profile of the flow with the distance from the wall, our aim is to only accurately predict the wall shear stress that could exist for a given average flow velocity in the pipe. This is purely because we are unable to verify the velocity (or turbulence) profile as a result of the lack of relevant experimental data.
2.3. Mesh
The computational grid for simulating fluids in horizontal pipes is shown in Figure 5. Instead of simulating the entire circular cross-section, two symmetry boundaries are used to simulate a quarter-pipe. The boundaries mathematically reduce the gradient across them to zero and allow no flux to leave or enter the quarter-pipe. The inlet has a specified velocity and turbulence intensity, whereas the outlet has a simple outflow condition with a diffusion gradient and a mass flow balance.
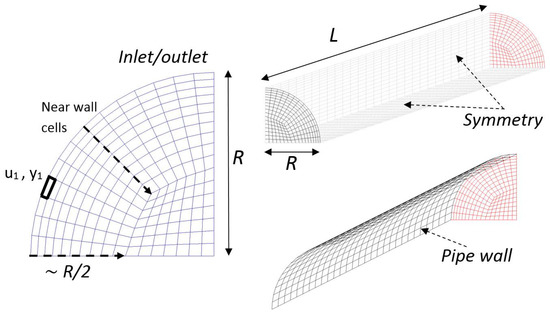
Figure 5.
The computational grid.
The pipe walls are modelled with the specified spear approach mentioned in Section 2.2, that is, or . As one can see in Figure 5, the cells along the pipe increase in height from the pipe’s wall towards the centre. This pattern is a part of the standard treatment used with wall functions while simulating turbulent boundary layers [17,40]. In every case, the grid follows the same pattern from the wall until half the radius, following which the cells are more uniformly arranged into an O-.
The height of the first cell, ( was previously used as the first grid point, which is located at half the height of the first cell) must be set as per guidelines similar to those for Newtonian fluids (see Section 1.3).
The and values were calculated for each test case, following which, the distance for the first grid point or was obtained by setting Equation (53) to values from 20 to 120. Once the first grid cell’s height was known, cells were added with an expansion ratio of between and until the cells reached the central O-, following which the O- was created. In either case, the cells along the pipe were sized to maintain an aspect ratio below 40. There is no specific literature on aspect ratios. However, on the basis of multiple guidelines available freely, the maximum aspect ratio was restricted to 40.
To ascertain the grid convergence, the height of the first grid point was varied between and (higher values of were possible only with higher Reynolds numbers, ). It is noted that for , for a converged value of the wall shear stress was closer to 20, whereas for , was at least 60 (as high as 200). Thus, the first grid point was placed progressively further from the wall (in terms of ) as the value increased.
For the standard Newtonian wall function, one should be aware that the first cell must be placed between (Newtonian definition of ) to avoid being completely within the fully laminar or turbulent regimes [14,35]. This has been corroborated through various studies. As a result of a lack of experimental or numerical evidence, it is impossible to conclude the same for a non-Newtonian fluid, and hence we refrain from discussing any trends in the relation between , and . Therefore, the data reported here is that obtained with values of (Herschel–Bulkley definition), beyond which the did not change (as mentioned previously, this increased with ).
3. Experiments
Table 1 presents an overview of the various experimental test cases considered in this article. All cases deal with Herschel–Bulkley domestic slurries in circular horizontal pipes. As per Equation (7), the unit of m for a given behaviour index n is .

Table 1.
The test cases considered for this article. The first two are from Slatter [13], is from Park et al. [48], and the last two belong to experimental data supplied by the co-authors [49].
In all simulations, the length of the pipe was set to L = 30 to 45 m (longer for a thicker pipe, ) to ensure that the flow reached a fully developed state and to avoid interference from the outflow boundary. The centreline velocity was monitored as it developed across the length of the pipe to a value that stopped varying with the downstream distance (after a certain distance from the inlet, thus reaching a fully developed state) before collecting any data.
Slatter [13] mentions a maximum experimental error of about in measuring the wall shear stress when it is about 1 Pa. As the flow velocity and hence the wall shear increase, the maximum error reduces to under for a wall shear of 10 Pa. The error in the rheological measurements is a maximum of [50]. Park et al. [48] mention that their rheological parameters were obtained by linear regression of viscometric data, with a coefficient of determination of .
The rheological parameters of the clay slurries and were determined using a Couette-flow co-axial rheometer of the Searle type, with a rotating inner cylinder and a stationary outer cylinder (Anton Paar MCR302; cup diameter of mm, bob diameter of 27 mm and bob length of mm; see www.anton-paar.comfordetails). (Clay slurries that were determined to possess a rheology similar to domestic slurry were used for the actual experiments.) The temperature was controlled to an accuracy of 0.1 °C using a Peltier system. After a rheogram was obtained using the viscometer, the rheological parameters were estimated for a Herschel–Bulkley behaviour with an absolute normalised residual of and a root-mean-square normalised residual of . Further, the pressure sensors had a maximum error of , and the flow meter that measured the volumetric flow rate to assess the flow velocity had an maximum error of . The experimental set-up is shown in Figure 6. The set-up involved a 100 mm pipe with a long horizontal section to permit the flow to reach a fully developed state, before the flow passed through two pressures sensors separated by a horizontal section of 15 m, two 90° bends and another horizontal section of m.
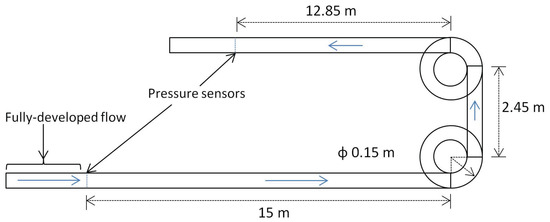
Figure 6.
A schematic of the experimental set-up showing the location of the pressure sensors and the dimensions of the various sections [49] (courtesy: Stichting Deltares).
The numerical solver was first validated against , and , following which, it was used to simulate the set-up shown in Figure 6. Upon simulating the fluid (see Table 1) for a range of velocities, the pressures calculated numerically matched their experimental counterparts at the locations shown in Figure 6, while accounting for the presence of two vertical pipe bends. This provided additional validation of the numerical method proposed in this article. More details on our studies on pipe bends will comprise another article in the future.
Figure 7 shows the residuals obtained for one test case. A simulation was considered as converged only after the residuals (not normalised) dropped below (in most cases below ). The sudden increase in the middle of the plot is the result of changing the wall function from the standard Newtonian function [18] to . In either case, the simulation reached convergence but the values of the wall shear predicted were very different (as described in Section 4).
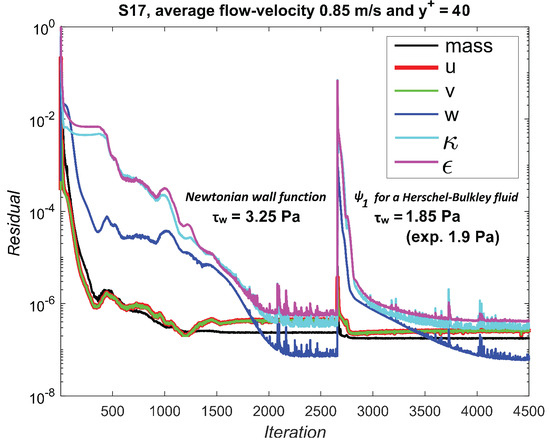
Figure 7.
Normalised residuals for one of the test cases. Applying improved the numerical prediction of the wall shear stress.
4. Observations
We present our observations using Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. Each figure has two y-axes. The left y-axis represents , while the right y-axis represents the Reynolds number . Therefore, each figure simultaneously shows the relationship of the velocity V on the x-axis with and . For simplicity, is shown with a dashed line with crosses at the relevant data points.
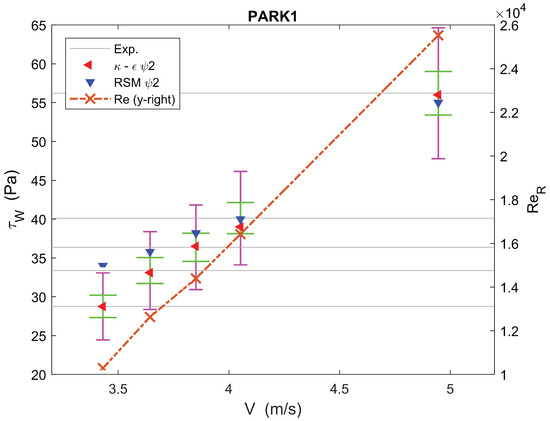
Figure 8.
Pa, , and mm.
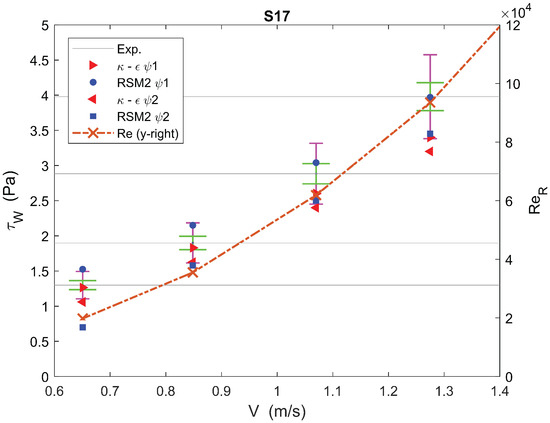
Figure 9.
Pa, , and mm.
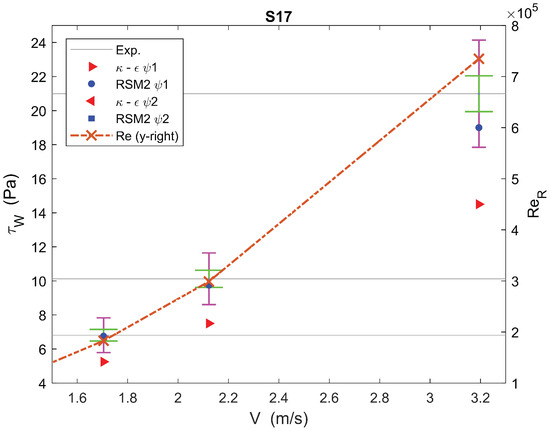
Figure 10.
Pa, , and mm.
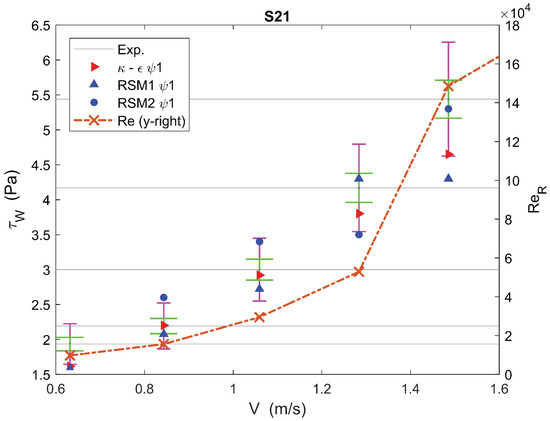
Figure 11.
Pa, , and mm.
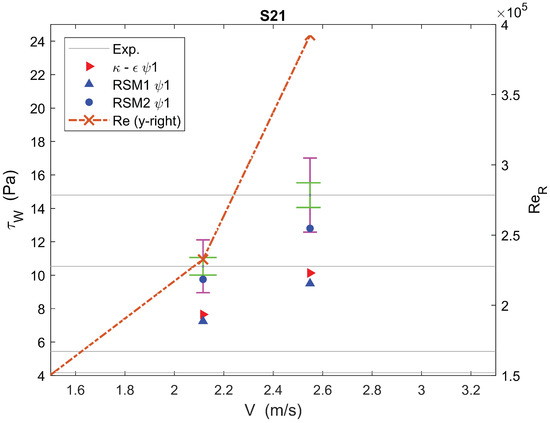
Figure 12.
Pa, , and mm.
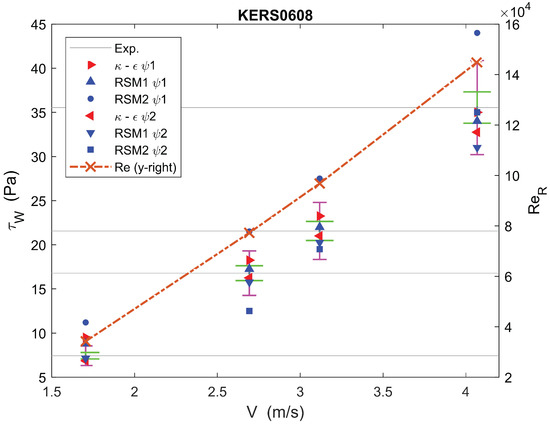
Figure 13.
Pa, , and mm.
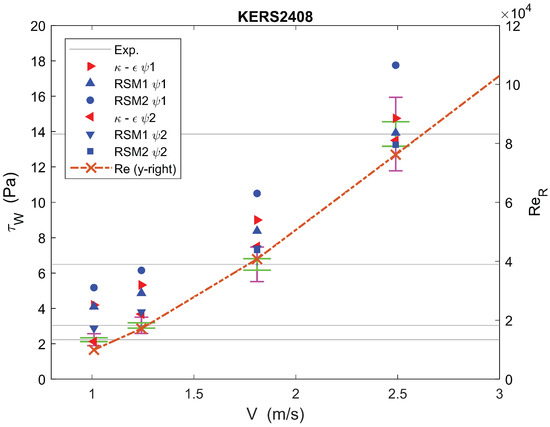
Figure 14.
Pa, , and mm.
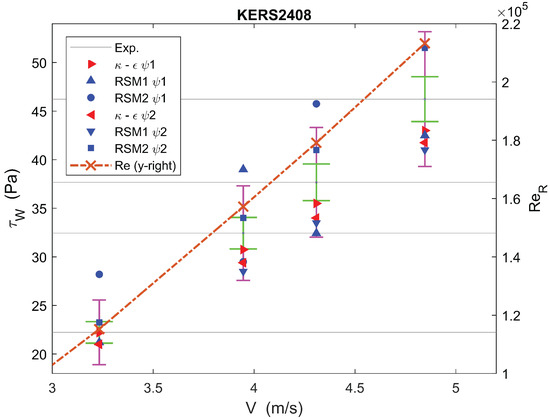
Figure 15.
Pa, , and mm.
The experimental values of are indicated with grey horizontal lines. We have chosen to use a line to mark the experimental to avoid cluttering the plots with too many markers. This does not imply that a given experimental value holds for all velocities V on the x-axis. Rather, the velocity at which a given experimental is known is made clear with a green error bar on the relevant grey line, representing a deviation from the experimental value, and with an additional magenta bar that indicates a deviation.
Finally, if a number of data points for a certain legend entry are missing, this means that the simulation did not converge or the numerically obtained data was very inaccurate and could not “fit within a concise plot”.
Figure 8 concerns the case , which had a very high value. Although not shown on the plot (for the sake of resolution), the use in this case led to an over-prediction in the shear stress. Upon using , the value was predicted more accurately. One notices that – remained accurate, whereas the accuracy of RSM1 increased with .
Figure 9 and Figure 10 represent the case . Although the value was low, n was also low, indicating a stronger non-Newtonian behaviour [11,12]. One notices that as increased, the accuracy of RSM2 with increased, whereas that of – with was reduced. At a very high Reynolds number (; see Figure 10), either RANS model was inaccurate. It is interesting to note that using in such a case (low ) led to an under-prediction in .
At a lower Reynolds number (), the accuracy of either RANS model could not be deduced with certainty, although the accuracy of – (see Figure 9) seemed to be acceptable. However, when the flow was more turbulent (the regime in which RANS models are generally valid), RSM was more accurate, possibly as a result of its anisotropic formulation that includes more physics than the isotropic –.
A similar trend is noted in Figure 11 and Figure 12, which pertain to the case . The accuracy of – was good at low Reynolds numbers (; see Figure 11) but diminished at higher Reynolds numbers. RSM2 showed a trend similar to that noted with . Further, RSM1 has also been added to elucidate the difference between RSM1 and RSM2 (see Section 2.1). RSM1 remained mostly inaccurate and could, in effect, be replaced by RSM2 or – depending on . It is important to note that as increased, in both and , the accuracy of both RSM2 and – was low, around .
represents a case that was mildly non-Newtonian with a high n (for , although was low, it was comparable to when was low). As shown in Figure 13, RSM2 was generally inaccurate. Although one sees at that RSM2 with was accurate, the general increasing trend of RSM2 (both and ) suggests that RSM2 was inaccurate at higher values of .
Further, RSM1 was much more accurate with , whereas with , it under-predicted . With regard to –, is the logical choice at lower velocities, as Pa was comparable to . However at higher velocities, becomes more accurate. Finally, as opposed to cases with lower values of n, – is noted to have been more accurate than RSM for .
in Figure 14 and Figure 15 is similar to with a high value of and a value that is comparable to at low velocities (low ). One notices that RSM2 was inaccurate with both and ; – seems to be the better choice with at lower velocities and at higher velocities, in keeping with what was observed for (both had a high value of n).
As noted for previously described cases, when increased to values above , the accuracy of all the methods was reduced, and the prediction deviated by more than from the experimental value. However, in this case, – still remained between and accurate.
We also simulated more test cases from Slatter [13] and observed the trends mentioned above. We have chosen to include only the cases mentioned in Table 1 for succinctness.
5. Conclusions and Outlook
On the basis of the mentioned observations, one may conclude that a combination of RANS modelling and a specified shear-based wall boundary condition suitable for non-Newtonian flows can provide accurate estimates (within in most cases) of the wall shear stress and the pressure drop through circular horizontal pipes carrying a Herschel–Bulkley fluid.
When used with the proposed specified shear boundary condition (), the RSM is observed to deliver more accurate results with fluids that have a smaller behaviour index or , alluding to a stronger nonlinear behaviour. On the other hand, – seems to work better with fluids that have a value of n greater than .
Further, the wall boundary condition must be modified () to account for the influence of a fluid’s yield stress or when it is comparable in magnitude to the wall shear stress or . Therefore, when is large, both RSM and – are observed to be accurate when used with , depending on the value of n. It is fair to mention that the accuracy of these numerical methods depends to a great extent on the rheological input. As observed in Slatter [13], models based on rheological inputs measured with laminar flows tend to deviate from experiments for turbulent regimes. It is therefore important to perform a sensitivity analysis of and in terms of the rheological inputs, which will also help to define the envelope within which these equations can be used. Further, the effect of the pipe diameter must be taken into account should these equations be extended to thicker pipes, as it is well known that flow regimes could change with increasing pipe diameter. We aim to address these issues in future publications.
Future work will additionally concern the extension of the specified shear functions for the study of the flow through bends in circular pipes carrying a Herschel–Bulkley slurry and possibly in an unsteady setting to study pulsatile effects. Lastly, using a commercial code adds restrictions to the numerical schemes that a user could use. For instance, upwind schemes used with RANS in ANSYS FLUENT are meant to guarantee numerical stability but may influence the final solution through numerical diffusion. Therefore, we aim to implement the specified shear conditions ( and ) in OpenFOAM, which could provide more flexibility in terms of using higher-order (third or higher) upwind schemes or a blend of central and upwind schemes.
Acknowledgments
This article is a result of the research carried out at the Delft University of Technology, Delft and was funded by NWO-domain TTW, Foundation Deltares, Stowa, Foundation RIONED, Waternet, Waterboard Zuiderzeeland, Grontmij and XYLEM. We acknowledge the support of the funding bodies and their contributions to this research.
Author Contributions
D.M. conducted the numerical simulations, whereas A.K.T.R. conducted the experiments for S17 and S21. Both D.M. and A.K.T.R., were supervised by J.v.L. and F.C.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chabbra, R.P.; Richardson, J.F. Non-Newtonian Flow in the Process Industries, 1st ed.; Butterworth-Heinemann: Oxford, UK, 1999. [Google Scholar]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid-Zeitschrift 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Oldroyd, J.G. A rational formulation of the equations of plastic flow for a Bingham solid. Math. Proc. Camb. Philos. Soc. 1947, 43, 100–105. [Google Scholar] [CrossRef]
- Skelland, A.H.P. Non-Newtonian Flow and Heat Transfer; John Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Govier, G.W.; Aziz, K. The Flow of Complex Mixtures in Pipes; R.E. Krieger Pub. Co.: New York, NY, USA, 1972. [Google Scholar]
- Bird, R.B.; Dai, G.C.; Yarusso, B.J. The rheology and flow of viscoplastic materials. Rev. Chem. Eng. 1983, 1, 1–70. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, Vol. 1: Fluid Mechanics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Heywood, N.I.; Cheng, D.C.H. Comparison of methods for predicting head loss in turbulent pipe flow of non-Newtonian fluids. Trans. Inst. Meas. Control 1984, 6, 33–45. [Google Scholar] [CrossRef]
- Torrance, B.M. Friction factors for turbulent non-Newtonian fluid flow in circular pipes. S. Afr. Mech. Eng. 1963, 13, 89–91. [Google Scholar]
- Hanks, R.W. Low Reynolds number turbulent pipeline flow of pseudohomogeneous slurries. In Proceedings Hydrotransport 5 Conference, Paper C2; BHRA Fluid Eng.: Cranfield, UK, 1978; pp. 8–11. [Google Scholar]
- Wilson, K.C.; Thomas, A.D. A new analysis of the turbulent flow of non-Newtonian fluids. Can. J. Chem. Eng. 1985, 63, 539–546. [Google Scholar] [CrossRef]
- Thomas, A.D.; Wilson, K.C. New analysis of non-Newtonian turbulent flow-yield-power-law fluids. Can. J. Chem. Eng. 1987, 65, 335–338. [Google Scholar] [CrossRef]
- Slatter, P.T. TranSitional and Turbulent Flow of Non-Newtonian Slurries in Pipes. Ph.D. Thesis, Department of Civil Engineering, University of Cape Town, Cape Town, South Africa, 1995. [Google Scholar]
- Ferziger, J.; Perić, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer Science and Business Media: Berlin, Germany, 2012. [Google Scholar]
- Davidson, P.A. Turbulence—An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Gavrilov, A.A.; Rudyak, V.Y. Reynolds-averaged modeling of turbulent flows of power-law fluids. J. Non-Newton. Fluid Mech. 2016, 227, 45–55. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling in CFD, 3rd ed.; DCW Industries: La Cañada Flintridge, CA, USA, 2006. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Gori, F.; Boghi, A. A three dimensional exact equation for the turbulent dissipation rate of Generalised Newtonian Fluids. Int. Commun. Heat Mass Transf. 2012, 39, 477–485. [Google Scholar] [CrossRef]
- Pinho, F.; Li, C.; Younis, B.; Sureshkumar, R. A low Reynolds number turbulence closure for viscoelastic fluids. J. Non-Newton. Fluid Mech. 2008, 154, 89–108. [Google Scholar] [CrossRef]
- Leighton, R.; Walker, D.T.; Stephens, T.; Garwood, G. Reynolds stress modelling for drag reducing viscoelastic flows. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Honolulu, HI, USA, 6–10 July 2003; Volume 1, pp. 735–744. [Google Scholar]
- Rudman, M.; Blackburn, H.M. Direct numerical simulation of turbulent non-Newtonian flow using a spectral element method. Appl. Math. Model. 2006, 30, 1229–1248. [Google Scholar] [CrossRef]
- Wilcox, D. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Malin, M.R. Turbulent pipe flow of power-law fluids. Int. Commun. Heat Mass Transf. 1997, 24, 977–988. [Google Scholar] [CrossRef]
- Malin, M.R. The turbulent flow of Bingham plastic fluids in smooth circular tubes. Int. Commun. Heat Mass Transf. 1997, 24, 793–804. [Google Scholar] [CrossRef]
- Malin, M.R. Turbulent pipe flow of Herschel-Bulkley fluids. Int. Commun. Heat Mass Transf. 1998, 25, 321–330. [Google Scholar] [CrossRef]
- Dodge, D.W.; Metzner, A.B. Turbulent flow of non-Newtonian systems. AIChE J. 1959, 5, 189–204. [Google Scholar] [CrossRef]
- Bartosik, A.S. Modification of κ-ϵ model for slurry flow with yield stress. In Proceedings of the 10th International Conference on Numerical Methods in Laminar and Turbulent Flows, Swansea, UK, 21–25 July 1997; Volume 10, pp. 265–274. [Google Scholar]
- Bartosik, A.S. Modelling of a turbulent flow using the Herschel-Bulkley rheological model. Chem. Process Eng. Inzynieria Chemiczna i Procesowa 2006, 27, 623–632. [Google Scholar]
- Clapp, R.M. Turbulent heat transfer in pseudoplastic non-Newtonian fluids. In International Developments of Heat Transfer Part III; The American Society of Mechanical Engineers: New York, NY, USA, 1961; pp. 652–661. [Google Scholar]
- Sawko, R. Mathematical and Computational Methods of Non-Newtonian Multiphase Flows. Ph.D. Thesis, School of Engineering, Cranfield University, Cranfield, UK, 2012. [Google Scholar]
- Singh, J.; Rudman, M.; Blackburn, H.M.; Chryss, A.; Pullum, L.; Graham, L.J.W. The importance of rheology characterization in predicting turbulent pipe flow of generalized Newtonian fluids. J. Non-Newton. Fluid Mech. 2016, 232, 11–21. [Google Scholar] [CrossRef]
- Gnambode, P.S.; Orlandi, P.; Ould-Rouiss, M.; Nicolas, X. Large-eddy simulation of turbulent pipe flow of power-law fluids. Int. J. Heat Fluid Flow 2015, 54, 196–210. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Schlichting, H. Boundary-Layer Theory, 8th ed.; Gersten, K., Ed.; Springer: Berlin, Germany, 2017. [Google Scholar]
- Prandtl, L. Zur turbulenten Strömung in glatten Röhren. Zeitschrift für Angewandte Mathematik und Mechanik 1925, 5, 136–139. [Google Scholar]
- Prandtl, L. Neure Ergebnisse der Turbulenzforschung. Zeitschrift des Vereines Deutscher Ingenieure 1933, 77, 105–114. [Google Scholar]
- von Kármán, T. Mechanische Ähnlichkeit Und Turbulenz. In Sonderdrucke aus den Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen: Mathematisch-Physische Klasse; Weidmannsche Buchh: Berlin, Germany, 1930. [Google Scholar]
- ANSYS. ANSYS FLUENT User’s Guide; Ansys Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Tanner, R.I.; Milthorpe, J.F. Numerical simulation of the flow of fluids with yield stress. In Proceedings of the Third International Conference on Numerical Methods in Laminar and Turbulent Flow, Seattle, WA, USA, 8–11 August 1983; pp. 680–690. [Google Scholar]
- Mitsoulis, E. Flows of viscoplastic materials: Models and computations. Rheol. Rev. 2007, 2007, 135–178. [Google Scholar]
- Rudman, M.; Blackburn, H.M.; Graham, L.J.W.; Pullum, L. Turbulent pipe flow of shear-thinning fluids. J. Non-Newton. Fluid Mech. 2004, 118, 33–48. [Google Scholar] [CrossRef]
- Metzner, A.B.; Reed, J.C. Flow of non-Newtonian fluids—Correlation of the laminar, transition and turbulent-flow regions. AIChE J. 1955, 1, 434–440. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-Profile Relationships in the Atmospheric Surface Layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Moeng, C.H. A large eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A scale-dependent dynamic model for large-eddy simulation: Application to a neutral atmospheric boundary layer. J. Fluid Mech. 2000, 415, 261–284. [Google Scholar] [CrossRef]
- Park, J.T.; Mannheimer, R.J.; Grimley, T.A.; Morrow, T.B. Pipe flow measurements of a transparent non-Newtonian slurry. J. Fluids Eng. 1989, 111, 331–336. [Google Scholar] [CrossRef]
- Thota Radhakrishnan, A.K.; van Lier, J.; Clemens, F.H.L.R. Available Upon Request, 2018; in press.
- Neill, R.I.G. The Rheology and Flow Behaviour of High Concentration Mineral Slurries. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 1988. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).