Numerical and Physical Investigation of the Performance of Turbulence Modeling Schemes around a Scour Hole Downstream of a Fixed Bed Protection
Abstract
:1. Introduction
2. Methodology
2.1. Laboratory Experiment
2.2. Numerical Investigation
2.2.1. Governing Equations
2.2.2. Turbulence Modeling
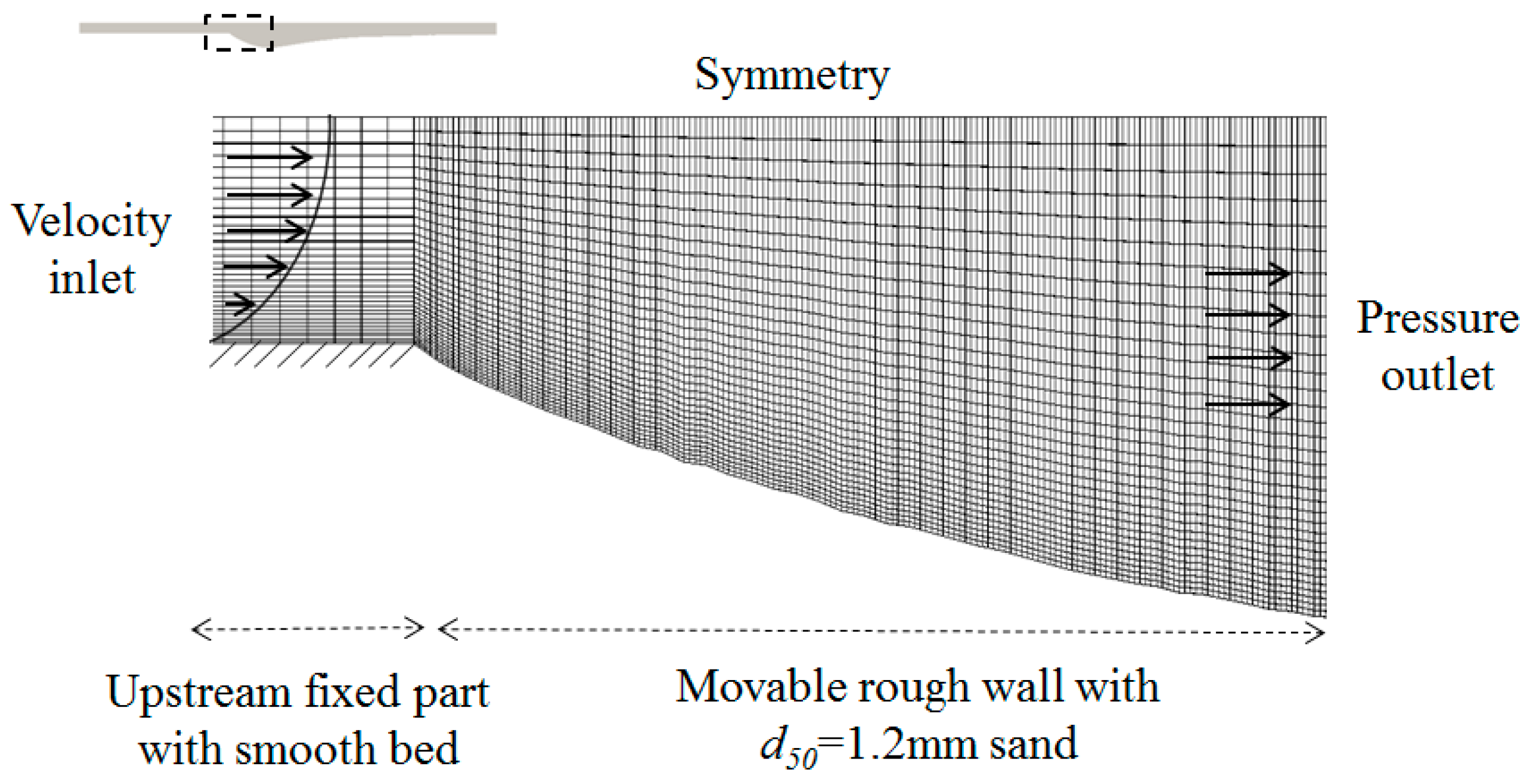
2.2.3. Numerical Setup
3. Results and Discussion
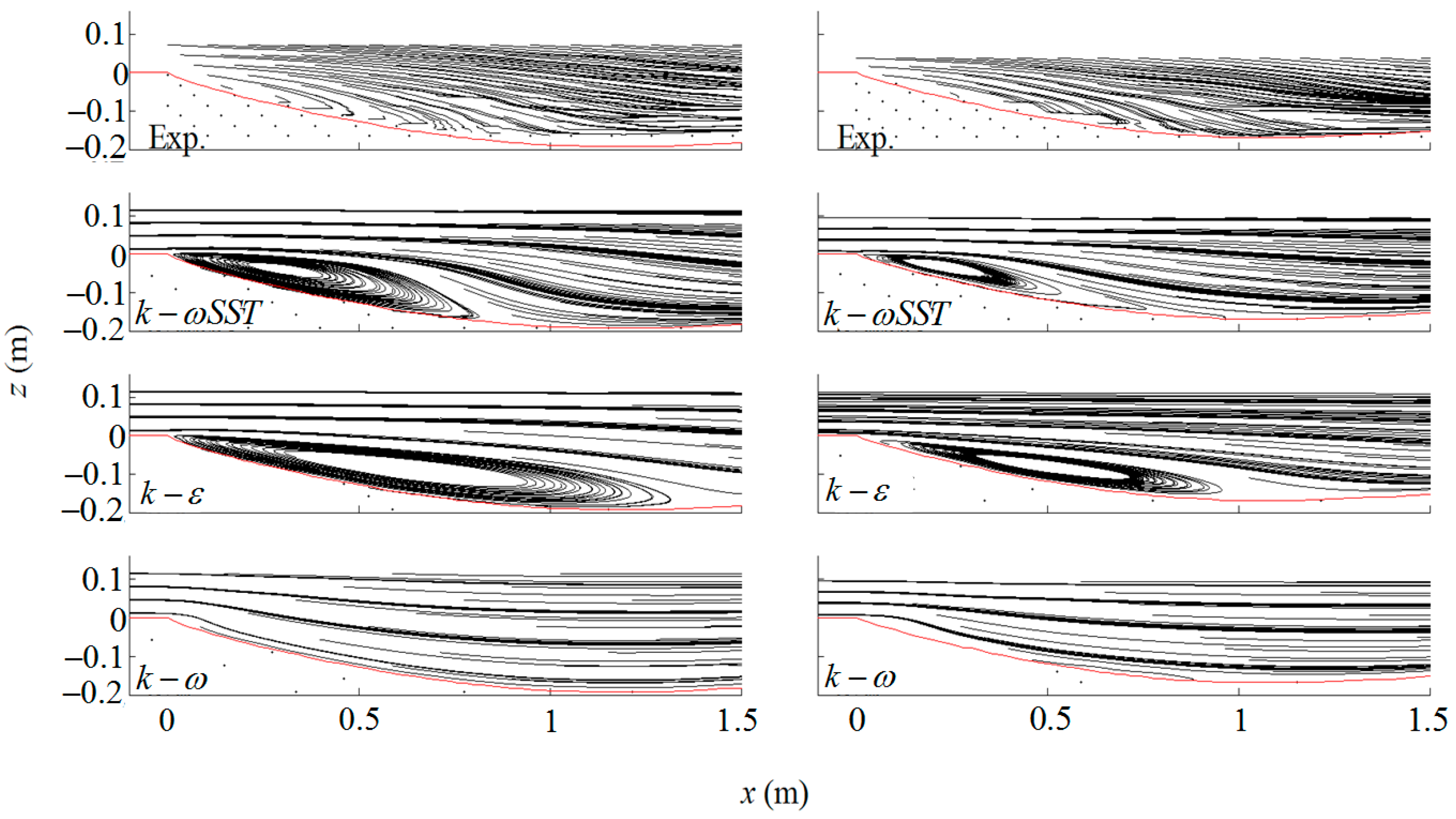
3.1. Streamline
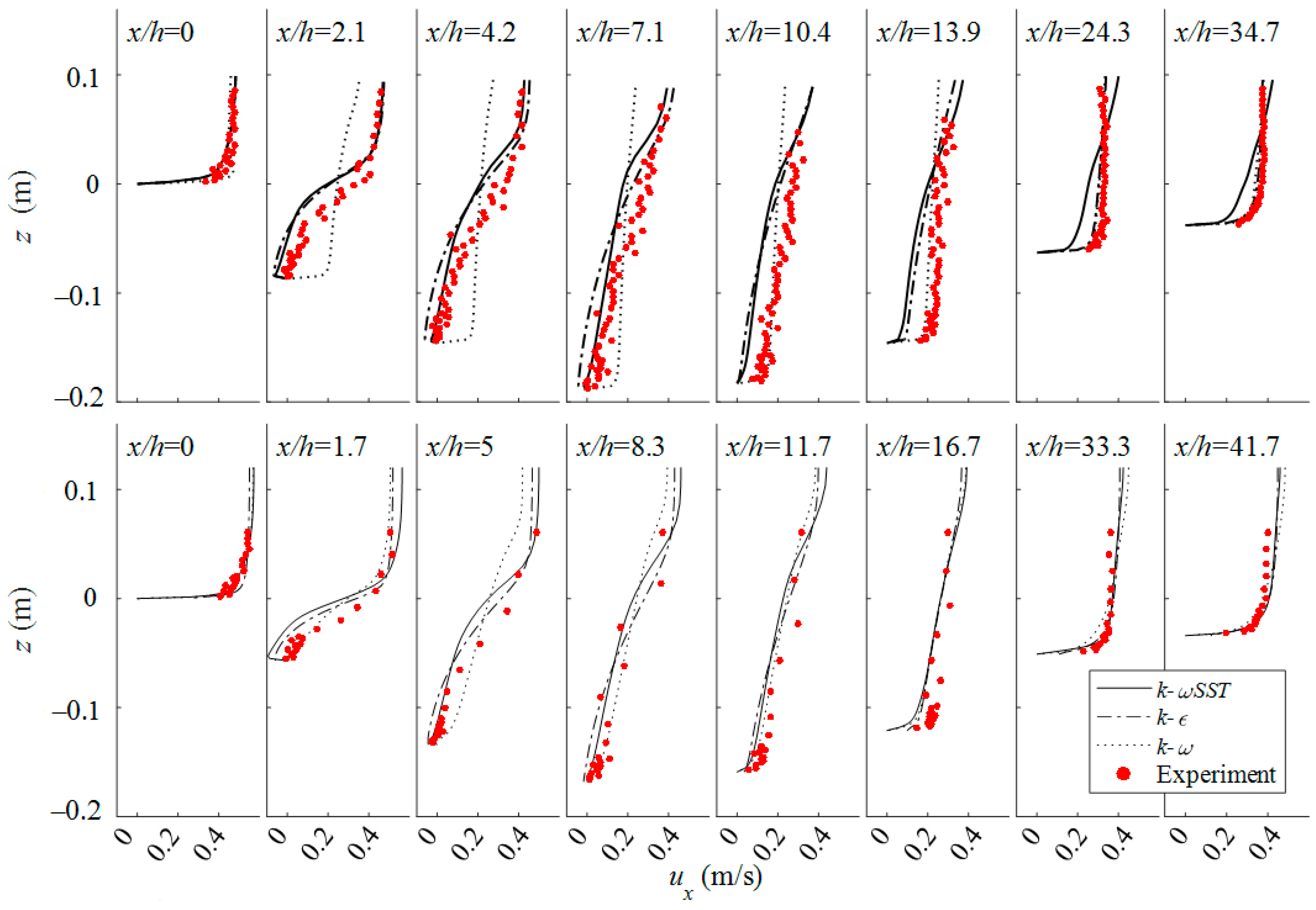
3.2. Velocity Profile
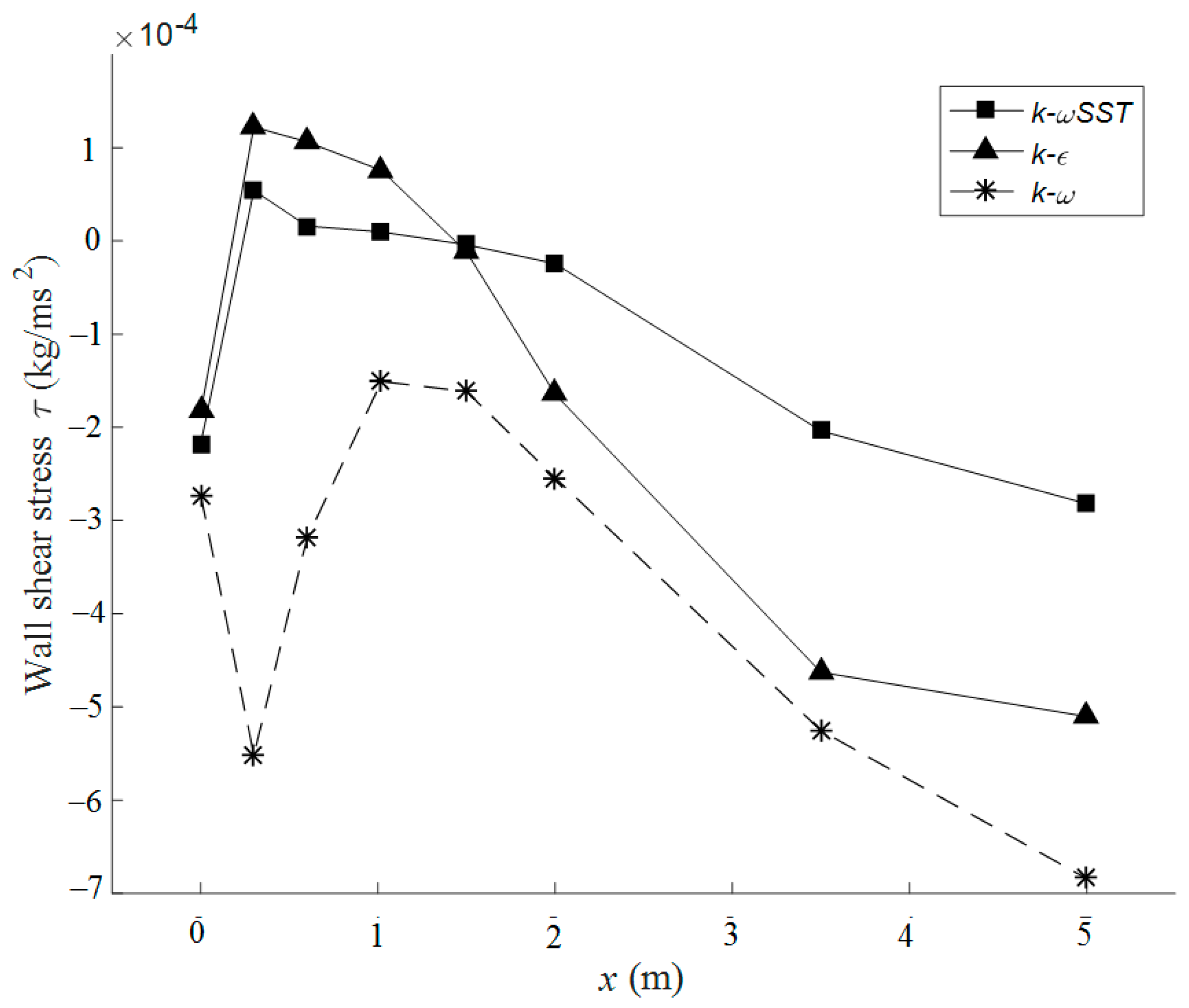
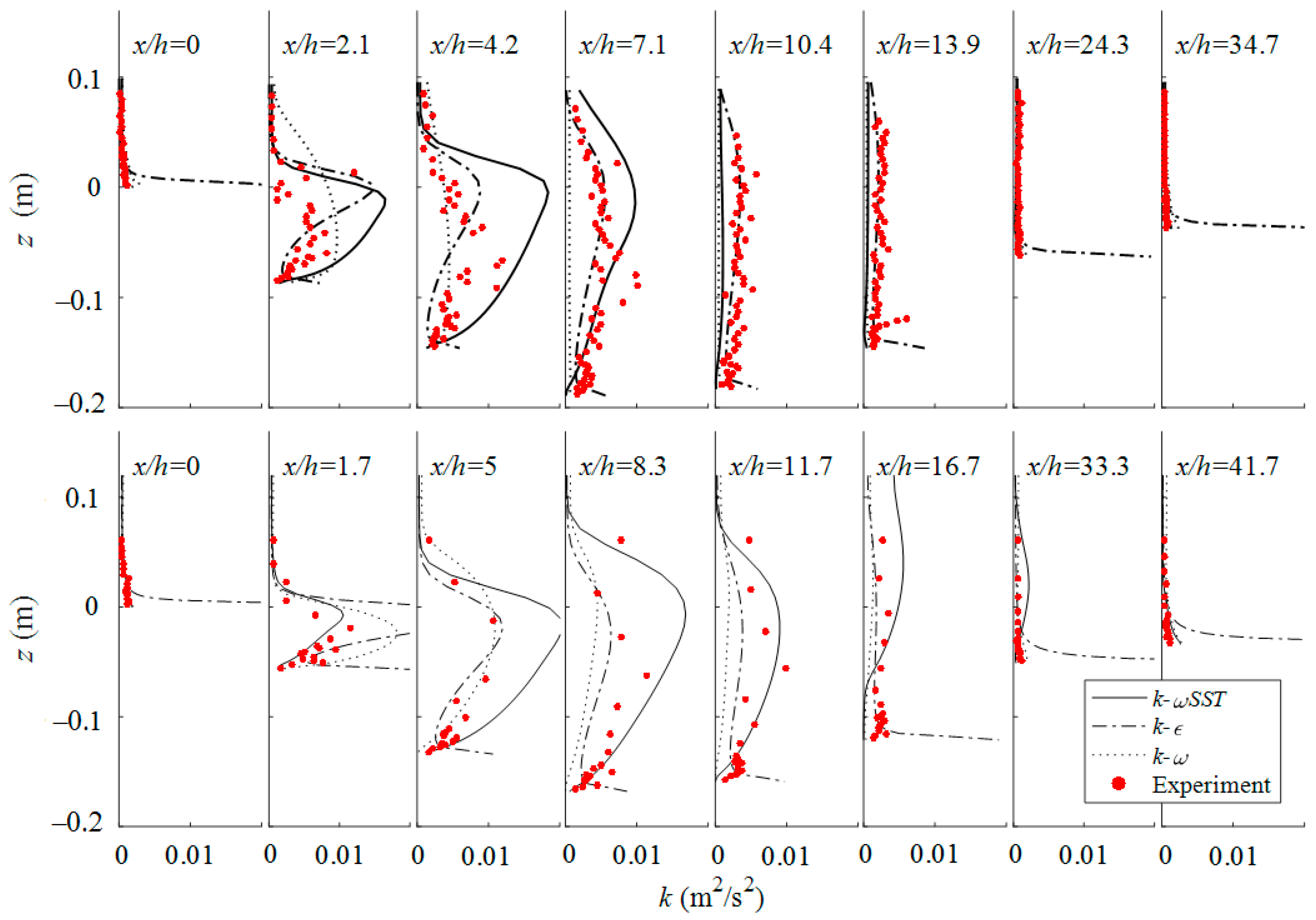
3.3. Turbulent Kinetic Energy
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shirole, A.; Holt, R. Planning for a comprehensive bridge safety assurance program. Transp. Res. Rec. 1991, 1290, 39–50. [Google Scholar]
- Guney, M.; Aksoy, A.; Bombar, G. Experimental study of local scour versus time around circular bridge pier. In Proceedings of the 6th International Advanced Technologies Symposium, Elazığ, Turkey, 16–18 May 2011. [Google Scholar]
- Dargahi, B. Controlling mechanism of local scouring. J. Hydraul. Eng. 1990, 116, 1197–1214. [Google Scholar] [CrossRef]
- Roy, D.; Matin, M.A. An assessment of local scour at floodplain and main channel of compound channel section. J. Civ. Eng. 2010, 38, 39–52. [Google Scholar]
- Ahn, J.; Yang, C.T. Determination of recovery factor for simulation of non-equilibrium sedimentation in reservoir. Int. J. Sediment Res. 2015, 30, 68–73. [Google Scholar] [CrossRef]
- Nagata, N.; Hosoda, T.; Nakato, T.; Muramoto, Y. Three-dimensional numerical model for flow and bed deformation around river hydraulic structures. J. Hydraul. Eng. 2005, 131, 1074–1087. [Google Scholar] [CrossRef]
- Liu, X.; Garcia, M.H. Three-dimensional numerical model with free water surface and mesh deformation for local sediment scour. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 203–217. [Google Scholar] [CrossRef]
- Konečný, P.; Ševčík, R. Comparison of turbulence models in OpenFOAM for 3D simulation of gas flow in solid propellant rocket engine. Adv. Mil. Technol. 2016, 11, 239–251. [Google Scholar] [CrossRef]
- Ali, A.; Sharma, R.K.; Ganesan, P.; Akib, S. Turbulence model sensitivity and scour gap effect of unsteady flow around pipe: A CFD study. Sci. World J. 2014, 2014, 412136. [Google Scholar] [CrossRef] [PubMed]
- Stahlmann, A. Numerical and experimental modelling of scour at foundation structures for offshore wind turbines. J. Ocean Wind Energy 2014, 1, 82–89. [Google Scholar]
- Park, S.W. Experimental Study of Local Scouring at the Downstream of River Bed Protection. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2016. [Google Scholar]
- Scholz, S. Study on Porous-Medium Wall Functions for k − ε and k − ω Turbulence Models. Bachelor’s Thesis, Stuttgart University, Stuttgart, Germany, 2014. [Google Scholar]
- Ota, K.; Sato, T.; Nakagawa, H. 3D Numerical model of sediment transport considering transition from bed-load motion to suspension—Application to a scour upstream of a cross-river structure. J. JSCE 2016, 4, 173–180. [Google Scholar] [CrossRef]
- Boussinesq, J.V. Cours d’Analyse Infinitésimale en vue des Applications Mécaniques et Physiques; Gauthier-Villars: Paris, France, 1887. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Prandtl, L. Bericht über Untersuchungen zur ausgebildeten Turbulenz. J. Appl. Math. Mech. 1925, 5, 136–139. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modelling for CFD, 1st ed.; DCW Industries, Inc.: La Canada, CA, USA, 1993. [Google Scholar]
- Wilcox, D.C. Re-assessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M.; Booij, R. Two-dimensional mathematical modelling of local-scour holes. J. Hydraul. Res. 1993, 31, 615–634. [Google Scholar] [CrossRef]
- Jellesma, M. Form Drag of Subaqueous Dune Configurations. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2013. [Google Scholar]


| Case | Q (m3/s) | h (m) | u (m/s) | d50 (m) | Re |
|---|---|---|---|---|---|
| Exp1 | 0.035 | 0.144 | 0.405 | 0.0012 | 58,300 |
| Exp2 | 0.12 | 0.486 | 58,300 |
| 1.44 | 1.92 | −0.33 | 0.09 | 1.0 | 1.3 |
| Case | Turbulence Model | Inlet Flow Vel. (m/s) | K (10−2 m2/s2) | (10−9 m2/s3) | (1/s) | (s) | (mm) | |
|---|---|---|---|---|---|---|---|---|
| Min | Max | |||||||
| 0.405 | 1.22 | 3.89 | 10−4 | 1.5 | 10 | |||
| 0.486 | 1.7 | 10.7 | ||||||
| 0.405 | 1.22 | 4.792 | ||||||
| 0.486 | 1.7 | 5.67 | ||||||
| SST1 | 0.405 | 1.22 | 4.792 | |||||
| SST2 | 0.486 | 1.7 | 5.67 | |||||
| Physical Case | Case Exp1 | Case Exp2 | ||||
|---|---|---|---|---|---|---|
| Numerical case | 1 | 1 | SST1 | 2 | 2 | SST2 |
| RMSE | 0.0561 | 0.0560 | 0.0407 | 0.0431 | 0.0448 | 0.0413 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.H.T.; Ahn, J.; Park, S.W. Numerical and Physical Investigation of the Performance of Turbulence Modeling Schemes around a Scour Hole Downstream of a Fixed Bed Protection. Water 2018, 10, 103. https://doi.org/10.3390/w10020103
Nguyen THT, Ahn J, Park SW. Numerical and Physical Investigation of the Performance of Turbulence Modeling Schemes around a Scour Hole Downstream of a Fixed Bed Protection. Water. 2018; 10(2):103. https://doi.org/10.3390/w10020103
Chicago/Turabian StyleNguyen, Thi Hoang Thao, Jungkyu Ahn, and Sung Won Park. 2018. "Numerical and Physical Investigation of the Performance of Turbulence Modeling Schemes around a Scour Hole Downstream of a Fixed Bed Protection" Water 10, no. 2: 103. https://doi.org/10.3390/w10020103
APA StyleNguyen, T. H. T., Ahn, J., & Park, S. W. (2018). Numerical and Physical Investigation of the Performance of Turbulence Modeling Schemes around a Scour Hole Downstream of a Fixed Bed Protection. Water, 10(2), 103. https://doi.org/10.3390/w10020103




