Study on the Applicability of the Hargreaves Potential Evapotranspiration Estimation Method in CREST Distributed Hydrological Model (Version 3.0) Applications
Abstract
1. Introduction
2. Study Area and Data Description
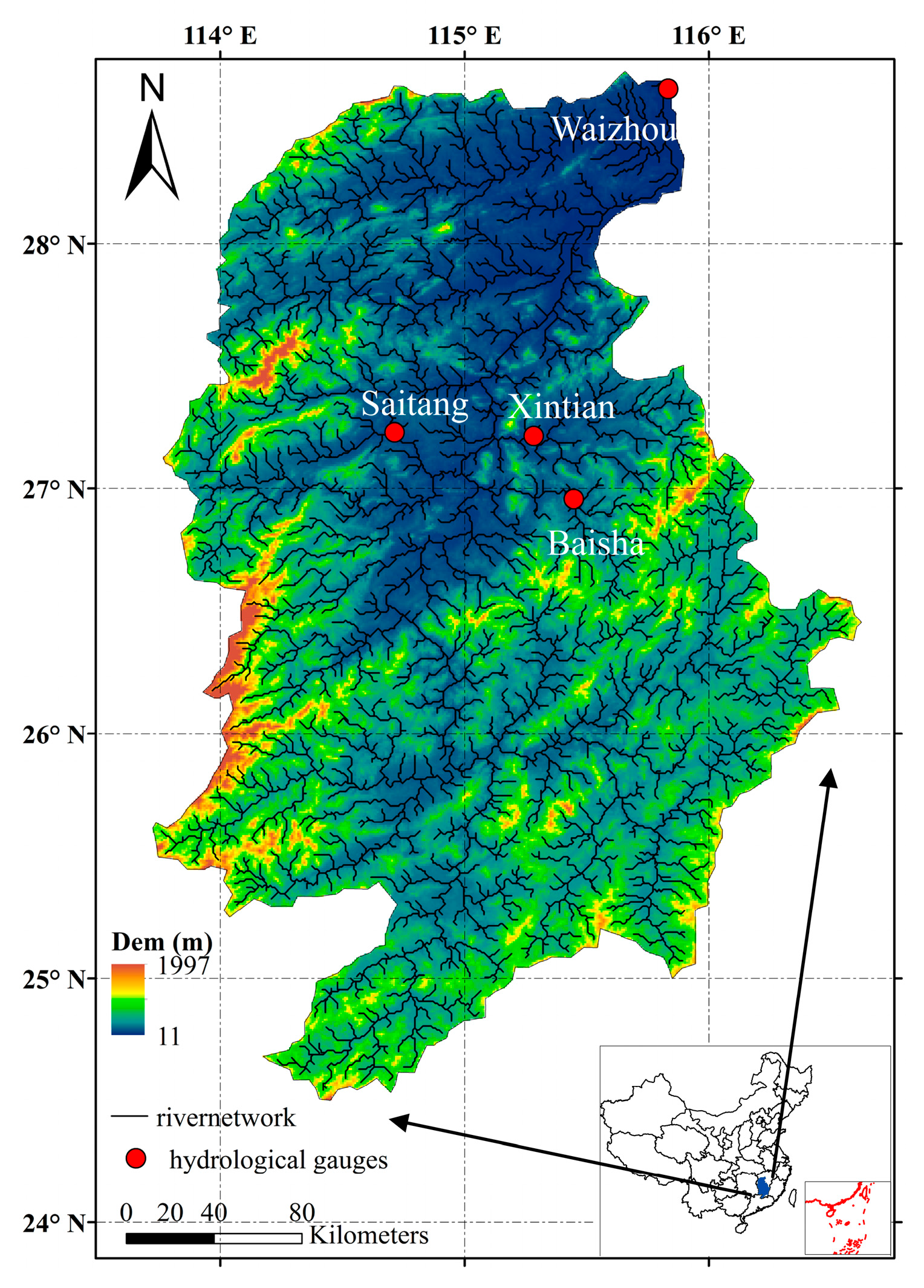
2.1. Study Area
2.2. Data
3. Methodology
3.1. Penman-Monteith Method
3.2. Hargreaves Method
3.3. CREST Distributed Hydrological Model Version 3.0
- Separating the soil layer into three layers and consider 3-layer tension water soil moisture and evapotranspiration computations.
- Adding a free water storage computation module with a free water distribution curve to describe the sub-grid variations of the free water storage.
- According to free water storage, separating runoff into three components, including overland flow, interflow, and ground water.
- Improving the flow concentration module into a four mechanisms-based cell-to-cell routing, including overland flow, interflow, ground water, and river channel flow routings. Based on the arrival time of each upstream grid cell to its downstream outlet grid cell, the generated runoff is routed down along the flow concentration path generated according to the 8-flow-direction method.
3.4. The Design of the Numerical Experiment
3.5. Statistical Metrics
4. Results and Discussion
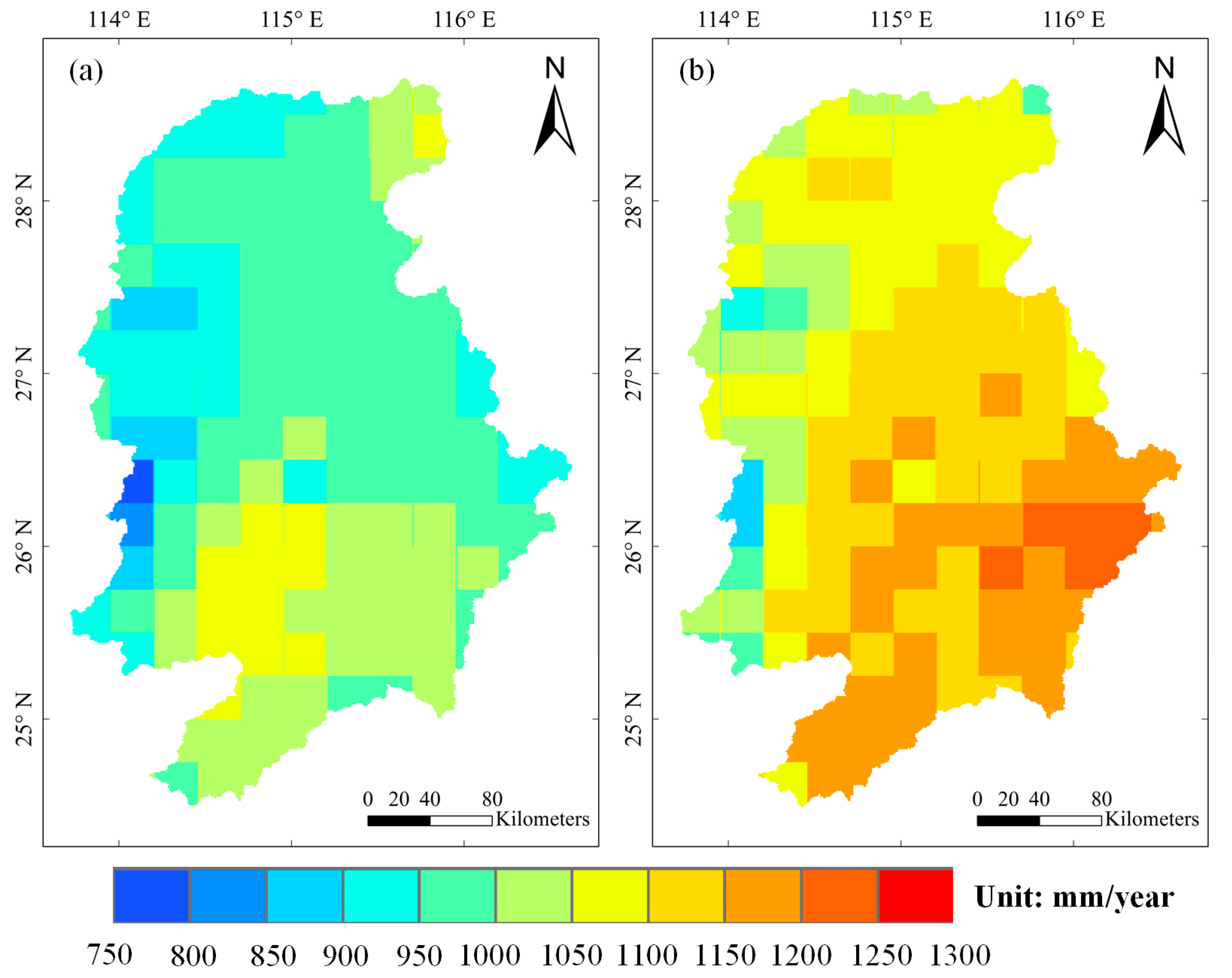
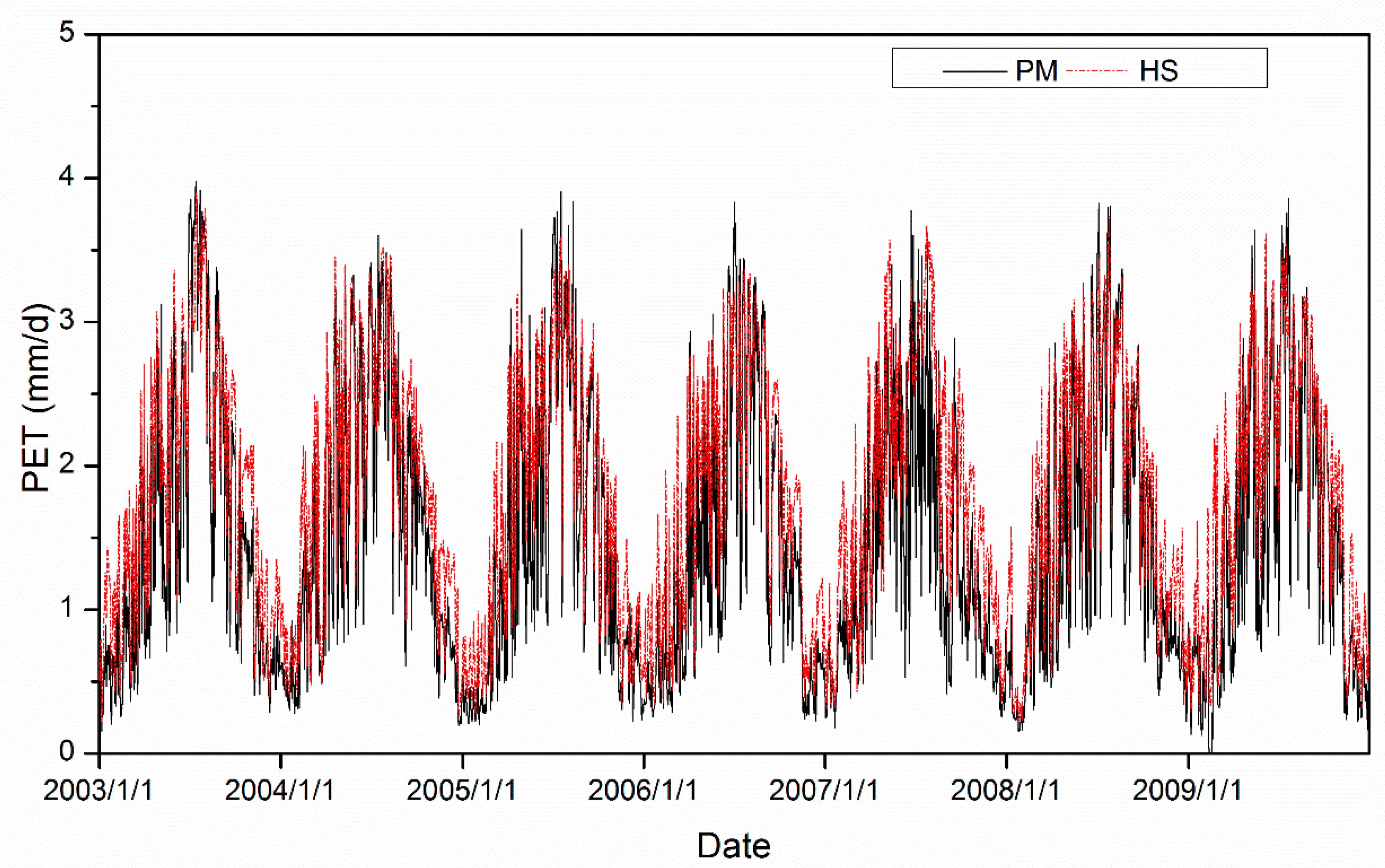
4.1. Intercomparison of Daily PET Among Two Datasets
4.2. Spatial Scale Effect of Pet to The Streamflow Simulation Based on CREST 3.0 Model
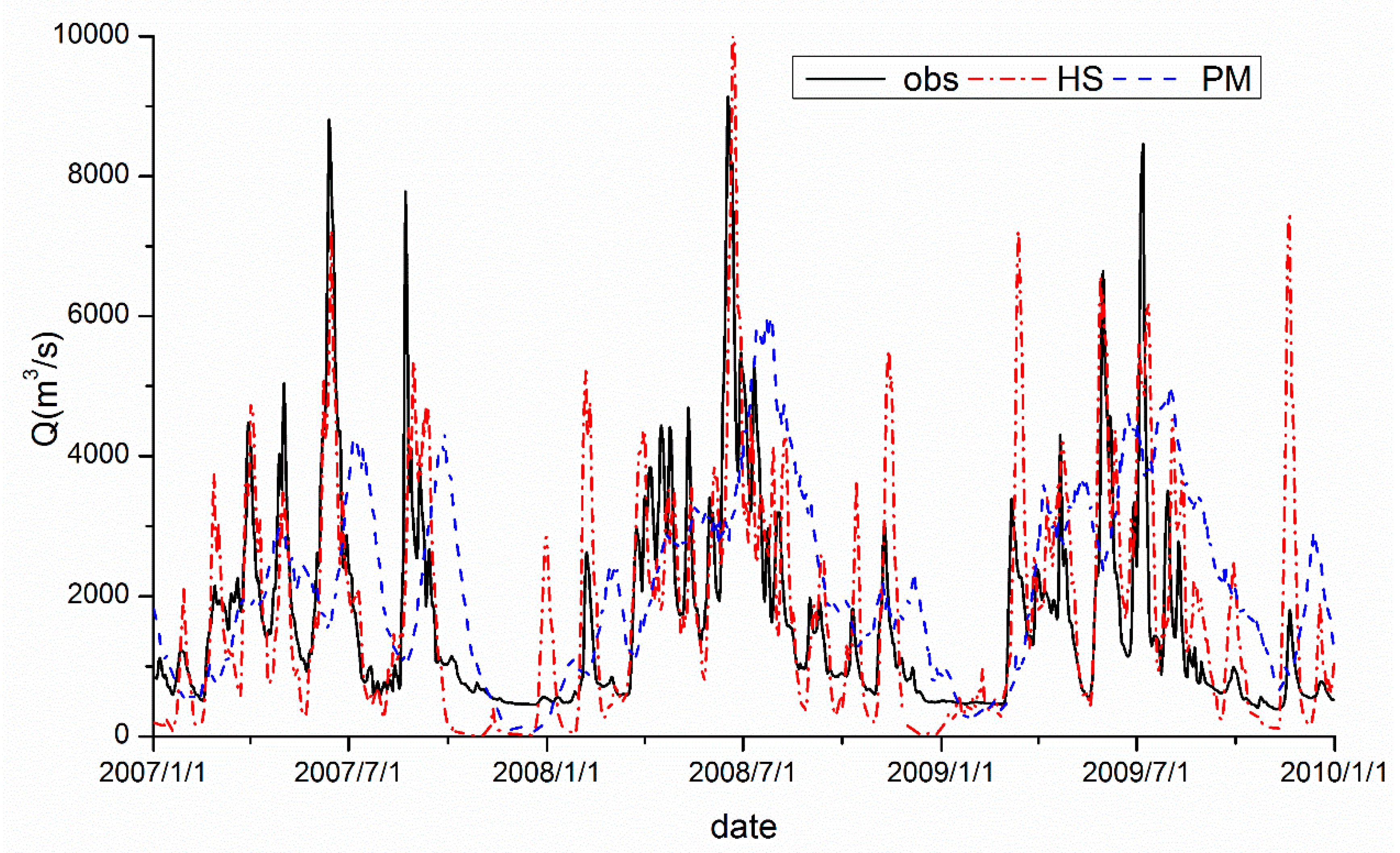
4.3. Comparison of Model Performance between PM and HS Methods in Streamflow Simulations (2003–2009)
5. Conclusions
- (1)
- The PET estimated by the PM and HS methods show large difference in spatial distribution. Two PET estimations are consistent in the lowest PET region, but vary much over the region with relatively high PET magnitude.
- (2)
- Two PET methods can reproduce the annual variations of the PET on daily time scale, but the magnitude of HS is higher than that of PM.
- (3)
- There is no significant discrepancy between HS and PM methods in CREST-based streamflow simulations with the same spatial scale by using BNU and ITPCAS meteorological forcing datasets. The BIAS and RMSE indicates that the performance of CREST model with 25 km spatial resolution is better than 10 km and 100 km.
- (4)
- Standard derivation (STD) of statistical metric for CREST model with PET products of different spatial resolutions indicates that the sensitivity of CREST model to the spatial scale of HS estimates is relatively lower than that of PM in the Ganjiang River Basin.
- (5)
- The comparison of hydrological simulations with 25 km ITPCAS data shows that the HS outperforms PM in streamflow simulation in this study area.
Author Contributions
Funding
Acknowledgement
Conflicts of Interest
References
- Wang, Z.; Xie, P.; Lai, C.; Chen, X.; Wu, X.; Zeng, Z.; Li, J. Spatiotemporal variability of reference evapotranspiration and contributing climatic factors in China during 1961–2013. J. Hydrol. 2017, 544, 97–108. [Google Scholar] [CrossRef]
- Andréassian, V.; Perrin, C.; Michel, C. Impact of imperfect potential evapotranspiration knowledge on the efficiency and parameters of watershed models. J. Hydrol. 2004, 286, 19–35. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Revuelto, J.; López-Moreno, J.I.; González-Hidalgo, J.C.; Moran-Tejeda, E.; Espejo, F. Reference evapotranspiration variability and trends in Spain, 1961–2011. Glob. Planet. Chang. 2014, 121, 26–40. [Google Scholar] [CrossRef]
- GaviláN, P.; EstéVez, J.; Berengena, J.N. Comparison of Standardized Reference Evapotranspiration Equations in Southern Spain. J. Irrig. Drain. Eng. 2008, 134, 1–12. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Hargreaves, G.H. Estimating Potential Evapotranspiration. J. Irrig. Drain. Div. ASCE 1982, 108, 225–230. [Google Scholar]
- Priestley, C.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Hargreaves, G.H. Accuracy of estimated reference crop evapotranspiration. J. Irrig. Drain. Eng. 1989, 115, 1000–1007. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Moeletsi, M.E.; Walker, S.; Hamandawana, H. Comparison of the Hargreaves and Samani equation and the Thornthwaite equation for estimating dekadal evapotranspiration in the Free State Province, South Africa. Phys. Chem. Earth Parts A/B/C 2013, 66, 4–15. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Mpallas, L.; Papaevangelou, G. Estimation of evapotranspiration using fuzzy systems and comparison with the Blaney-Criddle method. J. Environ. Sci. Technol. 2008, 1, 181–186. [Google Scholar]
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. Proc. Am. Soc. Civ. Eng. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar]
- McKenney, M.S.; Rosenberg, N.J. Sensitivity of some potential evapotranspiration estimation methods to climate change. Agric. For. Meteorol. 1993, 64, 81–110. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Federer, C.A.; Schloss, A.L. Potential evaporation functions compared on US watersheds: Possible implications for global-scale water balance and terrestrial ecosystem modeling. J. Hydrol. 1998, 207, 147–169. [Google Scholar] [CrossRef]
- Pereira, A.R.; Pruitt, W.O. Adaptation of the Thornthwaite scheme for estimating daily reference evapotranspiration. Agric. Water Manag. 2004, 66, 251–257. [Google Scholar] [CrossRef]
- Almorox, J.; Quej, V.H.; Martí, P. Global performance ranking of temperature-based approaches for evapotranspiration estimation considering Köppen climate classes. J. Hydrol. 2015, 528, 514–522. [Google Scholar] [CrossRef]
- Elferchichi, A.; Giorgio, G.; Lamaddalena, N.; Ragosta, M.; Telesca, V. Variability of Temperature and Its Impact on Reference Evapotranspiration: The Test Case of the Apulia Region (Southern Italy). Sustainability 2017, 9, 2337. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and evaluation of Hargreaves evapotranspiration equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating Reference Evapotranspiration Under Inaccurate Data Conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Yang, T.; Li, F.; Liang, K.; Hu, S.; Liu, C. Assessment of the Influences of Different Potential Evapotranspiration Inputs on the Performance of Monthly Hydrological Models under Different Climatic Conditions. J. Hydrometeorol. 2016, 17, 2259–2274. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 1—Can rainfall-runoff models effectively handle detailed potential evapotranspiration inputs? J. Hydrol. 2005, 303, 275–289. [Google Scholar] [CrossRef]
- Andersson, L. Improvements of runoff models what way to go? Hydrol. Res. 1992, 23, 315–332. [Google Scholar] [CrossRef]
- Parmele, L.H. Errors in output of hydrologic models due to errors in input potential evapotranspiration. Water Resour. Res. 1972, 8, 348–359. [Google Scholar] [CrossRef]
- Vázquez, R.F. Effect of potential evapotranspiration estimates on effective parameters and performance of the MIKE SHE-code applied to a medium-size catchment. J. Hydrol. 2003, 270, 309–327. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, J.; Jing, X.; Li, H. Study on SWBM and its application in semi-arid basins. Hydrology 2005, 25, 7–10. [Google Scholar]
- Thomas, H.A., Jr. Improved Methods for National tvater Assessment Water Resources Contract: WR15249270; US Water Resources Council: Washington, DC, USA, 1981.
- Wang, J.; Hong, Y.; Li, L.; Gourley, J.J.; Khan, S.I.; Yilmaz, K.K.; Adler, R.F.; Policelli, F.S.; Habib, S.; Irwn, D. The coupled routing and excess storage (CREST) distributed hydrological model. Hydrol. Sci. J. 2011, 56, 84–98. [Google Scholar] [CrossRef]
- Shen, X.; Hong, Y.; Zhang, K.; Hao, Z. Refining a distributed linear reservoir routing method to improve performance of the CREST model. J. Hydrol. Eng. 2016, 22, 04016061. [Google Scholar] [CrossRef]
- Kan, G.; Tang, G.; Yang, Y.; Hong, Y.; Li, J.; Ding, L.; He, X.; Liang, K.; He, L.; Li, Z. An improved coupled routing and excess storage (crest) distributed hydrological model and its verification in Ganjiang River Basin, China. Water 2017, 9, 904. [Google Scholar] [CrossRef]
- Gan, Y.; Liang, X.-Z.; Duan, Q.; Ye, A.; Di, Z.; Hong, Y.; Li, J. A systematic assessment and reduction of parametric uncertainties for a distributed hydrological model. J. Hydrol. 2018, 564, 697–711. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and hydrological comparisons between TRMM and GPM level-3 products over a midlatitude basin: Is day-1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Yang, K.; Jie, H.; Tang, W.; Qin, J.; Cheng, C.C.K. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Jie, H.; Qin, J.; Shi, J.; Du, J.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Chen, L.; Frauenfeld, O.W. Surface Air Temperature Changes over the Twentieth and Twenty-First Centuries in China Simulated by 20 CMIP5 Models. J. Clim. 2014, 27, 3920–3937. [Google Scholar] [CrossRef]
- Zhang, X.J.; Tang, Q.; Pan, M.; Tang, Y. A Long-Term Land Surface Hydrologic Fluxes and States Dataset for China. J. Hydrometeorol. 2014, 15, 2067–2084. [Google Scholar] [CrossRef]
- He, J.; Yang, K. China Meteorological Forcing Dataset. Cold Arid Reg. Sci. Data Cent. Lanzhou 2011. [Google Scholar] [CrossRef]
- Huang, C.; Zheng, X.; Tait, A.; Dai, Y.; Yang, C.; Chen, Z.; Li, T.; Wang, Z. On using smoothing spline and residual correction to fuse rain gauge observations and remote sensing data. J. Hydrol. 2014, 508, 410–417. [Google Scholar] [CrossRef]
- Li, T.; Zheng, X.; Dai, Y.; Yang, C.; Chen, Z.; Zhang, S.; Wu, G.; Wang, Z.; Huang, C.; Shen, Y. Mapping near-surface air temperature, pressure, relative humidity and wind speed over Mainland China with high spatiotemporal resolution. Adv. Atmos. Sci. 2014, 31, 1127–1135. [Google Scholar] [CrossRef]
- Chen, D.; Gao, G.; Xu, C.-Y.; Guo, J.; Ren, G. Comparison of the Thornthwaite method and pan data with the standard Penman-Monteith estimates of reference evapotranspiration in China. Clim. Res. 2005, 28, 123–132. [Google Scholar] [CrossRef]
- Wang, W.; Xing, W.; Shao, Q. How large are uncertainties in future projection of reference evapotranspiration through different approaches? J. Hydrol. 2015, 524, 696–700. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A comparison of six potential evapotranspiration methods for regional use in the southeastern united states 1. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Hargreaves, G.H. Defining and using reference evapotranspiration. J. Irrig. Drain. Eng. 1994, 120, 1132–1139. [Google Scholar] [CrossRef]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based Multi-satellite Precipitation Analysis over the Wangchu Basin of Bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Khan, S.I.; Adhikari, P.; Hong, Y.; Vergara, H.F.; Adler, R.; Policelli, F.; Irwin, D.; Korme, T.; Okello, L. Hydroclimatology of Lake Victoria region using hydrologic model and satellite remote sensing data. Hydrol. Earth Syst. Sci. 2011, 15, 107–117. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Hong, Y.; Tian, Y.; Policelli, F. Evaluation of global flood detection using satellite-based rainfall and a hydrologic model. J. Hydrometeorol. 2012, 13, 1268–1284. [Google Scholar] [CrossRef]
- Kan, G.; He, X.; Ding, L.; Li, J.; Hong, Y.; Zuo, D.; Ren, M.; Lei, T.; Liang, K. Fast hydrological model calibration based on the heterogeneous parallel computing accelerated shuffled complex evolution method. Eng. Optim. 2018, 50, 106–119. [Google Scholar] [CrossRef]
- Kannan, N.; White, S.; Worrall, F.; Whelan, M. Sensitivity analysis and identification of the best evapotranspiration and runoff options for hydrological modelling in SWAT-2000. J. Hydrol. 2007, 332, 456–466. [Google Scholar] [CrossRef]
- Burnash, R. The NWS river forecast system-catchment modeling. Comput. Models Watershed Hydrol. 1995, 188, 311–366. [Google Scholar]
- Oudin, L.; Perrin, C.; Mathevet, T.; Andréassian, V.; Michel, C. Impact of biased and randomly corrupted inputs on the efficiency and the parameters of watershed models. J. Hydrol. 2006, 320, 62–83. [Google Scholar] [CrossRef]
- Lingling, Z.; Jun, X.; Chongyu, X. A review of evapotranspiration estimation methods in hydrological models. Acta Geogr. Sin. 2013, 68, 127–136. [Google Scholar]
| Spatial Scale | Generated from BNU Forcing Data | Generated from ITPCAS Forcing Data |
|---|---|---|
| 10 km | (1) BNU-10 km-HS | (7) ITPCAS-10 km-HS |
| (2) BNU-10 km-PM | (8) ITPCAS-10 km-PM | |
| 25 km | (3) BNU-25 km-HS | (9) ITPCAS-25 km-HS |
| (4) BNU-25 km-PM | (10) ITPCAS-25 km-PM | |
| 100 km | (5) BNU-100 km-HS | (11) ITPCAS-100 km-HS |
| (6) BNU-100 km-PM | (12) ITPCAS-100 km-PM |
| Statistic Metrics | Equation | Perfect Value |
|---|---|---|
| Correlation coefficient (CC) | 1 | |
| Relative bias (BIAS) | 0 | |
| Root mean squared error (RMSE) | 0 | |
| Nash-Sutcliffe coefficient efficiency (NSCE) | 1 |
| Dataset Number | Data | BIAS (%) | CC | RMSE (m3/d) | NSCE |
|---|---|---|---|---|---|
| 1 | BNU-10 km-HS | 7.00 | 0.79 | 1227.21 | 0.56 |
| 2 | BNU-10 km-PM | 7.91 | 0.79 | 1221.89 | 0.57 |
| 3 | BNU-25 km-HS | 4.85 | 0.78 | 1213.47 | 0.57 |
| 4 | BNU-25 km-PM | 5.67 | 0.79 | 1210.85 | 0.58 |
| 5 | BNU-100 km-HS | 7.04 | 0.79 | 1216.84 | 0.57 |
| 6 | BNU-100 km-PM | −3.04 | 0.78 | 1237.51 | 0.56 |
| 7 | ITPCAS-10 km-HS | 7.87 | 0.79 | 1221.46 | 0.57 |
| 8 | ITPCAS-10 km-PM | 4.22 | 0.79 | 1227.25 | 0.56 |
| 9 | ITPCAS-25 km-HS | 3.88 | 0.80 | 1219.40 | 0.57 |
| 10 | ITPCAS-25 km-PM | 7.05 | 0.78 | 1236.55 | 0.56 |
| 11 | ITPCAS-100 km-HS | 6.23 | 0.75 | 1314.57 | 0.50 |
| 12 | TIPCAS-100 km-PM | −2.13 | 0.72 | 1328.21 | 0.49 |
| Dataset-Group | BIAS (%)-STD | CC-STD | RMSE (m3/d)-STD | NSCE-STD |
|---|---|---|---|---|
| BNU-HS | 1.02 | 0.0047 | 5.85 | 0.0047 |
| BNU-PM | 4.72 | 0.0047 | 10.94 | 0.0082 |
| ITPCAS-HS | 1.64 | 0.0216 | 44.39 | 0.033 |
| ITPCAS-PM | 3.84 | 0.0309 | 45.56 | 0.033 |
| Data | BIAS (%) | CC | RMSE (m3/d) | NSCE |
|---|---|---|---|---|
| ITPCAS-25 km-HS | 6.81 | 0.74 | 1163.65 | 0.37 |
| ITPCAS-25 km-PM | 29.35 | 0.36 | 1640.71 | −0.25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yang, Y.; Kan, G.; Hong, Y. Study on the Applicability of the Hargreaves Potential Evapotranspiration Estimation Method in CREST Distributed Hydrological Model (Version 3.0) Applications. Water 2018, 10, 1882. https://doi.org/10.3390/w10121882
Li Z, Yang Y, Kan G, Hong Y. Study on the Applicability of the Hargreaves Potential Evapotranspiration Estimation Method in CREST Distributed Hydrological Model (Version 3.0) Applications. Water. 2018; 10(12):1882. https://doi.org/10.3390/w10121882
Chicago/Turabian StyleLi, Zhansheng, Yuan Yang, Guangyuan Kan, and Yang Hong. 2018. "Study on the Applicability of the Hargreaves Potential Evapotranspiration Estimation Method in CREST Distributed Hydrological Model (Version 3.0) Applications" Water 10, no. 12: 1882. https://doi.org/10.3390/w10121882
APA StyleLi, Z., Yang, Y., Kan, G., & Hong, Y. (2018). Study on the Applicability of the Hargreaves Potential Evapotranspiration Estimation Method in CREST Distributed Hydrological Model (Version 3.0) Applications. Water, 10(12), 1882. https://doi.org/10.3390/w10121882







