How Ångström–Prescott Coefficients Alter the Estimation of Agricultural Water Demand in South Korea
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. FAO Penman–Monteith Equation
2.3. Ångström–Prescott Coefficients
2.4. Irrigation Water Requirement
2.5. Design Water Requirement
3. Results
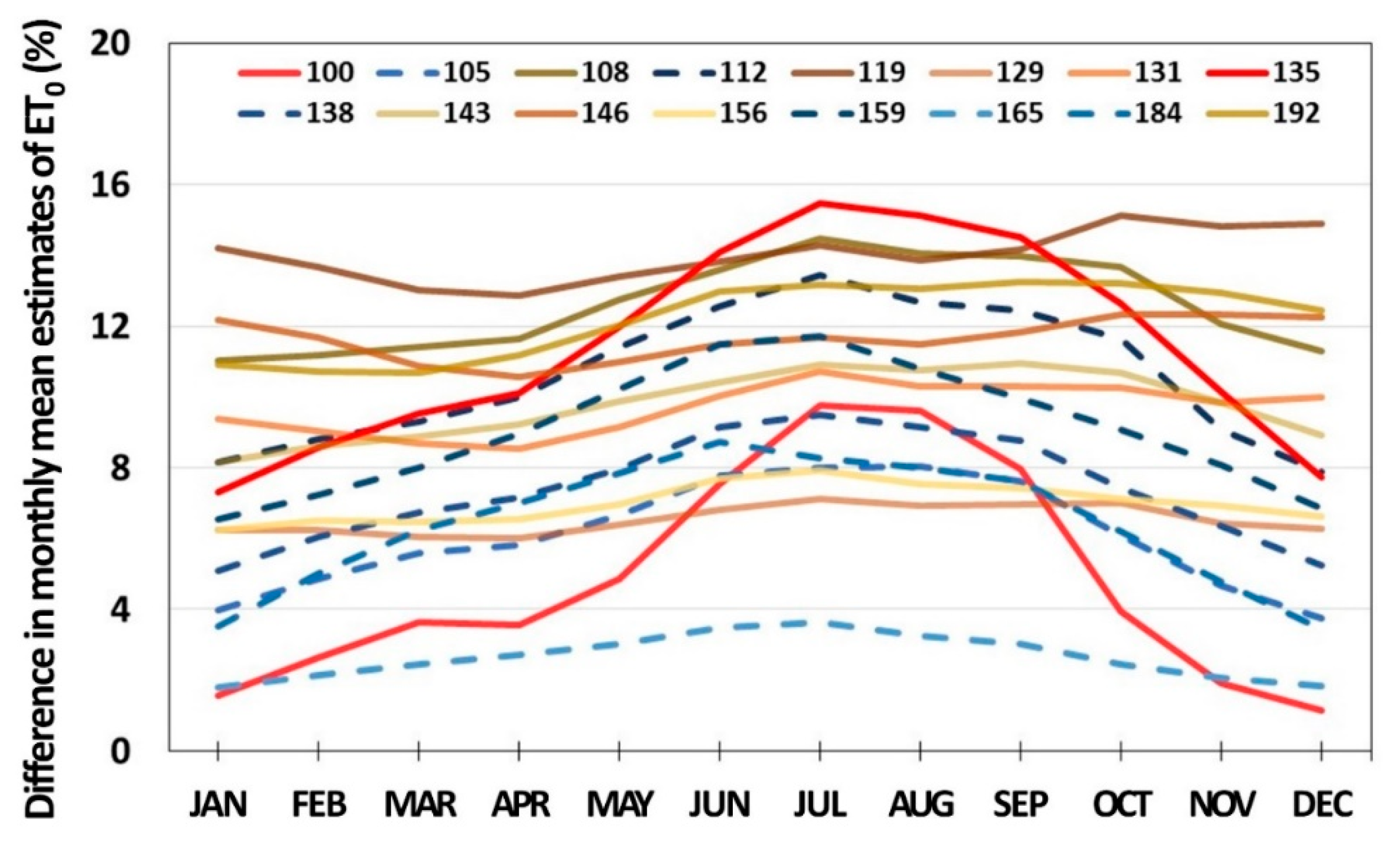
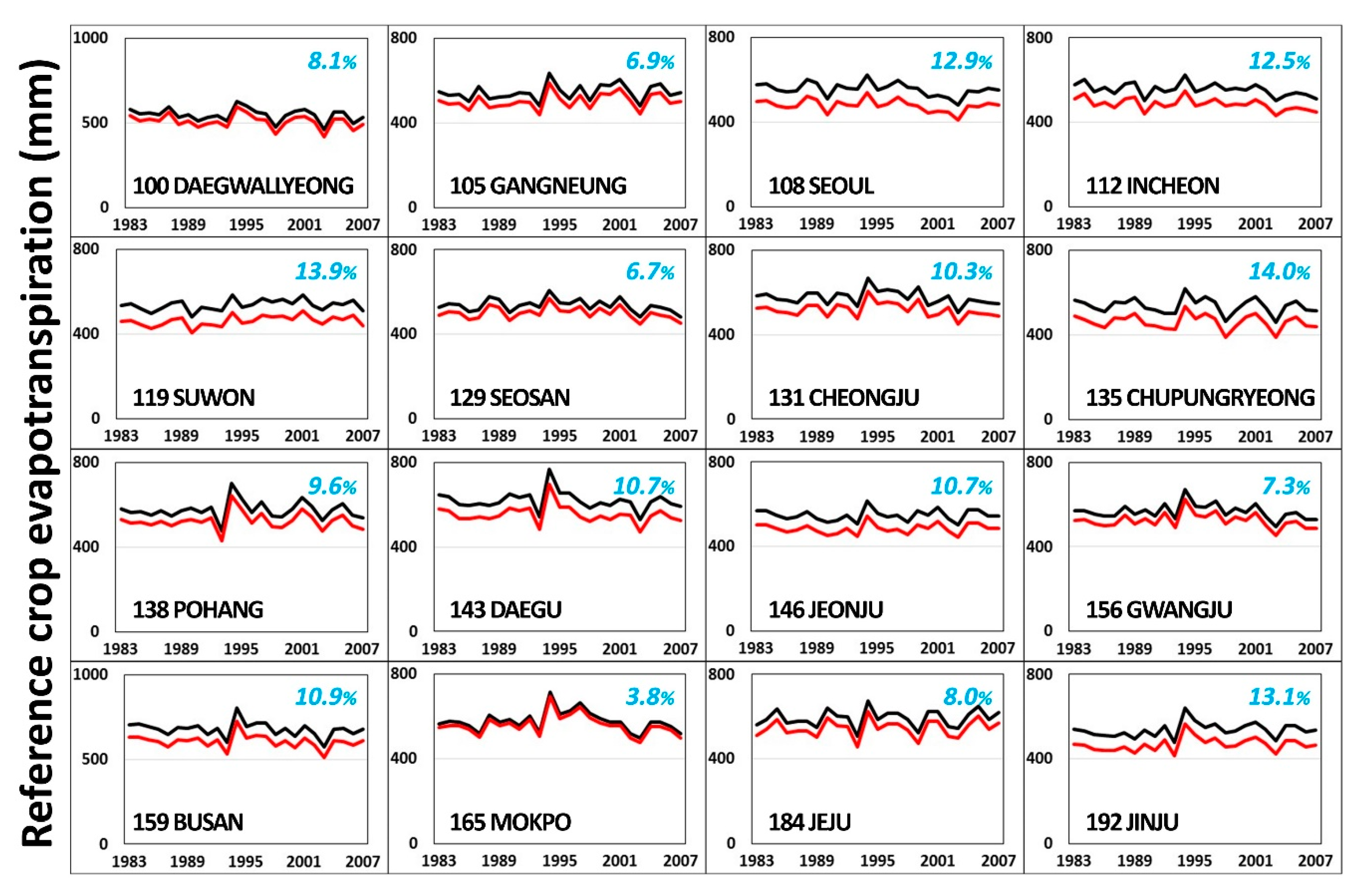
3.1. Reference Crop Evapotranspiration
3.2. Irrigation Water Requirement
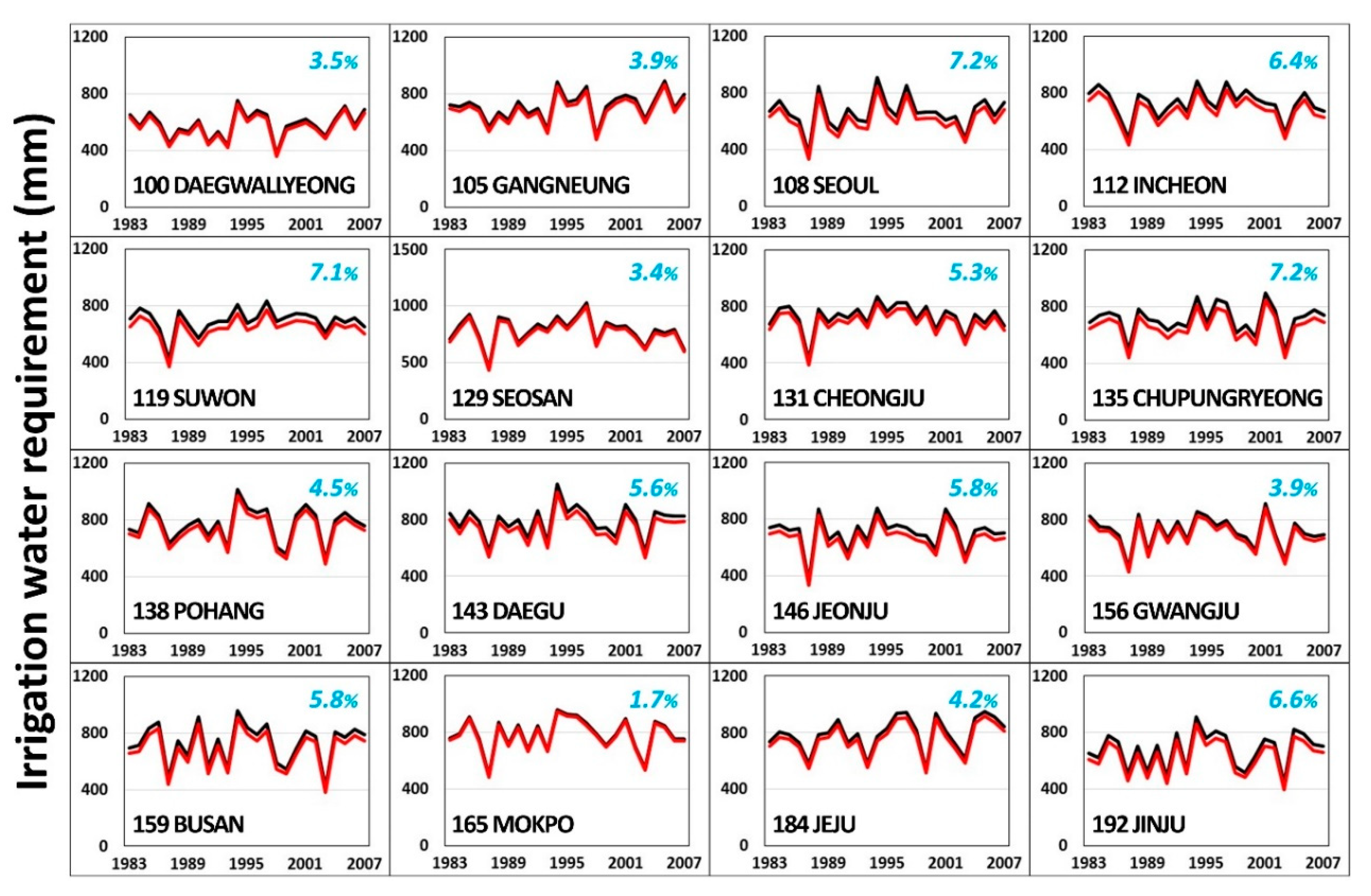
3.3. Design Water Requirement
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Döll, P. Vulnerability to the impact of climate change on renewable groundwater resources: A global-scale assessment. Environ. Res. Lett. 2009, 4, 035006. [Google Scholar] [CrossRef]
- de Fraiture, C.; Wichelns, D. Satisfying future water demands for agriculture. Agric. Water Manag. 2010, 97, 502–511. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. In FAO Irrigation and Drainage Paper No. 56; Food and Agricultural Organization (FAO): Rome, Italy, 1998. [Google Scholar]
- Chen, D.; Gao, G.; Xu, C.; Guo, J.; Ren, G. Comparison of the Thornthwaite method and pan data with the standard Penman-Monteith estimates of reference evapotranspiration in China. Clim. Res. 2005, 28, 123–132. [Google Scholar] [CrossRef]
- Cai, J.; Liu, Y.; Lei, T.; Pereira, L.S. Estimating reference evapotranspiration with the FAO Penman–Monteith equation using daily weather forecast messages. Agric. For. Meteorol. 2007, 145, 22–35. [Google Scholar] [CrossRef]
- Bojanowski, J.S.; Vrieling, A.; Skidmore, A.K. Calibration of solar radiation models for Europe using Meteosat Second Generation and weather station data. Agric. For. Meteorol. 2013, 176, 1–9. [Google Scholar] [CrossRef]
- Liu, X.; Mei, X.; Li, Y.; Wang, Q.; Zhang, Y.; Porter, J.R. Variation in reference crop evapotranspiration caused by the Ångström–Prescott coefficient: Locally calibrated versus the FAO recommended. Agric. Water Manag. 2009, 96, 1137–1145. [Google Scholar] [CrossRef]
- Podestá, G.P.; Núñez, L.; Villanueva, C.A.; Skansi, M.A. Estimating daily solar radiation in the Argentine Pampas. Agric. For. Meteorol. 2004, 123, 41–53. [Google Scholar] [CrossRef]
- Rahimi, I.; Bakhtiari, B.; Qaderi, K.; Aghababaie, M. Calibration of Angstrom Equation for Estimating Solar Radiation using Meta-Heuristic Harmony Search Algorithm (Case study: Mashhad-East of Iran). Energy Procedia 2012, 18, 644–651. [Google Scholar] [CrossRef]
- Sabziparvar, A.A.; Mousavi, R.; Marofi, S.; Ebrahimipak, N.A.; Heidari, M. An Improved Estimation of the Angstrom–Prescott Radiation Coefficients for the FAO56 Penman–Monteith Evapotranspiration Method. Water Resour. Manag. 2013, 27, 2839–2854. [Google Scholar] [CrossRef]
- Aladenola, O.O.; Madramootoo, C.A. Evaluation of solar radiation estimation methods for reference evapotranspiration estimation in Canada. Theor. Appl. Climatol. 2014, 118, 377–385. [Google Scholar] [CrossRef]
- Choi, M.-H.; Yun, J.-I.; Chung, U.-R.; Moon, K.-H. Performance of Angstrom-Prescott Coefficients under Different Time Scales in Estimating Daily Solar Radiation in South Korea. Korean J. Agric. For. Meteorol. 2010, 12, 232–237. [Google Scholar] [CrossRef]
- Yoo, S.-H.; Choi, J.-Y.; Jang, M.-W. Estimation of design water requirement using FAO Penman–Monteith and optimal probability distribution function in South Korea. Agric. Water Manag. 2008, 95, 845–853. [Google Scholar] [CrossRef]
- Pereira, L.S.; Alves, I. Crop Water Requirements. Encycl. Soils Environ. 2005, 322–334. [Google Scholar] [CrossRef]
- Bae, S.; Lee, S.-H.; Yoo, S.-H.; Kim, T. Analysis of Drought Intensity and Trends Using the Modified SPEI in South Korea from 1981 to 2010. Water 2018, 10, 327. [Google Scholar] [CrossRef]
- Ministry of Land, Transport and Maritime Affairs (MLTM). Long-Term Plans for Water Resources (2011–2020); MLTM: Gwacheon, Korea, 2010.
- Rubel, F.; Brugger, K.; Haslinger, K.; Auer, I. The climate of the European Alps: Shift of very high resolution Köppen-Geiger climate zones 1800–2100. Meteorol. Zeitschrift 2017, 26, 115–125. [Google Scholar] [CrossRef]
- Jensen, M.E.; Burman, R.D.; Allen, R.G. Evapotranspiration and Irrigation Water Requirements; ASCE Manual, No.70; American Society of Civil Engineers: New York, NY, USA, 1990. [Google Scholar]
- Yoo, S.H.; Choi, J.Y.; Jang, M.W. Estimation of paddy rice crop coefficient for FAO Penman–Monteith and modified Penman method. J. Korean Soc. Agric. Eng. 2006, 48, 13–23. [Google Scholar] [CrossRef]
- Lee, N.H. Simulating Daily Operation of Water Management System of Irrigation Districts. Ph.D. Thesis, Seoul National University, Seoul, Korea, 1989. [Google Scholar]
- International Rice Research Institute (IRRI). Annual Report for 1997; IRRI: Los Banos, Philippines, 1978. [Google Scholar]
- Dastane, N.G. Effective Rainfall in Irrigated Agriculture; Food and Agriculture Organization of the United Nations: Rome, Italy, 1978. [Google Scholar]
- Ministry of Agriculture and Forestry (MAF). Design Criteria of Land and Water Development Plan for Agriculture (Irrigation); MAF: Gwacheon, Korea, 1998.
- Chow, V.T. A general formula for hydrologic frequency analysis. Trans. Am. Geophys. Union 1951, 32, 231–237. [Google Scholar] [CrossRef]
- Lee, K.-H. Constructing a non-linear relationship between the incoming solar radiation and bright sunshine duration. Int. J. Climatol. 2010, 30, 1884–1892. [Google Scholar] [CrossRef]
- Palmer, W. Meteorological Droughts; Research paper, No. 45; US Department of Commerce Weather Bureau: Washington, DC, USA, 1965.
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I.; Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Yoo, S.-H.; Choi, J.-Y.; Nam, W.-H.; Hong, E. Analysis of design water requirement of paddy rice using frequency analysis affected by climate change in South Korea. Agric. Water Manag. 2012, 112, 33–42. [Google Scholar] [CrossRef]
- Hao, X.; Zhang, S.; Li, W.; Duan, W.; Fang, G.; Zhang, Y.; Guo, B. The Uncertainty of Penman-Monteith Method and the Energy Balance Closure Problem. J. Geophys. Res. Atmos. 2018, 123, 7433–7443. [Google Scholar] [CrossRef]
- Mokhtari, A.; Noory, H.; Vazifedoust, M. Performance of Different Surface Incoming Solar Radiation Models and Their Impacts on Reference Evapotranspiration. Water Resour. Manag. 2018, 32, 3053–3070. [Google Scholar] [CrossRef]
- Yoder, R.E.; Odhiambo, L.O.; Wright, W.C. Effects of Vapor-Pressure Deficit and Net-Irradiance Calculation Methods on Accuracy of Standardized Penman-Monteith Equation in a Humid Climate. J. Irrig. Drain. Eng. 2005, 131, 228–237. [Google Scholar] [CrossRef]

| Station ID | Station Name | Latitude (°N) | Longitude (°E) | Elevation (m) | Location | Climate Classification 1 | Ångström–Prescott Coefficients 2 | ||
|---|---|---|---|---|---|---|---|---|---|
| a | b | a + b | |||||||
| 100 | Daegwallyeong | 37.68 | 128.72 | 772.6 | Inland | Dfb | 0.175 | 0.559 | 0.734 |
| 105 | Gangneung | 37.75 | 128.89 | 26.0 | Coast | Cfa | 0.217 | 0.482 | 0.699 |
| 108 | Seoul | 37.57 | 126.97 | 85.7 | Inland | Cwa | 0.197 | 0.452 | 0.648 |
| 112 | Incheon | 37.48 | 126.62 | 69.0 | Coast | Cwa | 0.192 | 0.476 | 0.661 |
| 119 | Suwon | 37.27 | 126.99 | 34.8 | Inland | Cwa | 0.199 | 0.459 | 0.658 |
| 129 | Seosan | 36.78 | 126.49 | 28.9 | Inland | Cwa | 0.222 | 0.484 | 0.706 |
| 131 | Cheongju | 36.64 | 127.44 | 58.7 | Inland | Cwa | 0.198 | 0.491 | 0.689 |
| 135 | Chupungryeong | 36.22 | 127.99 | 243.7 | Inland | Cwa | 0.181 | 0.485 | 0.666 |
| 138 | Pohang | 36.03 | 129.38 | 3.9 | Coast | Cfa | 0.201 | 0.493 | 0.694 |
| 143 | Daegu | 35.88 | 128.65 | 53.5 | Inland | Cwa | 0.204 | 0.463 | 0.667 |
| 146 | Jeonju | 35.84 | 127.12 | 61.4 | Inland | Cfa | 0.206 | 0.470 | 0.676 |
| 156 | Gwangju | 35.17 | 126.89 | 72.4 | Inland | Cfa | 0.211 | 0.495 | 0.706 |
| 159 | Busan | 35.10 | 129.03 | 69.6 | Coast | Cwa | 0.200 | 0.471 | 0.671 |
| 165 | Mokpo | 34.82 | 126.38 | 38.0 | Coast | Cfa | 0.230 | 0.500 | 0.729 |
| 184 | Jeju | 33.51 | 126.53 | 20.5 | Coast | Cfa | 0.197 | 0.506 | 0.703 |
| 192 | Jinju | 35.16 | 128.04 | 30.2 | Inland | Cwa | 0.194 | 0.477 | 0.743 |
| Station ID | Station Name | A-P Coefficients | Daily | Monthly | Annual | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||||
| 100 | Daegwallyeong | Recommended | 2.1 (5.8%) 1,** | 24.0 (1.6%) | 29.6 (2.6%) | 51.7 (3.6%) | 91.3 (3.6%) | 109.3 (4.8%) * | 100.5 (7.6%) * | 95.4 (9.8%) | 87.6 (9.6%) * | 64.0 (7.9%) ** | 55.1 (4.0%) | 38.3 (1.9%) | 27.4 (1.2%) | 774.3 (5.8%) ** |
| Calibrated | 2.0 | 23.7 | 28.8 | 49.8 | 88.1 | 104.0 | 92.9 | 86.0 | 79.2 | 58.9 | 52.9 | 37.6 | 27.1 | 729.1 | ||
| 105 | Gangneung | Recommended | 2.7 (6.5%) ** | 42.3 (4.0%) | 46.4 (4.9%) | 70.6 (5.6%) | 104.9 (5.8%) | 124.4 (6.7%) * | 113.6 (7.8%) * | 114.9 (8.0%) | 107.9 (8.0%) * | 83.7 (7.6%) ** | 73.7 (6.1%) * | 54.5 (4.7%) | 46.3 (3.8%) | 983.3 (6.5%) ** |
| Calibrated | 2.5 | 40.7 | 44.2 | 66.6 | 98.8 | 116.1 | 104.7 | 105.7 | 99.2 | 77.3 | 69.2 | 52.0 | 44.6 | 919.1 | ||
| 108 | Seoul | Recommended | 2.5 (13.0%) ** | 26.5 (11.0%) ** | 36.3 (11.2%) ** | 64.0 (11.4%) ** | 97.3 (11.6%) ** | 121.0 (12.8%) ** | 122.5 (13.6%) ** | 109.5 (14.5%) ** | 113.6 (14.1%) ** | 90.0 (14.0%) ** | 66.4 (13.7%) ** | 38.7 (12.1%) ** | 26.8 (11.3%) ** | 912.6 (13.0%) ** |
| Calibrated | 2.2 | 23.6 | 32.2 | 56.7 | 86.0 | 105.6 | 105.9 | 93.7 | 97.6 | 77.4 | 57.3 | 34.1 | 23.8 | 793.8 | ||
| 112 | Incheon | Recommended | 2.5 (11.4%) ** | 29.2 (8.2%) * | 37.7 (8.8%) ** | 63.4 (9.3%) ** | 92.4 (10.0%) ** | 115.1 (11.4%) ** | 118.6 (12.6%) ** | 112.6 (13.4%) ** | 118.2 (12.7%) ** | 91.5 (12.5%) ** | 67.2 (11.6%) ** | 42.7 (9.1%) ** | 30.9 (7.9%) ** | 919.5 (11.4%) ** |
| Calibrated | 2.2 | 26.8 | 34.3 | 57.5 | 83.2 | 101.9 | 103.7 | 97.5 | 103.2 | 80.1 | 59.4 | 38.8 | 28.4 | 815.0 | ||
| 119 | Suwon | Recommended | 2.3 (13.9%) ** | 21.3 (14.2%) ** | 30.6 (13.7%) ** | 56.4 (13.0%) ** | 87.2 (12.8%) ** | 112.5 (13.4%) ** | 116.4 (13.8%) ** | 110.4 (14.3%) ** | 112.6 (13.9%) ** | 85.6 (14.2%) ** | 57.9 (15.1%) ** | 31.5 (14.8%) ** | 20.9 (14.9%) ** | 843.3 (13.9%) ** |
| Calibrated | 2.0 | 18.3 | 26.4 | 49.1 | 76.0 | 97.4 | 100.3 | 94.7 | 97.0 | 73.4 | 49.2 | 26.9 | 17.8 | 726.4 | ||
| 129 | Seosan | Recommended | 2.3 (6.6%) ** | 22.9 (6.2%) | 31.3 (6.3%) | 56.0 (6.0%) ** | 85.7 (6.0%) ** | 112.2 (6.4%) ** | 114.8 (6.8%) ** | 109.2 (7.1%) * | 114.1 (6.9%) * | 86.3 (7.0%) * | 60.3 (7.0%) ** | 34.0 (6.4%) * | 22.8 (6.3%) * | 849.8 (6.6%) ** |
| Calibrated | 2.2 | 21.5 | 29.3 | 52.7 | 80.6 | 105.0 | 107.0 | 101.4 | 106.2 | 80.3 | 56.1 | 31.8 | 21.4 | 793.3 | ||
| 131 | Cheongju | Recommended | 2.5 (9.8%) ** | 22.5 (9.4%) * | 33.0 (9.1%) * | 61.9 (8.7%) ** | 97.3 (8.5%) ** | 123.6 (9.2%) ** | 124.5 (10.0%) ** | 121.1 (10.7%) ** | 119.4 (10.3%) ** | 87.0 (10.3%) ** | 60.7 (10.2%) ** | 33.2 (9.9%) ** | 21.4 (10.0%) ** | 905.5 (9.8%) ** |
| Calibrated | 2.2 | 20.4 | 30.0 | 56.5 | 89.0 | 112.3 | 112.0 | 108.1 | 107.1 | 78.0 | 54.4 | 29.9 | 19.3 | 817.1 | ||
| 135 | Chupungryeong | Recommended | 2.5 (12.4%) ** | 33.2 (7.3%) * | 40.8 (8.6%) * | 68.7 (9.5%) * | 102.7 (10.1%) ** | 121.4 (12.0%) ** | 115.7 (14.1%) ** | 111.5 (15.5%) ** | 107.3 (15.1%) ** | 81.0 (14.5%) ** | 64.1 (12.6%) ** | 41.6 (10.1%) ** | 32.8 (7.7%) | 920.7 (12.4%) ** |
| Calibrated | 2.2 | 30.7 | 37.3 | 62.1 | 92.3 | 106.9 | 99.4 | 94.2 | 91.1 | 69.2 | 56.0 | 37.4 | 30.3 | 806.9 | ||
| 138 | Pohang | Recommended | 2.8 (7.9%) ** | 43.3 (5.1%) | 48.6 (6.1%) | 73.7 (6.7%) | 105.1 (7.2%) ** | 125.1 (8.0%) ** | 118.4 (9.2%) ** | 123.3 (9.5%) * | 119.0 (9.2%) * | 89.2 (8.8%) ** | 75.9 (7. 4%) * | 52.7 (6.4%) * | 42.9 (5.3%) | 1017.1 (7.9%) ** |
| Calibrated | 2.6 | 41.1 | 45.7 | 68.8 | 97.5 | 115.1 | 107.5 | 111.6 | 108.1 | 81.3 | 70.3 | 49.4 | 40.7 | 937.1 | ||
| 143 | Daegu | Recommended | 2.9 (10.0%) ** | 38.5 (8.1%) ** | 47.2 (8.6%) ** | 77.3 (8.9%) ** | 111.6 (9.2%) ** | 135.2 (9.9%) ** | 132.6 (10.4%) ** | 130.2 (10.9%) ** | 126.7 (10.8%) ** | 93.6 (11.0%) ** | 74.8 (10.7%) ** | 47.8 (9.8%) ** | 36.8 (8.9%) ** | 1052.3 (10.0%) ** |
| Calibrated | 2.6 | 35.4 | 43.2 | 70.4 | 101.3 | 121.9 | 118.8 | 116.0 | 113.0 | 83.3 | 66.8 | 43.1 | 33.6 | 946.7 | ||
| 146 | Jeonju | Recommended | 2.4 (11.5%) ** | 23.2 (12.2%) ** | 32.4 (11.7%) ** | 59.2 (10.9%) ** | 92.1 (10.6%) ** | 115.6 (11.0%) ** | 115.7 (11.5%) ** | 115.8 (11.7%) ** | 114.9 (11.5%) ** | 85.9 (11.8%) ** | 61.4 (12.3%) ** | 34.6 (12.3%) ** | 23.0 (12.3%) ** | 873.9 (11.5%) ** |
| Calibrated | 2.1 | 20.4 | 28.7 | 52.8 | 82.4 | 102.9 | 102.5 | 102.3 | 101.7 | 75.8 | 53.8 | 30.3 | 20.1 | 773.7 | ||
| 156 | Gwangju | Recommended | 2.5 (7.2%) ** | 28.4 (6.2%) ** | 37.0 (6.5%) * | 64.3 (6.5%) ** | 95.0 (6.5%) ** | 118.7 (7.0%) ** | 117.0 (7.7%) ** | 119.3 (7.9%) * | 120.2 (7.6%) * | 91.3 (7.4%) * | 68.8 (7.1%) ** | 39.6 (6.9%) ** | 27.4 (6.6%) * | 927.1 (7.2%) ** |
| Calibrated | 2.4 | 26.6 | 34.6 | 60.1 | 88.8 | 110.5 | 108.0 | 109.8 | 111.2 | 84.5 | 63.9 | 36.8 | 25.6 | 860.5 | ||
| 159 | Busan | Recommended | 2.9 (9.6%) ** | 50.8 (6.5%) ** | 56.6 (7.2%) * | 80.5 (8.0%) ** | 102.9 (9.0%) ** | 119.4 (10.2%) ** | 111.9 (11.5%) ** | 115.4 (11.7%) ** | 127.9 (10.8%) * | 100.3 (10.0%) ** | 87.2 (9.1%) ** | 61.5 (8.1%) ** | 51.4 (6.9%) ** | 1065.8 (9.6%) ** |
| Calibrated | 2.6 | 47.4 | 52.5 | 74.1 | 93.7 | 107.2 | 99.1 | 101.9 | 114.1 | 90.3 | 79.3 | 56.5 | 47.9 | 964.0 | ||
| 165 | Mokpo | Recommended | 2.7 (2.9%) ** | 38.2 (1.8%) | 43.4 (2.1%) | 67.9 (2.4%) | 94.7 (2.7%) | 115.6 (3.0%) | 114.3 (3.5%) | 118.3 (3.6%) | 129.3 (3.3%) | 100.6 (3.0%) | 85.7 (2.4%) | 55.5 (2.1%) | 39.4 (1.8%) | 1002.9 (2.9%) |
| Calibrated | 2.7 | 37.5 | 42.5 | 66.3 | 92.2 | 112.0 | 110.3 | 114.0 | 125.1 | 97.6 | 83.6 | 54.3 | 38.7 | 974.0 | ||
| 184 | Jeju | Recommended | 2.9 (7.0%) ** | 45.8 (3.5%) | 49.1 (5.0%) | 71.2 (6.2%) | 94.8 (7.0%) ** | 113.3 (7.9%) ** | 113.7 (8.7%) ** | 135.0 (8.3%) * | 131.1 (8.0%) * | 100.4 (7.6%) ** | 84.4 (6.2%) ** | 59.7 (4.8%) | 47.2 (3.5%) | 1045.7 (7.0%) ** |
| Calibrated | 2.7 | 44.2 | 46.6 | 66.7 | 88.1 | 104.4 | 103.8 | 123.9 | 120.6 | 92.8 | 79.2 | 56.8 | 45.6 | 972.7 | ||
| 192 | Jinju | Recommended | 2.5 (12.4%) ** | 30.9 (10.9%) ** | 39.9 (10.7%) ** | 65.8 (10.7%) ** | 92.0 (11.2%) ** | 113.1 (12.0%) ** | 111.3 (13.0%) ** | 115.3 (13.2%) ** | 113.9 (13.1%) ** | 83.7 (13.2%) ** | 63.2 (13.2%) ** | 37.6 (12.9%) ** | 28.2 (12.4%) ** | 895.0 (12.4%) ** |
| Calibrated | 2.1 | 27.5 | 35.6 | 58.8 | 81.7 | 99.5 | 96.9 | 100.1 | 99.1 | 72.6 | 54.8 | 32.7 | 24.7 | 784.1 | ||
| Average | Recommended | 2.6 (9.2%) | 32.6 (6.8%) | 40.0 (7.5%) | 65.8 (7.9%) | 96.7 (8.2%) | 118.5 (9.1%) | 116.3 (10.1%) | 116.1 (10.6%) | 116.5 (10.2%) | 88.4 (10.0%) | 69.2 (9.1%) | 44.0 (7.8%) | 32.9 (6.9%) | 936.8 (9.2%) | |
| Calibrated | 2.3 | 30.4 | 37.0 | 60.6 | 88.7 | 107.7 | 104.5 | 103.8 | 104.6 | 79.6 | 62.9 | 40.5 | 30.6 | 850.8 | ||
| Station ID | Station Name | Ångström–Prescott Coefficients | Mean (mm) | Max (mm) | Min (mm) | SD 1 | CV 1 | CS 1 | CK 1 |
|---|---|---|---|---|---|---|---|---|---|
| 100 | Daegwallyeong | Recommended | 583.9 (3.5%) 2 | 752.4 (3.1%) | 370.2 (2.9%) | 92.9 | 0.159 | −0.466 | 3.296 |
| Calibrated | 563.3 | 729.5 | 359.4 | 90.2 | 0.160 | −0.406 | 3.234 | ||
| 105 | Gangneung | Recommended | 715.8 (3.9%) | 891.1 (3.2%) | 497.6 (4.4%) | 97.0 | 0.136 | −0.340 | 3.523 |
| Calibrated | 688.2 | 862.9 | 475.6 | 95.0 | 0.138 | −0.352 | 3.521 | ||
| 108 | Seoul | Recommended | 662.8 (7.2%) | 908.1 (7.1%) | 370.2 (9.8%) | 114.0 | 0.172 | −0.157 | 4.608 |
| Calibrated | 614.8 | 844.0 | 334.0 | 107.9 | 0.175 | −0.181 | 4.569 | ||
| 112 | Incheon | Recommended | 729.6 (6.3%) | 883.1 (6.1%) | 475.7 (9.0%) | 98.9 | 0.136 | −0.822 | 4.335 |
| Calibrated | 683.3 | 828.9 | 433.0 | 95.2 | 0.139 | −0.854 | 4.402 | ||
| 119 | Suwon | Recommended | 695.1 (7.1%) * | 833.3 (7.1%) | 417.6 (10.7%) | 82.3 | 0.118 | −1.515 | 7.720 |
| Calibrated | 645.7 | 773.8 | 373.0 | 79.2 | 0.123 | −1.677 | 8.219 | ||
| 129 | Seosan | Recommended | 712.1 (3.4%) | 951.7 (3.2%) | 377.3 (5.7%) | 120.6 | 0.169 | −0.692 | 4.605 |
| Calibrated | 687.8 | 921.2 | 355.8 | 118.3 | 0.172 | −0.730 | 4.698 | ||
| 131 | Cheongju | Recommended | 725.8 (5.3%) | 869.1 (5.0%) | 420.9 (8.2%) | 93.2 | 0.128 | −1.534 | 6.960 |
| Calibrated | 687.5 | 825.8 | 386.3 | 91.0 | 0.132 | −1.598 | 7.194 | ||
| 135 | Chupungryeong | Recommended | 711.7 (7.2%) | 898.6 (6.1%) | 482.8 (9.0%) | 102.5 | 0.144 | −0.473 | 3.806 |
| Calibrated | 660.3 | 843.5 | 439.4 | 99.3 | 0.150 | −0.504 | 3.792 | ||
| 138 | Pohang | Recommended | 770.0 (4.5%) | 1012.1 (3.9%) | 514.7 (5.1%) | 121.2 | 0.157 | −0.385 | 3.091 |
| Calibrated | 735.4 | 973.1 | 488.4 | 118.2 | 0.161 | −0.372 | 3.087 | ||
| 143 | Daegu | Recommended | 792.3 (5.6%) | 1051.6 (5.3%) | 567.9 (6.4%) | 108.4 | 0.137 | −0.231 | 3.978 |
| Calibrated | 747.7 | 995.8 | 531.8 | 105.1 | 0.141 | −0.273 | 3.924 | ||
| 146 | Jeonju | Recommended | 704.4 (5.8%) | 880.2 (5.7%) | 361.3 (7.7%) | 111.3 | 0.158 | −1.148 | 6.083 |
| Calibrated | 663.2 | 830.3 | 333.6 | 107.0 | 0.161 | −1.124 | 6.065 | ||
| 156 | Gwangju | Recommended | 716.9 (3.9%) | 910.6 (3.2%) | 456.0 (5.0%) | 109.1 | 0.152 | −0.613 | 3.571 |
| Calibrated | 689.1 | 881.4 | 433.4 | 107.0 | 0.155 | −0.608 | 3.572 | ||
| 159 | Busan | Recommended | 728.9 (5.8%) | 960.8 (5.4%) | 415.5 (8.1%) | 140.8 | 0.193 | −0.620 | 2.966 |
| Calibrated | 686.6 | 909.1 | 381.7 | 136.5 | 0.199 | −0.632 | 2.975 | ||
| 165 | Mokpo | Recommended | 787.3 (1.7%) | 960.9 (1.5%) | 495.2 (2.3%) | 115.4 | 0.147 | −0.805 | 3.873 |
| Calibrated | 774.1 | 946.4 | 484.0 | 114.6 | 0.148 | −0.801 | 3.869 | ||
| 184 | Jeju | Recommended | 789.6 (4.1%) | 950.7 (3.7%) | 535.3 (3.8%) | 118.0 | 0.149 | −0.620 | 3.104 |
| Calibrated | 756.9 | 915.2 | 514.8 | 114.9 | 0.152 | −0.591 | 3.048 | ||
| 192 | Jinju | Recommended | 678.8 (6.6%) | 913.5 (6.1%) | 438.2 (8.8%) | 125.7 | 0.185 | −0.341 | 2.478 |
| Calibrated | 633.7 | 857.6 | 399.8 | 121.4 | 0.192 | −0.356 | 2.494 |
| Station ID | Station Name | Recommended Ångström–Prescott Coefficients | Calibrated Ångström–Prescott Coefficients | ||
|---|---|---|---|---|---|
| DWR (mm) | DRDY | DWR (mm) | DRDY | ||
| 100 | Daegwallyeong | 693.5 (3.4%) 1 | 2007 | 670.2 | 2007 |
| 105 | Gangneung | 831.2 (3.6%) | 1997 | 801.2 | 1997 |
| 108 | Seoul | 799.9 (6.9%) | 1988 | 744.4 | 2005 |
| 112 | Incheon | 843.2 (6.0%) | 1984 | 792.2 | 1999 |
| 119 | Suwon | 784.2 (6.9%) | 1984 | 730.2 | 1984 |
| 129 | Seosan | 852.1 (3.2%) | 1985 | 824.7 | 1985 |
| 131 | Cheongju | 826.4 (5.0%) | 1996 | 785.3 | 1996 |
| 135 | Chupungryeong | 832.6 (6.7%) | 1997 | 777.1 | 1997 |
| 138 | Pohang | 913.8 (4.2%) | 1985 | 875.7 | 1985 |
| 143 | Daegu | 922.1 (5.3%) | 1996 | 873.3 | 1996 |
| 146 | Jeonju | 828.7 (5.5%) | 2001 | 782.9 | 1988 |
| 156 | Gwangju | 844.3 (3.6%) | 1988 | 814.1 | 1994 |
| 159 | Busan | 893.2 (5.3%) | 1986 | 845.7 | 1986 |
| 165 | Mokpo | 920.0 (1.5%) | 1996 | 905.8 | 1996 |
| 184 | Jeju | 927.3 (3.9%) | 1996 | 891.2 | 1996 |
| 192 | Jinju | 828.3 (6.1%) | 2004 | 778.0 | 2004 |
| Average | 846.3 (4.8%) | 805.8 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, H.; Bhattarai, R.; Hwang, S.; Son, J.-G.; Jang, T. How Ångström–Prescott Coefficients Alter the Estimation of Agricultural Water Demand in South Korea. Water 2018, 10, 1851. https://doi.org/10.3390/w10121851
Jeong H, Bhattarai R, Hwang S, Son J-G, Jang T. How Ångström–Prescott Coefficients Alter the Estimation of Agricultural Water Demand in South Korea. Water. 2018; 10(12):1851. https://doi.org/10.3390/w10121851
Chicago/Turabian StyleJeong, Hanseok, Rabin Bhattarai, Syewoon Hwang, Jae-Gwon Son, and Taeil Jang. 2018. "How Ångström–Prescott Coefficients Alter the Estimation of Agricultural Water Demand in South Korea" Water 10, no. 12: 1851. https://doi.org/10.3390/w10121851
APA StyleJeong, H., Bhattarai, R., Hwang, S., Son, J.-G., & Jang, T. (2018). How Ångström–Prescott Coefficients Alter the Estimation of Agricultural Water Demand in South Korea. Water, 10(12), 1851. https://doi.org/10.3390/w10121851







