Field and Numerical Study of Resistance and Resilience on a Sea Breeze Dominated Beach in Yucatan (Mexico)
Abstract
1. Introduction
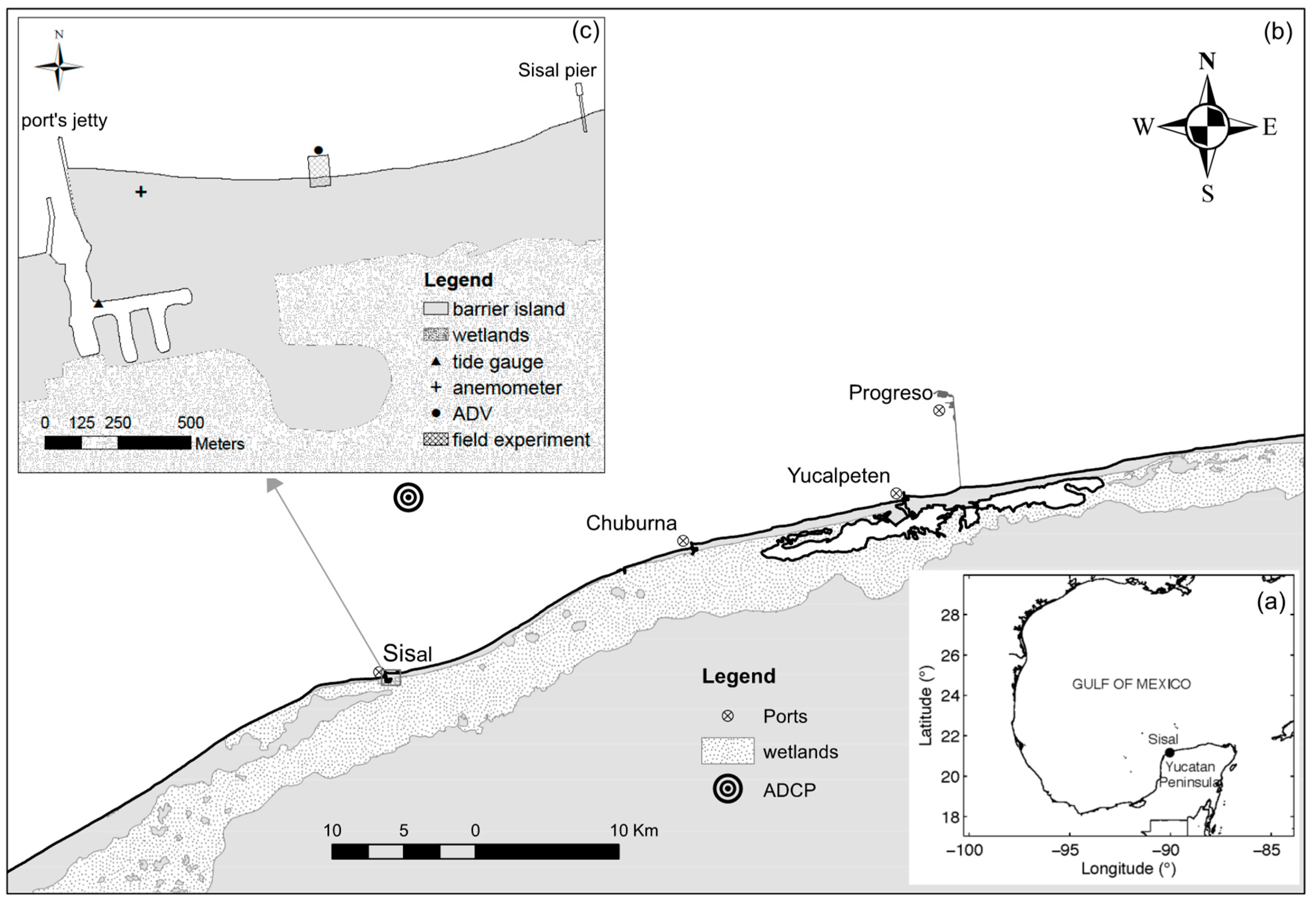
2. Study Area
3. Materials and Methods
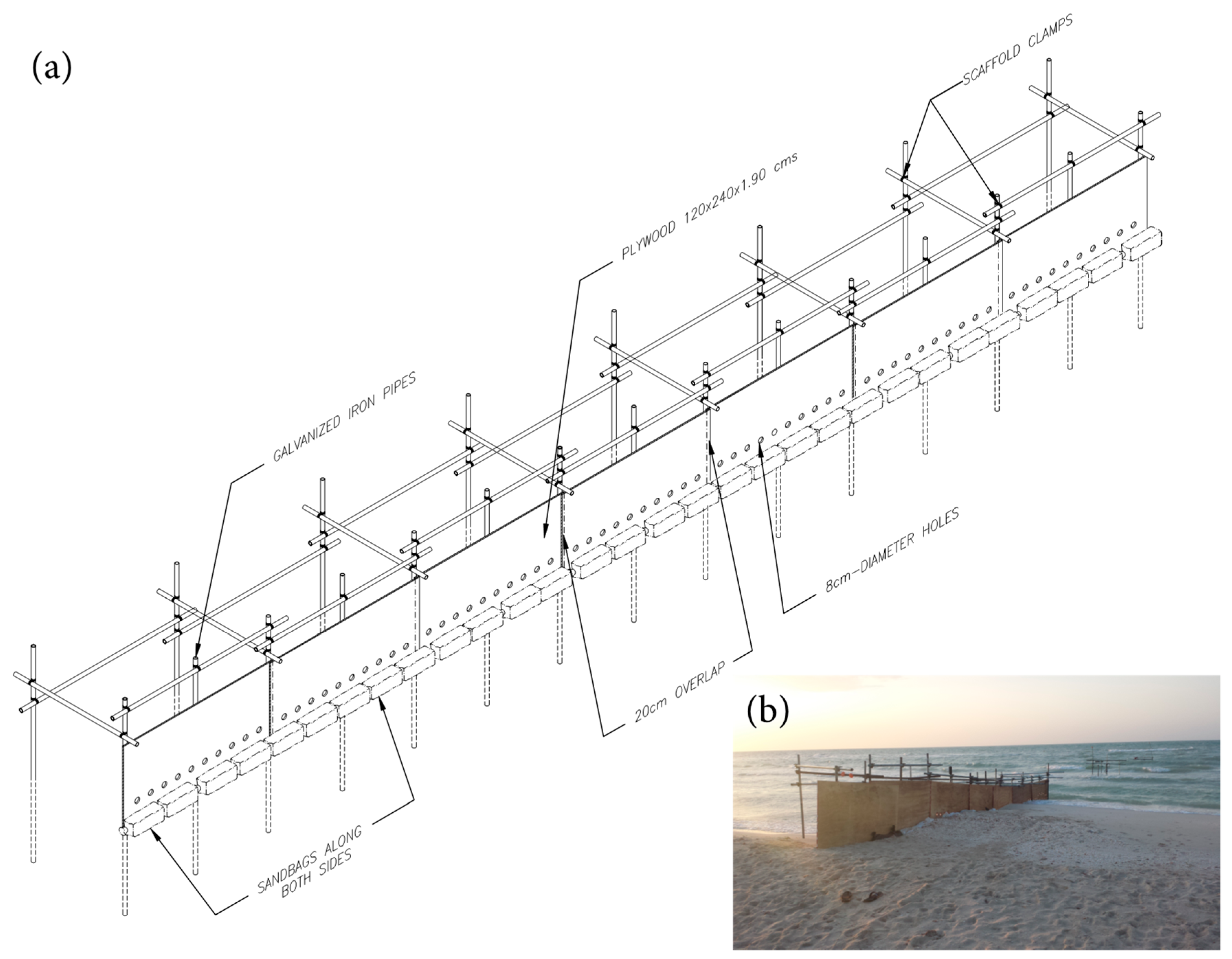
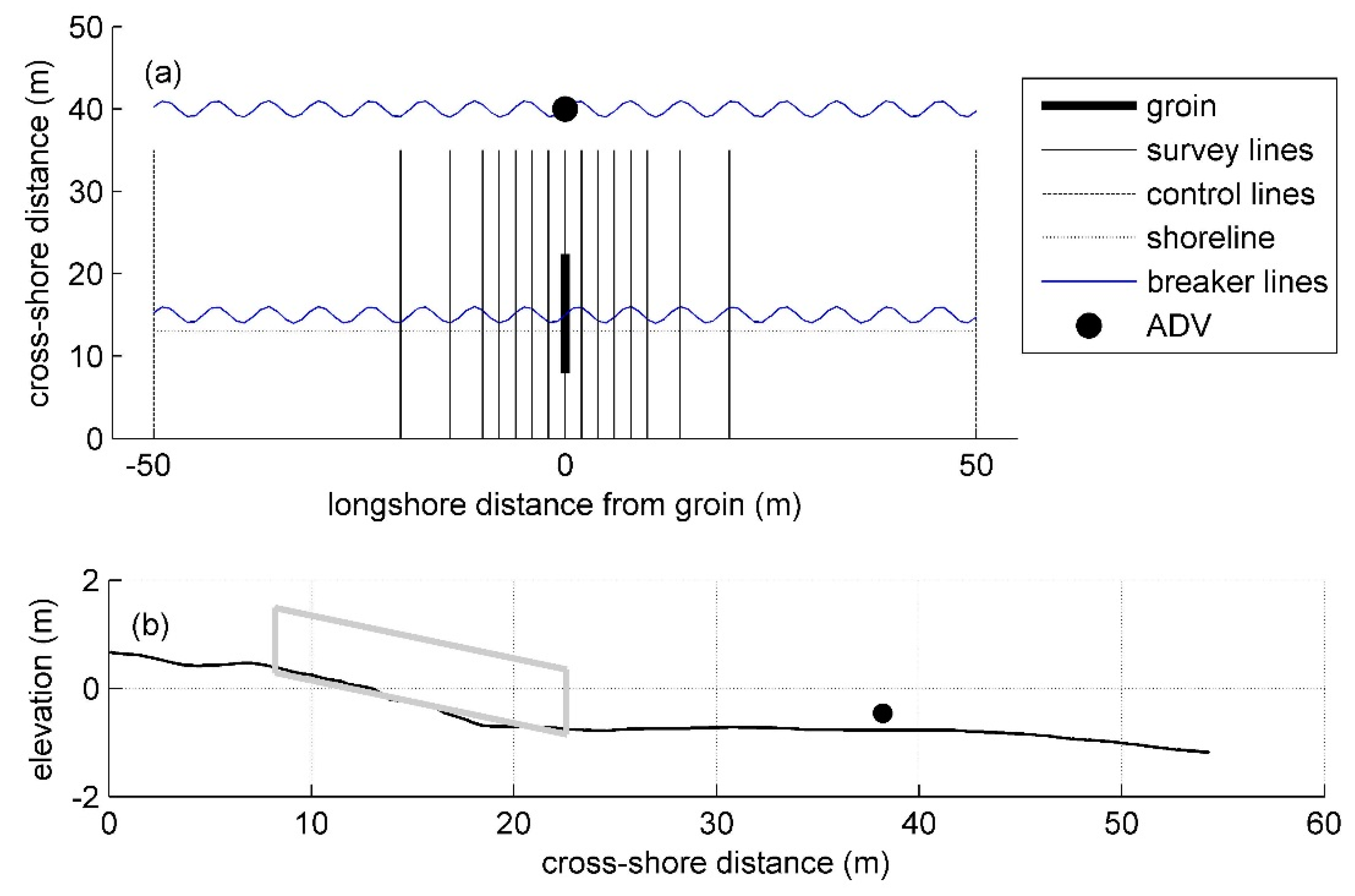
3.1. Field Experiment
3.1.1. Temporary Groin
3.1.2. Data Collection
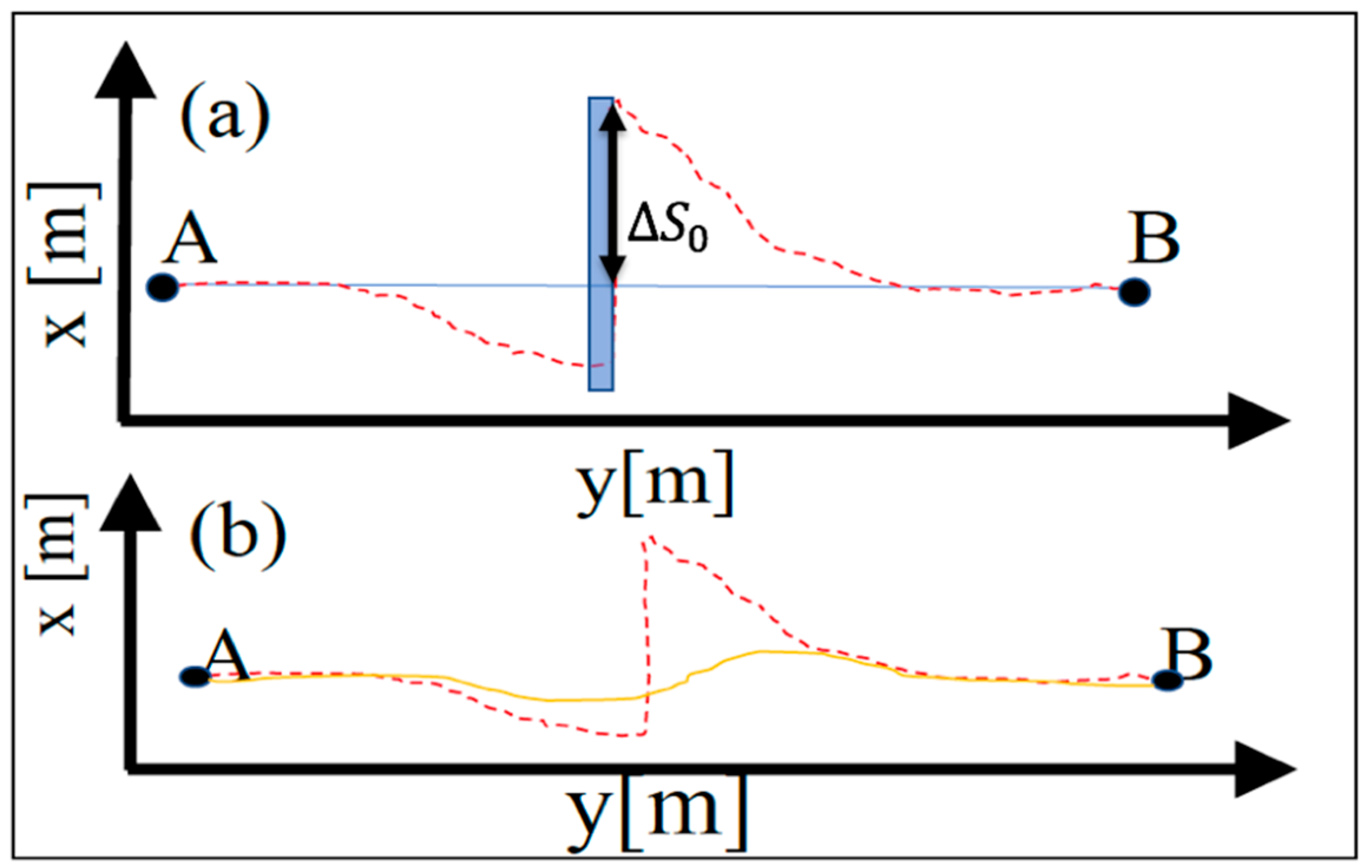
3.1.3. Field Data Analysis
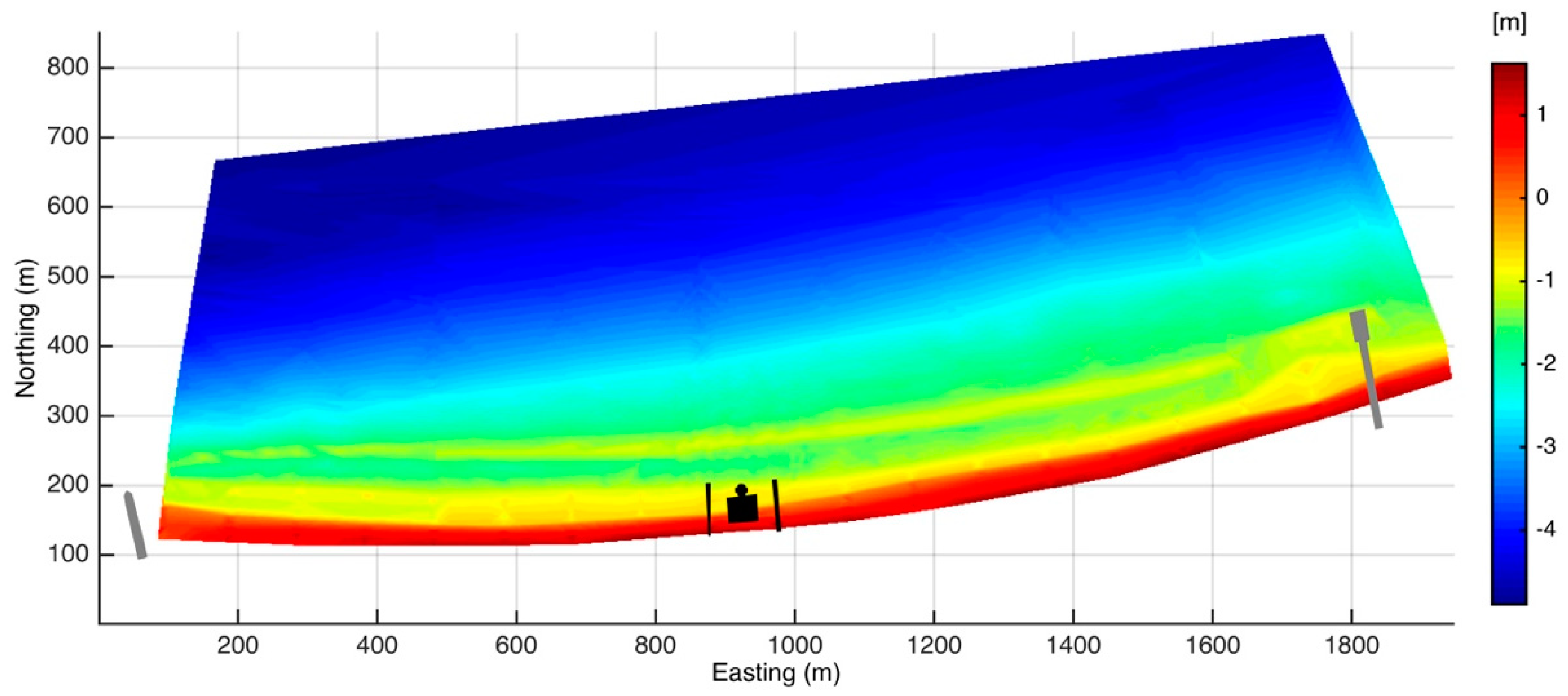
3.2. Numerical Model
3.2.1. Model Description
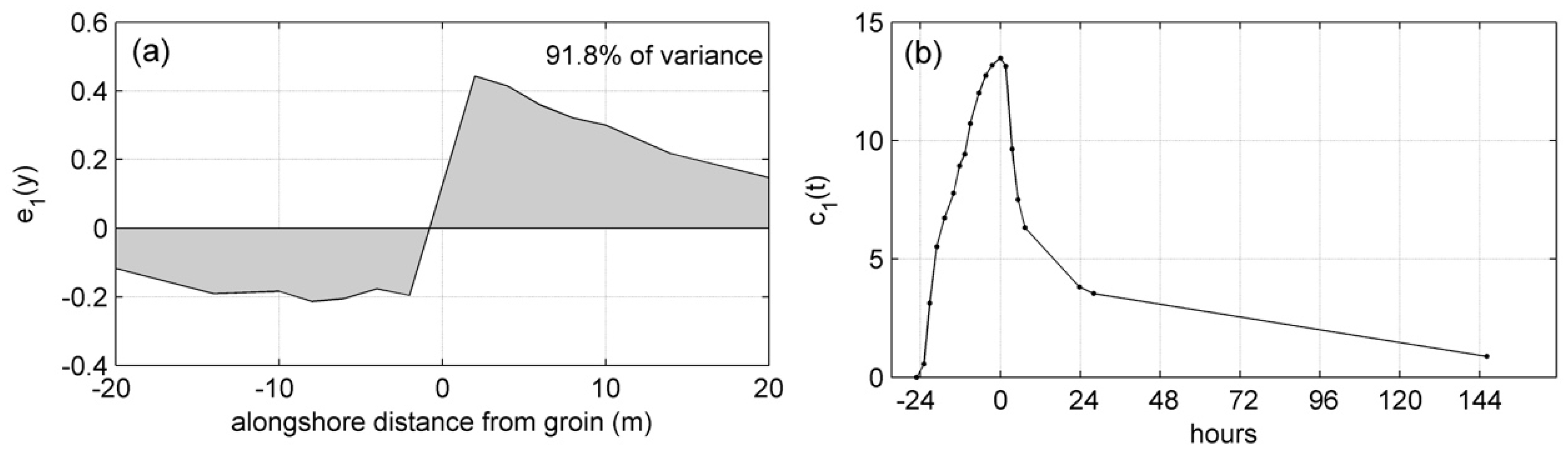
3.2.2. Data Analysis
4. Results
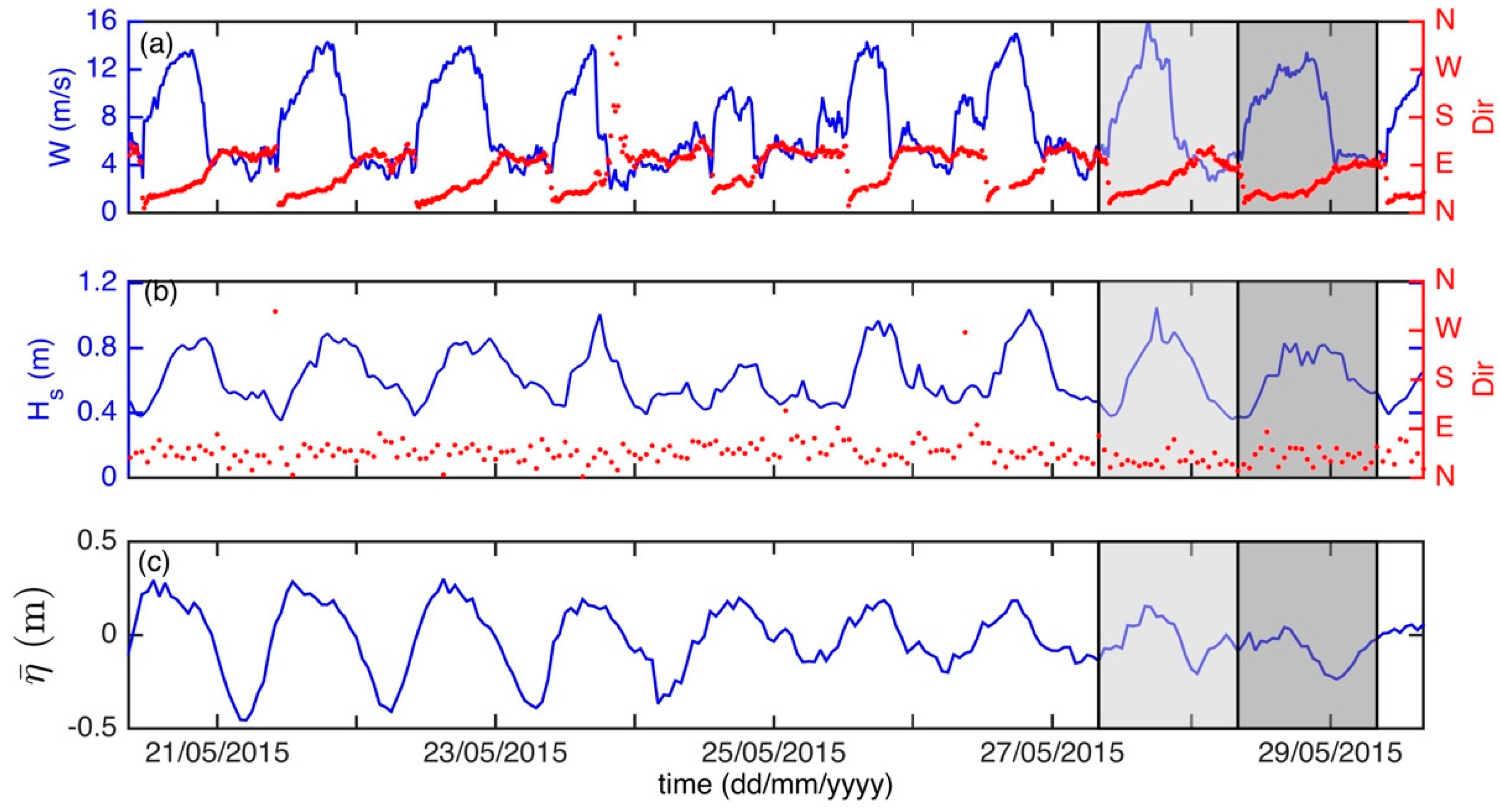
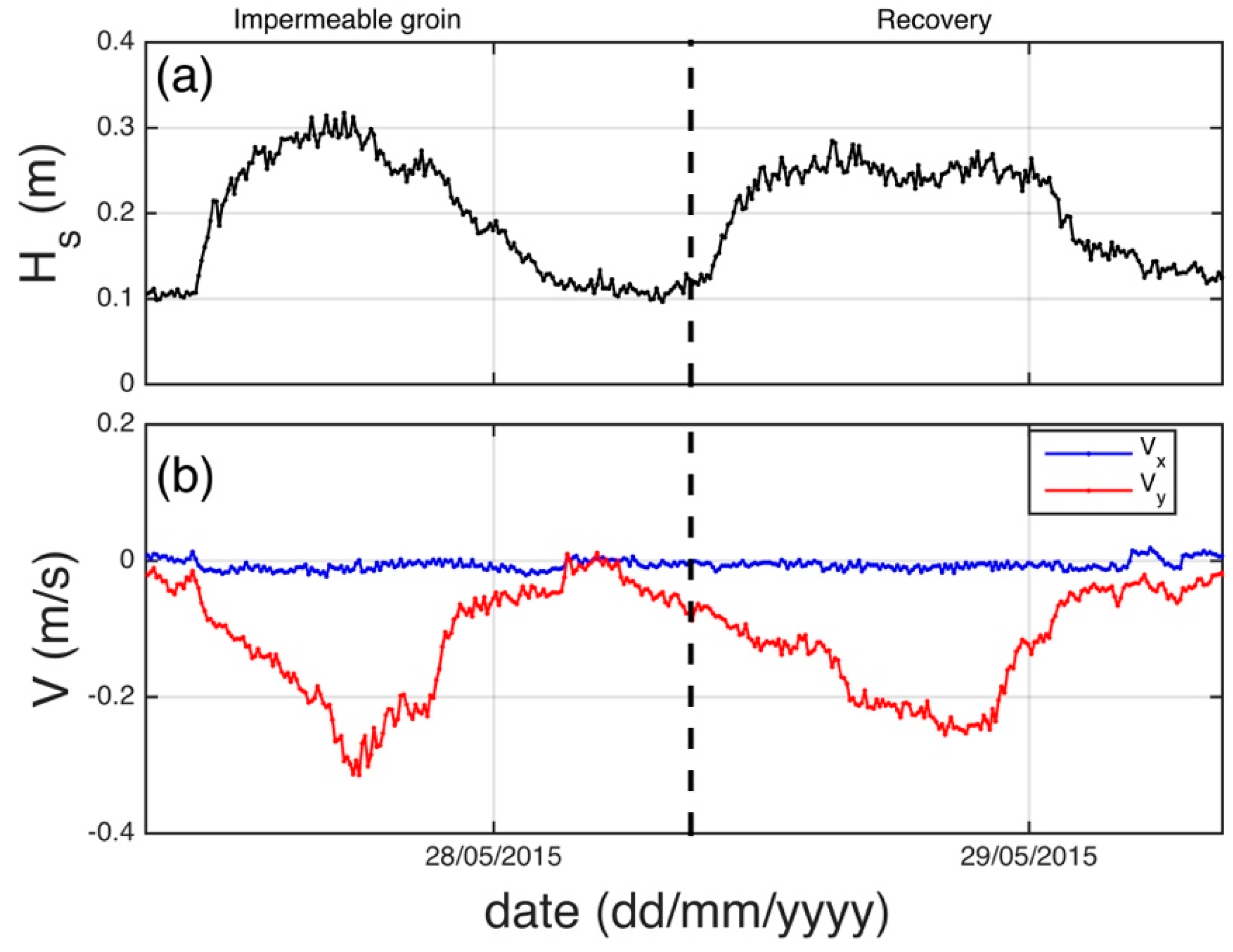
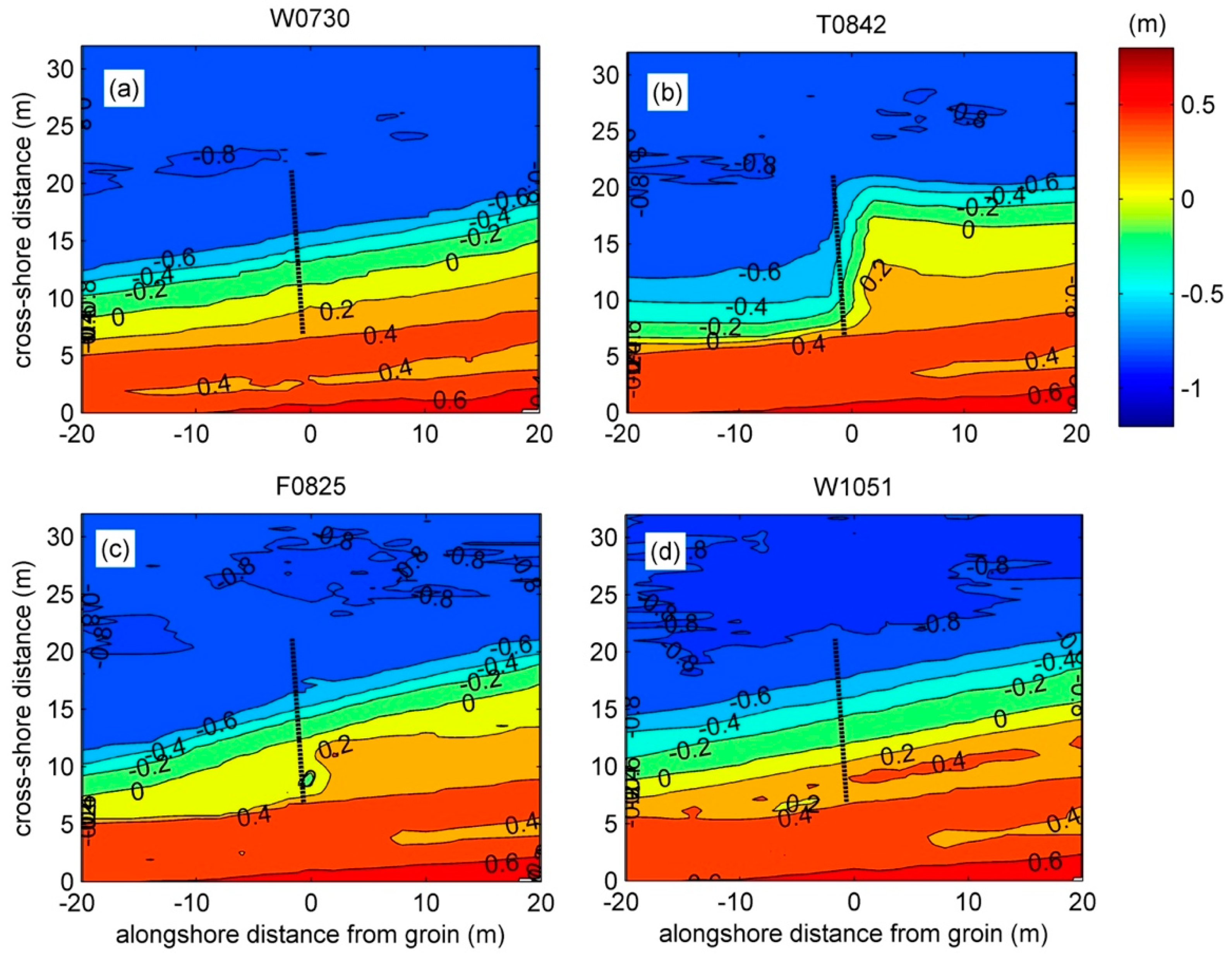
4.1. Field Observations
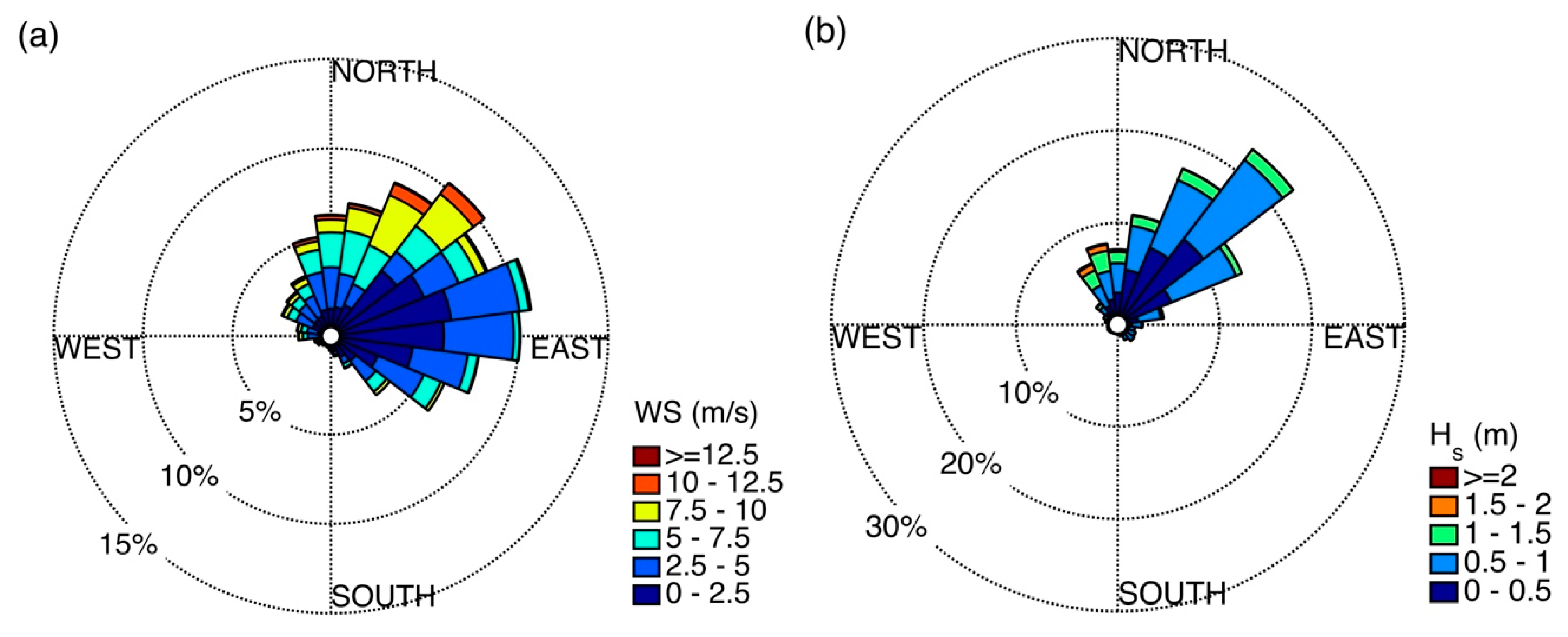
4.1.1. Forcing Conditions
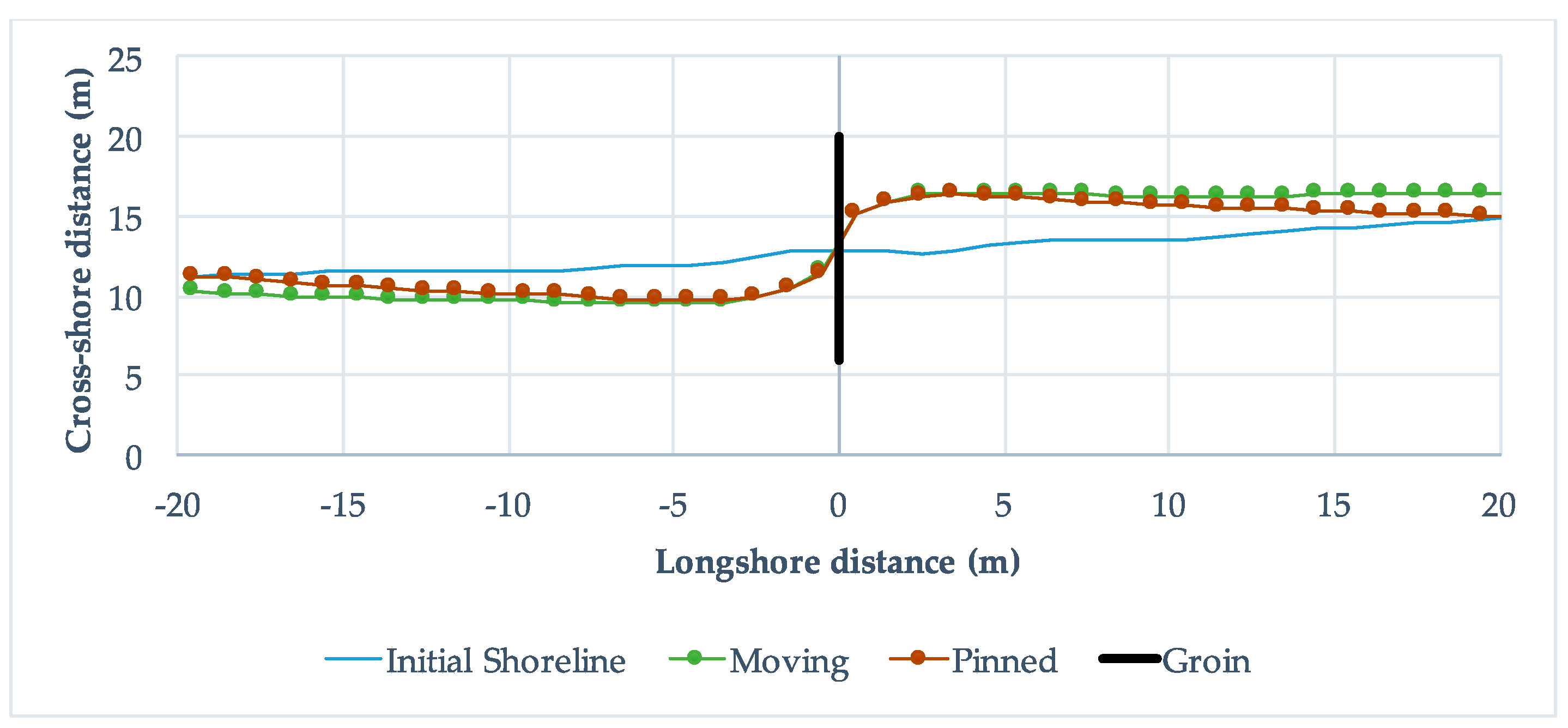
4.1.2. Observed Morphology Evolution
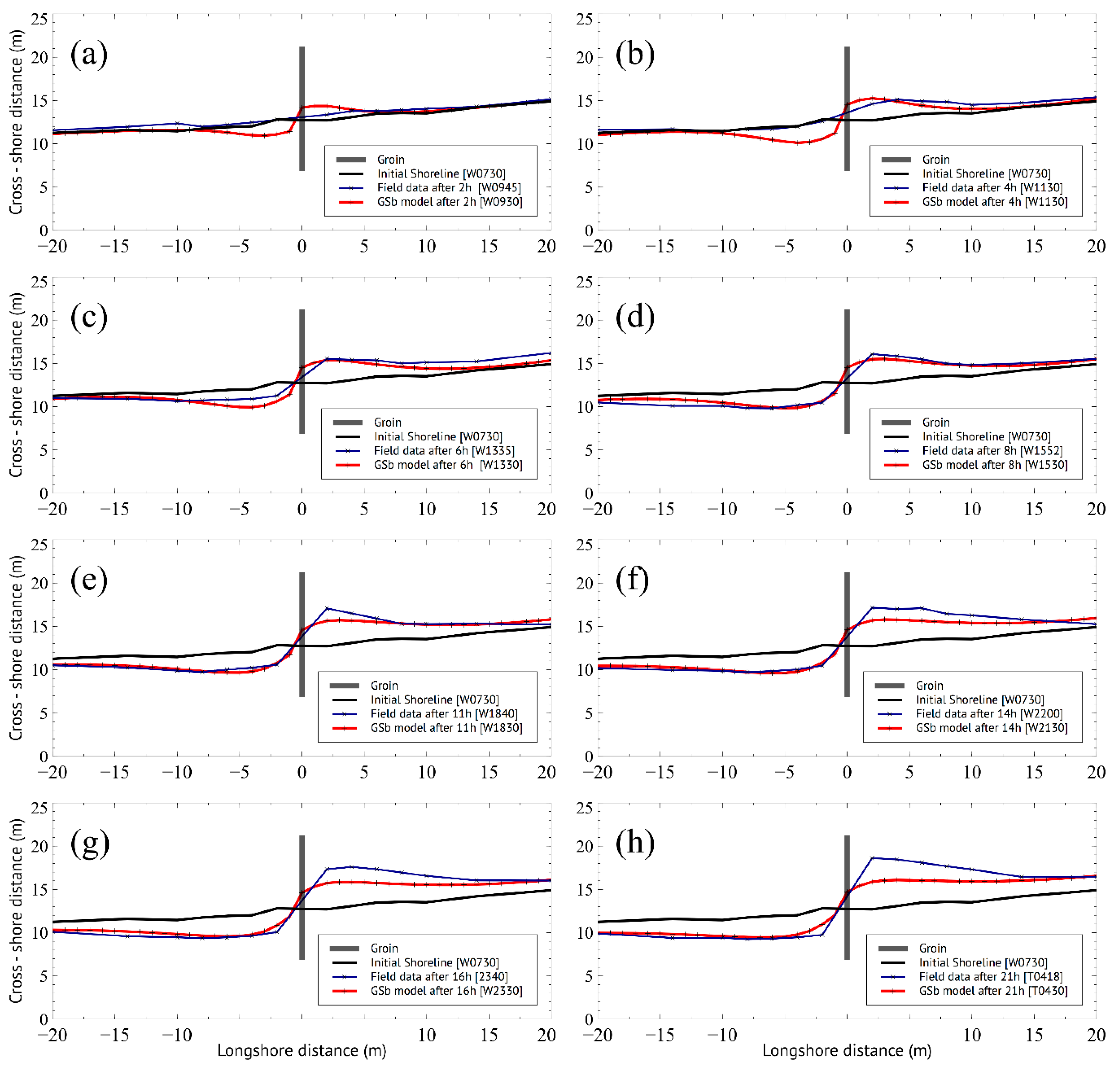
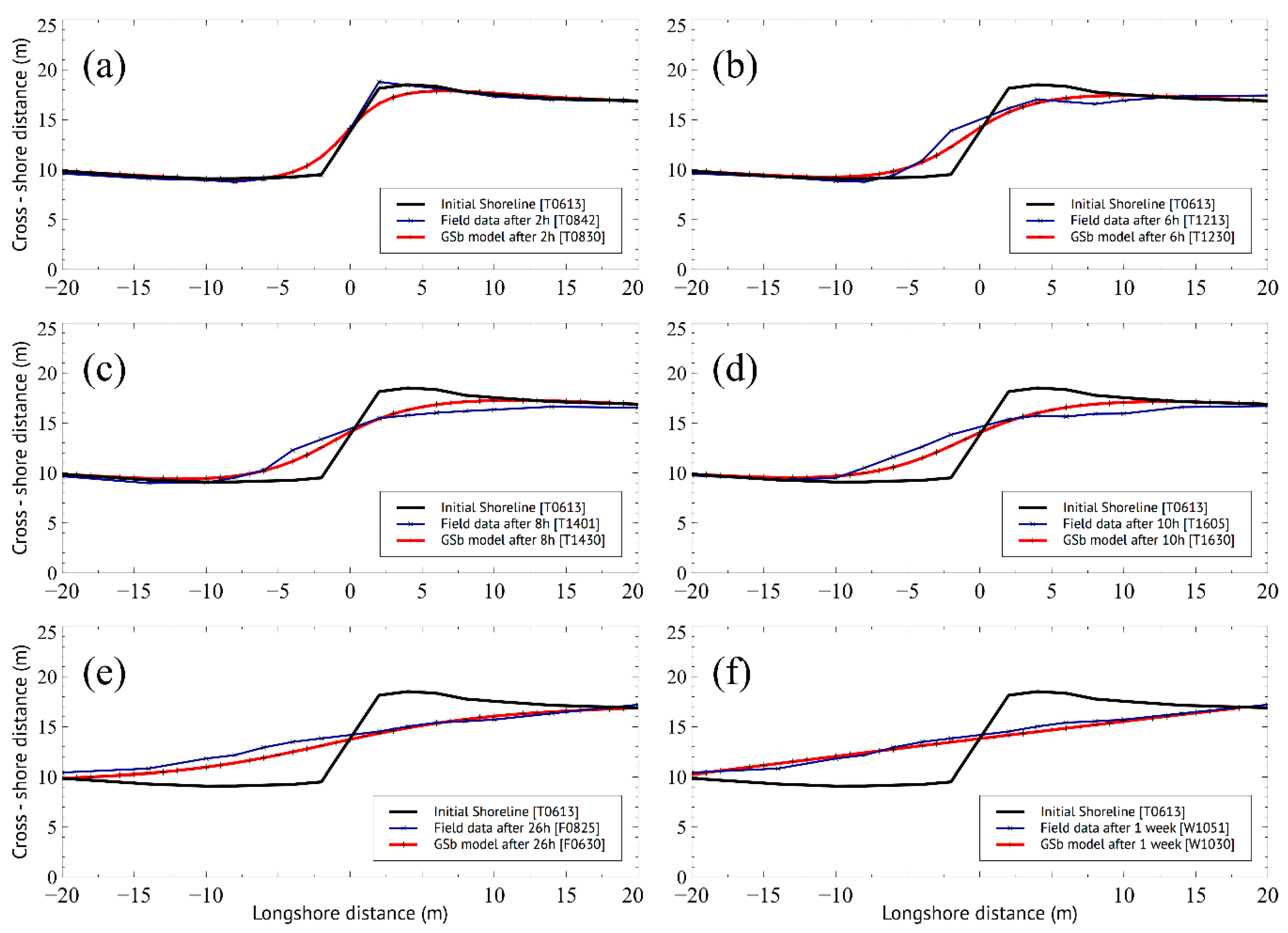
4.2. Numerical Modelling
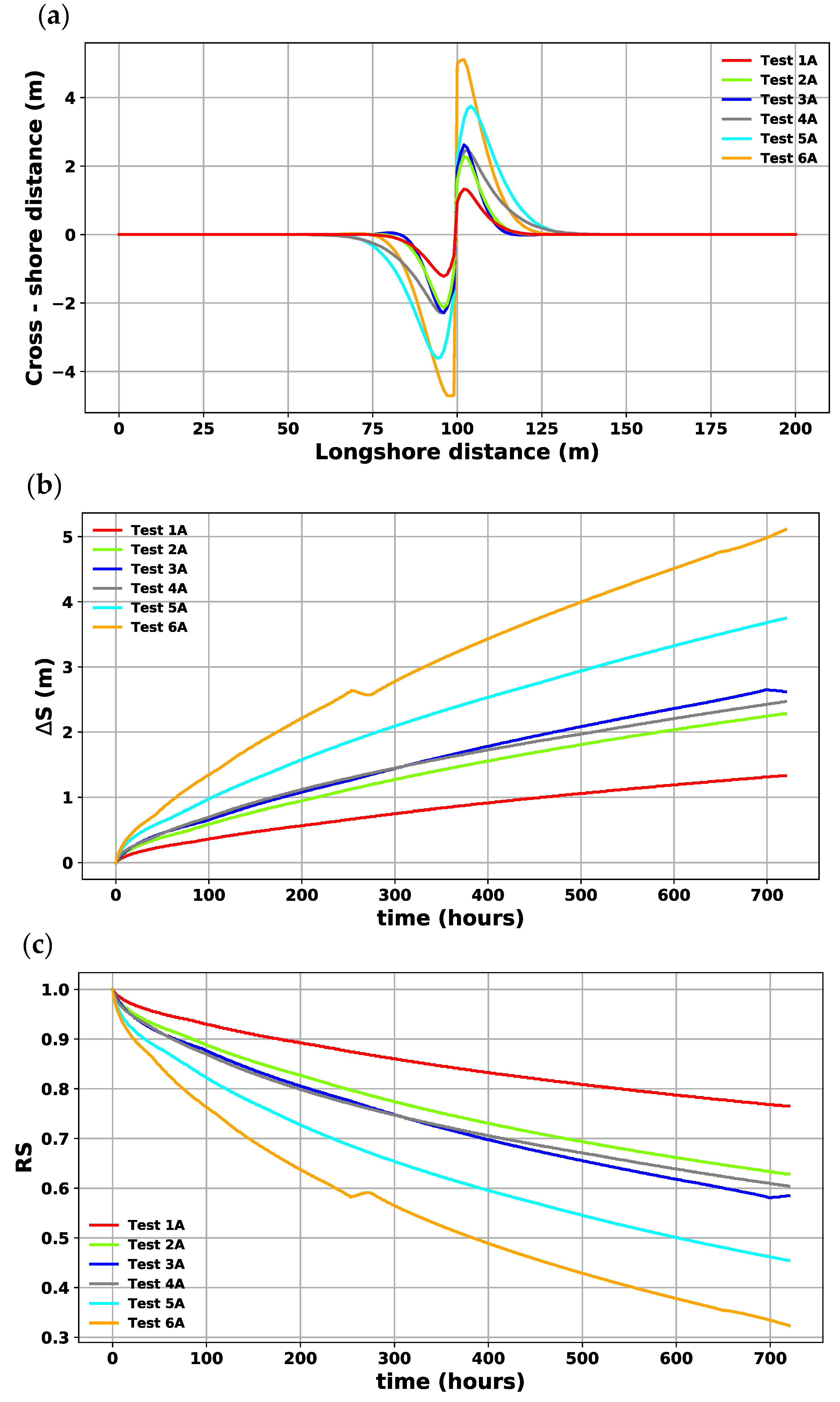
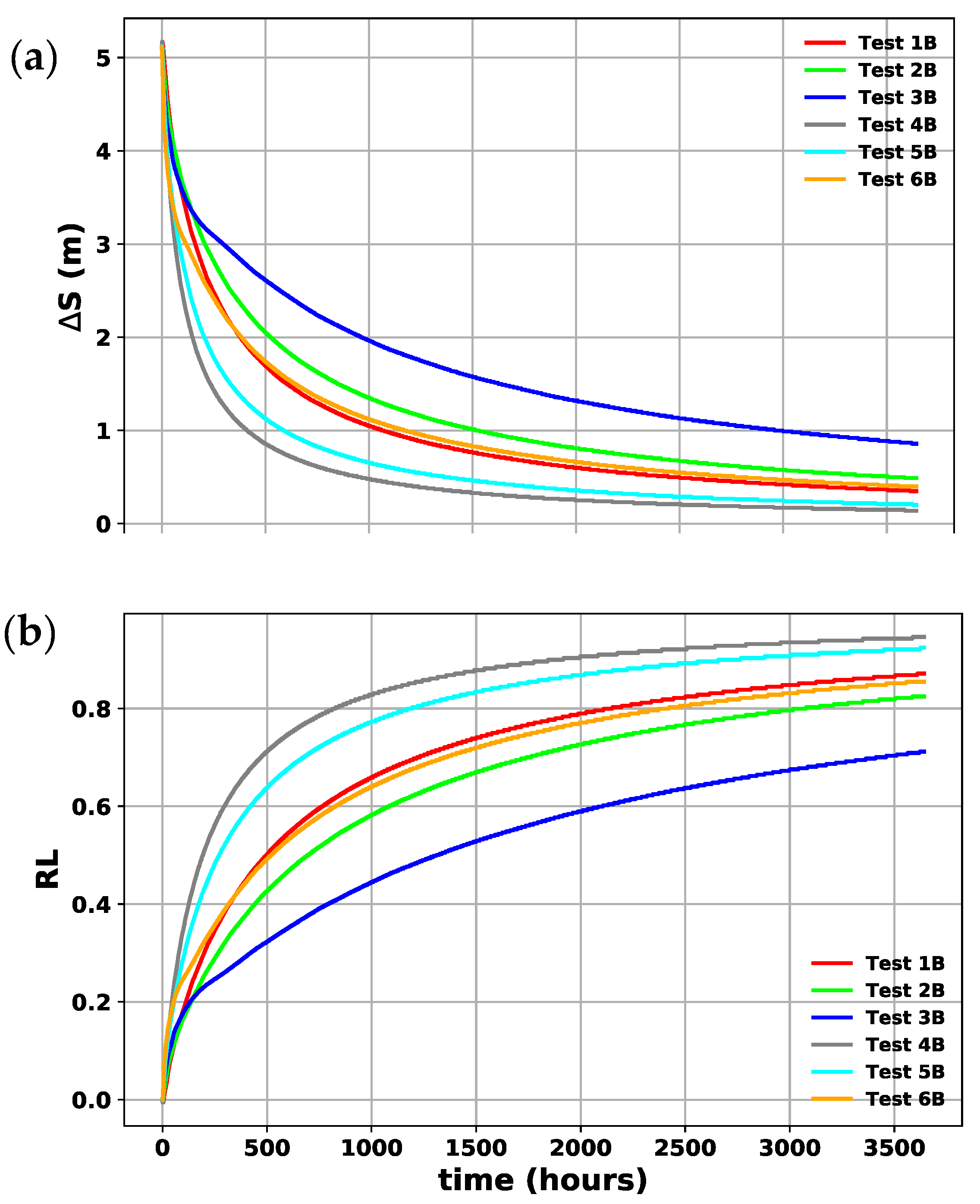
5. Discussion: Shoreline Stability
6. Conclusions
- (1)
- Analysis of high- spatial and temporal resolution field observations showed a high growth rate of the perturbation due to a groin disturbance and a lower decaying rate after the disturbance removal.
- (2)
- A new shoreline evolution model was calibrated with field observation and was able to reproduce both the perturbation growth and decay observed in the field.
- (3)
- A parametric numerical study suggests that shoreline resistance decreases with wave conditions enhancing alongshore sediment transport; whereas the resilience increases as a function of the alongshore diffusivity.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pimm, S.L. The complexity and the stability of ecosystems. Nature 1984, 307, 321–326. [Google Scholar] [CrossRef]
- Orwin, K.H.; Wardle, D.A. New indices for quantifying the resistance and resilience of soil biota to exogenous disturbances. Soil Biol. Biochem. 2004, 36, 1907–1912. [Google Scholar] [CrossRef]
- Folke, C. Resilience: The emergence of a perspective for social-ecological systems analyses. Glob. Environ. Chang. 2006, 16, 253–267. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and stability of ecological systems. Ann. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Garmezy, N.; Masten, A.S.; Tellegen, A. The study of stress and competence in children: A building block for developmental psychopathology. Child Dev. 1984, 55, 97–111. [Google Scholar] [CrossRef] [PubMed]
- Alexander, D.E. Resilience against earthquakes: Some practical suggestions for planners and managers. J. Seism. Earthq. Eng. 2012, 13, 109–115. [Google Scholar]
- Alexander, D.E. Resilience and disaster risk reduction: An etymological journey. Nat. Hazards Earth Syst. Sci. 2013, 13, 2707–2716. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; Sanchez Arcilla, A.; D’Alessandro, F.; Ilic, S.; James, M.; Fortes, C.J.E.M.; Sancho, F.; Schüttrumpf, H. Large-scale flume experiments on dune erosion processes. J. Hydraul. Res. 2011, 49, 20–30. [Google Scholar] [CrossRef]
- D’Alessandro, F.; Tomasicchio, G.R. Wave-dune interaction and beach resilience in large-scale physical model tests. Coast. Eng. 2016, 116, 15–25. [Google Scholar] [CrossRef]
- Smith, E.R.; D’Alessandro, F.; Tomasicchio, G.R.; Gailani, J.Z. Nearshore placement of a sand dredged mound. Coast. Eng. 2017, 126, 1–10. [Google Scholar] [CrossRef]
- Martinez, L.; Taramelli, A.; Silva, R. Resistance and Resilience: Facing the Multidimensional Challenges in Coastal Areas. J. Coast. Res. 2017, 77 (Suppl. 1), 1–6. [Google Scholar] [CrossRef]
- Lira-Pantoja, M.; Torres-Freyermuth, A.; Appendini, C.; Fernández, D.; Salles, P.; Mendoza, E.; López, J.; Pedrozo-Acuña, A. Chronic beach erosion induced by coastal structures in Chelem, Yucatan. Coast. Eng. Proc. 2012, 1, 125. [Google Scholar] [CrossRef]
- Medellín, G.; Mariño-Tapia, I.; Euán-Ávila, J. The influence of a seawall on postnourishment evolution in a sea-breeze-dominated microtidal beach. J. Coast. Res. 2015, 31, 1449–1458. [Google Scholar] [CrossRef]
- Meyer-Arendt, K.J. Recreational development and shoreline modification along the north coast of Yucatán, Mexico. Tour. Geogr. 2001, 3, 87–104. [Google Scholar] [CrossRef]
- Bodge, K.R.; Dean, R.G. Short-Term Impoundment of Longshore Sediment Transport; TR CERC-87-7; WES: Vicksburg, MS, USA, 1987. [Google Scholar]
- Wang, P.; Kraus, N.C. Longshore sediment transport rate measured by short-term impoundment. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 118–126. [Google Scholar] [CrossRef]
- Martin-Grandes, I.; Hughes, J.; Simmonds, D.J.; Chadwick, A.J.; Reeve, D.E. Novel methodology for one line model calibration using impoundment on mixed beach. Coast. Dyn. 2009. [Google Scholar] [CrossRef]
- Rosati, J.D.; Walton, T.L.; Bodge, K. Longshore Sediment Transport, in Coastal Engineering Manual, Part III; King, D.B., Ed.; Technical Report EM 1110-2-1100; U.S. Army Corps of Engineers: Washington, DC, USA, 2002. [Google Scholar]
- Elgar, S.; Raubenheimer, B.; Thomson, J.; Moulton, M. Resonance in an evolving hole in the swash zone. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 299–302. [Google Scholar] [CrossRef]
- Moulton, M.; Elgar, S.; Raubenheimer, B. A surf zone morphological diffusivity estimated from the evolution of excavated holes. Geophys. Res. Lett. 2014, 41, 4628–4636. [Google Scholar] [CrossRef]
- Moulton, M.; Elgar, S.; Raubenheimer, B.; Warner, J.C.; Kumar, N. Rip currents and alongshore flows in single channels dredged in the surf zone. J. Geophys. Res. Oceans 2017, 122, 3799–3816. [Google Scholar] [CrossRef]
- Torres-Freyermuth, A.; Puleo, J.A.; DiCosmo, N.; Allende-Arandia, M.E.; Chardón-Maldonado, P.; López-González, J.; Figueroa, B.; Ruiz de Alegría-Arzaburú, A.; Figlus, J.; Roberts, T.; et al. Nearshore hydrodynamics on a sea breeze dominated beach during intense wind events. Cont. Shelf Res. 2017, 151, 40–52. [Google Scholar] [CrossRef]
- Figueroa-Espinoza, B.; Salles, P.; Zavala, J. On the Wind Power Potential in the northwest of the Yucatan Peninsula in Mexico. Atmosfera 2014, 27, 77–89. [Google Scholar] [CrossRef]
- Pérez, E.P.; Magaña, V.; Caetano, E.; Kusunoki, S. Cold surge activity over the Gulf of Mexico in a warmer climate. Front. Earth Sci. 2014, 2, 19. [Google Scholar] [CrossRef]
- Appendini, C.M.; Pedrozo-Acuña, A.; Meza-Padilla, R.; Torres-Freyermuth, A.; Cerezo-Mota, R.; López-González, J.; Ruiz-Salcines, P. On the role of climate change on wind waves generated by tropical cyclones in the Gulf of Mexico. Coast. Eng. J. 2017, 59. [Google Scholar] [CrossRef]
- Martell-Dubois, R.; Silva-Casarin, R.; Mendoza-Baldwin, E.G.; Muñoz-Pérez, J.J.; Cerdeira-Estrada, S.; Escalante-Mancera, E.; Laiz, I. Spectral bimodality of waves produced by hurricanes in the Caribbean coastal zone off Mexico. Cienc. Mar. 2018, 44, 33–48. [Google Scholar] [CrossRef]
- Cuevas-Jiménez, A.; Euán-Ávila, J. Morphodynamics of carbonate beaches in the Yucatán Peninsula. Cienc. Mar. 2009, 35, 307–320. [Google Scholar] [CrossRef]
- Hubertz, J.M. Observations of local wind effects on longshore currents. Coast. Eng. 1986, 10, 275–288. [Google Scholar] [CrossRef]
- King, D.B. Wave and Beach Processes Modeling for Sabine Pass to Galveston Bay, Texas, Shoreline Erosion Feasibility Study; Technical Report ERDC/CHL TR-07-6; USACE Engineer Research and Development Center: Vicksburg, MS, USA, 2007; 150p. [Google Scholar]
- Burnette, C.; Dally, W.R. The Longshore Transport Enigma and Analysis of a 10-Year Record of Wind-Driven Nearshore Currents. J. Coast. Res. 2018, 34, 26–41. [Google Scholar] [CrossRef]
- Wellmann, N. Analysis of Near-Shore Sediment Samples from Sisal Beach (Mexico) Comparing Effects of Sea Breeze and el Norte Events. Ph.D. Thesis, Hochschule für Technik, Wirtschaft und Kultur Leipzig, Leipzig, Germany, 2014. [Google Scholar]
- Zavala-Hidalgo, J.; Morey, S.L.; O’Brien, J.O. Seasonal circulation on the western shelf of the Gulf of Mexico using a high-resolution numerical model. J. Geophys. Res. 2003, 108, 3389. [Google Scholar] [CrossRef]
- MEXICO97. Available online: https://www.ngs.noaa.gov/GEOID/MEXICO97/ (accessed on 20 August 2018).
- Medellín, G.; Medina, R.; Falqués, A.; González, M. Coastline sand waves on a low-energy beach at “El Puntal” spit, Spain. Mar. Geol. 2008, 250, 143–156. [Google Scholar] [CrossRef]
- Miller, J.K.; Dean, R.G. Shoreline Variability via Empirical Orthogonal Function Analysis: Part I Temporal and Spatial Characteristics. Coast. Eng. 2006, 54, 111–131. [Google Scholar] [CrossRef]
- Muñoz-Pérez, J.J.; Medina, R.; Tejedor, B. Evolution of longshore beach contour lines determined by the E.O.F. method. Sci. Mar. 2001, 65, 393–402. [Google Scholar] [CrossRef]
- Frey, A.E.; Connell, K.J.; Hanson, H.; Larson, M.; Thomas, R.C.; Munger, S.; Zundel, A. GenCade Version 1 Model Theory and User’s Guide; Technical Report ERDC/CHL TR-12-25; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2012. [Google Scholar]
- Bruun, P. Coast Erosion and the Development of Beach Profiles; Technical Memorandum N. 44; Department of the Army, Beach Erosion Board, Corps of Engineers: Washington, DC, USA, 1954.
- Dean, R.G. Equilibrium beach profiles: Characteristics and applications. J. Coast. Res. 1990, 71, 53–84. [Google Scholar]
- Tomasicchio, G.R.; Lamberti, A.; Guiducci, F. Stone movement on a reshaped profile. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; Volume 2, pp. 1625–1640. [Google Scholar]
- Lamberti, A.; Tomasicchio, G.R. Stone mobility and longshore transport at reshaping breakwaters. Coast. Eng. 1997, 29, 263–289. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; Archetti, R.; D’Alessandro, F.; Sloth, P. Long-shore transport at berm breakwaters and gravel beaches. Coast. Struct. 2007, 65–76. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; D’Alessandro, F.; Barbaro, G.; Malara, G. General longshore transport model. Coast. Eng. 2013, 71, 28–36. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; D’Alessandro, F.; Barbaro, G.; Musci, E.; De Giosa, T.M. Longshore transport at shingle beaches: An independent verification of the general model. Coast. Eng. 2015, 104, 69–75. [Google Scholar] [CrossRef]
- Ozasa, H.; Brampton, A.H. Mathematical modeling of beaches backed by seawalls. Coast. Eng. 1980, 4, 47–64. [Google Scholar] [CrossRef]
| Variable | Sensor | Manufacturer | Sampling Frequency | Start Date | End Date |
|---|---|---|---|---|---|
| Morphology | GPS | Leica Geosystems (Gallen, Switzerland) | 2–24 h | 27 May 2015 | 3 June 2015 |
| Waves | ADCP | RD Instruments (Poway, CA, USA) | 30 min | 27 May 2015 | 3 June 2015 |
| Surf zone currents | ADV Vector | Nortek (Rud, Norway) | 16 Hz | 27 May 2015 | 29 May 2015 |
| Sea level | Radar level sensor | OTT HydroMet (Kempten Germany) | 1 min | 27 May 2015 | 4 June 2015 |
| Winds | Weather station | Davis Vantage Pro 2 (Hayward, CA, USA) | 1 min | 27 May 2015 | 4 June 2015 |
| M | D | H | Hs (m) | Tp (s) | θ (°) | M | D | H | Hs (m) | Tp (s) | θ (°) | M | D | H | Hs (m) | Tp (s) | θ (°) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 27 | 7 | 0.54 | 3.7 | 41 | 5 | 29 | 17 | 0.47 | 2.5 | 71 | 6 | 1 | 3 | 0.57 | 3.3 | 36 | ||
| 5 | 27 | 8 | 0.51 | 3.6 | 51 | 5 | 29 | 18 | 0.49 | 2.9 | 67 | 6 | 1 | 4 | 0.53 | 3.4 | 37 | ||
| 5 | 27 | 9 | 0.5 | 3.8 | 26 | 5 | 29 | 19 | 0.55 | 3 | 30 | 6 | 1 | 5 | 0.5 | 3.1 | 56 | ||
| 5 | 27 | 10 | 0.48 | 3.6 | 38 | 5 | 29 | 20 | 0.61 | 3.3 | 45 | 6 | 1 | 6 | 0.4 | 4.5 | 29 | ||
| 5 | 27 | 11 | 0.5 | 3.4 | 36 | 5 | 29 | 21 | 0.66 | 3.7 | 16 | 6 | 1 | 7 | 0.4 | 4.1 | 34 | ||
| 5 | 27 | 12 | 0.47 | 3.2 | 26 | 5 | 29 | 22 | 0.71 | 3.4 | 41 | 6 | 1 | 8 | 0.33 | 4.3 | 36 | ||
| 5 | 27 | 13 | 0.47 | 2.7 | 77 | 5 | 29 | 23 | 0.7 | 3.6 | 65 | 6 | 1 | 9 | 0.32 | 4.3 | 13 | ||
| 5 | 27 | 14 | 0.42 | 3 | 51 | 5 | 30 | 0 | 0.6 | 3.3 | 62 | 6 | 1 | 10 | 0.28 | 4.3 | 12 | ||
| 5 | 27 | 15 | 0.38 | 3.8 | 19 | 5 | 30 | 1 | 0.56 | 3.5 | 36 | 6 | 1 | 11 | 0.27 | 3.7 | 358 | ||
| 5 | 27 | 16 | 0.39 | 4.1 | 43 | 5 | 30 | 2 | 0.59 | 3.9 | 43 | 6 | 1 | 12 | 0.28 | 3.8 | 62 | ||
| 5 | 27 | 17 | 0.46 | 2.7 | 24 | 5 | 30 | 3 | 0.71 | 3.3 | 52 | 6 | 1 | 13 | 0.31 | 3.5 | 41 | ||
| 5 | 27 | 18 | 0.62 | 1.4 | 32 | 5 | 30 | 4 | 0.75 | 3.4 | 45 | 6 | 1 | 14 | 0.31 | 3.3 | 48 | ||
| 5 | 27 | 19 | 0.68 | 3.5 | 28 | 5 | 30 | 5 | 0.76 | 3.5 | 83 | 6 | 1 | 15 | 0.24 | 3.8 | 14 | ||
| 5 | 27 | 20 | 0.74 | 3.6 | 22 | 5 | 30 | 6 | 0.72 | 3.4 | 8 | 6 | 1 | 16 | 0.24 | 4.1 | 22 | ||
| 5 | 27 | 21 | 0.8 | 3.7 | 26 | 5 | 30 | 7 | 0.69 | 3.3 | 63 | 6 | 1 | 17 | 0.22 | 4.2 | 358 | ||
| 5 | 27 | 22 | 0.85 | 3.8 | 24 | 5 | 30 | 8 | 0.64 | 1.4 | 13 | 6 | 1 | 18 | 0.19 | 4.2 | 6 | ||
| 5 | 27 | 23 | 1.05 | 4.2 | 32 | 5 | 30 | 9 | 0.6 | 3.6 | 71 | 6 | 1 | 19 | 0.3 | 2.5 | 260 | ||
| 5 | 28 | 0 | 0.84 | 4.5 | 19 | 5 | 30 | 10 | 0.53 | 4.2 | 27 | 6 | 1 | 20 | 0.2 | 4.1 | 11 | ||
| 5 | 28 | 1 | 0.83 | 3.8 | 55 | 5 | 30 | 11 | 0.49 | 4.2 | 14 | 6 | 1 | 21 | 0.18 | 4.2 | 10 | ||
| 5 | 28 | 2 | 0.9 | 3.4 | 70 | 5 | 30 | 12 | 0.52 | 2.9 | 45 | 6 | 1 | 22 | 0.26 | 2.3 | 64 | ||
| 5 | 28 | 3 | 0.85 | 3.3 | 30 | 5 | 30 | 13 | 0.45 | 3.7 | 33 | 6 | 1 | 23 | 0.42 | 2.7 | 22 | ||
| 5 | 28 | 4 | 0.78 | 3.8 | 32 | 5 | 30 | 14 | 0.46 | 3.8 | 15 | 6 | 2 | 0 | 0.46 | 3.2 | 9 | ||
| 5 | 28 | 5 | 0.74 | 3.9 | 47 | 5 | 30 | 15 | 0.45 | 1.6 | 53 | 6 | 2 | 1 | 0.41 | 3.2 | 23 | ||
| 5 | 28 | 6 | 0.66 | 4.3 | 28 | 5 | 30 | 16 | 0.41 | 3.2 | 9 | 6 | 2 | 2 | 0.47 | 5.2 | 357 | ||
| 5 | 28 | 7 | 0.57 | 1.4 | 32 | 5 | 30 | 17 | 0.44 | 4.3 | 19 | 6 | 2 | 3 | 0.41 | 3.3 | 352 | ||
| 5 | 28 | 8 | 0.48 | 4.6 | 20 | 5 | 30 | 18 | 0.46 | 2.7 | 17 | 6 | 2 | 4 | 0.35 | 3 | 37 | ||
| 5 | 28 | 9 | 0.47 | 3.4 | 46 | 5 | 30 | 19 | 0.52 | 3.2 | 56 | 6 | 2 | 5 | 0.31 | 3.8 | 2 | ||
| 5 | 28 | 10 | 0.43 | 4.5 | 25 | 5 | 30 | 20 | 0.58 | 3 | 14 | 6 | 2 | 6 | 0.27 | 3.4 | 32 | ||
| 5 | 28 | 11 | 0.39 | 4.2 | 31 | 5 | 30 | 21 | 0.61 | 3.5 | 44 | 6 | 2 | 7 | 0.39 | 1.4 | 11 | ||
| 5 | 28 | 12 | 0.36 | 3.8 | 25 | 5 | 30 | 22 | 0.67 | 3.7 | 39 | 6 | 2 | 8 | 0.23 | 2.7 | 22 | ||
| 5 | 28 | 13 | 0.38 | 3.6 | 12 | 5 | 30 | 23 | 0.75 | 3.8 | 32 | 6 | 2 | 9 | 0.21 | 3.2 | 46 | ||
| 5 | 28 | 14 | 0.37 | 3.9 | 25 | 5 | 31 | 0 | 0.76 | 3.9 | 16 | 6 | 2 | 10 | 0.16 | 3.3 | 28 | ||
| 5 | 28 | 15 | 0.38 | 4.1 | 18 | 5 | 31 | 1 | 0.71 | 3.7 | 21 | 6 | 2 | 11 | 0.12 | 3 | 66 | ||
| 5 | 28 | 16 | 0.45 | 2.9 | 43 | 5 | 31 | 2 | 0.78 | 3.8 | 39 | 6 | 2 | 12 | 0.13 | 2.6 | 146 | ||
| 5 | 28 | 17 | 0.53 | 3.1 | 55 | 5 | 31 | 3 | 0.72 | 3.5 | 32 | 6 | 2 | 13 | 0.2 | 2 | 47 | ||
| 5 | 28 | 18 | 0.63 | 3.2 | 84 | 5 | 31 | 4 | 0.67 | 3.7 | 28 | 6 | 2 | 14 | 0.21 | 2.1 | 58 | ||
| 5 | 28 | 19 | 0.63 | 3.5 | 51 | 5 | 31 | 5 | 0.6 | 3.7 | 48 | 6 | 2 | 15 | 0.19 | 2.5 | 239 | ||
| 5 | 28 | 20 | 0.63 | 3.4 | 20 | 5 | 31 | 6 | 0.54 | 3.4 | 45 | 6 | 2 | 16 | 0.15 | 2.1 | 76 | ||
| 5 | 28 | 21 | 0.83 | 3.7 | 37 | 5 | 31 | 7 | 0.53 | 3.9 | 360 | 6 | 2 | 17 | 0.27 | 2.1 | 80 | ||
| 5 | 28 | 22 | 0.77 | 4.1 | 55 | 5 | 31 | 8 | 0.56 | 2.8 | 70 | 6 | 2 | 18 | 0.29 | 1.9 | 41 | ||
| 5 | 28 | 23 | 0.83 | 3.4 | 54 | 5 | 31 | 9 | 0.51 | 4.2 | 32 | 6 | 2 | 19 | 0.29 | 2.3 | 52 | ||
| 5 | 29 | 0 | 0.69 | 3.4 | 53 | 5 | 31 | 10 | 0.49 | 3.6 | 32 | 6 | 2 | 20 | 0.29 | 2.4 | 64 | ||
| 5 | 29 | 1 | 0.78 | 3.6 | 34 | 5 | 31 | 11 | 0.52 | 1.5 | 61 | 6 | 2 | 21 | 0.34 | 2.4 | 62 | ||
| 5 | 29 | 2 | 0.7 | 3.9 | 19 | 5 | 31 | 12 | 0.43 | 4.5 | 28 | 6 | 2 | 22 | 0.36 | 2.3 | 54 | ||
| 5 | 29 | 3 | 0.81 | 3.8 | 56 | 5 | 31 | 13 | 0.41 | 4.1 | 31 | 6 | 2 | 23 | 0.36 | 2.6 | 40 | ||
| 5 | 29 | 4 | 0.82 | 3.9 | 38 | 5 | 31 | 14 | 0.39 | 3.1 | 51 | 6 | 3 | 0 | 0.32 | 2.7 | 69 | ||
| 5 | 29 | 5 | 0.77 | 4.1 | 30 | 5 | 31 | 15 | 0.35 | 4.8 | 37 | 6 | 3 | 1 | 0.38 | 2.6 | 55 | ||
| 5 | 29 | 6 | 0.77 | 4.1 | 54 | 5 | 31 | 16 | 0.31 | 3.9 | 41 | 6 | 3 | 2 | 0.32 | 2.7 | 82 | ||
| 5 | 29 | 7 | 0.76 | 4.1 | 29 | 5 | 31 | 17 | 0.33 | 1.9 | 352 | 6 | 3 | 3 | 0.27 | 2.7 | 353 | ||
| 5 | 29 | 8 | 0.6 | 3.9 | 43 | 5 | 31 | 18 | 0.43 | 2.7 | 55 | 6 | 3 | 4 | 0.29 | 2.6 | 51 | ||
| 5 | 29 | 9 | 0.61 | 3.7 | 38 | 5 | 31 | 19 | 0.54 | 3 | 17 | 6 | 3 | 5 | 0.26 | 2.7 | 62 | ||
| 5 | 29 | 10 | 0.57 | 3.6 | 45 | 5 | 31 | 20 | 0.58 | 3.4 | 49 | 6 | 3 | 6 | 0.27 | 2 | 52 | ||
| 5 | 29 | 11 | 0.54 | 3.7 | 17 | 5 | 31 | 21 | 0.57 | 3.4 | 53 | 6 | 3 | 7 | 0.26 | 9.4 | 282 | ||
| 5 | 29 | 12 | 0.52 | 3.2 | 28 | 5 | 31 | 22 | 0.66 | 3.4 | 26 | 6 | 3 | 8 | 0.24 | 2.9 | 53 | ||
| 5 | 29 | 13 | 0.53 | 3.5 | 57 | 5 | 31 | 23 | 0.65 | 3.5 | 25 | 6 | 3 | 9 | 0.27 | 1.8 | 21 | ||
| 5 | 29 | 14 | 0.45 | 3.6 | 30 | 6 | 1 | 0 | 0.7 | 3.8 | 25 | 6 | 3 | 10 | 0.24 | 3.4 | 222 | ||
| 5 | 29 | 15 | 0.39 | 3.3 | 49 | 6 | 1 | 1 | 0.69 | 3.7 | 53 | ||||||||
| 5 | 29 | 16 | 0.44 | 1.5 | 25 | 6 | 1 | 2 | 0.67 | 3.7 | 49 |
| Longshore Distance from Groin (m) | −20 | −14 | −10 | −8 | −6 | −4 | −2 | 2 | 4 | 6 | 8 | 10 | 14 | 20 | RMSE | |
| Cross-shore Distance from Baseline (m) | Initial Shoreline | 11.3 | 11.6 | 11.5 | 11.8 | 11.9 | 12.0 | 12.8 | 12.7 | 13.1 | 13.5 | 13.6 | 13.5 | 14.2 | 14.9 | |
| Field data at 23 h | 9.9 | 9.3 | 9.1 | 9.1 | 9.2 | 9.3 | 9.5 | 18.1 | 18.5 | 18.3 | 17.8 | 17.5 | 17.1 | 16.9 | ||
| GSb, KGSb = 0.005 | 10.1 | 9.8 | 9.5 | 9.4 | 9.5 | 10.0 | 11.2 | 15.7 | 16.2 | 16.4 | 16.5 | 16.4 | 16.4 | 16.6 | 3.825 | |
| GSb, KGSb = 0.01 | 10.1 | 9.8 | 9.4 | 9.4 | 9.4 | 10.2 | 11.4 | 15.8 | 16.3 | 16.4 | 16.4 | 16.4 | 16.4 | 16.6 | 3.817 | |
| GSb, KGSb = 0.05 | 10.1 | 9.4 | 9.3 | 9.8 | 9.8 | 11.6 | 12.5 | 17.0 | 16.7 | 16.5 | 16.4 | 16.4 | 16.4 | 16.6 | 4.127 | |
| GSb, KGSb = 0.1 | 10.1 | 8.9 | 10.2 | 11.2 | 11.2 | 12.8 | 13.3 | 18.1 | 16.8 | 16.8 | 16.6 | 16.5 | 16.5 | 16.6 | 5.269 |
| Case | H1/50 (m) | θ (°) | ΔS(t0) (m) | RS(t0) | Q × 10−5 (m3/s) |
|---|---|---|---|---|---|
| Test 1A | 0.232 | 15 | 1.33 | 0.765 | 1.52 |
| Test 2A | 0.232 | 30 | 2.28 | 0.629 | 2.45 |
| Test 3A | 0.232 | 45 | 2.62 | 0.585 | 2.46 |
| Test 4A | 0.310 | 15 | 2.47 | 0.604 | 4.03 |
| Test 5A | 0.310 | 30 | 3.75 | 0.454 | 6.47 |
| Test 6A | 0.310 | 45 | 5.11 | 0.324 | 6.50 |
| Case | H1/3 (m) | H1/50 (m) | θo (°) | (°) | × 10−2 (m2/s) | RL(ti) | |
|---|---|---|---|---|---|---|---|
| Test 1B | 0.150 | 0.232 | 0.34 | 15 | 3.74 | 0.88 | 0.865 |
| Test 2B | 0.150 | 0.232 | 0.33 | 30 | 6.76 | 0.77 | 0.815 |
| Test 3B | 0.150 | 0.232 | 0.31 | 45 | 8.71 | 0.67 | 0.689 |
| Test 4B | 0.200 | 0.310 | 0.43 | 15 | 3.89 | 1.60 | 0.945 |
| Test 5B | 0.200 | 0.310 | 0.42 | 30 | 7.40 | 1.43 | 0.920 |
| Test 6B | 0.200 | 0.310 | 0.39 | 45 | 10.29 | 1.14 | 0.844 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medellín, G.; Torres-Freyermuth, A.; Tomasicchio, G.R.; Francone, A.; Tereszkiewicz, P.A.; Lusito, L.; Palemón-Arcos, L.; López, J. Field and Numerical Study of Resistance and Resilience on a Sea Breeze Dominated Beach in Yucatan (Mexico). Water 2018, 10, 1806. https://doi.org/10.3390/w10121806
Medellín G, Torres-Freyermuth A, Tomasicchio GR, Francone A, Tereszkiewicz PA, Lusito L, Palemón-Arcos L, López J. Field and Numerical Study of Resistance and Resilience on a Sea Breeze Dominated Beach in Yucatan (Mexico). Water. 2018; 10(12):1806. https://doi.org/10.3390/w10121806
Chicago/Turabian StyleMedellín, Gabriela, Alec Torres-Freyermuth, Giuseppe Roberto Tomasicchio, Antonio Francone, Peter A. Tereszkiewicz, Letizia Lusito, Leonardo Palemón-Arcos, and José López. 2018. "Field and Numerical Study of Resistance and Resilience on a Sea Breeze Dominated Beach in Yucatan (Mexico)" Water 10, no. 12: 1806. https://doi.org/10.3390/w10121806
APA StyleMedellín, G., Torres-Freyermuth, A., Tomasicchio, G. R., Francone, A., Tereszkiewicz, P. A., Lusito, L., Palemón-Arcos, L., & López, J. (2018). Field and Numerical Study of Resistance and Resilience on a Sea Breeze Dominated Beach in Yucatan (Mexico). Water, 10(12), 1806. https://doi.org/10.3390/w10121806









