A New Tool to Estimate Inundation Depths by Spatial Interpolation (RAPIDE): Design, Application and Impact on Quantitative Assessment of Flood Damages
Abstract
1. Introduction
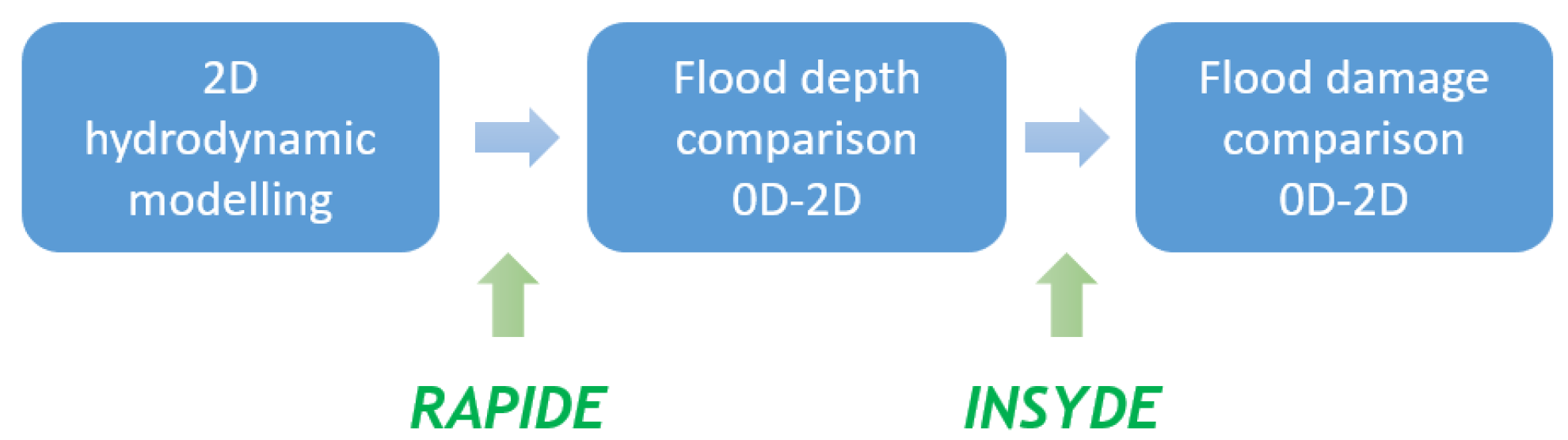
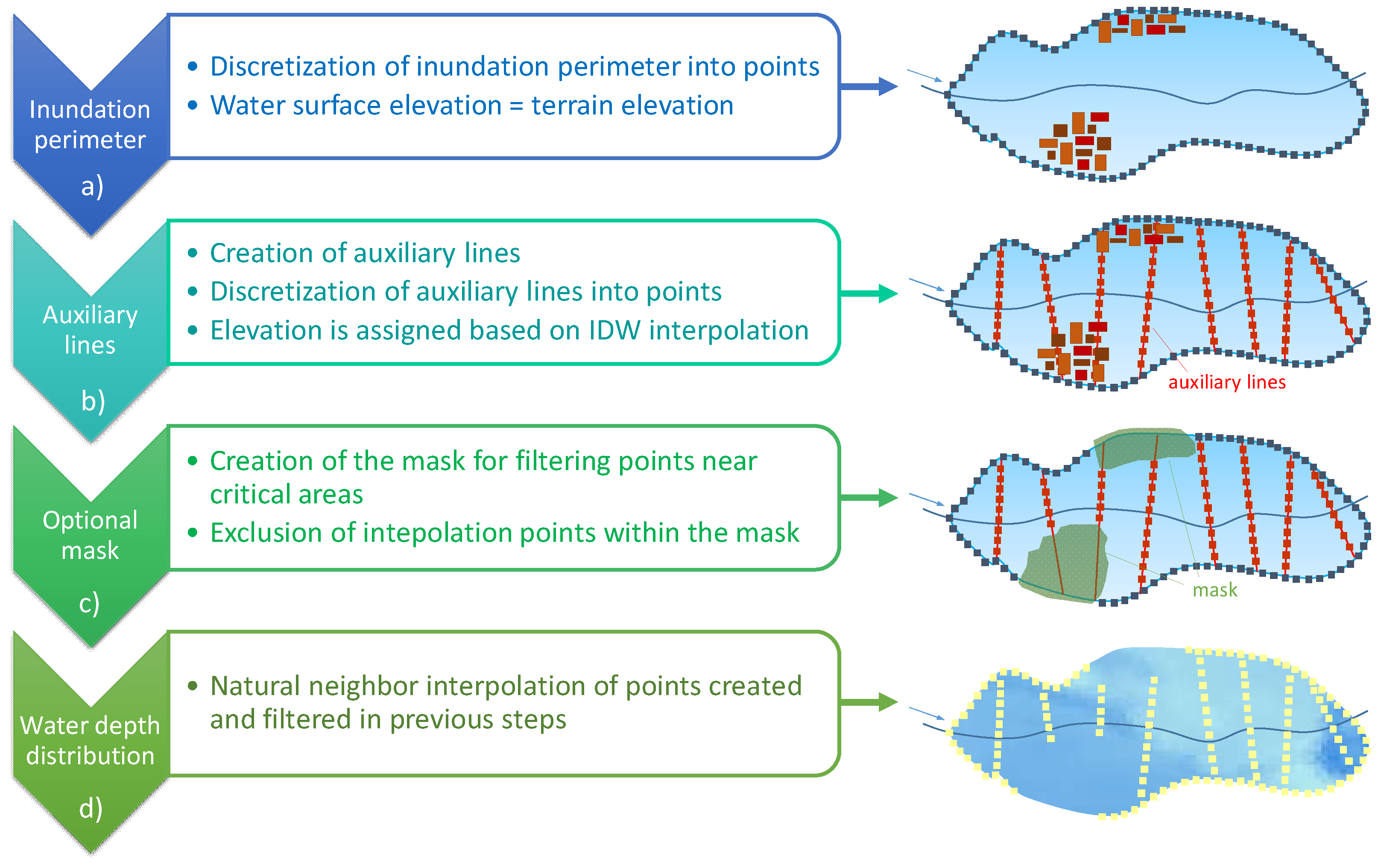
2. RAPIDE: RAPid GIS Tool for Inundation Depth Estimation
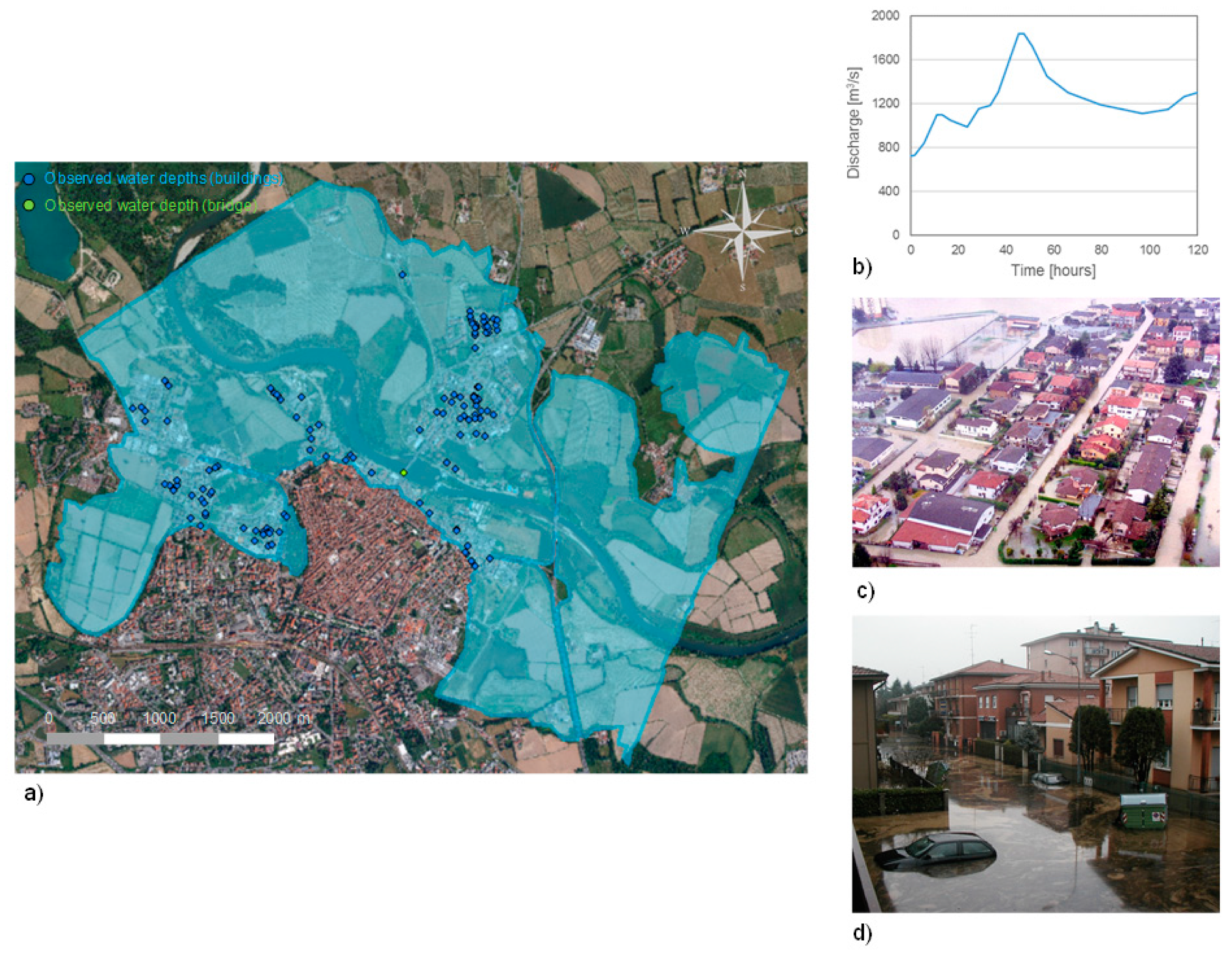
3. Case Study: 2002 Adda River Flood Event
- Measured water levels at the ancient bridge of the town of Lodi;
- Observed water depths in more than 260 georeferenced points within the inundated area (Figure 3a), deriving from indications provided by municipal technicians and by citizens in the damage compensation forms, as well as from interpretation of photographs taken during or immediately after the event (these water depth measurements could be affected by average errors of about 20–30 cm, given the type and quality of the observations);
- Documented oil spills in some zones of the inundated area (Figure 3d);
- Observed losses for 271 residential buildings, deriving from damage compensation forms compiled by citizens, for a total of 3.77 M€ (as of year 2002).
4. Hazard Modelling of the 2002 Adda Flood
4.1. 2D Hydraulic Model
- the average of the differences between simulated and observed water depths (AD);
- the absolute average of the differences between simulated and observed water depths (AAD);
- the Nash-Sutcliffe Efficiency (NSE) [27], defined as:where WDOi and WDSi are, respectively, the observed and simulated water depth at location i, while is the mean observed water depth. The NSE may range between −∞ and 1 (goal value);
- the flood area index (FAI) [28], defined as:where A11, A01 and A10 respectively represent the numbers of pixels for which both simulation and observation indicate “wet”, simulation indicates “wet” and observation indicates “dry”, and simulation indicates “dry” and observation indicates “wet”. The FAI may range between 0 and 1 (goal value).
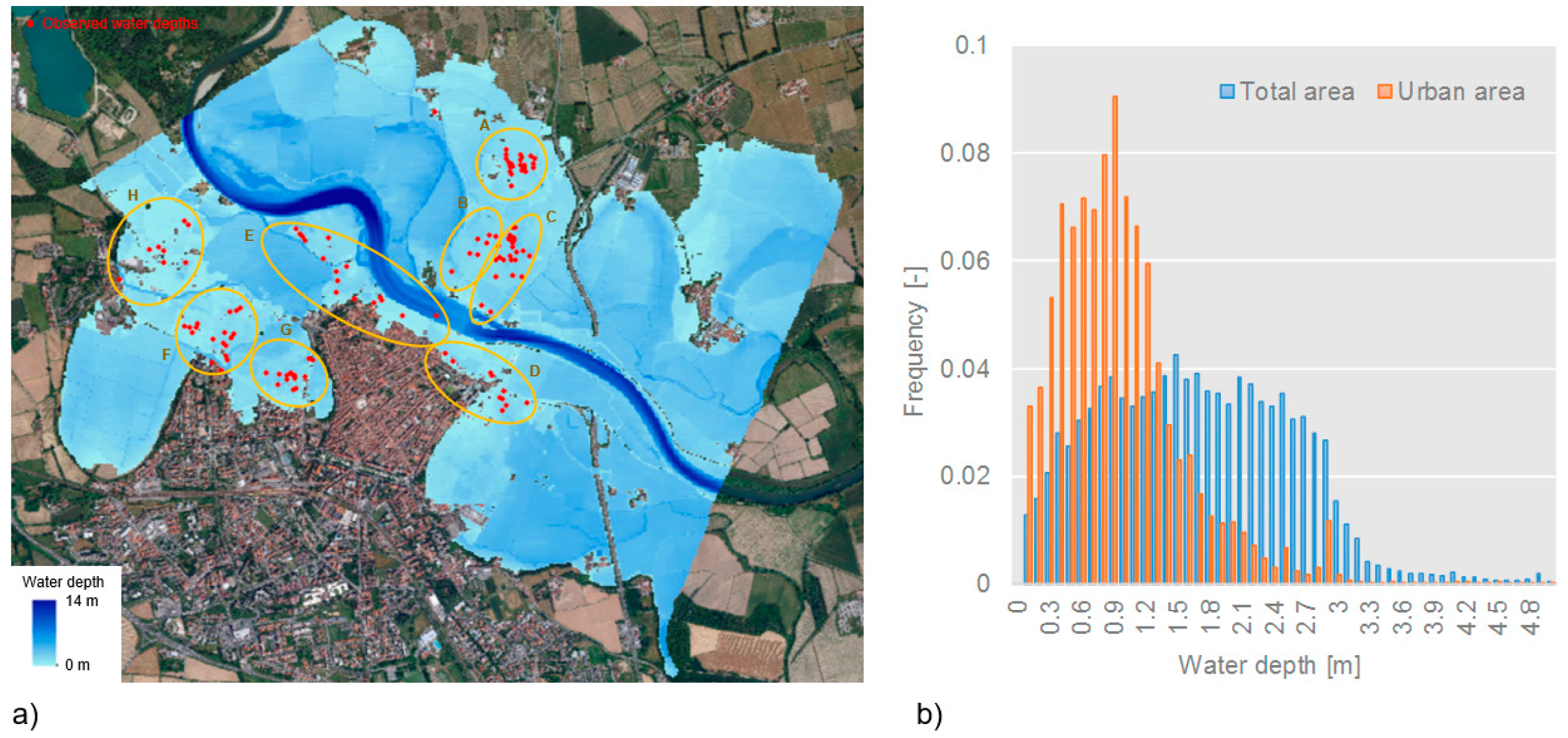
4.2. RAPIDE Model
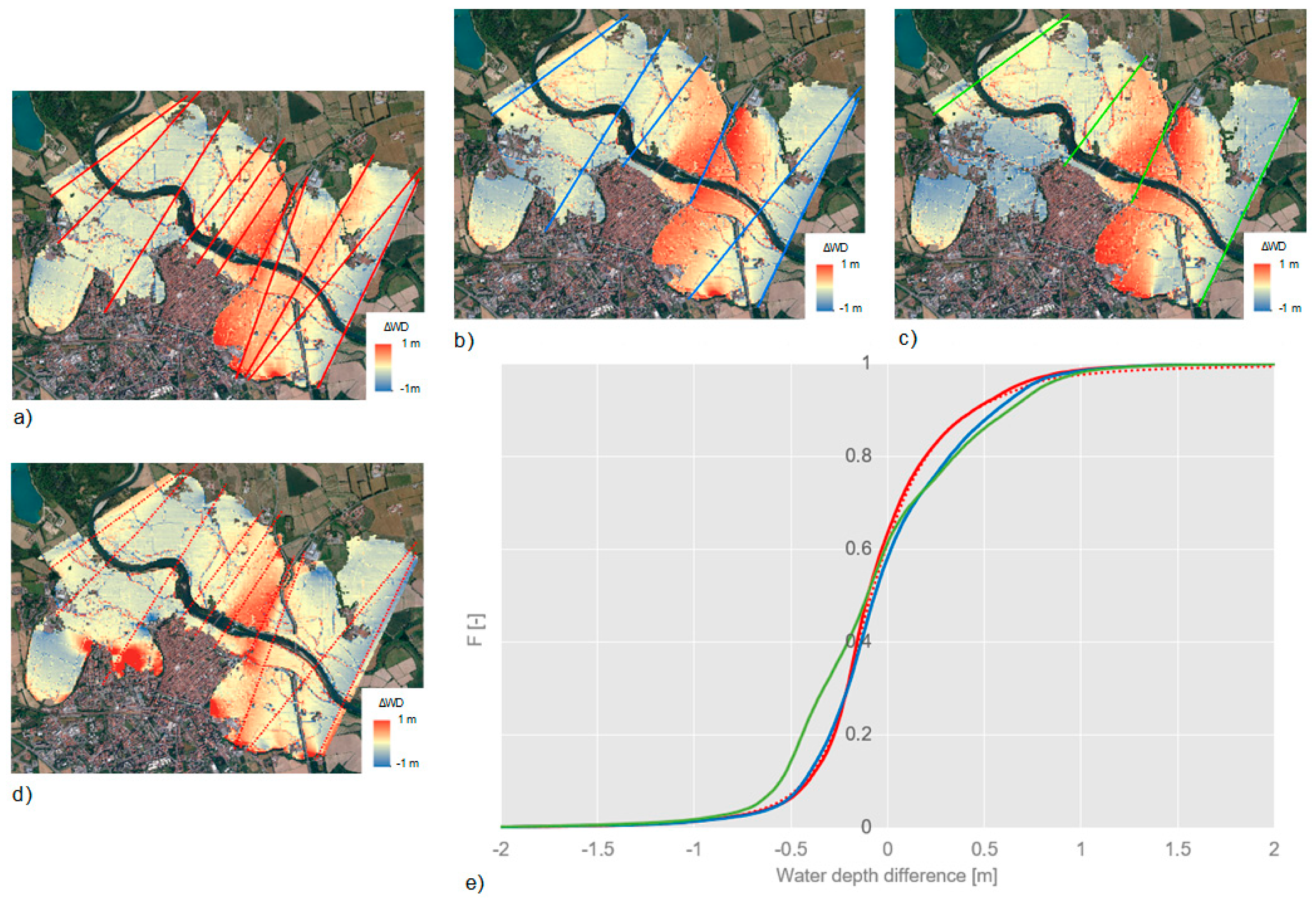
- the number of selected auxiliary lines (that is inversely proportional to the spacing between these lines): three scenarios with increasing mean spacing (from 450 m to 1.3 km, corresponding approximately to 3 and 10 times the Adda’s main channel width) were considered (i.e., ‘narrow’, ‘large’ and ‘very large spacing’ cases (Figure 5)); the last two configurations were obtained by deleting lines from the ‘narrow spacing’ case and without changing their positions;
- the use of a mask: the default condition for all the tested scenarios included the use of a polygon mask derived from the regional land-use map filtered for built-up areas (Figure 5d); the upstream and downstream boundaries of the inundated area (where it was known that water depth was not null) were masked as well; the ‘narrow spacing’ case was then tested also without the use of this mask;
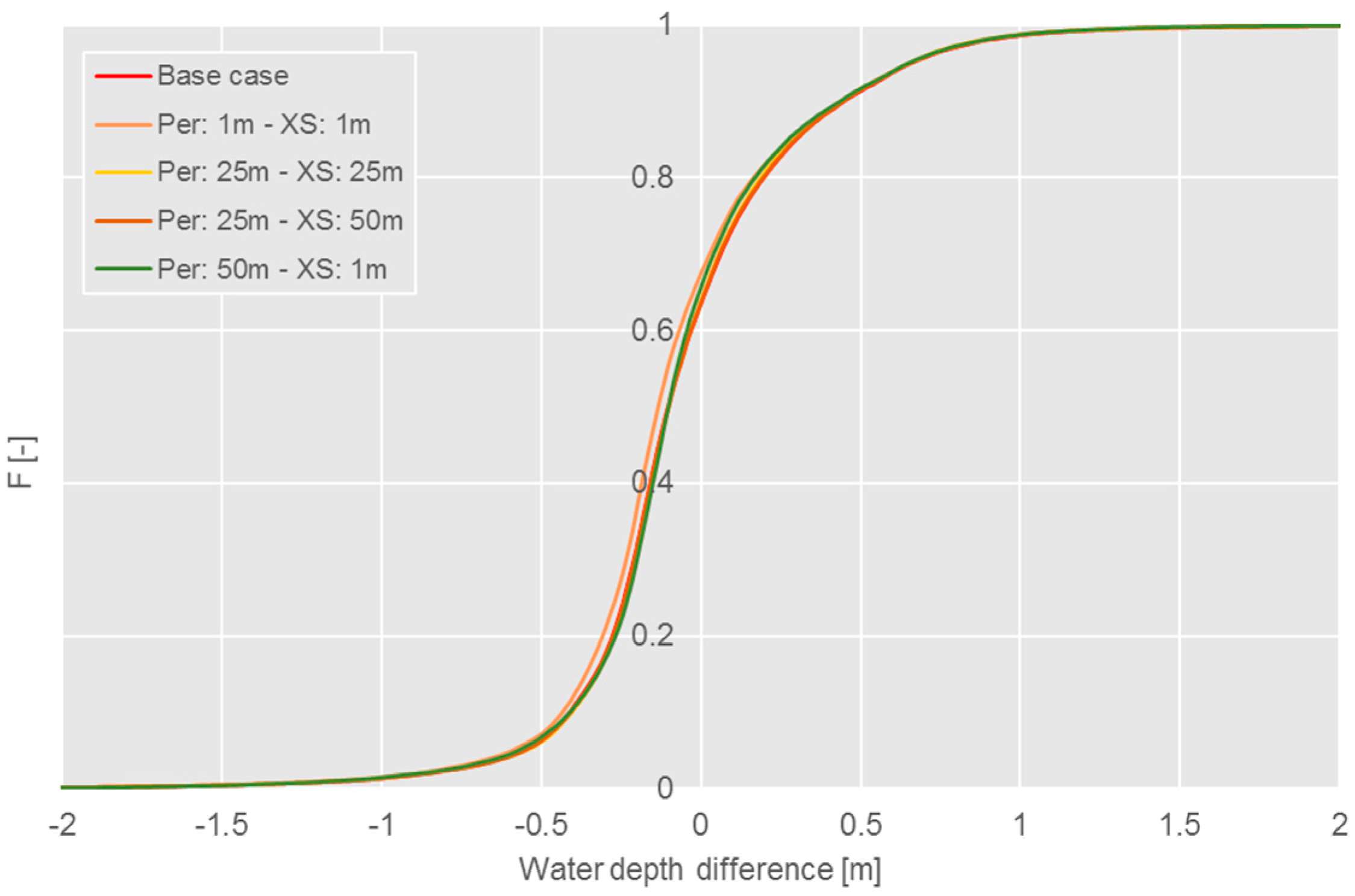
- the resolution used for the discretization of the flood perimeter and auxiliary lines: in the RAPIDE toolbox the user can change the default values for the resolution of the discretization, equal to 25 m and 1 m for flood the perimeter and auxiliary lines, respectively; based on the ‘narrow spacing’ case, different conditions were tested, varying the resolution between 1 m and 50 m for the perimeter and up to 50 m for the lines;
- the location of the auxiliary lines: a total of 25 configurations were generated and tested; the number of possible configurations was mainly limited by the requirements of perpendicularity to the channel axis, non-intersection with other drawn lines, intersection with the flood perimeter in two points over the external boundary and physical meaning of the lines.
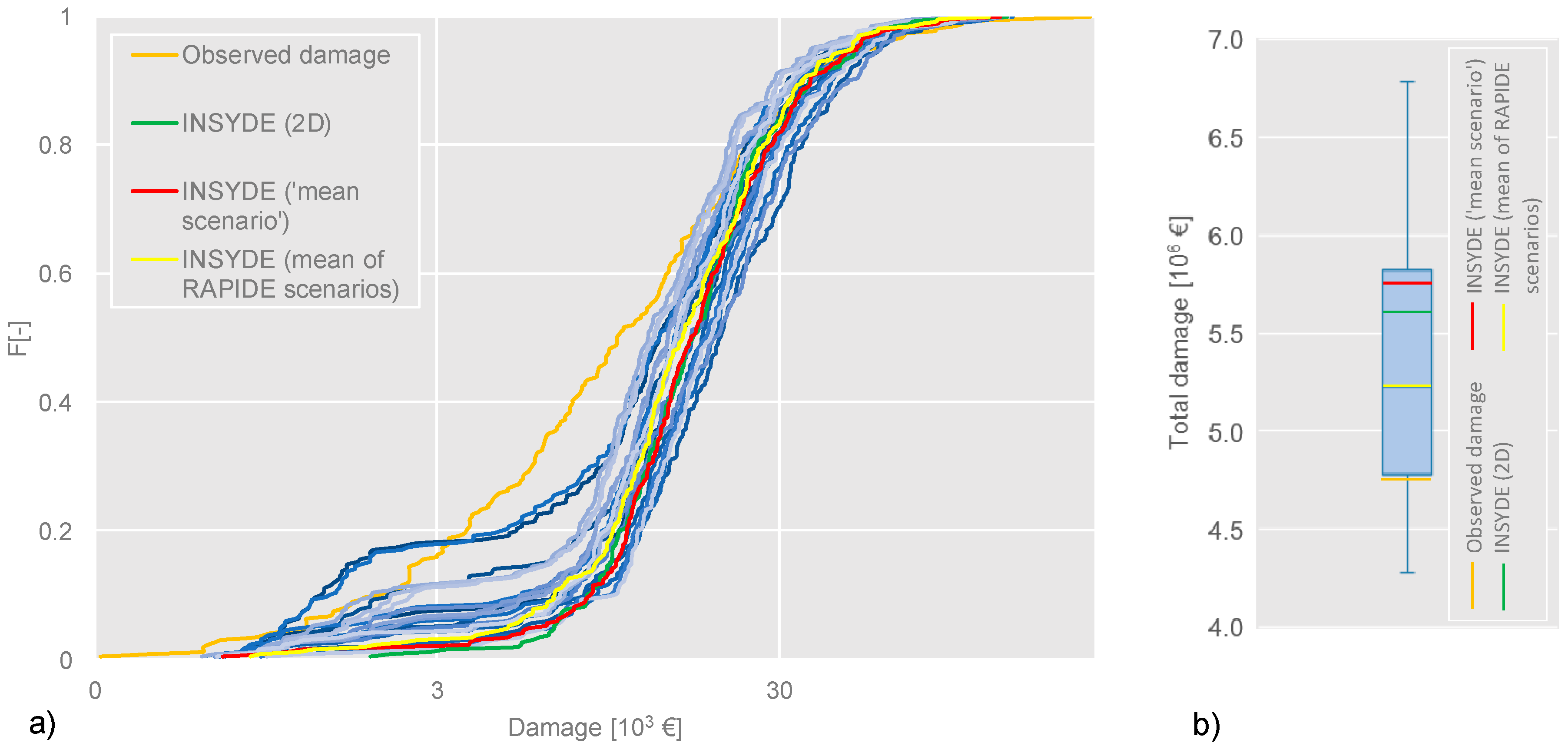
5. Damage Modelling of the 2002 Adda Flood
- the geometric characteristics (i.e., footprint area, external perimeter, basement area, number of floors) and finishing level of the buildings were derived from cadastral data;
- the building type (i.e., apartment, semi-detached or detached house), level of maintenance and year of construction were assigned to different buildings, based on the urban development plan of the town of Lodi;
- the building material (i.e., reinforced concrete or masonry) was assigned considering the most frequent type observed in each census zone of Lodi, based on ISTAT data, as shown in [31].
6. Discussion and Recommendations
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Plate, E.J. Flood risk management for setting priorities in decision making. In Extreme Hydrological Events: New Concepts for Security; Vasiliev, O.F., van Gelder, P.H.A.J.M., Plate, E.J., Bolgov, M.V., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 21–44. ISBN 978-1-4020-5739-7. [Google Scholar]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Assessment of economic flood damage. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Armenakis, C.; Du, E.X.; Natesan, S.; Persad, R.A.; Zhang, Y. Flood risk assessment in urban areas based on spatial analytics and social factors. Geosciences 2017, 7, 123. [Google Scholar] [CrossRef]
- Lugeri, N.; Kundezewicz, Z.W.; Genovese, E.; Hochrainer, S.; Radziejewski, M. River flood risk and adaption in Europe—Assessment of the present status. Mitig. Adapt. Strateg. Glob. Chang. 2010, 15, 621–639. [Google Scholar] [CrossRef]
- Horrit, M.S.; Bates, P.D. Predicting floodplain inundation: Raster-based modelling versus the finite-element approach. Hydrol. Process. 2001, 15, 825–842. [Google Scholar] [CrossRef]
- Horrit, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Büchele, B.; Kreibich, H.; Kron, A.; Thieken, A.; Ihringer, J.; Oberle, P.; Merz, B.; Nestmann, F. Flood-risk mapping: Contribution towards an enhanced assessment of extreme events and associated risks. Nat. Hazards Earth Syst. Sci. 2006, 6, 485–503. [Google Scholar] [CrossRef]
- Pender, G. Briefing: Introducing the flood risk management research consortium. In Proceedings of the Institution of Civil Engineers—Water Management; Thomas Telford Ltd.: London, UK, 2006; Volume 159, pp. 3–8. [Google Scholar]
- Woodhead, S.; Asselman, N.; Zech, Y.; Soares-Frazão, S.; Bates, P.; Kortenhaus, A. Evaluation of Inundation Models-Limits and Capabilities of Models. FLOODSite Report T08-07-01. 2007. Available online: http://www.floodsite.net/html/partner_area/project_docs/T08_07_01_Inundation_Model_Evaluation_M8_1_V1_7_P15.pdf (accessed on 7 December 2018).
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Modell. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Vojinovic, Z.; Tutulic, D. On the use of 1D and coupled 1D-2D modelling approaches for assessment of flood damage in urban areas. Urban Water J. 2009, 6, 183–199. [Google Scholar] [CrossRef]
- de Moel, H.; van Alphen, J.; Aerts, J.C.J.H. Flood maps in Europe—Methods, availability and use. Nat. Hazards Earth Syst. Sci. 2009, 9, 289–301. [Google Scholar] [CrossRef]
- Ward, P.J.; Jongman, B.; Weiland, F.S.; Bouwman, A.; van Beek, R.; Bierkens, M.F.; Ligtvoet, W.; Winsemius, H.C. Assessing flood risk at the global scale: Model setup, results, and sensitivity. Environ. Res. Lett. 2013, 8, 044019. [Google Scholar] [CrossRef]
- McGrath, H.; Bourgon, J.F.; Proulx-Bourque, J.S.; Nastev, M.; El Ezz, A.A. A comparison of simplified conceptual models for rapid web-based flood inundation mapping. Nat. Hazards 2018, 93, 905–920. [Google Scholar] [CrossRef]
- Autoritàdi Bacino del Fiume, P. Piano per la Valutazione e la Gestione del Rischio di Alluvioni. Mappatura della Pericolosità e Valutazione del Rischio; Report II.A; Autorità di Bacino del Fiume Po: Parma, Italy, 2016; 29p. [Google Scholar]
- Scorzini, A.R.; Leopardi, M. River basin planning: From qualitative to quantitative flood risk assessment: The case of Abruzzo Region (central Italy). Nat. Hazards 2017, 88, 71–93. [Google Scholar] [CrossRef]
- Teng, J.; Vaze, J.; Dutta, D.; Marvanek, S. Rapid inundation modelling in large floodplains using LiDAR DEM. Water Resour. Manag. 2015, 29, 2619–2636. [Google Scholar] [CrossRef]
- Lhomme, J.; Sayers, P.; Gouldby, B.; Samuels, P.; Wills, M.; Mulet-Marti, J. Recent development and application of a rapid flood spreading method. In Flood Risk Management: Research and Practice; Samuels, P., Huntington, S., Allsop, W., Harrop, J., Eds.; Taylor & Francis Group: London, UK, 2008. [Google Scholar]
- Nobre, A.D.; Cuartas, L.A.; Hodnett, M.; Rennó, C.D.; Rodrigues, G.; Silveira, A.; Waterloo, M.; Saleska, S. Height Above the Nearest Drainage—A hydrologically relevant new terrain model. J. Hydrol. 2011, 404, 13–29. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, Y.F.; Munasinghe, D.; Fang, Z.; Tsang, Y.P.; Cohen, S. Comparative analysis of inundation mapping approaches for the 2016 flood in the Brazos River, Texas. J. Am. Water Resour. Assoc. 2018, 54, 820–833. [Google Scholar] [CrossRef]
- Cohen, S.; Brakenridge, G.R.; Kettner, A.; Bates, B.; Nelson, J.; McDonald, R.; Huang, Y.F.; Munasinghe, D.; Zhang, J. Estimating floodwater depths from flood inundation maps and topography. J. Am. Water Resour. Assoc. 2017, 54, 847–858. [Google Scholar] [CrossRef]
- Gatti, F. Stima del Rischio Alluvionale per le Attività Economiche: Il Caso Studio di Olbia (OT). Master’s Thesis, Università degli Studi di Milano, Milan, Italy, 2016; p. 91. [Google Scholar]
- Pastormerlo, M. SWAM (Surface Water Analysis Method): Un Metodo Speditivo per la Modellazione di un Evento Alluvionale. Master’s Thesis, Università degli Studi di Milano, Milan, Italy, 2016; p. 112. [Google Scholar]
- Dottori, F.; Figueiredo, R.; Martina, M.L.V.; Molinari, D.; Scorzini, A.R. INSYDE: A synthetic, probabilistic flood damage model based on explicit cost analysis. Nat. Hazards Earth Syst. Sci. 2016, 16, 2577–2591. [Google Scholar] [CrossRef]
- Rossetti, S.; Cella, O.W.; Lodigiani, V. Studio idrologico-idraulico del tratto del f. adda inserito nel territorio comunale. In Relazione Idrologico-Idraulica; Atti del P.G.T. del comune di Lodi: Lodi, Italy, 2010; p. 101. [Google Scholar]
- Steffler, P.M.; Blackburn, J. River2D—Two-Dimensional Depth Averaged Model of River Hydrodynamics and Fish Habitat; University of Alberta: Edmonton, AB, Canada, 2002. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Dung, N.V.; Merz, B.; Bárdossy, A.; Thang, T.D.; Apel, H. Multi-objective automatic calibration of hydrodynamic models utilizing inundation maps and gauge data. Hydrol. Earth Syst. Sci. 2011, 15, 1339–1354. [Google Scholar] [CrossRef]
- Dressler, M. Art of Surface Interpolation; Technical University of Liberec Faculty of Mechatronics and Interdisciplinary Engineering Studies: Liberec, Czech Republic, 2009. [Google Scholar]
- Galliani, M.; Scorzini, A.R.; Molinari, D.; Minucci, G. Flood damage model validation and the level of detail of input data quality: The case of the 2002 flood in Lodi (northern Italy). In Proceedings of the 5th IAHR Europe Congress, Trento, Italy, 12–14 June 2018. [Google Scholar]
- Molinari, D.; Scorzini, A.R. On the influence of input data quality to flood damage estimation: The performance of the INSYDE model. Water 2017, 9, 688. [Google Scholar] [CrossRef]
- Freni, G.; La Loggia, G.; Notaro, V. Uncertainty in urban flood damage assessment due to urban drainage modelling and depth–damage curve estimation. Water Sci. Technol. 2010, 61, 2979–2993. [Google Scholar] [CrossRef]
- de Moel, H.; Aerts, J.C.J.H. Effect of uncertainty in land use, damage models and inundation depth on flood damage estimates. Nat. Hazards 2011, 58, 407–425. [Google Scholar] [CrossRef]
- Brémond, P.; Grelot, F.; Agenais, A.L. Review Article: Economic evaluation of flood damage to agriculture—Review and analysis of existing methods. Nat. Hazards Earth Syst. Sci. 2013, 13, 2493–2512. [Google Scholar] [CrossRef]
| Indicator | Cluster | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | Average | |
| AD (m) | 0.09 | −0.01 | 0.34 | 0.17 | −0.39 | −0.18 | −0.16 | −0.23 | −0.04 |
| AAD (m) | 0.21 | 0.29 | 0.42 | 0.33 | 0.57 | 0.36 | 0.37 | 0.41 | 0.37 |
| NSE | 0.24 | 0.42 | −1.03 | 0.39 | −0.04 | −0.19 | −0.11 | −0.31 | −0.18 |
| Hazard Parameter | 2D Model | RAPIDE |
|---|---|---|
| Water depth (h) | Water depth distribution as of output from 2D model | Water depth distribution as of output from RAPIDE |
| Flow velocity (v) | Flow velocity distribution as of output from 2D model | Default value in INSYDE (0.5 m/s) |
| Flood duration (d) | Default value in INSYDE (24 h) | |
| Water quality (q) | As from documented observations during the event | |
| Presence of sediment (s) | Default value in INSYDE (fine-grained sediment) | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scorzini, A.R.; Radice, A.; Molinari, D. A New Tool to Estimate Inundation Depths by Spatial Interpolation (RAPIDE): Design, Application and Impact on Quantitative Assessment of Flood Damages. Water 2018, 10, 1805. https://doi.org/10.3390/w10121805
Scorzini AR, Radice A, Molinari D. A New Tool to Estimate Inundation Depths by Spatial Interpolation (RAPIDE): Design, Application and Impact on Quantitative Assessment of Flood Damages. Water. 2018; 10(12):1805. https://doi.org/10.3390/w10121805
Chicago/Turabian StyleScorzini, Anna Rita, Alessio Radice, and Daniela Molinari. 2018. "A New Tool to Estimate Inundation Depths by Spatial Interpolation (RAPIDE): Design, Application and Impact on Quantitative Assessment of Flood Damages" Water 10, no. 12: 1805. https://doi.org/10.3390/w10121805
APA StyleScorzini, A. R., Radice, A., & Molinari, D. (2018). A New Tool to Estimate Inundation Depths by Spatial Interpolation (RAPIDE): Design, Application and Impact on Quantitative Assessment of Flood Damages. Water, 10(12), 1805. https://doi.org/10.3390/w10121805






