Performance Assessment of General Circulation Model in Simulating Daily Precipitation and Temperature Using Multiple Gridded Datasets
Abstract
1. Introduction
2. Materials and Methods
2.1. Geography and Climate of Pakistan
2.2. Data and Sources
2.2.1. Gridded Datasets
2.2.2. Coupled Model Intercomparison Project Phase 5 (CMIP5) General Circulation Model (GCM) Datasets
3. Methodology
3.1. Procedure
- (1)
- The GCMs are evaluated and ranked using SU at each grid point (total 36 grid points at 2° × 2° resolution to cover whole Pakistan, Figure 1) according to their capability to replicate gridded temperature and precipitation data for the period 1979–2005.
- (2)
- The GCMs are ranked based on their positions at different grid points using a weighting technique, where more weight is given to GCMs which archive a higher rank in most of the grid points. A separate list of rank is prepared for each climatic variable (maximum and minimum temperature and precipitation) and each gridded dataset.
- (3)
- The common GCMs appeared above the 50-th percentile of all GCMs in each list are identified as the most appropriate ensemble for the projection of temperature and precipitation of Pakistan.
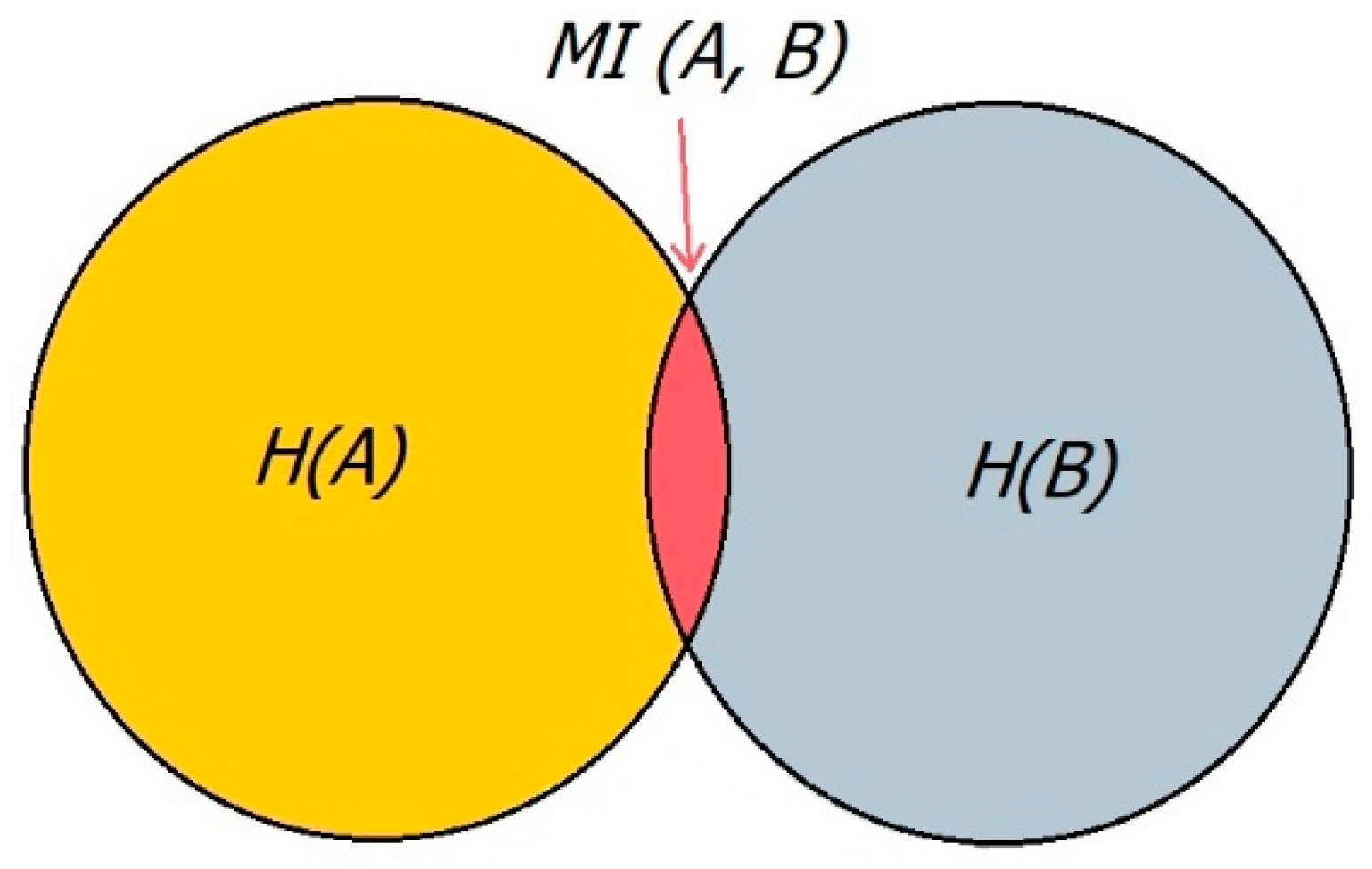
3.2. Symmetric Uncertainty (SU)
3.3. Ranking of GCMs using Weighting Method
4. Results
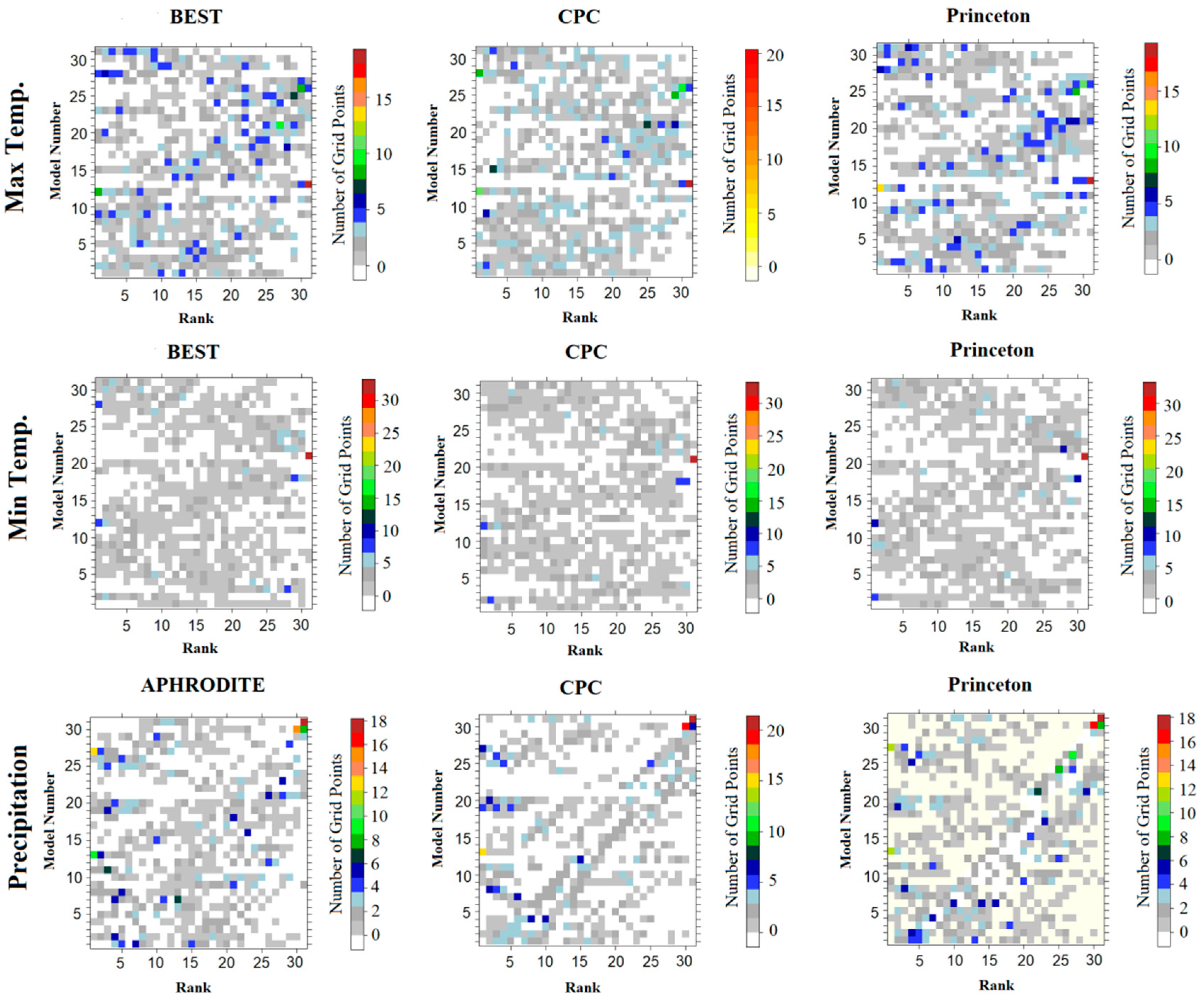
4.1. Ranking of GCMs
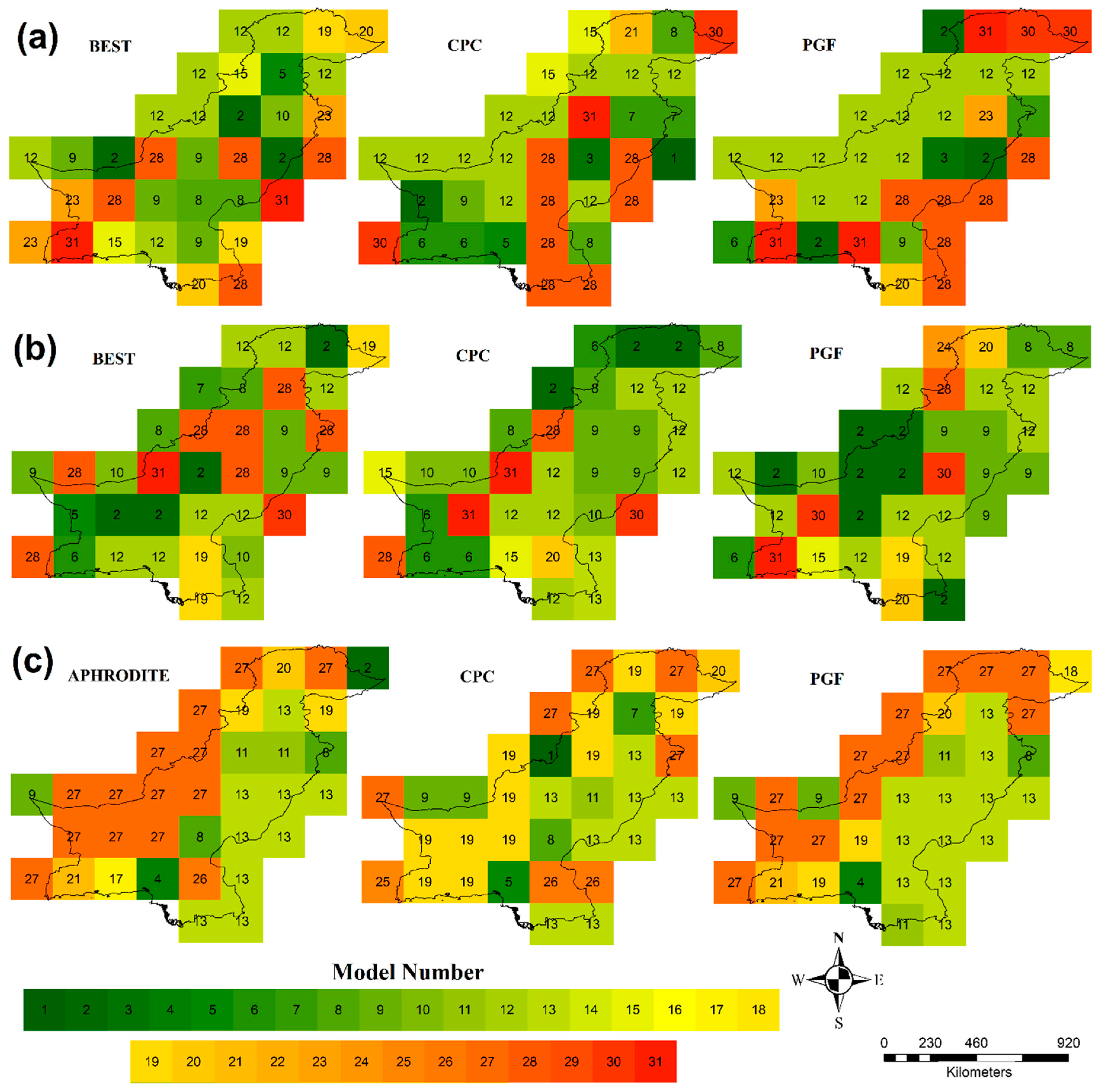
4.2. Spatial Distribution of Top Ranked GCMs
4.3. Ranking of GCMs for Pakistan
4.4. Selection of GCM Ensemble
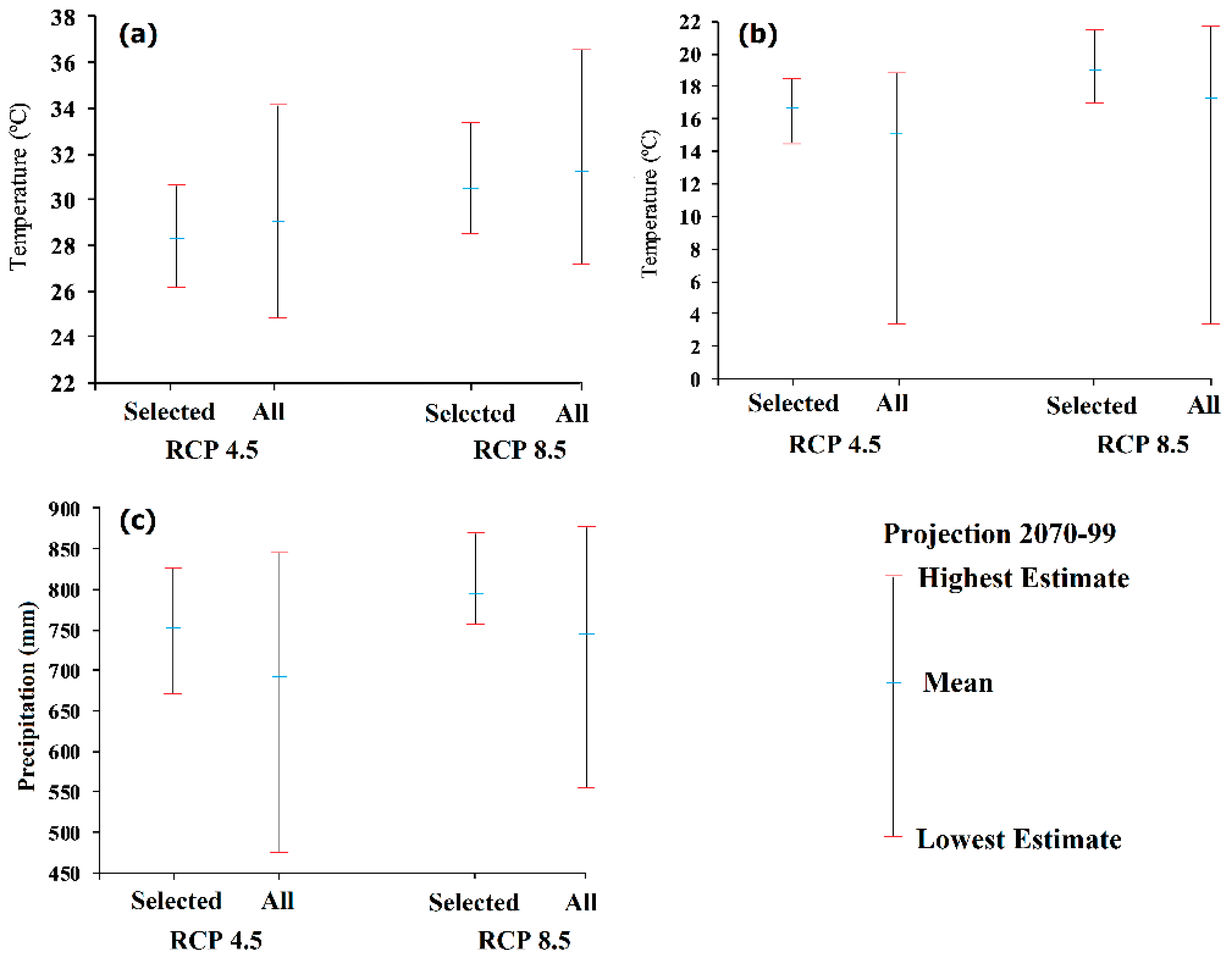
4.5. Future Projections using GCM Ensemble
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yip, S.; Ferro, C.A.; Stephenson, D.B.; Hawkins, E. A simple, coherent framework for partitioning uncertainty in climate predictions. J. Clim. 2011, 24, 4634–4643. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.; Chandler, R.; Kendon, E.; Widmann, M.; Brienen, S.; Rust, H.; Sauter, T.; Themeßl, M. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Lutz, A.F.; ter Maat, H.W.; Biemans, H.; Shrestha, A.B.; Wester, P.; Immerzeel, W.W. Selecting representative climate models for climate change impact studies: An advanced envelope-based selection approach. Int. J. Climatol. 2016, 36, 3988–4005. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Wang, X.-J. Selection of climate models for projection of spatiotemporal changes in temperature of Iraq with uncertainties. Atmos. Res. 2018, 213, 509–522. [Google Scholar] [CrossRef]
- Pour, S.H.; Shahid, S.; Chung, E.-S.; Wang, X.-J. Model output statistics downscaling using support vector machine for the projection of spatial and temporal changes in rainfall of Bangladesh. Atmos. Res. 2018, 213, 149–162. [Google Scholar] [CrossRef]
- Mote, P.; Brekke, L.; Duffy, P.B.; Maurer, E. Guidelines for constructing climate scenarios. Eos Trans. Am. Geophys. Union 2011, 92, 257–258. [Google Scholar] [CrossRef]
- Srinivasa Raju, K.; Nagesh Kumar, D. Ranking general circulation models for India using TOPSIS. J. Water Clim. Chang. 2015, 6, 288–299. [Google Scholar] [CrossRef]
- Warszawski, L.; Frieler, K.; Huber, V.; Piontek, F.; Serdeczny, O.; Schewe, J. The inter-sectoral impact model intercomparison project (ISI–MIP): Project framework. Proc. Natl. Acad. Sci. USA 2014, 111, 3228–3232. [Google Scholar] [CrossRef]
- Hidalgo, H.G.; Das, T.; Dettinger, M.; Cayan, D.; Pierce, D.; Barnett, T.; Bala, G.; Mirin, A.; Wood, A.; Bonfils, C. Detection and attribution of streamflow timing changes to climate change in the western United States. J. Clim. 2009, 22, 3838–3855. [Google Scholar] [CrossRef]
- Raju, K.S.; Sonali, P.; Kumar, D.N. Ranking of CMIP5-based global climate models for India using compromise programming. Theor. Appl. Climatol. 2017, 128, 563–574. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Ali, R.; Harun, S.; Wang, X. Evaluation of the performance of gridded precipitation products over Balochistan Province, Pakistan. Désalin. Water Treat. 2017, 79, 73–86. [Google Scholar] [CrossRef]
- Talavera, L. An evaluation of filter and wrapper methods for feature selection in categorical clustering. In Advances in Intelligent Data Analysis VI; Springer: Berlin/Heidelberg, Germany, 2005; pp. 440–451. [Google Scholar]
- Maxino, C.; McAvaney, B.; Pitman, A.; Perkins, S. Ranking the AR4 climate models over the Murray-Darling Basin using simulated maximum temperature, minimum temperature and precipitation. Int. J. Climatol. J. R. Meteorol. Soc. 2008, 28, 1097–1112. [Google Scholar] [CrossRef]
- Perkins, S.; Pitman, A.; Holbrook, N.; McAneney, J. Evaluation of the AR4 climate models’ simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. J. Clim. 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Knutti, R.; Masson, D.; Gettelman, A. Climate model genealogy: Generation CMIP5 and how we got there. Geophys. Res. Lett. 2013, 40, 1194–1199. [Google Scholar] [CrossRef]
- Yokoi, S.; Takayabu, Y.N.; Nishii, K.; Nakamura, H.; Endo, H.; Ichikawa, H.; Inoue, T.; Kimoto, M.; Kosaka, Y.; Miyasaka, T. Application of cluster analysis to climate model performance metrics. J. Appl. Meteorol. Climatol. 2011, 50, 1666–1675. [Google Scholar] [CrossRef]
- Jiang, X.; Waliser, D.E.; Xavier, P.K.; Petch, J.; Klingaman, N.P.; Woolnough, S.J.; Guan, B.; Bellon, G.; Crueger, T.; DeMott, C. Vertical structure and physical processes of the Madden–Julian oscillation: Exploring key model physics in climate simulations. J. Geophys. Res. Atmos. 2015, 120, 4718–4748. [Google Scholar] [CrossRef]
- Min, S.K.; Hense, A. A Bayesian approach to climate model evaluation and multi-model averaging with an application to global mean surface temperatures from IPCC AR4 coupled climate models. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Afshar, A.A.; Hasanzadeh, Y.; Besalatpour, A.; Pourreza-Bilondi, M. Climate change forecasting in a mountainous data scarce watershed using CMIP5 models under representative concentration pathways. Theor. Appl. Climatol. 2017, 129, 683–699. [Google Scholar] [CrossRef]
- Xuan, W.; Ma, C.; Kang, L.; Gu, H.; Pan, S.; Xu, Y.-P. Evaluating historical simulations of CMIP5 GCMs for key climatic variables in Zhejiang Province, China. Theor. Appl. Climatol. 2017, 128, 207–222. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X. Intercomparison of near-surface temperature and precipitation extremes in AMIP-2 simulations, reanalyses, and observations. J. Clim. 2005, 18, 5201–5223. [Google Scholar] [CrossRef]
- Gleckler, P.J.; Taylor, K.E.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Johnson, F.; Sharma, A. Measurement of GCM skill in predicting variables relevant for hydroclimatological assessments. J. Clim. 2009, 22, 4373–4382. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.P.; Kirshner, S. Daily rainfall projections from general circulation models with a downscaling nonhomogeneous hidden Markov model (NHMM) for south-eastern Australia. Hydrol. Process. 2013, 27, 3663–3673. [Google Scholar] [CrossRef]
- Rupp, D.E.; Abatzoglou, J.T.; Hegewisch, K.C.; Mote, P.W. Evaluation of CMIP5 20th century climate simulations for the Pacific Northwest USA. J. Geophys. Res. Atmos. 2013, 118, 10884–10906. [Google Scholar] [CrossRef]
- Gu, H.; Yu, Z.; Wang, J.; Wang, G.; Yang, T.; Ju, Q.; Yang, C.; Xu, F.; Fan, C. Assessing CMIP5 general circulation model simulations of precipitation and temperature over China. Int. J. Climatol. 2015, 35, 2431–2440. [Google Scholar] [CrossRef]
- Reichler, T.; Kim, J. How well do coupled models simulate today’s climate? Bull. Am. Meteorol. Soc. 2008, 89, 303–312. [Google Scholar] [CrossRef]
- Witten, I.H.; Paynter, G.W.; Frank, E.; Gutwin, C.; Nevill-Manning, C.G. KEA: Practical Automated Keyphrase Extraction. In Design and Usability of Digital Libraries: Case Studies in the Asia Pacific; IGI Global: Hershey, PA, USA, 2005; pp. 129–152. [Google Scholar]
- Khan, N.; Shahid, S.; Ismail, T.; Ahmed, K.; Nawaz, N. Trends in heat wave related indices in Pakistan. Stoch. Environ. Res. Risk Assess. 2018. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Nawaz, N. Impacts of climate variability and change on seasonal drought characteristics of Pakistan. Atmos. Res. 2018, 214, 364–374. [Google Scholar] [CrossRef]
- Khan, N.; Shahid, S.; bin Ismail, T.; Wang, X.-J. Spatial distribution of unidirectional trends in temperature and temperature extremes in Pakistan. Theor. Appl. Climatol. 2018, 1–15. [Google Scholar] [CrossRef]
- Rohde, R.; Muller, R.; Jacobsen, R.; Muller, E.; Perlmutter, S.; Rosenfeld, A.; Wurtele, J.; Groom, D.; Wickham, C. A new estimate of the average Earth surface land temperature spanning 1753 to 2011. Geoinform. Geostat. Overv. 2013. [Google Scholar] [CrossRef]
- Xie, P.; Chen, M.; Shi, W. CPC unified gauge-based analysis of global daily precipitation. In Proceedings of the Preprints, 24th Conference on Hydrology, Atlanta, GA, USA, 17–21 January 2010. [Google Scholar]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef]
- Chaney, N.; Herman, J.; Reed, P.; Wood, E. Flood and drought hydrologic monitoring: The role of model parameter uncertainty. Hydrol. Earth Syst. Sci. 2015, 19, 3239–3251. [Google Scholar] [CrossRef]
- Yatagai, A.; Arakawa, O.; Kamiguchi, K.; Kawamoto, H.; Nodzu, M.I.; Hamada, A. A 44-year daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Sola 2009, 5, 137–140. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Palazzi, E.; Von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu–Kush Karakoram Himalaya: Observations and future scenarios. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Berkeley Earth Surface Temperature. Available online: http://www.berkeleyearth.org (accessed on 1 June 2018).
- Climate Prediction Centre. Available online: http://www.cpc.ncep.noaa.gov/ (accessed on 1 June 2018).
- Asian Precipitation—Highly Resolved Observational Data Integration toward Evaluation, (Monsoon Asia). Available online: http://www.chikyu.ac.jp/precip/english/products.html (accessed on 1 June 2018).
- Princeton Global Meteorological Forcing Dataset. Available online: http://www.hydrology.princeton.edu (accessed on 1 June 2018).
- Intergovernmental Panel on Climate Change. Available online: http://www.ipcc-data.org/sim/gcm_monthly/AR5/Reference-Archive.html (accessed on 1 June 2018).
- Wang, L.; Ranasinghe, R.; Maskey, S.; van Gelder, P.M.; Vrijling, J. Comparison of empirical statistical methods for downscaling daily climate projections from CMIP5 GCMs: A case study of the Huai River Basin, China. Int. J. Climatol. 2016, 36, 145–164. [Google Scholar] [CrossRef]
- Novaković, J. Toward optimal feature selection using ranking methods and classification algorithms. Yugosl. J. Oper. Res. 2016, 21, 119–135. [Google Scholar] [CrossRef]
- Singh, B.; Kushwaha, N.; Vyas, O.P. A feature subset selection technique for high dimensional data using symmetric uncertainty. J. Data Anal. Inf. Process. 2014, 2, 95–105. [Google Scholar] [CrossRef]
- Kannan, S.S.; Ramaraj, N. A novel hybrid feature selection via Symmetrical Uncertainty ranking based local memetic search algorithm. Knowl.-Based Syst. 2010, 23, 580–585. [Google Scholar] [CrossRef]
- Shreem, S.S.; Abdullah, S.; Nazri, M.Z.A. Hybrid feature selection algorithm using symmetrical uncertainty and a harmony search algorithm. Int. J. Syst. Sci. 2016, 47, 1312–1329. [Google Scholar] [CrossRef]

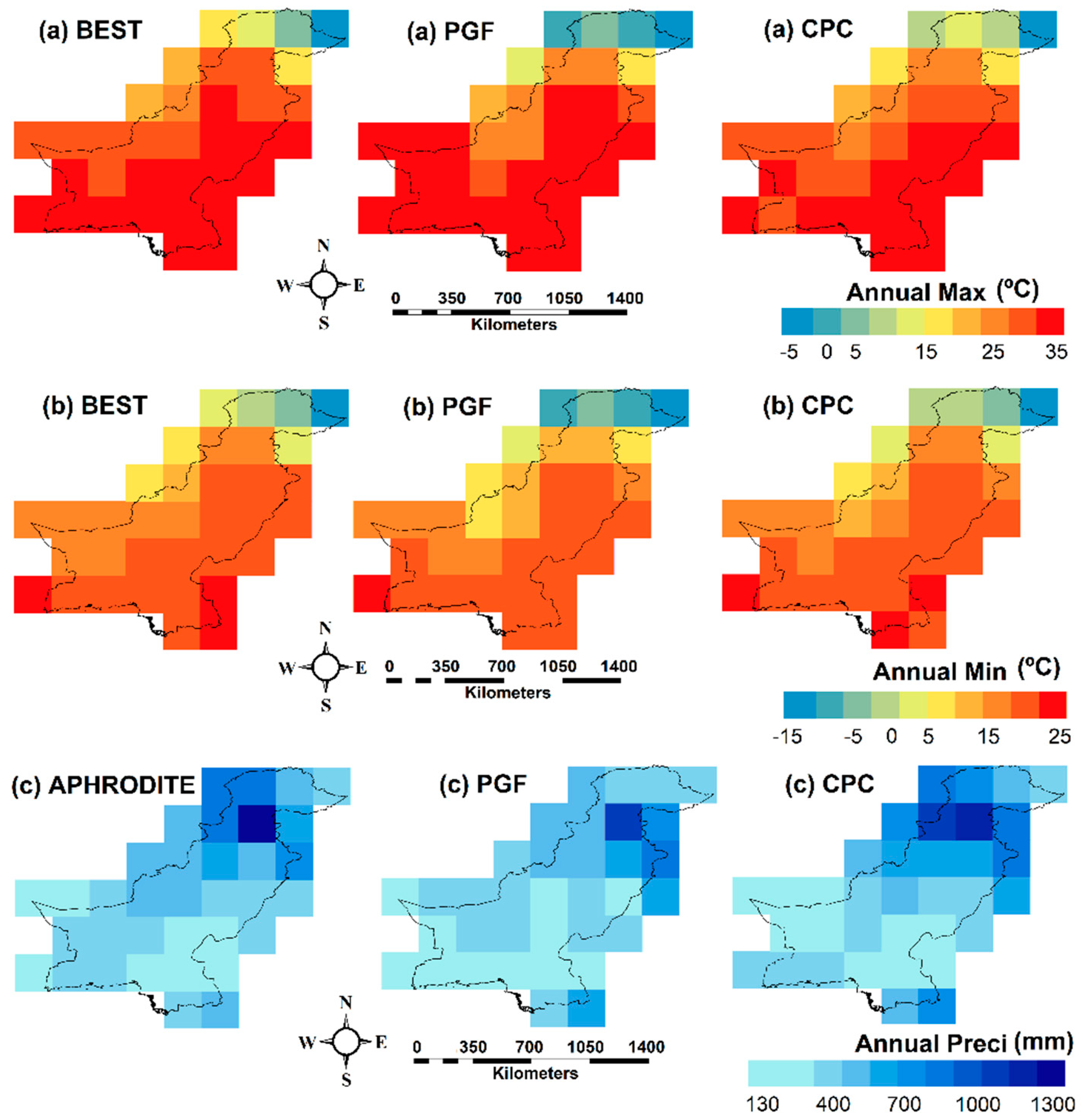
| Products | Source | Period | Spatial Resolution | Climate Variable |
|---|---|---|---|---|
| BEST [33] | Berkley Earth Surface Temperature [40] | (1960–2013) | 1° × 1° | Daily Temp. |
| CPC [34] | Climate Prediction Centre [41] | (1979–present) | 0.5° × 0.5° | Daily Temp. and Precipitation |
| APHRODITE [37] | Asian Precipitation—Highly Resolved Observational Data Integration Toward Evaluation, (Monsoon Asia) [42] | (1951–2007) | 0.5° × 0.5° | Daily Precipitation |
| PGF [35] | Princeton Global Meteorological Forcing [43] | (1948–2010) | 0.25° × 0.25° | Daily Temp. and Precipitation |
| GCM No. | GCM Name | Developer | Resolution |
|---|---|---|---|
| 1 | ACCESS1-0 | Commonwealth Scientific and Industrial Research Organisation–Bureau of Meteorology, Australia | 1.9 × 1.2 |
| 2 | ACCESS1-3 | ||
| 3 | bcc-csm1-1-m | Beijing Climate Centre, China | 2.8 × 2.8 |
| 4 | bcc-csm1-1 | 1.1 × 1.1 | |
| 5 | BNU-ESM | Beijing Normal University, China | 2.8 × 2.8 |
| 6 | CanESM2 | Canadian Centre for Climate Modelling and Analysis, Canada | 2.8 × 2.8 |
| 7 | CCSM4 | National Centre for Atmospheric Research USA | 0.94 × 1.25 |
| 8 | CESM1(BGC) | 0.94 × 1.25 | |
| 9 | CMCC-CM | Centro Euro-Mediterraneo sui Cambiamenti Climatici, Italy | 0.7 × 0.7 |
| 10 | CMCC-CMS | 1.9 × 1.9 | |
| 11 | CNRM-CM5 | Centre National de Recherches Météorologiques, Centre, France | 1.4 × 1.4 |
| 12 | CSIRO-Mk3-6-0 | Commonwealth Scientific and Industrial Research Organization, Australia | 1.9 × 1.9 |
| 13 | EC-EARTH | EC-EARTH consortium published at the Irish Centre for High-End Computing, Netherlands/Ireland | 1.1 × 1.1 |
| 14 | FGOALS-g2 | Institute of Atmospheric Physics, Chinese Academy of Sciences, China | 2.8 × 2.8 |
| 15 | GFDL-CM3 | Geophysical Fluid Dynamics Laboratory, USA | 2.5 × 2.0 |
| 16 | GFDL-ESM2G | 2.5 × 2.0 | |
| 17 | GFDL-ESM2M | 2.5 × 2.0 | |
| 18 | GISS-E2-R | NASA/GISS (Goddard Institute for Space Studies), USA | 2.5 × 2.0 |
| 19 | HadGEM2-CC | Met Office Hadley Centre, UK | 1.9 × 1.2 |
| 20 | HadGEM2-ES | 1.9 × 1.2 | |
| 21 | INMCM4.0 | Institute of Numerical Mathematics, Russia | 2.0 × 1.5 |
| 22 | IPSL-CM5A-LR | Institut Pierre Simon Laplace, France | 3.7 × 1.9 |
| 23 | IPSL-CM5A-MR | 2.5 × 1.3 | |
| 24 | IPSL-CM5B-LR | 3.7 × 1.9 | |
| 25 | MIROC-ESM-CHEM | The University of Tokyo, National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | 2.8 × 2.8 |
| 26 | MIROC-ESM | 2.8 × 2.8 | |
| 27 | MIROC5 | 1.4 × 1.4 | |
| 28 | MPI-ESM-LR | Max Planck Institute for Meteorology, Germany | 1.9 × 1.9 |
| 29 | MPI-ESM-MR | 1.9 × 1.9 | |
| 30 | MRI-CGCM3 | Meteorological Research Institute, Japan | 1.1 × 1.1 |
| 31 | NorESM1-M | Meteorological Institute, Norway | 2.5 × 1.9 |
| GCM No. | Model Name | Score (SU) | Rank (SU) | Score (R2) | Score (NRMSE) | Average (R2 + NRMSE) | Rank (R2 + NRMSE) |
|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | 1.66 | 15 | 3.01 | 3.77 | 3.39 | 15 |
| 2 | ACCESS1-3 | 6.77 | 3 | 3.07 | 5.98 | 4.02 | 6 |
| 3 | bcc-csm1-1 | 0.00 | 18 | 3.30 | 1.90 | 2.60 | 21 |
| 4 | bcc-csm1-1-m | 0.00 | 18 | 2.84 | 3.53 | 3.19 | 18 |
| 5 | BNU-ESM | 2.69 | 10 | 3.06 | 3.53 | 3.29 | 16 |
| 6 | CanESM2 | 2.21 | 12 | 3.98 | 3.04 | 3.51 | 12 |
| 7 | CCSM4 | 1.70 | 14 | 4.50 | 2.49 | 3.49 | 13 |
| 8 | CESM1-BGC | 3.48 | 7 | 5.48 | 1.58 | 3.53 | 11 |
| 9 | CMCC-CM | 5.64 | 5 | 2.84 | 4.92 | 3.88 | 8 |
| 10 | CMCC-CMS | 0.00 | 18 | 5.07 | 2.40 | 3.73 | 9 |
| 11 | CNRM-CM5 | 0.00 | 18 | 3.16 | 1.51 | 2.33 | 24 |
| 12 | CSIRO-Mk3-6-0 | 14.25 | 1 | 3.88 | 5.69 | 4.79 | 3 |
| 13 | EC-EARTH | 0.00 | 18 | 1.94 | 2.22 | 2.08 | 28 |
| 14 | FGOALS-g2 | 0.00 | 18 | 3.29 | 3.10 | 3.20 | 17 |
| 15 | GFDL-CM3 | 3.43 | 8 | 4.01 | 2.77 | 3.39 | 14 |
| 16 | GFDL-ESM2G | 0.00 | 18 | 1.49 | 1.06 | 1.28 | 30 |
| 17 | GFDL-ESM2M | 0.00 | 18 | 1.83 | 2.99 | 2.41 | 23 |
| 18 | GISS-E2-R | 0.00 | 18 | 4.93 | 3.47 | 4.20 | 4 |
| 19 | HadGEM2-CC | 1.83 | 13 | 4.24 | 2.87 | 3.56 | 10 |
| 20 | HadGEM2-ES | 2.99 | 9 | 2.52 | 3.38 | 2.95 | 20 |
| 21 | INMCM4 | 0.00 | 18 | 1.76 | 3.26 | 2.51 | 22 |
| 22 | IPSL-CM5A-LR | 0.00 | 18 | 1.92 | 2.59 | 2.26 | 25 |
| 23 | IPSL-CM5A-MR | 3.93 | 6 | 2.98 | 5.13 | 4.05 | 5 |
| 24 | IPSL-CM5B-LR | 0.00 | 18 | 1.08 | 3.38 | 2.23 | 26 |
| 25 | MIROC5 | 1.41 | 17 | 3.50 | 2.42 | 2.96 | 19 |
| 26 | MIROC-ESM | 0.00 | 18 | 0.76 | 2.11 | 1.44 | 29 |
| 27 | MIROC-ESM-CHEM | 1.41 | 16 | 0.92 | 3.47 | 2.19 | 27 |
| 28 | MPI-ESM-LR | 11.37 | 2 | 4.69 | 5.33 | 5.01 | 1 |
| 29 | MPI-ESM-MR | 0.00 | 18 | 0.00 | 1.68 | 0.84 | 31 |
| 30 | MRI-CGCM3 | 2.66 | 11 | 3.17 | 4.75 | 3.96 | 7 |
| 31 | NorESM1-M | 6.30 | 4 | 5.10 | 4.50 | 4.80 | 2 |
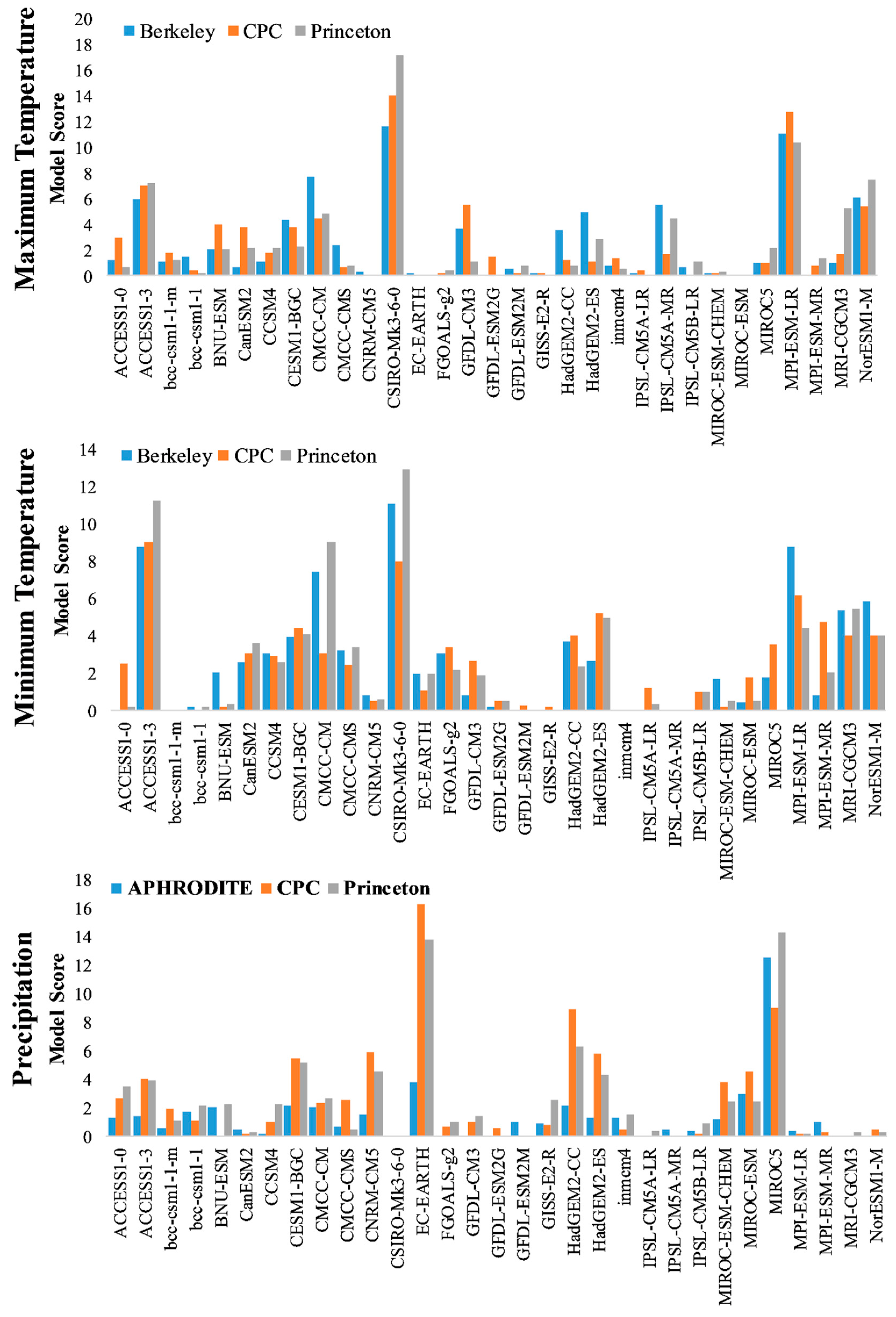
| Model | Max Temperature | Min Temperature | Precipitation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BEST | CPC | PGF | Score | BEST | CPC | PGF | Score | APH | CPC | PGF | Score | |
| ACCESS1-0 | 1.3 | 3.0 | 0.7 | 1.7 | 0.0 | 2.5 | 0.2 | 0.9 | 1.3 | 2.7 | 3.5 | 2.5 |
| ACCESS1-3 | 6.0 | 7.0 | 7.3 | 6.8 | 8.7 | 9.0 | 11.2 | 9.7 | 1.5 | 4.0 | 3.9 | 3.1 |
| bcc-csm1-1-m | 1.2 | 1.8 | 1.2 | 1.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5 | 1.9 | 1.1 | 1.2 |
| bcc-csm1-1 | 1.5 | 0.5 | 0.3 | 0.7 | 0.2 | 0.0 | 0.2 | 0.1 | 1.7 | 1.1 | 2.2 | 1.6 |
| BNU-ESM | 2.1 | 4.0 | 2.0 | 2.7 | 2.0 | 0.2 | 0.3 | 0.9 | 2.0 | 0.0 | 2.2 | 1.4 |
| CanESM2 | 0.7 | 3.8 | 2.2 | 2.2 | 2.5 | 3.1 | 3.6 | 3.1 | 0.5 | 0.2 | 0.3 | 0.3 |
| CCSM4 | 1.1 | 1.8 | 2.2 | 1.7 | 3.0 | 2.9 | 2.6 | 2.8 | 0.2 | 1.0 | 2.3 | 1.2 |
| CESM1-BGC | 4.3 | 3.8 | 2.3 | 3.5 | 3.9 | 4.4 | 4.1 | 4.1 | 2.2 | 5.4 | 5.1 | 4.2 |
| CMCC-CM | 7.7 | 4.5 | 4.8 | 5.6 | 7.4 | 3.1 | 9.0 | 6.5 | 2.0 | 2.3 | 2.7 | 2.3 |
| CMCC-CMS | 2.4 | 0.7 | 0.7 | 1.3 | 3.2 | 2.4 | 3.4 | 3.0 | 0.7 | 2.6 | 0.5 | 1.2 |
| CNRM-CM5 | 0.3 | 0.0 | 0.0 | 0.1 | 0.9 | 0.5 | 0.6 | 0.7 | 1.5 | 5.9 | 4.5 | 4.0 |
| CSIRO-Mk3-6-0 | 11.6 | 14.0 | 17.2 | 14.3 | 11.1 | 8.0 | 12.9 | 10.7 | 0.0 | 0.0 | 0.0 | 0.0 |
| EC-EARTH | 0.2 | 0.0 | 0.0 | 0.1 | 2.0 | 1.0 | 1.9 | 1.6 | 3.8 | 16.3 | 13.8 | 11.3 |
| FGOALS-g2 | 0.0 | 0.2 | 0.5 | 0.2 | 3.0 | 3.4 | 2.2 | 2.9 | 0.0 | 0.7 | 1.0 | 0.6 |
| GFDL-CM3 | 3.7 | 5.5 | 1.1 | 3.4 | 0.8 | 2.7 | 1.9 | 1.8 | 0.0 | 1.0 | 1.4 | 0.8 |
| GFDL-ESM2G | 0.0 | 1.5 | 0.0 | 0.5 | 0.2 | 0.5 | 0.5 | 0.4 | 0.0 | 0.5 | 0.0 | 0.2 |
| GFDL-ESM2M | 0.5 | 0.2 | 0.8 | 0.5 | 0.0 | 0.3 | 0.0 | 0.1 | 1.0 | 0.0 | 0.0 | 0.3 |
| GISS-E2-R | 0.3 | 0.2 | 0.0 | 0.2 | 0.0 | 0.2 | 0.0 | 0.1 | 0.9 | 0.8 | 2.5 | 1.4 |
| HadGEM2-CC | 3.5 | 1.2 | 0.8 | 1.8 | 3.7 | 4.0 | 2.3 | 3.3 | 2.2 | 8.9 | 6.3 | 5.8 |
| HadGEM2-ES | 5.0 | 1.1 | 2.9 | 3.0 | 2.6 | 5.2 | 4.9 | 4.3 | 1.3 | 5.8 | 4.4 | 3.8 |
| INMCM4 | 0.8 | 1.3 | 0.5 | 0.9 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.5 | 1.5 | 1.1 |
| IPSL-CM5A-LR | 0.3 | 0.4 | 0.0 | 0.2 | 0.0 | 1.3 | 0.3 | 0.5 | 0.0 | 0.0 | 0.3 | 0.1 |
| IPSL-CM5A-MR | 5.5 | 1.7 | 4.5 | 3.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.2 |
| IPSL-CM5B-LR | 0.7 | 0.0 | 1.2 | 0.6 | 0.0 | 1.0 | 1.0 | 0.7 | 0.3 | 0.2 | 0.9 | 0.5 |
| MIROC-ESM-CHEM | 0.2 | 0.2 | 0.3 | 0.2 | 1.7 | 0.2 | 0.5 | 0.8 | 1.2 | 3.8 | 2.4 | 2.4 |
| MIROC-ESM | 0.0 | 0.0 | 0.0 | 0.0 | 0.5 | 1.8 | 0.5 | 0.9 | 3.0 | 4.5 | 2.5 | 3.3 |
| MIROC5 | 1.1 | 1.0 | 2.1 | 1.4 | 1.8 | 3.5 | 0.0 | 1.8 | 12.5 | 9.0 | 14.2 | 11.9 |
| MPI-ESM-LR | 11.0 | 12.7 | 10.4 | 11.4 | 8.7 | 6.2 | 4.4 | 6.4 | 0.3 | 0.2 | 0.2 | 0.2 |
| MPI-ESM-MR | 0.0 | 0.8 | 1.4 | 0.7 | 0.8 | 4.7 | 2.0 | 2.5 | 1.0 | 0.3 | 0.0 | 0.4 |
| MRI-CGCM3 | 1.0 | 1.7 | 5.2 | 2.7 | 5.4 | 4.0 | 5.4 | 4.9 | 0.0 | 0.0 | 0.3 | 0.1 |
| NorESM1-M | 6.1 | 5.4 | 7.5 | 6.3 | 5.8 | 4.0 | 4.0 | 4.6 | 0.0 | 0.5 | 0.3 | 0.3 |
| GCM | Max Temperature | Min Temperature | Precipitation |
|---|---|---|---|
| ACCESS1-0 | 1.7 | 0.0 | 2.5 |
| ACCESS1-3 | 6.8 | 9.7 | 3.1 |
| bcc-csm1-1 | 0.0 | 0.0 | 1.6 |
| bcc-csm1-1-m | 0.0 | 0.0 | 1.2 |
| BNU-ESM | 2.7 | 0.0 | 1.4 |
| CanESM2 | 2.2 | 3.1 | 0.0 |
| CCSM4 | 1.7 | 2.8 | 0.0 |
| CESM1-BGC | 3.5 | 4.1 | 4.2 |
| CMCC-CM | 5.6 | 6.5 | 2.3 |
| CMCC-CMS | 0.0 | 3.0 | 1.2 |
| CNRM-CM5 | 0.0 | 0.0 | 4.0 |
| CSIRO-Mk3-6-0 | 14.3 | 10.7 | 0.0 |
| EC-EARTH | 0.0 | 0.0 | 11.3 |
| FGOALS-g2 | 0.0 | 2.9 | 0.0 |
| GFDL-CM3 | 3.4 | 1.8 | 0.0 |
| GFDL-ESM2G | 0.0 | 0.0 | 0.0 |
| GFDL-ESM2M | 0.0 | 0.0 | 0.0 |
| GISS-E2-R | 0.0 | 0.0 | 1.4 |
| HadGEM2-CC | 1.8 | 3.3 | 5.8 |
| HadGEM2-ES | 3.0 | 4.3 | 3.8 |
| INMCM4 | 0.0 | 0.0 | 0.0 |
| IPSL-CM5A-LR | 0.0 | 0.0 | 0.0 |
| IPSL-CM5A-MR | 3.9 | 0.0 | 0.0 |
| IPSL-CM5B-LR | 0.0 | 0.0 | 0.0 |
| MIROC5 | 1.4 | 1.8 | 11.9 |
| MIROC-ESM | 0.0 | 0.0 | 3.3 |
| MIROC-ESM-CHEM | 0.0 | 0.0 | 2.4 |
| MPI-ESM-LR | 11.4 | 6.4 | 0.0 |
| MPI-ESM-MR | 0.0 | 2.5 | 0.0 |
| MRI-CGCM3 | 2.7 | 4.9 | 0.0 |
| NorESM1-M | 6.3 | 4.6 | 0.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, N.; Shahid, S.; Ahmed, K.; Ismail, T.; Nawaz, N.; Son, M. Performance Assessment of General Circulation Model in Simulating Daily Precipitation and Temperature Using Multiple Gridded Datasets. Water 2018, 10, 1793. https://doi.org/10.3390/w10121793
Khan N, Shahid S, Ahmed K, Ismail T, Nawaz N, Son M. Performance Assessment of General Circulation Model in Simulating Daily Precipitation and Temperature Using Multiple Gridded Datasets. Water. 2018; 10(12):1793. https://doi.org/10.3390/w10121793
Chicago/Turabian StyleKhan, Najeebullah, Shamsuddin Shahid, Kamal Ahmed, Tarmizi Ismail, Nadeem Nawaz, and Minwoo Son. 2018. "Performance Assessment of General Circulation Model in Simulating Daily Precipitation and Temperature Using Multiple Gridded Datasets" Water 10, no. 12: 1793. https://doi.org/10.3390/w10121793
APA StyleKhan, N., Shahid, S., Ahmed, K., Ismail, T., Nawaz, N., & Son, M. (2018). Performance Assessment of General Circulation Model in Simulating Daily Precipitation and Temperature Using Multiple Gridded Datasets. Water, 10(12), 1793. https://doi.org/10.3390/w10121793








