1. Introduction
Approximately 20–25% of the global population depends largely or entirely on groundwater obtained from karst aquifers [
1]. For proper water management and protection, it is important to understand and be able to predict groundwater flow in karst. Numerical modeling is an efficient method for describing many physical phenomena and is frequently used in traditional hydrogeology. However, the existence of a highly permeable conduit network embedded in a less permeable rock matrix results in a highly heterogeneous permeability distribution and makes karst different from other aquifers [
2]. Moreover, this duality in the permeability results in different flow conditions and makes karst particularly difficult to model. The conduit system occupies only a small portion of the total aquifer but has a major impact on the hydraulic behavior of the karst system [
3]. Normally, most of the recharge water is collected and transmitted toward the spring by the conduit network [
1]. The karst conduits are characterized by fast, mostly turbulent flow, which can be free surface (partially saturated conduit) or pressurized (fully saturated conduit). The remaining part of the aquifer is characterized by a system of small fissures and pores and is herein referred to as the karst matrix (generally, one can speak about a triple-porosity system: conduits, fractures, and a porous matrix; however, for flow modeling purposes, the latter two are usually combined and referred to as the matrix). The matrix is important for water storage and attenuation of contaminants. In contrast with conduits, the flow in the matrix is generally laminar (seepage) but can be both saturated and unsaturated. The complexity of the karst aquifers is further increased by the existence of many special karst forms (such as caves, sinkholes, and epikarst) and the fact that there is interaction between conduit and matrix systems. During drought season, the pressure in conduits is generally lower than the pressure in the matrix, and conduits are recharged by groundwater stored in the matrix. In contrast, during storm flow intervals, the pressure in the conduits increases faster than in the surrounding matrix, and a substantial pressure difference between the matrix and conduit occurs. The flow in conduits normally becomes pressurized, and hydraulic head inversion occurs; i.e., the conduit network starts to recharge the matrix storage.
In recent years, many approaches for modeling groundwater flow in karst have been suggested (e.g., [
4,
5,
6]). Generally, they are divided into two main groups [
3]: spatially lumped (hydrological) and spatially distributed (hydraulic) models. In the following, only a short overview of the mentioned approaches is given; for more detailed descriptions, we refer to [
7,
8]. Spatially lumped models transform recharge events (input) into spring hydrographs (output). They are often called global models since they consider the system as a single unit and simulate the global hydraulic behavior of the entire system. These models are relatively simple to use and do not require detailed knowledge about the system; however, they do not simulate actual physical processes and cannot account for spatial variability within an aquifer. To account for spatial variations in the involved parameters (e.g., permeability or recharge distribution) and flow variables (e.g., pressure or velocity), spatially distributed (physical-based) models are needed. The physical processes of flow are described via partial differential equations (PDEs), and numerical (discretization) techniques are used to solve initial-boundary value problems (IBVPs). The solution of a particular IBVP is given by the flow variables, which have both spatial and temporal variability.
Among the different approaches suggested within the spatially distributed models (e.g., Kovács and Sauter [
7], Hartmann et al. [
8]), the focus of this work is the so-called (coupled) discrete-continuum (DC) or hybrid approach. In this approach, karst conduits are discretized as one-dimensional elements, and governing equations similar to the one for hydraulic networks are used to describe the (usually pressurized) flow in the conduit network. The low-permeability matrix is discretized in three dimensions, and the Darcy flow is generally assumed to be valid. The coupling between two domains is established via a first-order exchange term governed by the conduit-matrix head difference [
9] or by assuming continuous heads [
10]. The first DC model was presented by Király [
11], and example applications of DC models include [
9,
10,
12,
13,
14,
15,
16,
17,
18,
19,
20], among others. The most popular and widely used DC model is the conduit flow process (CFP) model [
21] integrated into MODFLOW-2005 [
22]. CFP is an open-source finite difference solver that has been documented for wider use and developed to account for dual-porosity nature, such as that observed in karst aquifers. The flow in the karst matrix is based on the classical MODFLOW approach, whereas the turbulent conduit flow is based on the Darcy–Weisbach equation. Partially filled conduits are simulated as fully saturated pipes by using a corrected diameter. However, most of the MODFLOW-CFP applications were performed under fully saturated conditions. The main reason for considering only fully saturated conditions is the robustness of the numerical simulations. It is well known that a high nonlinearity of soil properties in the unsaturated zone can produce severe convergence problems [
23]. Similarly, the transition between a free surface and pressurized flow can affect the numerical behavior in terms of robustness and correctness [
17]. Thus, it can be stated that MODFLOW-CFP has been designed and used as a compromise between practical applicability and numerical stability. Further, the two advanced karst flow models were presented by de Rooij [
24] and de Rooij et al. [
25]. First, in his thesis [
24], the turbulent conduit flow was coupled with a laminar matrix flow via a finite element model that accounted for variable saturation in both flow domains. The coupling was imposed by head continuity on the matrix–conduit interface. Later, a novel model in which surface flow was added to the previously mentioned subsurface system was developed [
25]. The subsurface equations remained the same, but the conduit-matrix coupling was based on Peaceman’s well index. Finite-difference discretization was used, and certain numerical problems mentioned in [
24] were avoided. Both models were applied to hypothetical karst systems.
The DC approach can be generally considered as the most advanced among practically used models. While still being computationally acceptable, it accounts for a heterogeneity and duality of karst and can be used to better understand complicated hydrodynamic processes as well as for testing different conceptual models. However, in addition to the complexity of developing reliable numerical models, this approach requires large input data, which usually limits its practical application [
7]. The shape and position of the conduit network and a reasonable distribution of hydraulic parameters and recharge are necessary to obtain realistic results. Moreover, the verification of such complex numerical models is quite difficult, but it is still important before their practical usage. Since analytical solutions are not available (except for some trivial cases) and collected field data are generally insufficient for true verification, laboratory experiments are one possible logical choice. Based on the literature, there seems to have been only a few attempts to construct laboratory analogues of karst. Models such as those presented by Öllős and Németh [
26] and Wu and Hunkeler [
27] were constructed to analyze flows dominated by a conduit network. In Faulkner et al. [
28], the authors demonstrated a laboratory model that is capable of simulating coupled conduit-matrix conditions. It was used to analyze both groundwater flow and solute transport, and their numerical model has been verified with measured results. However, the overall dimensions (0.6 × 0.26 × 0.02 m) of their model make it essentially two-dimensional and applicable only for laminar flow in conduits. Recently, the authors in Castro [
29] presented a 3D sandbox with overall dimensions 1.044 × 0.419 × 0.434 m. The sandbox was filled with homogeneous porous material, and a perforated steel pipe with an external diameter of 0.019 m was used to simulate karst conduit. Steady-state experiments under saturated flow conditions were performed, and collected data were used for the validation of MODFLOW-CFP.
Thus, the purpose of this work is twofold. First, our aim is to develop a novel computational model based on a nonconventional numerical method. The model is of the discrete-continuum type and accounts for variably saturated conditions in both flow domains. Since groundwater flow modeling in karst is quite complex, we believe that advancement in a pure mathematical and numerical sense is important for future improvement in modeling capabilities in karst hydrogeology. Moreover, in such a complex area, critical consideration of the used methods and obtained results is necessary. Furthermore, as a second objective, a three-dimensional physical model was constructed. Although it is not an exact representation of a realistic karst system, the presented unique and quite complex physical karst flow model can be used for verification and validation of different mathematical and numerical models. The most important features of karst systems, such as laminar porous medium flow (through both unsaturated and saturated zones), turbulent conduit flow (both free surface and pressurized conditions), as well as groundwater exchange between two systems, can be captured. Different boundary conditions and recharge characteristics, in addition to many other possibilities, enable the testing of different flow conditions. The pressure distribution in a karst matrix and discharge from both systems were continuously measured during experiments.
The paper is organized as follows:
Section 2 describes the mathematical background of the governing equations used in numerical models. In
Section 3, a novel numerical approach is presented, and discretization of the governing equations is demonstrated in detail. In
Section 4, examples from the literature are used to verify the matrix and conduit solvers without their interaction. In
Section 5, experimental results from the physical model are compared with results obtained via a numerical model. Finally,
Section 6 discusses the obtained results and some future perspectives, while
Section 7 concludes the work. In addition, a detailed description of the novel physical model and presented experimental results are available online via
supplementary materials.
2. Mathematical Models
Generally, the same physical laws (i.e., conservation of mass and momentum) govern both matrix and conduit flows. However, for practical purposes, they often have to be simplified.
Thus, the matrix system is modeled as a continuum using the Darcy law and the representative elementary volume (REV) concept [
30]. Additionally, in many practical applications, the variably saturated flow equation [
31,
32] (often referred to as Richards’ equation) is capable of accurately simulating flow through both saturated and unsaturated zone.
Flow in the conduits is generally described with a system of 3D Navier–Stokes equations. However, the solution of the full 3D equations is very demanding, and the possible free surface flow condition necessitates special approaches. Additionally, the flow in conduits is usually turbulent, and the scale of interest is large [
33,
34]. All these reasons, together with the fact that the geometry of the karst conduits is very complex and, in most cases, unknown, lead to simplified mathematical models. Thus, as in usual approaches for a hydraulic network and open-channel flow modeling [
35,
36], the flow in karst conduits is treated as one-dimensional.
Since flow equations of the two systems (i.e., matrix and conduit) are governed by different partial differential equations (PDEs) and dimensionality, mathematical models have to be coupled. This section describes mathematical models for matrix flow, conduit flow, and the conduit–matrix interface.
In the following, uppercase () and lowercase () will be used to distinguish between matrix and conduit hydraulic and pressure heads, respectively.
2.1. Variably Saturated Flow in a Karst Matrix
The mathematical model for flow in the karst matrix is based on the governing equation for variably saturated subsurface flow in a porous medium [
21,
31,
37]:
where
is the specific storage coefficient (L
),
is the volumetric water content (-),
is the porosity (-),
H is the hydraulic (piezometric) head (L),
is the relative permeability (-),
is the saturated hydraulic conductivity tensor (L T
), and
is the volumetric flux per unit volume representing sources and (or) sinks (T
). Let [
] be the time interval of interest,
be a bounded domain, and
and
be domain boundaries with Dirichlet and Neumann boundary conditions, respectively. The appropriate initial and boundary conditions are given by
where
(-) is the outward normal vector and
,
, and
are prescribed initial and boundary condition functions. To solve Equations (
1)–(4), constitutive relationships for describing the unsaturated flow and storage properties must be defined. In this work, we use the bimodal constrained form of the van Genuchten–Mualem model [
38,
39].
The water content is expressed through the effective saturation
(-):
where
is the pressure head (
) (L),
z is the elevation head (L),
is the residual volumetric water content, and
is the saturated volumetric water content (often assumed to be equal to the porosity). Generally, the saturation and volumetric water content are related by the porosity, i.e.,
.
The relationship between the water content and pressure head (retention function) is given by
where each mode of the curve is given by [
40]
The specific moisture capacity is given as a function of the effective saturation:
The relative permeability is given as a function of the effective saturation:
where
is the inverse of the air entry pressure head (L
),
is the pore size distribution index (
) (-),
is the parameter defined as
(-), and
is an additional fitting parameter (-), called the tortuosity parameter, which is often set to
. This model is a weighted superposition of two van Genuchten functions, where the weighting factors
are subject to
and
. This function is much more suitable to fit data that do not perfectly follow the van Genuchten unimodal shape and will be used in this work to describe soil properties of our physical model. Note that the bimodal model also covers the commonly used unimodal van Genuchten model by simply setting
and
.
2.2. Variably Saturated Flow in Karst Conduits
The one-dimensional flow in karst conduits in the
l-direction is given by
where
C is the capacity term (L),
h is the hydraulic (piezometric) head (L),
l is the spatial longitudinal coordinate (L),
is the conveyance factor (L
T
), and
is a sink/source term (L
T
). Appropriate initial and boundary conditions are given by
where
,
, and
are prescribed initial and boundary condition functions. The nonlinear diffusion Equation (
10) is usually called the noninertia wave equation and can be derived by neglecting inertia terms in the general momentum equation and combining with the mass conservation equation [
24]. The noninertia wave equation can be used to describe both free surface and pressurized flows by modifying the capacity term (de Rooij et al. [
25]):
where
W is the top width of the flow (L),
is the density of the water (M L
),
g is the acceleration of the gravity (L T
),
is the cross-section flow area (L
), and
is the compressibility of water (L T
M
). The conveyance factor
is given by the Manning equation [
41]:
where
is Manning’s roughness coefficient (L
T) and
R is the hydraulic radius (L), defined as
, where
is the wetted perimeter (L). The variables
W,
, and
in the general case depend on the geometry of the conduit cross-section and water depth
(L). For a circular conduit with radius
(L), they are given by
2.3. Exchange of Water Between the Matrix and Conduit Flow
The exchange of water is established by defining a linear flux relation on the interface between different flow systems (e.g., Liedl et al. [
9]):
where
H and
h are, as defined before, the hydraulic heads in the matrix and conduit, and
is the exchange coefficient (T
), which is usually determined via calibration. From a mathematical point of view,
is expressed as a scalar value while being aware that its direction coincides with the normal direction of the conduit–matrix interface. Expression (
19) will be used to couple the matrix and conduit flow systems. The incorporation of this term into both the matrix and conduit flow equations will be explained in more detail in the next section.
5. Verification of the CV-IGA Karst Flow Model With Experimental Data
In this section, the experimental setup is introduced, and the experimental results are compared with the numerical results. The details of the physical model and additional experimental results can be found in the
supplementary materials.
5.1. Experimental Setup
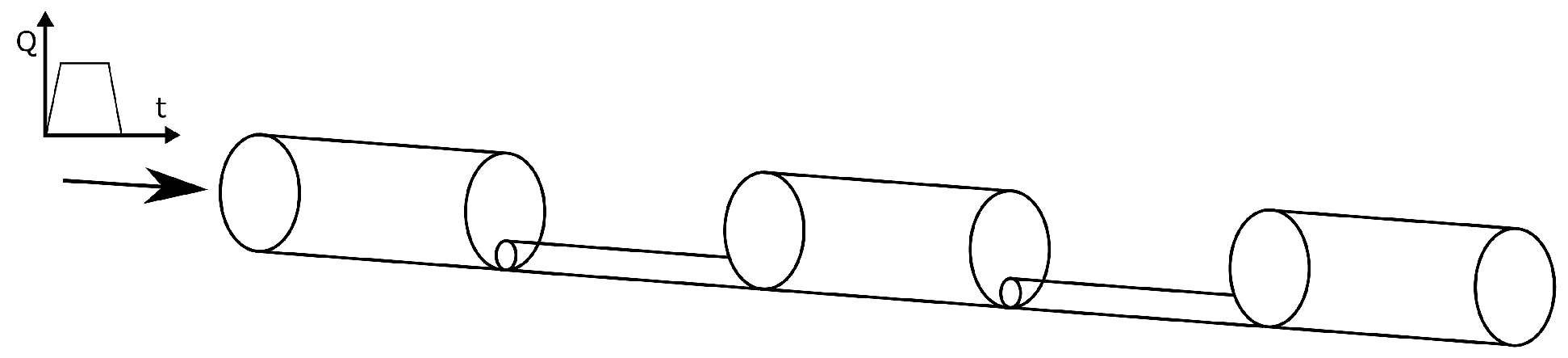
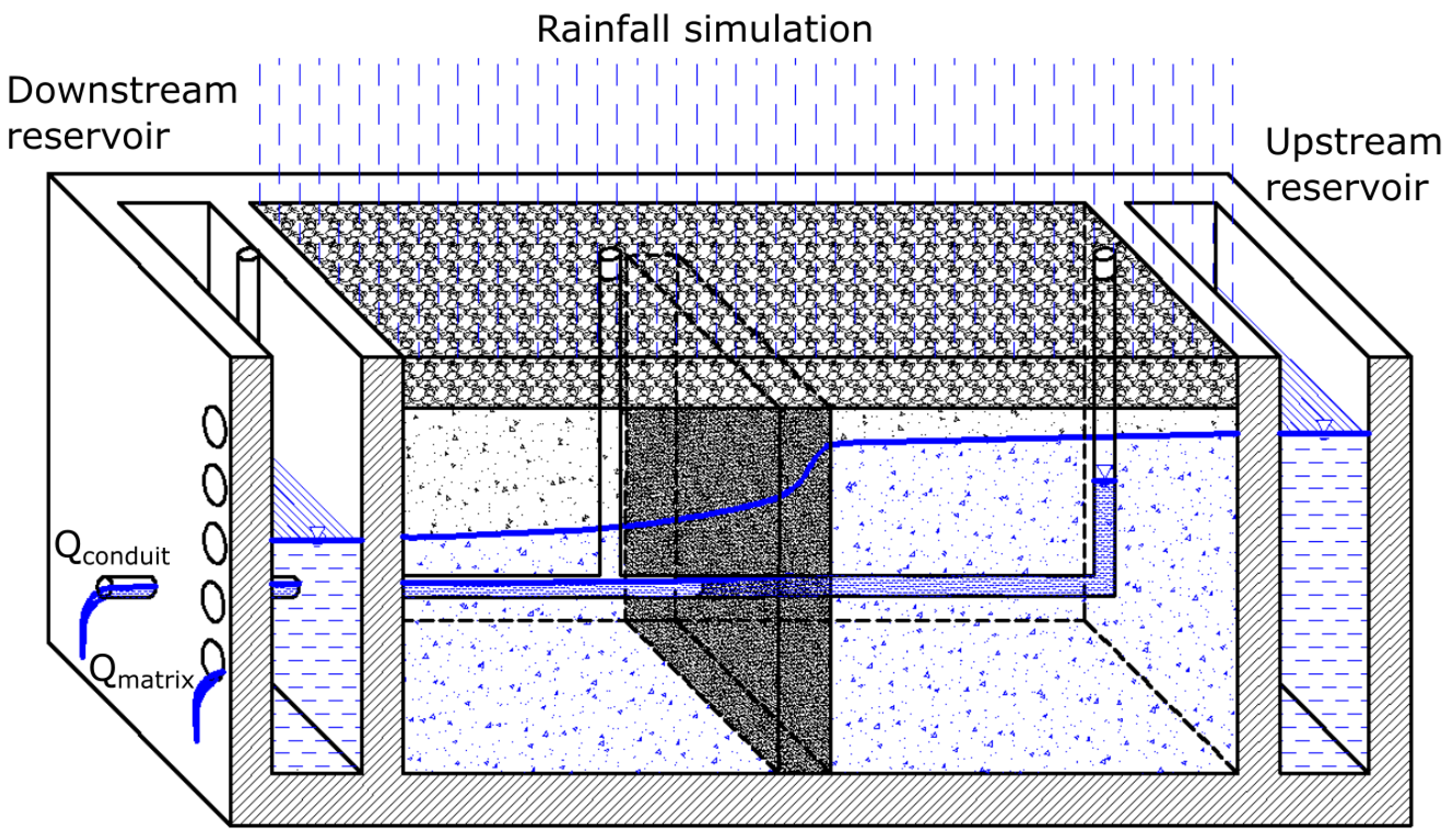
The physical model (
Figure 6) is made of a concrete construction with overall dimensions 5.66 × 2.95 × 2.00 m. Two water reservoirs, as shown in
Figure 7, are used to specify the water levels (boundary conditions) on the upstream and downstream ends of the model. Between reservoirs, the model is filled by heterogeneous porous material, which is used to simulate the karst matrix. Three types of materials are used: coarse quartz sand (CQS—67%), fine quartz sand (FQS—14%), and gravel (G—19%). The top 25 cm of the soil is filled by gravel to simulate epikarst effects. This layer prevents surface runoff and enables the investigation of additional effects, such as fast infiltration and ponding on the interface with lower-permeability materials. In the middle of the model, there is a zone of fine quartz sand, which is used to produce a pressure drop and to decrease the overall matrix velocities. The rest is mostly filled by coarse quartz sand, but there are also particular zones with two other materials to magnify heterogeneity effects (
Figure 8). Plastic perforated pipes are installed through the porous medium and are used to simulate karst conduits, whereas vertical branches are directly connected with conduits to simulate sinkholes. There are three independent conduit systems; however, during the experiment, only one conduit system is activated. The perforated parts of the pipes are surrounded by fine quartz sand and covered with geotextile to prevent perforations from clogging. On the top of the concrete construction, there are sprinklers and shower heads for rainfall simulation. The flow (computational) domain of the matrix excludes walls and reservoirs, and the dimensions are
,
, and
m.
During the experiment, there is continuous measurement of discharges and pressures. The discharge is measured on the downstream ends of the model for both the matrix and conduit systems. The matrix discharge is regarded as the overall discharge from the porous medium that overflows from the downstream reservoir. The conduit discharge is measured on the outlet as sketched in
Figure 7. In the comparison with realistic karst aquifers, the conduit outlet could be regarded as a main spring, whereas the matrix discharge can be considered as the total water that flows beside the main spring, regarding the porous matrix, fractures, and small conduits. Measurement of the matrix discharge enables information that is generally unknown in practice. In addition to discharge, the pressure distribution is measured at 44 fixed points by pipes that are installed through the foundation slab and rise vertically. These pipes are perforated only on their ends (inside the porous medium) and are denoted as piezometers. Additionally, 25 fully perforated vertical pipes are installed starting from the soil surface; they are denoted as boreholes. Since these pipes are fully perforated, borehole packers are used to isolate part of the pipe (approximately 10 cm) at a specific depth. A pressure sensor or water hose can be installed at any depth of borehole and used for pressure measurements or performing partially penetrating pumping tests, respectively.
The soil parameters for three different material types are presented in
Table 1. The soil samples were sent to a specialized laboratory for measurements of the saturated and unsaturated soil parameters. However, because of the extremely high conductivity, the results for gravel (G) were not obtained. Therefore, Darcy experiments were performed for all three materials and, in addition to obtained values in laboratory (for CQS and FQS), used to determine the range of hydraulic conductivities for each material. Then, additional steady-state experiments (included in the supplementary materials) were performed, and numerical calibration was used to define the final values of the saturated conductivities. The numerical calibration revealed moderate anisotropy of vertical conductivities, which is important to consider, especially because conduit-matrix interaction produces significant velocities in the vertical direction. All values adopted during the numerical calibration were inside the range of measured values. The laboratory measurements of unsaturated soil properties were available for CQS and FQS, and bimodal van Genuchten curves (presented in
Section 2.1) were used since classical (unimodal) van Genuchten curves were not able to fit the data accurately. For G, there were no measurements, and the parameters were determined by guidelines from the literature and numerical calibration. The specific storage coefficient (
) values were taken from the literature.
As mentioned above, there are three different conduit systems installed in the model, labeled C1, C2, and C3, that have differences in the shape, the pipe diameter, and the number and size of perforations. If any of these conduits is clogged at the outlet, its influence on the matrix flow is minor and therefore can be neglected; this was confirmed by the numerical model. Three types of PVC pipes were used, and the Manning coefficients are defined by the manufacturer for Conduit C1, Conduit C3, and the unperforated part of Conduit C2. For the perforated part of C2, which is corrugated, there was no specified value. Therefore, numerical calibration was needed; moreover, specific flow conditions (significant lateral inflow) inside the model prevented reliable empirical determination from being performed outside the model.
The physical karst flow model enables different experimental setups including different water levels in reservoirs, different rain distribution and intensity, and pumping/extracting water from any of boreholes. Additionally, many different flow conditions can be achieved to test numerical models; for example, there are both saturated and unsaturated flow conditions in the matrix, flow in the conduits can be free surface or pressurized, and interaction between the matrix and conduit can be tested for different conditions. In the following, we present two test cases with comparisons between experimental and numerical results.
5.2. Comparison between Numerical and Experimental Results
In this section, the CV-IGA karst flow model is used to simulate experimental data obtained with the novel 3D physical model. The water levels in both the upstream and downstream reservoirs are implemented as Dirichlet boundary conditions by specifying constant head values. Above the water levels in the reservoirs (up to the top of the soil), the no-flow (flux ) Neumann boundary condition is used since there is no development of the seepage face. The same no-flow condition is used on remaining boundaries except on the top soil layer, where rain is specified by a nonzero flux value. Evaporation is neglected due to the short duration of the experiment. The conduit upstream boundary is defined as a no-flow condition, whereas the downstream boundary depends on the flow conditions.
5.2.1. Test Case 1
In the first test case, we considered a straight circular pipe with perforations uniformly distributed along the pipe (Conduit C1). The position of the conduit was defined by the starting and ending coordinates of the pipe bottom,
and
. The conduit diameter was 0.0155 m, and the Manning roughness coefficient was
0.009 m
s. The water levels in two reservoirs were kept fixed at
m and
m. Since for this test case, the conduit flow was pressurized, the Dirichlet boundary condition at the outlet was defined by the hydraulic head value, which is equal to the conduit top elevation (the atmospheric pressure at the outlet). Numerical results were obtained using matrix spatial discretization
m and
m, whereas the conduit discretization was set as
m. The same time step
min was used for both matrix and conduit solvers, and the matrix–conduit exchange coefficient was set after calibration to
s
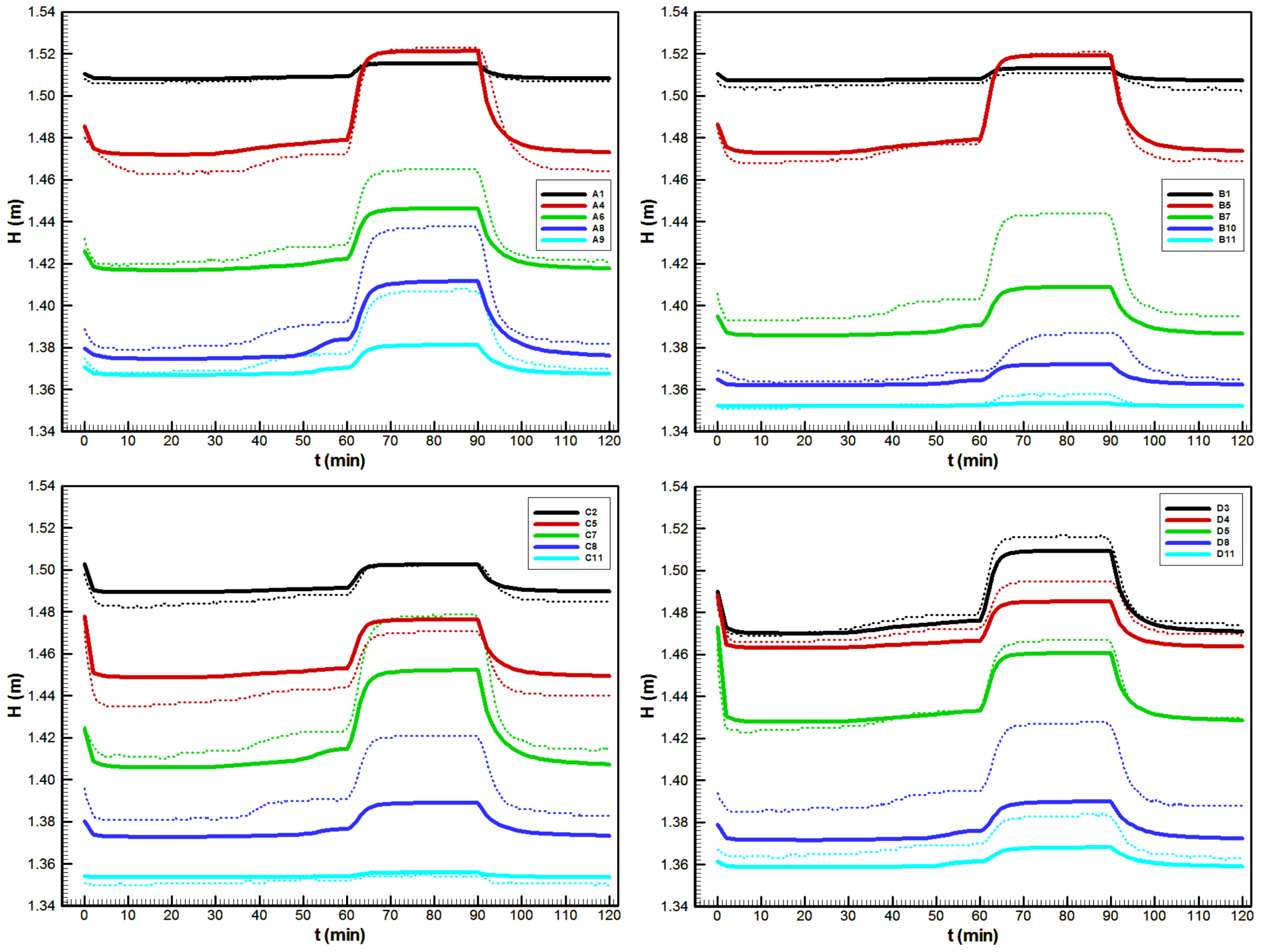
. Comparisons between the measured and calculated values for discharges and selected hydraulic heads are shown in
Figure 9 and
Figure 10, respectively. Detailed experimental results for all piezometers can be found in the
supplementary materials.
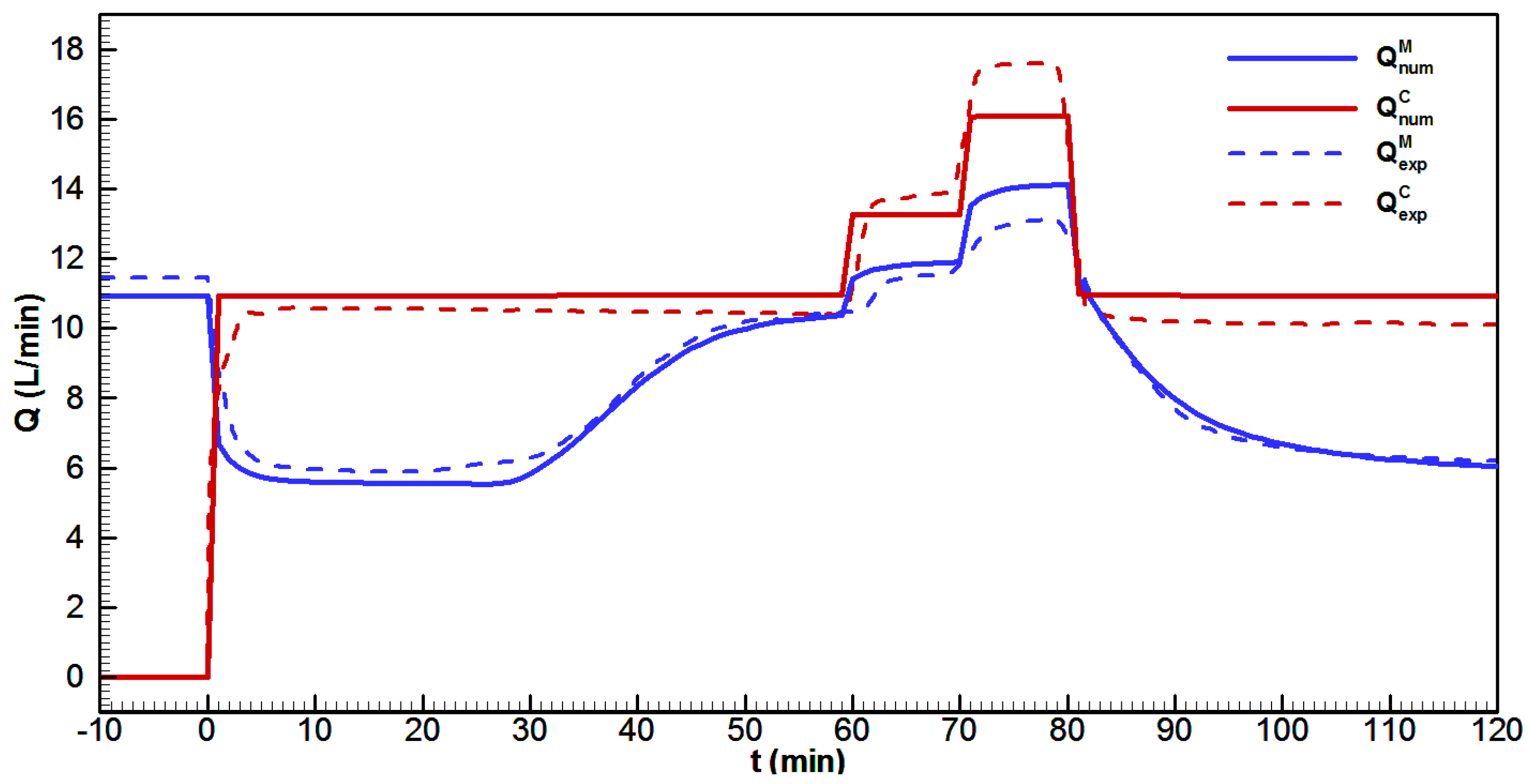
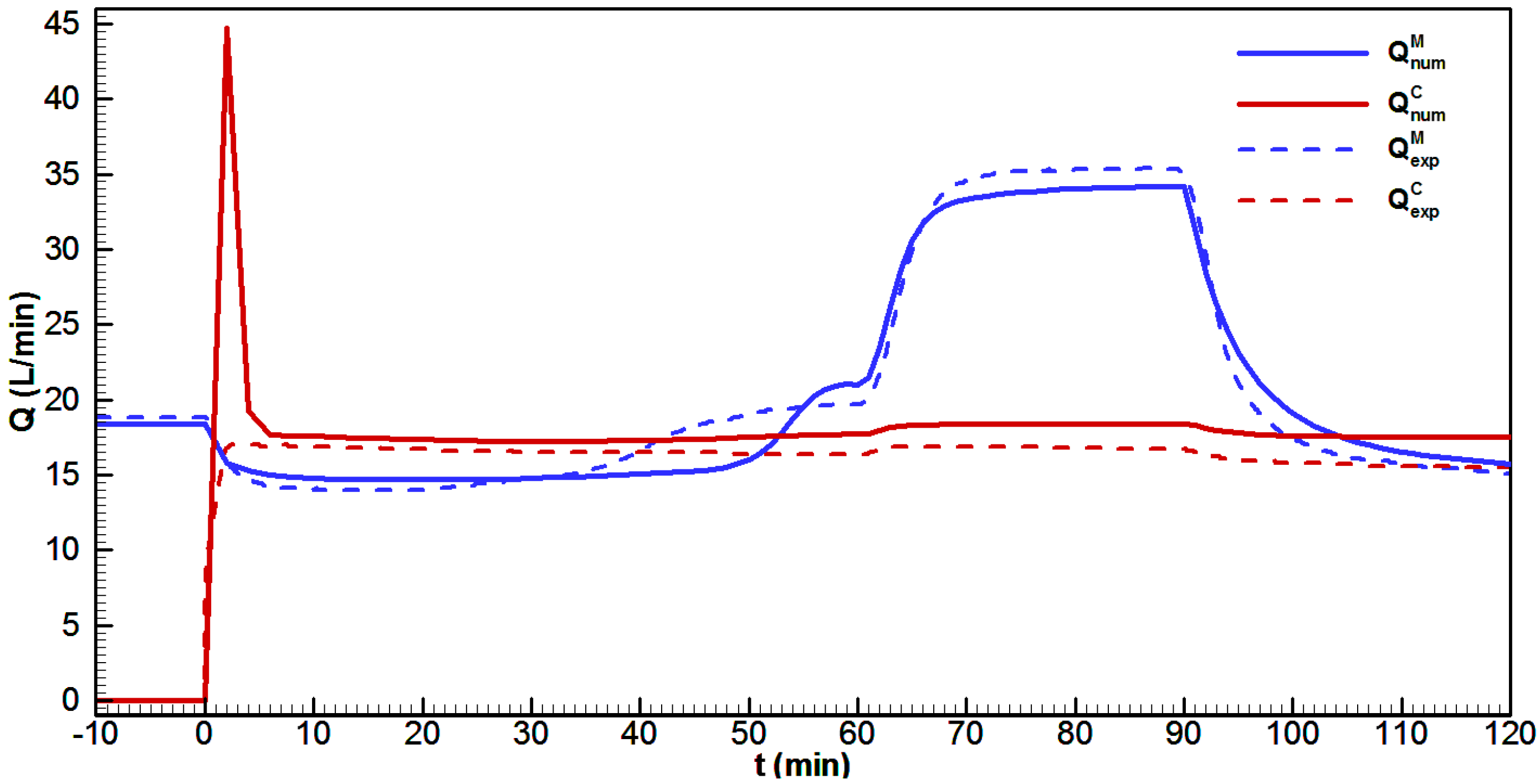
Before the measurement was started, the steady-state matrix flow (blue line) was established, while the conduit outlet was clogged (see
Figure 9).
was defined as the moment at which Conduit C1 was opened. Both the conduit (red line) and matrix responses were very fast due to high matrix conductivities. Basically, the conduit represented a highly permeable zone and drained groundwater from the surrounding porous medium. At
min, the sprinkler rainfall with a total discharge of 10.17 L/min started, whereas its influence on the matrix discharge began to be visible approximately 10 min later. This delay was mostly because of slow water infiltration through the unsaturated zone. Further, the matrix discharge was slowly raising and started to approach a steady-state value after
min, whereas the conduit discharge remained practically the same. The reason for this is as follows. The conduit discharge can be increased by increasing the matrix pressure in the vicinity of the conduit. However, due to high overall matrix permeability and moderate rainfall intensity, the increase in the matrix pressure around the conduit is not sufficiently high to be visible on conduit discharge. Thus, to achieve more significant variations of a matrix–conduit exchange, the direct recharge (5.80 L/min) through a conduit sinkhole (connected with the upstream end of the conduit) was started at
min. The applied direct recharge produced an increase in the conduit’s pressure, and significant effects on both the matrix and conduit flow were achieved. The numerical results reveal that increased conduit pressure produced by the direct recharge only reduced exchange discharge, and there was still no flow from the conduit toward the matrix (head inversion). The total increase in conduit discharge was smaller than the applied recharge because the matrix inflow was reduced. Moreover, at
min, the direct recharge was increased from 5.80 to 14.65 L/min, and a further increase in the conduit pressure produced head inversion, but only in the upstream part of the model. At
min, both rainfall and direct recharge were turned off, while measurements were continued until the end of the experiment (
min).
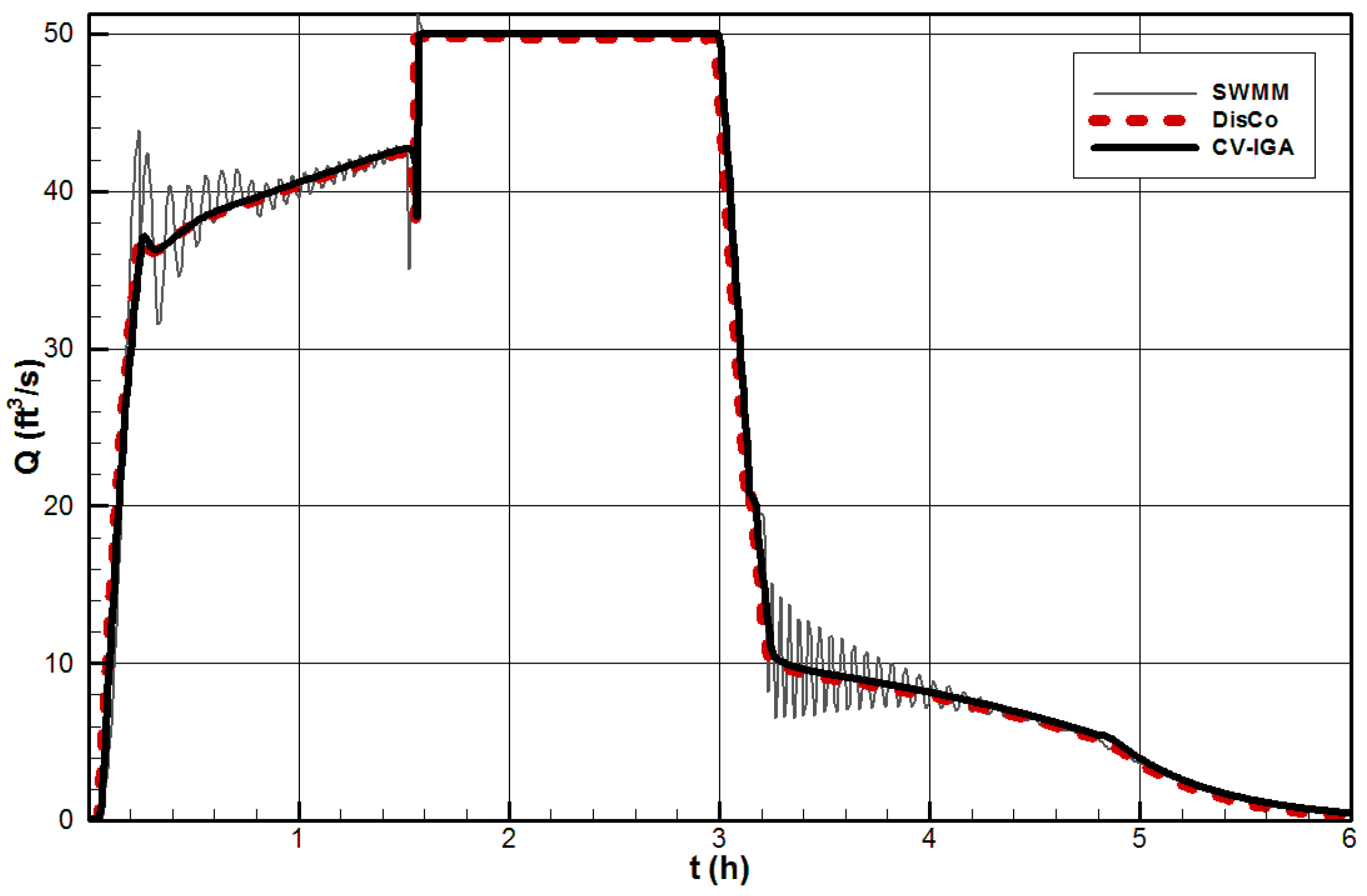
The hydrograph comparison shows that the numerical model follows the behavior of the experimental results. The differences are mostly inside the range of measurement error, which is estimated to be around 1.0 L/min. The numerical results are sharper then the experimental ones, which are smoothed by the measuring equipment.
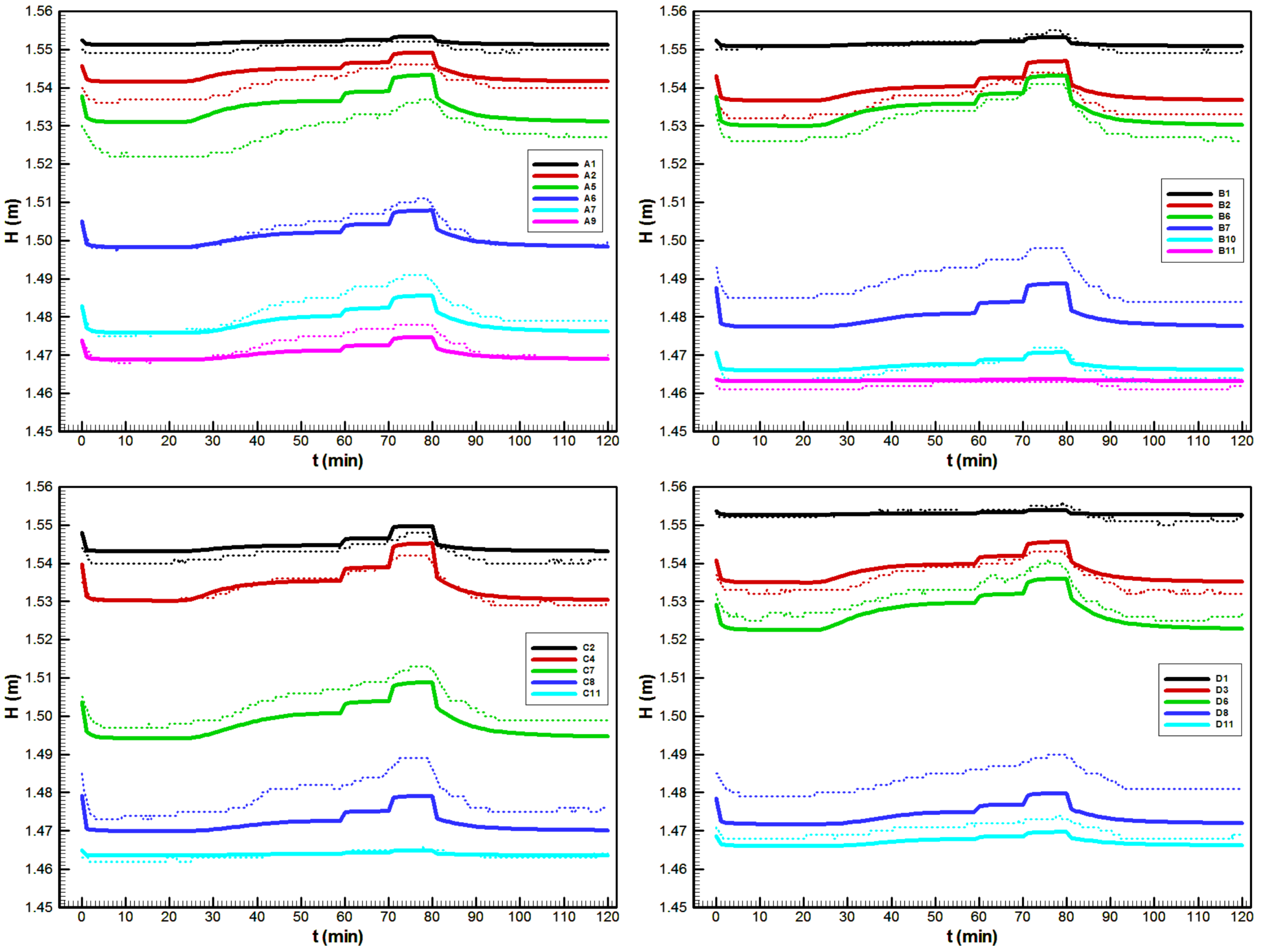
The hydraulic head comparison in
Figure 10 also demonstrates good agreement of the results. The precision of the measurements was mostly influenced by the precision of photogrammetry and was approximately 1.5 cm. For most results, this error is lower.
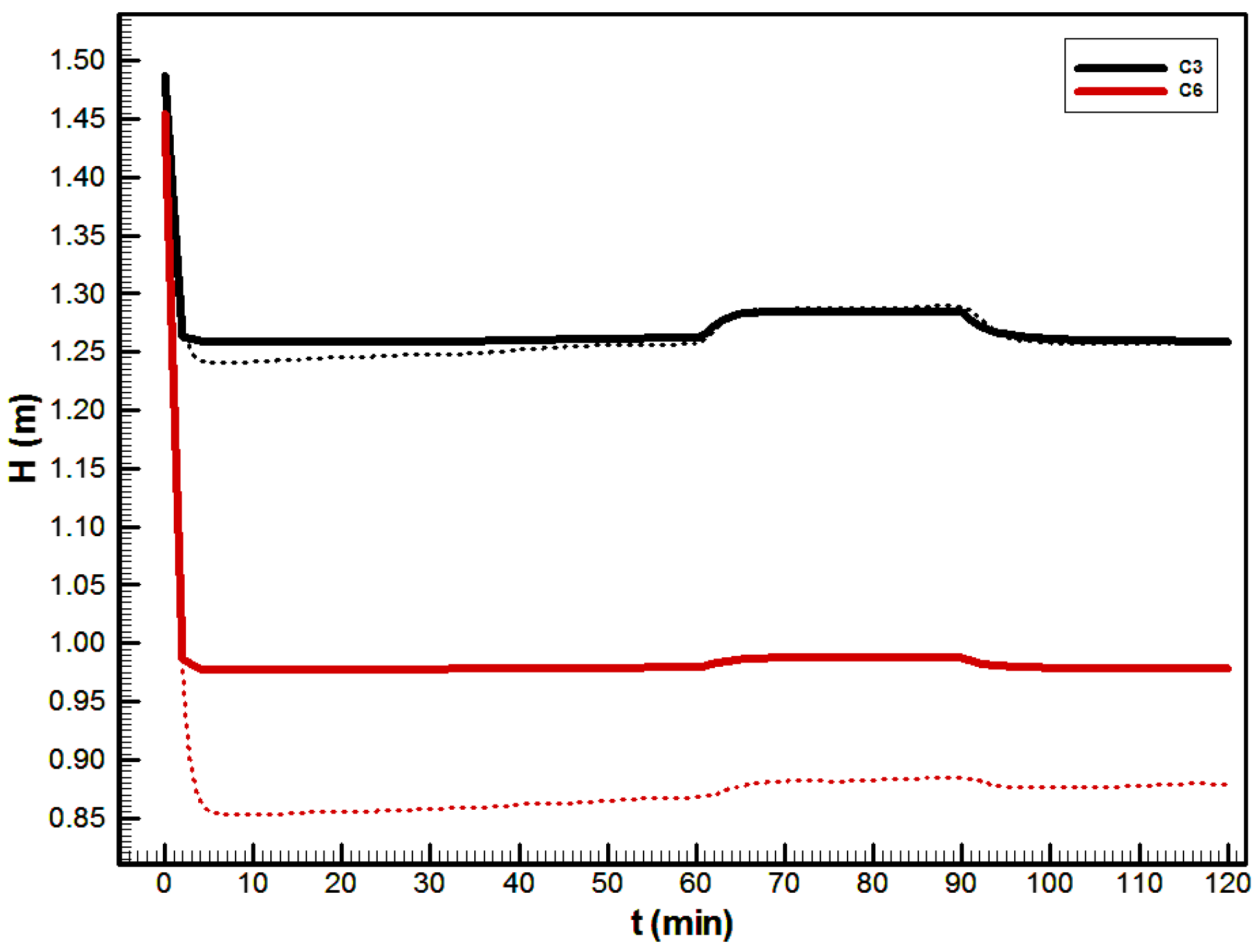
Figure 11 shows the hydraulic head comparison for two piezometers that are closest to Conduit C1 and mostly influenced by the matrix–conduit interaction. Again, the experimental results are slightly smoothed mostly because of the time lag produced by filling the piezometers. These results clearly demonstrate that the numerical model is capable of capturing the realistic flow dynamics of the physical model.
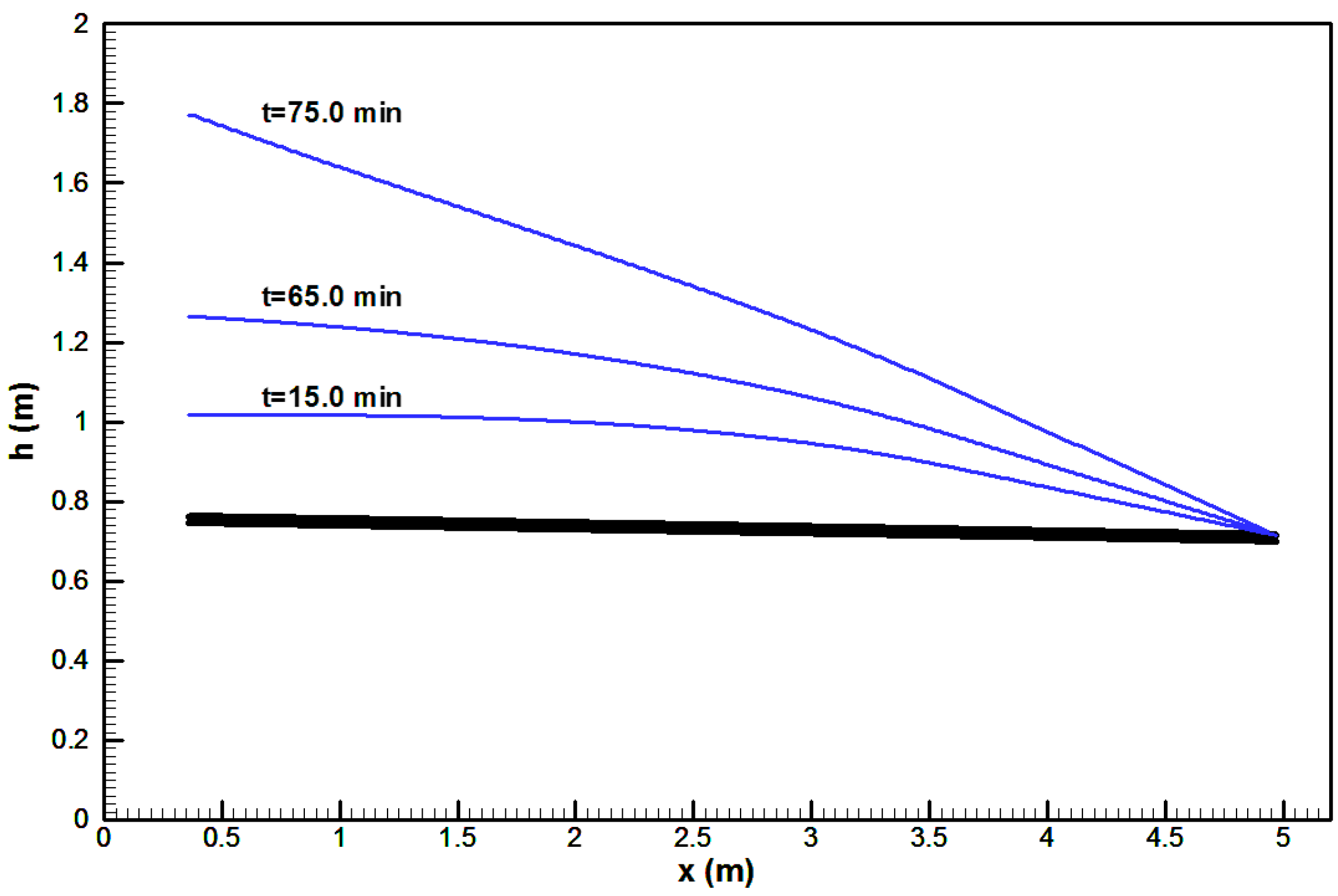
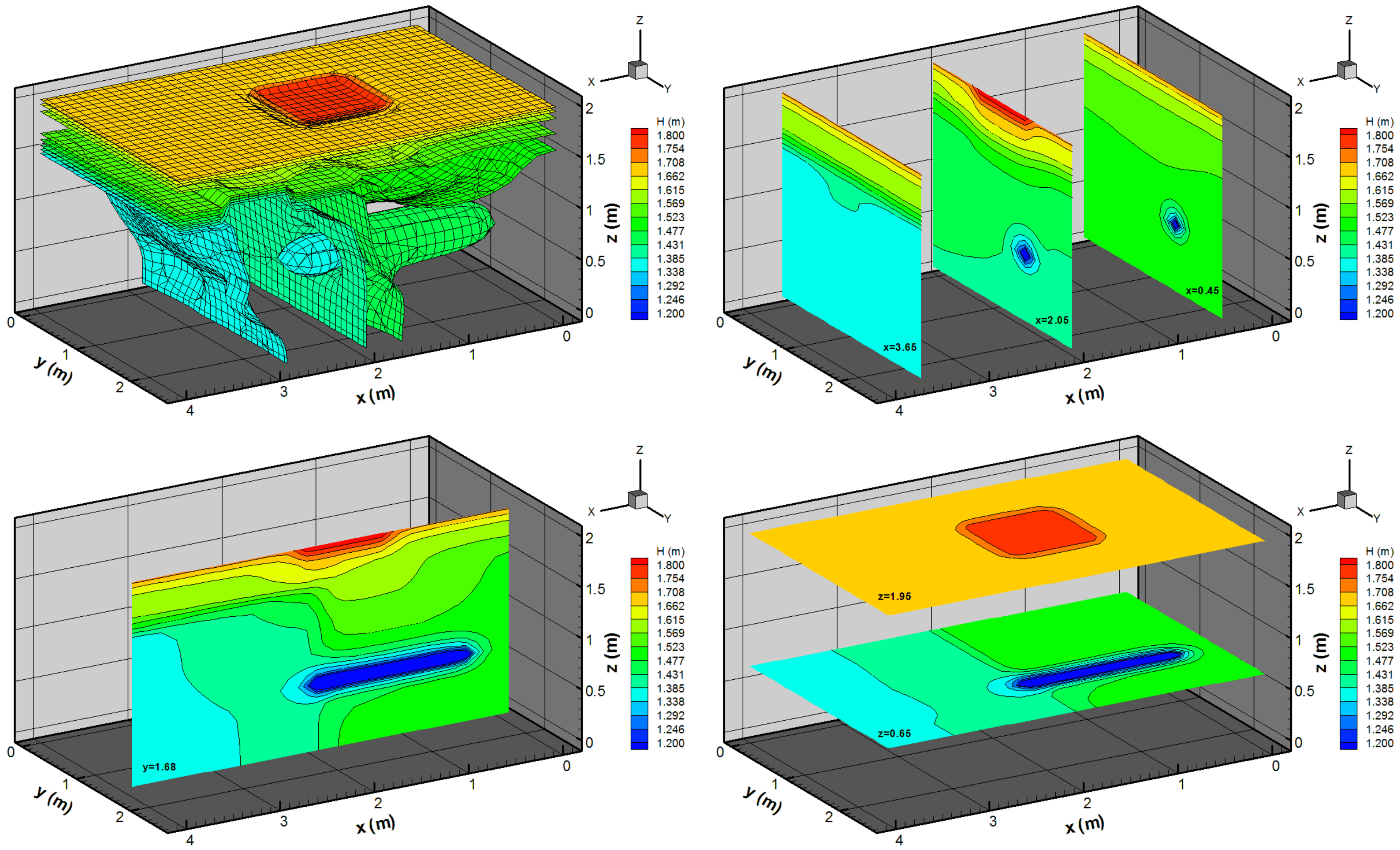
Further,
Figure 12 demonstrates conduit solutions in three representative time steps. These results confirm that head inversion can only happen from
70–80 min because, for the remaining time, the hydraulic head in the conduit is lower than the minimum matrix head defined by the downstream reservoir (
m). Additionally, the calculated Reynolds number at the conduit outlet was between 15,000 and 22,000 during simulation.
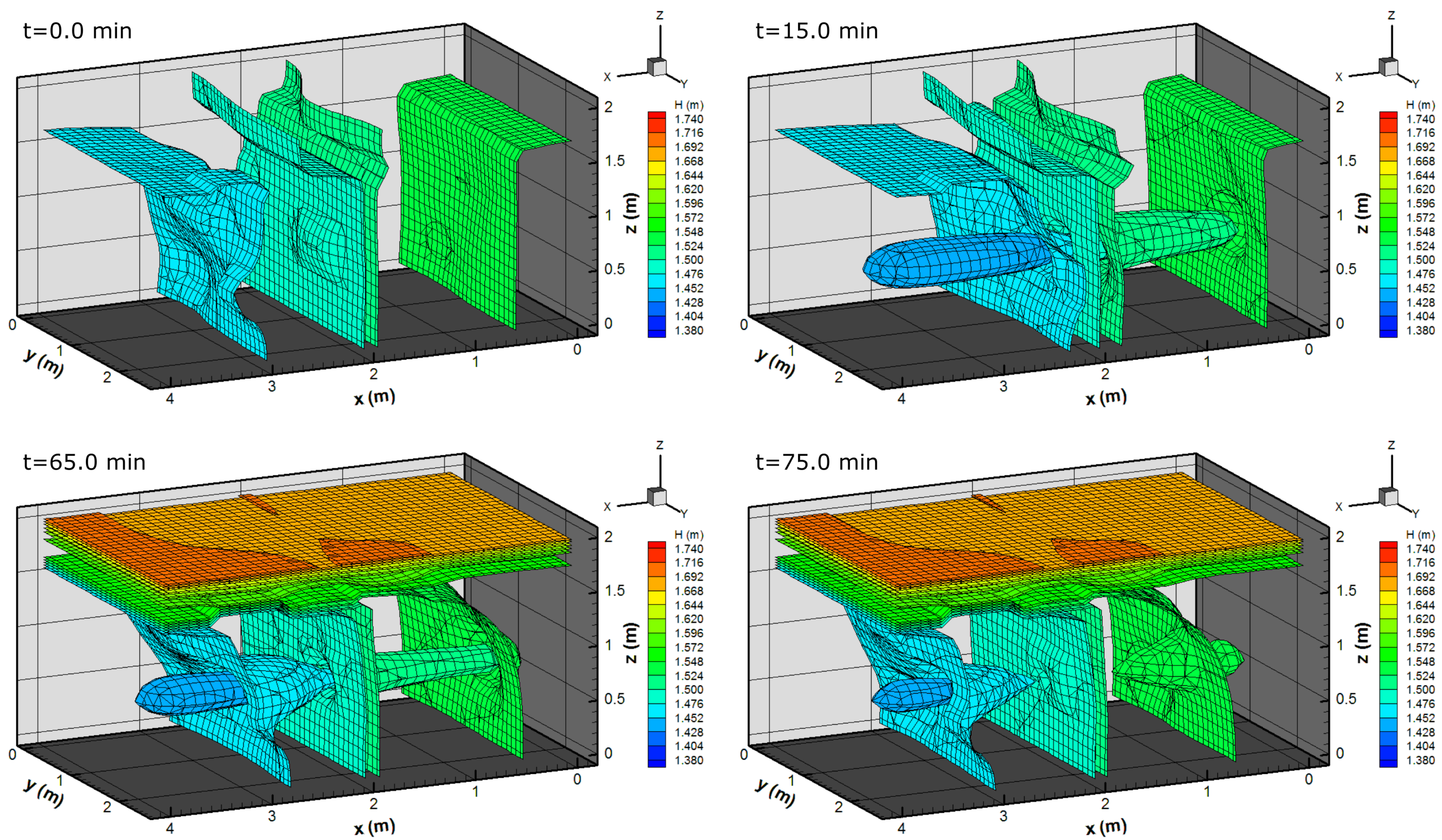
Finally,
Figure 13 demonstrates the matrix’s hydraulic head solutions at different time steps. At
min (before conduit opening), the steady-state matrix solution is shown, whereas at
min, a high conduit influence on the matrix flow is clearly visible. At
min, the matrix is influenced both by rainfall and the direct recharge from the conduit, whereas at
min the direct recharge is increased, and head inversion is visible in the upstream part of the model.
5.2.2. Test Case 2
For the second test case, we used a straight circular pipe with a larger diameter that was perforated only at the upstream part of the model (Conduit C2). The position of the conduit was defined by the starting and ending coordinates of the pipe bottom
and
, while the conduit was perforated only for
. The conduit diameter was 0.042 m, and the Manning roughness coefficients were
0.044 m
s and
0.015 m
s for the perforated and unperforated parts, respectively. The water levels in two reservoirs were kept fixed at
m and
m. Since for this test case, there was free surface flow at the conduit outlet, the free outfall boundary condition [
57] was used. This condition was implemented as a Dirchlet boundary condition, where the hydraulic head was calculated using a smaller value between the critical and normal water depth. The same numerical discretization was used as in the previous test case, while the exchange coefficient was set after calibration
s
. The measured and calculated values for discharges and hydraulic heads are shown in
Figure 14 and
Figure 15, respectively.
As for the previous test case, the steady state matrix flow (blue lines) was established before the start of measurements. At
, Conduit C2 was opened, and conduit discharge (red lines) was increased instantaneously. In the first time step, the numerical model showed a much higher discharge value then that obtained by experiment. This value was the outcome of the initial conduit emptying. Because of the larger pipe diameter, there was a free surface (partially filled) flow at the downstream end; thus, the conduit needed to release excessive water, which was initially stored in the conduit. The measuring equipment used for experimental data was not able to capture this effect (see how discharges are measured in the
supplementary materials). Additionally, this behavior was not observed in the previous test case (Conduit C1) because of a smaller pipe diameter and the fact that flow in the conduit remained pressurized.
At time min, the water depth at outlet boundary was measured to be 19 mm, while the numerical model predicted a value of 22 mm. At min, sprinkler rainfall of total discharge 12.00 L/min started. At this time, the rainfall influence on the matrix discharge was observed later than indicated by the experimental data. The good agreement of rainfall infiltration obtained in the first test case suggests that the main cause could be coarse quartz sand (CQS), which dominated in the additional infiltration area that was saturated in the previous test case (the water table was lower in this case). Even though the water retention curve for this material was obtained in the laboratory, it is well known that the accurate measurement of soil parameters in the unsaturated zone is a very difficult task. For example, the soil hysteresis or initial saturation deviations can significantly affect results due to the high nonlinearity of water retention curves.
Moreover, as in the previous case, the rainfall did not significantly affect conduit discharge; thus, at min, the rainfall intensity was increased by turning on two additional shower heads. The total discharge of 42.30 L/min was distributed on the square area defined by two corner points and , while keeping the same sprinkler rainfall (12.00 L/min) distributed on the overall top area. This high-intensity rain then produced a fast and significant increase in the matrix discharge, but an increase in the conduit discharge was also observed. The maximum matrix discharge value was slightly underestimated by the numerical model, which was followed by underestimated pressures in the downstream part of the model, meaning that concentrated rainfall influence was distributed differently than was predicted by the numerical model. The imperfection of the measurements of rainfall distribution and the model’s heterogeneity are likely the main reasons for these differences. The increase in conduit discharge was significantly smaller than in the matrix because the high matrix permeability was able to collect most of the rainfall water and prevented a significant increase in matrix pressures. Both the sprinkler and shower heads rains were turned off at min, while measurements were continued until the end of the experiment, min.
In this case, the head variations were more pronounced. The pressure drop introduced by opening the conduit was higher than in the previous case, and high-intensity rainfall produced an increase of the head up to 6 cm. The general behavior of the hydraulic head was quite realistic, but as mentioned before, the accuracy was lower in the downstream part of the model. The same two piezometers as in the previous case were the most dynamic and are shown separately in
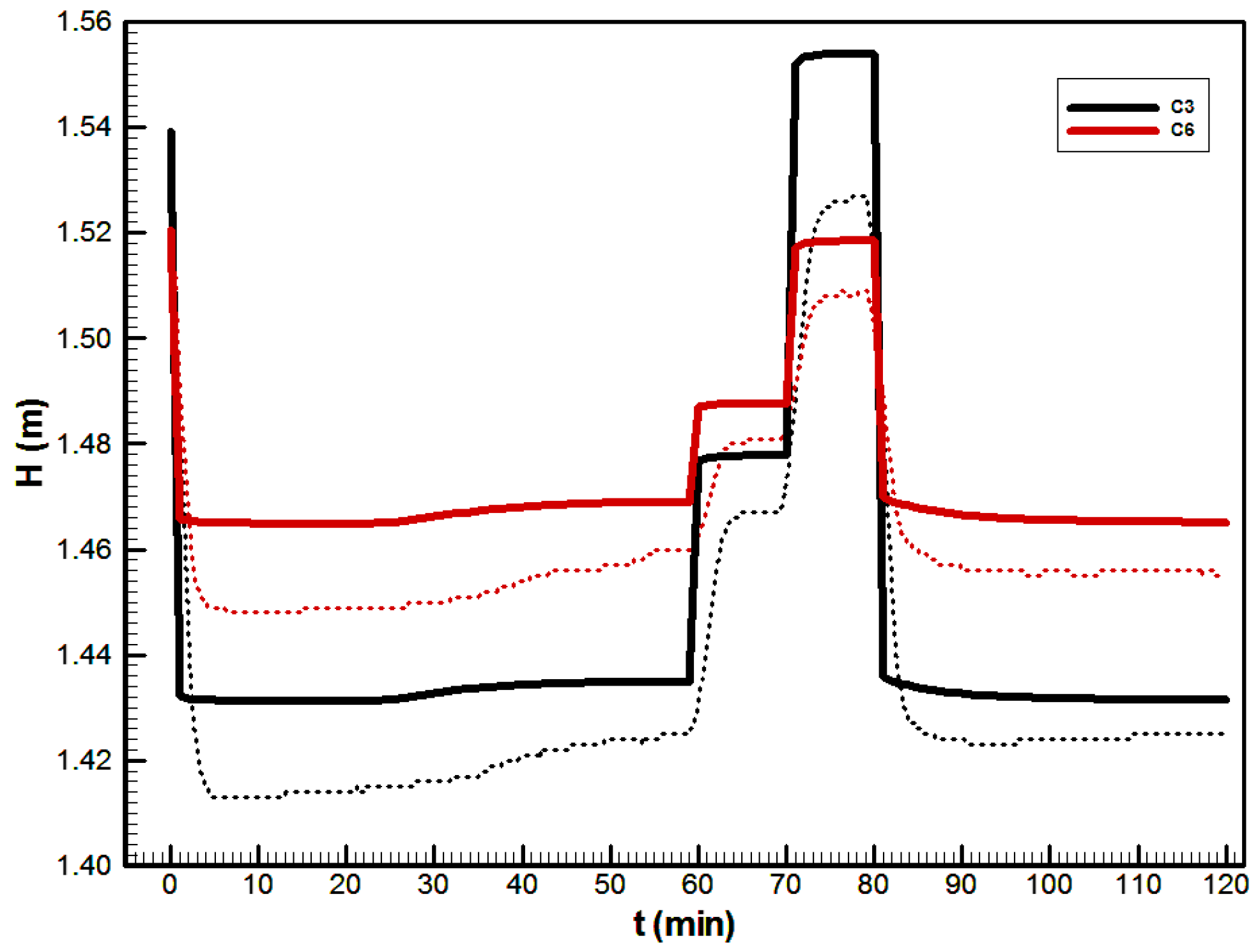
Figure 16. Even though Conduit C2 was only partially perforated, it produced a large amount of conduit discharge, followed by a significantly large pressure drop (especially observed by Piezometer C6 in
Figure 16). The free surface flow caused by high pipe conductivity and a larger percentage of perforated area were the main reasons for this behavior. The highest pressured drop measured by piezometers was 0.61 m, while the numerical model had a predicted value of 0.48 m. Even though discrete-continuum models are not capable of the detailed resolution of flow interface, it seems that this model quite realistically simulates the hydrodynamics of the physical model.
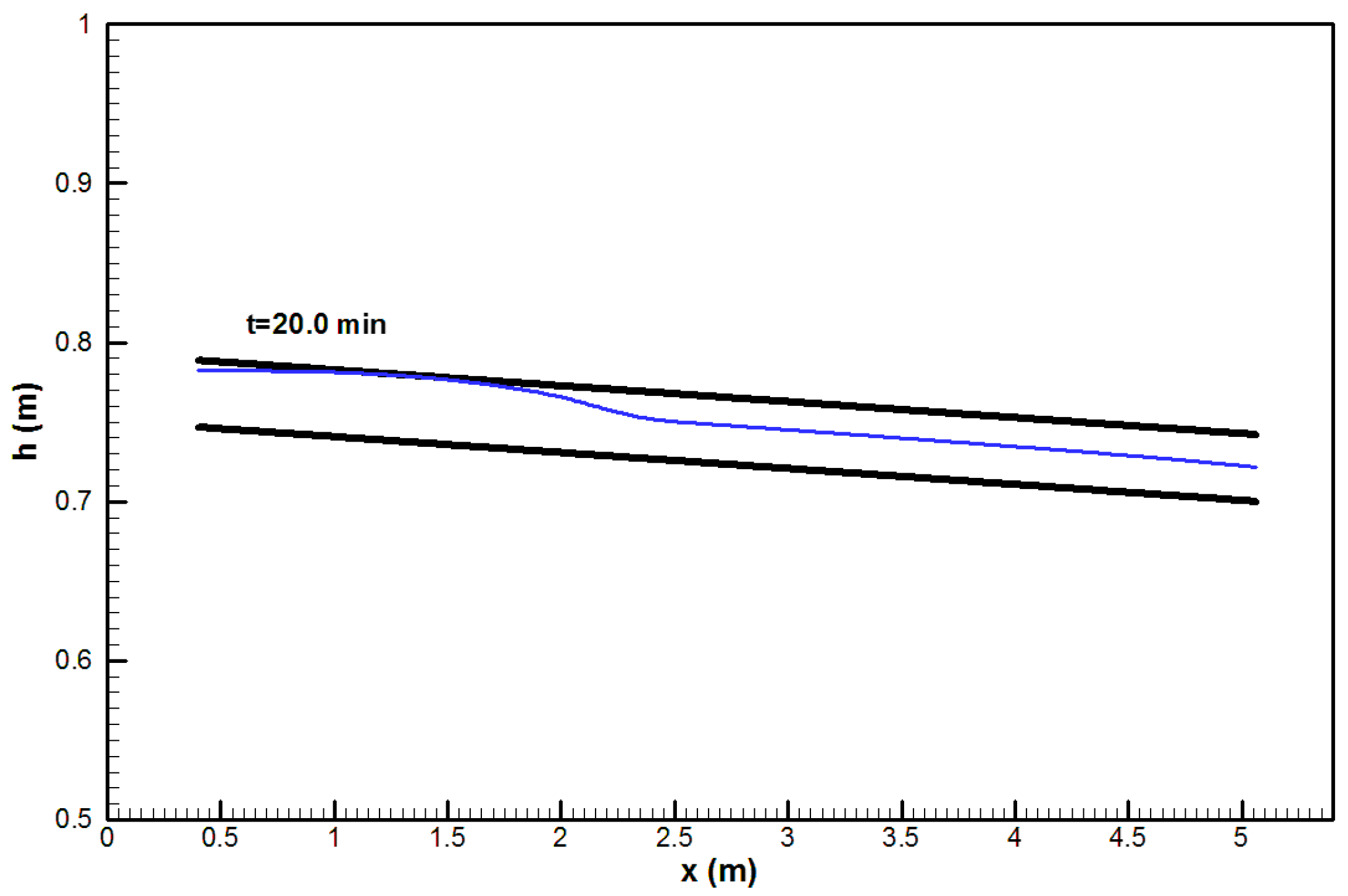
Figure 17 demonstrates the numerical solution for the hydraulic head inside the conduit where it dominated free surface flow. However, in part of the conduit, the water surface reached the top of the conduit, and flow was slightly pressurized. The conduit solution is shown only for one time step because there are no significant changes in the hydraulic head during the solution. Finally,
Figure 18 presents the matrix solution at
min.
6. Discussion
In this paper, we present the development of the hybrid (discrete-continuum) karst flow model. With respect to the wide range of karst-distributed models (continuum, discrete, hybrid, etc.…), these hybrid models have the potential to describe many karst complex properties, especially karst heterogeneity, which includes the usually uncertain conduit geometry and soil properties of a matrix. Moreover, if we take into account the description of different flow regimes in conduits (turbulent flow) and the matrix (laminar Darcy flow), as well as their complex relationship, hybrid models temporally serve as the best candidate for realistic karst flow modeling. The two main issues that appear most important for the development of realistic hybrid karst flow models are as follows: (a) its numerical complexity, which requires the solving of high nonlinearity, the preserving of numerical stability, and an adequate description of karst multiphysics, and (b) uncertain measurements and sparse collection of input data causing the difficult (in many cases, impossible) verification of karst flow models under realistic catchment conditions.
Complex karst flow modeling usually requires even more than the “state-of-the-art” modern numerical techniques. This is the main reason why, in this work, a new karst flow model was developed using some important ingredients: (a) control-volume formulation, which ensures local and global mass balance (e.g., finite element usually enables only global mass balance); (b) Fup basis functions inside relatively novel isogeometric analysis (IGA) (Hughes et al. [
42], Cottrell et al. [
43]), which enable the description of geometry, high approximation properties, the continuity of velocities and fluxes, and efficient multiresolution adaptive algorithms (Gotovac et al. [
45]); and (c) the handling of high nonlinearity, which requires a presented segregated iterative algorithm, and very “careful” modeling between the matrix and conduit separate solvers ninvolving underrelaxation for increased stability. Possible further improvements include the solving of the large system of nonlinear equations due to the description of the large catchment area. One possible direction is incorporating this algorithm into the open source code Petiga (Dalcin et al. [
58]), which is based on robust parallel nonlinear library PETSc (Balay et al. [
59]) and IGA. Furthermore, one bottleneck is the high nonlinearity introduced by Richards’ equation as well as the definition and measurements of unsaturated curves. A new improved description of the unsaturated zone is highly desirable. Last but not least, the definition of the exchange flux is still an open research topic. In this paper, we used a classical linear relationship depending on the head differences and questionable first-order exchange parameter. Some improvements using the Peaceman well index are given for example in de Rooij et al. [
25].
The realistic verification of the karst flow models is also an open research topic, especially for distributed models such as the presented one. Realistic verification includes knowledge of a wide range of parameters and karst properties (for example, Croatian karst aquifers in Jadro and Ombla catchments; see Bonacci [
60]). The most needed data are conduit geometry (diameters, positions, and network structure), matrix heterogeneity (conductivity and porosity), unsaturated matrix properties in terms of van Genuchten curves and uncertainty of its parameters, boundary conditions such as matrix inland conditions and outlet conduit condition, uncertainty of rainfall distribution, etc. Due to usual lack of collected data, its great number, and the relatively large number of needed calibration parameters, realistic verification is definitely complex and usually an extremely difficult task. Therefore, as a first step for the verification of the presented karst flow model, it was performed in this case under controlled laboratory conditions.
Therefore, a large 3D physical karst flow model was constructed (5.66 × 2.95 × 2.00 m). To the best of our knowledge, this is the first such model that enables many of the mentioned karst flow characteristics and a detailed knowledge of most of the mentioned input data (see other, simpler laboratory models in Faulkner et al. [
28] and Castro [
29]). Despite the still presented uncertainty in soil properties (see also the
supplementary materials), most of the input data are defined by measurements and “fine-tuning” by additional smaller flow test experiments given in the
supplementary materials. Thus, verification is performed on two different flow test cases, where the only parameters that were calibrated during the presented experiments were the matrix–conduit exchange coefficient and roughness in the perforated part of the larger Conduit C2. Since it is a substantial improvement in comparison with realistic flow conditions in karst, the presented verification can be regarded as the first attempt for the realistic verification of karst flow models.
The two flow test cases were presented, and numerical results were confronted with experimental data. In the first test case, the matrix flow was disturbed by opening the smaller conduit (diameter: 0.0155 m). The activation of the conduit produced a decrease in both the matrix discharge and the heads since the conduit represents a highly permeable zone and redirected a significant amount of flow. The total discharge (from both the matrix and the conduit) was significantly higher, whereas the conduit flow was pressurized due to the small conduit diameter and sufficient exchange capacity. Moreover, moderate rainfall was applied to test nonlinear infiltration through the unsaturated zone, while direct recharge was used as an additional test for water exchange between the matrix and conduit. While conduits drained the matrix during most of the experiment, the numerical results show that, for a maximum applied direct recharge (from –80 min), there was head inversion in the upstream part, where the conduit recharged the matrix. The numerical results are in excellent agreement during most of the experiment and inside the measurement error. The largest deviation from the measurement results was observed during direct recharge through the conduit. This can also be due to measurement error; however, there is a possibility that an exchange term that uses a constant exchange coefficient (i.e., linear dependency of exchange discharge with head difference) is not capable of accurately capturing this range of pressure variations. However, it can be stated that the overall dynamics of the physical model were realistically and accurately simulated by the numerical model.
In the second test case, the matrix flow interacted with the partially perforated pipe/conduit (diameter: 0.042 m). This setup was shown to be more demanding for flow modeling. The free surface conduit flow that used a demanding and unknown outlet boundary condition, a longer infiltration depth, a higher and concentrated rainfall intensity, and larger discharge rates followed by large pressure variations in the matrix are some of the main differences that represent serious challenges for the numerical model. Again, the model captured complex physics very realistically. The largest difference occurred in the model response to applied rainfall. For this case, the water table was lower, and, due to a deeper infiltration depth, the influence on the matrix discharge was observed later than in the experiment. The watering of dry soil represents a very serious problem and is highly influenced by (always) uncertain van Genuchten parameters and imperfection in rainfall distribution. Further, the concentrated high-intensity rainfall produced a lower matrix discharge than measured. Measurement errors are likely to be more pronounced for higher flow rates values, but the underestimation of the hydraulic head in the downstream part of the model suggests that the model response to this rainfall was different than in the physical model. The imperfection of rainfall distribution, the complex heterogeneity, and the complex physics of infiltration above the water table are the greatest challenges in obtaining accurate results. Finally, measurement errors for both test cases were considered to be dominated by photogrammetry errors, which were estimated at approximately 1.5 cm for head and 1.0 L/min for discharges.
The two presented test cases were significantly different and captured many complicated processes that occur in real karst aquifers. The numerical model was mostly inside the range of measurement precision, and the observed experimental behavior was realistically simulated, which is an encouraging result and demonstrates the robustness of the developed numerical model. Finally, the first test case used approximately 60 min of CPU time, while the second test case needed approximately 81 min. Both calculations were performed by serial computing on a single processor (Intel Core i7, 2.60 GHZ).
We are planning to use the presented karst flow model to investigate the sensitivity and validity of the water exchange term. The exchange coefficient is the main calibration parameter that directly determines the matrix–conduit exchange. We have verified our numerical model in the sense that it can produce accurate and realistic results by calibrating the exchange parameter; however, the serious sensitivity analysis of this parameter was not considered. Thus, we are also planning to use different experimental setups and investigate how obtained values of exchange parameters describe different flow conditions on the scale of our physical model. This is an important topic for practical application since numerical karst flow models are needed for the prediction of different scenarios and not only for understanding and reproducing obtained measured data. Finally, the quality of the velocity results of our karst flow model will enable more realistic analysis of tracer tests and contaminant transport.
7. Conclusions
In this work, a novel numerical model for groundwater flow modeling in karst aquifers is presented. The hybrid (discrete-continuum) approach is used as the best candidate for realistic karst flow modeling. Due to the high nonlinearity introduced by the unsaturated zone, most karst flow models neglect important hydrodynamic behavior above the water table. Thus, in this work, matrix flow is described by a more realistic variably saturated flow equation (usually called Richards’ equation). Additionally, the mixed form of the equation is used to obtain a mass conservative solution in both the saturated and unsaturated zones. The flow in the karst conduits is represented as one-dimensional and captured by a noninertia wave equation. This equation conveniently describes both the free surface and pressurized flow conditions by simply modifying the capacity term in governing equations. Since two flow domains (i.e., matrix and conduit) are governed by different partial differential equations (as well as dimensionality), the equations need to be coupled. The coupling is established on a classical first-order exchange term, which is proportional to the head difference on the matrix-conduit interface.
A novel numerical technique based on control-volume formulation and Fup basis functions was used for spatial discretization and labeled control-volume isogeometric analysis (CV-IGA). Fup basis functions belong to the class of atomic functions and can be regarded as infinitely differentiable B-splines. The application of Fup functions enables higher continuity and smoothness of the solution, while control-volume formulation retains the conservation property of governing equations. The karst flow model is based on a segregated (iteratively coupled) scheme, in which each flow domain is solved independently by using the last known solution of the other domain to calculate the exchange term.
A particular difficulty with complex 3D karst flow models is the verification and validation process due to lack of input (such as conduits geometry and parameters of aquifer) and measured (head distribution and discharges) data. Therefore, in this work, a novel 3D physical karst flow model able to reproduce many important flow features in karst is presented. This physical model enables substantial improvement in comparison with real aquifers, especially in terms of the detailed knowledge of mentioned input and measured data. Two complex experimental setups were used and simulated by the numerical model. The numerical model was mostly inside the range of measurement precision and has been capable of realistically simulating demanding flow in the physical model.