Numerical Model of Supersaturated Total Dissolved Gas Dissipation in a Channel with Vegetation
Abstract
1. Introduction
2. Materials and Methods
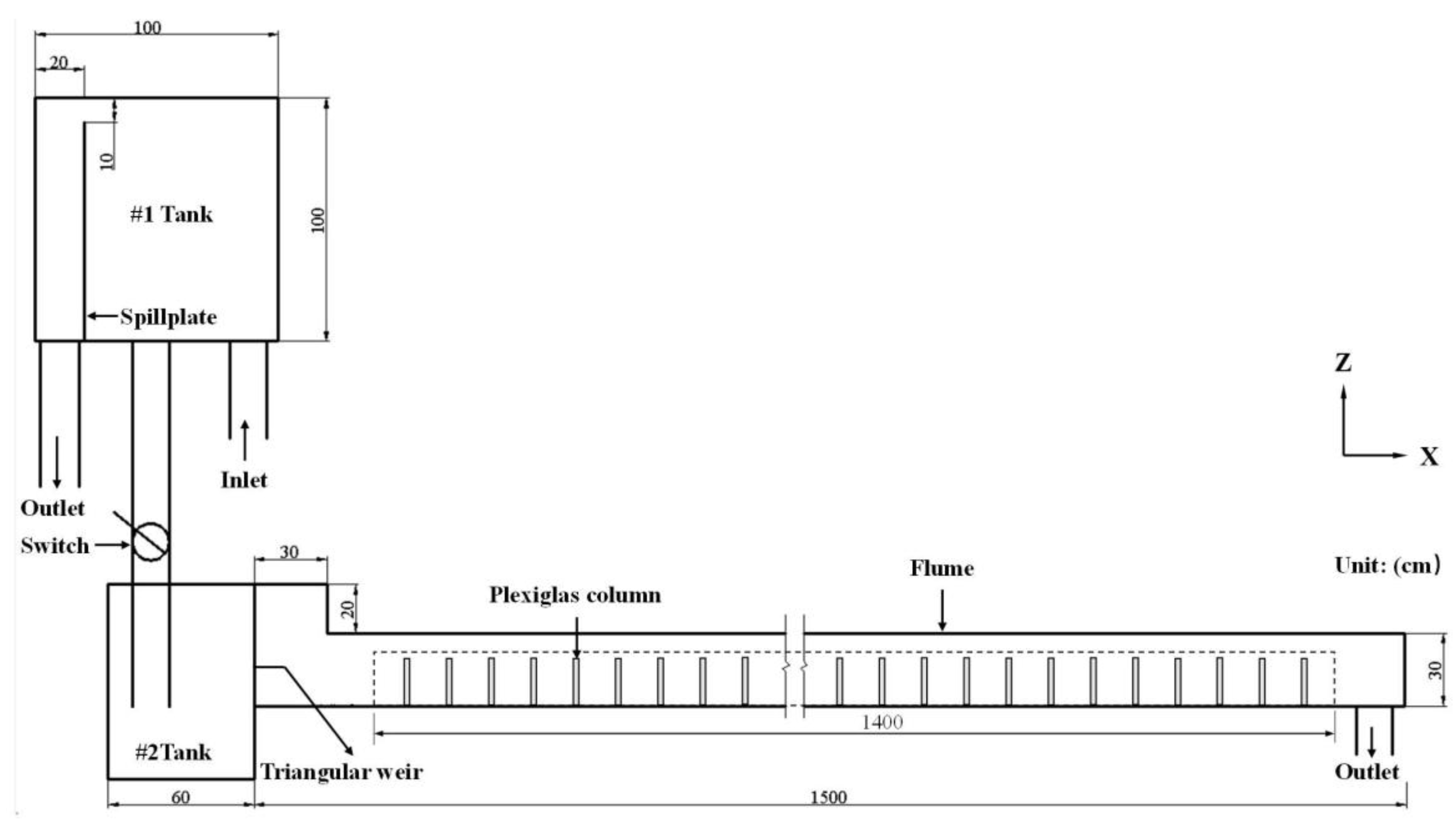
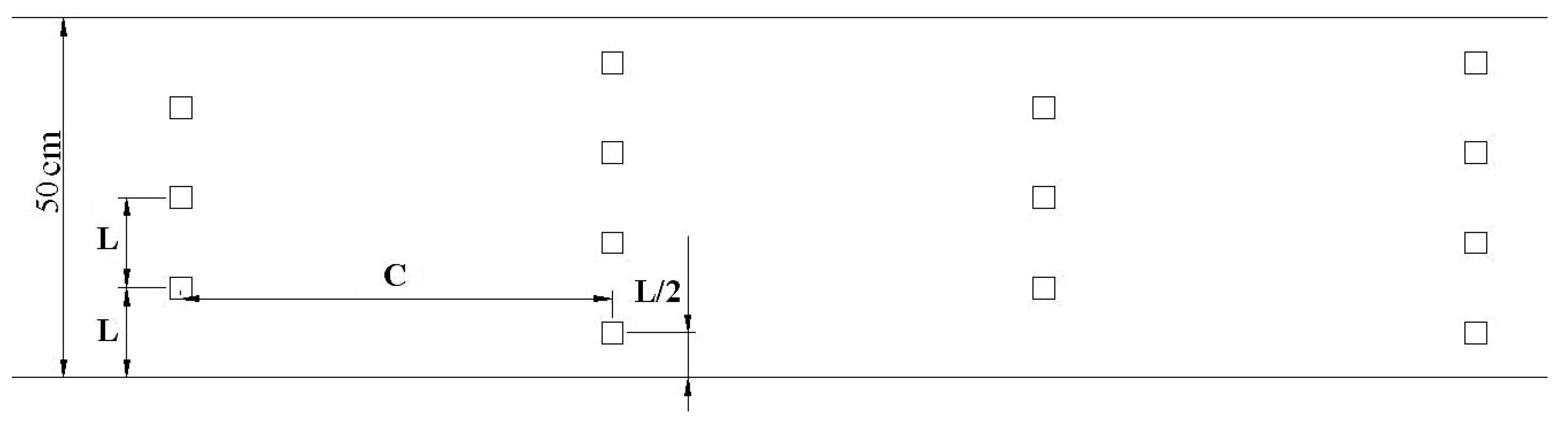
2.1. Study Case
2.2. Model Assumption
2.3. Model Equations
2.3.1. Continuity Equation
2.3.2. Momentum Equation
2.3.3. k-ε Equations
2.3.4. Transportation Equation of TDG
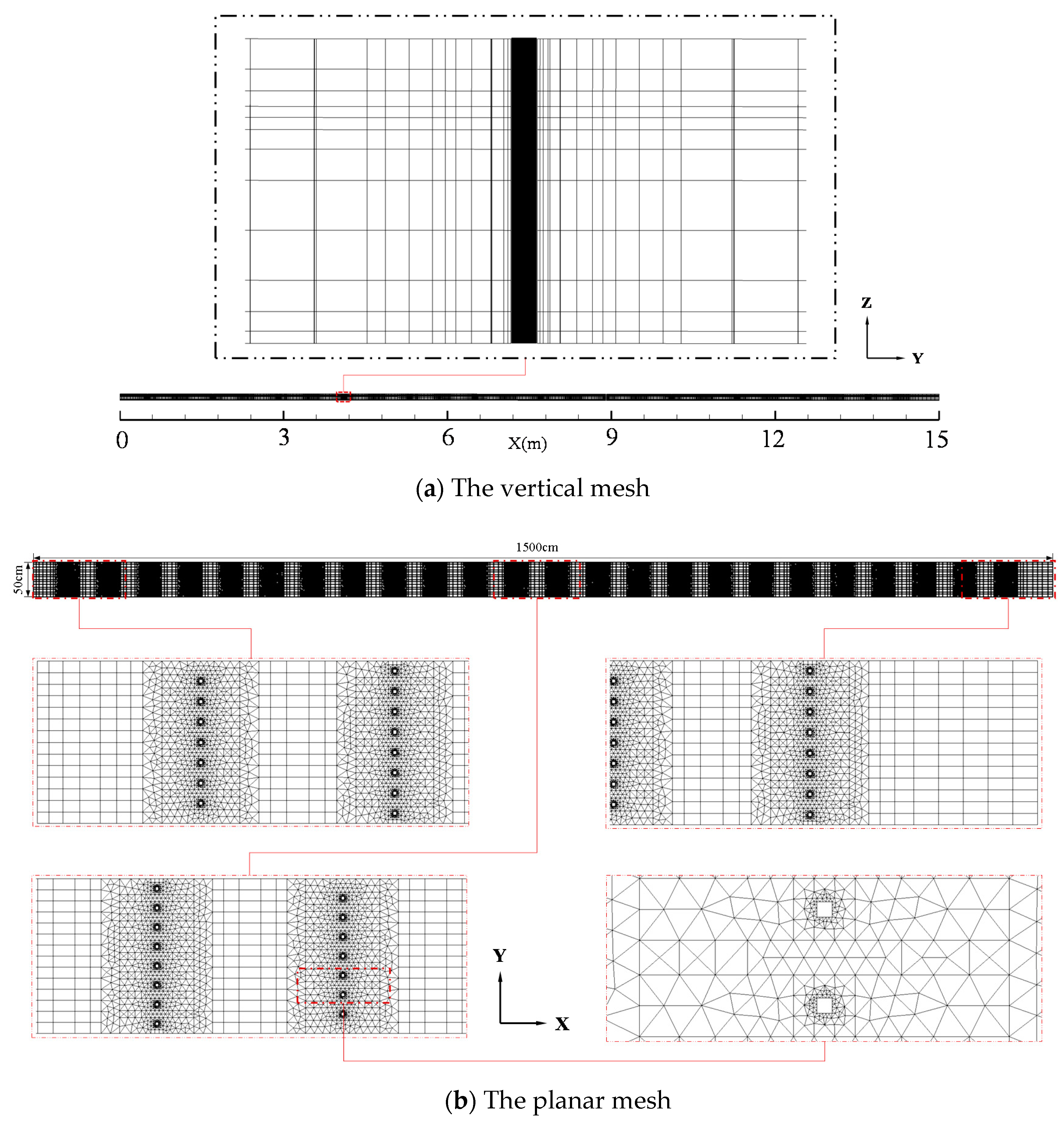
2.4. Compute Region and Meshes
2.5. Boundary Conditions
2.5.1. Boundary Conditions of Flow Field
2.5.2. Boundary Conditions of the TDG Concentration Field
2.6. Model Parameters
2.6.1. Parameterizing the TDG Source Term
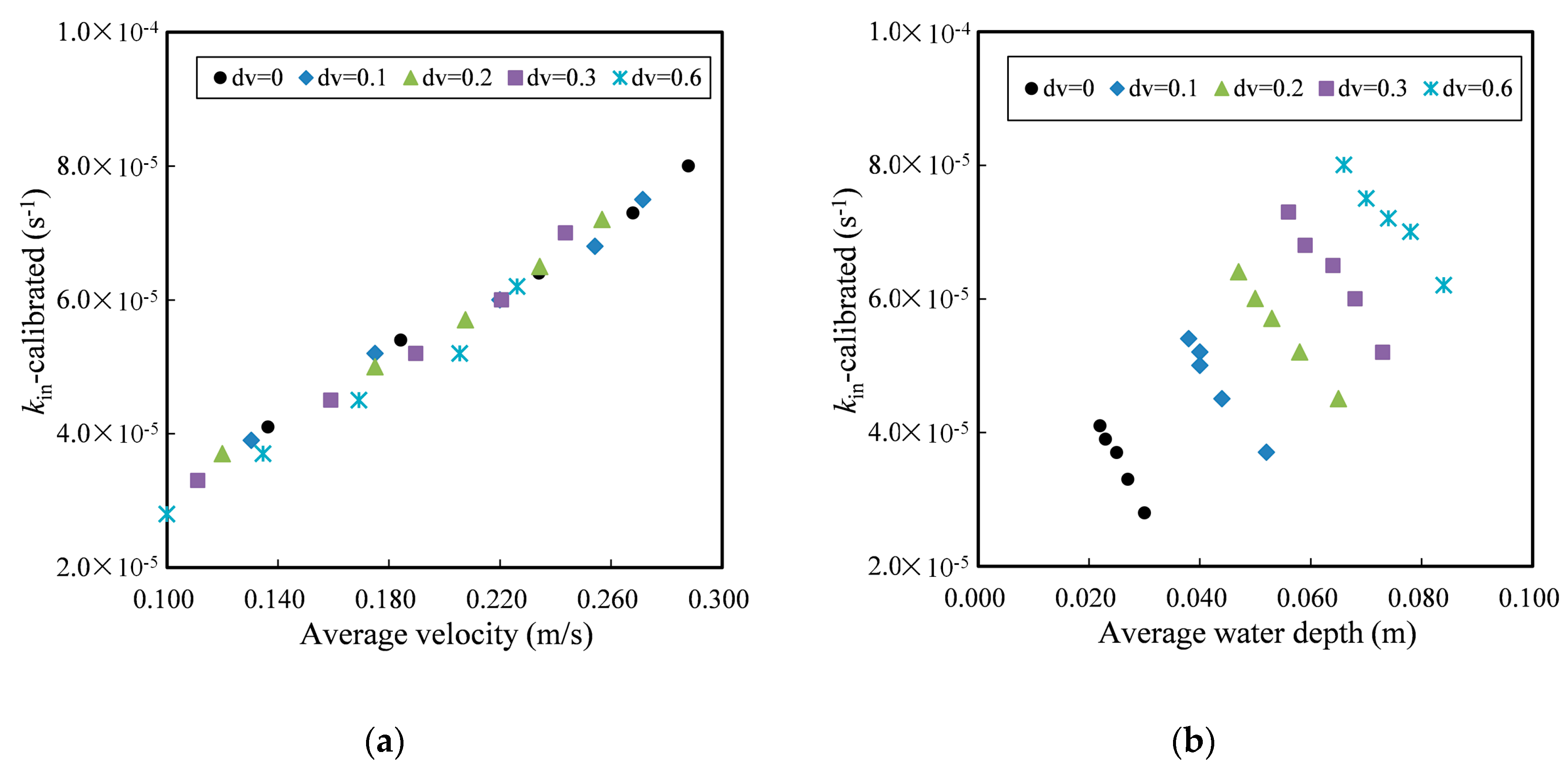
2.6.2. The Formula of Inner Dissipation Coefficient
2.7. Verification of the Model
2.7.1. Verification Case
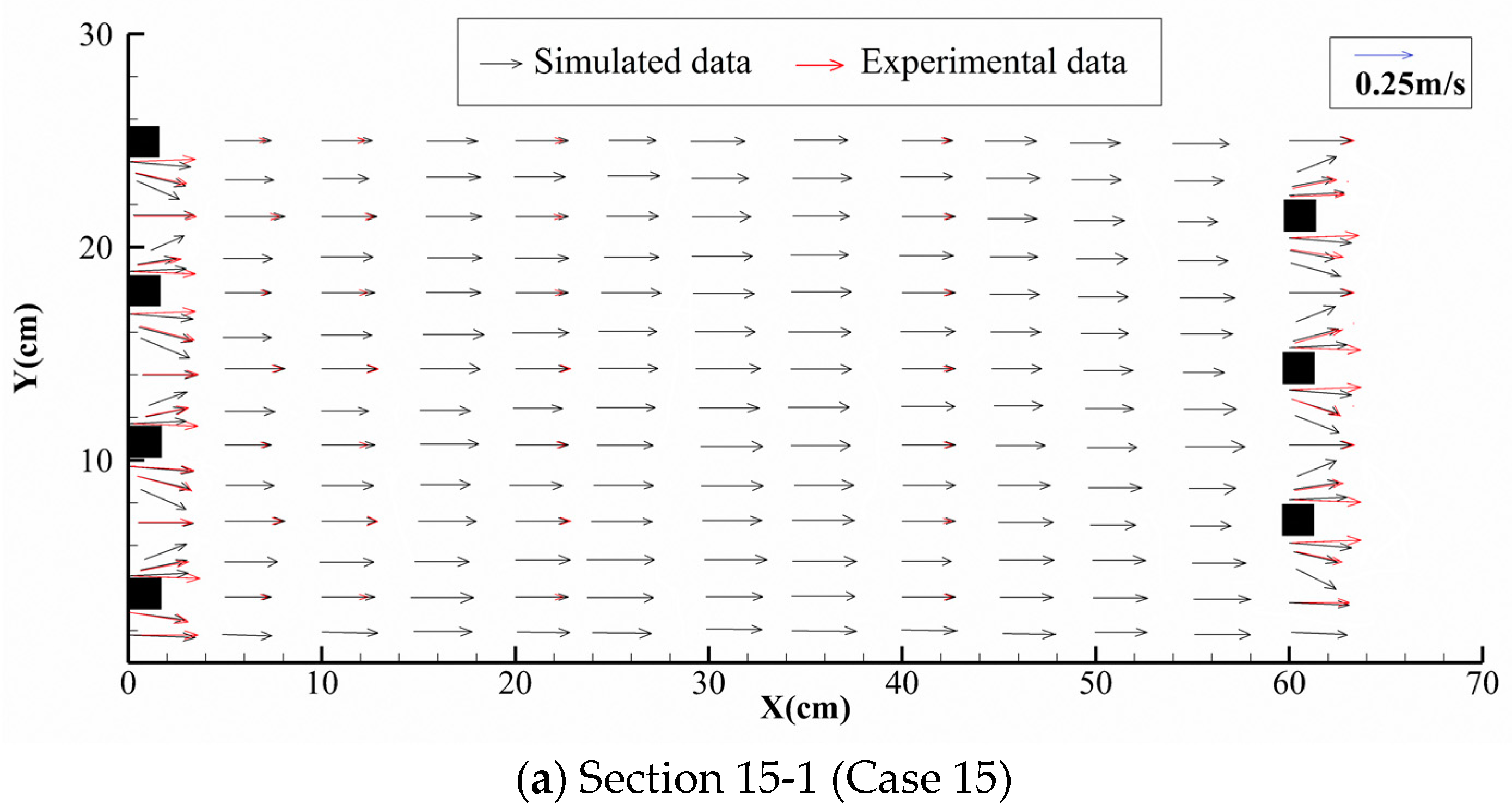
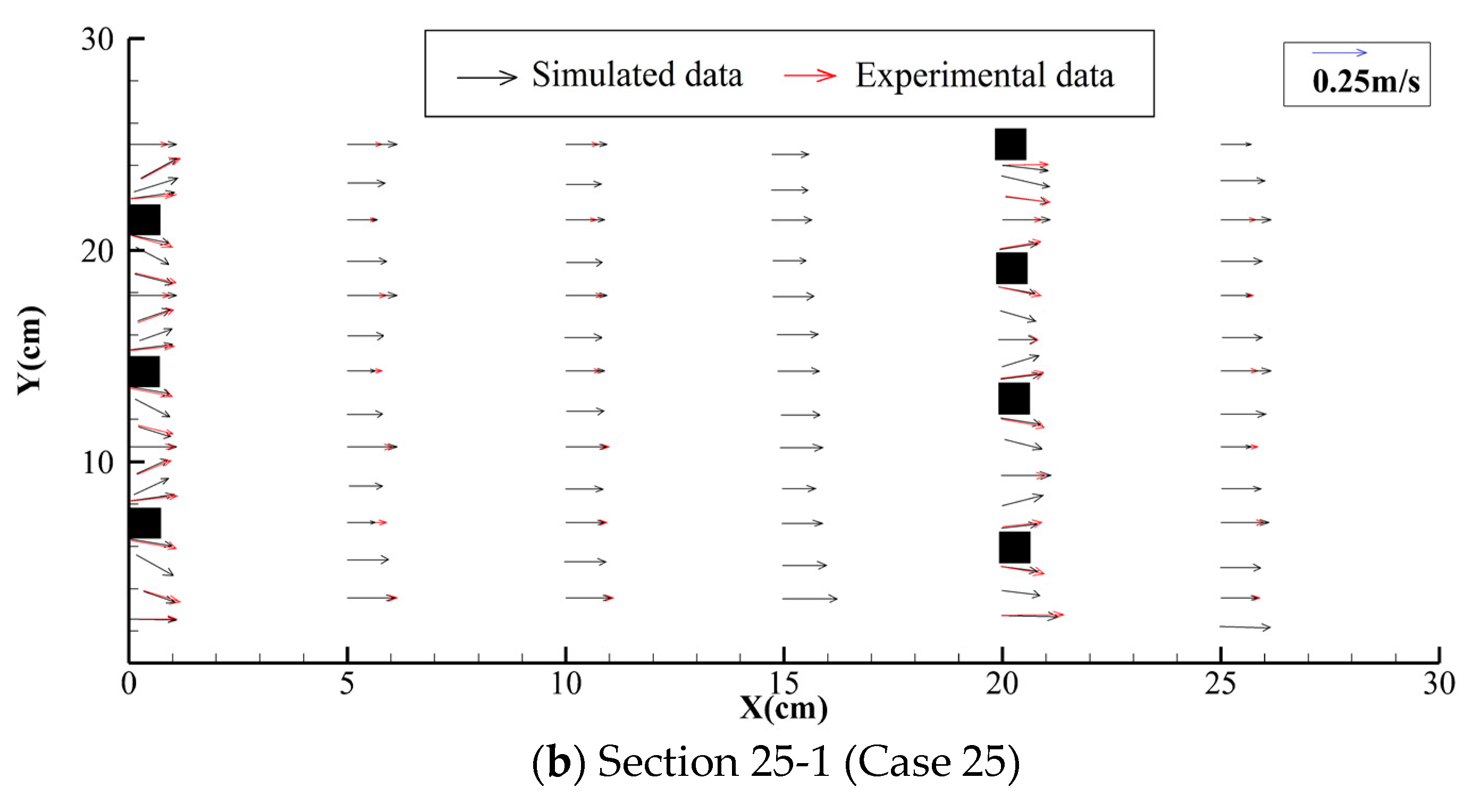
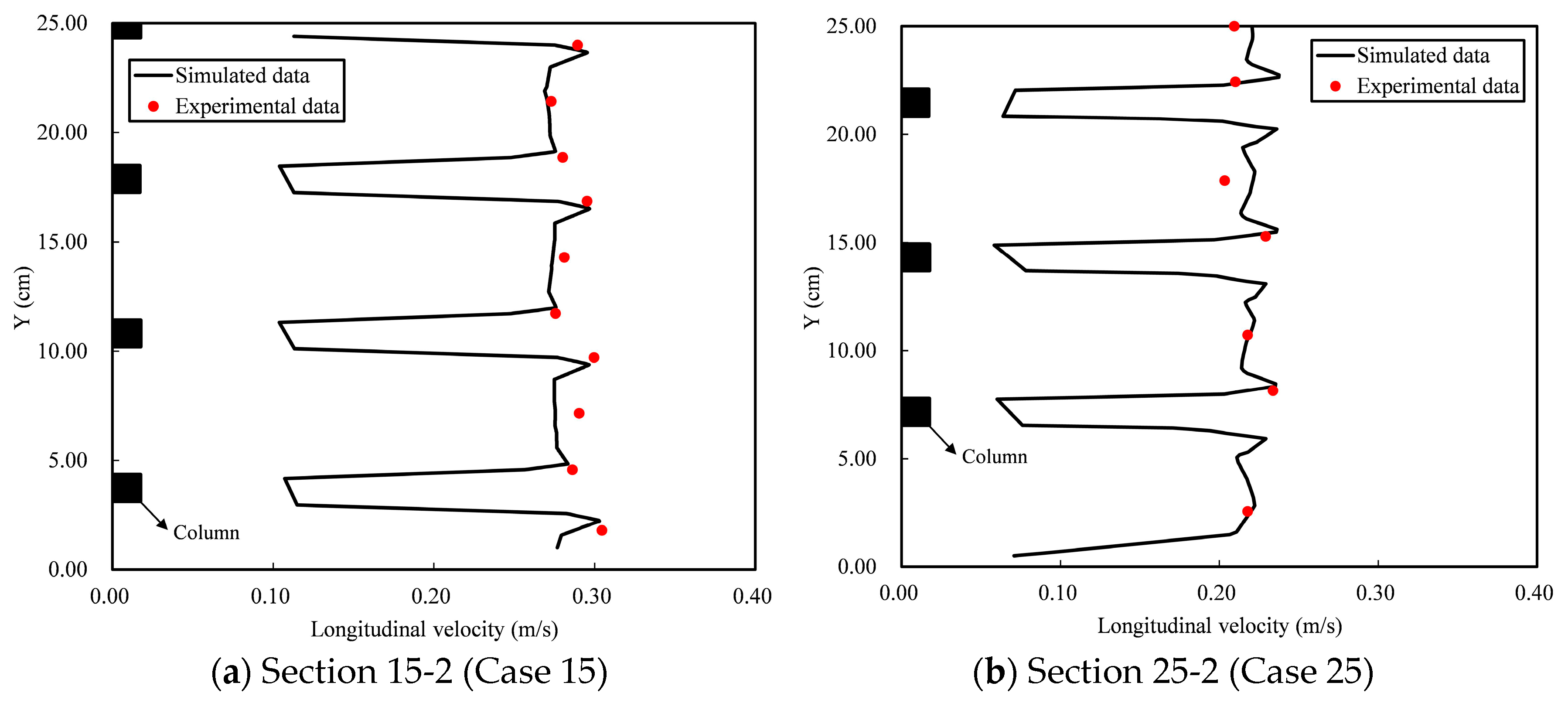
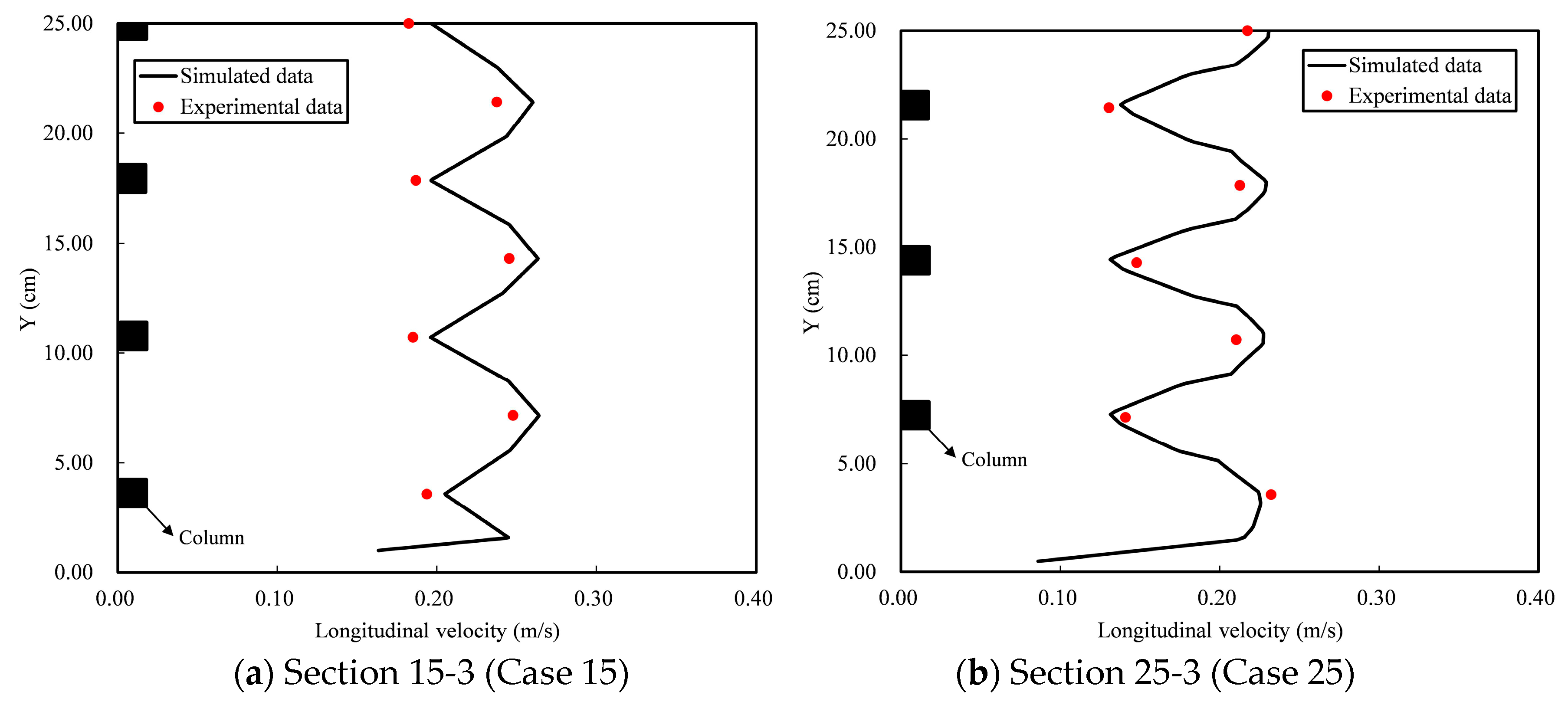
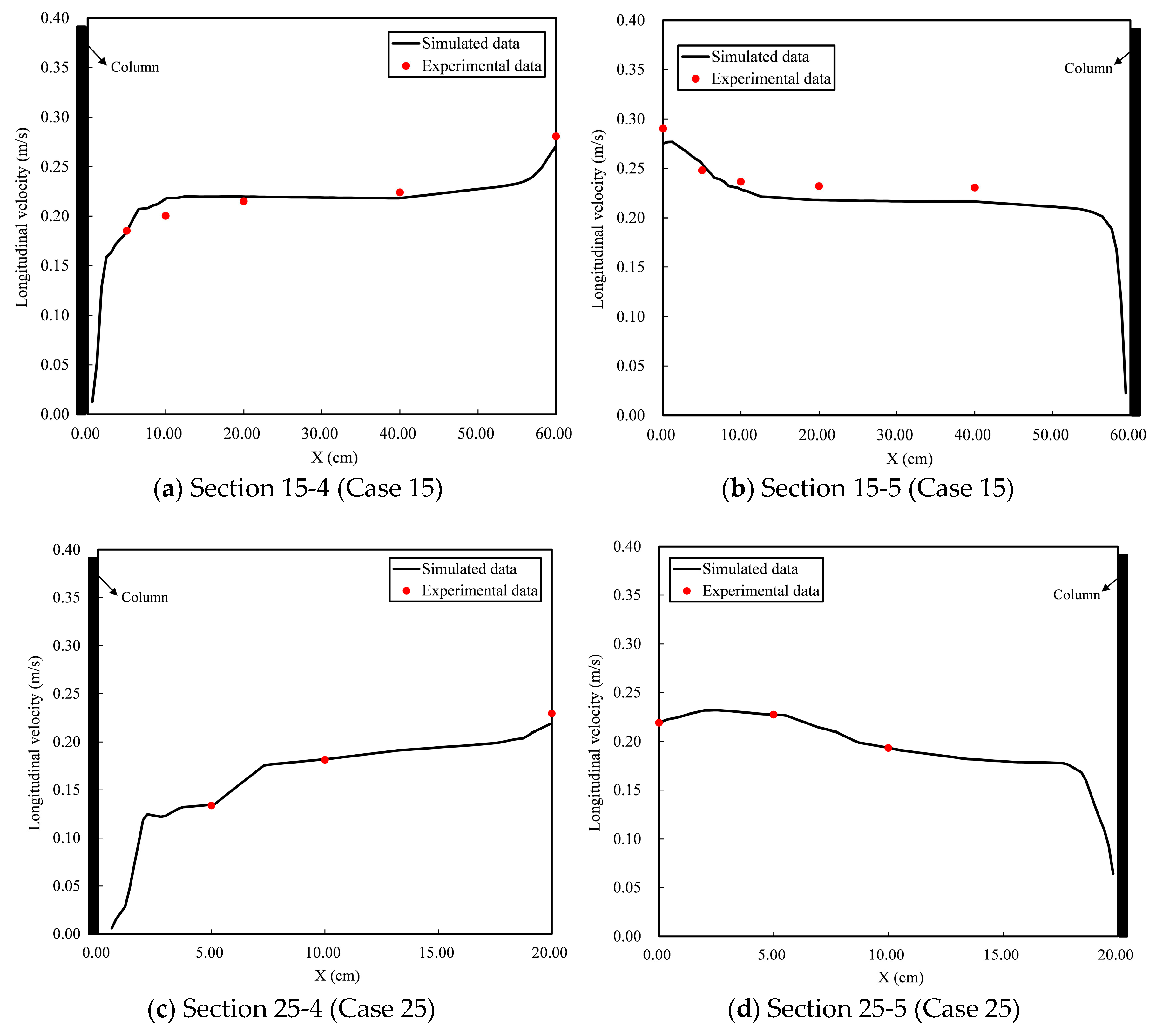
2.7.2. Verification Results of the Flow Field
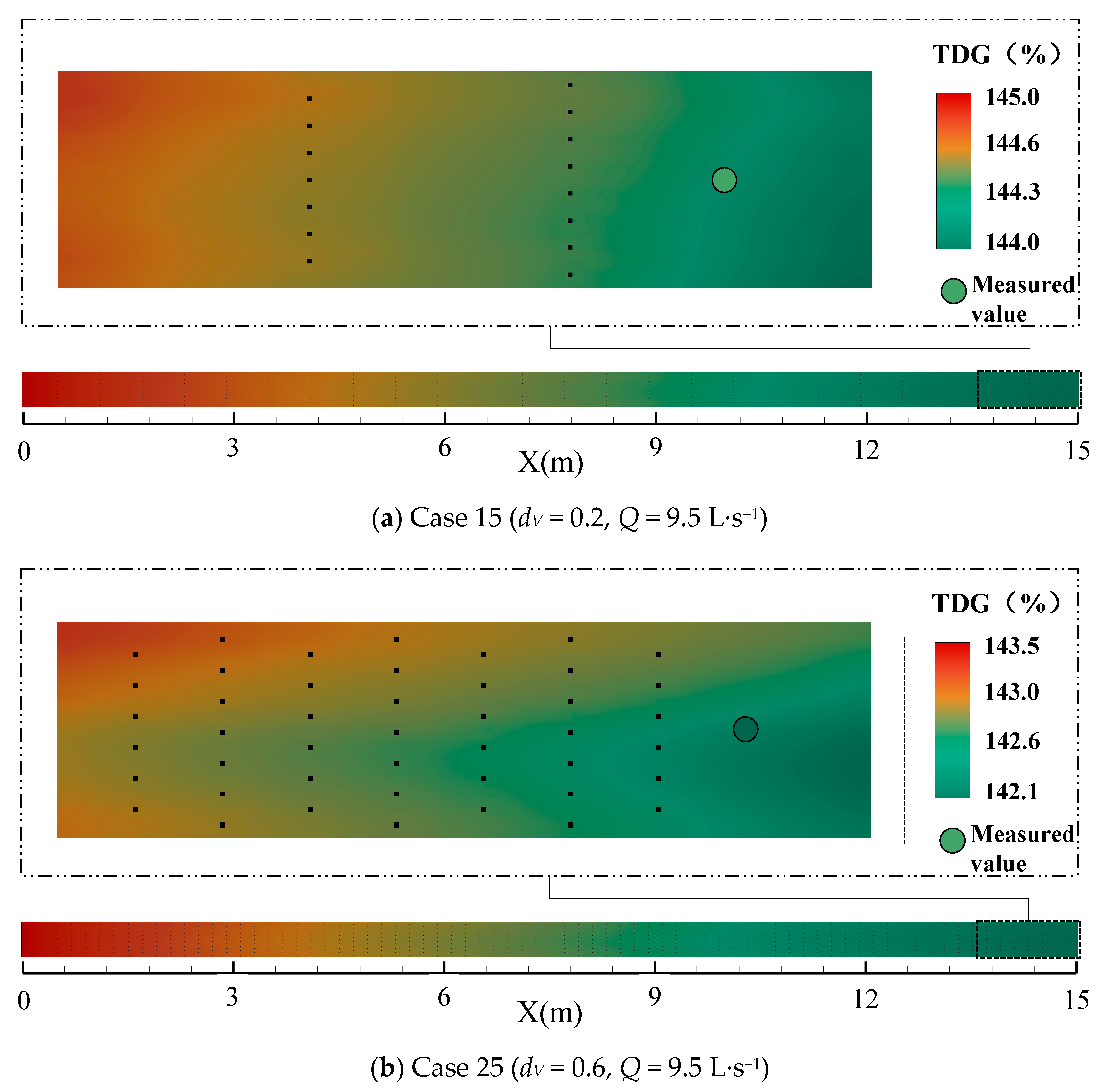
2.7.3. Verification Results of the TDG Concentration Field
3. Results and Discussions
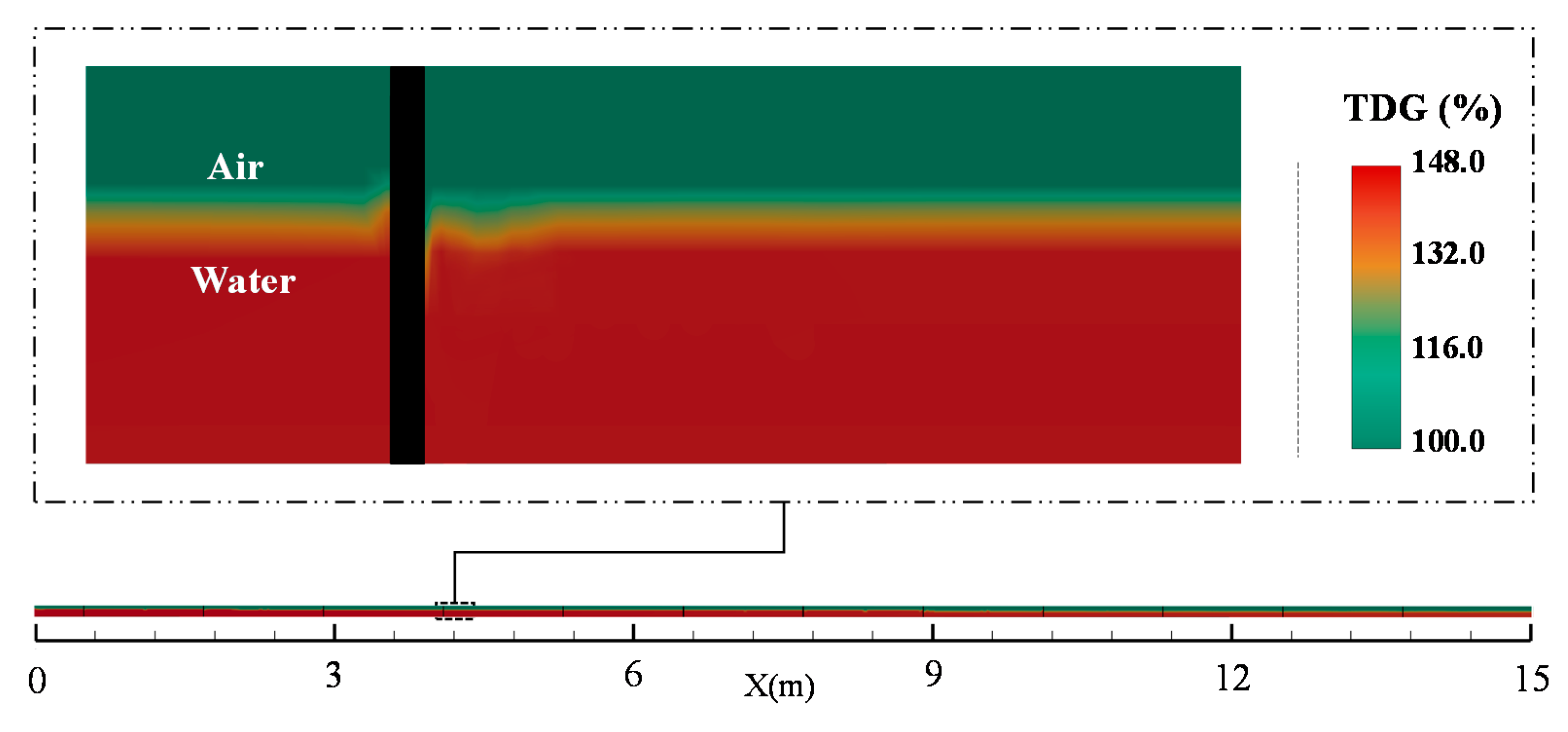
3.1. The Distribution of Supersaturated TDG around a Column
3.2. Vertical Distribution of Supersaturated TDG
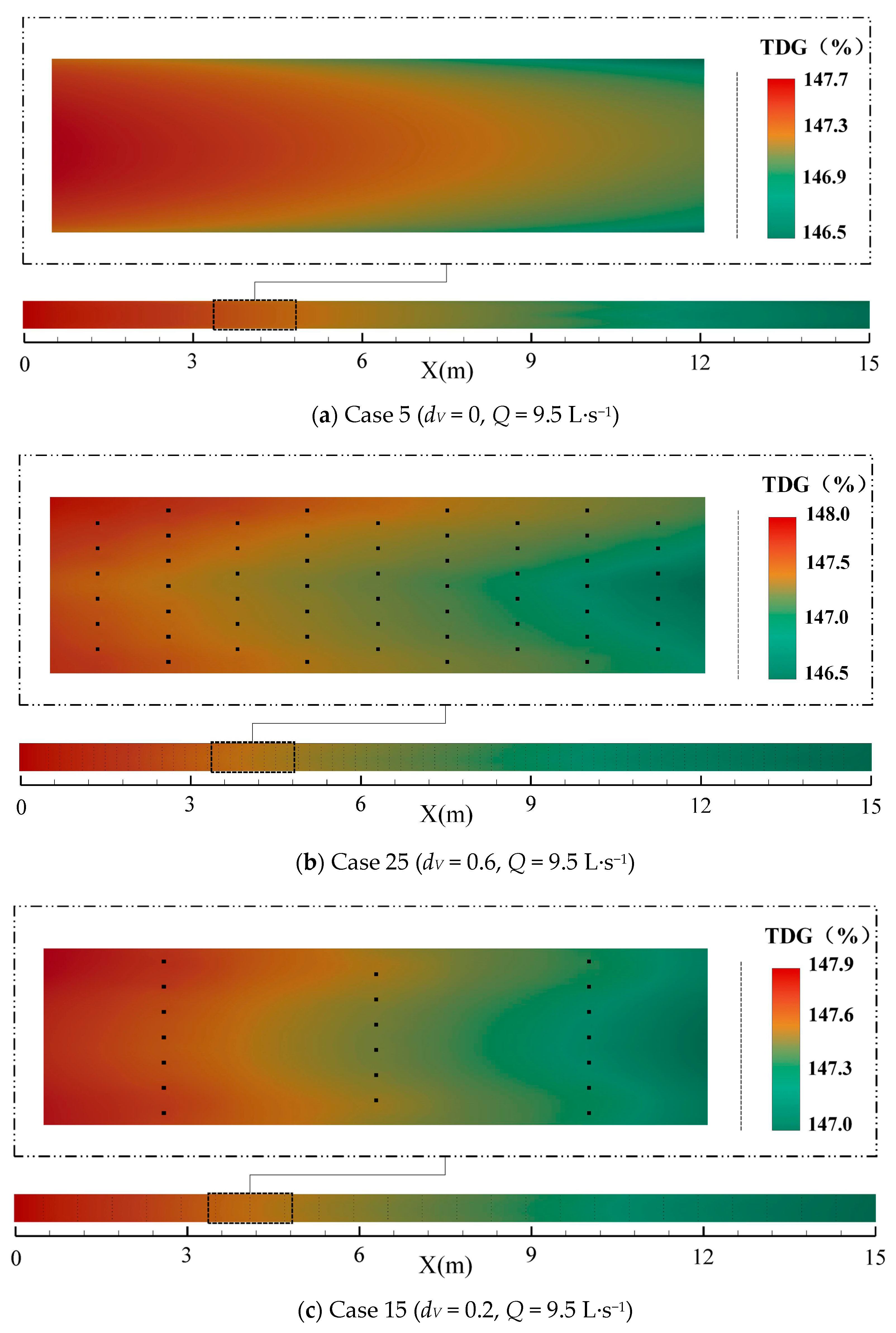
3.3. Planar Distribution of Supersaturated TDG
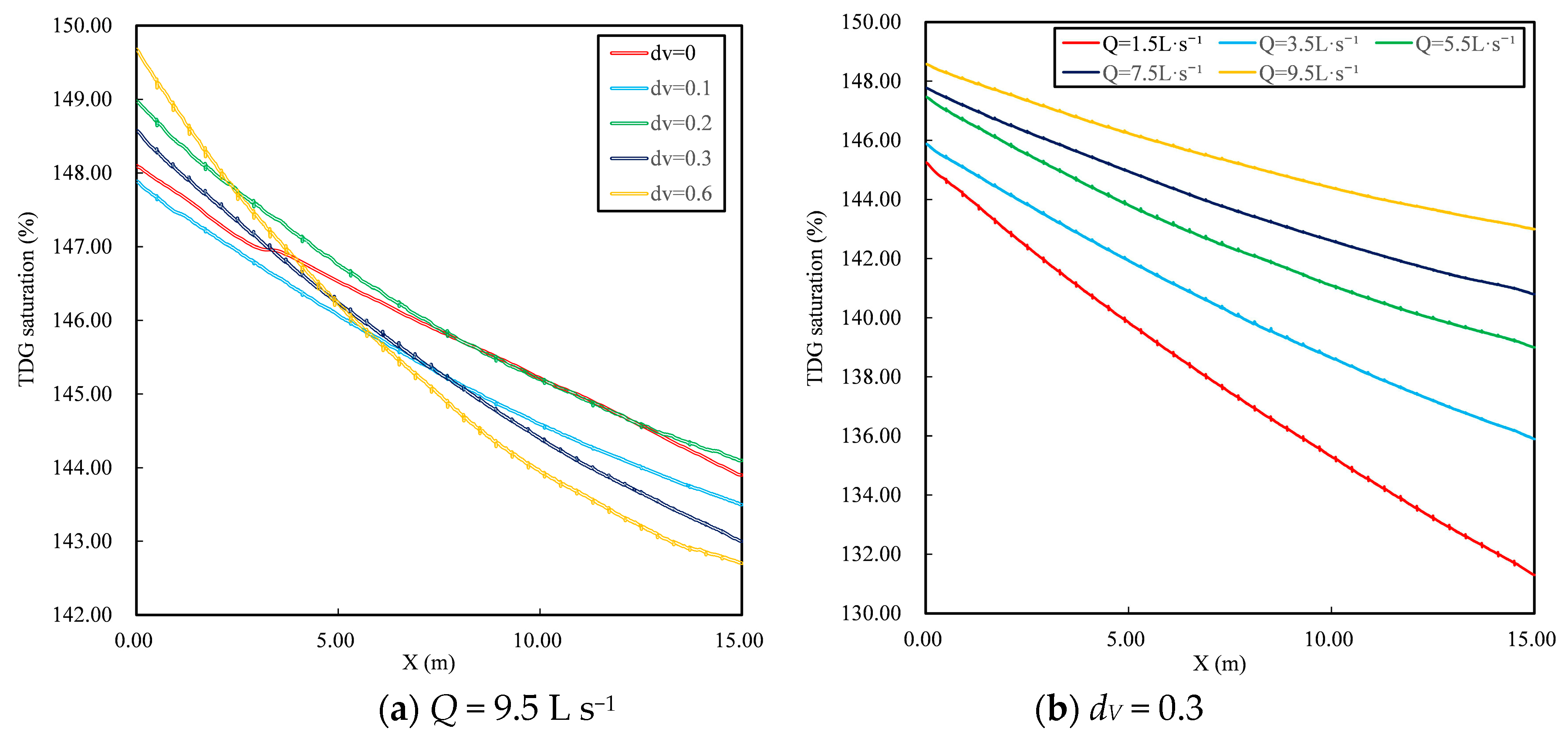
3.3.1. The Longitudinal Distribution of Supersaturated TDG
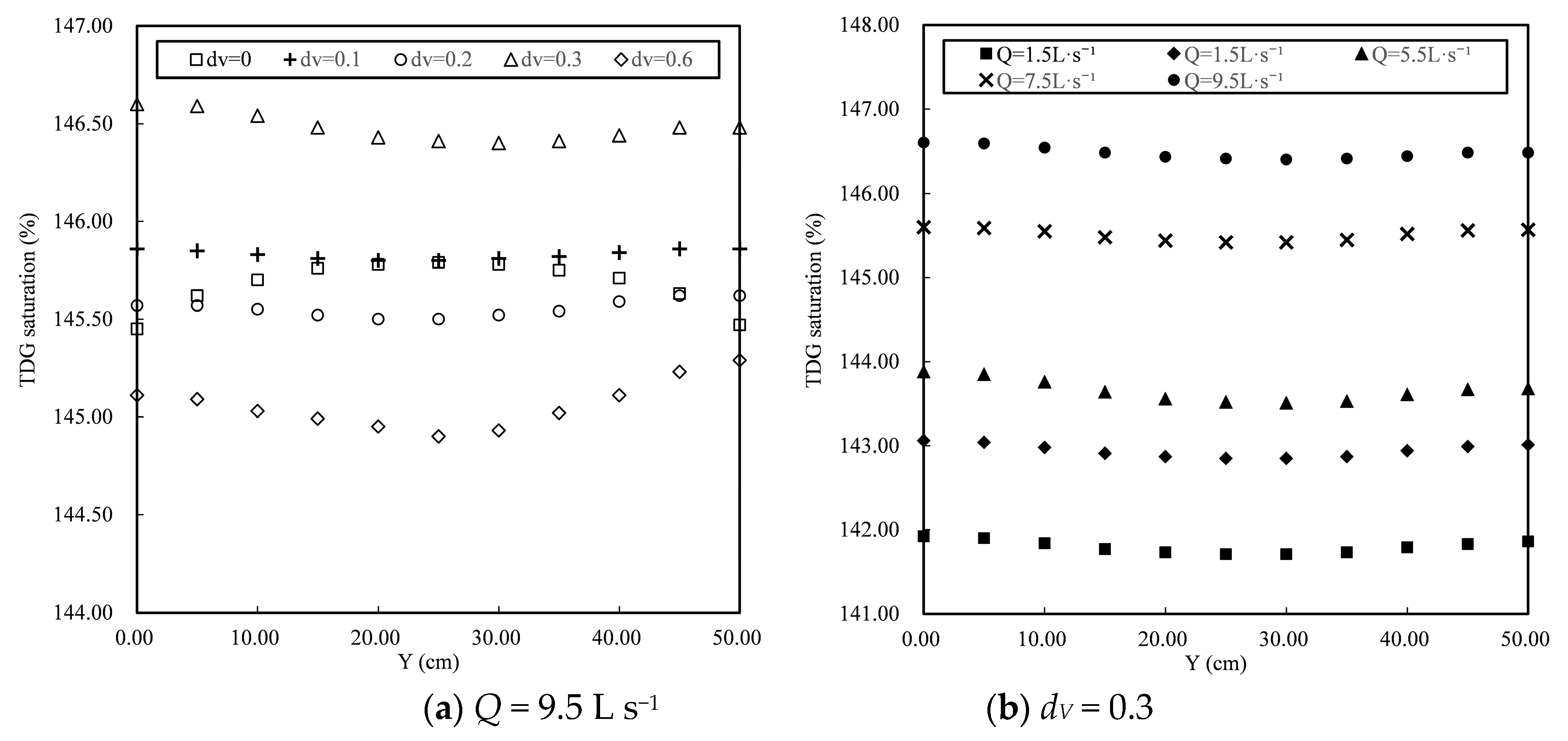
3.3.2. The Lateral Distribution of Supersaturated TDG
4. Conclusions and Prospect
- (1)
- A three-dimensional two-phase flow dynamics model was established to study the complex characteristics of three-dimensional flow under the effects of vegetation, and the model was verified by measurements of flow velocity in vegetation-affected flows in the experiments. The verification results indicated that the numerical simulation results of each section were basically consistent with the measured flow velocity distribution, and the calculation error of flow velocity was within 0.019 m·s−1.
- (2)
- Dividing the dissipation process of supersaturated TDG in vegetation-affected flows into the liquid-gas free surface transfer and the inner dissipation, a three-dimensional supersaturated TDG transportation and dissipation model considering the influence of vegetation was established. In this model, the inner dissipation coefficient was introduced to characterize the inner dissipation of supersaturated TDG. A formula based on the average velocity, the average hydrodynamic radius, Reynolds number and vegetation density was developed to predict the inner dissipation coefficient of supersaturated TDG. The prediction model was verified with two individual cases, and this verification demonstrated that the simulation results of the dissipation process of supersaturated TDG in the flume were very close to the measured values. The transportation and dissipation model of supersaturated TDG established in this paper can be used to predict the transportation and dissipation process of supersaturated TDG dissipation in vegetation-affected flows.
- (3)
- The simulation results show that the water-blocking effect caused by a column formed an obvious area of low TDG saturation behind the column. In the vertical direction, the TDG saturation in the surface water was slightly lower than that in the subsurface water, and TDG saturation in the subsurface water decreased as the water depth increased. At the same time, affected by the water-blocking effect of the vegetation group, TDG saturation presented a distribution characterized by high values in the middle and low values on both sides in the lateral direction. In the longitudinal direction, the TDG saturation decreased gradually with downstream extent but showed serrated distribution characteristics in the region behind the column.
- (4)
- Because the existing measurement and numerical simulation methods have difficulty reflecting the influence of real vegetation on the flow field and the supersaturated TDG transportation and dissipation process, a Plexiglas vertical column with a square cross section was selected to simulate rigid hydrophilic plants. The effects of vegetation’s flexible characteristics and the presence of leaves on the transportation and dissipation processes of supersaturated TDG in flowing water remain to be studied. Limited by laboratory conditions, only small-scale mechanism experiments have been carried out. The parameters used in the three-dimensional TDG transportation and dissipation model were also calibrated by the experimental results. The applicability of this model for simulating the transportation and dissipation process of supersaturated TDG under vegetation-affected flows in large-scale flows remains to be further studied.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wydoski, R.S.; Wick, E.J. Flooding and aquatic ecosystems. In Inland Flood Hazards: Human, Riparian, and Aquatic Communities; Wohl, E.E., Ed.; Cambridge University Press: New York, NY, USA, 2011; pp. 238–268. [Google Scholar]
- Reolid, M.; Rodríguez-Tovar, F.J.; Nagy, J. Ecological replacement of Valanginian agglutinated foraminifera during a maximum flooding event in the Boreal realm (Spitsbergen). Cretac. Res. 2012, 33, 196–204. [Google Scholar] [CrossRef]
- Heydel, F.; Engels, J.G.; Feigs, J.T.; Vásquez, E.; Rudolph, B.; Rohwer, J.; Jensen, K. Adaptation to tidal flooding and rapid genetic divergence between a narrow endemic grass species and its widespread congener lead to an early stage of ecological speciation. Perspect. Plant Ecol. 2017, 27, 57–67. [Google Scholar] [CrossRef]
- Bendix, J.; Cowell, C.M. Fire, floods and woody debris: Interactions between biotic and geomorphic processes. Geomorphology 2010, 116, 297–304. [Google Scholar] [CrossRef]
- Chaleeraktrakoon, C.; Chinsomboon, Y. Dynamic rule curves for flood control of a multipurpose dam. J. Hydro-Environ. Res. 2015, 9, 133–144. [Google Scholar] [CrossRef]
- Talukdar, S.; Pal, S. Impact of dam on inundation regime of flood plain wetland of punarbhaba river basin of barind tract of Indo-Bangladesh. Int. Soil Water Conserv. Res. 2017, 5, 109–121. [Google Scholar] [CrossRef]
- Tao, J.P.; Yang, Z.; Cai, Y.P.; Wang, X.; Chang, J.B. Spatiotemporal response of pelagic fish aggregations in their spawning grounds of middle Yangtze to the flood process optimized by the Three Gorges Reservoir operation. Ecol. Eng. 2017, 103, 86–94. [Google Scholar] [CrossRef]
- Quirino, B.A.; Carniatto, N.; Guglielmetti, R.; Fugi, R. Changes in diet and niche breadth of a small fish species in response to the flood pulse in a Neotropical floodplain lake. Limnologica 2017, 62, 126–131. [Google Scholar] [CrossRef]
- Lemke, M.J.; Hagy, H.M.; Dungey, K.; Casper, A.F.; Lemke, A.M.; VanMiddlesworth, T.D.; Kent, A. Echoes of a flood pulse: Short-term effects of record flooding of the Illinois River on floodplain lakes under ecological restoration. Hydrobiologia 2017, 804, 151–175. [Google Scholar] [CrossRef]
- Bolland, J.D.; Nunn, A.D.; Lucas, M.C.; Cowx, I.G. The habitat use of young-of-the-year fishes during and after floods of varying timing and magnitude in a constrained lowland river. Ecol. Eng. 2015, 75, 434–440. [Google Scholar] [CrossRef]
- Li, R.; Li, J.; Li, K.F.; Deng, Y.; Feng, J.J. Prediction for supersaturated total dissolved gas in high-dam hydropower projects. Sci. China Ser. E 2009, 52, 3661–3667. [Google Scholar] [CrossRef]
- Feng, J.J.; Li, R.; Ma, Q.; Wang, L.L. Experimental and field study on dissipation coefficient of supersaturated total dissolved gas. J. Cent. South Univ. 2014, 21, 1995–2003. [Google Scholar] [CrossRef]
- Kamal, R.; Zhu, D.Z.; Mcarthur, M.; Leake, A. Field study on the dissipation of supersaturated total dissolved gases in a cascade reservoir system. In Proceedings of the World Environmental and Water Resources Congress 2016, West Palm Beach, FL, USA, 22–26 May 2016; pp. 452–460. [Google Scholar]
- Weitkamp, D.E.; Sullivan, R.D.; Swant, D.; DosSantos, J. Gas Bubble Disease in Resident Fish of the Lower Clark Fork River. Trans. Am. Fish. Soc. 2003, 132, 865–876. [Google Scholar] [CrossRef]
- Wang, Y.M.; Liang, R.F.; Tuo, Y.C.; Li, K.F.; Hodegs, B.R. Tolerance and Avoidance Behavior towards Gas Supersaturation in Rock Carp Procypris rabaudi with a History of Previous Exposure. N. Am. J. Aquac. 2015, 77, 478–484. [Google Scholar] [CrossRef]
- Li, R.; Hodegs, B.R.; Feng, J.J.; Yong, X.D. Comparison of supersaturated total dissolved gas dissipation with dissolved oxygen dissipation and reaeration. J. Environ. Eng. 2013, 139, 385–390. [Google Scholar] [CrossRef]
- Ou, Y.M.; Li, R.; Hodges, B.R.; Feng, J.J.; Pu, C.X. Impact of temperature on the dissipation process of supersaturated total dissolved gas in flowing water. Fresenius Environ. Bull. 2016, 25, 1927–1934. [Google Scholar]
- Huang, J.P.; Li, R.; Feng, J.J.; Xu, W.L.; Wang, L.L. Relationship investigation between the dissipation process of supersaturated total dissolved gas and wind effect. Ecol. Eng. 2016, 95, 430–437. [Google Scholar] [CrossRef]
- Ou, Y.M.; Li, R.; Tuo, Y.C.; Niu, J.L.; Feng, J.J.; Pu, C.X. The promotion effect of aeration on the dissipation of supersaturated total dissolved gas. Ecol. Eng. 2016, 95, 245–251. [Google Scholar] [CrossRef]
- Shen, X.; Li, R.; Huang, J.P.; Feng, J.J.; Hodges, B.R.; Li, K.F.; Xu, W.L. Shelter construction for fish at the confluence of a river to avoid the effects of total dissolved gas supersaturation. Ecol. Eng. 2016, 97, 642–648. [Google Scholar] [CrossRef]
- Witt, A.; Stewart, K.; Hadjerioua, B. Predicting Total Dissolved Gas Travel Time in Hydropower Reservoirs. J. Environ. Eng. 2017, 143, 06017011. [Google Scholar] [CrossRef]
- Yuan, Y.Q.; Feng, J.J.; Li, R.; Huang, Y.H.; Huang, J.P.; Wang, Z.H. Modelling the promotion effect of vegetation on the dissipation of supersaturated total dissolved gas. Ecol. Model. 2018, 386, 89–97. [Google Scholar] [CrossRef]
- Pickett, J.; Rueda, H.; Herold, M. Total Maximum Daily Load for Total Dissolved Gas in the Mid-Columbia River and Lake Roosevelt; U.S. Environmental Protection Agency and Washington State Department of Ecology: Washington, DC, USA, 2004; pp. 1–79.
- Perkins, W.A.; Richmond, M.C. MASS2, Modular Aquatic Simulation System in Two Dimensions: Theory and Numerical Methods; Pacific Northwest National Laboratory Report; Pacific Northwest National Laboratory: Washington, DC, USA, 2004; pp. 1–73.
- Johnson, E.L.; Clabough, T.S.; Peery, C.A.; Bennett, D.H.; Bjornn, T.C.; Caudill, C.C.; Richmond, M.C. Estimating adult Chinook salmon exposure to dissolved gas supersaturation downstream of hydroelectric dams using telemetry and hydrodynamic models. River Res. Appl. 2010, 23, 963–978. [Google Scholar] [CrossRef]
- Ma, Q.; Li, R.; Zhang, Q.; Hodges, B.R.; Feng, J.J.; Yang, H.X. Two-Phase Flow Simulation of Supersaturated Total Dissolved Gas in the Plunge Pool of a High Dam. Environ. Prog. Sustain. 2016, 35, 1139–1148. [Google Scholar] [CrossRef]
- Witt, A.; Magee, T.; Stewart, K.; Hadjerioua, B. Development and implementation of an optimization model for hydropower and total dissolved gas in the Mid-Columbia River System. J. Water Res. Plan. 2017, 143, 04017063. [Google Scholar] [CrossRef]
- Feng, J.J.; Li, R.; Liang, R.F.; Shen, X. Eco-environmentally friendly operational regulation: An effective strategy to diminish the TDG supersaturation of reservoirs. Hydrol. Earth Syst. Sci. 2014, 10, 14355–14390. [Google Scholar] [CrossRef]
- Aberle, J.; Järvelä, J. Hydrodynamics of Vegetated Channels, In Rivers-Physical, Fluvial and Environmental Processess; Springer International Publishing Switzerland: Bern, Switzerland, 2015; pp. 255–277. [Google Scholar]
- Nepf, H.M. Flow and Transport in Regions with Aquatic Vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Najafabadi, E.F.; Gallichand, J. Effects of accelerating and decelerating flows in a channel with vegetated banks and gravel bed. Int. J. Sediment Res. 2012, 27, 188–200. [Google Scholar] [CrossRef]
- Serio, F.D.; Meftah, M.B.; Mossa, M.; Termini, D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2017, 120, 98–113. [Google Scholar] [CrossRef]
- Hamidifar, H.; Omid, M.H.; Keshavarzi, A. Kinetic energy and momentum correction coefficients in straight compound channels with vegetated floodplain. J. Hydrol. 2016, 537, 10–17. [Google Scholar] [CrossRef]
- Dijk, W.M.V.; Teske, R.; Lageweg, W.I.V.D.; Kleinhans, M.G. Effects of vegetation distribution on experimental river channel dynamics. Water Resour. Res. 2013, 49, 7558–7574. [Google Scholar] [CrossRef]
- Yang, J.Q.; Kerger, F.; Neph, H.M. Estimation of the bed shear stress in vegetated and bare channels with smooth beds. Water Resour. Res. 2015, 51, 3647–3663. [Google Scholar] [CrossRef]
- Richet, J.B.; Ouvry, J.F.; Saunier, M. The role of vegetative barriers such as fascines and dense shrub hedges in catchment management to reduce runoff and erosion effects: Experimental evidence of efficiency, and conditions of use. Ecol. Eng. 2016, 103, 455–469. [Google Scholar] [CrossRef]
- Liu, C.; Nepf, H. Sediment deposition within and around a finite patch of model vegetation over a range of channel velocity. Water Resour. Res. 2016, 52, 600–612. [Google Scholar] [CrossRef]
- Hu, Z.H.; Lei, J.R.; Liu, C.; Nepf, H. Wake structure and sediment deposition behind models of submerged vegetation with and without flexible leaves. Adv. Water Resour. 2018, 118, 28–38. [Google Scholar] [CrossRef]
- Lu, J.; Dai, H.C. Three dimensional numerical modeling of flows and scalar transport in a vegetated channel. J. Hydro-Environ. Res. 2017, 16, 27–33. [Google Scholar] [CrossRef]
- Lu, J.; Dai, H.C. Numerical modeling on pollution transport in flexible vegetation. Appl. Math. Model. 2018, 64, 93–105. [Google Scholar] [CrossRef]
- Huang, Y.H. Impact of Vegetation on the Dissipation Process of Supersaturated Total Dissolved Gas. Master’s Thesis, Sichuan University, Sichuan, China, 2017. (In Chinese). [Google Scholar]
- Huai, W.X.; Hu, Y.; Zeng, Y.H.; Han, J. Velocity distribution for open channel flows with suspended vegetation. Adv. Water Resour. 2012, 49, 56–61. [Google Scholar] [CrossRef]
- Yang, Z.H.; Bai, F.P.; Huai, W.X.; An, R.D.; Wang, H.Y. Modelling open-channel flow with rigid vegetation based on two-dimensional shallow water equations using the lattice Boltzmann method. Ecol. Eng. 2017, 106, 75–81. [Google Scholar] [CrossRef]
- Beudin, A.; Kalra, T.S.; Ganju, N.K.; Wamer, J.C. Development of a coupled wave-flow-vegetation interaction model. Comput. Geosci. 2016, 100, 76–86. [Google Scholar] [CrossRef]
- Politano, M.S.; Carrica, P.M.; Turan, C.; Weber, L. A multidimensional two-phase flow model for the total dissolved gas downstream of spillways. J. Hydraul. Res. 2007, 45, 165–177. [Google Scholar] [CrossRef]
- Politano, M.S.; Carrica, P.; Weber, L. A multiphase model for the hydrodynamics and total dissolved gas in tailraces. Int. J. Multiph. Flow 2009, 35, 1036–1050. [Google Scholar] [CrossRef]
- Fu, X.L.; Li, D.; Zhang, X.F. Simulations of the three-dimensional total dissolved gas saturation downstream of spillways under unsteady conditions. J. Hydrodyn. 2010, 22, 598–604. [Google Scholar] [CrossRef]
- Geldert, D.A.; Gulliver, J.S.; Wilhelms, S.C. Modeling dissolved gas supersaturation below spillway plunge pools. J. Hydraul. Eng. 1998, 124, 513–521. [Google Scholar] [CrossRef]

| Case No. | Flow (L·s−1) | The Vegetation Density | Lateral Space Ly (10−2 m) | Longitudinal Space Lx (10−2 m) | The Flow Depth h (10−2 m) | TDG Saturation of Entry Section (%) |
|---|---|---|---|---|---|---|
| 1 | 1.5 | 0 | / | / | 2.2 | 144.5 |
| 2 | 3.5 | 0 | / | / | 3.8 | 144.4 |
| 3 | 5.5 | 0 | / | / | 4.7 | 145.6 |
| 4 | 7.5 | 0 | / | / | 5.6 | 147.1 |
| 5 | 9.5 | 0 | / | / | 6.6 | 148.1 |
| 6 | 1.5 | 0.1 | 12.5 | 60 | 2.5 | 144.2 |
| 7 | 3.5 | 0.1 | 12.5 | 60 | 4.4 | 144.6 |
| 8 | 5.5 | 0.1 | 12.5 | 60 | 5.3 | 144.5 |
| 9 | 7.5 | 0.1 | 12.5 | 60 | 6.4 | 146.6 |
| 10 | 9.5 | 0.1 | 12.5 | 60 | 7.5 | 147.9 |
| 11 | 1.5 | 0.2 | 7.1 | 60 | 2.8 | 144.9 |
| 12 | 3.5 | 0.2 | 7.1 | 60 | 4.6 | 147.4 |
| 13 | 5.5 | 0.2 | 7.1 | 60 | 5.8 | 148.5 |
| 14 | 7.5 | 0.2 | 7.1 | 60 | 7.2 | 148.6 |
| 15 | 9.5 | 0.2 | 7.1 | 60 | 8.6 | 149.0 |
| 16 | 1.5 | 0.3 | 12.5 | 20 | 3.1 | 145.3 |
| 17 | 3.5 | 0.3 | 12.5 | 20 | 4.7 | 145.9 |
| 18 | 5.5 | 0.3 | 12.5 | 20 | 6.6 | 147.5 |
| 19 | 7.5 | 0.3 | 12.5 | 20 | 7.8 | 147.8 |
| 20 | 9.5 | 0.3 | 12.5 | 20 | 9.0 | 148.6 |
| 21 | 1.5 | 0.6 | 7.1 | 20 | 3.2 | 145.7 |
| 22 | 3.5 | 0.6 | 7.1 | 20 | 5.9 | 147.5 |
| 23 | 5.5 | 0.6 | 7.1 | 20 | 7.6 | 148.5 |
| 24 | 7.5 | 0.6 | 7.1 | 20 | 8.4 | 149.3 |
| 25 | 9.5 | 0.6 | 7.1 | 20 | 9.6 | 149.7 |
| Case No. | Flow Rate (L·s−1) | Vegetation Density | TDG Saturation Upstream (%) | TDG Saturation Downstream (%) | kin (s−1) |
|---|---|---|---|---|---|
| 1 | 1.5 | 0 | 144.5 | 137.2 | 4.5 × 10−5 |
| 2 | 3.5 | 0 | 144.4 | 138.9 | 5.5 × 10−5 |
| 3 | 5.5 | 0 | 145.6 | 140.2 | 6.0 × 10−5 |
| 4 | 7.5 | 0 | 147.1 | 142.0 | 6.5 × 10−5 |
| 5 | 9.5 | 0 | 148.1 | 143.9 | 7.8 × 10−5 |
| 6 | 1.5 | 0.1 | 144.2 | 135.2 | 4.3 × 10−5 |
| 7 | 3.5 | 0.1 | 144.6 | 137.8 | 5.2 × 10−5 |
| 8 | 5.5 | 0.1 | 144.5 | 138.3 | 5.8 × 10−5 |
| 9 | 7.5 | 0.1 | 146.6 | 141.1 | 6.3 × 10−5 |
| 10 | 9.5 | 0.1 | 147.9 | 143.5 | 7.5 × 10−5 |
| 11 | 1.5 | 0.2 | 144.9 | 133.5 | 4.0 × 10−5 |
| 12 | 3.5 | 0.2 | 147.4 | 139.2 | 5.0 × 10−5 |
| 13 | 5.5 | 0.2 | 148.5 | 141.5 | 5.5 × 10−5 |
| 14 | 7.5 | 0.2 | 148.6 | 142.6 | 6.0 × 10−5 |
| 15 | 9.5 | 0.2 | 149.0 | 144.1 | 7.2 × 10−5 |
| 16 | 1.5 | 0.3 | 145.3 | 131.3 | 3.7 × 10−5 |
| 17 | 3.5 | 0.3 | 145.9 | 135.9 | 4.7 × 10−5 |
| 18 | 5.5 | 0.3 | 147.5 | 139.0 | 5.2 × 10−5 |
| 19 | 7.5 | 0.3 | 147.8 | 140.8 | 5.8 × 10−5 |
| 20 | 9.5 | 0.3 | 148.6 | 143.0 | 7.0 × 10−5 |
| 21 | 1.5 | 0.6 | 145.7 | 128.2 | 3.0 × 10−5 |
| 22 | 3.5 | 0.6 | 147.5 | 134.2 | 4.1 × 10−5 |
| 23 | 5.5 | 0.6 | 148.5 | 138.0 | 4.5 × 10−5 |
| 24 | 7.5 | 0.6 | 149.3 | 140.2 | 5.0 × 10−5 |
| 25 | 9.5 | 0.6 | 149.7 | 142.7 | 6.3 × 10−5 |
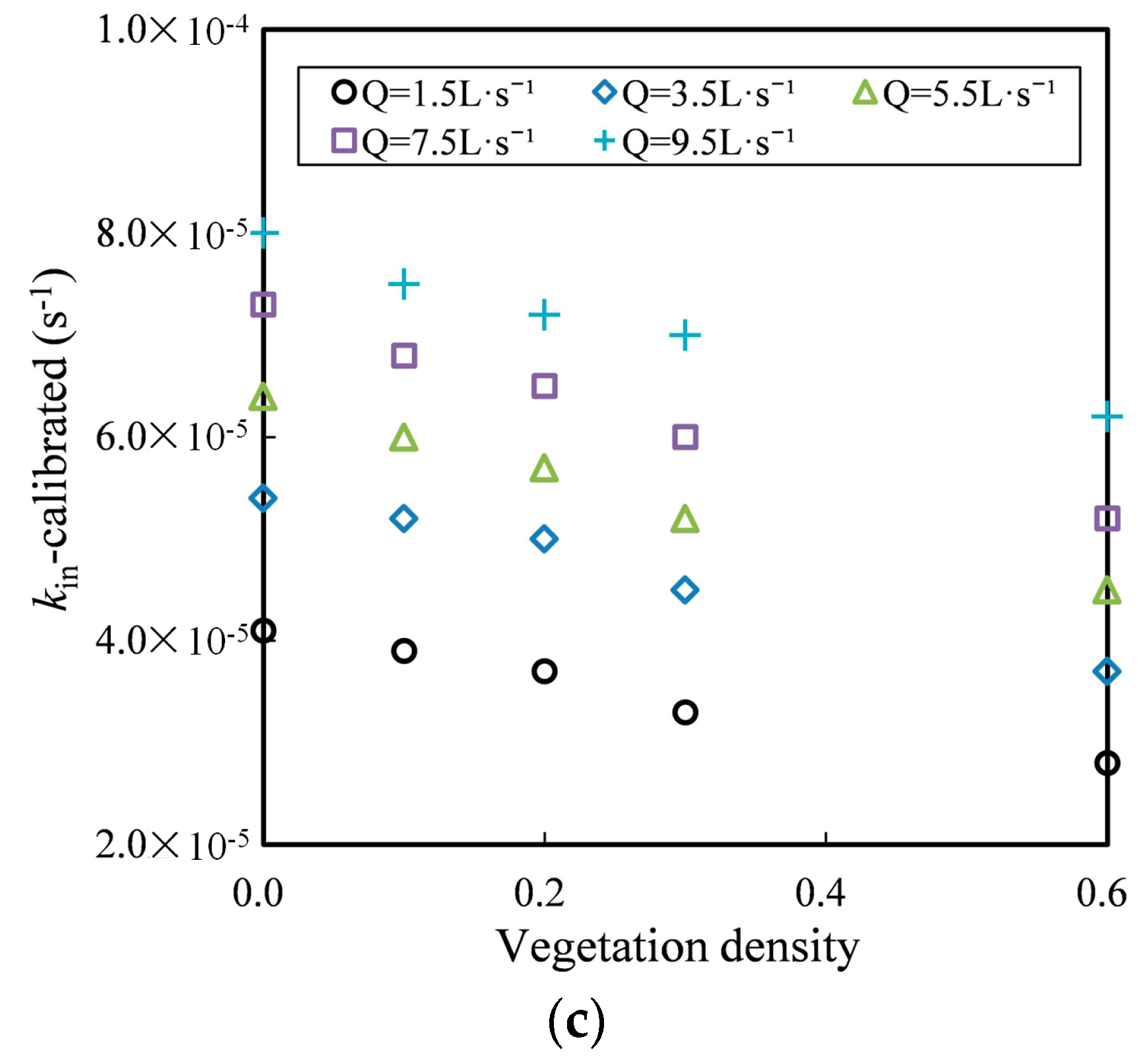
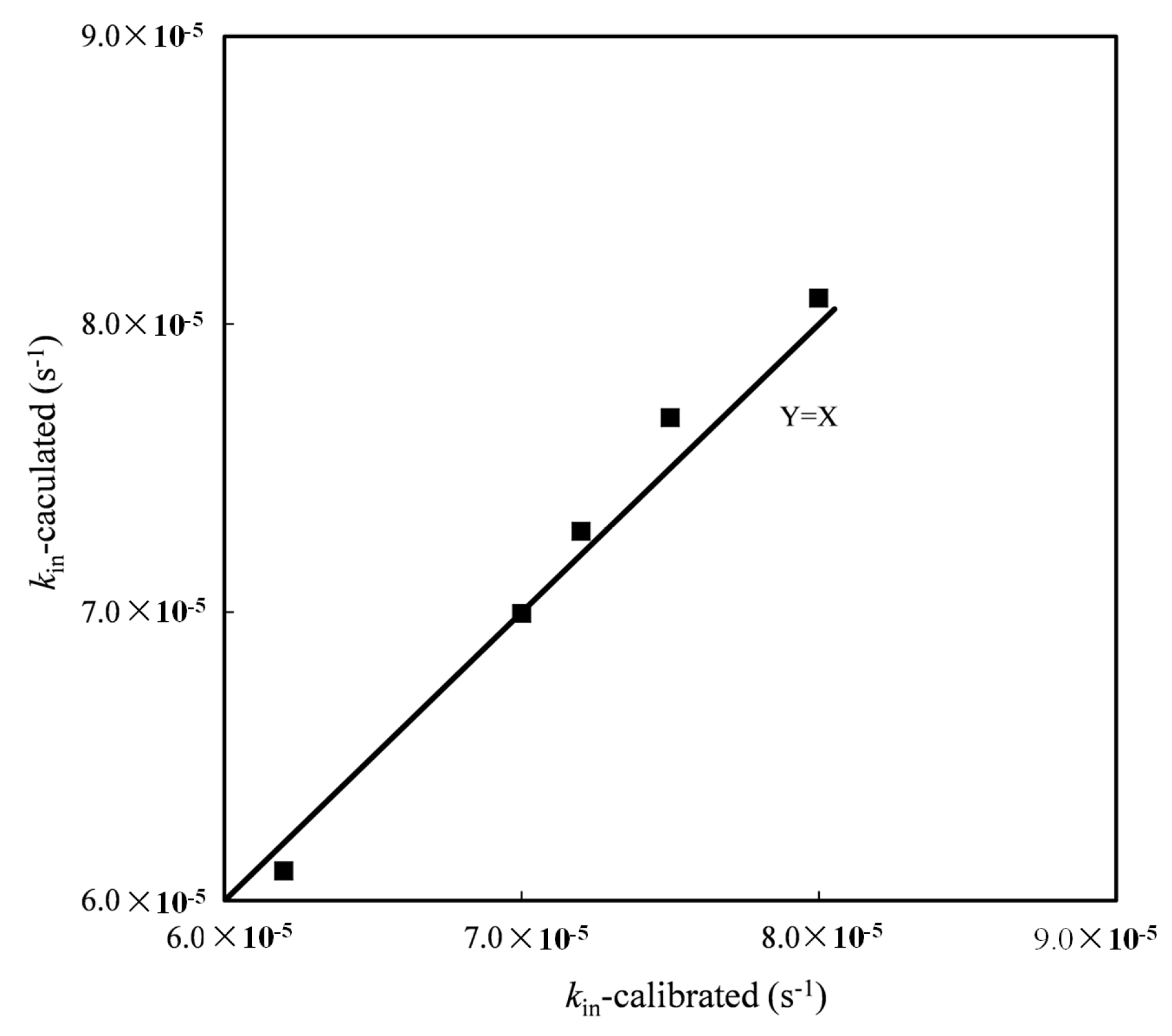
| Case No. | Flow (L·s−1) | Vegetation Density | kin Calculated (s−1) | kin Calibrated (s−1) |
|---|---|---|---|---|
| 5 | 9.5 | 0 | 8.1 × 10−5 | 8.0 × 10−5 |
| 10 | 9.5 | 0.1 | 7.7 × 10−5 | 7.5 × 10−5 |
| 15 | 95 | 0.2 | 7.3 × 10−5 | 7.2 × 10−5 |
| 20 | 9.5 | 0.3 | 7.0 × 10−5 | 7.0 × 10−5 |
| 25 | 9.5 | 0.6 | 6.1 × 10−5 | 6.2 × 10−5 |
| Case No. | Flow (m3·s−1) | The Water Depth of Inlet Section (10−2 m) | The TDG Saturation of Inlet Section (%) |
|---|---|---|---|
| 15 | 0.0095 | 7.4 | 149.0 |
| 25 | 0.0095 | 8.4 | 149.7 |
| Section No. | Mean Error (m/s) | RSD (%) | STD | RMSE (m/s) |
|---|---|---|---|---|
| Section 15-1 | 0.018 | 7.2 | 0.02 | 0.023 |
| Section 15-2 | 0.019 | 6.5 | 0.02 | 0.009 |
| Section 15-3 | 0.015 | 6.8 | 0.02 | 0.004 |
| Section 15-4 | 0.008 | 3.3 | 0.01 | 0.006 |
| Section 15-5 | 0.013 | 6.4 | 0.02 | 0.008 |
| Section 25-1 | 0.017 | 8.6 | 0.02 | 0.019 |
| Section 25-2 | 0.010 | 4.7 | 0.01 | 0.007 |
| Section 25-3 | 0.012 | 6.8 | 0.01 | 0.004 |
| Section 25-4 | 0.011 | 5.5 | 0.01 | 0.008 |
| Section 25-5 | 0.011 | 6.4 | 0.01 | 0.002 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Huang, Y.; Feng, J.; Li, R.; An, R.; Huang, J. Numerical Model of Supersaturated Total Dissolved Gas Dissipation in a Channel with Vegetation. Water 2018, 10, 1769. https://doi.org/10.3390/w10121769
Yuan Y, Huang Y, Feng J, Li R, An R, Huang J. Numerical Model of Supersaturated Total Dissolved Gas Dissipation in a Channel with Vegetation. Water. 2018; 10(12):1769. https://doi.org/10.3390/w10121769
Chicago/Turabian StyleYuan, Youquan, Yinghan Huang, Jingjie Feng, Ran Li, Ruidong An, and Juping Huang. 2018. "Numerical Model of Supersaturated Total Dissolved Gas Dissipation in a Channel with Vegetation" Water 10, no. 12: 1769. https://doi.org/10.3390/w10121769
APA StyleYuan, Y., Huang, Y., Feng, J., Li, R., An, R., & Huang, J. (2018). Numerical Model of Supersaturated Total Dissolved Gas Dissipation in a Channel with Vegetation. Water, 10(12), 1769. https://doi.org/10.3390/w10121769






