Case Study on Application of the Step with Non-Uniform Heights at the Bottom Using a Numerical and Experimental Model
Abstract
1. Introduction
2. Physical Model and Problem Description
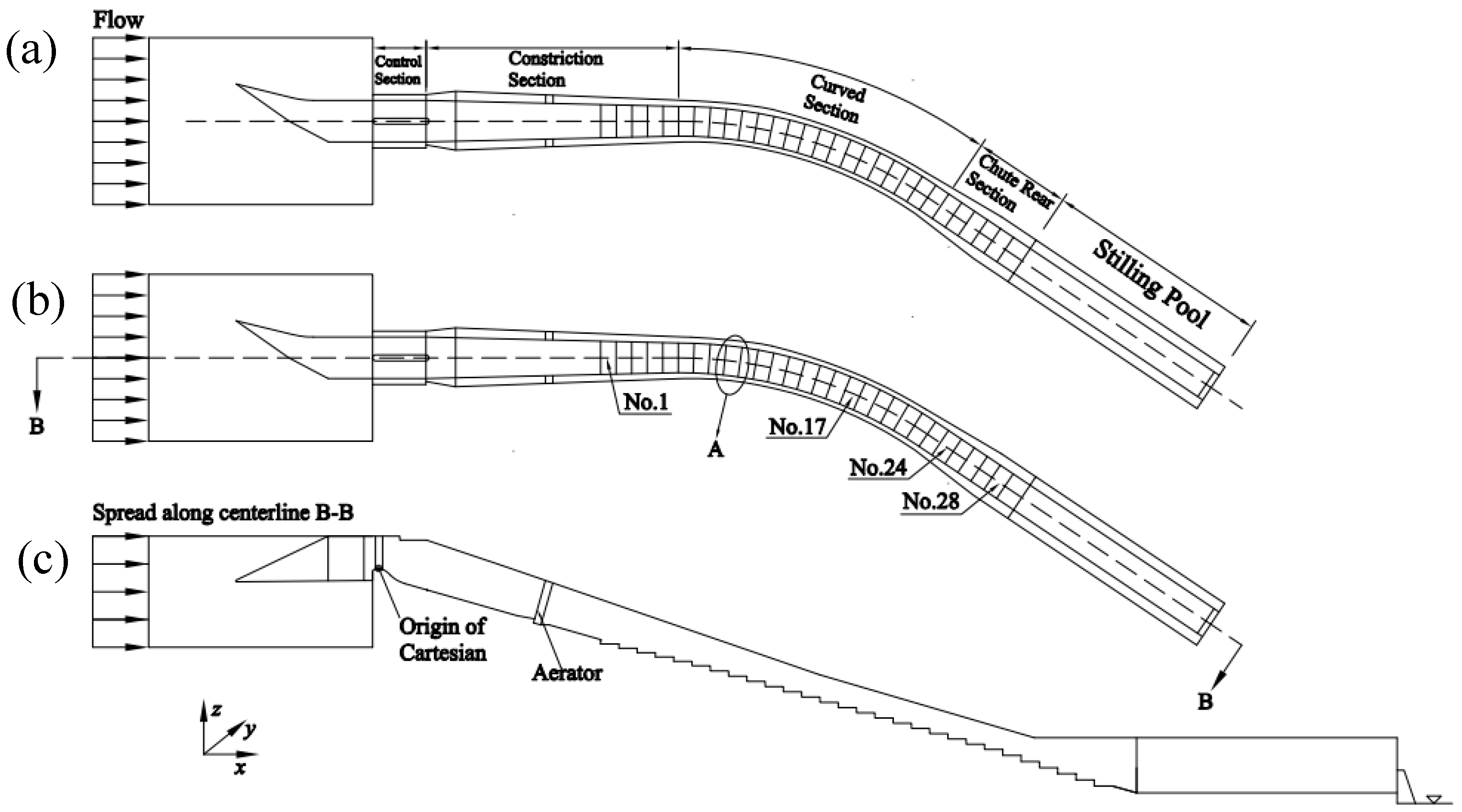
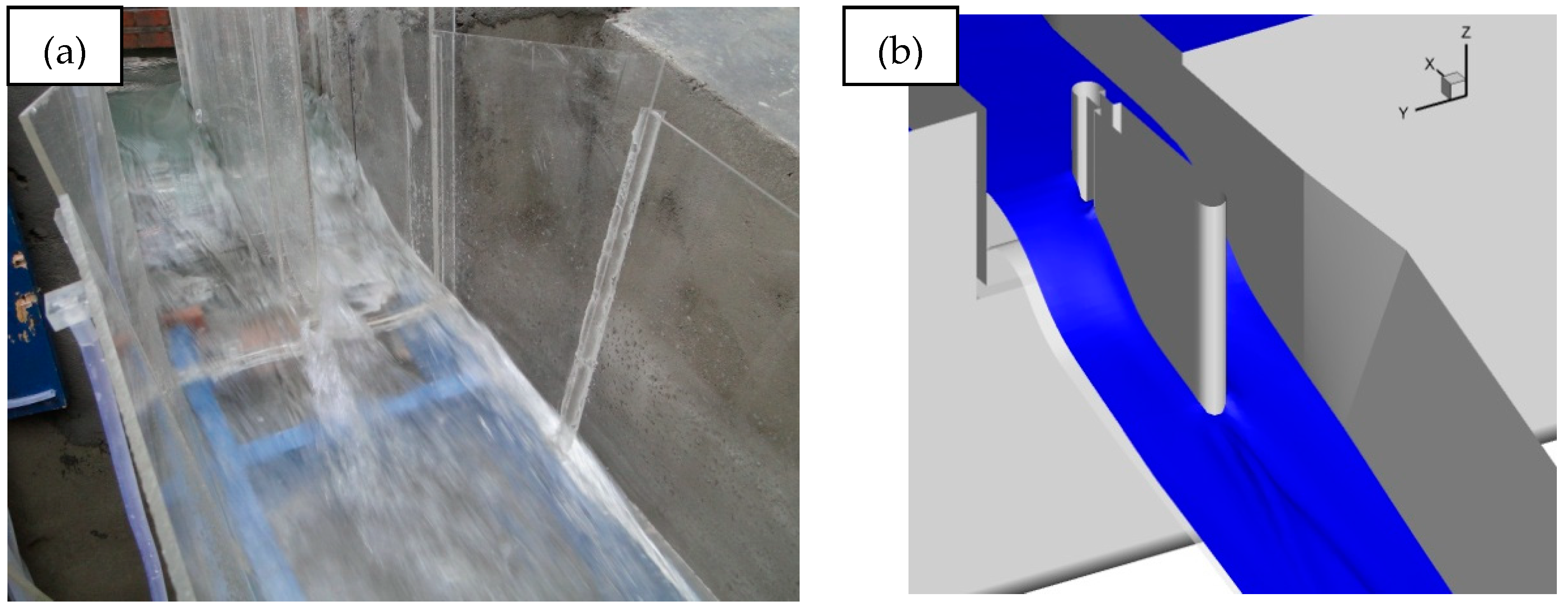
2.1. Physical Model
2.2. Problem Description
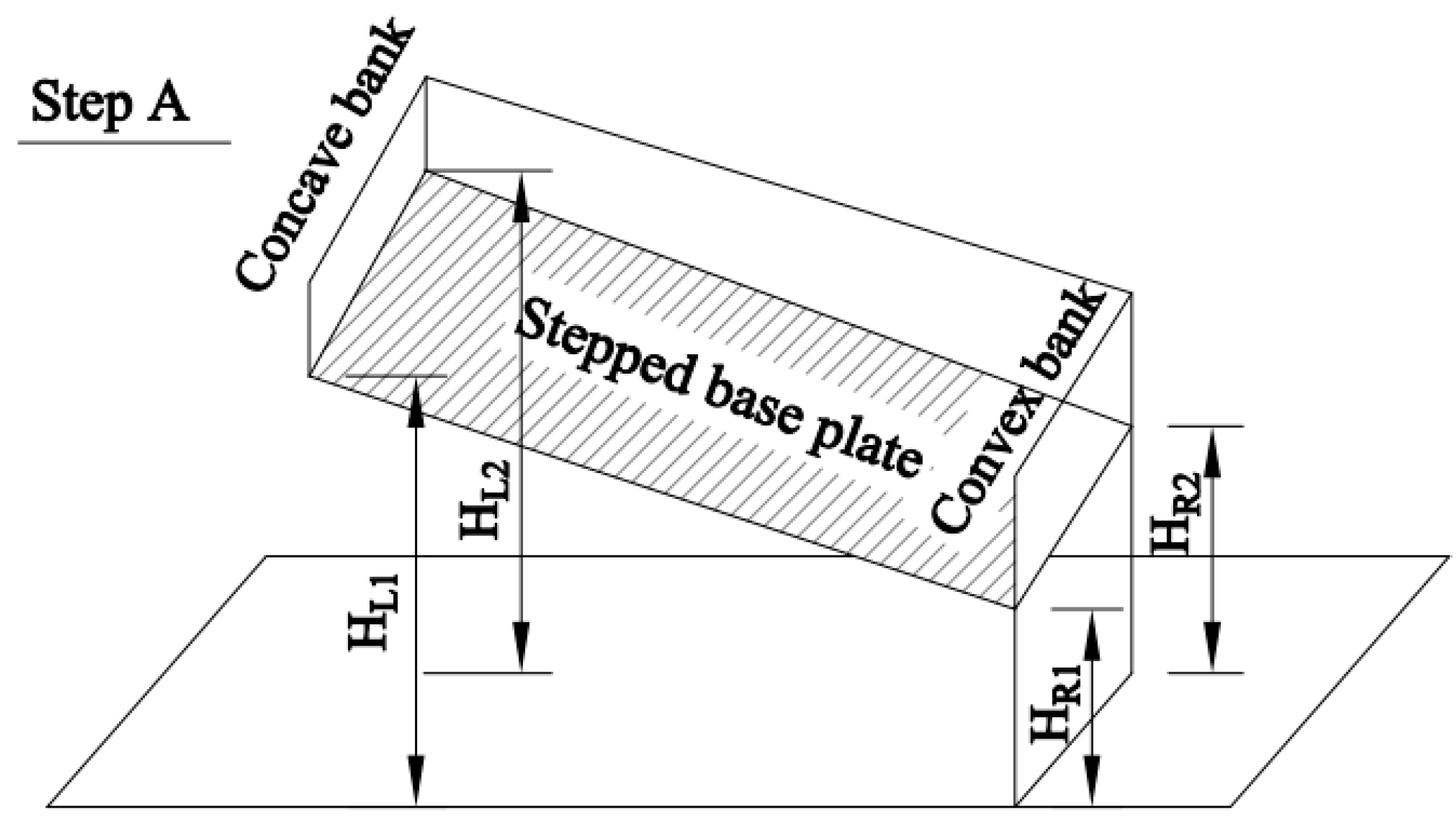
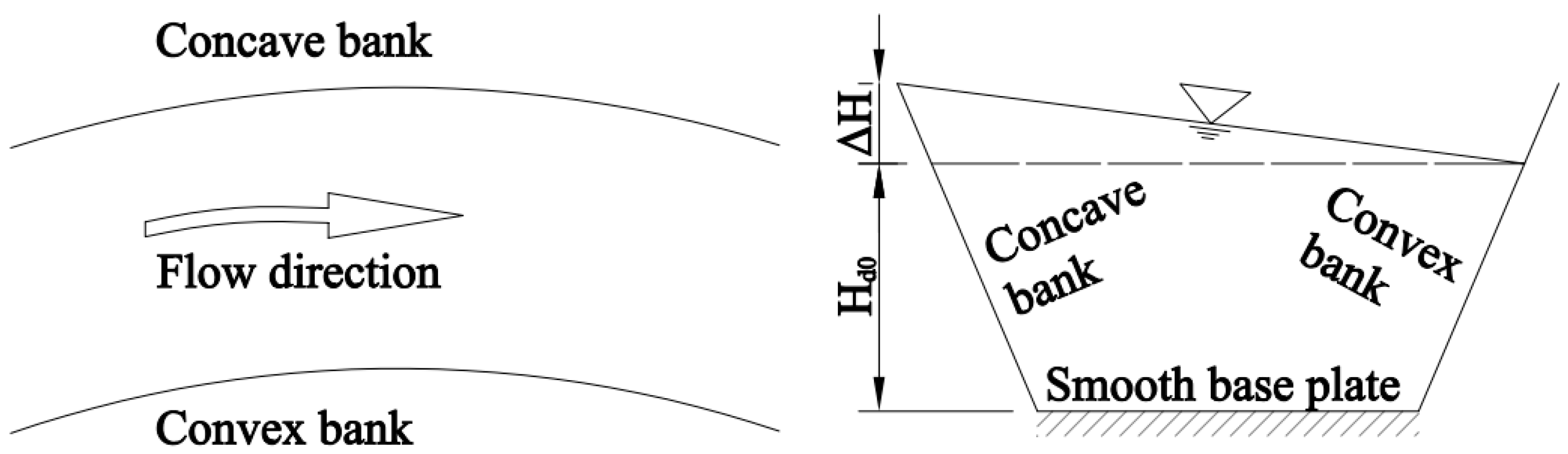
2.3. Effects of the Non-Uniform Steps
3. Numerical Methodology and Model Validation
3.1. Numerical Methodology
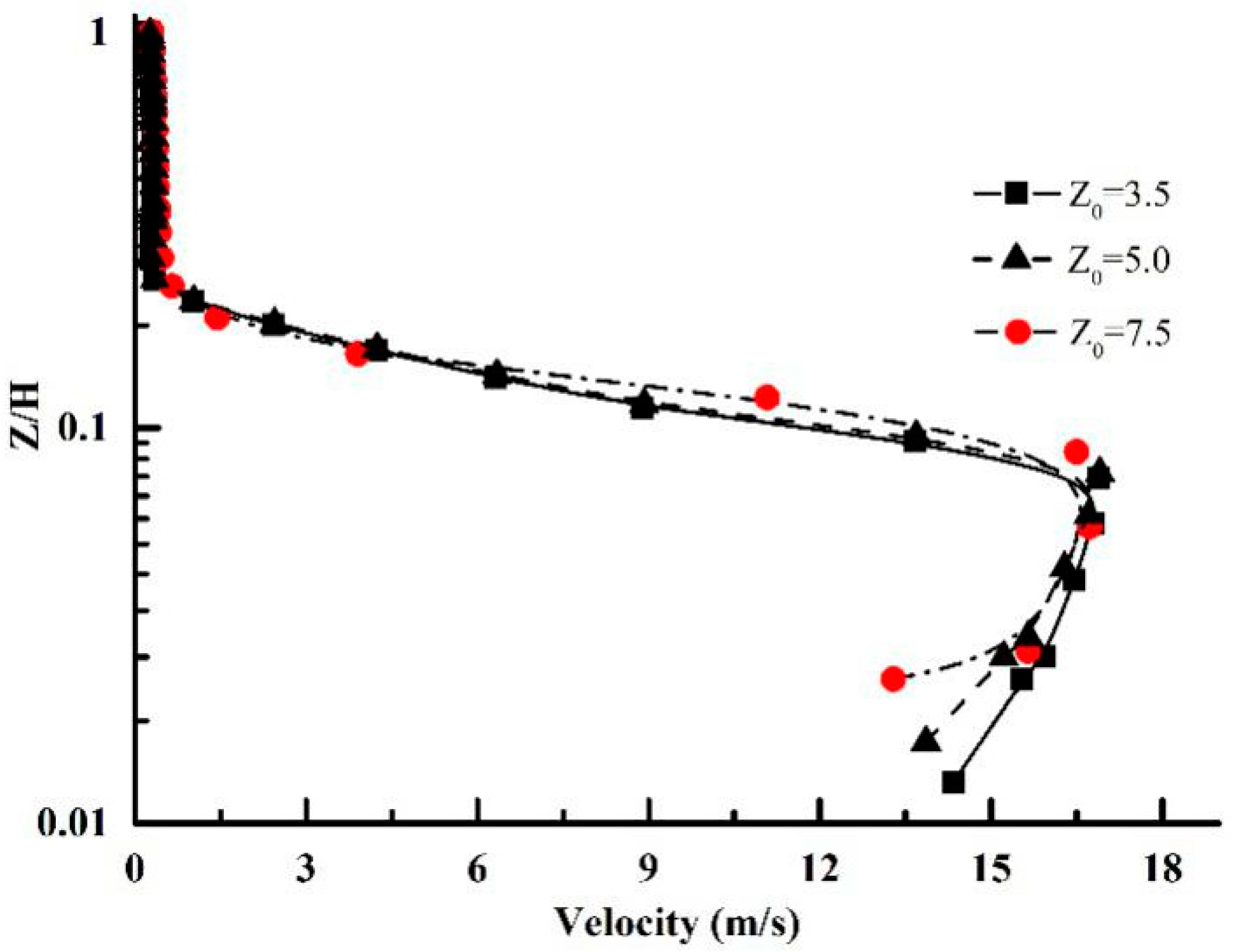
3.2. Mesh Tests and Model Validation
4. Results and Discussion
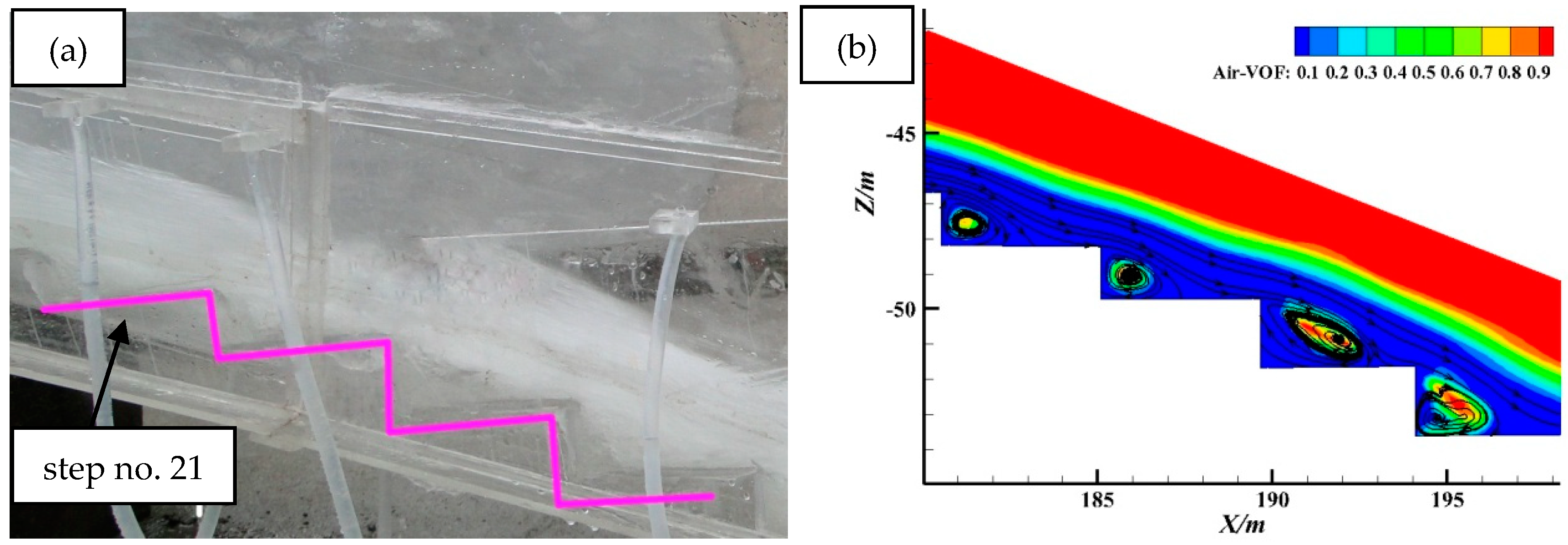
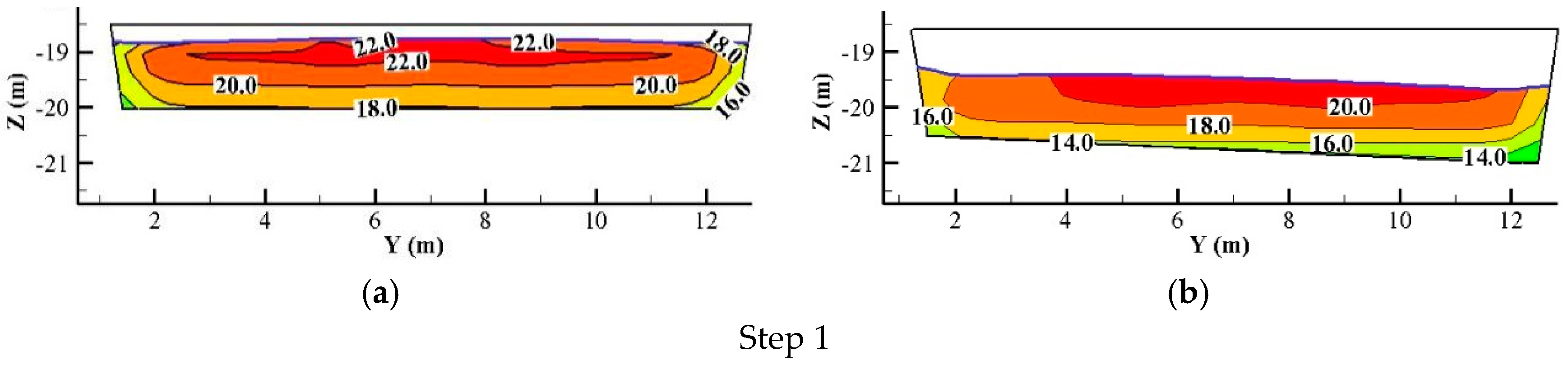
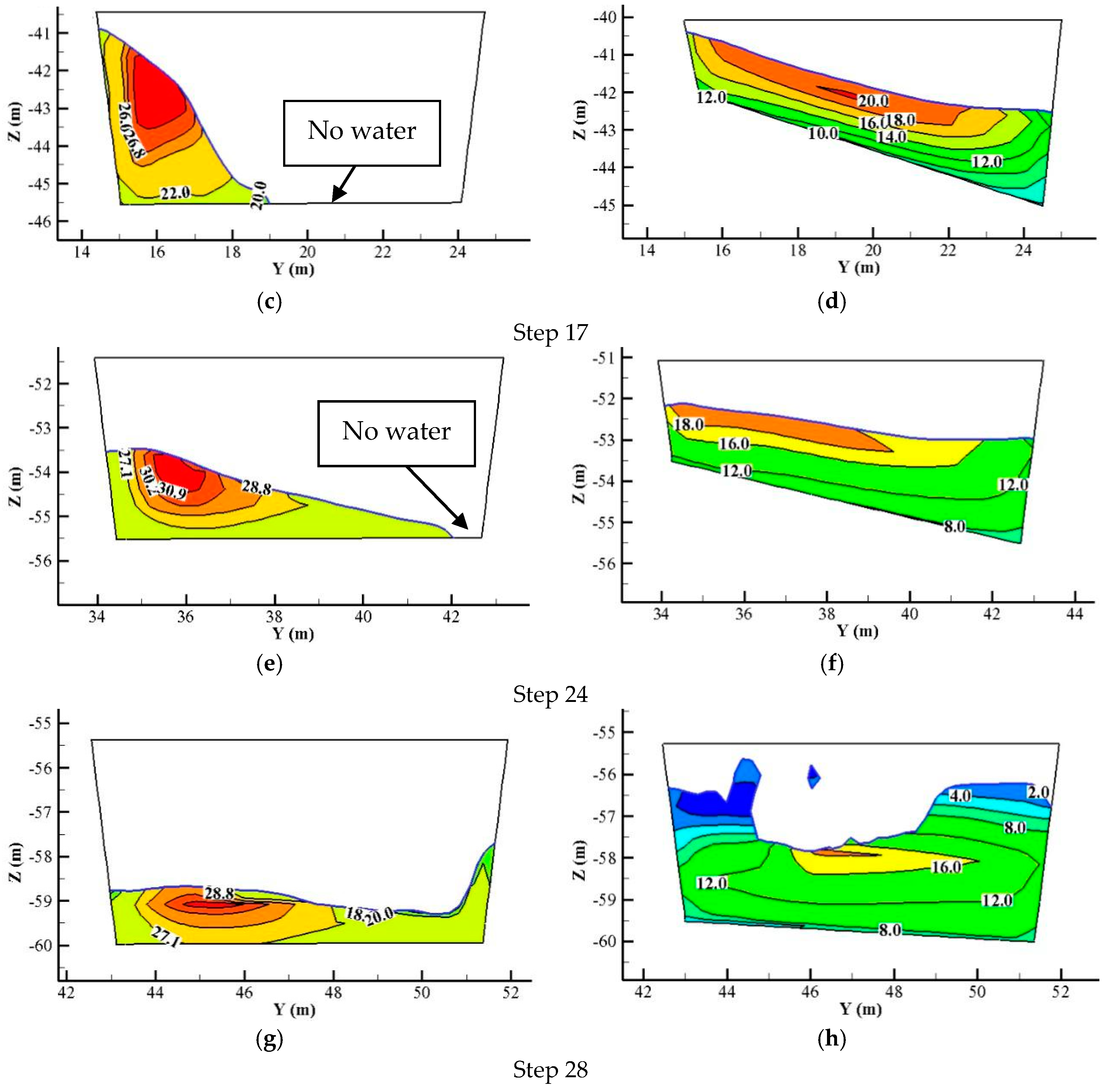
4.1. Main Flow Region
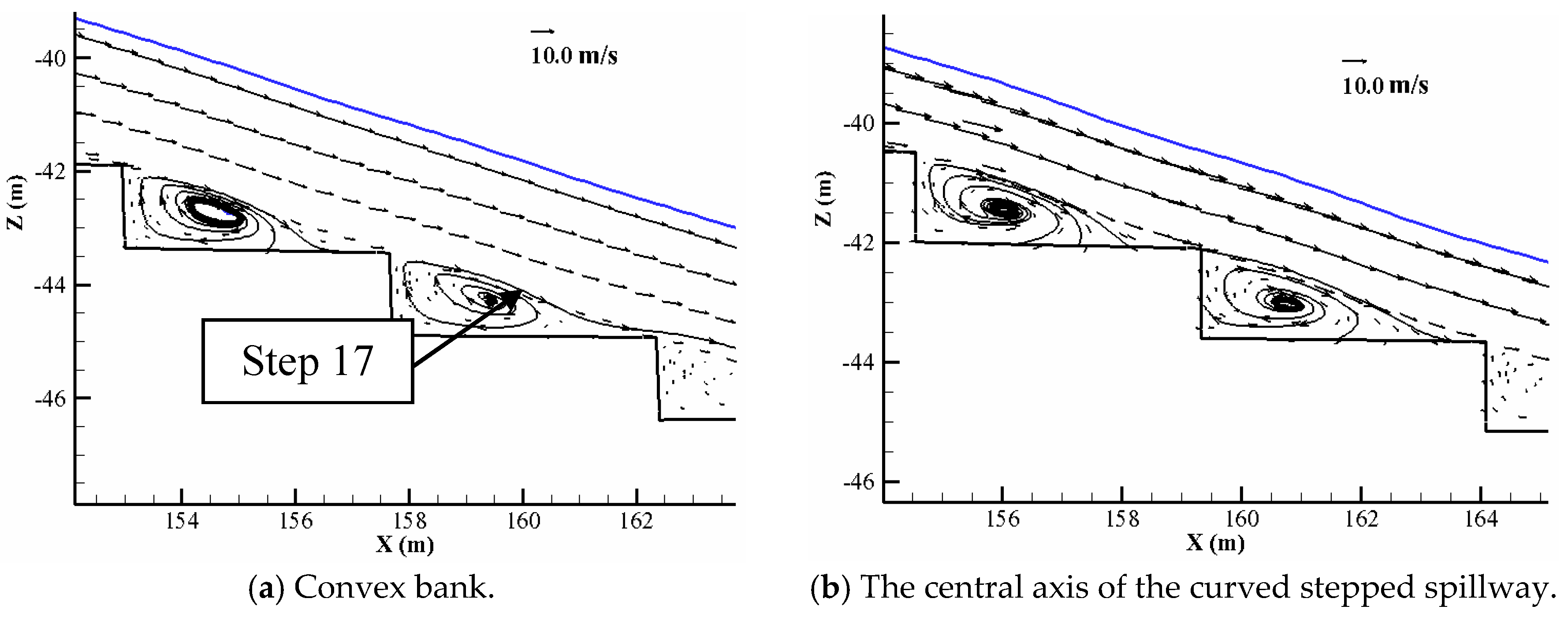
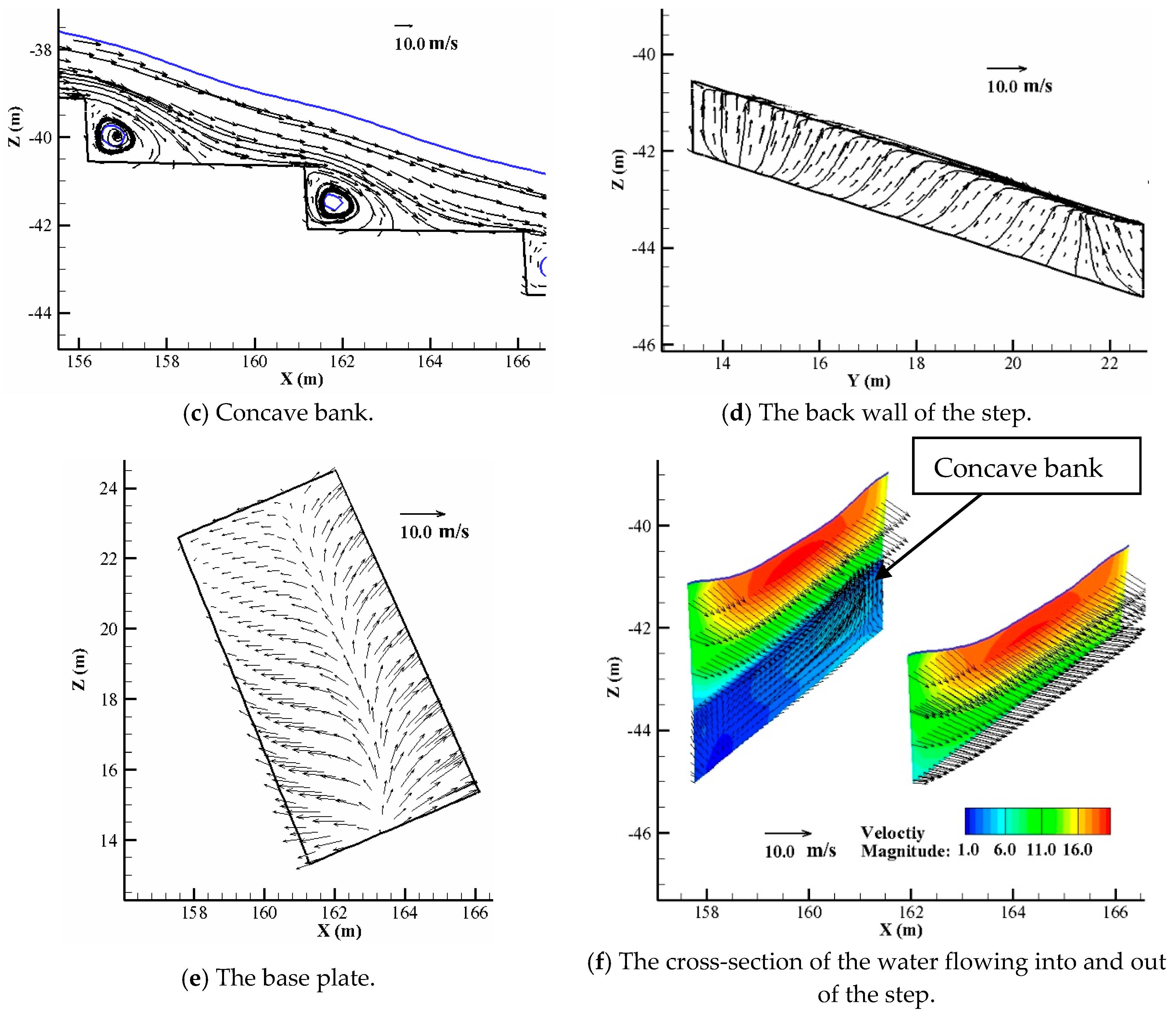
4.2. Flow Pattern on a Step
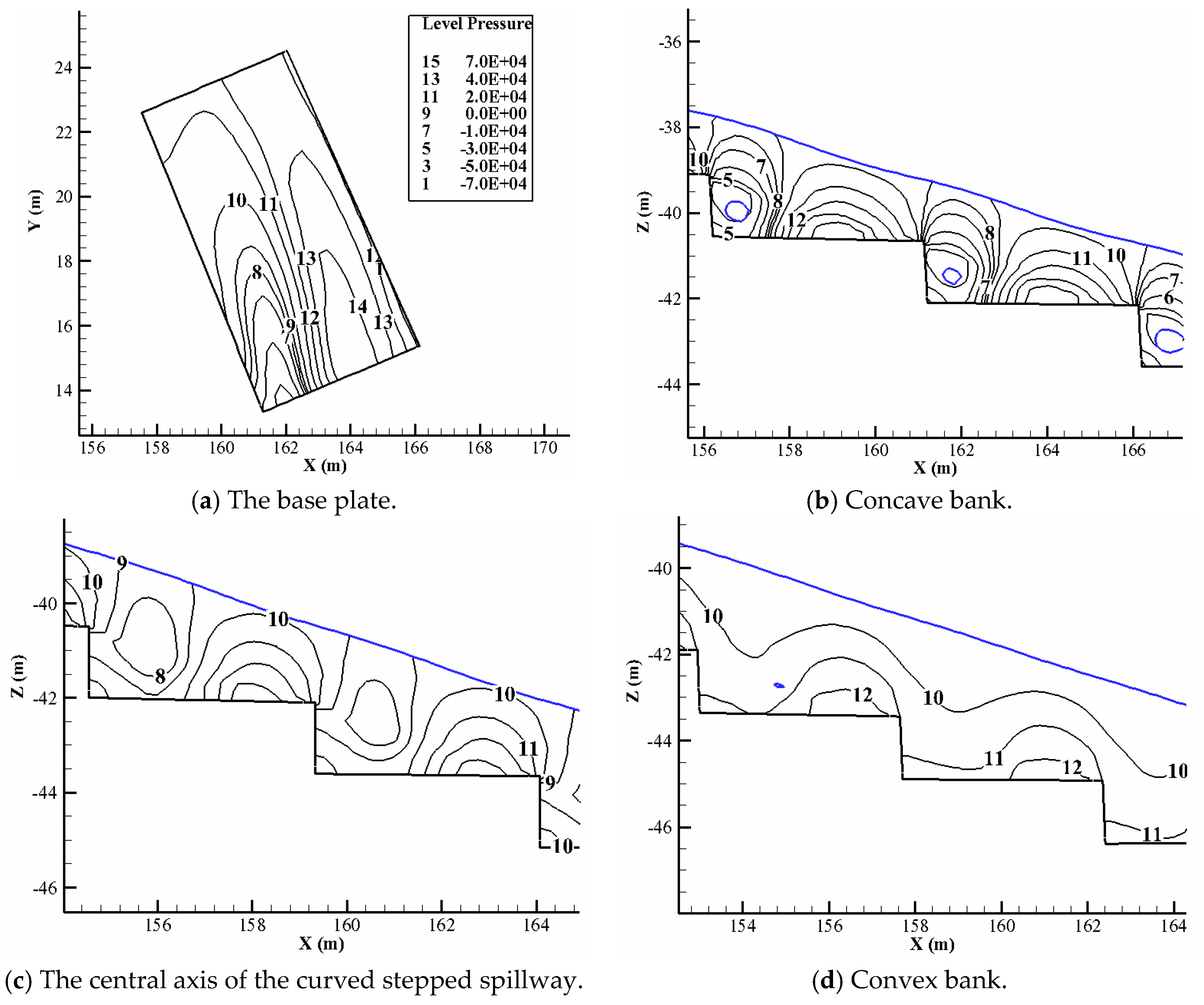
4.3. Cavitation Characteristics
4.4. Energy Loss
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ye, J.; McCorquodale, J.A. Simulation of curved open channel flows by 3D hydrodynamic model. J. Hydraul. Eng. 1998, 124, 687–698. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of skimming flows over stepped channels and spillways. J. Hydraul. Res. 1994, 32, 445–460. [Google Scholar] [CrossRef]
- Chinnarasri, C.; Wongwises, S. Flow Patterns and Energy Dissipation over Various Stepped Chutes. J. Irrig. Drain. Eng. 2006, 132, 70–76. [Google Scholar] [CrossRef]
- Sorensen, R.M. Stepped spillway hydraulic model investigation. J. Hydraul. Eng. 1985, 111, 1461–1472. [Google Scholar] [CrossRef]
- Shvainshtein, A.M. Stepped spillways and energy dissipation. Hydrotech. Constr. 1999, 33, 275–282. [Google Scholar] [CrossRef]
- Christodoulou, G.C. Energy dissipation on stepped spillways. J. Hydraul. Eng. 1993, 119, 644–650. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Energy dissipation down a stepped spillway with nonuniform step heights. J. Hydraul. Eng. 2011, 137, 1543–1548. [Google Scholar] [CrossRef]
- Pegram, G.G.S.; Officer, A.K.; Mottram, S.R. Hydraulics of skimming flow on modeled stepped spillways. J. Hydraul. Eng. 1999, 125, 500–510. [Google Scholar] [CrossRef]
- Ostad Mirza, M.J.; Matos, J.; Pfister, M.; Schleiss, A.J. Effect of an abrupt slope change on air entrainment and flow depths at stepped spillways. J. Hydraul. Res. 2017, 55, 362–375. [Google Scholar] [CrossRef]
- Meireles, I.C.; Bombardelli, F.A.; Matos, J. Air entrainment onset in skimming flows on steep stepped spillways: An analysis. J. Hydraul. Res. 2014, 52, 375–385. [Google Scholar] [CrossRef]
- Zhang, G.; Chanson, H. Hydraulics of the developing flow region of stepped spillways. II: Pressure and velocity fields. J. Hydraul. Eng. 2016, 142, 04016016. [Google Scholar] [CrossRef]
- Chen, Q.; Dai, G.; Liu, H. Volume of fluid model for turbulence numerical simulation of stepped spillway overflow. J. Hydraul. Eng. 2002, 128, 683–688. [Google Scholar] [CrossRef]
- Ye, M.; Wu, C.; Chen, Y.; Zhou, Q. Case study of an S-shaped spillway using physical and numerical models. J. Hydraul. Eng. 2006, 132, 892–898. [Google Scholar] [CrossRef]
- Tabbara, M.; Chatila, J.; Awwad, R. Computational simulation of flow over stepped spillways. Comput. Struct. 2005, 83, 2215–2224. [Google Scholar] [CrossRef]
- Toro, J.P.; Bombardelli, F.A.; Paik, J. Detached eddy simulation of the nonaerated skimming flow over a stepped spillway. J. Hydraul. Eng. 2017, 143, 04017032. [Google Scholar] [CrossRef]
- Toro, J.P.; Bombardelli, F.A.; Paik, J.; Meireles, I.; Amador, A. Characterization of turbulence statistics on the non-aerated skimming flow over stepped spillways: A numerical study. Environ. Fluid Mech. 2016, 16, 1195–1221. [Google Scholar] [CrossRef]
- Rozovskiĭ, I.L. Flow of Water in Bends of Open Channels; Academy of Sciences of the Ukrainian SSR: Kiev, Ukraine, 1957. [Google Scholar]
- Wu, Y.F.; Zhu, J.Y. Exposed bottom phenomenon of curved channels with rapid flows. Adv. Sci. Technol. Water Resour. 2011, 31, 9–12. (In Chinese) [Google Scholar]
- Rodi, W. Turbulence Models and Their Application in Hydraulics; Routledge: London, UK, 2017. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, Y.; Luo, L. Numerical simulation of air-water two-phase flow over stepped spillways. Sci. China Ser. E Technol. Sci. 2006, 49, 674–684. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Two-phase flow characteristics of stepped spillways. J. Hydraul. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Li, D.; Yang, Q.; Ma, X.; Dai, G. Free Surface Characteristics of Flow around Two Side-by-Side Circular Cylinders. J. Mar. Sci. Eng. 2018, 6, 75. [Google Scholar] [CrossRef]
- Jin, X.; Lin, P. Viscous effects on liquid sloshing under external excitations. Ocean Eng. 2018. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Chanson, H.; Brattberg, T. Experimental Study of the Air-Water Shear Flow in a Hydraulic Jump. Int. J. Multiph. Flow 2000, 26, 583–607. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of skimming flows on stepped chutes: The effects of inflow conditions? J. Hydraul. Res. 2006, 44, 51–60. [Google Scholar] [CrossRef]
- Chatila, J.; Tabbara, M. Computational modeling of flow over an ogee spillway. Comput. Struct 2004, 82, 1805–1812. [Google Scholar] [CrossRef]
- Reinauer, R.; Hager, W.H. Supercritical bend flow. J. Hydraul. Eng. 1997, 123, 208–218. [Google Scholar] [CrossRef]
- Rajaratnam, N. Skimming flow in stepped spillways. J. Hydraul. Eng. 1990, 116, 587–591. [Google Scholar] [CrossRef]
- Chamani, M.R.; Rajaratnam, N. Characteristics of skimming flow over stepped spillways. J. Hydraul. Eng. 1999, 125, 361–368. [Google Scholar] [CrossRef]
- Iyer, C.O.; Ceccio, S.L. The influence of developed cavitation on the flow of a turbulent shear layer. Phys. Fluids 2002, 14, 3414–3431. [Google Scholar] [CrossRef]
- O’Hern, T.J. An experimental investigation of turbulent shear flow cavitation. J. Fluid Mech. 1990, 215, 365–391. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Frizell, K.W.; Renna, F.M.; Matos, J. Cavitation potential of flow on stepped spillways. J. Hydraul. Eng. 2012, 139, 630–636. [Google Scholar] [CrossRef]
- Chen, Q.; Dai, G.; Liu, H. Turbulence numerical simulation for the stepped spillway overflow. Tianjin Daxue Xuebao/J. Tianjin Univ. Sci. Technol. 2002, 35, 23–27. [Google Scholar]
- Juny, M.S.; Pomares, J.; Dolz, J. Pressure field in skimming flow over a stepped spillway. In Proceedings of the International Workshop on Hydraulics of Stepped Spillways, Zurich, Switzerland, 22–24 March 2000; Minor, H.E., Hager, W.H., Eds.; AA Balkema: Rotterdam, The Netherlands, 2000; pp. 137–146. [Google Scholar]
- Sanchez-Juny, M.; Blade, E.; Dolz, J. Pressures on a stepped spillway. J. Hydraul. Res. 2007, 45, 505–511. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y.; Takahashi, M. Flow characteristics of skimming flows in stepped channels. J. Hydraul. Eng. 2004, 130, 860–869. [Google Scholar] [CrossRef]






| Prototype | Physical Model | |||
|---|---|---|---|---|
| Index | Water Level in Upstream (m) | Discharge (m3/s) | Water Level in Upstream (m) | Discharge (L/s) |
| Case 1 | 516.09 | 272.00 | 12.90 | 26.87 |
| Case 2 | 517.00 | 348.08 | 12.92 | 34.40 |
| Case 3 | 518.36 | 477.64 | 12.96 | 47.20 |
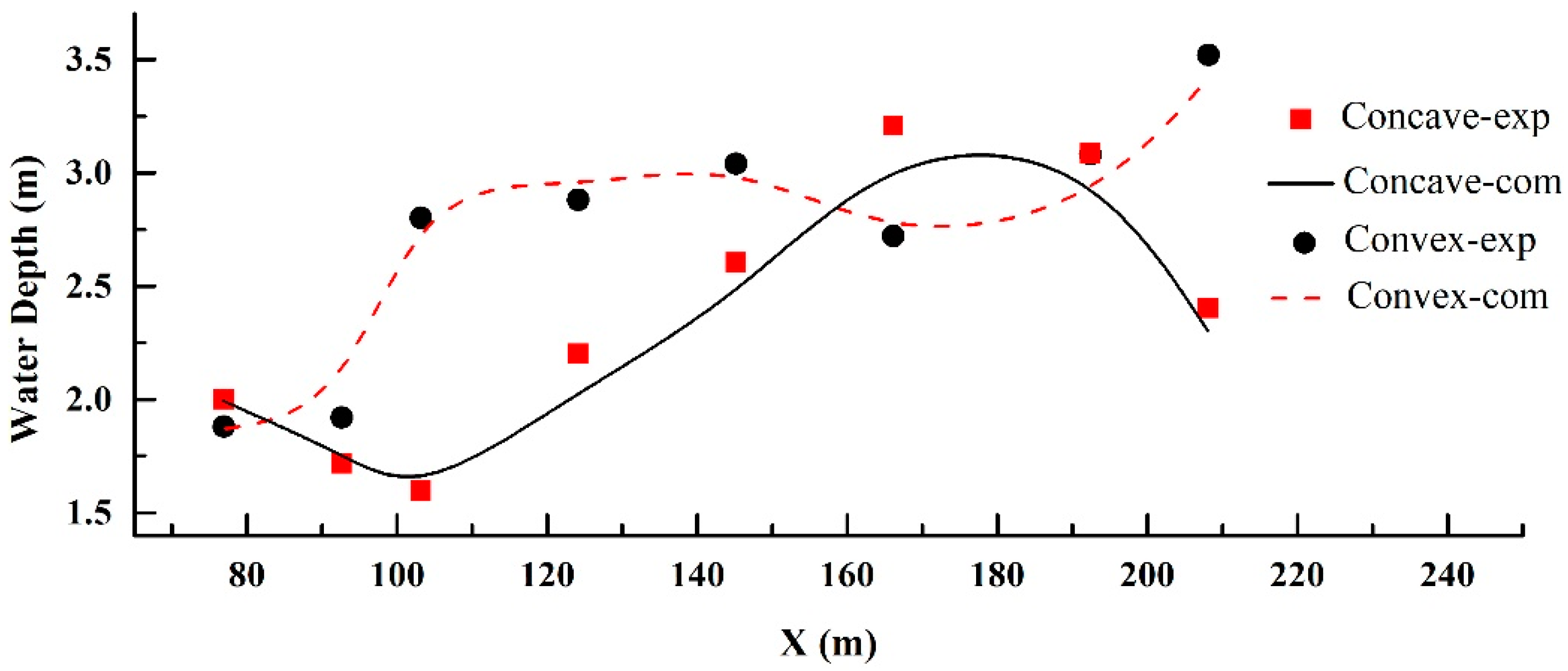
| Smooth Spillway | Curved Stepped Spillway | ||||
|---|---|---|---|---|---|
| Axial Distance (m) | Water Level (m) | Axial Distance (m) | Water Level (m) | ||
| Concave | Convex | Concave | Convex | ||
| 103.66 | 1.44 | 1.28 | 103.16 | 1.12 | 1.80 |
| 126.73 | 2.40 | 0.52 | 124.16 | 1.60 | 2.60 |
| 149.81 | 5.32 | 0.16 | 145.16 | 1.80 | 2.40 |
| 161.35 | 5.92 | 0.08 | 166.16 | 2.60 | 2.20 |
| 194.97 | 3.60 | 0.40 | 192.41 | 2.20 | 2.60 |
| 206.51 | 1.60 | 0.92 | 208.16 | 2.00 | 2.80 |
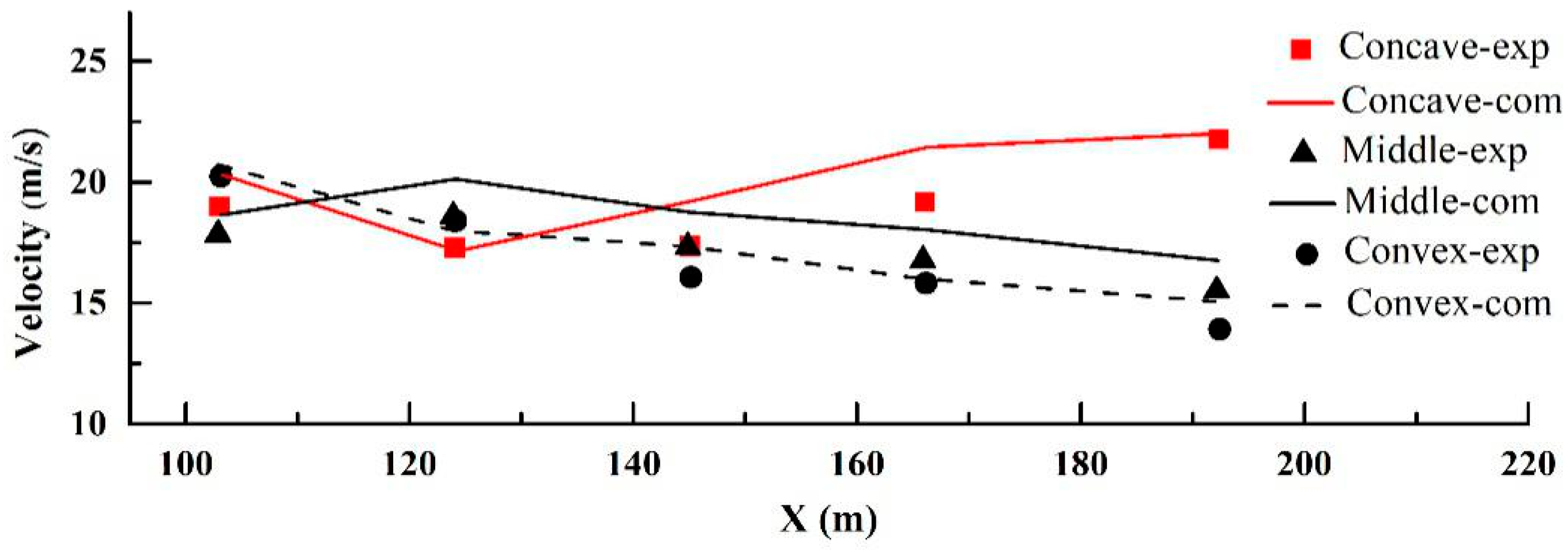
| Axial Distance (m) | Velocity Distribution (m/s) | ||
|---|---|---|---|
| Concave | Middle | Convex | |
| 103.16 | 16.57 | 16.63 | 16.70 |
| 124.16 | 16.76 | 18.97 | 16.95 |
| 145.16 | 17.14 | 17.77 | 15.68 |
| 166.16 | 19.04 | 18.09 | 15.18 |
| 192.41 | 19.61 | 15.81 | 14.29 |
| 208.16 | 16.57 | 16.63 | 16.70 |
| Index | Velocity on the Weir Crest (m/s) | Water depth on the Weir Crest (cm) | Fr |
|---|---|---|---|
| Smooth | 1.15 | 8.78 | 1.16 |
| Stepped | 1.15 | 8.78 | 1.16 |
| Index | Velocity of Flow into the Curved Section (m/s) | Water Depth of Flow into the Curved Section (cm) | Fr |
|---|---|---|---|
| Smooth | 2.00 | 5.00 | 2.86 |
| Stepped | 2.00 | 5.00 | 2.86 |
| Case | Water Depth (h0) (m) | Mean Velocity (V0) (m/s) | Energy (E) (m) | Relative Energy Loss (ΔE/E′) |
|---|---|---|---|---|
| Smooth curved spillway | 1.25 | 27.4 | 39.51 | 0.66 |
| Stepped curved spillway | 2.0 | 15.0 | 13.47 | 1.93 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Yang, Q.; Ma, X.; Dai, G. Case Study on Application of the Step with Non-Uniform Heights at the Bottom Using a Numerical and Experimental Model. Water 2018, 10, 1762. https://doi.org/10.3390/w10121762
Li D, Yang Q, Ma X, Dai G. Case Study on Application of the Step with Non-Uniform Heights at the Bottom Using a Numerical and Experimental Model. Water. 2018; 10(12):1762. https://doi.org/10.3390/w10121762
Chicago/Turabian StyleLi, Dengsong, Qing Yang, Xudong Ma, and Guangqing Dai. 2018. "Case Study on Application of the Step with Non-Uniform Heights at the Bottom Using a Numerical and Experimental Model" Water 10, no. 12: 1762. https://doi.org/10.3390/w10121762
APA StyleLi, D., Yang, Q., Ma, X., & Dai, G. (2018). Case Study on Application of the Step with Non-Uniform Heights at the Bottom Using a Numerical and Experimental Model. Water, 10(12), 1762. https://doi.org/10.3390/w10121762





