Improved Building Treatment Approach for Urban Inundation Modeling: A Case Study in Wuhan, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Improved Building Treatment Approach (IBTA)
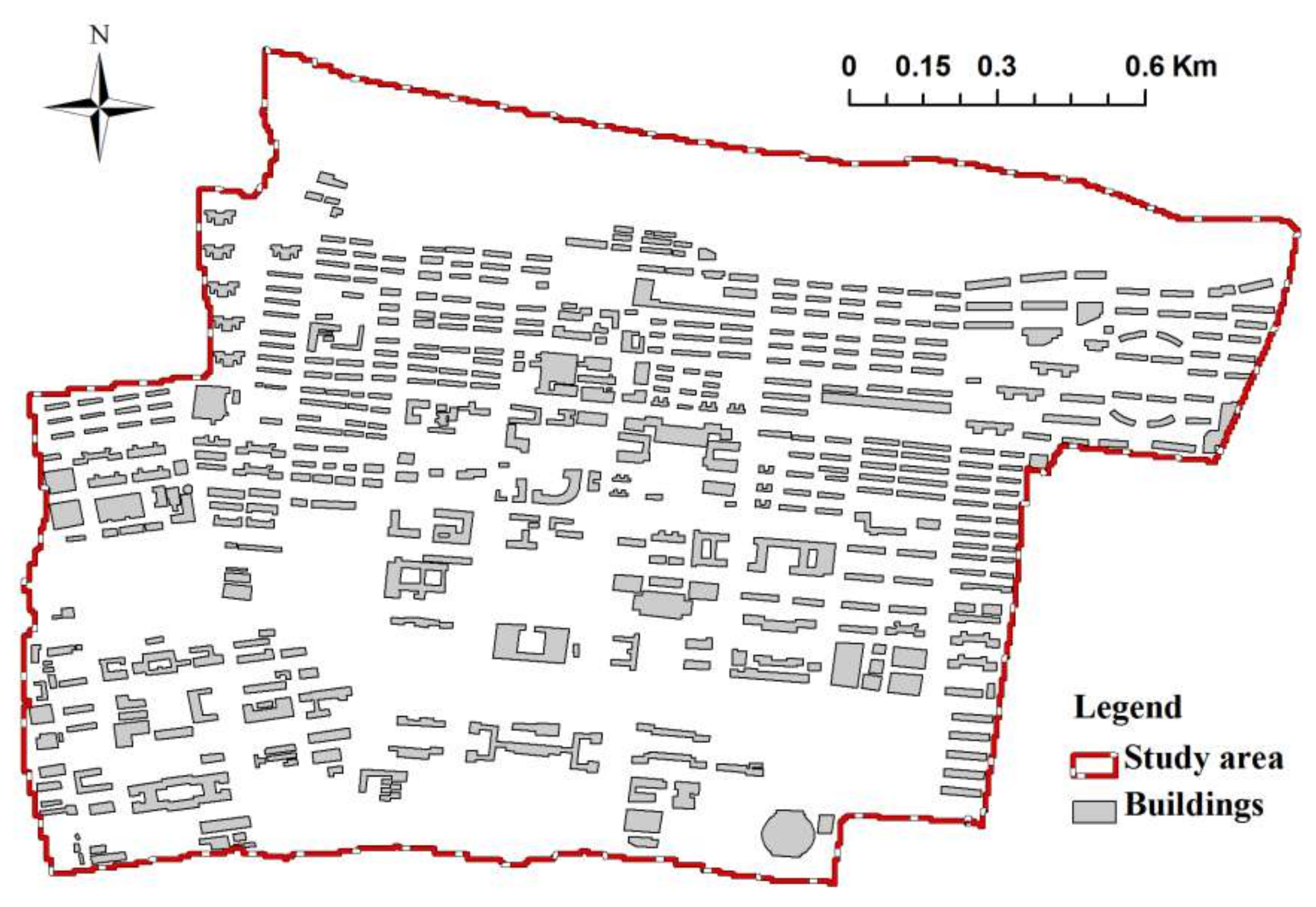
2.2. Study Area
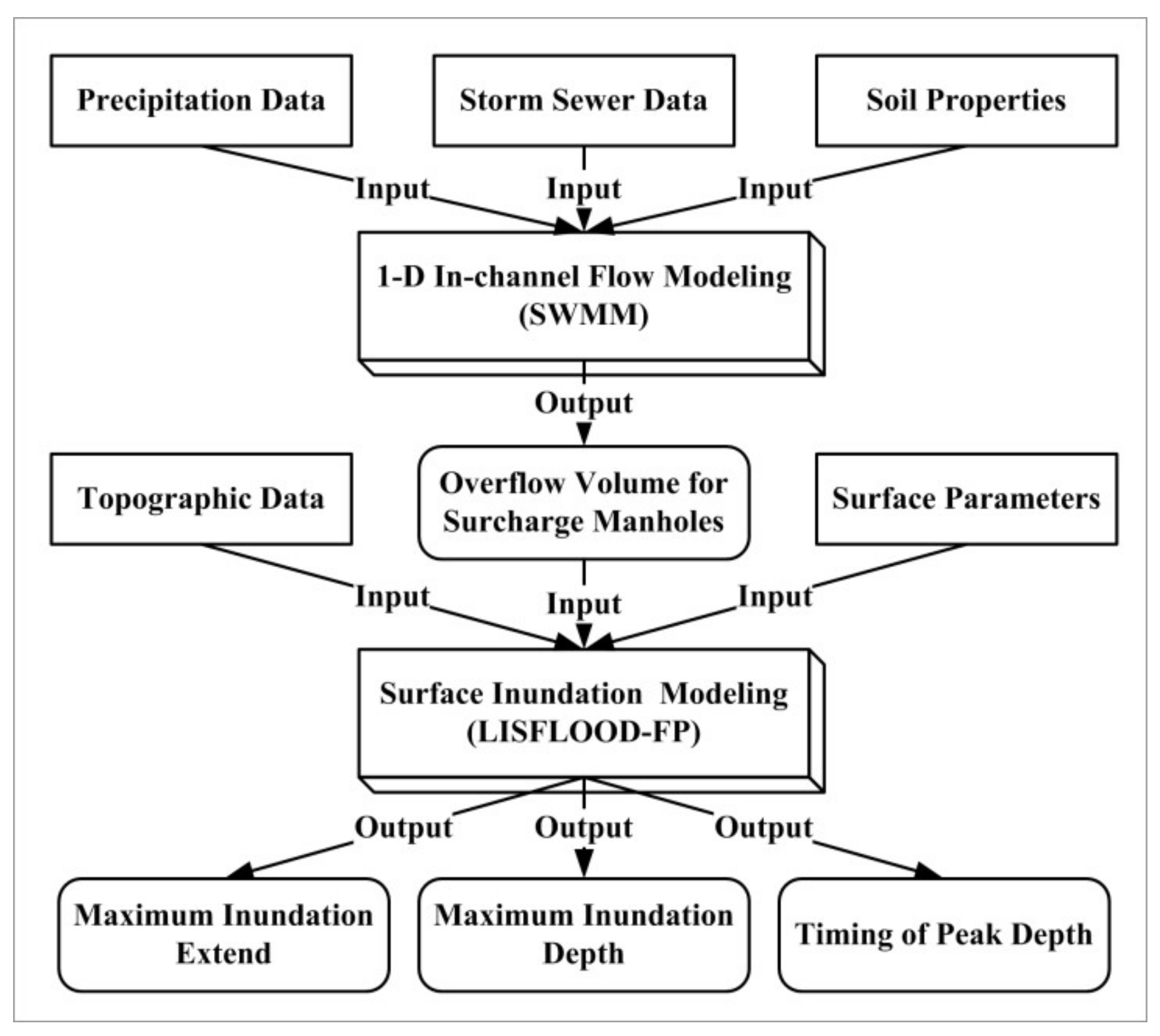
2.3. Inundation Model
2.4. Data Sources and Preprocessing
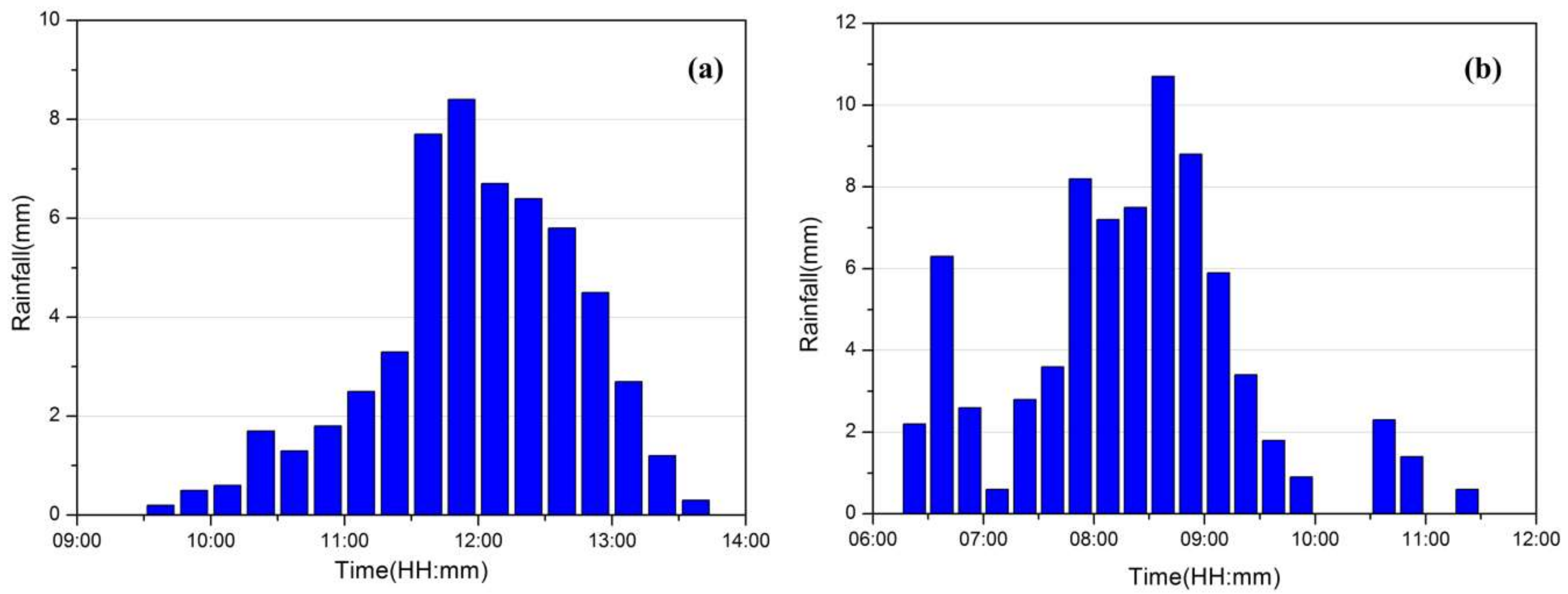
2.4.1. Precipitation Data
2.4.2. Topographic Data
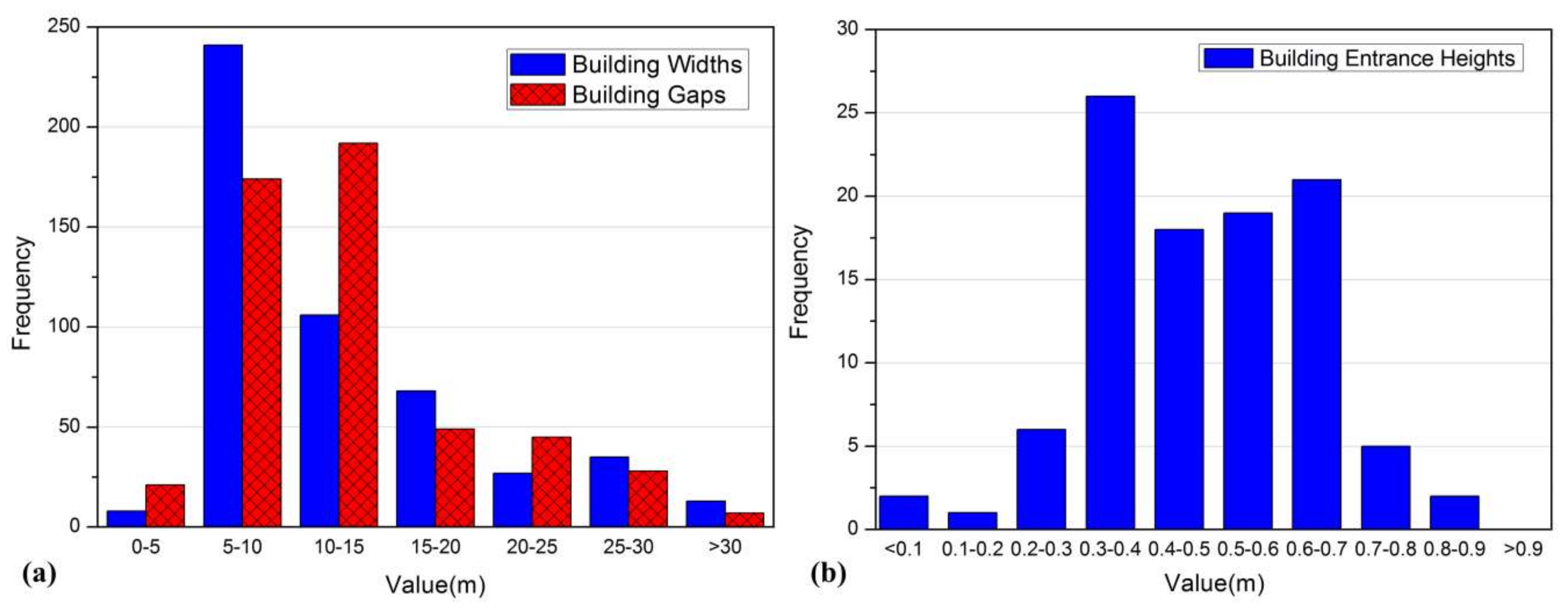
2.4.3. Buildings Data
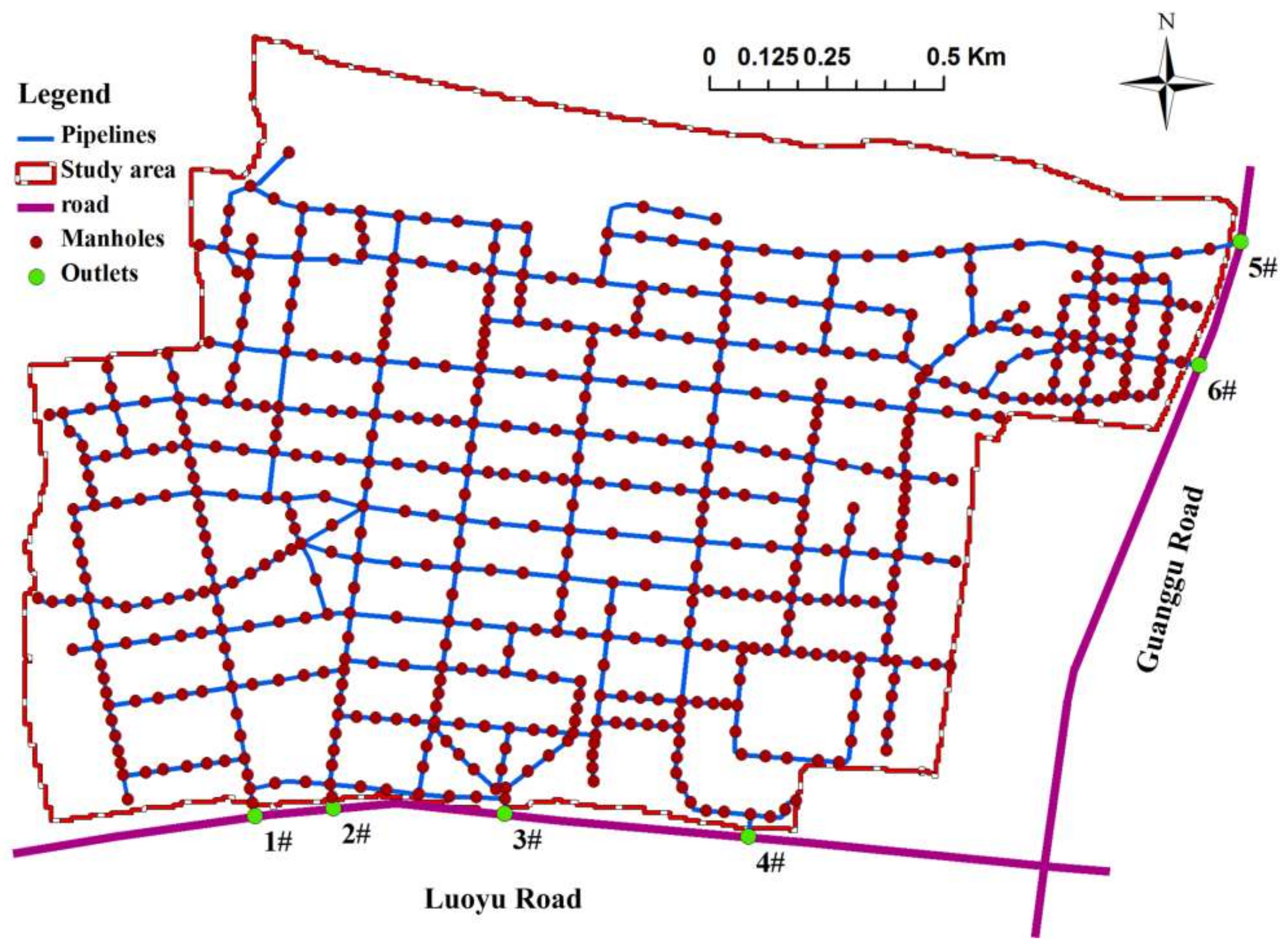
2.4.4. Storm Sewer Data
2.4.5. Terrain Preprocessing
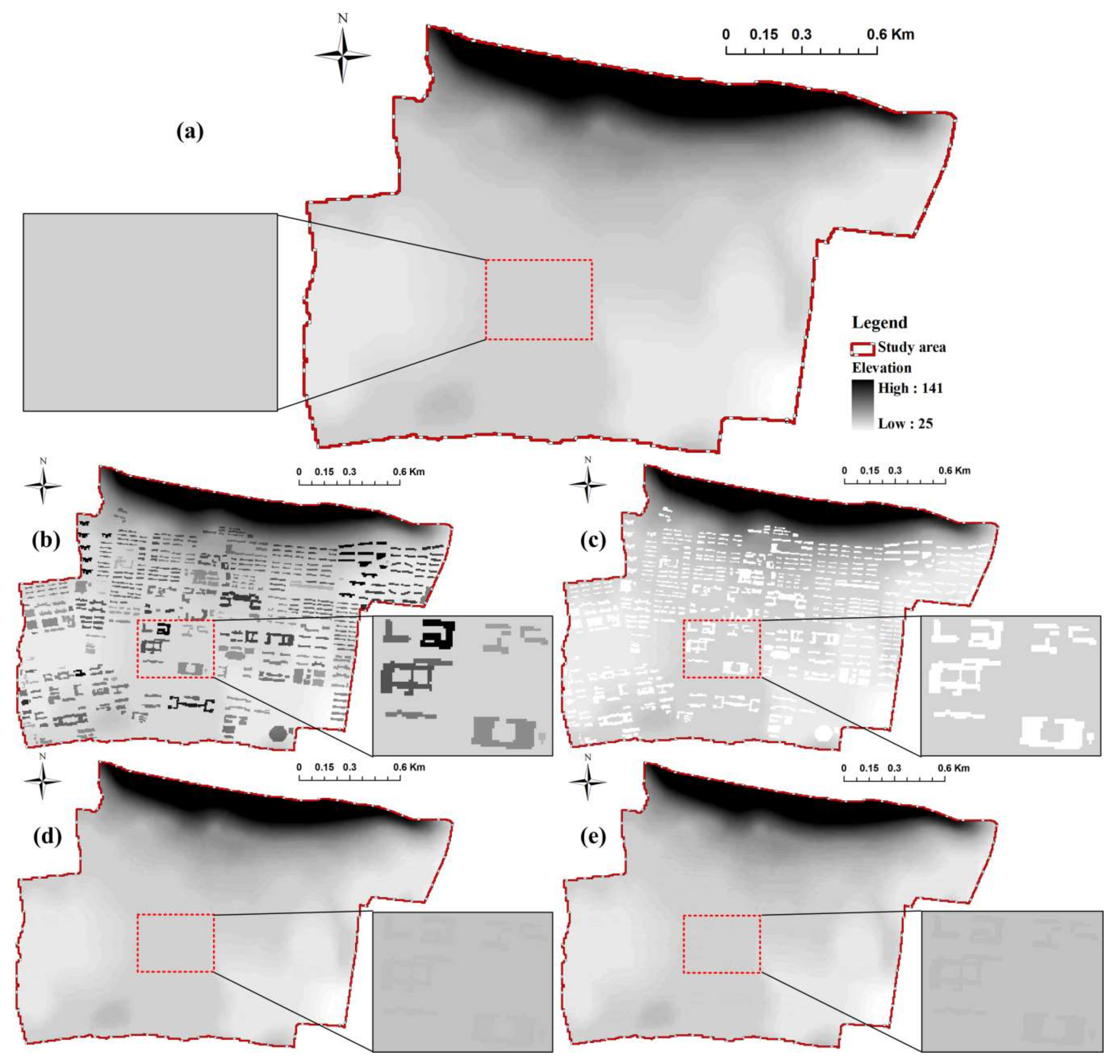
- BB method: DEM cells that are occupied by buildings were raised by the roof height of the buildings. The result is shown in Figure 5b.
- BH method: Areas demarked as buildings in the bare-earth DEM were removed, and thus mesh holes were formed that were aligned with building footprints (see Figure 5c).
- IBTA0.4 method: DEM cells that fall within building footprints were raised by a fixed value of 0.4 m, reflected the height of the entrance of the building ground floors, as shown in Figure 5d.
- IBTA0.6 method: The only difference between IBTA0.6 and IBTA0.4 is that for IBTA0.6 the building elevation was set to 0.6 m higher than the local ground level elevation (instead of 0.4 m for IBTA0.4). The results can be seen in Figure 5e.
- IBTA0.4R method: The terrain processing approach of the IBTA0.4R method is same as that of IBTA0.4.
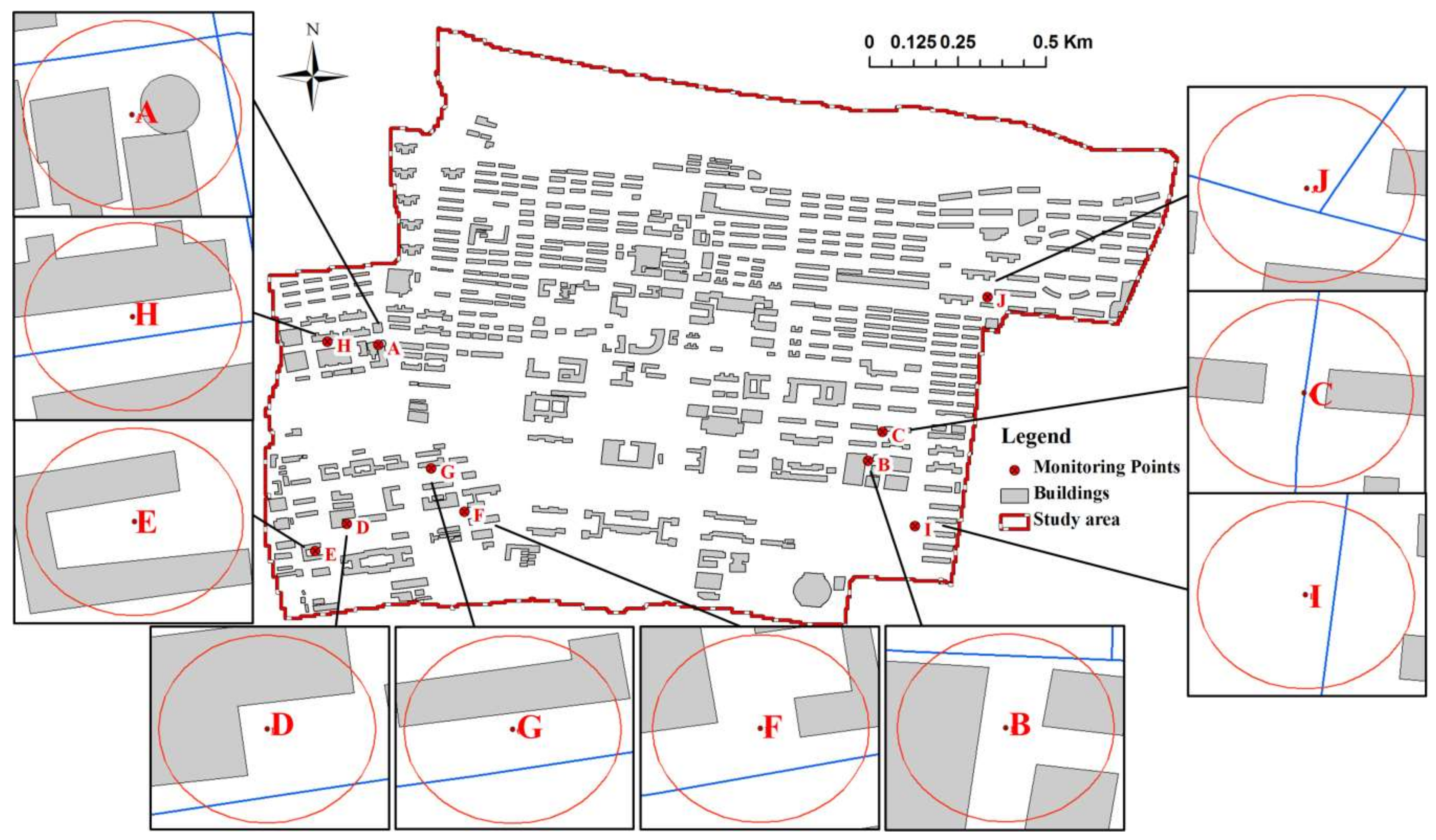
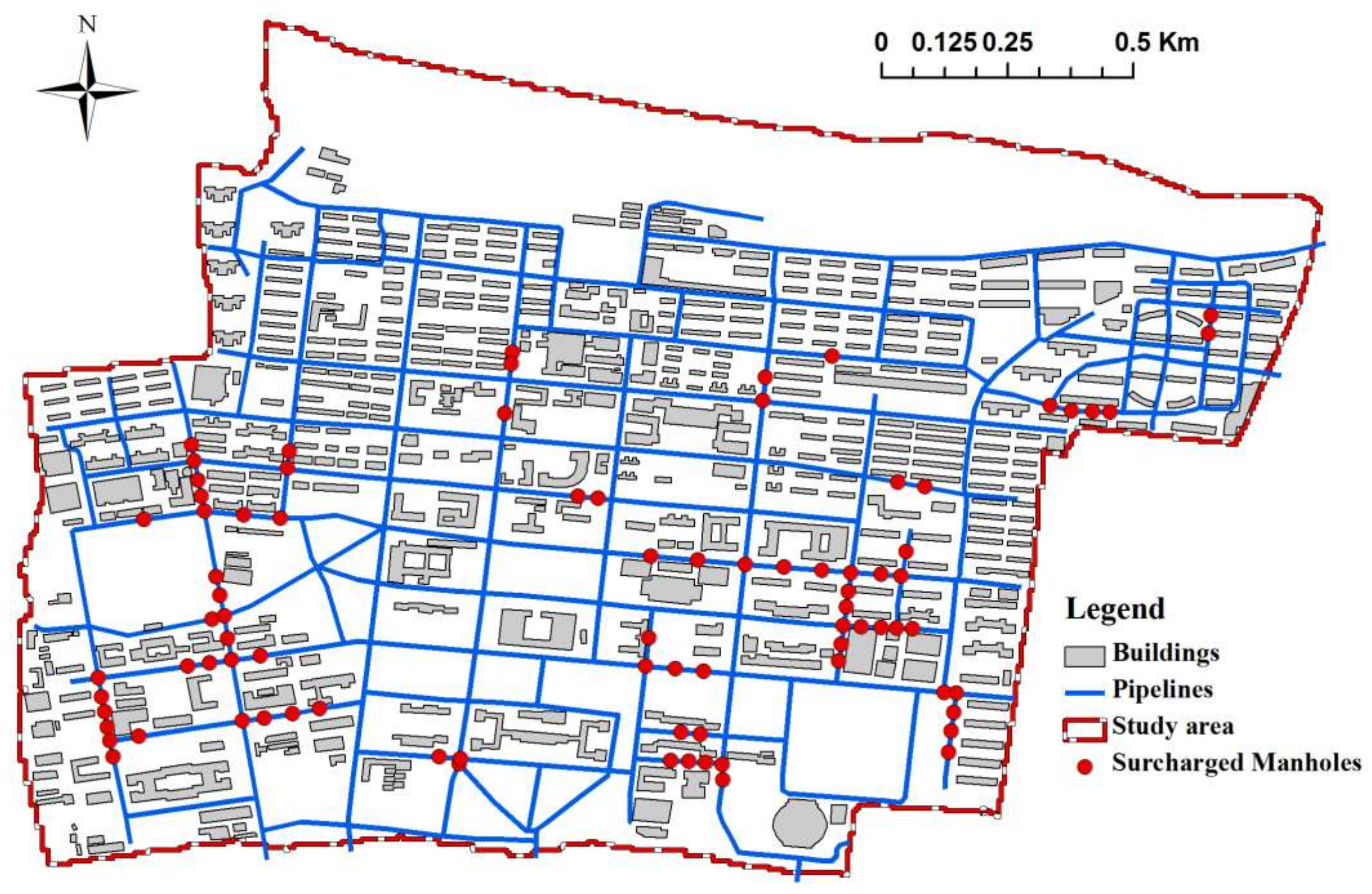
2.4.6. Observed Data and Monitoring Points
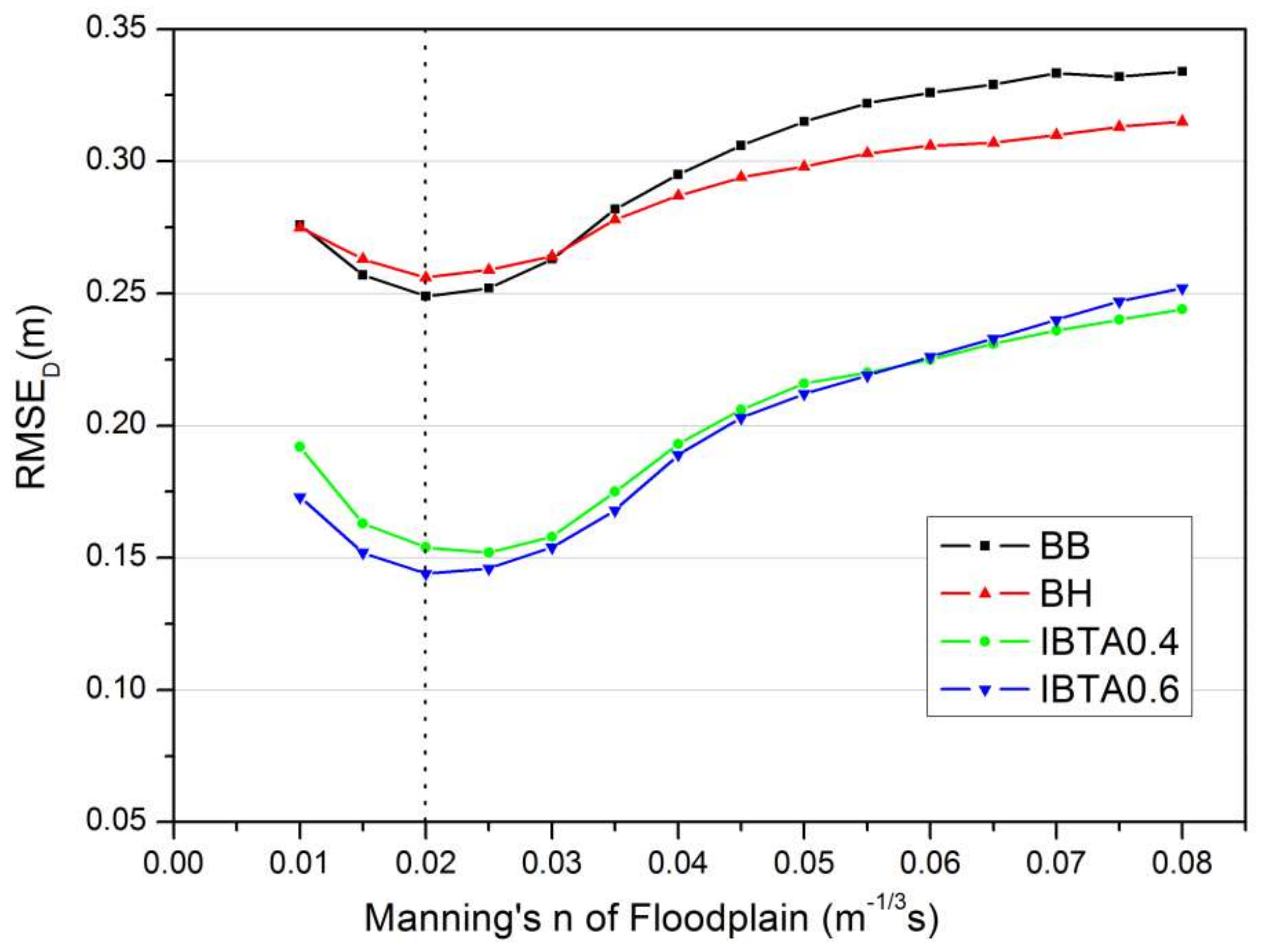
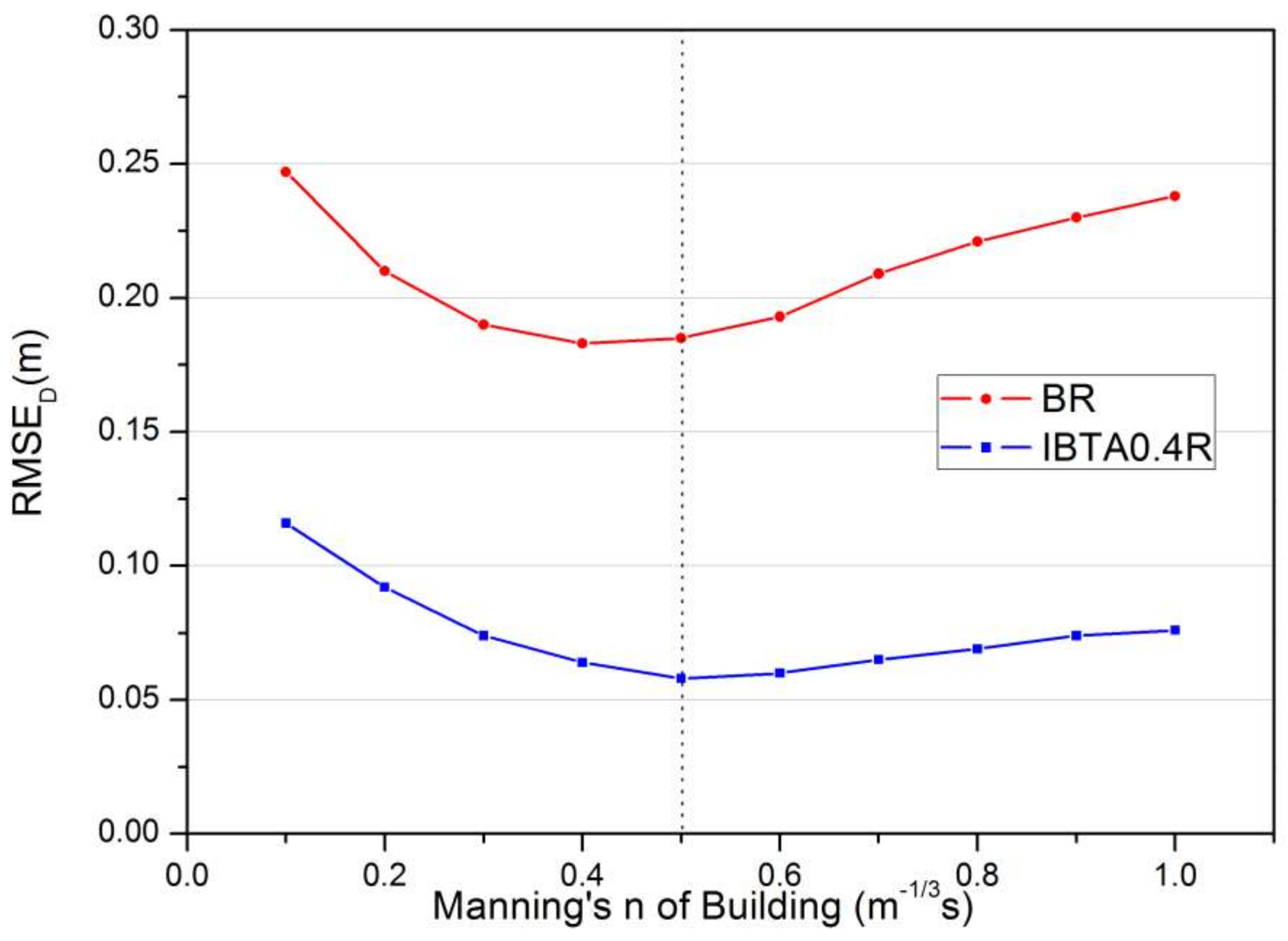
2.5. Model Calibration and Validation
2.5.1. Calibration
2.5.2. Validation
3. Results and Discussions
3.1. Model Sensitivity to Building Treatment Method
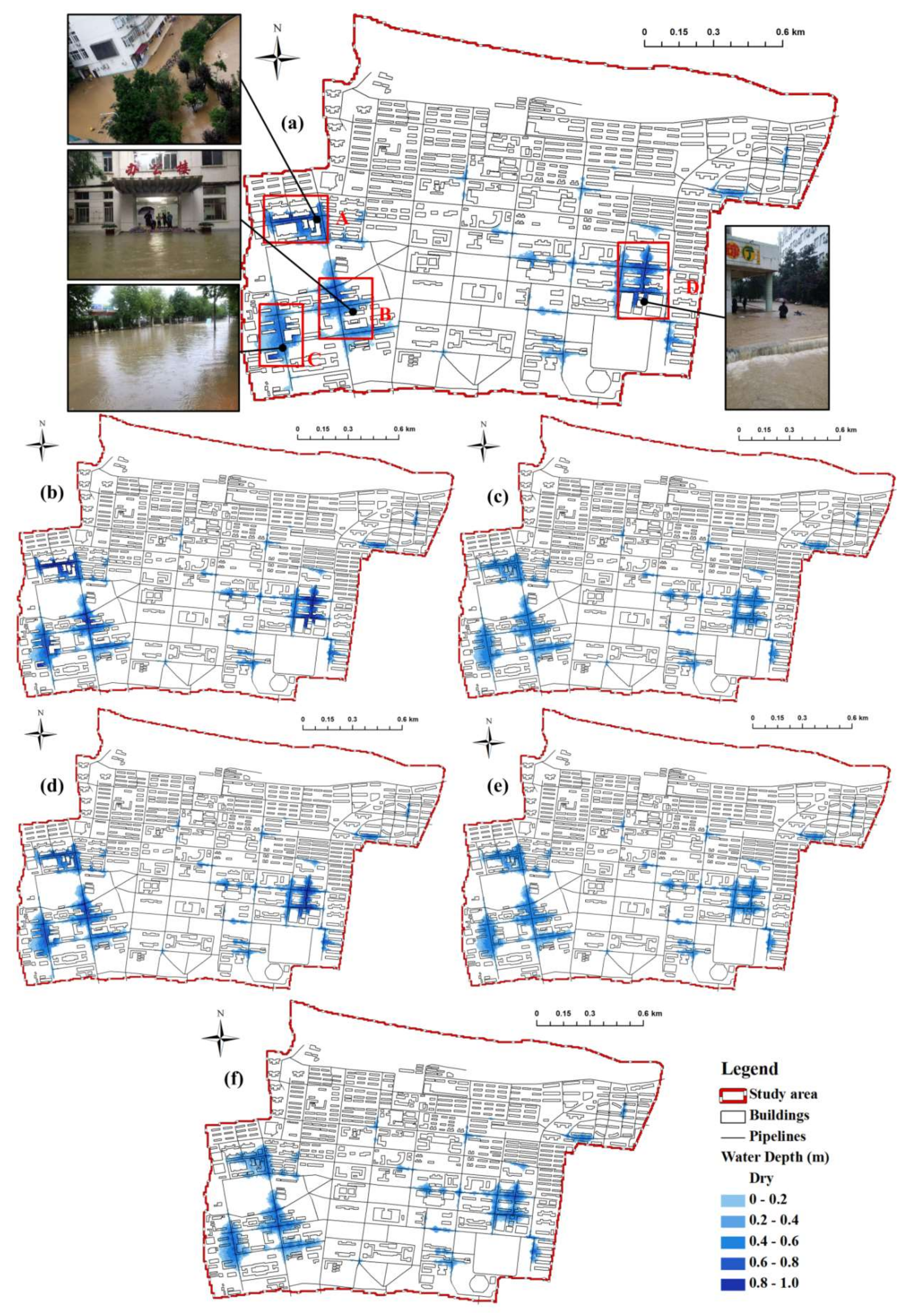
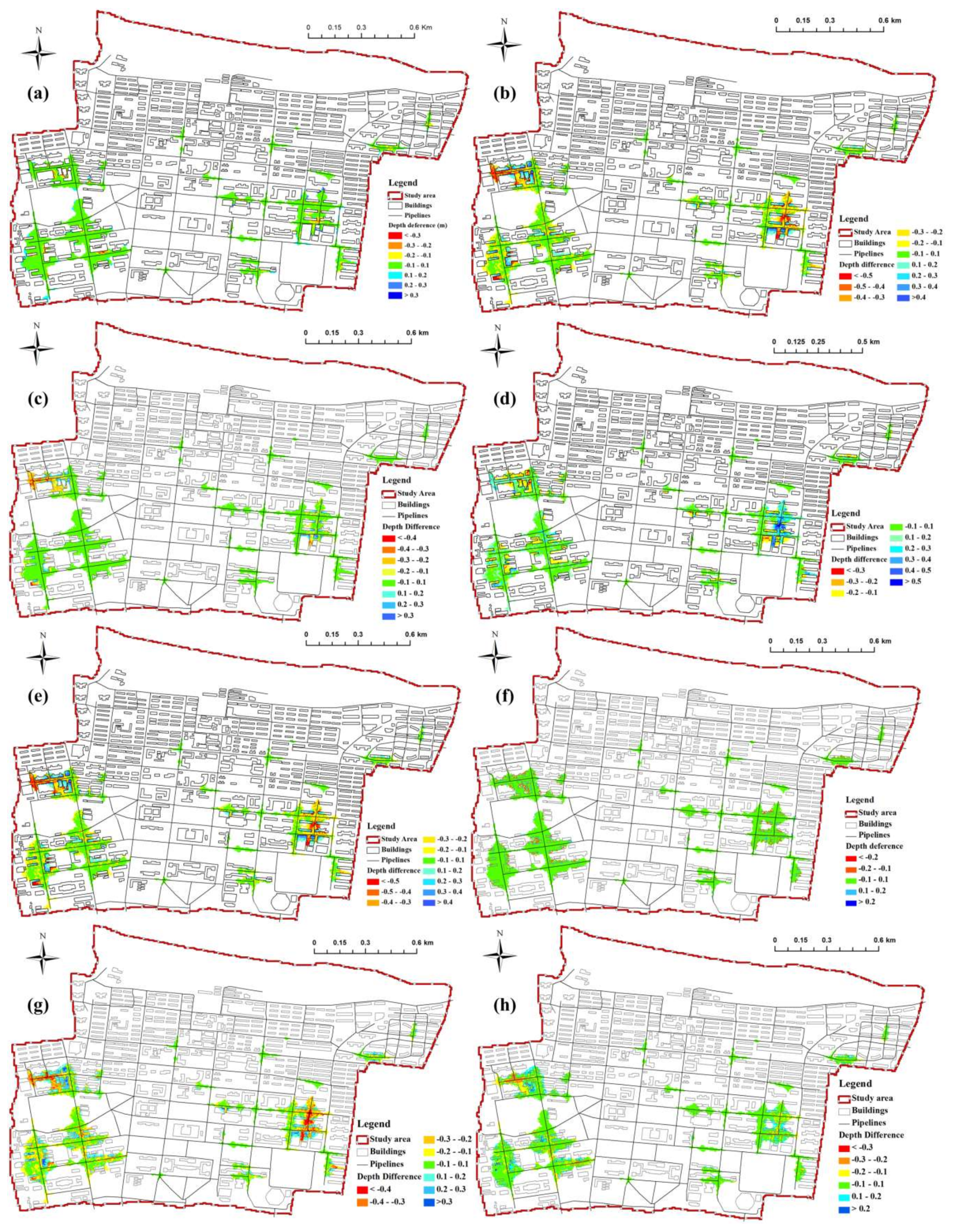
- BB-BH methods: No remarkable difference in maximum inundation extent could be found between the BH and BB methods. Both methods present extensive and torrential inundation within regions A to D (see Figure 13a,b). Nevertheless, the BH method produces a slightly smaller inundation zone compared to the BB method along the western and southern edge of region C (Figure 14a). Moreover, the BH method produces a slightly larger maximum inundation depth compared to the BB method along the building footprints and gaps, especially in regions A and D with dense building coverage. Considering the small distinction between the BH and BB simulations, the BB method serves as the benchmark of these two methods when compared to other methods.
- IBTA0.4-BB methods: There are significant differences in the simulated maximum inundation area and depth between the IBTA0.4 and BB methods (see Figure 13a,c and Figure 14b). The BB method generally produces higher inundation depths than IBTA0.4, particularly for the area between the crowded buildings alongside the road. Specifically, the BB method demonstrates a torrential inundation at Nanyi Road (region A), which is surround by cafeterias and apartment buildings, and the highest inundation depth reaches over 0.8 m (Figure 13a). On the other hand, Nanyi Road is flooded by water with a maximum inundation depth below 0.6 m in the modeling scenario simulated by IBTA0.4. Similar differences can be found around the Coal Combustion Laboratory in the southwest corner of region C. The BB method simulated much higher inundation depths in the recess of the laboratory building than IBTA0.4. Furthermore, in the IBTA0.4 simulation, we note that fair amounts of the area within the buildings are simulated to be wet, which is not the case in BB simulations. The discrepancies in simulations of localized inundation area and depth are attributed to the different values of building elevation used in these two methods. For IBTA0.4, the inner areas of the buildings are available for storage when the inundation depth rises to 0.4 m, while the flow water is still confined between the outer walls of buildings in the BB method, leading to the increase in water depths. Additionally, we note that IBTA0.4 also simulates smaller maximum inundation area and depths at Xiwu Road, which is located at the western edge of region A and intersects with Nanyi Road at its western endpoint. This is primarily because the buildings alongside Nanyi Road act to redirect the southward- and northward-moving surface flow to the west in the BB method; therefore, more water reaches Xiwu Road in this case. These results indicate that the localized simulated inundation areas and depths are sensitive to the building treatment method.
- IBTA0.6-BB methods: As shown in Figure 13a,d and Figure 14c, the IBTA0.6 and BB methods also produce varying simulated maximum inundation areas and depths. The greatest differences between the two methods also occurred mainly at locations near dense buildings in regions A and D, yet to a smaller degree than that in Figure 14b. Moreover, the simulated maximum inundation area and depths of IBTA0.6 agree well with those of the BB method in most of regions B and C, which is markedly different from the results shown in Figure 14b. This is because, for the IBTA0.6 method, the simulated maximum inundation depth in most parts of regions B and C is below 0.6 m, in which case the buildings are still treated as a solid block, and results in similar inundation depths to the BB method. Nevertheless, as shown by the discrepancies in the simulation results illustrated in Figure 14c, the model sensitivity to the building treatment method becomes more pronounced.
- IBTA0.6-IBTA0.4 methods: There are considerable differences in both maximum inundation area and depth between the IBTA0.6 and IBTA0.4 simulations, and especially in the local areas around the building features (Figure 13c,d and Figure 14d). Overall, IBTA0.6 produces deeper flood water along the road, but shallower or no inundation inside buildings, compared to the IBTA0.4 method. This is attributed to the increase in threshold of building entrance height (from 0.4 m to 0.6 m) when the IBTA0.6 method is used. With the increase of building elevation, less flux enters the buildings, and the overlooked building storage volume leads to increased pooling along the road and in other lowlands outside of building, thus resulting in more severe inundation. Therefore, it can be inferred that the storage and blockage effects of buildings are affected by the changes in threshold used for terrain preprocessing.
- IBTA0.4R-IBTA0.4 methods: The simulated maximum inundation areas and depths differ very little between the IBTA0.4R and IBTA0.4 methods, except in some areas within and along the building footprints where patches of red and blue colors appear in Figure 14f. IBTA0.4R always produces greater inundation depths but smaller flooding extent inside buildings than the IBTA0.4 method. This is ascribed to the building resistance effect represented in the IBTA0.4R method by changing the Manning’s n value at building’s position, in which case water flow into buildings is inhibited by the presence of inner walls, furniture and closed doors. It can be inferred that beyond the storage and blockage effect, the inner resistance effect of the buildings should also not be ignored in urban inundation modeling.
- BR-IBTA0.6 methods: Remarkable differences in the simulated maximum inundation area and depth can be found between the modeling scenarios of BR and IBTA0.6, particularly in the dense building areas of regions A and D (see Figure 14g). The BR method generally produces smaller maximum inundation depths than IBTA0.6 along the roads and alleyways between densely-spaced buildings, but higher inundation depths inside buildings. This is a result of the absence of building blockage effect in the BR method. In IBTA0.6, DEM cells fall within building features and can obstruct flow and block flood flows from reaching the interior spaces of the buildings when the water level is below 0.6 m, in contrast to the BR method which can only resist flow. In the BR method, significant volumes of water enter and move through the buildings without any solid obstruction. Therefore, less water accumulates and flows along the roads and alleyways between buildings, leading to lower inundation depths.
- BR-IBTA0.4R methods: As shown in Figure 14h, the differences in the simulated maximum inundation area and depth between BR and IBTA0.4R methods are smaller than those in Figure 14g, especially in region D with dense building coverage. This is mainly because the building blockage effect is decreased in IBTA0.4R by using a lower threshold of building entrance height. It can be seen from Figure 13 and Figure 14 that as the full grid area remains available for water storage, the BR method generally simulates lower inundation depth and greater lateral spreading than the other methods. These results are similar to those of Schubert and Sanders [36], suggesting the significant role played by solid obstruction in the flood wave propagation and the importance of an accurate representation of building blockage effect in urban inundation modeling.
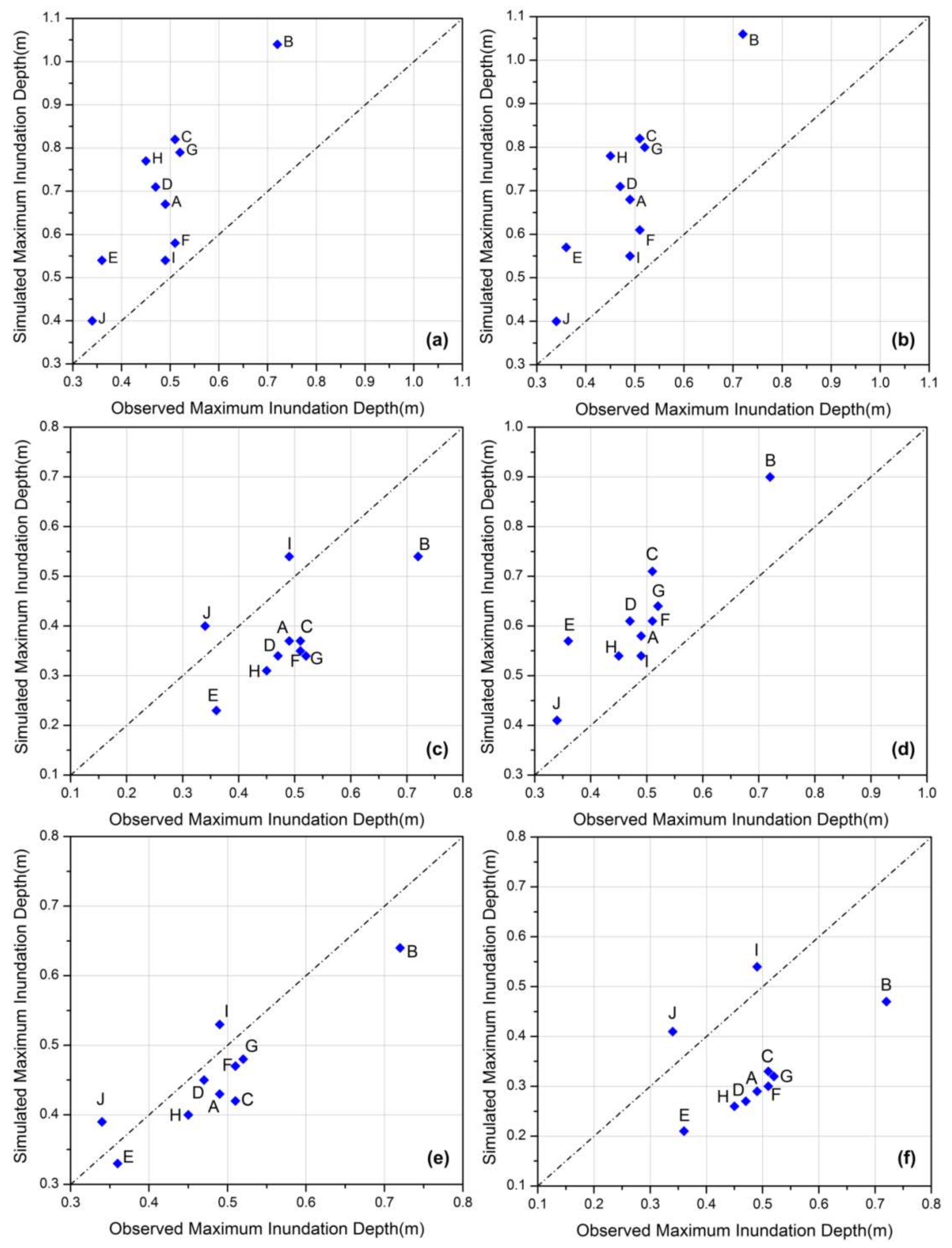
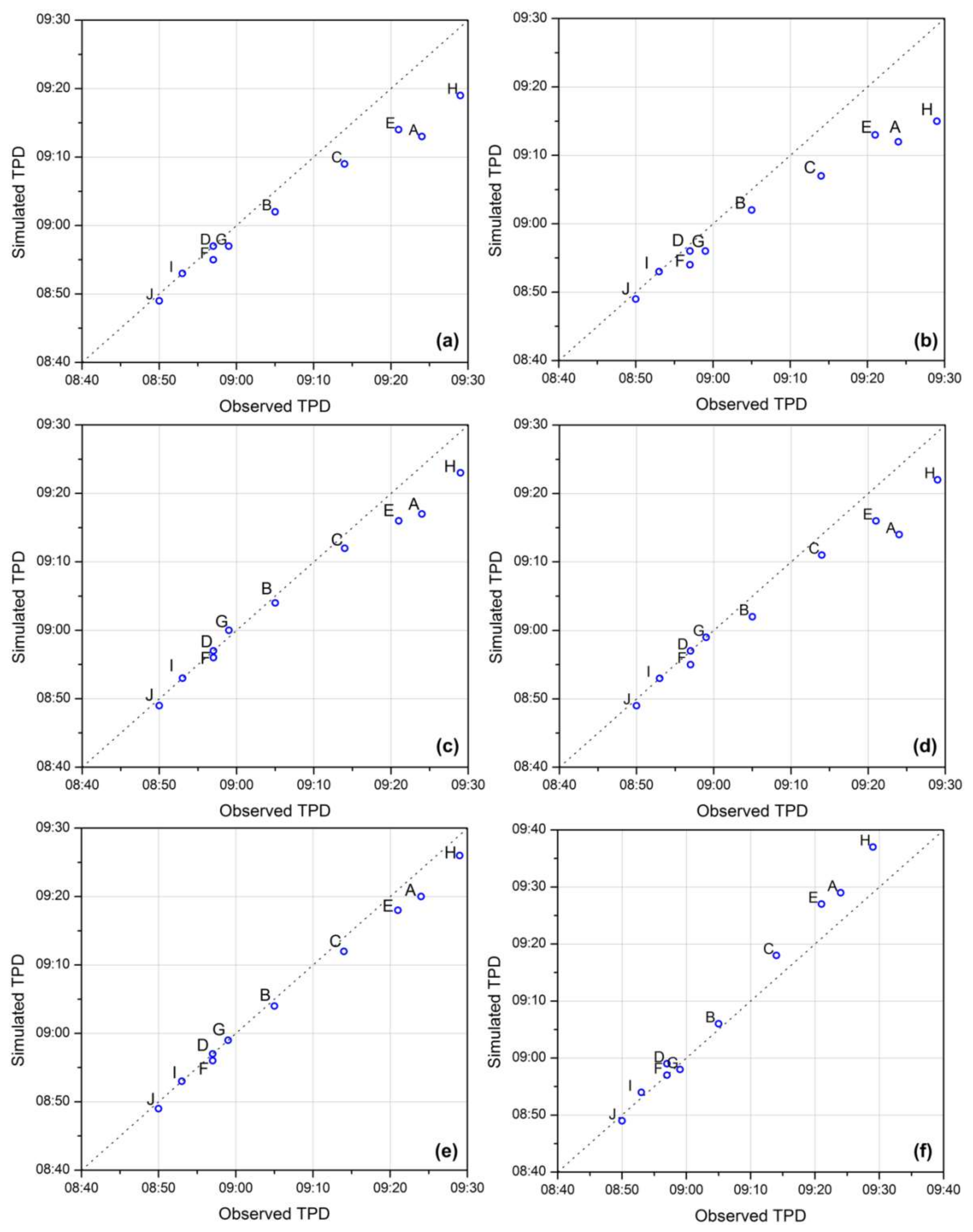
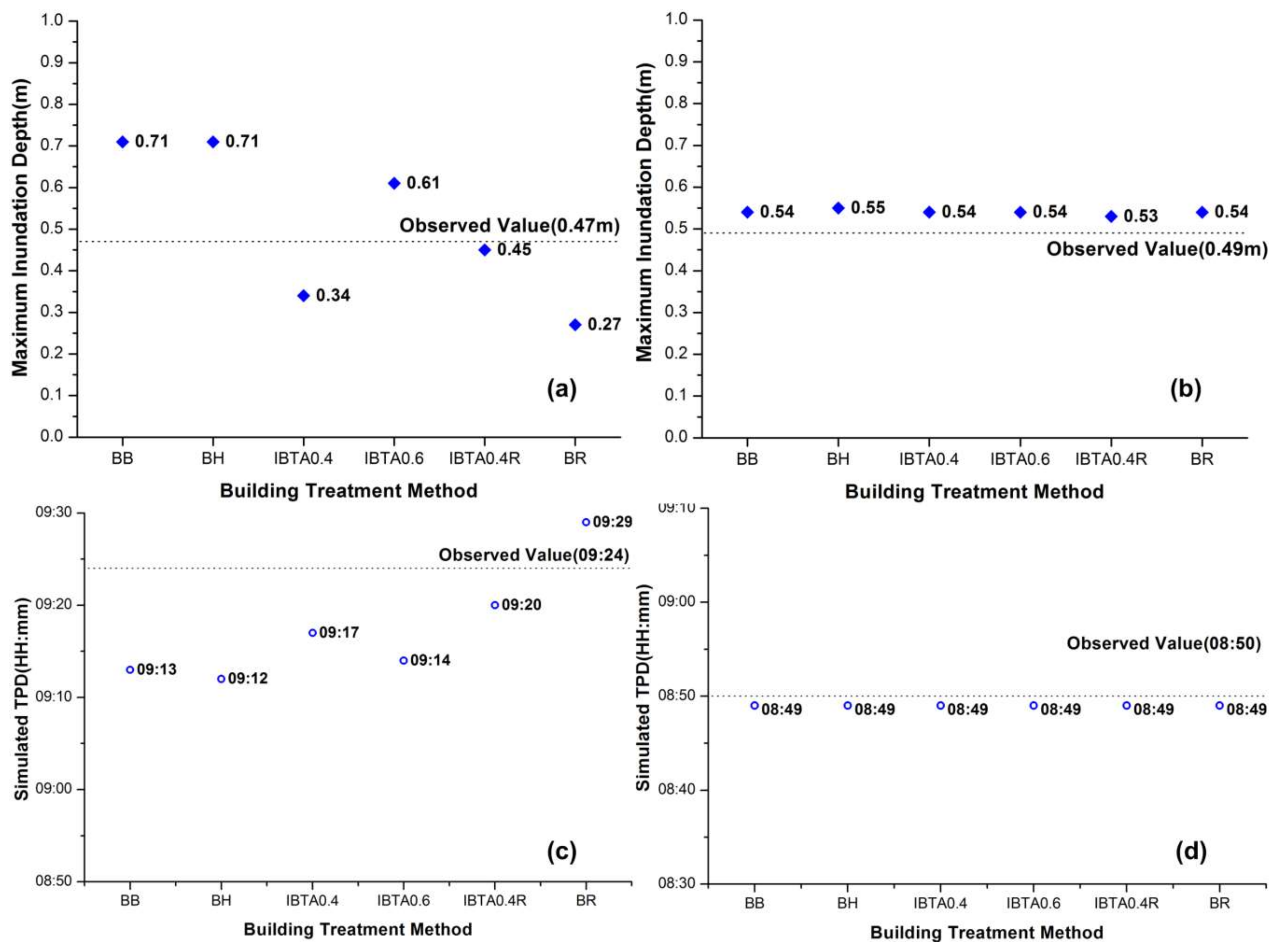
3.2. Performance of Building Treatment Methods
4. Conclusions
- The model results of the maximum inundation depth, extent and timing of the peak depth all exhibited sensitivity to the building treatment method in dense building regions of the study area. However, this sensitivity is reduced in open areas without dense building surroundings (points I and J).
- As the blockage, storage and resistance effects of buildings were both adequately represented, IBTA0.4R produced the best performance across all building treatment methods considered in this study when assessed against the measurement values of the flood event.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hsu, M.H.; Chen, S.H.; Chang, T.J. Inundation simulation for urban drainage basin with storm sewer system. J. Hydrol. 2000, 234, 21–37. [Google Scholar] [CrossRef]
- Wu, X.; Yu, D.; Wilby, R.L. An evaluation of the impacts of land surface modification, storm sewer development, and rainfall variation on waterlogging risk in Shanghai. Nat. Hazards 2012, 63, 305–323. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.; Yin, Z.; Wang, J.; Xu, S. Modelling the anthropogenic impacts on fluvial flood risks in a coastal mega-city: A scenario-based case study in Shanghai, China. Landsc. Urban Plan. 2015, 136, 144–155. [Google Scholar] [CrossRef]
- Gallegos, H.A.; Schubert, J.E.; Sanders, B.F. Two-dimensional, high-resolution modeling of urban dam-break flooding: A case study of Baldwin Hills, California. Adv. Water Resour. 2009, 32, 1323–1335. [Google Scholar] [CrossRef]
- Tsubaki, R.; Fujita, I. Unstructured grid generation using LiDAR data for urban flood inundation modelling. Hydrol. Process. 2010, 24, 1404–1420. [Google Scholar] [CrossRef]
- Du, J.; Qian, L.; Rui, H.; Zuo, T.; Zheng, D.; Xu, Y.; Xu, C. Assessing the effects of urbanization on annual runoff and flood events using an integrated hydrological modeling system for Qinhuai River basin, China. J. Hydrol. 2012, 464, 127–139. [Google Scholar] [CrossRef]
- Alfieri, L.; Feyen, L.; Baldassarre, G.D. Increasing flood risk under climate change: A pan-European assessment of the benefits of four adaptation strategies. Clim. Chang. 2016, 136, 507–521. [Google Scholar] [CrossRef]
- Kelman, I.; Spence, R. An overview of flood actions on buildings. Eng. Geol. 2004, 73, 297–309. [Google Scholar] [CrossRef]
- Middelmann-Fernandes, M.H. Flood damage estimation beyond stage–damage functions: An Australian example. J. Flood Risk Manag. 2010, 3, 88–96. [Google Scholar] [CrossRef]
- Fewtrell, T.J.; Bates, P.D.; Horritt, M.; Hunter, N.M. Evaluating the effect of scale in flood inundation modelling in urban environments. Hydrol. Process. 2010, 22, 5107–5118. [Google Scholar] [CrossRef]
- Biancamaria, S.; Bates, P.D.; Boone, A.; Mognard, N.M. Large-scale coupled hydrologic and hydraulic modelling of the Ob river in Siberia. J. Hydrol. 2009, 379, 136–150. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Interactions between subgrid-scale resolution, feature representation and grid-scale resolution in flood inundation modelling. Hydrol. Process. 2011, 25, 36–53. [Google Scholar] [CrossRef]
- Mignot, E.; Paquier, A.; Haider, S. Modeling floods in a dense urban area using 2D shallow water equations. J. Hydrol. 2006, 327, 186–199. [Google Scholar] [CrossRef]
- Hine, D.; Hall, J.W. Information gap analysis of flood model uncertainties and regional frequency analysis. Water Resour. Res. 2010, 46, W01514. [Google Scholar] [CrossRef]
- Phillips, B.C.; Yu, S.; Thompson, G.R.; De Silva, N. 1D and 2D Modelling of Urban Drainage Systems using XP-SWMM and TUFLOW. In Proceedings of the 10th International Conference on Urban Drainage, Copenhagen, Denmark, 21–26 August 2005; pp. 21–26. [Google Scholar]
- Mciwem, K.B. JFLOW: A multiscale two-dimensional dynamic flood model. Water Environ. J. 2010, 20, 79–86. [Google Scholar]
- Bates, P.D.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Lamb, R.; Crossley, A.; Waller, S. A fast 2D floodplain inundation model. Water Manag. 2009, 162, 363–370. [Google Scholar]
- Neal, J.; Schumann, G.; Bates, P.D. A subgrid channel model for simulating river hydraulics and floodplain inundation over large and data sparse areas. Water Resour. Res. 2012, 48, W11506. [Google Scholar] [CrossRef]
- Schumann, J.P.; Neal, J.C.; Voisin, N.; Andreadis, K.M.; Pappenberger, F.; Phanthuwongpakdee, N.; Hall, A.C.; Bates, P.D. A first large-scale flood inundation forecasting model. Water Resour. Res. 2013, 49, 6248–6257. [Google Scholar] [CrossRef]
- Neal, J.; Schumann, G.; Fewtrell, T.; Budimir, M.; Bates, P.D.; Mason, D. Evaluating a new LISFLOOD-FP formulation with data from the summer 2007 floods in Tewkesbury, UK. J. Flood Risk Manag. 2011, 4, 88–95. [Google Scholar] [CrossRef]
- Mason, D.C.; Cobby, D.M.; Horritt, M.S.; Bates, P.D. Floodplain friction parameterization in two-dimensional river flood models using vegetation heights derived from airborne scanning laser altimetry. Hydrol. Process. 2003, 17, 1711–1732. [Google Scholar] [CrossRef]
- Fewtrell, T.J.; Duncan, A.; Sampson, C.C.; Neal, J.C.; Bates, P.D. Benchmarking urban flood models of varying complexity and scale using high resolution terrestrial LiDAR data. Phys. Chem. Earth 2011, 36, 281–291. [Google Scholar] [CrossRef]
- Sampson, C.C.; Fewtrell, T.J.; Duncan, A.; Shaad, K.; Horritt, M.S.; Bates, P.D. Use of terrestrial laser scanning data to drive decimetric resolution urban inundation models. Adv. Water Resour. 2012, 41, 1–17. [Google Scholar] [CrossRef]
- Ozdemir, H.; Sampson, C.C.; De Almeida, G.A.M.; Bates, P.D. Evaluating scale and roughness effects in urban flood modelling using terrestrial LIDAR data. Hydrol. Earth Syst. Sci. 2013, 17, 4015–4030. [Google Scholar] [CrossRef]
- Neal, J.; Villanueva, I.; Wright, N.; Willis, T.; Fewtrell, T.; Bates, P.D. How much physical complexity is needed to model flood inundation? Hydrol. Process. 2012, 26, 2264–2282. [Google Scholar] [CrossRef]
- Yin, J.; Lin, N.; Yu, D. Coupled modeling of storm surge and coastal inundation: A case study in New York City during Hurricane Sandy. Water Resour. Res. 2016, 52, 8685–8699. [Google Scholar] [CrossRef]
- Gallien, T.W.; Schubert, J.E.; Sanders, B.F. Predicting tidal flooding of urbanized embayments: A modeling framework and data requirements. Coast. Eng. 2011, 58, 567–577. [Google Scholar] [CrossRef]
- Brown, J.D.; Spencer, T.; Moeller, I. Modeling storm surge flooding of an urban area with particular reference to modeling uncertainties: A case study of Canvey Island, United Kingdom. Water Resour. Res. 2007, 43, 93–104. [Google Scholar] [CrossRef]
- Schubert, J.E.; Sanders, B.F.; Smith, M.J.; Wright, N.G. Unstructured mesh generation and landcover-based resistance for hydrodynamic modeling of urban flooding. Adv. Water Resour. 2008, 31, 1603–1621. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.G.; Liang, D.; Falconer, R.A.; Lin, B.; Waller, S.; et al. Benchmarking 2D Hydraulic Models for Urban Flood Simulations. Water Manag. 2008, 161, 13–30. [Google Scholar]
- Aronica, G.T.; Lanza, L.G. Drainage efficiency in urban areas: A case study. Hydrol. Process. 2010, 19, 1105–1119. [Google Scholar] [CrossRef]
- Aronica, G.T.; Tucciarelli, T.; Nasello, C. 2D Multilevel Model for Flood Wave Propagation in Flood-Affected Areas. J. Water Resour. Plan. Manag. 1998, 124, 210–217. [Google Scholar] [CrossRef]
- Chen, A.S.; Evans, B.; Djordjević, S.; Savic, D.A. A coarse-grid approach to representing building blockage effects in 2D urban flood modelling. J. Hydrol. 2012, 426, 1–16. [Google Scholar] [CrossRef]
- Chen, A.S.; Evans, B.; Djordjević, S.; Savic, D.A. Multi-layered coarse grid modelling in 2D urban flood simulations. J. Hydrol. 2012, 470, 1–11. [Google Scholar] [CrossRef]
- Schubert, J.E.; Sanders, B.F. Building treatments for urban flood inundation models and implications for predictive skill and modeling efficiency. Adv. Water Resour. 2012, 41, 49–64. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.; Guo, S.; Liao, W.; Zeng, Z.; Chen, X. Scenario-based projections of future urban inundation within a coupled hydrodynamic model framework: A case study in Dongguan City, China. J. Hydrol. 2017, 547, 428–442. [Google Scholar] [CrossRef]
- Schmitt, T.G.; Thomas, M.; Ettrich, N. Analysis and modeling of flooding in urban drainage systems. J. Hydrol. 2004, 299, 300–311. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.S.; Djordjevic, S.; Savic, D.A. Comparison of 1D/1D and 1D/2D coupled (sewer/surface) hydraulic models for urban flood simulation. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Peterson, E.W.; Wicks, C.M. Assessing the importance of conduit geometry and physical parameters in karst systems using the storm water management model (SWMM). J. Hydrol. 2006, 329, 294–305. [Google Scholar] [CrossRef]
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model (SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Hunter, N.M.; Horritt, M.S.; Bates, P.D.; Wilson, M.D.; Werner, M.G.F. An adaptive time step solution for raster-based storage cell modelling of floodplain inundation. Adv. Water Resour. 2005, 28, 975–991. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Dottori, F.; Todini, E. Developments of a flood inundation model based on the cellular automata approach: Testing different methods to improve model performance. Phys. Chem. Earth 2011, 36, 266–280. [Google Scholar] [CrossRef]
- Sampson, C.C.; Bates, P.D.; Neal, J.C.; Horritt, M.S. An automated routing methodology to enable direct rainfall in high resolution shallow water models. Hydrol. Process. 2013, 27, 467–476. [Google Scholar] [CrossRef]
- De Almeida, G.A.M.; Bates, P.D. Applicability of the local inertial approximation of the shallow water equations to flood modeling. Water Resour. Res. 2013, 49, 4833–4844. [Google Scholar] [CrossRef]
- Yu, D.; Coulthard, T.J. Evaluating the importance of catchment hydrological parameters for urban surface water flood modelling using a simple hydro-inundation model. J. Hydrol. 2015, 524, 385–400. [Google Scholar] [CrossRef]

| Monitoring Point | Flood Event of 20 June 2016 | Flood Event of 1 July 2016 | BCR (%) | ||
|---|---|---|---|---|---|
| Maximum Inundation Depth | Peak Depth Time | Maximum Inundation Depth | Peak Depth Time | ||
| A | 0.37 m | 12:32 | 0.49 m | 09:24 | 43.8% |
| B | 0.61 m | 12:16 | 0.72 m | 09:05 | 44.7% |
| C | 0.39 m | 12:22 | 0.51 m | 09:14 | 22.1% |
| D | 0.34 m | 12:06 | 0.47 m | 08:57 | 45.1% |
| E | 0.22 m | 12:29 | 0.36 m | 09:21 | 38.2% |
| F | 0.42 m | 12:05 | 0.51 m | 08:57 | 25.7% |
| G | 0.40 m | 12:08 | 0.52 m | 08:59 | 26.5% |
| H | 0.35 m | 12:38 | 0.45 m | 09:29 | 31.9% |
| I | 0.36 m | 12:03 | 0.49 m | 08:53 | 4.9% |
| J | 0.22 m | 12:01 | 0.34 m | 08:50 | 0% |
| Model Parameters | Type | Calibrated Value |
|---|---|---|
| Manning’s n value for pipelines | Cast iron pipe | 0.012 |
| Concrete pipe | 0.014 | |
| Plastic pipe | 0.014 | |
| Manning’s n value for overland flow | Floodplain | 0.02 |
| Buildings (BR and IBTA0.4) | 0.5 | |
| Depression storage | Impervious surfaces | 1.5 mm |
| Pervious surfaces | 3.8 mm | |
| Horton infiltration parameters | Maximum infiltration rate | 76.5 mm/h |
| Minimum infiltration rate | 3.9 mm/h | |
| Decay constant | 6 h–1 | |
| Drying time | 7 d |
| Building Treatment Method | RMSED | ||
|---|---|---|---|
| All | Points I and J | ||
| BB | Calibration | 0.24 m | 0.05 m |
| Validation | 0.23 m | 0.06 m | |
| BH | Calibration | 0.25 m | 0.05 m |
| Validation | 0.24 m | 0.06 m | |
| IBTA0.4 | Calibration | 0.15 m | 0.05 m |
| Validation | 0.14 m | 0.06 m | |
| IBTA0.6 | Calibration | 0.14 m | 0.04 m |
| Validation | 0.14 m | 0.06 m | |
| IBTA0.4R | Calibration | 0.06 m | 0.04 m |
| Validation | 0.06 m | 0.05 m | |
| BR | Calibration | 0.19 m | 0.06 m |
| Validation | 0.18 m | 0.06 m | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Tan, F.; Zhang, Y. Improved Building Treatment Approach for Urban Inundation Modeling: A Case Study in Wuhan, China. Water 2018, 10, 1760. https://doi.org/10.3390/w10121760
Shen J, Tan F, Zhang Y. Improved Building Treatment Approach for Urban Inundation Modeling: A Case Study in Wuhan, China. Water. 2018; 10(12):1760. https://doi.org/10.3390/w10121760
Chicago/Turabian StyleShen, Ji, Fangbi Tan, and Yongzhi Zhang. 2018. "Improved Building Treatment Approach for Urban Inundation Modeling: A Case Study in Wuhan, China" Water 10, no. 12: 1760. https://doi.org/10.3390/w10121760
APA StyleShen, J., Tan, F., & Zhang, Y. (2018). Improved Building Treatment Approach for Urban Inundation Modeling: A Case Study in Wuhan, China. Water, 10(12), 1760. https://doi.org/10.3390/w10121760





