Mechanism of Steady and Unsteady Piping in Coastal and Hydraulic Structures with a Sloped Face
Abstract
1. Introduction
2. Unsteady Piping Experiments
2.1. Experimental Setup
2.2. Soil Characteristics
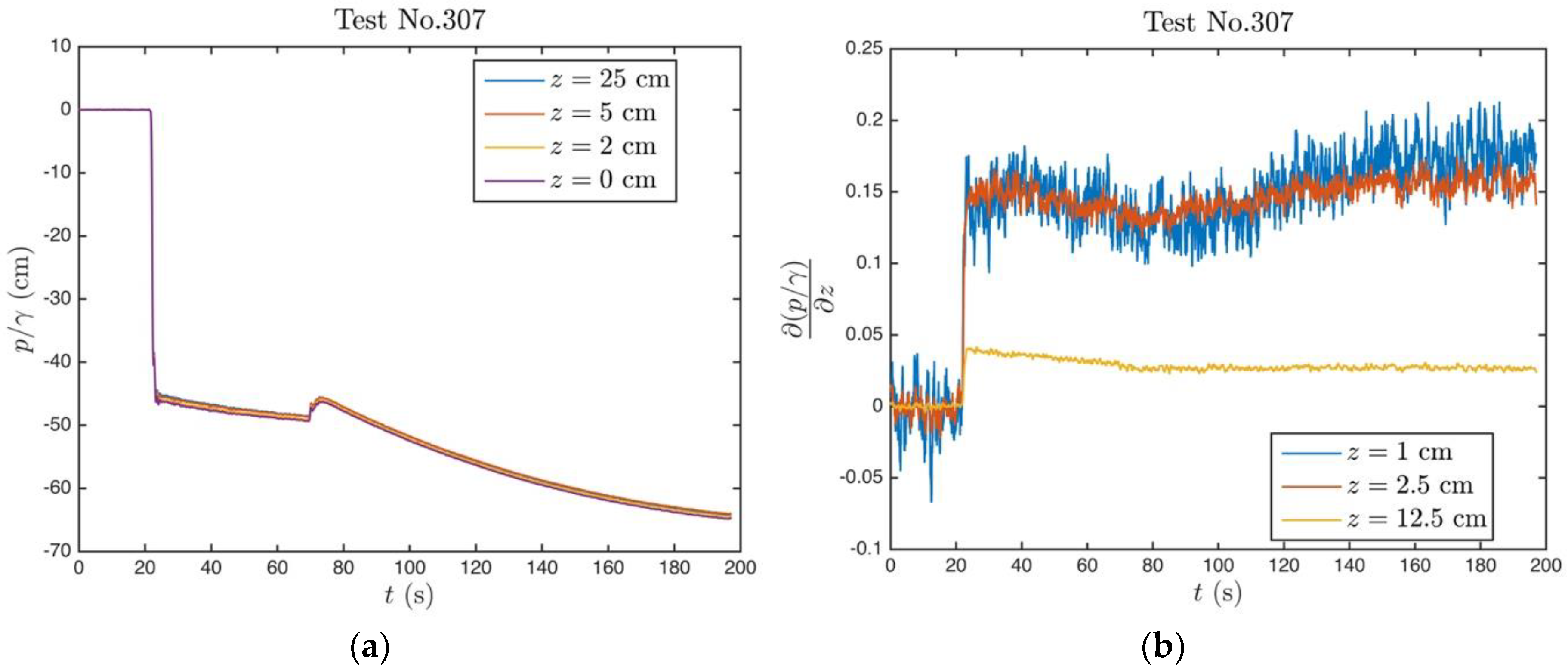
2.3. Experimental Procedure
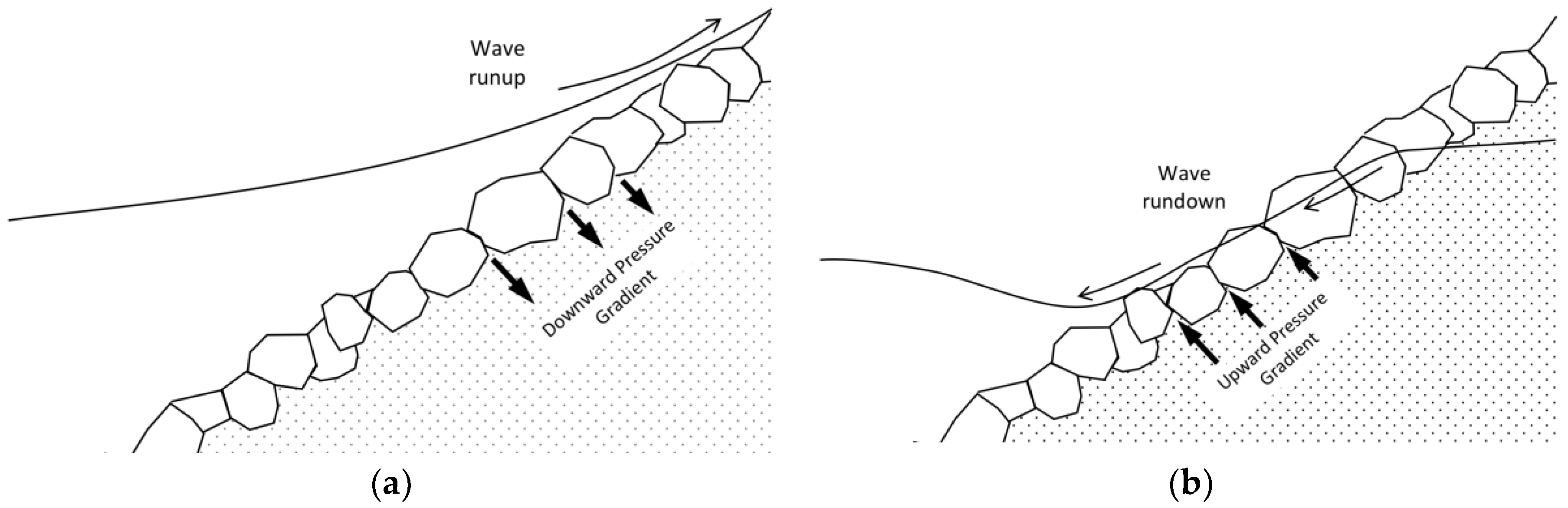
3. Force-Balance Equation on a Soil Element
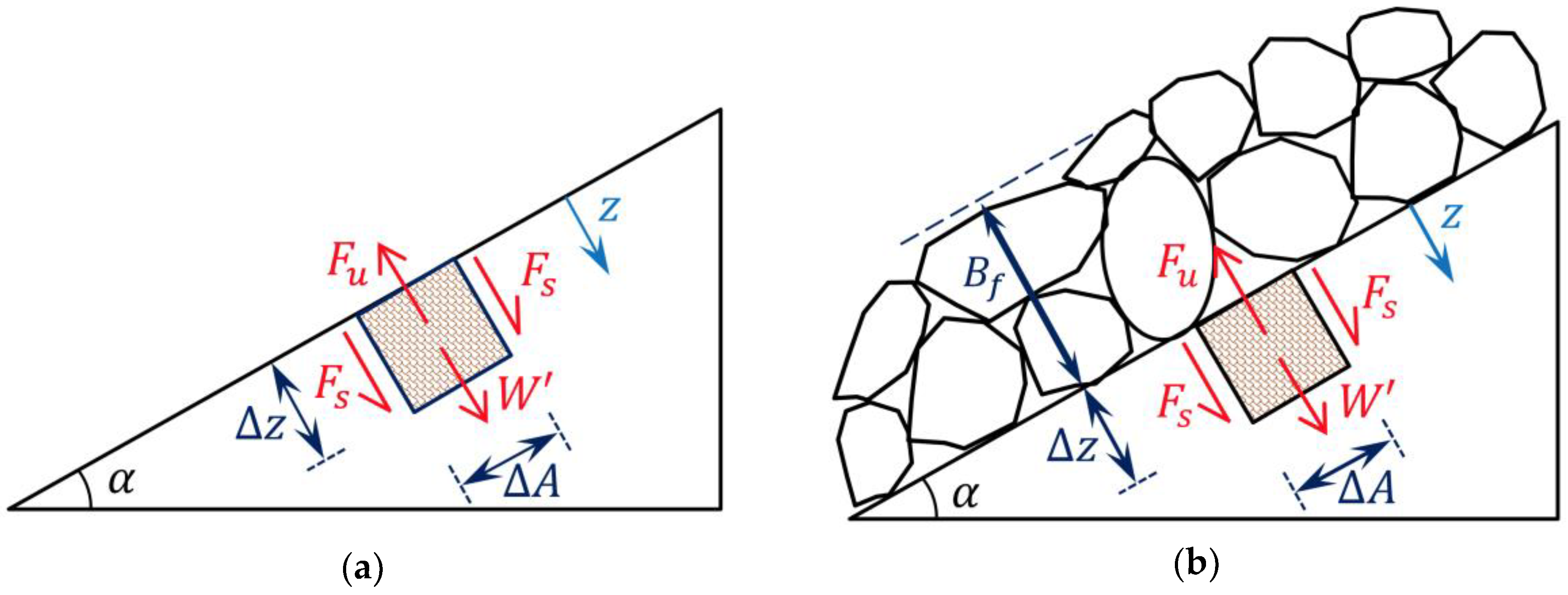
3.1. Force-Balance Equation for a Sloped-Face Soil Parcel Without a Filter Layer
3.2. Force-Balance Equation for a Sloped-Face Soil Parcel Protected by a Filter Layer
4. Results
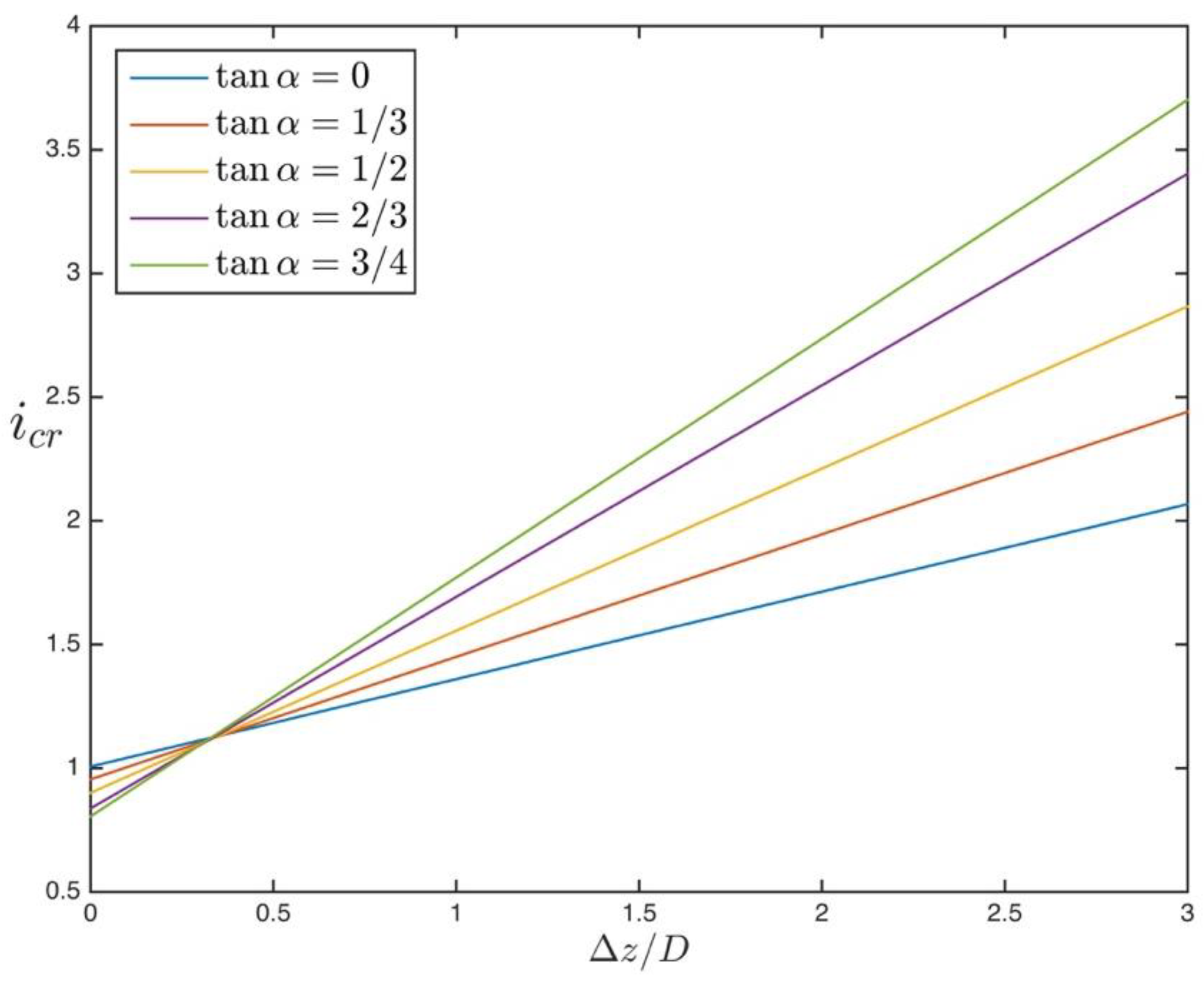
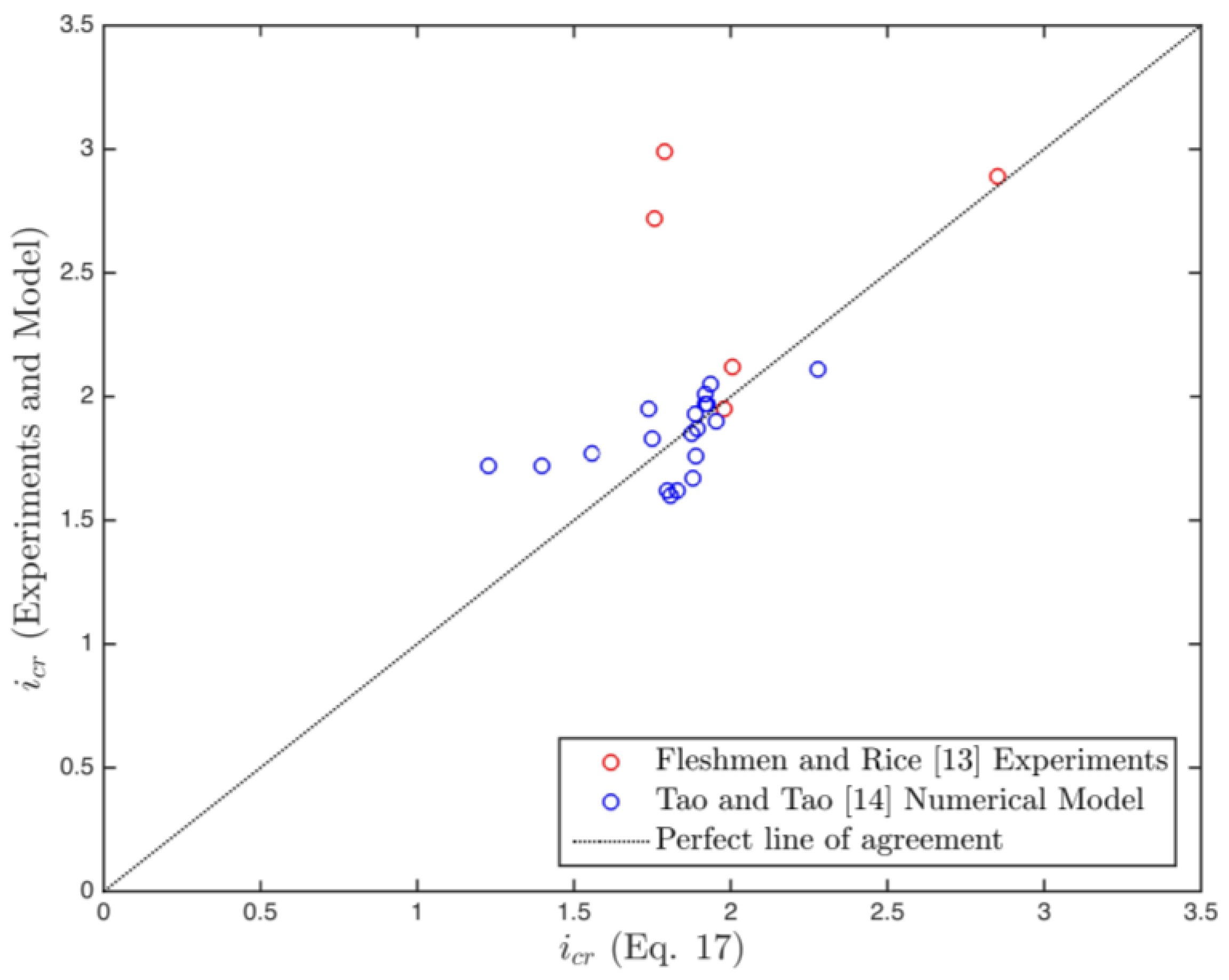
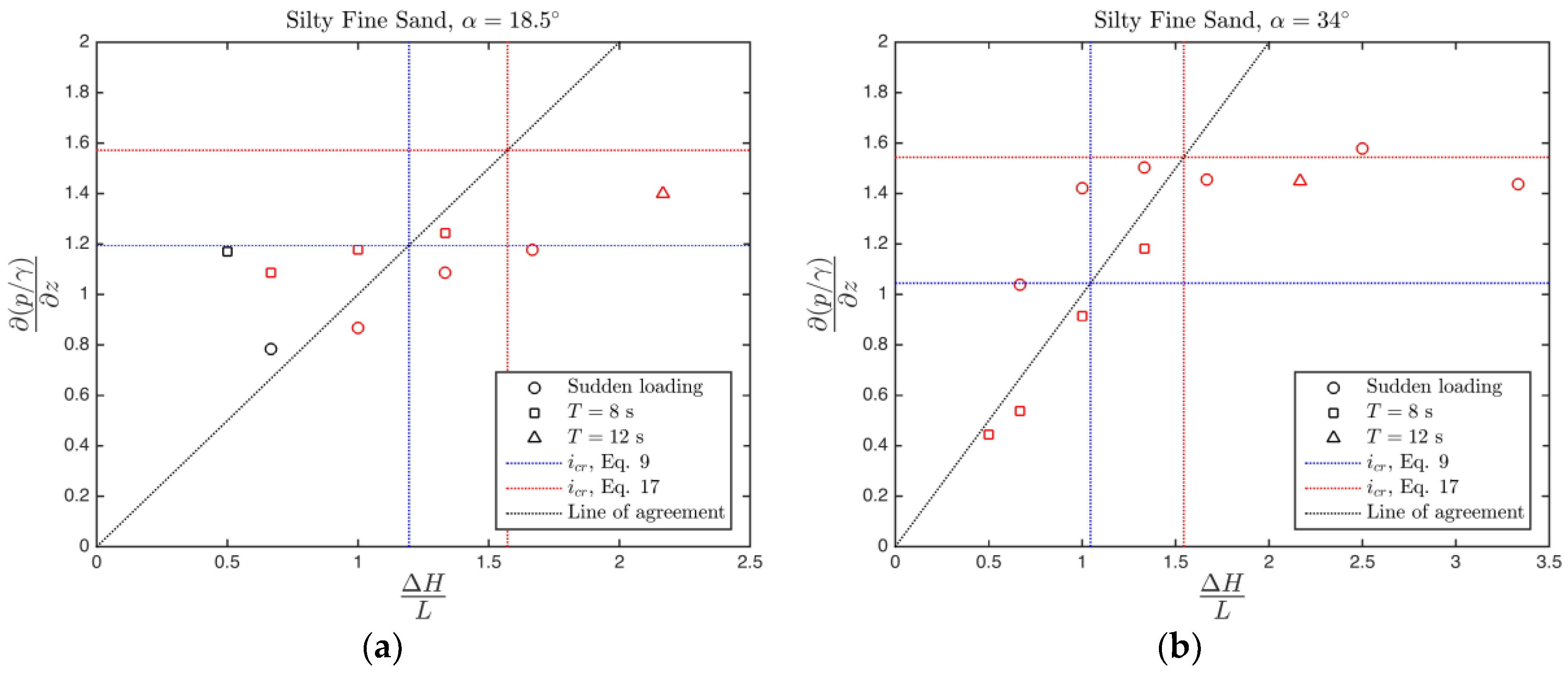
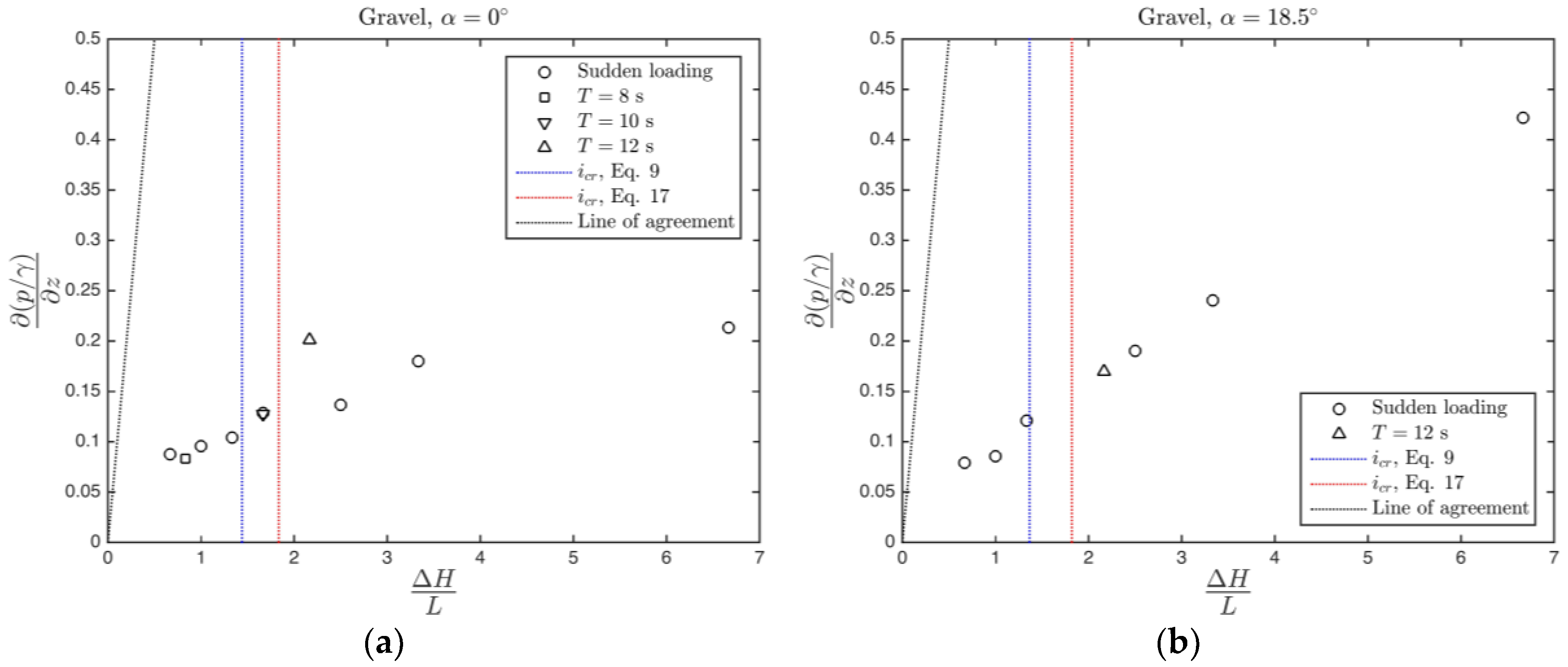
4.1. Comparison of the Steady Piping Criterion with the Available Data
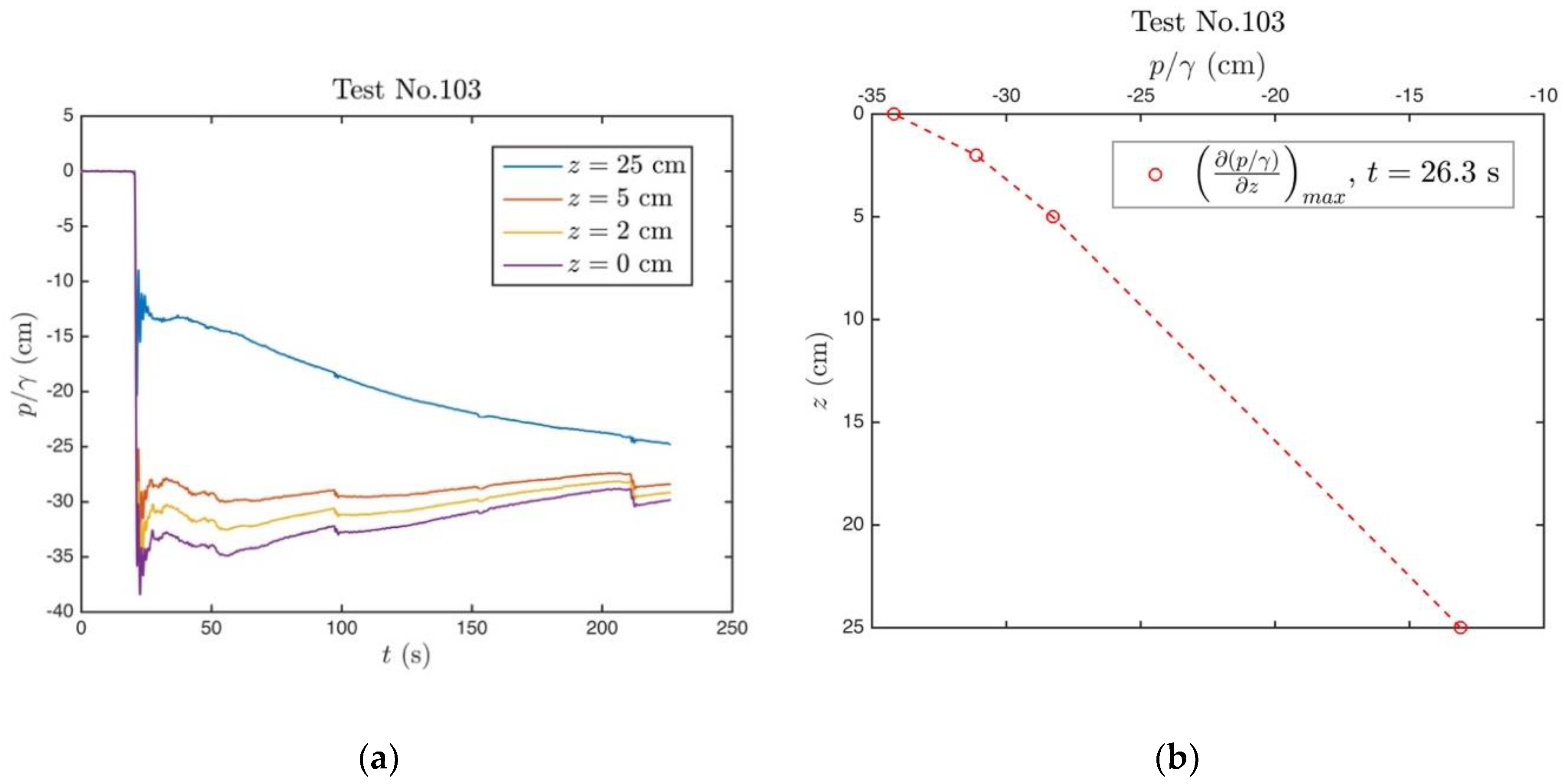
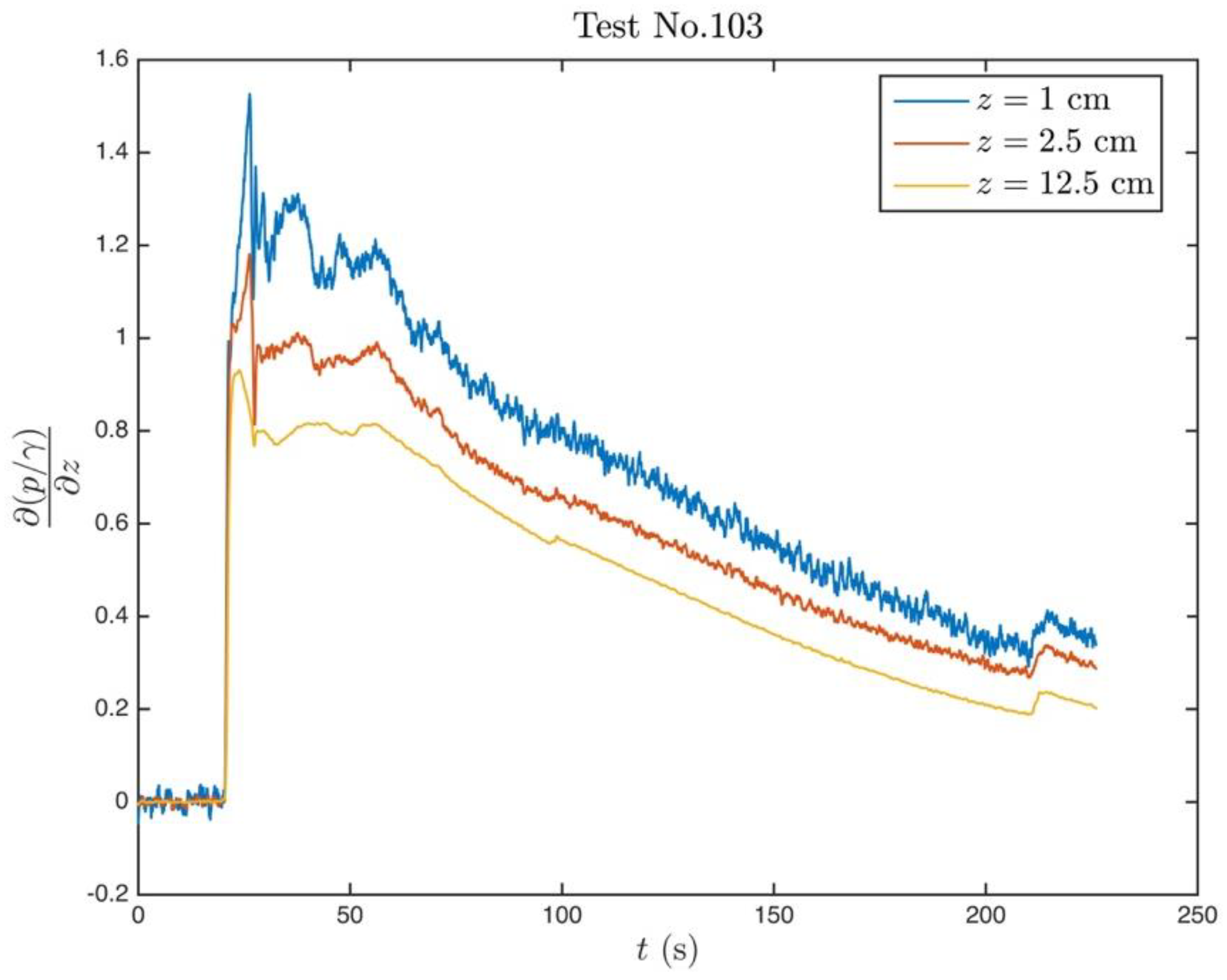
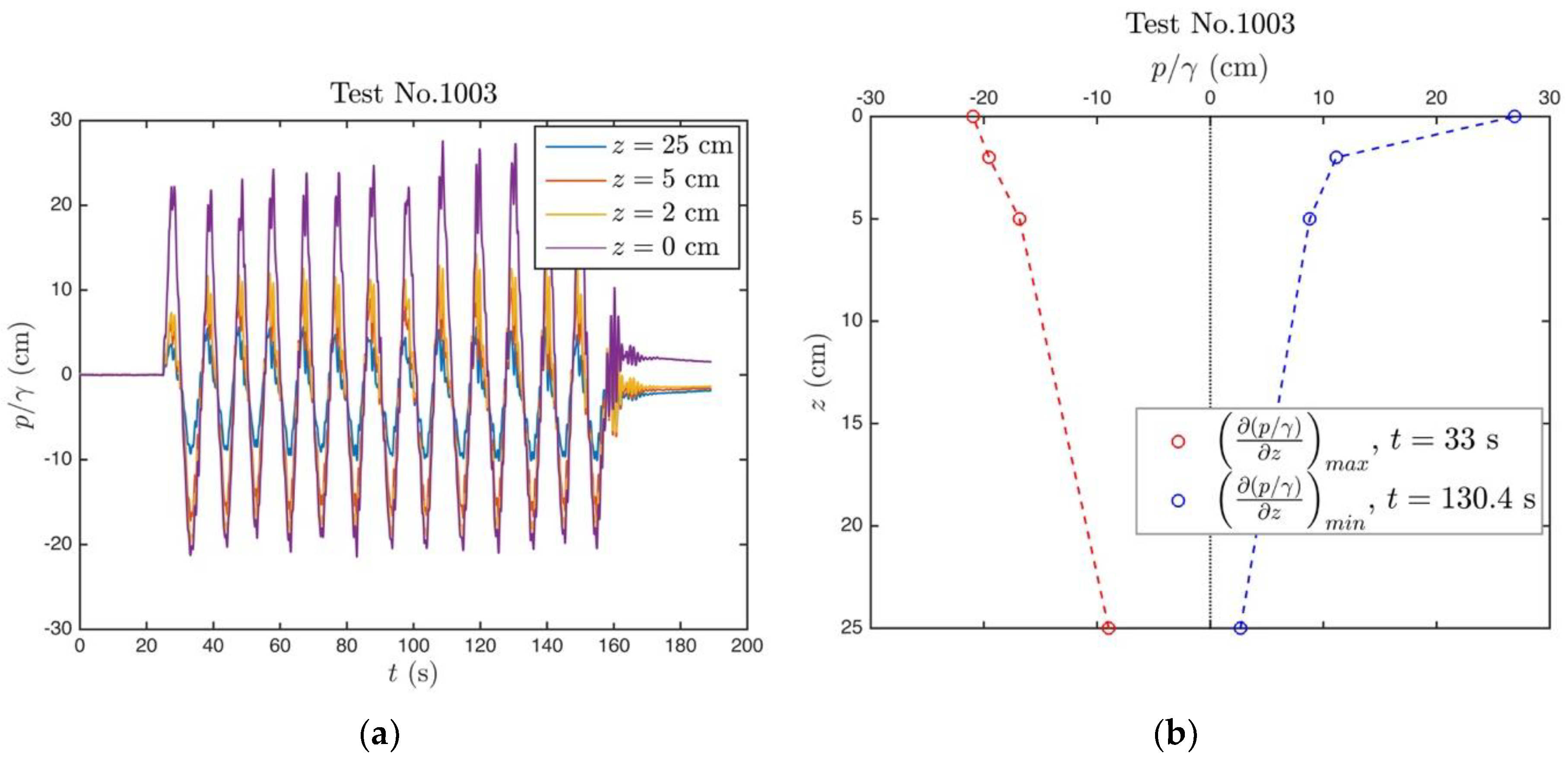
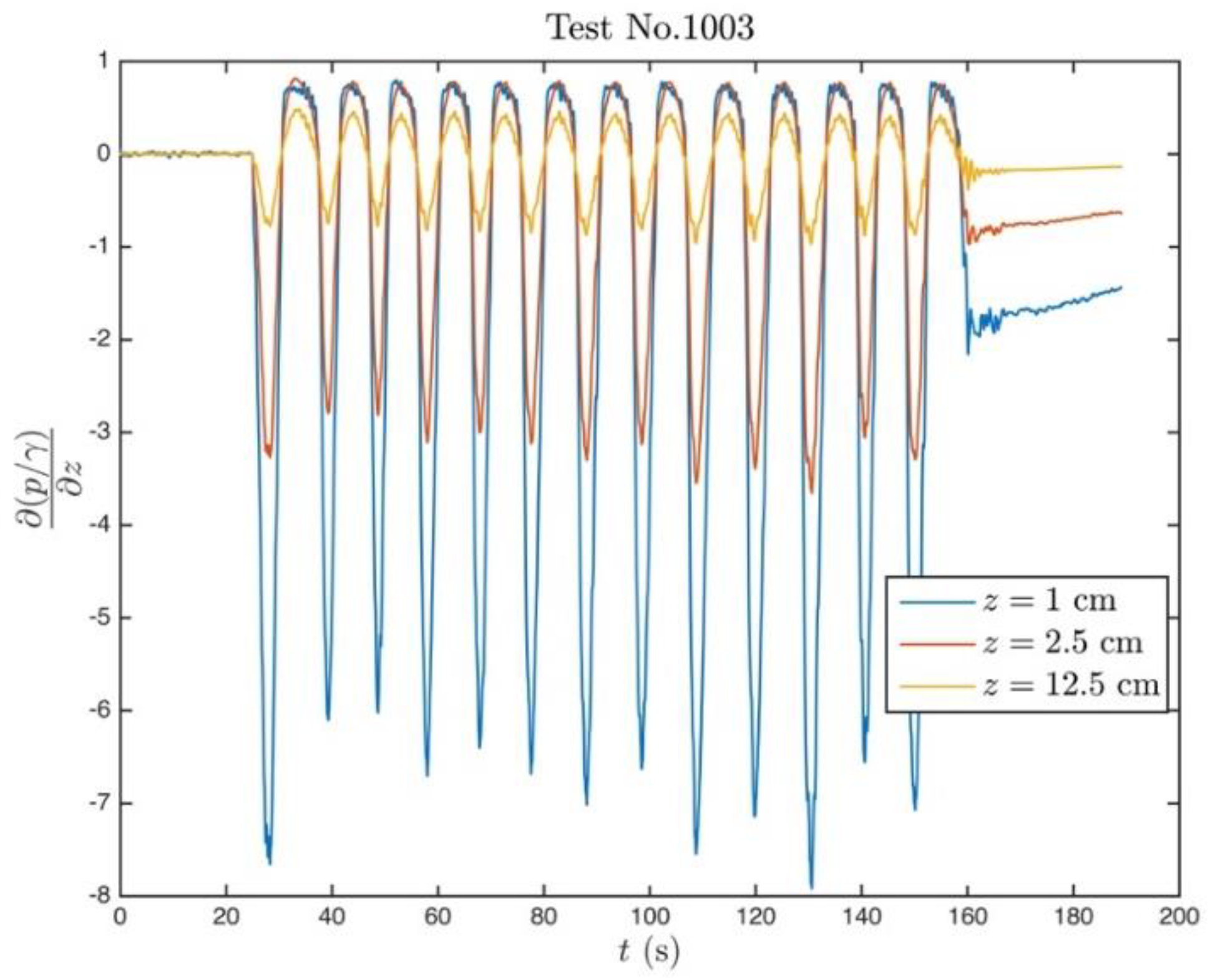
4.2. Experimental Findings on Unsteady Piping
5. Discussion and Remarks for Practical Applications
- The grain size ratio of the filter layer to the base soil must comply with the filter criteria given in Equations (1)–(4). This would ensure that the base soil will not be able to move through the grains of the filter layer without clogging the pores but the pore water can be drained easily through the filter. Hence, piping resistance would be enhanced.
- It was seen that the hydraulic conductivity is an important parameter in piping, especially when the hydraulic gradient acts unsteadily. Therefore, the selection of low hydraulic conductivity base soils (especially for coastal structures) must be omitted if possible (see also [2]).
- The thickness of the filter layer must be carefully determined. To this end, the criterion given with Equation (20) can be used to define the minimum filter layer thickness . The thickness of the base soil parcel, , can be taken as zero to omit the uncertainties and to stay on the safe side. Equations (18) and (22) can be used to determine the active lateral earth pressure coefficient () and the filter pore size (), respectively. It should be noted that the criterion for the total failure of the entire soil column given by [24] and defined in Equation (24) comes out to be less critical than the piping criterion ().
6. Conclusions
- In the case of steady hydraulic loading, the comparison of the force-balance equation (Equation (17)) and the available data from the literature shows that friction forces are effective in resisting against piping. However, there are quite many uncertainties in estimating the friction forces. Therefore, it may be safer to resort to the force balance equation with zero friction (Equation (9)) for design purposes when there is no filter layer. The effect of filter layer on increasing the friction forces is formulated (Equation (20)) in terms of the filter layer thickness.
- The mechanisms of piping under steady and unsteady hydraulic loadings are quite different since the inertia terms become effective in the unsteady loading case. Generally speaking, soil is more prone to piping in the case of unsteady hydraulic loading. This was also shown by Tomlinson and Vaid [3] when they increased the hydraulic gradient in a rapid manner and got piping under a much lower hydraulic gradient compared to the gradually increasing case.
- Experimental findings showed that the period of oscillatory hydraulic loading did not have a significant effect on the results for the tested periods of loading ( s). Additionally, the sudden hydraulic loading did not generate a distinctly different effect on the soil compared to the oscillatory.
- The hydraulic conductivity of the soil becomes very important for piping vulnerability under unsteady hydraulic gradients, such that low conductivity soil was seen to be much more susceptible to piping. As the hydraulic conductivity gets higher, the soil becomes more resistant to piping under unsteady hydraulic loading. Therefore, the usage of low hydraulic conductivity soils in coastal structures must be omitted, as also suggested by the design guidelines [2].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Richards, K.S.; Reddy, K.R. Critical appraisal of piping phenomena in earth dams. Bull. Eng. Geol. Environ. 2007, 66, 381–402. [Google Scholar] [CrossRef]
- CIRIA (Construction Industry Research, Information Association). The Rock Manual: The Use of Rock in Hydraulic Engineering; CIRIA Report; CIRIA: London, UK, 2007. [Google Scholar]
- Tomlinson, S.S.; Vaid, Y.P. Seepage forces and confining pressure effects on piping erosion. Can. Geotech. J. 2000, 37, 1–13. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1943; p. 510. [Google Scholar]
- de Graauw, A.F.; van der Meulen, T.; van der Does de Bye, M.R. Granular filters: Design criteria. J. Waterw. Port Coast. Ocean Eng. ASCE 1984, 110, 80–96. [Google Scholar] [CrossRef]
- Sumer, B.M.; Nielsen, A.W. Sinking failure of scour protection at wind turbine foundation. Proc. ICE-Energy 2013, 166, 170–188. [Google Scholar] [CrossRef]
- Ojha, C.S.P.; Singh, V.P.; Adrian, D.H. Determination of Critical Head in Soil Piping. J. Hydraul. Eng. 2003, 129, 511–518. [Google Scholar] [CrossRef]
- El Shamy, U.; Aydin, F. Multiscale modeling of flood-induced piping in river levees. J. Geotech. Geoenviron. Eng. 2008, 134, 1385–1398. [Google Scholar] [CrossRef]
- Abdelhamid, Y.; El Shamy, U. Pore-scale modeling of fine-particle migration in granular filters. Int. J. Geomech. 2015, 16, 04015086. [Google Scholar] [CrossRef]
- Ko, D.; Kang, J. Experimental Studies on the Stability Assessment of a Levee Using Reinforced Soil Based on a Biopolymer. Water 2018, 10, 1059. [Google Scholar] [CrossRef]
- Sterpi, D. Effects of the erosion and transport of fine particles due to seepage flow. Int. J. Geomech. 2008, 3, 111–122. [Google Scholar] [CrossRef]
- Jacobson, T. An Analysis on Soil Properties on Predicting Critical Hydraulic Gradients for Piping Progression in Sandy Soils. Master’s Thesis, Utah State University, Logan, UT, USA, 2013. [Google Scholar]
- Fleshman, M.; Rice, J. Laboratory modeling of the mechanisms of piping erosion initiation. J. Geotech. Geoenviron. Eng. 2014, 04014017. [Google Scholar] [CrossRef]
- Tao, J.; Tao, H. Factors Affecting Piping Erosion Resistance: Revisited with a Numerical Modeling Approach. Int. J. Geomech. 2017, 17, 04017097. [Google Scholar] [CrossRef]
- Kirca, V.S.O.; Caglar, B.; Bagci, T.; Kilci, E.; Kabdasli, M.S. Use of Steel Slag in Rubble-Mound Marine Structures. In Proceedings of the 3rd Iron and Steel Symposium (UDCS’17), Karabuk, Turkey, 3–5 April 2017; pp. 307–313. [Google Scholar]
- Wang, Y.; Li, C.; Zhou, X.; Wei, X. Seepage Piping Evolution Characteristics in Bimsoils-An Experimental Study. Water 2017, 9, 458. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Hu, Y.; Xiao, Y. Optimization of Multiple Seepage Piping Parameters to Maximize the Critical Hydraulic Gradient in Bimsoils. Water 2017, 9, 787. [Google Scholar] [CrossRef]
- Honjo, Y.; Veneziano, D. Improved filter criterion for cohesionless soils. J. Geotech. Eng. ASCE 1989, 115, 75–94. [Google Scholar] [CrossRef]
- Okita, Y.; Nikigaki, M. Filtration processes observed with g-ray density meter. In Filters in Geotechnical and Hydraulic Engineering; Brauns, J., Heibaum, M., Schuler, U., Eds.; A.A. Balkema: Rotterdam, The Netherlands, 1992. [Google Scholar]
- Nielsen, A.W.; Probst, T.; Petersen, T.U.; Sumer, B.M. Sinking of armour layer around a vertical cylinder exposed to waves and current. Coast. Eng. 2015, 100, 58–66. [Google Scholar] [CrossRef]
- Sumer, B.M.; Sen, M.B.; Karagali, I.; Ceren, B.; Fredsøe, J.; Sottile, M.; Zillioli, L.; Fuhrman, D.R. Flow and sediment transport induced by a plunging solitary wave. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Sumer, B.M.; Guner, H.A.; Hansen, N.M.; Fuhrman, D.R.; Fredsøe, J. Laboratory observations of flow and sediment transport induced by plunging regular waves. J. Geophys. Res. Oceans 2013, 118, 6161–6182. [Google Scholar] [CrossRef]
- Jensen, B.; Christensen, E.D.; Sumer, B.M. Pressure-induced forces and shear stresses on rubble mound breakwater armour layers in regular waves. Coast. Eng. 2014, 91, 60–75. [Google Scholar] [CrossRef]
- Alcérreca-Huerta, J.C.; Oumeraci, H. Soil stability analysis for wave-induced momentary liquefaction beneath porous bonded revetments. Coast. Eng. 2018, 138, 22–35. [Google Scholar] [CrossRef]
- Kilci, E.; Kirca, V.S.O. A Modified Piping Criterion for Determination of Effective Filter Thickness under Revetment Slopes. In Proceedings of the 13th Advances in Civil Engineering Congress, Izmir, Turkey, 12–14 September 2018. [Google Scholar]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; John Wiley & Sons: New York, NY, USA, 1948. [Google Scholar]
- Lambe, T.W.; Whitman, R.V. Soil Mechanics (SI Version); John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Fair, G.M.; Hatch, L.P.; Hudson, H.E. Fundamental factors governing the streamline flow of water through sand [with discussion]. J. (Am. Water Works Assoc.) 1933, 25, 1551–1565. [Google Scholar] [CrossRef]
- Uno, T.; Kamiya, K.; Matsushima, T. The relationship between particle size and void diameter. In Proceedings of the Geofilters’96 Conference, Montreal, QC, Canada, 29–31 May 1996; pp. 67–74. [Google Scholar]
- Burcharth, H.F.; Andersen, O.K. On the one-dimensional steady and unsteady porous flow equations. Coast. Eng. 1995, 24, 233–257. [Google Scholar] [CrossRef]


| Soil Type | (m/s) | |||||
|---|---|---|---|---|---|---|
| Silty Fine Sand | 3.00 | 0.2 | 3.1 | 0.37 | 40 | |
| Medium Sand | 2.65 | 0.7 | 2.5 | 0.39 | 38 | |
| Gravel | 3.40 | 12 | 1.8 | 0.40 | 44 |
| No. | Soil Type | Type of Hydraulic Loading | Surface Angle, | (s) | Piping? | |
|---|---|---|---|---|---|---|
| 101 | Medium Sand | Sudden | 0 | 0.15 | N/A | No |
| 102 | Sudden | 0 | 0.30 | N/A | No | |
| 103 | Sudden | 0 | 0.50 | N/A | Yes | |
| 104 | Sudden | 0 | 0.75 | N/A | Yes | |
| 105 | Sudden | 0 | 0.40 | N/A | Yes | |
| 201 | Oscillatory | 0 | 0.10 | 8 | No | |
| 202 | Oscillatory | 0 | 0.15 | 8 | No | |
| 203 | Oscillatory | 0 | 0.20 | 8 | No | |
| 204 | Oscillatory | 0 | 0.25 | 8 | No | |
| 205 | Oscillatory | 0 | 0.30 | 8 | No | |
| 206 | Oscillatory | 0 | 0.35 | 8 | No | |
| 207 | Oscillatory | 0 | 0.40 | 8 | No | |
| 208 | Oscillatory | 0 | 0.40 | 12 | Yes | |
| 209 | Oscillatory | 0 | 0.50 | 12 | Yes | |
| 901 | Silty Fine Sand | Sudden | 0 | 0.20 | N/A | No |
| 902 | Sudden | 0 | 0.30 | N/A | No | |
| 903 | Sudden | 0 | 0.40 | N/A | Yes | |
| 904 | Sudden | 0 | 0.50 | N/A | Yes | |
| 905 | Sudden | 0 | 0.75 | N/A | Yes | |
| 1001 | Oscillatory | 0 | 0.15 | 8 | No | |
| 1002 | Oscillatory | 0 | 0.20 | 8 | No | |
| 1003 | Oscillatory | 0 | 0.30 | 10 | Yes | |
| 1004 | Oscillatory | 0 | 0.40 | 10 | Yes | |
| 1005 | Oscillatory | 0 | 0.50 | 10 | Yes | |
| 1006 | Oscillatory | 0 | 0.65 | 12 | Yes | |
| 1101 | Sudden | 18.5 | 0.20 | N/A | No | |
| 1102 | Sudden | 18.5 | 0.30 | N/A | Yes | |
| 1103 | Sudden | 18.5 | 0.40 | N/A | Yes | |
| 1104 | Sudden | 18.5 | 0.50 | N/A | Yes | |
| 1201 | Oscillatory | 18.5 | 0.15 | 8 | No | |
| 1202 | Oscillatory | 18.5 | 0.20 | 8 | Yes | |
| 1203 | Oscillatory | 18.5 | 0.30 | 8 | Yes | |
| 1204 | Oscillatory | 18.5 | 0.40 | 8 | Yes | |
| 1205 | Oscillatory | 18.5 | 0.65 | 12 | Yes | |
| 1301 | Sudden | 34.0 | 0.20 | N/A | Yes | |
| 1302 | Sudden | 34.0 | 0.30 | N/A | Yes | |
| 1303 | Sudden | 34.0 | 0.40 | N/A | Yes | |
| 1304 | Sudden | 34.0 | 0.50 | N/A | Yes | |
| 1305 | Sudden | 34.0 | 0.75 | N/A | Yes | |
| 1306 | Sudden | 34.0 | 1.00 | N/A | Yes | |
| 1401 | Oscillatory | 34.0 | 0.15 | 8 | Yes | |
| 1402 | Oscillatory | 34.0 | 0.20 | 8 | Yes | |
| 1403 | Oscillatory | 34.0 | 0.30 | 8 | Yes | |
| 1404 | Oscillatory | 34.0 | 0.40 | 8 | Yes | |
| 1405 | Oscillatory | 34.0 | 0.65 | 12 | Yes | |
| 301 | Gravel | Sudden | 0 | 0.20 | N/A | No |
| 302 | Sudden | 0 | 0.30 | N/A | No | |
| 303 | Sudden | 0 | 0.40 | N/A | No | |
| 304 | Sudden | 0 | 0.50 | N/A | No | |
| 305 | Sudden | 0 | 0.75 | N/A | No | |
| 306 | Sudden | 0 | 1.00 | N/A | No | |
| 307 | Sudden | 0 | 2.00 | N/A | No | |
| 401 | Oscillatory | 0 | 0.25 | 8 | No | |
| 402 | Oscillatory | 0 | 0.50 | 10 | No | |
| 403 | Oscillatory | 0 | 0.65 | 12 | No | |
| 501 | Sudden | 18.5 | 0.20 | N/A | No | |
| 502 | Sudden | 18.5 | 0.30 | N/A | No | |
| 503 | Sudden | 18.5 | 0.40 | N/A | No | |
| 504 | Sudden | 18.5 | 0.75 | N/A | No | |
| 505 | Sudden | 18.5 | 1.00 | N/A | No | |
| 506 | Sudden | 18.5 | 2.00 | N/A | No | |
| 601 | Oscillatory | 18.5 | 0.65 | 12 | No | |
| 701 | Sudden | 34.0 | 2.00 | N/A | No | |
| 801 | Oscillatory | 34.0 | 0.65 | 12 | No |
| Ref. | Data No. | Soil Type | |||||
|---|---|---|---|---|---|---|---|
| [13] | 1 | Ottawa 20–30 sand | 2.64 | 35 | 0.35 | 2.49 | 1.95 |
| [13] | 2 | Ottawa graded sand | 2.64 | 35 | 0.35 | 2.49 | 2.12 |
| [13] | 3 | Angular 20–30 sand | 2.64 | 37 | 0.43 | 2.49 | 2.72 |
| [13] | 4 | Angular graded sand | 2.64 | 38 | 0.42 | 2.49 | 2.99 |
| [13] | 5 | No. 100 garnet sand | 3.87 | 39 | 0.47 | 2.49 | 2.89 |
| [14] | 1 | N/A | 2.65 | 26.57 | 0.36 | 2.47 | 1.67 |
| [14] | 2 | N/A | 2.65 | 26.57 | 0.38 | 2.47 | 1.39 |
| [14] | 3 | N/A | 2.65 | 26.57 | 0.38 | 2.47 | 1.36 |
| [14] | 4 | N/A | 2.65 | 26.57 | 0.40 | 2.47 | 1.29 |
| [14] | 5 | N/A | 2.65 | 26.57 | 0.40 | 2.47 | 1.29 |
| [14] | 6 | N/A | 2.65 | 26.57 | 0.39 | 2.47 | 1.32 |
| [14] | 7 | N/A | 2.65 | 26.57 | 0.38 | 0.59 | 1.26 |
| [14] | 8 | N/A | 2.65 | 26.57 | 0.38 | 1.11 | 1.28 |
| [14] | 9 | N/A | 2.65 | 26.57 | 0.38 | 1.55 | 1.29 |
| [14] | 10 | N/A | 2.65 | 26.57 | 0.37 | 2.53 | 1.45 |
| [14] | 11 | N/A | 2.65 | 26.57 | 0.37 | 3.52 | 1.68 |
| [14] | 12 | N/A | 2.65 | 0.00 | 0.35 | 2.40 | 1.23 |
| [14] | 13 | N/A | 2.65 | 14.04 | 0.37 | 2.51 | 1.38 |
| [14] | 14 | N/A | 2.65 | 26.57 | 0.37 | 2.55 | 1.45 |
| [14] | 15 | N/A | 2.65 | 36.87 | 0.38 | 2.58 | 1.53 |
| [14] | 16 | N/A | 2.65 | 0.00 | 0.36 | 2.47 | 1.32 |
| [14] | 17 | N/A | 2.65 | 14.04 | 0.37 | 2.51 | 1.42 |
| [14] | 18 | N/A | 2.65 | 26.57 | 0.37 | 2.53 | 1.45 |
| [14] | 19 | N/A | 2.65 | 26.57 | 0.37 | 2.55 | 1.45 |
| [14] | 20 | N/A | 2.65 | 26.57 | 0.37 | 2.53 | 0.16 |
| [14] | 21 | N/A | 2.65 | 26.57 | 0.38 | 2.56 | 1.51 |
| [14] | 22 | N/A | 2.65 | 26.57 | 0.39 | 2.58 | 1.38 |
| [14] | 23 | N/A | 2.65 | 26.57 | 0.39 | 2.62 | 1.32 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirca, V.S.O.; Kilci, R.E. Mechanism of Steady and Unsteady Piping in Coastal and Hydraulic Structures with a Sloped Face. Water 2018, 10, 1757. https://doi.org/10.3390/w10121757
Kirca VSO, Kilci RE. Mechanism of Steady and Unsteady Piping in Coastal and Hydraulic Structures with a Sloped Face. Water. 2018; 10(12):1757. https://doi.org/10.3390/w10121757
Chicago/Turabian StyleKirca, V. S. Ozgur, and R. Evren Kilci. 2018. "Mechanism of Steady and Unsteady Piping in Coastal and Hydraulic Structures with a Sloped Face" Water 10, no. 12: 1757. https://doi.org/10.3390/w10121757
APA StyleKirca, V. S. O., & Kilci, R. E. (2018). Mechanism of Steady and Unsteady Piping in Coastal and Hydraulic Structures with a Sloped Face. Water, 10(12), 1757. https://doi.org/10.3390/w10121757





