Abstract
Although steady uniform friction formulas have been introduced to the framework of a one-dimensional (1D) hydrodynamic model for centuries, the error of friction calculation inevitably undermines the performance of flood routing. Based on successful results of unsteady channel friction research studies, a newly proposed unsteady friction model is introduced to establish a modified 1D hydrodynamic model (namely, the modified SVN model). With the help of a carefully designed parameter calibration method, the performance of the modified SVN model was compared with that of the original SVN model in a simulation test for a hydraulic experiment. This study’s results revealed that compared with the original SVN model, the modified SVN model could achieve a better simulation in both the flow depth and the sectional averaged velocity simulations. Furthermore, it could reduce the peak value error and the time-at-peak error as well, indicating that the use of an unsteady friction model can efficiently improve the performance of a 1D hydrodynamic model.
1. Introduction
Based on Saint-Venant equations, the one-dimensional (1D) hydrodynamic model is a fundamental tool for the simulation of 1D flow movement in the case of river or open channel flows [,]. It has been widely used in the fields of hydraulic simulation like flood forecasting and waterway engineering [,]. The partial differential equations for rivers and channels can help us better understand the unsteady flow behavior and prevent the potential damage of flood events. However, the performance of the 1D hydrodynamic model critically depends on the frictional calculation accuracy. In the case of unsteady flow, flow unsteadiness and flow non-uniformity make the frictional resistance become more complex. As a result, friction factors (e.g., the Chezy coefficient or the Manning roughness factor) become very hard to identify and the error of friction calculation inevitably undermines the performance of flood routing [].
Two types of approaches have been developed to address this problem. First, many advanced optimal algorithms have been applied to calibrate the parameter of friction term. For example, the influence coefficient algorithm was introduced by Becker and Yeh for the parameter identification problem in unsteady open channel flow []. The genetic algorithm (GA) was introduced by Giustolisi to determine the Chezy coefficient in corrugated channels []. A numerical method based on the adjoint equation algorithm was proposed by Ding and Wang to identify Manning’s n in river networks []. Further information about identifying friction factors can be found in Liu [], Nocedal and Wright [], Ding et al. [], Zou et al. [], etc. Despite the fact that parameter calibration algorithms take advantage of optimal control theories, it seems that a calibrating friction factor as a constant is not enough to compensate all the discrepancies between model calculations and observations []. Second, many real-time parameter updating methods have been used to dynamically update the friction factor in the engineering field. For example, Hsu et al. proposed an iteration Manning roughness factor updating technique for real-time flood forecasting []. Bao and Zhao applied the Kalman filter to deal with the roughness coefficient updating problem []. In addition, Liu et al. presented a multi-segmental roughness coefficient updating method to consider both spatial distribution and a time-varying process of roughness coefficient in the channel from Cuntan to Wanxian in Three Gorges of the Yangtze River []. These dynamic routing models with real-time roughness updating methods give good results for hydraulic simulations. However, because the updated friction factors of the present time step are usually quite different from those of the previous time step, the results deteriorate markedly when the updated parameter is used for hydraulic forecasting [].
Neither carefully designed parameter calibration algorithms nor dynamically updating methods can significantly improve the accuracy of friction calculation, indicating that the classic friction models like the Chezy formula and the Manning formula only work for steady uniform flows but not for unsteady flows. If one neglects the impact of flow unsteadiness on frictional resistance, the friction coefficients become grey-box parameters []. Rouse [], Yen [], and Ding et al. [] argued that in the case of unsteady flow, friction parameters such as the Chezy coefficient and the Manning roughness factor actually include the components of surface friction resistance, form resistance, wave resistance, and resistance due to flow unsteadiness. As a result, these coefficients are very unstable and unpredictable in an unsteady flow regime []. Many studies in the literature are devoted to developing new models for calculating 1D unsteady channel friction, like Tu and Graf [], Rowiński et al. [], Mrokowska et al. [], and Bao et al. []. The proposed unsteady friction models contain the terms of time and space derivatives of hydraulic parameters, which better demonstrate the dependence of unsteady friction on flow unsteadiness and flow non-uniformity. Nevertheless, on one hand, most studies considered the problem of unsteady friction as the inverse problem of flood routing. Hence, the unsteady friction formulas proposed in them are derived from the momentum equation of Saint-Venant equations. These equations cannot be used to calculate the friction term of the 1D hydrodynamic model. On the other hand, although some of the proposed formulas can be used to compute the friction slope in the 1D hydrodynamic model, these formulas are more complex than the Chezy and Manning formulas. For example, Bao et al. proposed a 1D unsteady friction formula based on dimensional analysis instead of the inverse analysis of momentum equation []. However, in their proposal, more empirical parameters were introduced to describe the dependence of unsteady friction on spatio-temporal derivatives of hydraulic parameters. It is known that the determination of empirical parameters is very difficult due to the high nonlinearity of the 1D hydrodynamic model. Hence, the estimation of friction parameters would be more difficult and time-consuming when the proposed unsteady friction model is used as a substitute for the Chezy or Manning formula. It is evident that the advantages of using these unsteady friction models in the 1D hydrodynamic model have not yet been discussed.
To uncover the potential advantages of unsteady friction formulas, a modified 1D hydrodynamic model is proposed in this paper, referred to as the modified SVN model, based on the unsteady friction formula presented by Bao et al. []. Since the steady uniform component of the unsteady friction model is the same as the Chezy formula, a classic 1D hydrodynamic model with the friction calculator of the Chezy formula is used for comparison, referred to as the original SVN model. The performances of the modified and the original SVN models are compared using a dataset of hydraulic experiments, where a genetic algorithm-based parameter calibration method is used to overcome the difficulties of empirical parameter estimation.
2. Flume Experiments and Data
The hydraulic experiments were conducted in a 20.0 m long, 0.3 m wide, and 0.4 m high glass-made flume with a recirculating water system in the hydraulic laboratory of Hydraulic and Hydro-Power Engineering, Hohai University. The experiment setup is shown in Figure 1. The water recirculation system consists of the glass-made flume, a recycle pond, a large water tank, and two pumps. The pump between the flume and the large water tank was used to pump water into the flume. In order to relieve the vibration to the flume, a flexible tube was used for connecting the water pump and the flume. A small water tank was placed ahead of the flume to straighten the incoming flow and eliminate large eddies, which made the flow state across the experimental range more stable and without significant ripples. The used water passed through the tail gate and then entered the cycle pond. It entered the large tank through another pump for reutilization. In addition, gravel was paved evenly on the bottom to simulate a rough riverbed []. The flume bed remained flat throughout the experiments. Three observation cross sections were placed along the flume at an interval of 5 m, referred to as cross sections #1, #2, and #3. The incoming flow was controlled using a hydraulic valve and its discharge was measured using a pipe ultrasonic flow meter with a precision of 0.5% [].
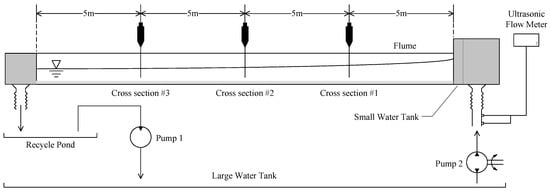
Figure 1.
Experiment flume with its recirculation system.
In order to obtain the cross-sectional averaged velocity, a NORTEK Acoustic Doppler Velocimeter (ADV) (Nortek, Vangkroken 2, 1351 Rud, Norway) was used to measure instantaneously the vertical distributions of point velocities at each cross section []. The sampling rate and number of the ADV were set to 50 Hz and 5000, respectively, according to Niño et al. []. The relationships of the cross-sectional averaged velocity versus a fixed-point velocity were carefully calibrated at cross sections #1, #2, and #3, referred to as V−V* relationships. They are expressed using Equations (1), (2), and (3), respectively:
where V* is the averaged velocity over a time which is detected by the ADV at a fixed point and V is the cross-sectional averaged velocity. Fitting curves are displayed in Figure 2, where the coefficients of determination are 0.9990, 0.9695, and 0.9937, respectively.
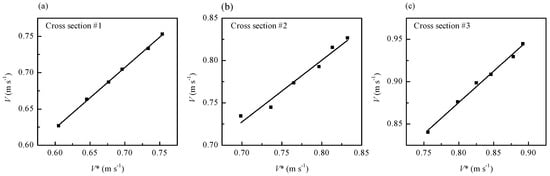
Figure 2.
Fitting curves of velocity at fixed points versus the cross-sectional averaged velocity (V−V* relationships): (a) the V–V* relationship at cross section #1; (b) the V–V* relationship at cross section #2; (c) the V–V* relationship at cross section #3.
In the unsteady flow experiments, the discharge of incoming flow which was controlled by the hydraulic valve gradually rose from the base value, reached its peak value, and then fell back to the original one, simulating flood events of single-peak hydrographs. In all, 10 different man-made flood events were conducted. Each flood event was performed within 3–4 min. The discharge of incoming flow in the No. 1 experiments (1-1, 1-2, 1-3, 1-4, 1-5) was in the range of 60–110 (m3/h), and the discharge in the No. 2 experiments (2-1, 2-2, 2-3, 2-4, 2-5) was in the range of 60–100 (m3/h). During the unsteady flow experiments, both the cross-sectional averaged velocity V and the flow depth D were recorded every 5 s and the observation precision was evaluated using a posteriori error inspection method. According to the principle of conservation of mass, variables at each cross section should be compatible with following water balance equation:
where the left side equation is the accumulative discharge of inflow (i.e., ∑Qin), B is the width of the flume, L is the length of the part ahead of the cross section, D(t) is the flow depth series, V(t) is the average velocity series, (T) is the average stage of the part ahead of the cross section at the end of experiment, and (0) is average stage of the part ahead of the cross section at the beginning of the experiment. According to Equation (4), the ∑Qin can be calculated based on the time series of D(t) and V(t), referred to as calculated accumulative discharge. Moreover, ∑Qin was measured using the pipe ultrasonic flow meter as well. Therefore, the relative error of ∑Qin in each experimental flood event can be obtained, as shown in Table 1.

Table 1.
Relative error between the observed and calculated accumulative discharges at each cross section in man-made flood events.
Table 1 shows that the relative error between the calculated accumulative discharge and the observed one is less than 4%, mostly controlled within 2% (86.7%). This illustrates that the observations of D(t) and V(t) at each cross section are reasonable. With the dataset of hydraulic experiments, the characteristic of unsteady flow is simply illustrated. This study’s experiments showed that the wave crests passed through cross sections #1, #2, and #3 in sequence. As an example, the flow depth hydrographs of the No. 1-1 flood event are shown in Figure 3.
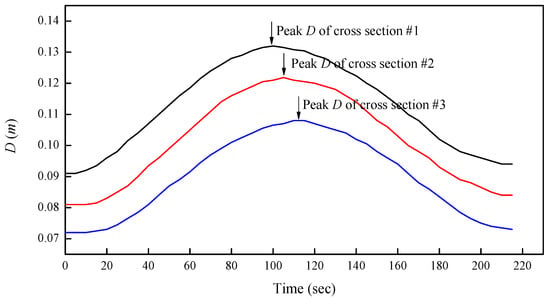
Figure 3.
The flow depth hydrographs of the No. 1-1 flood event.
In addition, the relationships between the cross-sectional averaged velocity and the flow depth displayed an anticlockwise loop-shaped curve in the experiments (see Figure 4).
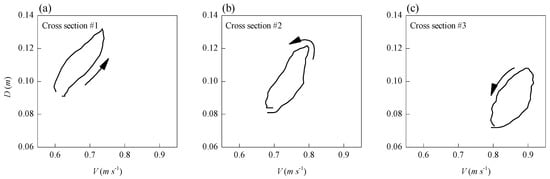
Figure 4.
The relationships between cross-sectional averaged velocity and the flow depth at: (a) cross section #1, (b) cross section #2, and (c) cross section #3 in flood event No. 1-1.
3. Methods
3.1. Extended Chezy Formula
In engineering practice, empirical steady uniform friction formulas are widely used to estimate the unsteady friction slope of open channels and rivers []. For example, the Chezy formula can be written as:
where Sc is the friction slope computed with the Chezy formula, V is the cross-sectional averaged velocity, R is the hydraulic radius, and C is the Chezy coefficient. The relationships among Chezy’s C, Manning’s n, and the Fanning friction factor f can be written as follows:
where n is the Manning roughness coefficient, f is the Fanning friction factor, and g is the gravitational acceleration.
However, the frictional resistance of unsteady flow is more complex than that of steady uniform flow. A symbolic function which was deduced by Rouse [] reported that the Fanning friction factor f is associated with several dimensionless hydraulic parameters, as follows:
where Re is the Reynolds number, K is the relative roughness, η is a dimensionless parameter that describes the effect of the cross-sectional geometric shape, N is the dimensionless flow non-uniformity factor, Fr is Froude number, and U is the dimensionless flow unsteadiness factor.
Equation (7) is a general equation for both steady uniform and unsteady frictional resistances. In Equation (7), some dimensionless parameters such as Re, Fr, K, and η are also the factors which affect the frictional resistance of steady uniform flow. On the other hand, the other parameters like U and N which represent the impacts of flow unsteadiness and flow non-uniformity are the additional factors that emerge in the case of unsteady flow. Therefore, they can be reorganized as the following expression:
where f is the Fanning friction factor, F1 is a function of the factors which affect both steady uniform and unsteady frictions, and F2 contains the factors which only affect unsteady friction, which depends on time and space derivatives of hydraulic parameters, such as ∂D/∂x, ∂D/∂t, ∂V/∂x, and ∂V/∂t. Based on dimensional analysis, a modified friction model for unsteady flow has been proposed by Bao et al. []. The modified model states the following:
where D is the flow depth, V is the cross-sectional averaged velocity, and Sm is the friction slope calculated by the modified friction model, in which the steady uniform component of the modified model is the same as the Chezy formula. Moreover, it considers the effect of flow non-uniformity and flow unsteadiness by additional components related to ∂D/∂x, ∂D/∂t, and ∂V/∂t. Thus, the modified friction model can be regarded as an extension of the Chezy formula, namely, the extended Chezy formula. Since it is not deduced from the momentum equation of the Saint-Venant equations, the extended Chezy formula can be recognized as a substitute for the Chezy formula or Manning formula to modify the friction calculation of a 1D hydrodynamic model.
3.2. Modified SVN Model
Saint-Venant equations as one-dimensional shallow water equations are derived from the conservation of mass and the dynamic relation for momentum conservation principles, which can be applied to unsteady flow appropriately []. Its expressions can be written as follows:
where D is the flow depth, V is the cross-sectional averaged velocity, S0 is the bed slope, Sf is the friction slope, and g is the gravitational acceleration. In this paper, the extended Chezy formula is used to compute the friction term in the momentum equation of the Saint-Venant equations. That is, the Sf is computed using Equation (9). Therefore, a new version of a 1D hydrodynamic model is proposed, which is referred to as the modified SVN model.
The numerical solution of the modified SVN model can be obtained at given initial and boundary conditions. In this paper, the Preissmann implicit difference method was used for discretization, in which the arithmetic average method and the weighted average method are applied in spatial partial derivative approximation and temporal partial derivative approximation, respectively [,,]:
where f represents a certain variable such as flow depth and cross-sectional averaged velocity. θ is the difference coefficient. Its range is 0.5 ≤ θ ≤ 1 []. The superscripts represent time t. n and n + 1 are the current moment and the next moment, respectively. The subscripts represent location x. j and j + 1 are the two adjoining cross sections, in which jth cross section locates upstream of the j + 1th cross section. and .
Friction is of great importance in hydrodynamic modelling. Since it is one of the major sources of uncertainties in flood routing, every finding on friction formula modification may help modelers to cope with this uncertainty. Hence, the extended Chezy formula is employed to compute the friction slope in Equation (16), establishing a modified SVN model. In the process of discretization, four hydraulic variables of the two adjacent cross sections are organized into two equations [,]:
where Equations (15) and (16) are the two discretized equations derived from the continuity equation and the momentum equation between the jth and the j + 1th cross sections, respectively. Subscript j and j + 1 represent the index of sections. pa1j, pb1j, pk1j, pd1j, pe1j, pa2j, pb2j, pk2j, pd2j, and pe2j are coefficients. They are determined by the current state of the hydraulic parameters and the four parameters involved in the extended Chezy formula, (pa1j… pe1j, pa2j… pe2j) = f (q, Vj, Dj, Vj+1, Dj+1, c0, c1, c2, c3). In addition, ∆Vj, ∆Dj, ∆Vj+1, and ∆Dj+1 are the increment of the next time relative to the current moment.
3.3. Original SVN Model
It is possible to substitute the Chezy formula into the Saint-Venant equations, set 1/C2 = c0, and then obtain the classic 1D hydrodynamic model. In this paper, it is referred to as the original SVN model. Similarly, the numerical solution of the original SVN model can be derived using the Preissmann differencing method to scatter its governing equations. Obviously, the discretized equation of the continuity equation is the same as Equation (15). On the other hand, the discretized equation of the momentum equation is different from Equation (16) due to the different friction formula, which can be expressed as follows:
where, pa3j, pb3j, pk3j, pd3j, and pe3j are coefficients. Their calculation formulas are the same as pa2j, pb2j, pk2j, pd2j, and pe2j in the case of c1 = c2 = c3 = 0.
For a river or open channel which has N cross sections, both the original and modified SVN models are (2N − 2) equations with 2N unknown variables. Therefore, at the given initial conditions, two boundary conditions are needed for solving equations. In this study, the initial conditions were obtained by the linear interpolation method using the observations of the upstream and downstream cross sections (i.e., cross sections #1 and #3). In addition, the cross-sectional averaged velocity of cross section #1 and the flow depth of cross section #3 served as boundary conditions.
3.4. A Genetic Algorithm (GA)-Based Parameter Calibration Method
It is known that the determination of empirical parameters is very difficult due to the high nonlinearity of 1D hydrodynamic models. Therefore, the estimation of friction parameters would be more difficult and time-consuming since the extended Chezy friction model in the modified SVN model has more empirical parameters that must be calibrated compared with the Chezy formula. In order to overcome the difficulty of parameter estimation, a GA-based parameter calibration method is proposed in this paper. GA is an adaptive optimized algorithm of probability search which simulates heredity and evolution of biology in the wild. According to the natural evolution rules of “Survival of the fittest” and genetic choice theory, the algorithm begins from a random population and evolves to an increasingly good approximation. GA-based methods have been widely used in the parameter calibration of complex and nonlinear problems []. For example, Lei et al. [] and Tang et al. [] successfully calibrated numerical models using a GA algorithm in complex river networks.
For both the original and modified SVN models, when they are used to simulate man-made flood events, there must be an optimal group of parameters which make the model calculation best fit the experimental observation. Hence, the calibration problem is recognized as an optimization problem. In this study, based on the given initial and boundary conditions, the cross-sectional averaged velocity and the flow depth of cross section #2 were calculated. The objective function can be written as follows:
where m is the number of experimental flood events (for this study, m = 10 and all 10 flood events were used for parameter calibrations); n is the sequence length of the jth experimental flood event; V2,i and D2,i are the observed cross-sectional averaged velocity and flow depth at cross section #2 during the jth experiment, whereas and are the computed ones; and αj is a weighing coefficient between the cross-sectional averaged velocity and flow depth, which is determined by the relative magnitude of the cross-sectional averaged velocity and flow depth []. It is given by Equation (20). ck is the kth parameter to be calibrated and and are the lower bound and the upper bound, respectively. The frictional slope of the modified SVN model is computed using the extended Chezy formula and four parameters must be calibrated (p = 4), whereas the friction slope of the original SVN model is computed using the Chezy formula and only one parameter must be calibrated (p = 1):
where V2,i and D2,i are the observed cross-sectional averaged velocity and flow depth at cross section #2.
In this paper, the GA-based parameter calibration method was designed based on the University of Sheffield’s Genetic Algorithm Toolbox []. The binary system coding mode was adopted to encode parameters during the parameter calibration. The length of coding that corresponded to each of the parameters was 20. As there were four parameters in the modified SVN model, the length of the individual was 80 (L = 80), whereas in the original SVN model, there was only one parameter and the length of the individual was 20 (L = 20). The process of applying a genetic algorithm for parameter calibration is summarized as follows, with the parameters of GA presented in Table 2.

Table 2.
Parameters involved in the genetic algorithm (GA)-based parameter calibration method.
- Generating the initial community: at the beginning of the algorithm, a population of size N is randomly generated and enters the loop.
- Calculating the fitness of parent: after decoding the genetic code of each individual, the parameters are obtained. Then, flood events are simulated using the modified or original SVN model with the parameters to get the value of the objective function. Finally, the mapped method is adopted to calculate the fitness according to the objective function result.
- Generating offspring by crossing and mutation operation: genes are selected by using the roulette method in which the selection probability is proportional to the fitness of parent individuals. In addition, a certain size of offspring population is generated by crossing and mutation, where the simplex crossover operator is used to perform the crossing operation, with the crossover probability being Px, and the mutation operator is used based on the discrete mutation operator, with the mutation probability being Pm. The ratio of the offspring population to parent population is GGAP, where GGAP = 0.95. Hence, the number of the offspring population is GGAP × N.
- Competition restructuring operation between parent and offspring: according to the principle of survival of the fittest, GGAP × N low fitness parent individuals will be eliminated by offspring ones, that is, 5% excellent individuals of parent and all of offspring will be recombined to form a new population.
- Judging whether the termination conditions are satisfied: if the hereditary algebra is greater than the maximum number of generations M, choose the best individual decoding output in the current population as the optimal approximation solution of the original problem; otherwise, substitute the current population as a parent into the next round of cycle operation, and return to step (2).
The technical flowchart is shown in Figure 5.
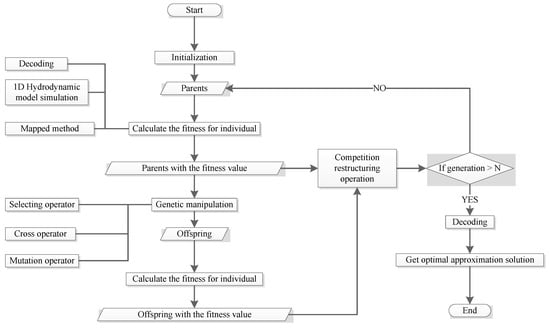
Figure 5.
Flow chart of the genetic algorithm.
3.5. Efficiency Criteria
The Nash–Sutcliffe model efficiency coefficient (NSE), the relative peak value error (RPE) and the relative time-at-peak error (RTE) are used to assess the model accuracy [,]. The formulas are as follows:
where Xc(i) and Xo(i) represent the ith calculated value and the observed value, respectively, is the average observed value, and n is the length of X series. NSE indicates how well the observed values match the simulated ones and can range from −∞ to 1; larger NSE values indicate a better model performance. PXc is the calculated peak value, PXo is the observed peak value, and RPE > 0 indicates that the calculated peak value is greater than the observed one, and vice versa. PTc is the time of calculated peak occurrence, PTo is the time of observed peak occurrence, RTE is the relative time-at-peak error, and RTE > 0 indicates that the calculated peak lags behind the observed peak, and vice versa.
4. Results and Discussion
4.1. Model Calibration
The parameters of both the original and modified SVN models were carefully identified using the proposed GA-based parameter calibration method. Figure 6 illustrates the relationship between the best objective function value and the generation during the parameter calibration for both the original and modified SVN models. It can be seen that the best objective function value decreases with the increasing level of generation. Moreover, this gradual decline trend of the best objective function value ends with a stable state. Therefore, it can be concluded that the proposed parameter calibration method is convergent.
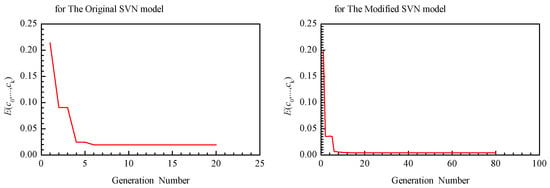
Figure 6.
The decline trend of the best objective function value during the parameter calibration.
The optimal values of the empirical parameters are listed in Table 3, where the lower and upper bounds of c0 are given after using the Chezy formula. However, the lower and upper bounds of other empirical parameters in the extended Chezy formula could not be estimated due to a lack of similar applications. In this paper, they were determined using the trial and error method.

Table 3.
Parameter calibration details for the modified and original models.
Moreover, because this paper compared the performance of the original and modified SVN models according to the numerical experiment, the accuracy of the solution was crucial. Mass balance is a good measure for the quality of the computation. In this paper, the relative error (REM) was computed to evaluate the conservation of mass for the measuring segment from cross section #1 to cross section #3. REM is defined as the ratio of the non-conservative discharge and inflow discharge, whereas the concept non-conservative discharge consists of the net outflow and the rate of change in storage []. This study’s results showed that REM ranged from 0.3‰ to 0.8‰ in the original SVN model and from 0.4‰ to 0.8‰ in the modified SVN model. This indicated that the non-conservative mass error introduced from the numerical methods was negligible.
4.2. Performance of the Original SVN Model
The optimal parameter values were then inserted into the numerical model (i.e., the original and modified SVN models), and the man-made flood events in the experiment were simulated. The model performance was evaluated by computing the NSE, RPE and RTE between the model calculations and observations at cross section #2. Table 4 shows the NSEs, RPEs, and RTEs of the original SVN model for each flood event. According to Table 4, the averaged absolute value (AAV) of the NSEs for flow depth simulating was 0.81. In addition, the AAVs of the RPEs and RTEs were 4.0% and 5.6%, respectively. Generally, although a good agreement was obtained between observed and simulated flow depths in the original SVN model, there was some pronounced error in the simulations for the peak of flow depth. Specifically, the RPEs between the calculated and observed flow depth were negative at each flood event, whereas the RTEs were positive. This indicated that the peak of the simulated flow depth in the original SVN model lagged behind the observed one and that the simulated maximum flow depth was smaller than that of the observed one.

Table 4.
The Nash–Sutcliffe model efficiency coefficients (NSEs), relative peak value errors (RPEs), and relative time-at-peak errors (RTEs) of the original SVN model.
The AVV of the NSEs for the sectional averaged velocity simulation was 0.52, much lower than that for the flow depth simulation. This indicated that the original SVN model could not simulate the sectional averaged velocity accurately. Since the AAVs of the RPEs and RTEs were 4.0% and 6.5%, respectively, there was some pronounced error in the peak simulation as well. Specifically, the RPEs for the sectional averaged velocity were negative at each flood event, indicating that the simulated maximum sectional averaged velocity was smaller than the observed one. Furthermore, randomly distributed RTEs showed that different flood events had different time-at-peak errors in the sectional averaged velocity simulation.
In order to investigate the mechanism behind the poor performance of the original SVN model, the authors re-ran the original SVN model with three different parameters: c0 = 0.0013 (the objective function value = 0.0196), c0 = 0.0018 (the objective function value = 0.0441), and c0 = 0.0008 (the objective function value = 0.0448). Then, the performances of the original SVN model with different parameters were compared (see Figure 7). According to Figure 7, it can be concluded that although c0 = 0.0013 could achieve the best overall model performance according to the objective function value, it was not the best parameter for each situation. For example, c0 = 0.0013 was good for flow depth simulating, whereas c0 = 0.0018 was better for the sectional averaged velocity simulation. Moreover, c0 = 0.0013 was a better choice for the Nos. 2-1 and 2-2 flood events, whereas for the Nos. 1-1 and 1-2 flood events, c0 = 0.0018 was the preferred parameter because it could improve the performance of the sectional averaged velocity simulation without hurting the agreement between observed and simulated flow depths. Hence, not only the flow depth simulation and the sectional averaged velocity simulation had preferred different parameters, but also different flood events had preferred different parameters. In such a case, it is very difficult to obtain an ideal parameter which can support good performance for both the flow depth simulation and the sectional averaged velocity simulation and obtain a sound agreement for every flood event.
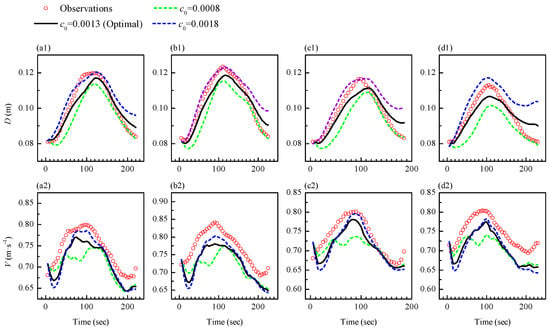
Figure 7.
Simulation results of the original SVN model with different parameter values: (a1) flow depth hydrograph and (a2) sectional averaged velocity hydrograph for No. 1-1 flood event; (b1) flow depth hydrograph and (b2) sectional averaged velocity hydrograph for No. 1-2 flood event; (c1) flow depth hydrograph and (c2) sectional averaged velocity hydrograph for No. 2-1 flood event; and (d1) flow depth hydrograph and (d2) sectional averaged velocity hydrograph for No. 2-2 flood event.
4.3. Performance of the Modified SVN Model
The performance of the modified SVN model was evaluated using NSE, RPE, and RTE as well, as is shown in Table 5. By comparing the results of the modified SVN model in Table 5 with those of the original SVN model in Table 4, one notes that the AAV of NSEs for the flow depth simulation was 0.81 in the original SVN model results and that it was increased to 0.96 in the modified SVN model. The maximum increase in NSE for flow depth simulation was from 0.63 to 0.91 in the No. 2-2 flood event. Moreover, the AAV of NSEs in the sectional averaged velocity simulation has improved from 0.52 to 0.84. The maximum increase was from 0.4 to 0.88 in the No. 2-5 flood event. Therefore, the NSE values were increased in both the flow depth simulation and the sectional averaged velocity simulation. As a result, the agreement between observations and simulations in the modified SVN model is better than those in the original SVN model.

Table 5.
The NSEs, RPEs, and RTEs of the modified SVN model.
Furthermore, compared with the original SVN model, the modified SVN model reduced the AAV of RPEs from 4.0% to 1.65% for the flow depth simulation and from 4.0% to 0.77% for the sectional averaged velocity simulation. In addition, the AAV of RTEs in the original SVN model was 5.6% for the flow depth simulation and 6.5% for the sectional average velocity simulation, but they were reduced to 1.60% and 4.91%, respectively, in the results of the modified SVN model. The modified SVN model reduced the peak value error and the time-at-peak error in both the flow depth simulation and the sectional averaged velocity simulation.
From the above results, the modified SVN model had higher NSEs and lower RPEs and RTEs than the original SVN model in both simulations of the flow depth and the sectional averaged velocity. It can be concluded that the modified SVN model performs better than the original SVN model. It also indicates that the extended Chezy formula is reasonable.
Figure 8 shows the results of the modified SVN model compared with the original model and the observations. On one hand, Figure 8 confirms that by employing the extended Chezy formula, the modified SVN model can provide a better performance. On the other hand, Figure 8 reveals that some errors remain in the simulation result. For example, for both the modified and original SVN models, there is a decrease in the calculated velocity in the first time steps. It is known that in the numerical experiment, except for the friction calculation, errors will be introduced by the initial and boundary conditions as well. In this paper, this situation was analyzed as follows.
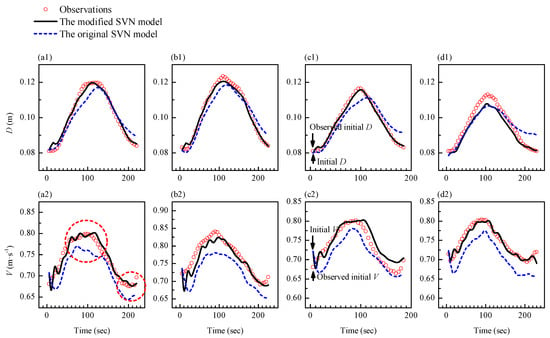
Figure 8.
Simulation results of the modified and original SVN models during the four flood events: (a1) flow depth hydrograph and (a2) sectional averaged velocity hydrograph for No. 1-1 flood event; (b1) flow depth hydrograph and (b2) sectional averaged velocity hydrograph for No. 1-2 flood event; (c1) flow depth hydrograph and (c2) sectional averaged velocity hydrograph for No. 2-1 flood event; and (d1) flow depth hydrograph and (d2) sectional averaged velocity hydrograph for No. 2-2 flood event.
In the numerical experiment, the initial conditions (V and D and time t = 0) were obtained by the linear interpolation method using data from the upstream and downstream cross sections (i.e., cross sections #1 and #3). However, according to Figure 8, the initial V of cross section #2 which was obtained by the linear interpolation method was greater than the observed one, whereas the initial D of cross section #2 which was obtained by the linear interpolation method was slightly less than the observed one (see Figure 8(c1,c2), for example). To counteract the effects of initial condition errors, the calculated velocity decreased and the calculated water depth increased in the first time steps. However, the initial condition error did not result in the failure of the numerical experiment. As the calculation continued, the effect of the initial condition error became less and less important. According to Figure 8, the impact of the initial condition error lasted about four time steps. By comparing the residuals of D and V in the first four time steps and that of the remaining time steps, the additional residual which was introduced by the initial condition error was obtained. Generally, it had an impact on the objective function in the range of 3%–5%. Following the same logic, except for the initial condition error, the result of numerical experiments was also affected by the boundary condition error. It is known that measuring cross-sectional averaged velocity is more difficult than observing water depth. In the numerical experiment, some fluctuations in the calculated averaged velocity hydrographs occurred due to the error in the averaged velocity measurement of cross section #3 (downstream boundary condition). In addition, because the friction slope computed by the extended Chezy formula was based not only on V and D but also on ∂D/∂x, ∂D/∂t and ∂V/∂t, the modified SVN model which employed the extended Chezy formula to compute the friction slope was more sensitive to the error in the averaged velocity measurement of cross section #3 (see Figure 8(a2), for example). In a further study, more data assimilation techniques should be introduced to eliminate the influence of the observation error.
5. Conclusions
In this paper, a newly proposed 1D unsteady friction formula was introduced to the framework of a 1D hydrodynamic model to establish the modified SVN model. With the help of a GA-based parameter calibration algorithm, the performance of the modified SVN model was compared with that of the original SVN model in a simulation test for a hydraulic experiment. The results revealed the following:
The GA-based parameter calibration method was convergent and could identify the empirical parameters efficiently. However, in the original SVN model, not only the flow depth simulation and the sectional averaged velocity simulation had preferred different parameters, but also different flood events had preferred different parameters. In such a case, it is very difficult to obtain an ideal parameter which can support good performance for both the flow depth simulation and the sectional averaged velocity simulation and obtain a sound agreement for every flood event. As a result, although the optimal parameter c0 = 0.0013 can achieve the best overall model performance, it is not the best parameter for each situation.
Compared with the original SVN model, the modified SVN model can achieve a better simulation in both the flow depth and the sectional averaged velocity simulations. Furthermore, it can reduce the peak value error and the time-at-peak error as well. The modified SVN model is better than the original SVN model. It also indicates that the extended Chezy formula can be used as a substitute for steady uniform friction formulas in the framework of a 1D hydrodynamic model.
This paper provides a simple test verifying the advantages of using the extended Chezy formula in a 1D hydrodynamic model. Despite the fact that similar flume experiments have been widely used to investigate unsteady channel flow behavior, a laboratorial channel is relatively short. For this reason, the flow unsteadiness and flow non-uniformity are limited. Further investigation should concentrate more on flood simulations for field measurements.
Author Contributions
J.Z. and W.B. designed the experiments; J.Z. performed the experiments; Y.L. and L.C. analyzed the data; and J.Z. and M.B. wrote the manuscript. All the authors discussed the structure of the paper.
Funding
This work was supported by the Postgraduate Research & Practice Innovation Program of Jiangsu Province (grant KYCX17_0423), the Fundamental Research Funds for Central Universities (grant 2017B684X14), the National Key R&D Program of China (grant 2016YFC0402703), and the National Natural Science Foundation of China (grant 51709077).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Papancolaou, A.N.; Bdour, A.; Wicklein, E. One-dimensional hydrodynamic/sediment transport model applicable to steep mountain streams. J. Hydraul. Res. 2004, 42, 357–375. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Bao, W.M.; Qu, S.M.; Yu, Z.B. One-dimensional hydrodynamic model accounting for tidal effect. Hydrol. Res. 2012, 43, 113–122. [Google Scholar] [CrossRef]
- Mcdowell, D.M.; Ball, D.J. The dynamic simulation of unsteady frictional flow in tidal estuaries. Proc. Inst. Civ. Eng. 1971, 50, 129–138. [Google Scholar]
- Zhang, S.H.; Xu, D.; Li, Y.N. One-dimensional complete hydrodynamic model for border irrigation based on hybrid numerical method. Irrig. Sci. 2011, 29, 93–102. [Google Scholar] [CrossRef]
- Bozzi, S.; Passoni, G.; Bernardara, P.; Goutal, N.; Arnaud, A. Roughness and discharge uncertainty in 1D water level calculations. Environ. Model. Assess. 2015, 20, 343–353. [Google Scholar] [CrossRef]
- Becker, L.; Yeh, W.W.G. Identification of parameters in unsteady open channel flows. Water Resour. Res. 1972, 8, 956–965. [Google Scholar] [CrossRef]
- Giustolisi, O. Using genetic programming to determine Chèzy resistance coefficient in corrugated channels. J. Hydroinform. 2004, 6, 157–173. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, S.S.Y. Identification of Manning’s roughness coefficients in channel network using adjoint analysis. Int. J. Comput. Fluid Dyn. 2005, 19, 3–13. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, J. Calculation of field Manning′s roughness coefficient. Agric. Water Manag. 2001, 49, 153–161. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: Berlin, Germany, 1999; pp. 29–76. [Google Scholar]
- Ding, Y.; Jia, Y.; Wang, S.S.Y. Identification of Manning’s roughness coefficients in shallow water flows. J. Hydraul. Eng. 2004, 130, 501–510. [Google Scholar] [CrossRef]
- Zou, X.; Navon, I.M.; Berger, M.; Phua, K.H.; Schlick, T.; Dimet, F.X.L. Numerical experience with limited-memory Quasi-Newton and Truncated Newton methods. SIAM J. Optim. 2006, 3, 582–608. [Google Scholar] [CrossRef]
- Graf, W.H.; Song, T. Bed-shear stress in non-uniform and unsteady open-channel flows. J. Hydraul. Res. 1995, 33, 699–704. [Google Scholar] [CrossRef]
- Hsu, M.H.; Liu, W.C.; Fu, J.C. Dynamic routing model with real-time roughness updating for flood forecasting. J. Hydraul. Eng. 2006, 132, 605–619. [Google Scholar] [CrossRef]
- Bao, H.J.; Zhao, L.N. Hydraulic model with roughness coefficient updating method based on Kalman filter for channel flood forecast. Water Sci. Eng. 2011, 4, 13–23. [Google Scholar]
- Liu, X.; Xingya, X.U.; Lai, R.; Huang, L.; Zhang, Y.; Fang, H. Real-time channel flood forecasting model with multi-segmental roughness coefficients updating dynamically based on ensemble Kalman filter. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Ngaina, J.N.; Njoroge, J.M.; Mutua, F.; Mutai, B.K.; Opere, A.O. Real time flood forecasting in river Nzoia using ensemble Kalman filter. In Proceedings of the 11th KMS Conference, Nairobi, Kenya, 12–16 November 2013. [Google Scholar]
- Bellos, V.; Nalbantis, I.; Tsakiris, G. Friction modeling of flood flow simulations. J. Hydraul. Eng. 2018, 144, 04018073. [Google Scholar] [CrossRef]
- Rouse, H. Critical analysis of open-channel resistance. J. Hydraul. Div. 1965, 91, 1–23. [Google Scholar]
- Yen, B.C. Open channel flow resistance. J. Hydraul. Eng. 2002, 128, 20–39. [Google Scholar] [CrossRef]
- Tu, H.; Graf, W.H. Friction in unsteady open-channel flow over gravel beds. J. Hydraul. Res. 1993, 31, 99–110. [Google Scholar]
- Rowiński, P.M.; Czernuszenko, W.; Marc, J.M. Time-dependent shear velocities in channel. Hydrol. Sci. J. 2000, 45, 881–895. [Google Scholar] [CrossRef]
- Mrokowska, M.M.; Rowiński, P.M.; Kalinowska, M.B. A methodological approach of estimating resistance to flow under unsteady flow conditions. Hydrol. Earth Syst. Sci. 2015, 19, 4041–4053. [Google Scholar] [CrossRef]
- Bao, W.; Zhou, J.; Xiang, X.; Jiang, P.; Bao, M. A hydraulic friction model for one-dimensional unsteady channel flows with experimental demonstration. Water 2018, 10, 43. [Google Scholar] [CrossRef]
- Mrokowska, M.M.; Rowiński, P.M.; Książek, L.; Strużyński, A.; Wyrębek, M.; Radecki-Pawlik, A. Flume experiments on gravel bed load transport in unsteady flow—Preliminary results. In Hydrodynamic and Mass Transport at Freshwater Aquatic Interfaces; Springer: Berlin, Germany, 2016; pp. 221–233. [Google Scholar]
- Lynnworth, L.C.; Liu, Y. Ultrasonic flowmeters: Half-century progress report, 1955–2005. Ultrasonics 2006, 44, e1371–e1378. [Google Scholar] [CrossRef] [PubMed]
- Niño, Y.; García, C.M.; Cantero, M.I.; García, M.H. Turbulence measurements with acoustic Doppler velocimeters. J. Hydraul. Eng. 2005, 131, 1062–1073. [Google Scholar]
- Schlichting, H. Boundary-Layer Theory, 7th ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Traver, R.G.; Miller, A.C. Modeling unsteady one dimensional open channel flow using the slope friction form of the Saint-Venant equations. In Hydraulic Engineering (1987); ASCE: Reston, VA, USA, 2015. [Google Scholar]
- Sart, C.; Baume, J.P.; Malaterre, P.O.; Guinot, V. Adaptation of preissmann’s scheme for transcritical open channel flows. J. Hydraul. Res. 2010, 48, 428–440. [Google Scholar] [CrossRef]
- Zhang, D.W.; Dong, Z.C. Study on application of Preissmann implicit scheme in flood routing of Xinyi river. J. Water Resour. Archit. Eng. 2004, 4, 12. [Google Scholar]
- Hu, Q.Y.; Wang, C.H. Stability analysis of four-point linear implicit scheme of Saint-Venant equations. J. Hohai Univ. 2011, 39, 397–401. [Google Scholar]
- Wang, X.H.; Zhang, Q.; Yang, F.S. Application of the priessmann implicit scheme to flood routing in lower Weihe River. J. Northwest Hydro Electr. Power 2003, 19, 1–4. [Google Scholar]
- Mu, J.B.; Zhang, X.F. Real-time flood forecasting method with 1-D unsteady flow model. J. Hydrodyn. Ser. B 2007, 19, 150–154. [Google Scholar] [CrossRef]
- Sun, N.; Li, Z.L.; Li, Z. Inversion of channel’s roughness and integrated leakage coefficient based on genetic algorithm. J. Water Resour. Archit. Eng. 2009, 7, 88–90. [Google Scholar]
- Lei, Y.; Tang, H.W.; Zhou, Y.L.; Liu, G.; Chen, M. Application of genetic algorithm for back analysis of roughness parameters in river. J. Hydrodyn. 2008, 23, 612–617. [Google Scholar]
- Tang, H.W.; Xin, X.K.; Dai, W.H.; Xiao, Y. Parameter identification for modeling river network using a genetic algorithm. J. Hydrodyn. Ser. B 2010, 22, 246–253. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, F.W.; Huang, B.D. Improvement and Application of GA Toolbox Designed by University of Sheffield Based on Matlab. Mech. Eng. 2010, 10, 31–33. [Google Scholar]
- Bao, W.M.; Zhang, X.Q.; Qu, S.M. Dynamic correction of roughness in the hydrodynamic model. J. Hydrodyn. Ser. B 2009, 21, 255–263. [Google Scholar] [CrossRef]
- Hsi, M.H.; Fu, J.C.; Liu, W.C. Flood routing with real-time stage correction method for flash flood forecasting in the Tanshui River, Taiwan. J. Hydrol. 2003, 283, 267–280. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).