Impact of Different Reanalysis Data and Parameterization Schemes on WRF Dynamic Downscaling in the Ili Region
Abstract
1. Introduction
2. Materials and Methods
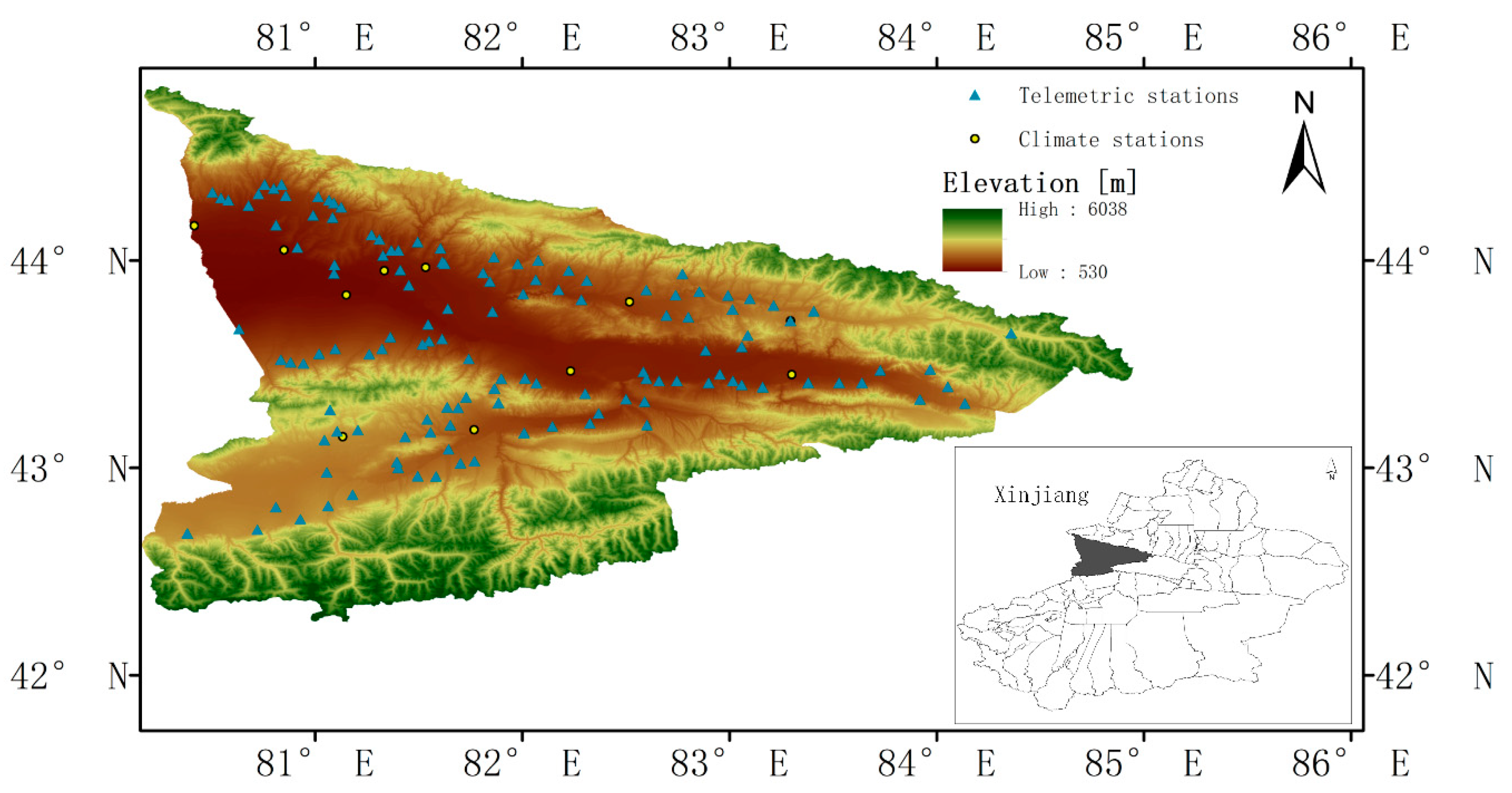
2.1. Study Area and Observational Data
2.2. Model Configuration and Experimental Design
2.3. Evaluation Statistics
3. Results
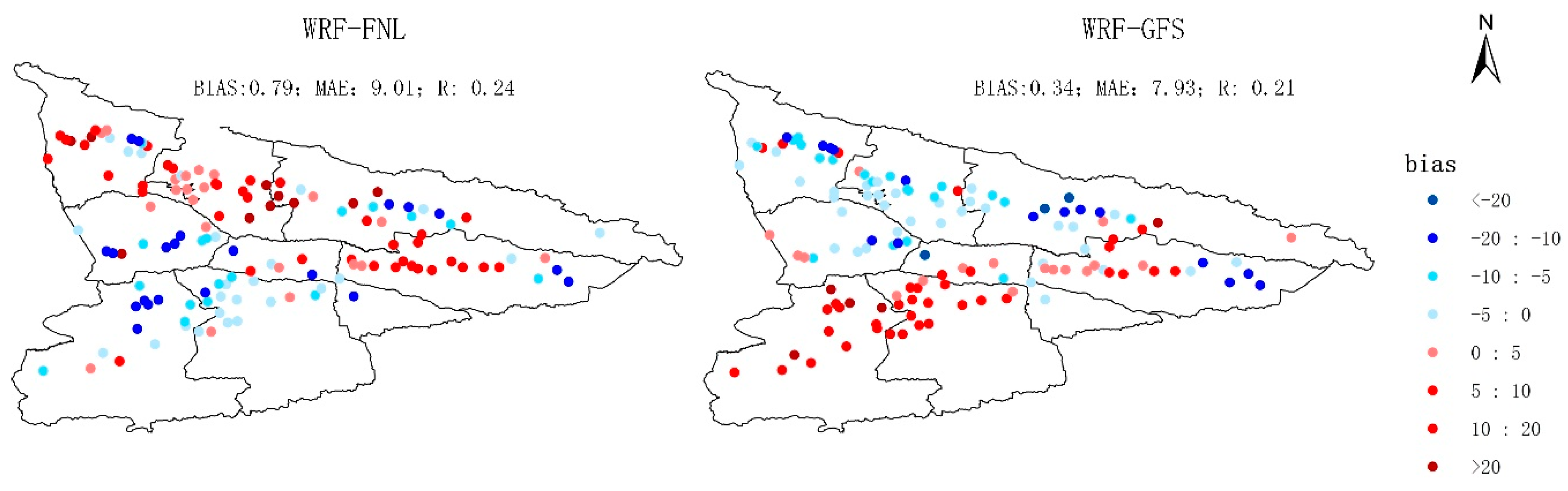
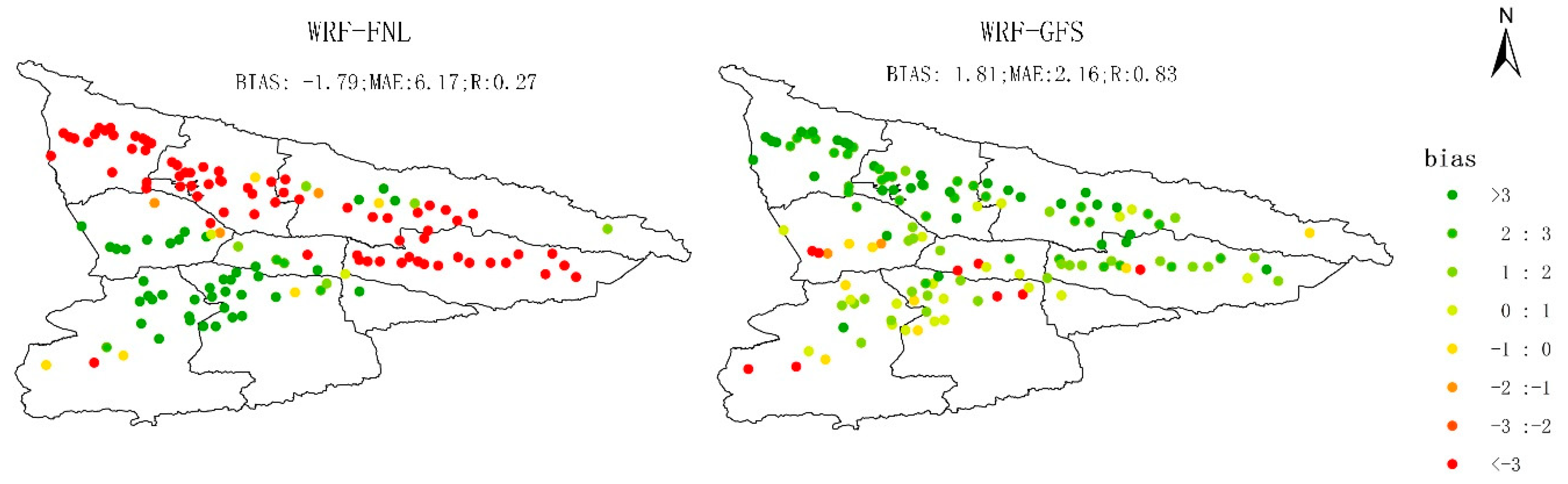
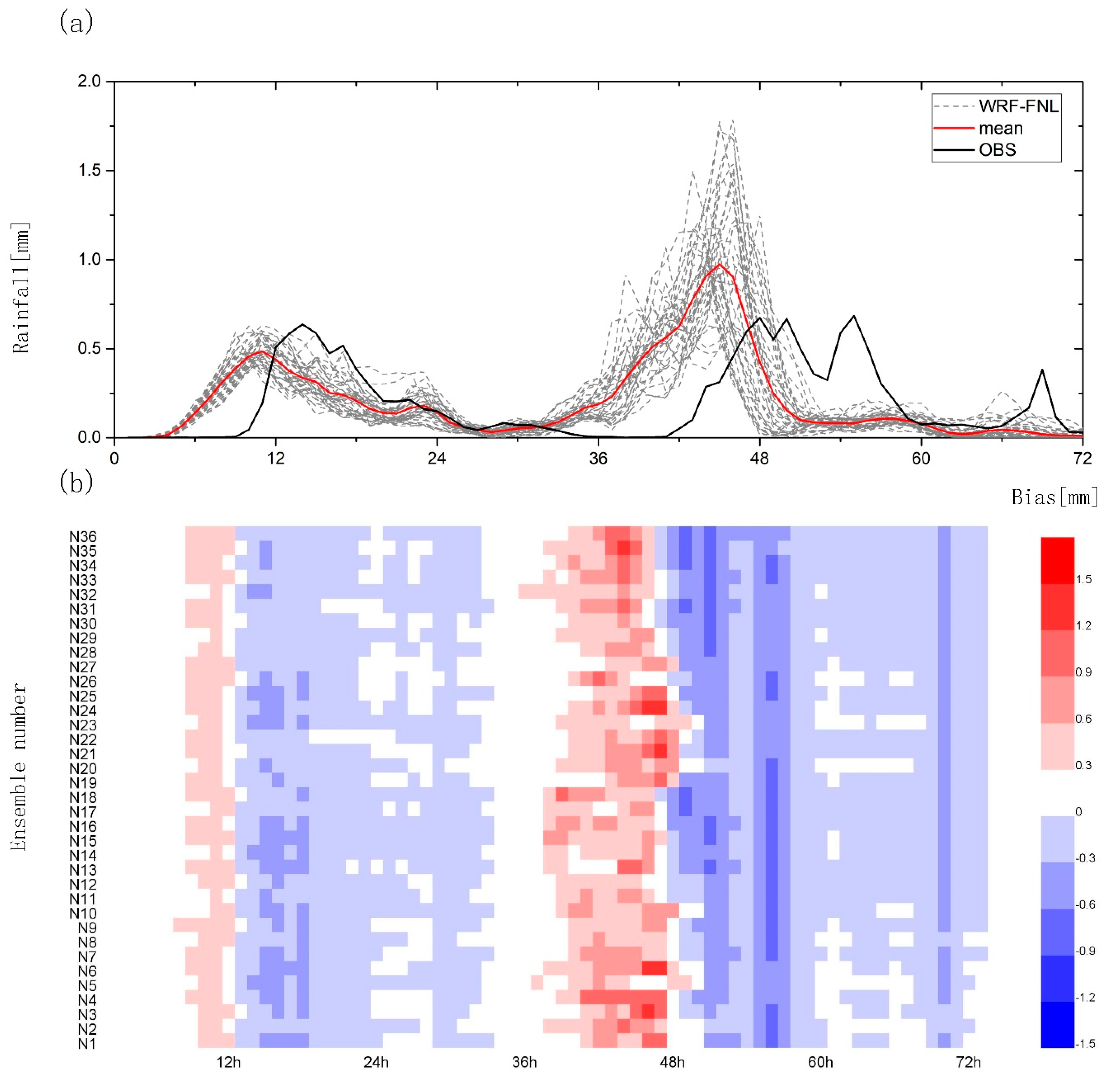
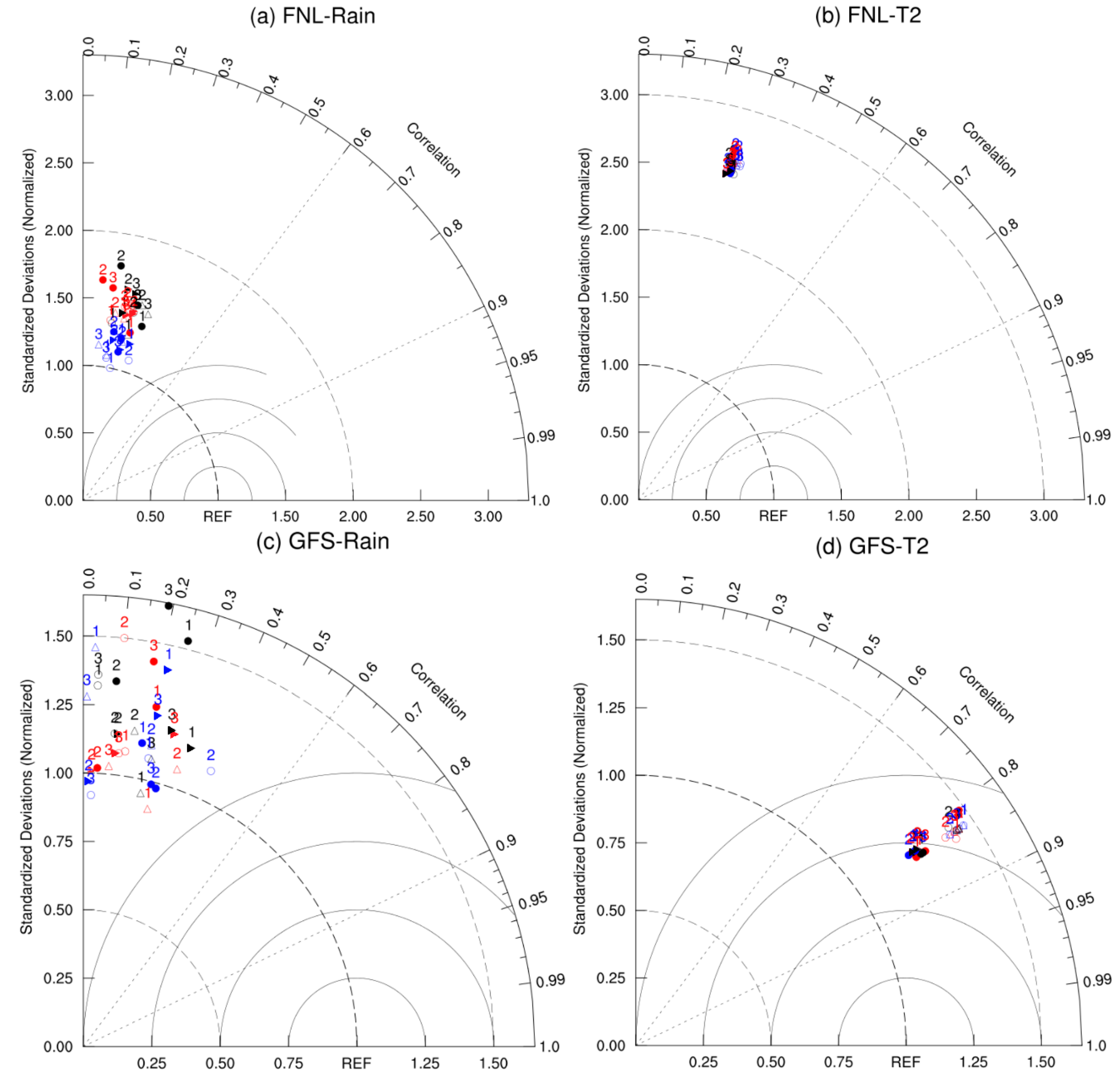
3.1. Verification of WRF Simulations
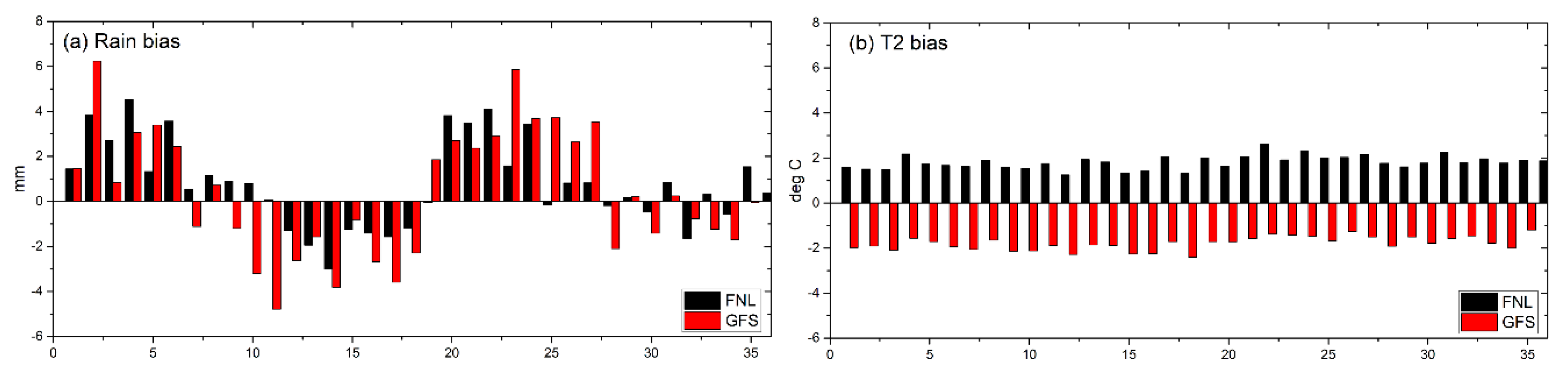
3.1.1. Climatological Spatial Pattern of Precipitation and 2-m Temperature
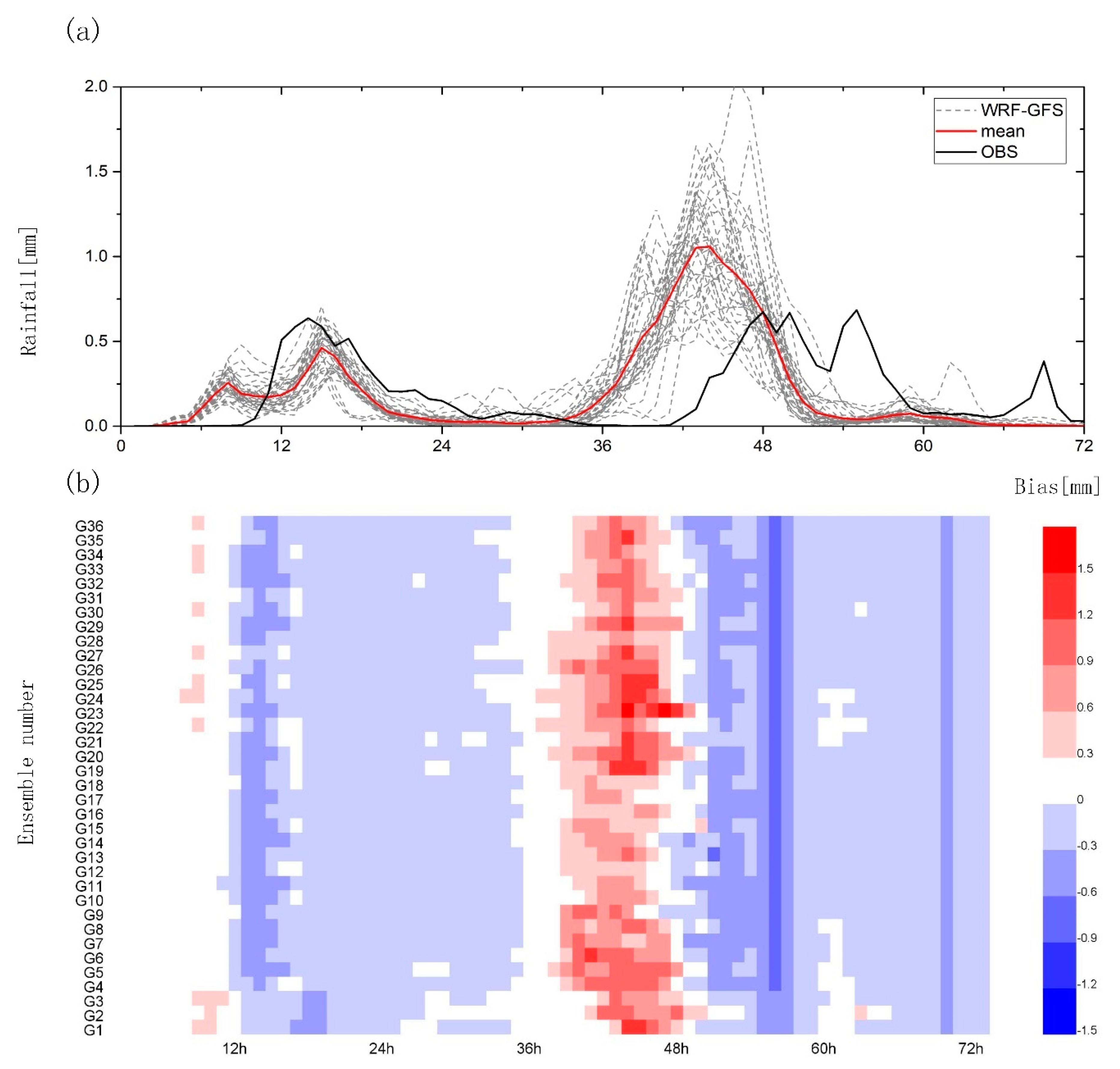
3.1.2. Temporal Characteristics of Rainfall Events
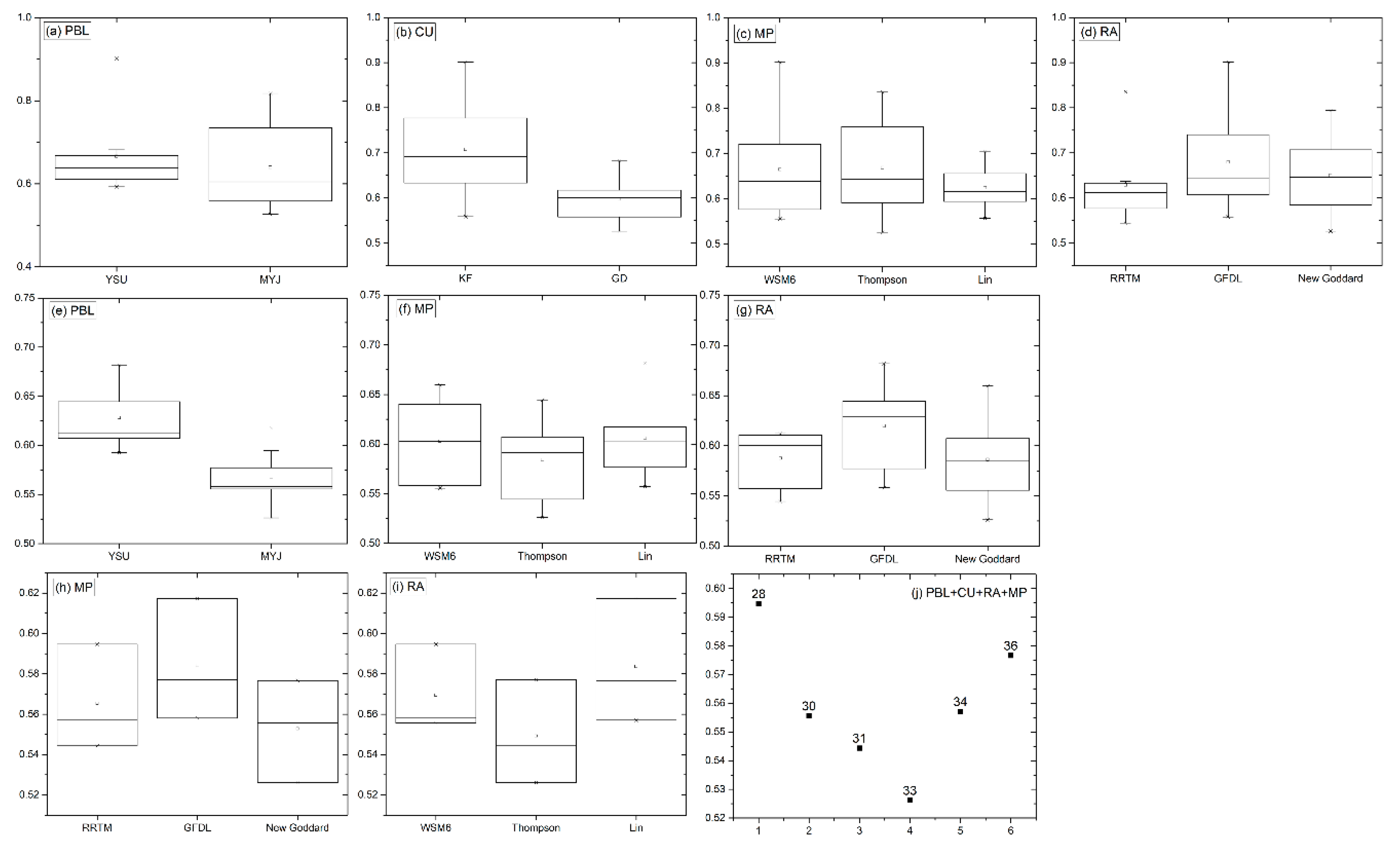
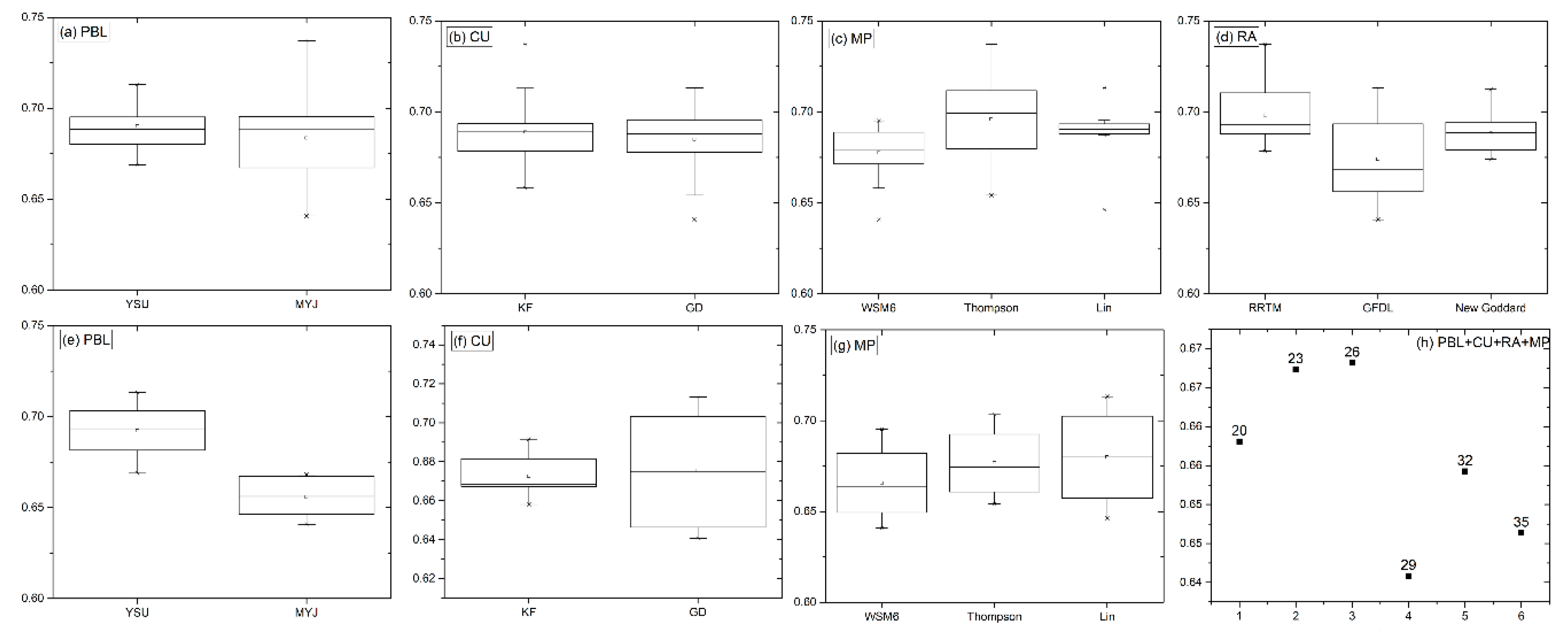
3.2. Impact of Different Parameterization Schemes
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Huang, D.; Gao, S. Impact of different reanalysis data on WRF dynamical downscaling over China. Atmos. Res. 2018, 200, 25–35. [Google Scholar] [CrossRef]
- Chawla, I.; Osuri, K.K.; Mujumdar, P.P.; Niyogi, D. Assessment of the Weather Research and Forecasting (WRF) model for simulation of extreme rainfall events in the upper Ganga Basin. Hydrol. Earth Syst. Sci. 2018, 22, 1095–1117. [Google Scholar] [CrossRef]
- Kondowe, A.L. Impact of Convective Parameterization Schemes on the Quality of Rainfall Forecast over Tanzania Using WRF-Model. Nat. Sci. 2014, 6, 691–699. [Google Scholar] [CrossRef]
- Misenis, C.; Zhang, Y. An examination of sensitivity of WRF/Chem predictions to physical parameterizations, horizontal grid spacing, and nesting options. Atmos. Res. 2010, 97, 315–334. [Google Scholar] [CrossRef]
- Liu, C.; Ikeda, K.; Thompson, G.; Rasmussen, R.; Dudhia, J. High-Resolution Simulations of Wintertime Precipitation in the Colorado Headwaters Region: Sensitivity to Physics Parameterizations. Mon. Weather Rev. 2011, 139, 3533–3553. [Google Scholar] [CrossRef]
- Yucel, I.; Onen, A.; Yilmaz, K.K.; Gochis, D.J. Calibration and evaluation of a flood forecasting system: Utility of numerical weather prediction model, data assimilation and satellite-based rainfall. J. Hydrol. 2015, 523, 49–66. [Google Scholar] [CrossRef]
- Ravazzani, G.; Amengual, A.; Ceppi, A.; Homar, V.; Romero, R.; Lombardi, G. Potentialities of ensemble strategies for flood forecasting over the Milano urban area. J. Hydrol. 2016, 539, 237–253. [Google Scholar] [CrossRef]
- Wu, M.; Lin, G. The very short-term rainfall forecasting for a mountainous watershed by means of an ensemble numerical weather prediction system in Taiwan. J. Hydrol. 2017, 546, 60–70. [Google Scholar] [CrossRef]
- Madhulatha, A.; Rajeevan, M. Impact of different parameterization schemes on simulation of mesoscale convective system over south-east India. Meteorol. Atmos. Phys. 2018, 130, 49–65. [Google Scholar] [CrossRef]
- Singh, K.S.; Bonthu, S.; Purvaja, R.; Robin, R.S.; Kannan, B.A.M.; Ramesh, R. Prediction of heavy rainfall over Chennai Metropolitan City, Tamil Nadu, India: Impact of microphysical parameterization schemes. Atmos. Res. 2018, 202, 219–234. [Google Scholar] [CrossRef]
- Argüeso, D.; Hidalgomuñoz, J.M.; Gámizfortis, S.R.; Estebanparra, M.J.; Dudhia, J.; Castrodíez, Y. Evaluation of WRF Parameterizations for Climate Studies over Southern Spain Using a Multistep Regionalization. J. Clim. 2011, 24, 5633–5651. [Google Scholar] [CrossRef]
- Evans, J.P.; Ekström, M.; Ji, F. Evaluating the performance of a WRF physics ensemble over South-East Australia. Clim. Dyn. 2012, 39, 1241–1258. [Google Scholar] [CrossRef]
- Jankov, I.; Gallus, W.A., Jr.; Segal, M.; Shaw, B.; Koch, S.E. The impact of Different WRF Model Physical Parameterizations and Their Interactions on Warm Season MCS Rainfall. Am. Meteorol. Soc. 2005, 20, 1048–1060. [Google Scholar] [CrossRef]
- Flaounas, E.; Bastin, S.; Janicot, S. Regional climate modelling of the 2006 West African monsoon: sensitivity to convection and planetary boundary layer parameterisation using WRF. Clim. Dyn. 2011, 36, 1083–1105. [Google Scholar] [CrossRef]
- Banks, R.F.; Tiana-Alsina, J.; Baldasano, J.M.; Rocadenbosch, F.; Papayannis, A.; Solomos, S. Sensitivity of boundary-layer variables to PBL schemes in the WRF model based on surface meteorological observations, lidar, and radiosondes during the HygrA-CD campaign. Atmos. Res. 2016, 176, 185–201. [Google Scholar] [CrossRef]
- Tiwari, S.; Kar, S.C.; Bhatla, R. Dynamic downscaling over western Himalayas: Impact of cloud microphysics schemes. Atmos. Res. 2018, 201, 1–16. [Google Scholar] [CrossRef]
- Anil Kumar, R.; Dudhia, J.; Bhowmik, S.K. Evaluation of Physics options of the Weather Research and Forecasting (WRF) Model to simulate high impact heavy rainfall events over Indian Monsoon region. Geofizika 2010, 27, 101–125. [Google Scholar]
- Heikkilä, U.; Sandvik, A.; Sorteberg, A. Dynamical downscaling of ERA-40 in complex terrain using the WRF regional climate model. Clim. Dyn. 2011, 37, 1551–1564. [Google Scholar] [CrossRef]
- Pennelly, C.; Reuter, G.; Flesch, T. Verification of the WRF model for simulating heavy precipitation in Alberta. Atmos. Res. 2014, 135, 172–192. [Google Scholar] [CrossRef]
- Zhang, X.; Xiong, Z.; Zheng, J.; Ge, Q. High-resolution precipitation data derived from dynamical downscaling using the WRF model for the Heihe River Basin, northwest China. Theor. Appl. Climatol. 2018, 131, 1249–1259. [Google Scholar] [CrossRef]
- Mendoza, P.A.; Clark, M.P.; Mizukami, N.; Newman, A.J.; Barlage, M.; Gutmann, E.D. Effects of Hydrologic Model Choice and Calibration on the Portrayal of Climate Change Impacts. J. Hydrometeorol. 2015, 16, 762–780. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Carvalho, A.C.; Carvalheiro, L.; Rocha, A.; Castanheira, J.M. On the influence of physical parameterisations and domains configuration in the simulation of an extreme precipitation event. Dyn. Atmos. Ocean. 2014, 68, 35–55. [Google Scholar] [CrossRef]
- Hong, S.Y. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2005, 134, 2318–2341. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. Convective Parameterization for Mesoscale Models: The Kain–Fritsch Scheme. The Representation of Cumulus Convection in Numerical Models. Am. Meteorol. Soc. 1993, 165–170. [Google Scholar]
- Grell, G.A.; Dévényi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29, 587–590. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A Revised Approach to Ice Microphysical Processes for the Bulk Parameterization of Clouds and Precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Thompson, G.; Rasmussen, R.M.; Manning, K. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a new snow parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Lin, Y.L. Bulk parameterization of the snow field in a cloud model. J. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter Monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Fels, S.B.; Schwarzkopf, M.D. An efficient, accurate algorithm for calculating CO2 15 micron band cooling rates. J. Geophys. Res. Ocean 1981, 86, 1205–1232. [Google Scholar] [CrossRef]
- Chou, M.D.; Suarez, M.J. A solar radiation parameterization for atmospheric studies, NASA TM-104606. Nasa Tech. Memo 1999, 15. [Google Scholar]
| Model Options | Dataset or Value |
|---|---|
| Domains | 2 |
| Grid resolution (spacing) | 27:9 KM |
| Initial conditions | 1. Final Analysis (FNL) (1° × 1°, 6 h); 2. Global Forecast System GFS (0.5° × 0.5°, 6 h) |
| boundary layer (PBL) schemes | 1. Yonsei University (YSU); 2. the Mellor–Yamada–Janjic (MYJ) |
| Cumulus (CU) schemes | 1. Kain–Fritsch (KF); 2. Grell–Devenyi (GD) |
| Microphysics (MP)schemes | 1. the WRF Single Moment 6-class (WSM6); 2. Thompson (THM); 3. Purdue Lin (Lin) |
| Shortwave/Longwave radiation (RA)schemes | 1. Dudhia/Rapid Radiative Transfer Model (RRTM); 2. The Geophysical Fluid Dynamics Laboratory (GFDL)/The Geophysical Fluid Dynamics Laboratory (GFDL); 3. New Goddard/New Goddard |
| Member | PBL | CU | MP | RA |
|---|---|---|---|---|
| 1 | YSU | KF | WSM6 | Dudhia/RRTM |
| 2 | YSU | KF | WSM6 | GFDL/GFDL |
| 3 | YSU | KF | WSM6 | New Goddard/New Goddard |
| 4 | YSU | KF | THM | Dudhia/RRTM |
| 5 | YSU | KF | THM | GFDL/GFDL |
| 6 | YSU | KF | THM | New Goddard/New Goddard |
| 7 | YSU | KF | Lin | Dudhia/RRTM |
| 8 | YSU | KF | Lin | GFDL/GFDL |
| 9 | YSU | KF | Lin | New Goddard/New Goddard |
| 10 | YSU | GD | WSM6 | Dudhia/RRTM |
| 11 | YSU | GD | WSM6 | GFDL/GFDL |
| 12 | YSU | GD | WSM6 | New Goddard/New Goddard |
| 13 | YSU | GD | THM | Dudhia/RRTM |
| 14 | YSU | GD | THM | GFDL/GFDL |
| 15 | YSU | GD | THM | New Goddard/New Goddard |
| 16 | YSU | GD | Lin | Dudhia/RRTM |
| 17 | YSU | GD | Lin | GFDL/GFDL |
| 18 | YSU | GD | Lin | New Goddard/New Goddard |
| 19 | MYJ | KF | WSM6 | Dudhia/RRTM |
| 20 | MYJ | KF | WSM6 | GFDL/GFDL |
| 21 | MYJ | KF | WSM6 | New Goddard/New Goddard |
| 22 | MYJ | KF | THM | Dudhia/RRTM |
| 23 | MYJ | KF | THM | GFDL/GFDL |
| 24 | MYJ | KF | THM | New Goddard/New Goddard |
| 25 | MYJ | KF | Lin | Dudhia/RRTM |
| 26 | MYJ | KF | Lin | GFDL/GFDL |
| 27 | MYJ | KF | Lin | New Goddard/New Goddard |
| 28 | MYJ | GD | WSM6 | Dudhia/RRTM |
| 29 | MYJ | GD | WSM6 | GFDL/GFDL |
| 30 | MYJ | GD | WSM6 | New Goddard/New Goddard |
| 31 | MYJ | GD | THM | Dudhia/RRTM |
| 32 | MYJ | GD | THM | GFDL/GFDL |
| 33 | MYJ | GD | THM | New Goddard/New Goddard |
| 34 | MYJ | GD | Lin | Dudhia/RRTM |
| 35 | MYJ | GD | Lin | GFDL/GFDL |
| 36 | MYJ | GD | Lin | New Goddard/New Goddard |
| Variable | Absolute Error | WRF-GFS Experiment | WRF-FNL Experiment | ||
|---|---|---|---|---|---|
| Mean | Number of Stations | Mean | Number of Stations | ||
| precipitation | >20 mm | 23.34 mm | 8 | 28.16 mm | 10 |
| 10–20 mm | 14.06 mm | 30 | 13.81 mm | 40 | |
| <10 mm | 4.63 mm | 93 | 4.28 mm | 81 | |
| 2-m temperature | >4 °C | 4.63 °C | 10 | 7.67 °C | 95 |
| 2–4 °C | 2.89 °C | 58 | 2.98 °C | 21 | |
| <2 °C | 1.09 °C | 63 | 1.1 °C | 15 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Mu, Z. Impact of Different Reanalysis Data and Parameterization Schemes on WRF Dynamic Downscaling in the Ili Region. Water 2018, 10, 1729. https://doi.org/10.3390/w10121729
Zhou Y, Mu Z. Impact of Different Reanalysis Data and Parameterization Schemes on WRF Dynamic Downscaling in the Ili Region. Water. 2018; 10(12):1729. https://doi.org/10.3390/w10121729
Chicago/Turabian StyleZhou, Yulin, and Zhenxia Mu. 2018. "Impact of Different Reanalysis Data and Parameterization Schemes on WRF Dynamic Downscaling in the Ili Region" Water 10, no. 12: 1729. https://doi.org/10.3390/w10121729
APA StyleZhou, Y., & Mu, Z. (2018). Impact of Different Reanalysis Data and Parameterization Schemes on WRF Dynamic Downscaling in the Ili Region. Water, 10(12), 1729. https://doi.org/10.3390/w10121729




