A Stochastic Simulation Model for Monthly River Flow in Dry Season
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Methods
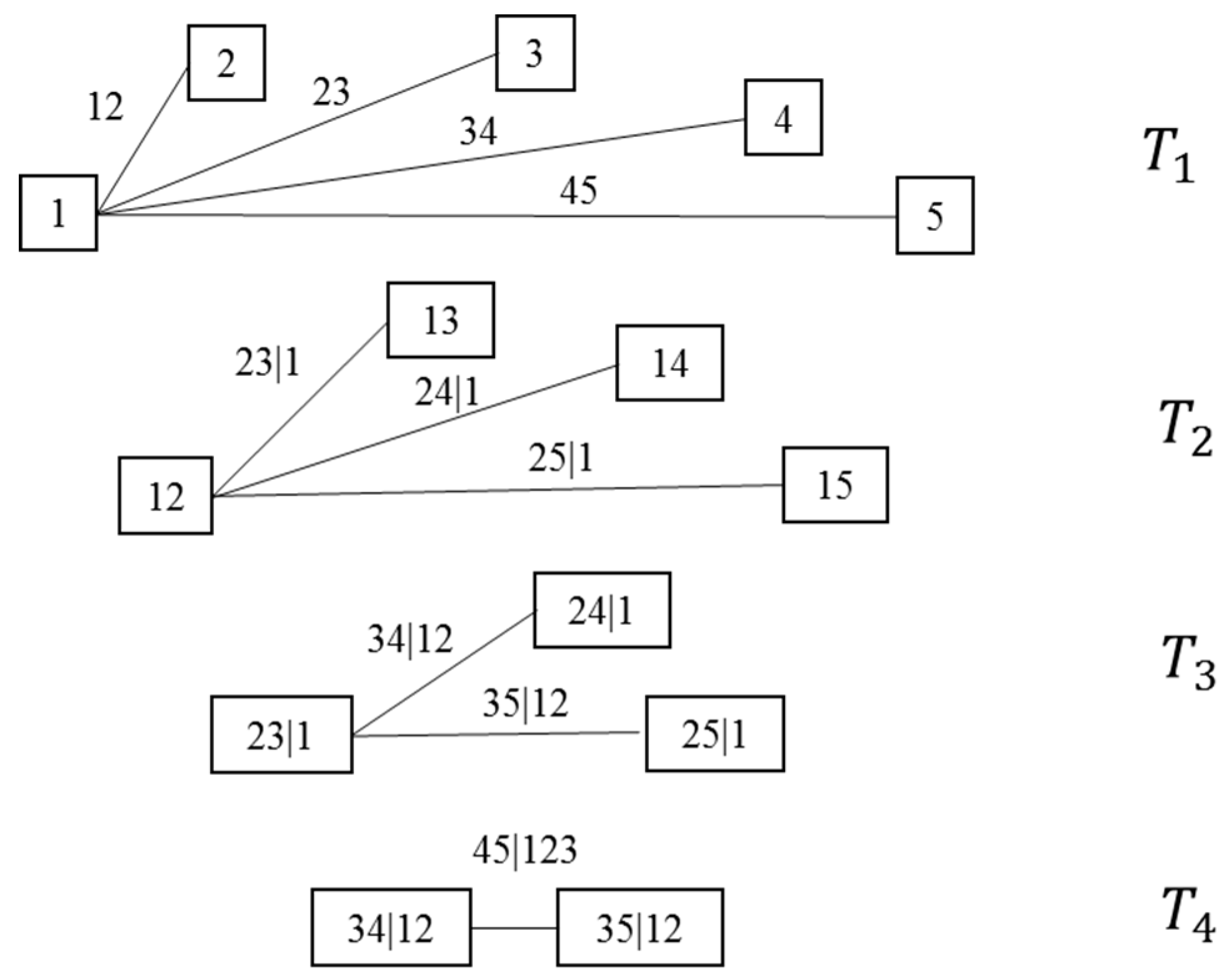
2.2.1. Canonical Vine Copulas
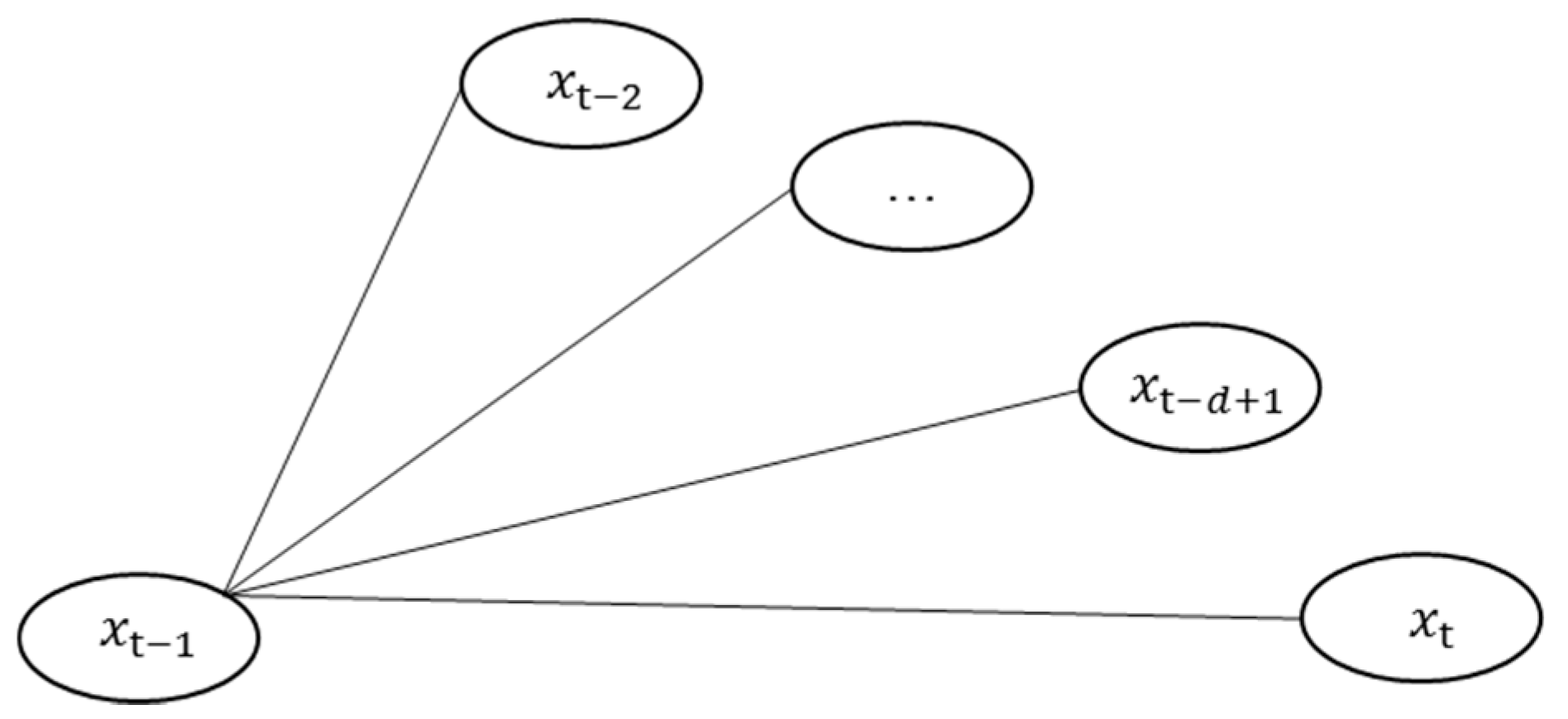
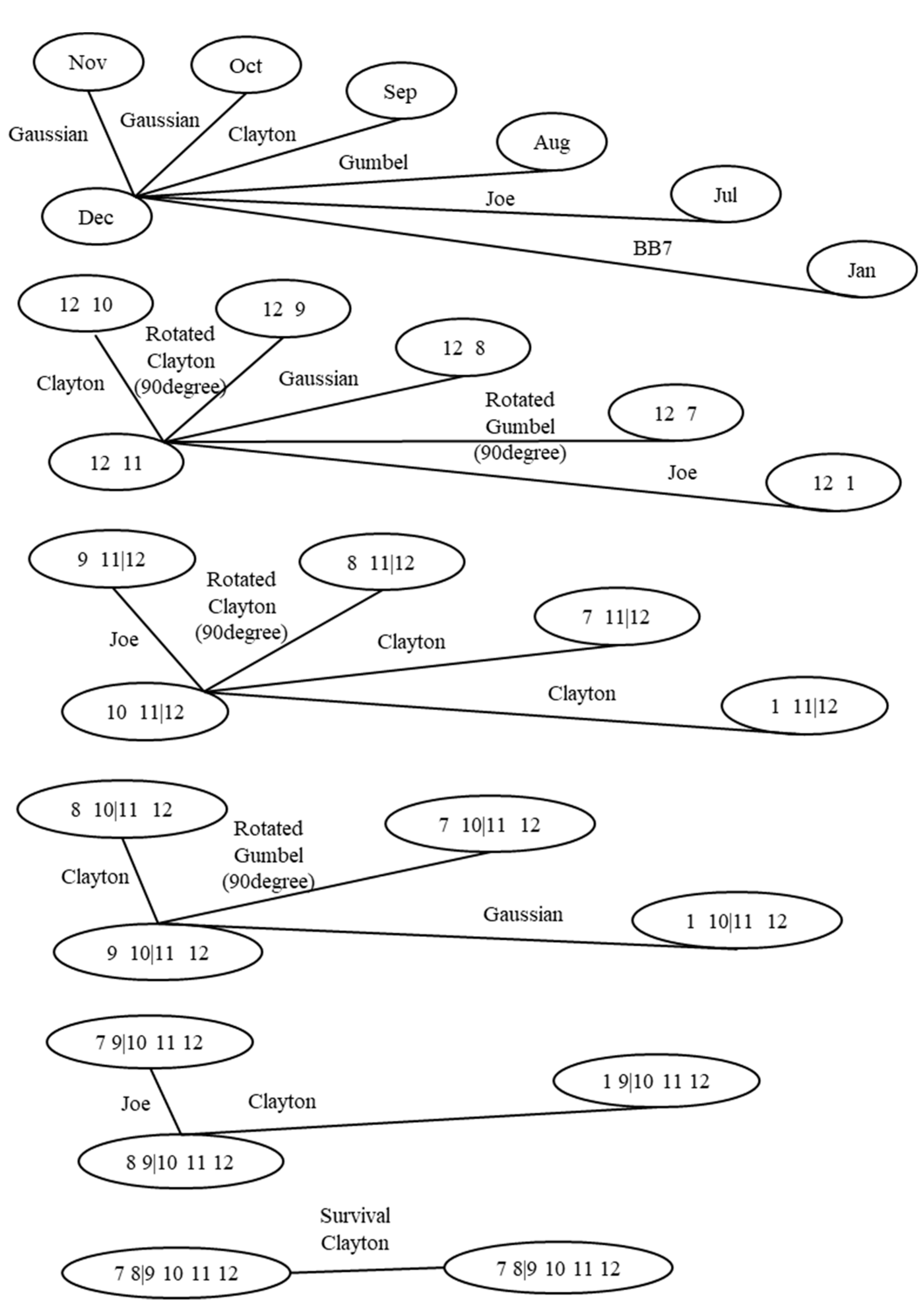
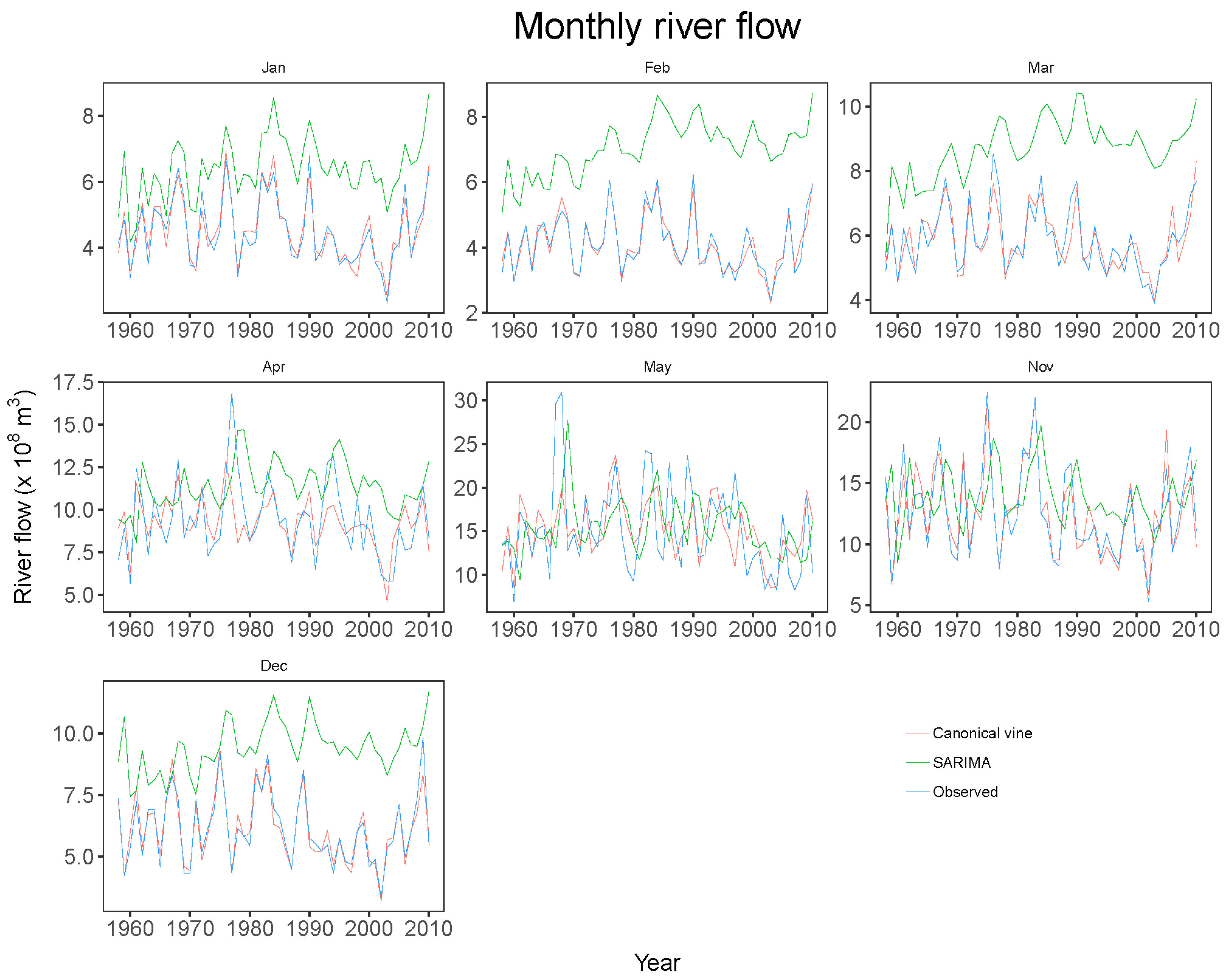
2.2.2. Monthly River Flow Simulation Using Canonical Vine Copulas
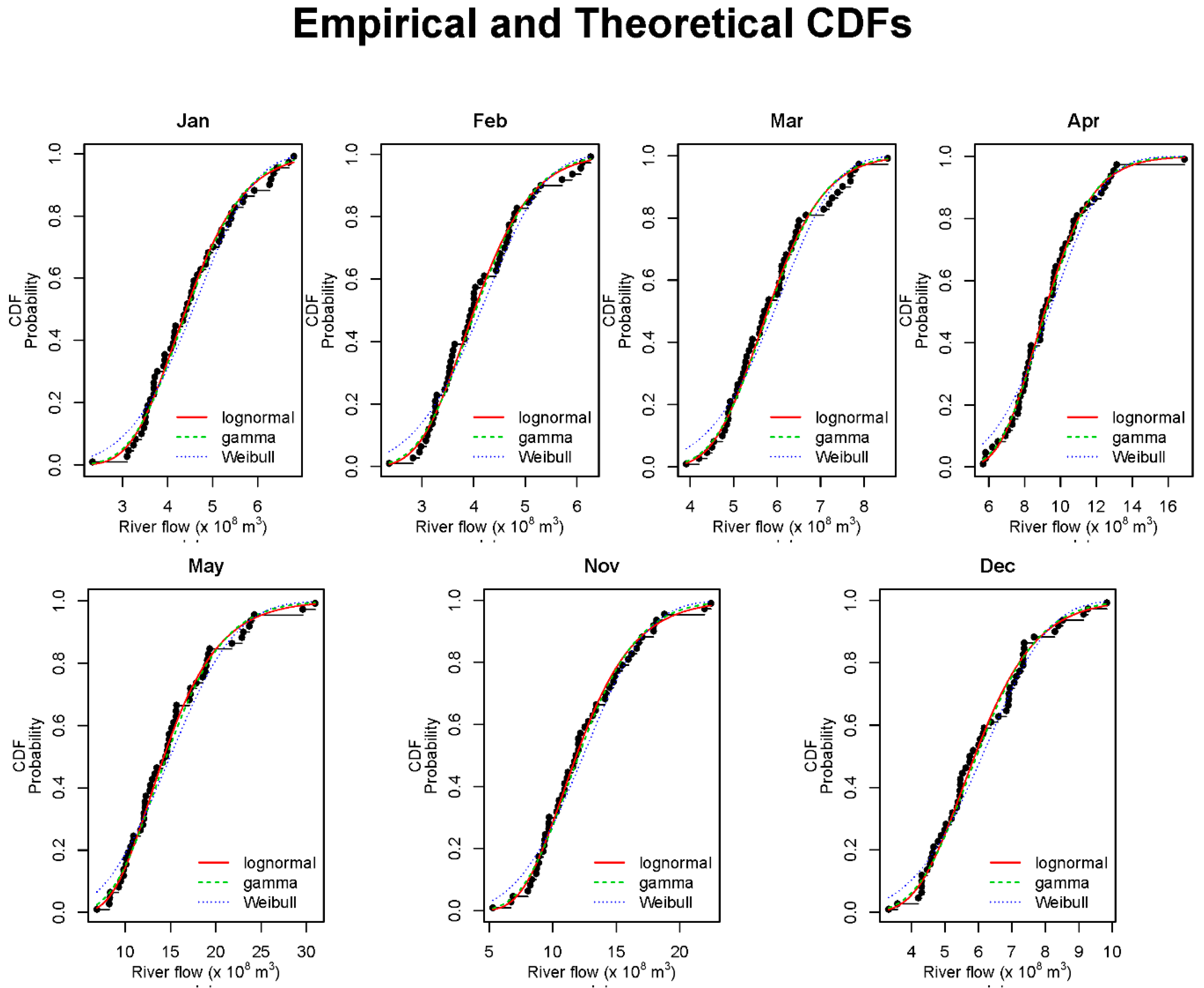
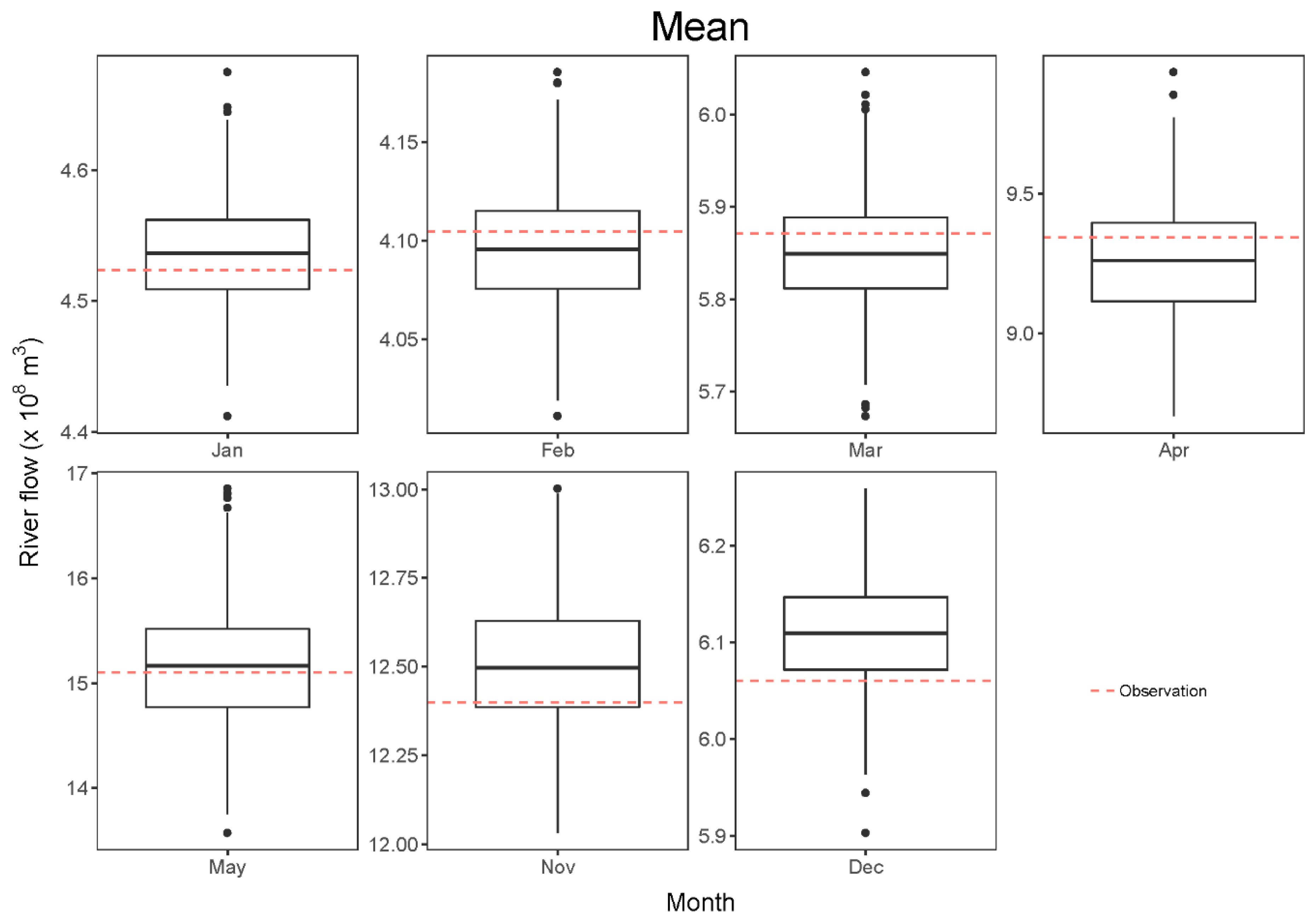
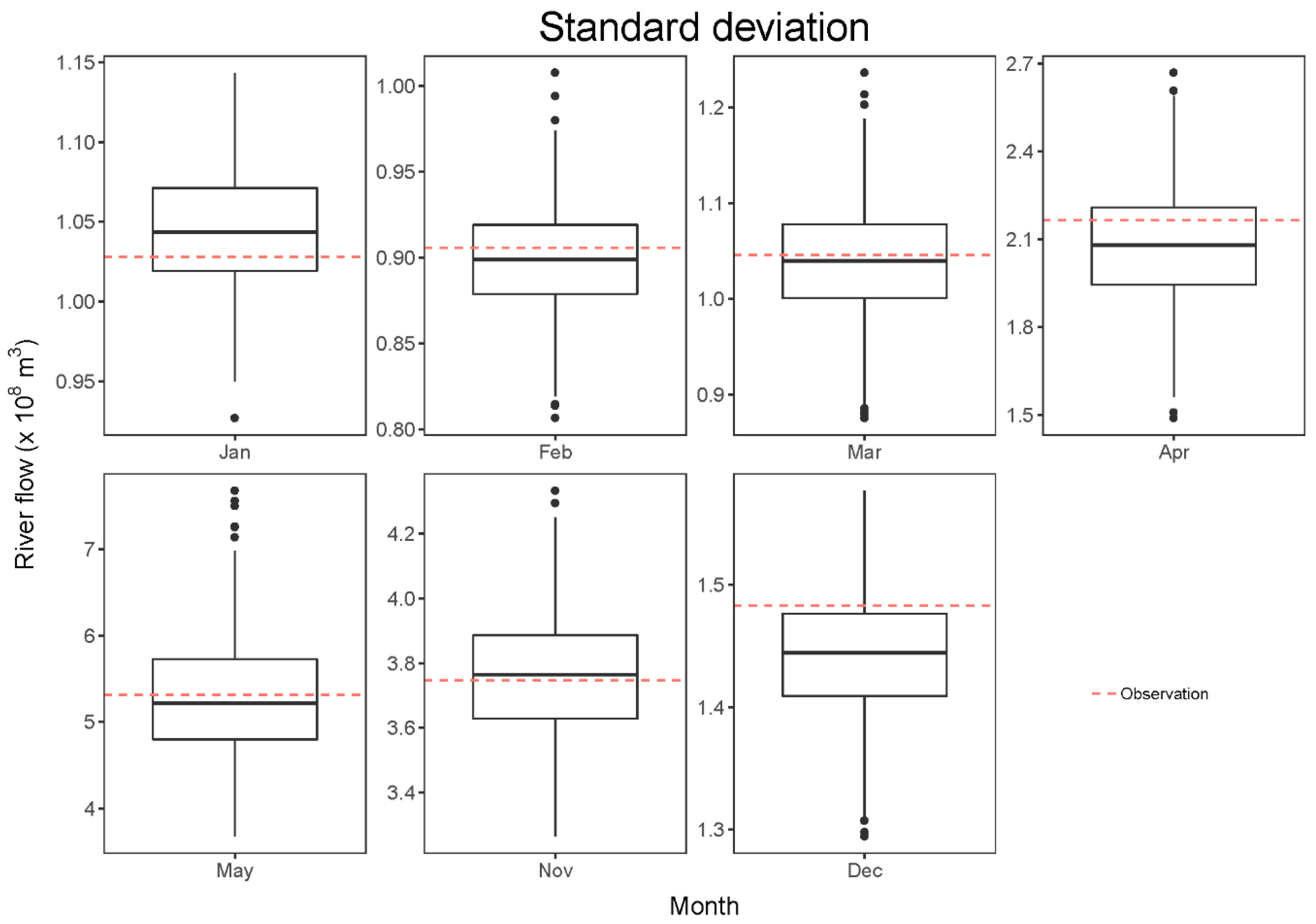
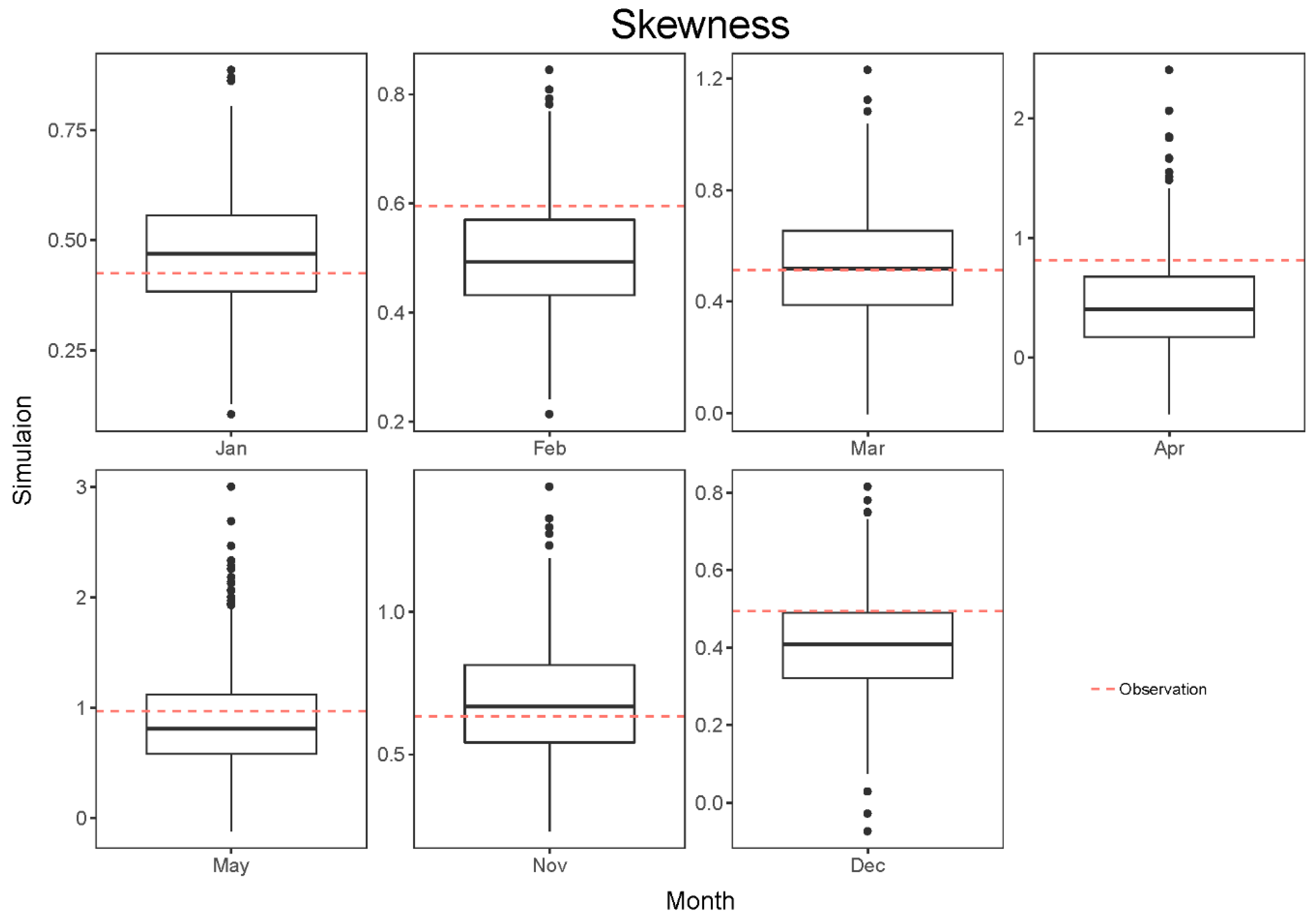
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hutchins, M.; Abesser, C.; Prudhomme, C.; Elliott, J.; Bloomfield, J.; Mansour, M.; Hitt, O. Combined impacts of future land-use and climate stressors on water resources and quality in groundwater and surface waterbodies of the upper Thames river basin, UK. Sci. Total Environ. 2018, 631, 962–986. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Zhong, P.A.; Sun, Y.; Yeh, W.W.G. Real-Time Optimal Flood Control Decision Making and Risk Propagation Under Multiple Uncertainties. Water Resour. Res. 2017, 53, 10635–10654. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Fu, M.; Wang, C.; Mohtar, W.H.M.W.; Deo, R.C.; El-Shafie, A. Application of the Hybrid Artificial Neural Network Coupled with Rolling Mechanism and Grey Model Algorithms for Streamflow Forecasting Over Multiple Time Horizons. Water Resour. Manag. 2018, 32, 1883–1899. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Liu, Z.; Yang, G.; Zhong, Y.; Liu, D. Uncertainty analysis of bivariate design flood estimation and its impacts on reservoir routing. Water Resour. Manag. 2018, 32, 1795–1809. [Google Scholar] [CrossRef]
- Ahani, A.; Shourian, M.; Rad, P.R. Performance Assessment of the Linear, Nonlinear and Nonparametric Data Driven Models in River Flow Forecasting. Water Resour. Manag. 2018, 32, 383–399. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Maskey, M.; Shrestha, D.L. Instance-based learning compared to other data-driven methods in hydrological forecasting. Hydrol. Process. 2008, 22, 275–287. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: San Francisco, CA, USA, 1970. [Google Scholar]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Lall, U.; Sharma, A. A Nearest Neighbor Bootstrap For Resampling Hydrologic Time Series. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mishra, A.; Trenberth, K.E. Climate Change and Drought: A Perspective on Drought Indices. Curr. Clim. Chang. Rep. 2018, 4, 145–163. [Google Scholar] [CrossRef]
- Zhu, F.; Zhong, P.-A.; Sun, Y. Multi-criteria group decision making under uncertainty: Application in reservoir flood control operation. Environ. Model. Softw. 2018, 100, 236–251. [Google Scholar] [CrossRef]
- Balistrocchi, M.; Bacchi, B. Derivation of flood frequency curves through a bivariate rainfall distribution based on copula functions: Application to an urban catchment in northern Italy’s climate. Hydrol. Res. 2017, 48, 749–762. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Liu, Z.; Chen, K.; Chang, F.-J.; Xiong, F. Bivariate seasonal design flood estimation based on copulas. J. Hydrol. Eng. 2017, 22, 05017028. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; He, S.; Guo, J.; Hong, X.; Liu, Z. A copula-based analysis of projected climate changes to bivariate flood quantiles. J. Hydrol. 2018, 566, 23–42. [Google Scholar] [CrossRef]
- Wang, W.; Dong, Z.; Si, W.; Zhang, Y.; Xu, W. Two-Dimension Monthly River Flow Simulation Using Hierarchical Network-Copula Conditional Models. Water Resour. Manag. 2018, 32, 3801–3820. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Zhou, J.; Zhang, J. Copula-based method for multisite monthly and daily streamflow simulation. J. Hydrol. 2015, 528, 369–384. [Google Scholar] [CrossRef]
- Smith, M.S. Copula modelling of dependence in multivariate time series. Int. J. Forecast. 2015, 31, 815–833. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. Improved Bayesian multimodeling: Integration of copulas and Bayesian model averaging. Water Resour. Res. 2014, 50, 9586–9603. [Google Scholar] [CrossRef]
- Kong, X.; Huang, G.; Fan, Y.; Li, Y. Maximum entropy-Gumbel-Hougaard copula method for simulation of monthly streamflow in Xiangxi river, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 833–846. [Google Scholar] [CrossRef]
- Singh, V.P.; Zhang, L. Copula–entropy theory for multivariate stochastic modeling in water engineering. Geosci. Lett. 2018, 5, 6. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, X.; Guan, Y. A multivariate conditional model for streamflow prediction and spatial precipitation refinement. J. Geophys. Res. Atmos. 2015, 120. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Probability density decomposition for conditionally dependent random variables modeled by vines. Ann. Math. Artif. Intell. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Pereira, G.A.A.; Veiga, Á.; Erhardt, T.; Czado, C. A periodic spatial vine copula model for multi-site streamflow simulation. Electr. Power Syst. Res. 2017, 152, 9–17. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, J.; Jin, J.; Weinberg, J.; Bao, Z.; Liu, C.; Liu, Y.; Yan, X.; Song, X.; Zhai, R. Impacts of climate change on water resources in the Yellow River basin and identification of global adaptation strategies. Mitig. Adapt. Strateg. Glob. Chang. 2017, 22, 67–83. [Google Scholar] [CrossRef]
- Wang, T.; Yang, D.; Qin, Y.; Wang, Y.; Chen, Y.; Gao, B.; Yang, H. Historical and future changes of frozen ground in the upper Yellow River Basin. Glob. Planet. Chang. 2018, 162, 199–211. [Google Scholar] [CrossRef]
- Hu, Y.; Maskey, S.; Uhlenbrook, S.; Zhao, H. Streamflow trends and climate linkages in the source region of the Yellow River, China. Hydrol. Process. 2011, 25, 3399–3411. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: New York, NY, USA, 1997. [Google Scholar]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Gumbel, E.J. Distributions des valeurs extrêmes en plusieurs dimensions. Publ. Inst. Stat. Univ. Paris 1960, 9, 171–173. [Google Scholar]
- Frank, M.J. On the simultaneous associativity of F (x, y) andx+y − F (x, y). Aequ. Math. 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Joe, H. Families of m-Variate Distributions with Given Margins and m(m−1)/2 Bivariate Dependence Parameters. Lect. Notes-Monogr. Ser. 1996, 28, 120–141. [Google Scholar]
- Neslen, R. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bedford, T.; Cooke, R.M. Vines: A New Graphical Model for Dependent Random Variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Gao, S.; Liu, P.; Pan, Z.; Ming, B.; Guo, S.; Xiong, L. Derivation of low flow frequency distributions under human activities and its implications. J. Hydrol. 2017, 549, 294–300. [Google Scholar] [CrossRef]
- Wang, D.; Cai, X. Detecting human interferences to low flows through base flow recession analysis. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Pereira, G.; Veiga, Á. PAR(p)-vine copula based model for stochastic streamflow scenario generation. Stoch. Environ. Res. Risk Assess. 2017, 32, 833–842. [Google Scholar] [CrossRef]
- Wagenmakers, E.J.; Farrell, S. AIC model selection using Akaike weights. Psychon. Bull. Rev. 2004, 11, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Posada, D.; Buckley, T.R. Model selection and model averaging in phylogenetics: Advantages of Akaike information criterion and Bayesian approaches over likelihood ratio tests. Syst. Biol. 2004, 53, 793–808. [Google Scholar] [CrossRef] [PubMed]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. Int. Symp. Inf. Theory 1973, 267–281. [Google Scholar]
- Akaike, H. A Bayesian extension of the minimum AIC procedure of autoregressive model fitting. Biometrika 1979, 66, 237–242. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.P.; Mishra, A.K. Monthly river flow simulation with a joint conditional density estimation network. Water Resour. Res. 2013, 49, 3229–3242. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]

| Copula | C(u,u*) | Generator φ(t) | Tail Dep. (Lower, Upper) | Parameter Range |
|---|---|---|---|---|
| Gaussian | ||||
| Student-t | ||||
| Clayton Copula | ||||
| Gumbel Copula | ||||
| Frank Copula | ||||
| Joe | ||||
| Clayton-Gumbel | ||||
| Joe-Gumbel | ||||
| Joe-Clayton | ||||
| Joe-Frank |
| Jan | Feb | Mar | Apr | May | Nov | Dec | |
|---|---|---|---|---|---|---|---|
| Gamma | 0.93 | 0.75 | 0.97 | 0.98 | 0.80 | 0.93 | 0.79 |
| Lognormal | 0.95 | 0.84 | 0.99 | 0.99 | 0.98 | 0.99 | 0.68 |
| Weibull | 0.66 | 0.34 | 0.59 | 0.62 | 0.35 | 0.51 | 0.61 |
| Lag1 | Lag2 | Lag3 | Lag4 | Lag5 | Lag6 | Lag7 | Lag8 | Lag9 | Lag10 | Lag11 | Lag12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jan | 0.747 | 0.722 | 0.702 | 0.586 | 0.459 | 0.449 | 0.147 | 0.146 | 0.117 | 0.213 | 0.092 | 0.135 |
| Feb | 0.803 | 0.746 | 0.681 | 0.665 | 0.574 | 0.447 | 0.423 | 0.126 | 0.223 | 0.174 | 0.233 | 0.135 |
| Mar | 0.681 | 0.693 | 0.656 | 0.617 | 0.594 | 0.501 | 0.393 | 0.310 | 0.113 | 0.116 | 0.075 | 0.167 |
| Apr | 0.340 | 0.336 | 0.371 | 0.280 | 0.333 | 0.308 | 0.217 | 0.255 | 0.198 | 0.114 | 0.096 | 0.142 |
| May | 0.454 | 0.284 | 0.312 | 0.311 | 0.262 | 0.287 | 0.256 | 0.241 | 0.061 | 0.099 | 0.040 | 0.111 |
| Jun | 0.356 | 0.187 | 0.308 | 0.345 | 0.298 | 0.342 | 0.350 | 0.350 | 0.268 | 0.152 | 0.159 | 0.022 |
| Jul | 0.372 | 0.203 | 0.154 | 0.361 | 0.374 | 0.350 | 0.368 | 0.354 | 0.363 | 0.286 | 0.139 | 0.126 |
| Aug | 0.384 | 0.055 | 0.115 | 0.142 | 0.108 | 0.073 | 0.092 | 0.076 | 0.126 | 0.099 | 0.022 | −0.052 |
| Sep | 0.382 | 0.222 | 0.005 | 0.096 | 0.100 | 0.091 | 0.045 | 0.086 | 0.031 | 0.082 | 0.087 | 0.066 |
| Oct | 0.602 | 0.356 | 0.282 | 0.023 | 0.024 | 0.045 | 0.103 | 0.044 | 0.082 | 0.008 | 0.066 | 0.050 |
| Nov | 0.781 | 0.530 | 0.416 | 0.286 | 0.097 | 0.073 | 0.094 | 0.150 | 0.059 | 0.092 | 0.017 | 0.096 |
| Dec | 0.795 | 0.695 | 0.549 | 0.417 | 0.296 | 0.126 | 0.153 | 0.126 | 0.235 | 0.111 | 0.160 | 0.094 |
| SARIMA | Canonical Vine | |
|---|---|---|
| MAE | 3.14 | 1.21 |
| RMSE | 3.79 | 2.48 |
| NSE | −0.76 | 0.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Dong, Z.; Zhu, F.; Cao, Q.; Chen, J.; Yu, X. A Stochastic Simulation Model for Monthly River Flow in Dry Season. Water 2018, 10, 1654. https://doi.org/10.3390/w10111654
Wang W, Dong Z, Zhu F, Cao Q, Chen J, Yu X. A Stochastic Simulation Model for Monthly River Flow in Dry Season. Water. 2018; 10(11):1654. https://doi.org/10.3390/w10111654
Chicago/Turabian StyleWang, Wenzhuo, Zengchuan Dong, Feilin Zhu, Qing Cao, Juan Chen, and Xiao Yu. 2018. "A Stochastic Simulation Model for Monthly River Flow in Dry Season" Water 10, no. 11: 1654. https://doi.org/10.3390/w10111654
APA StyleWang, W., Dong, Z., Zhu, F., Cao, Q., Chen, J., & Yu, X. (2018). A Stochastic Simulation Model for Monthly River Flow in Dry Season. Water, 10(11), 1654. https://doi.org/10.3390/w10111654






