Using SCADA to Detect and Locate Bursts in a Long-Distance Water Pipeline
Abstract
1. Introduction
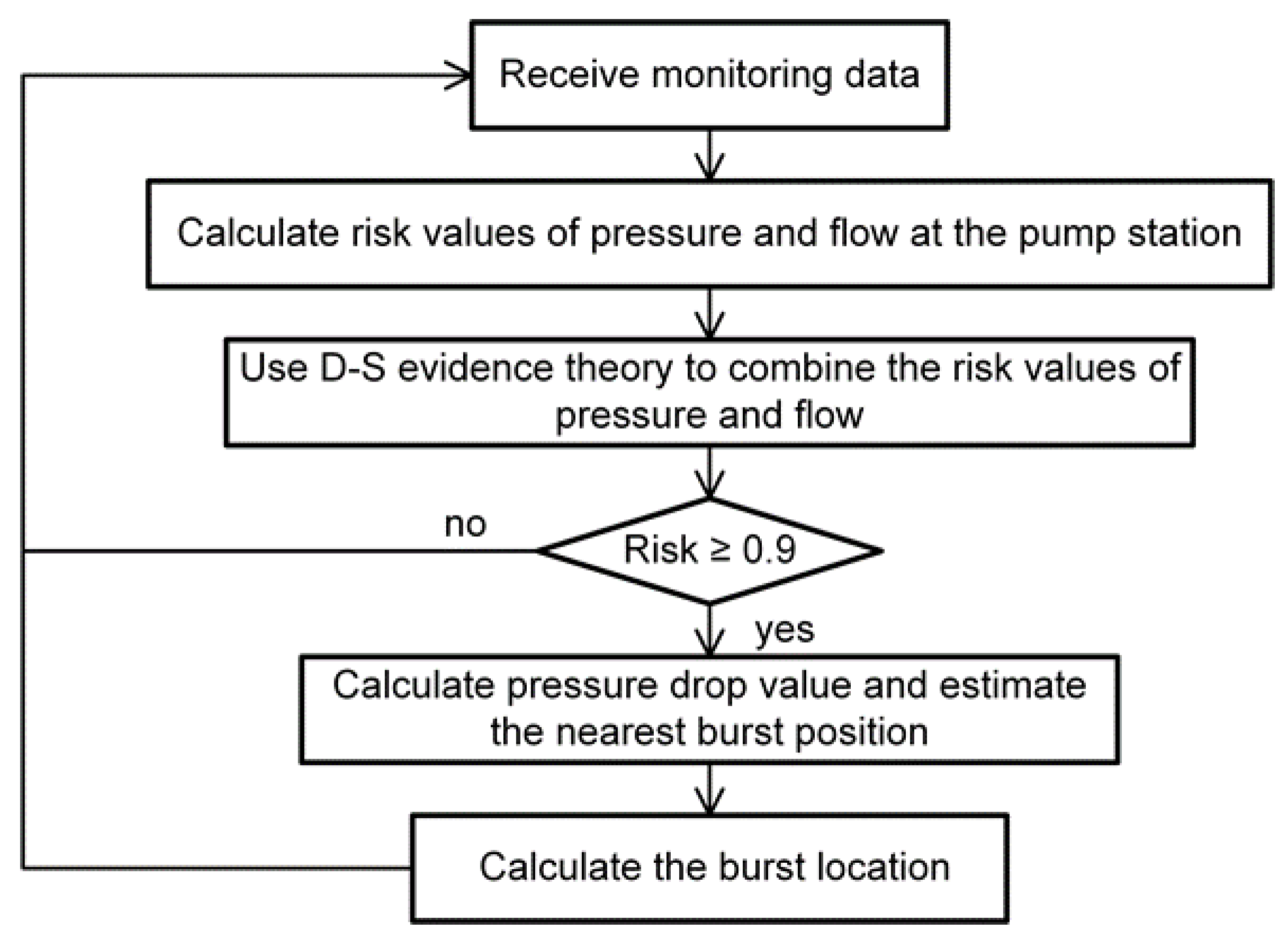
2. Pipe Burst Detection
2.1. State Changes of Pressure and Flow at Pumping Station
- State 1
- When the number of operating pumps increases, the pressure and flow both increase (ΔP and ΔQ are positive);
- State 2
- When some pumps are shut off, the pressure drops and the flow also decreases (ΔP and ΔQ are negative);
- State 3
- If the flow decreases, the pressure rises when the number of pumps operating remains constant (ΔQ is negative and ΔP is positive); and
- State 4
- If the flow increases, the pressure descends when the number of pumps stays constant (ΔQ is positive and ΔP is negative).
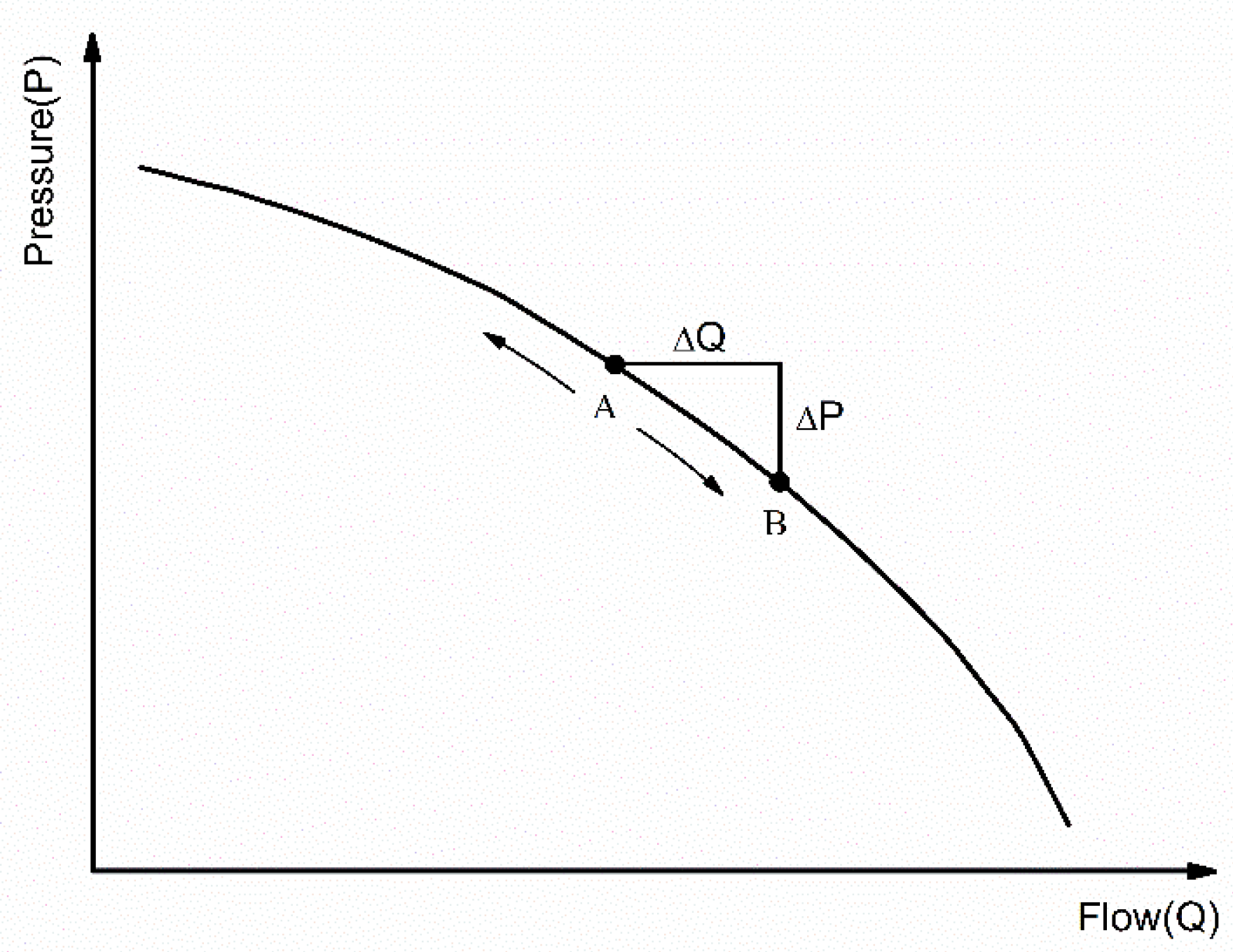
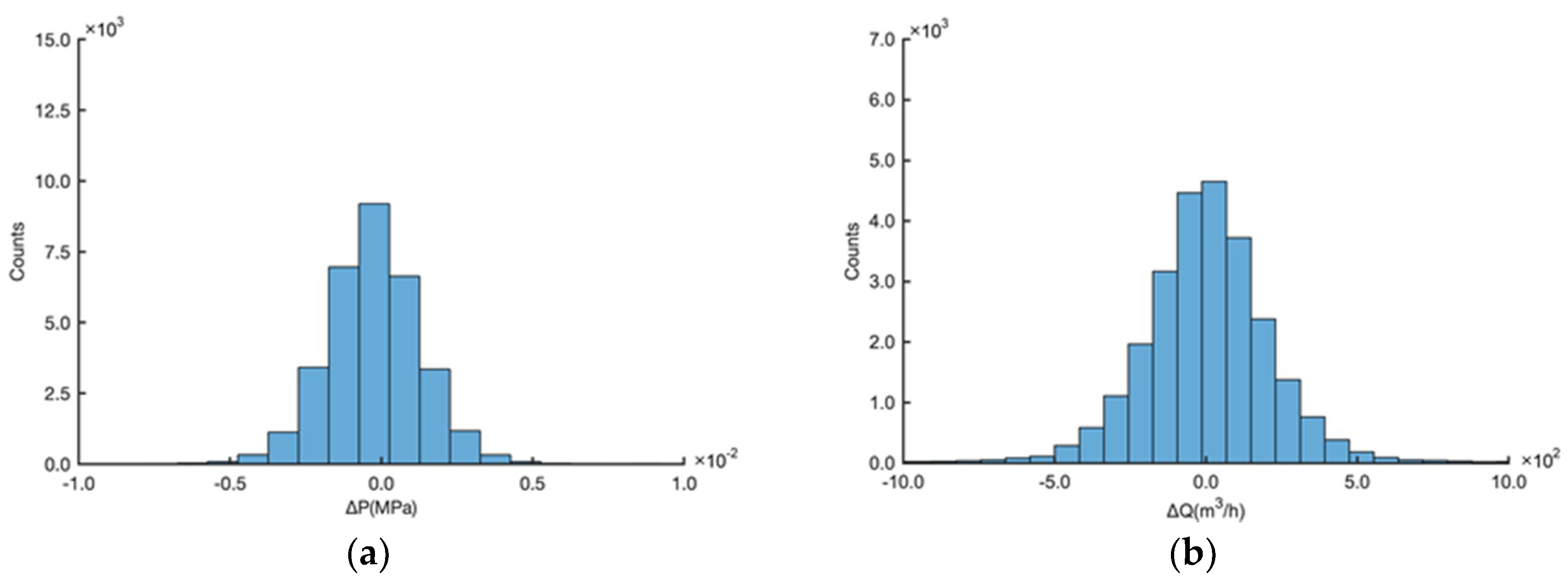
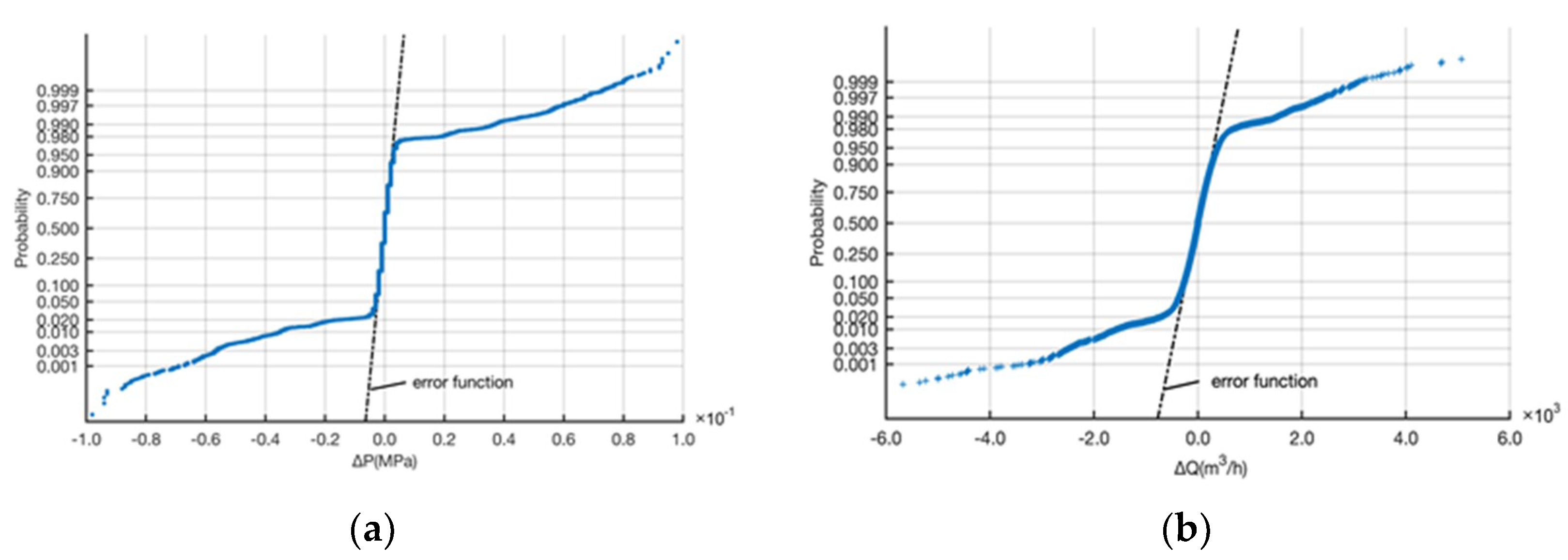
2.2. Pressure and Flow Fluctuation Distributions
2.3. Abnormality Risk Function
2.4. Combining Pressure and Flow Risk Functions
3. Pipe Burst Localization
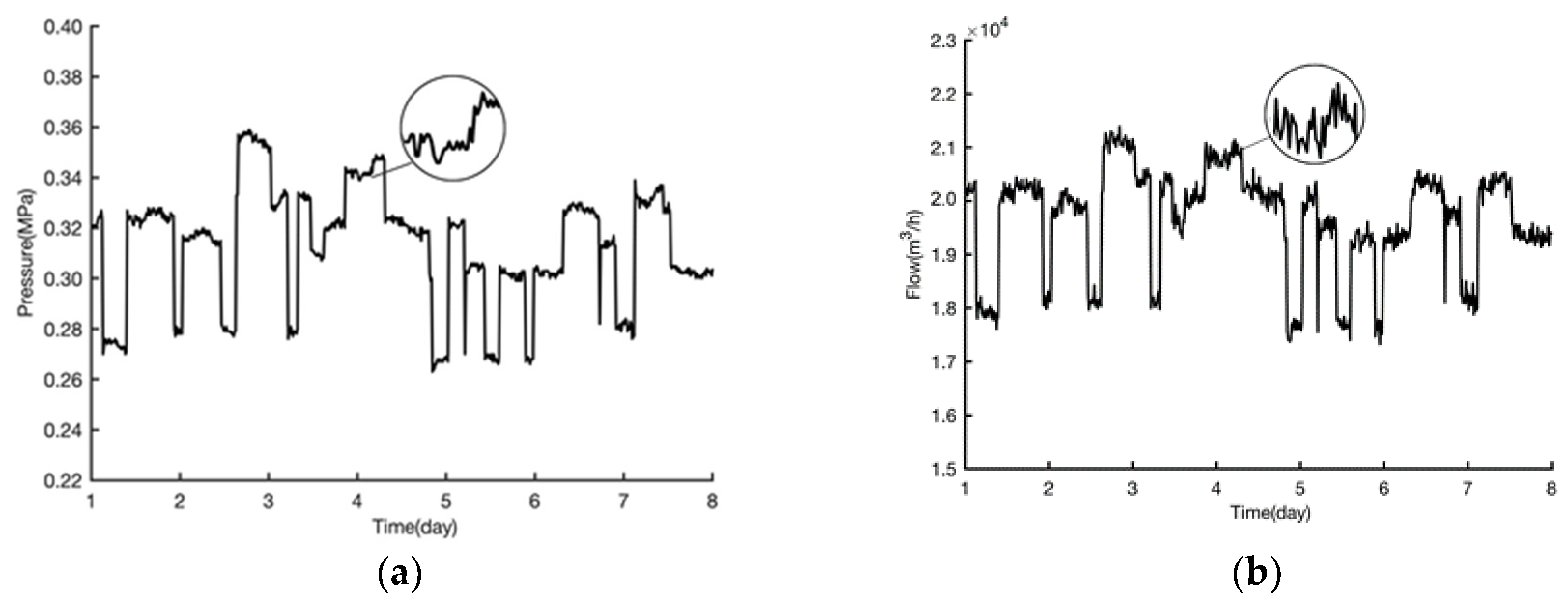
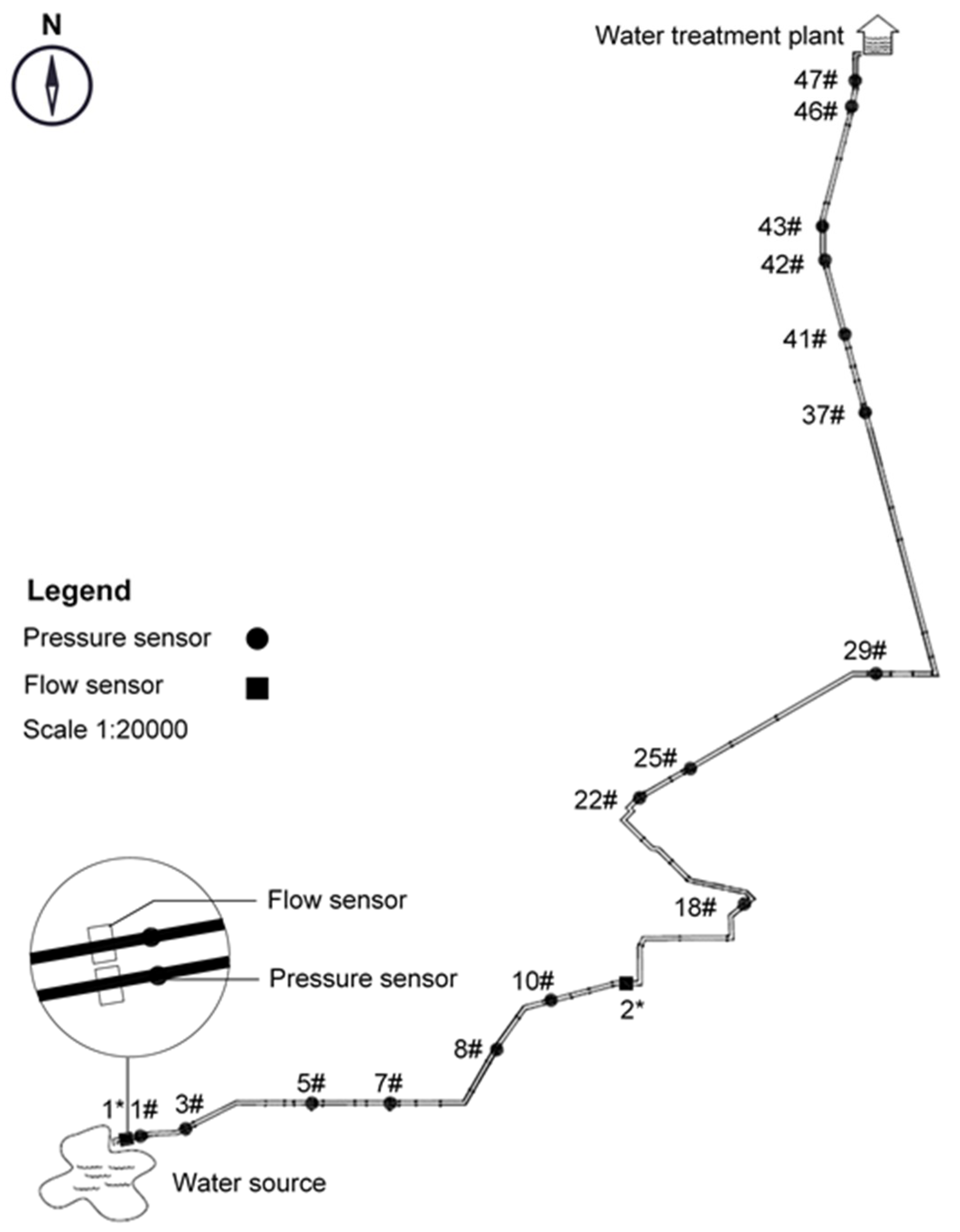
4. Case Study
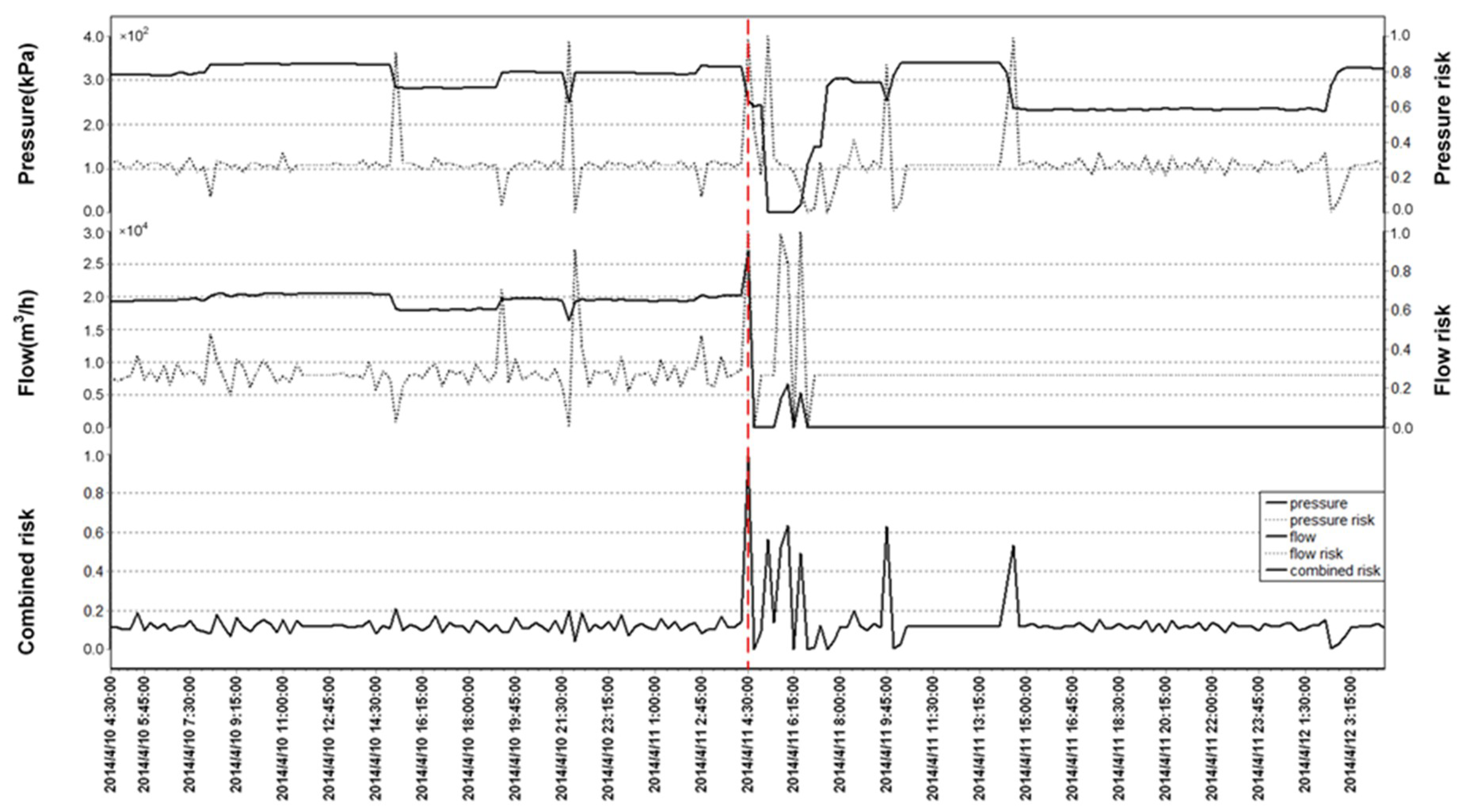
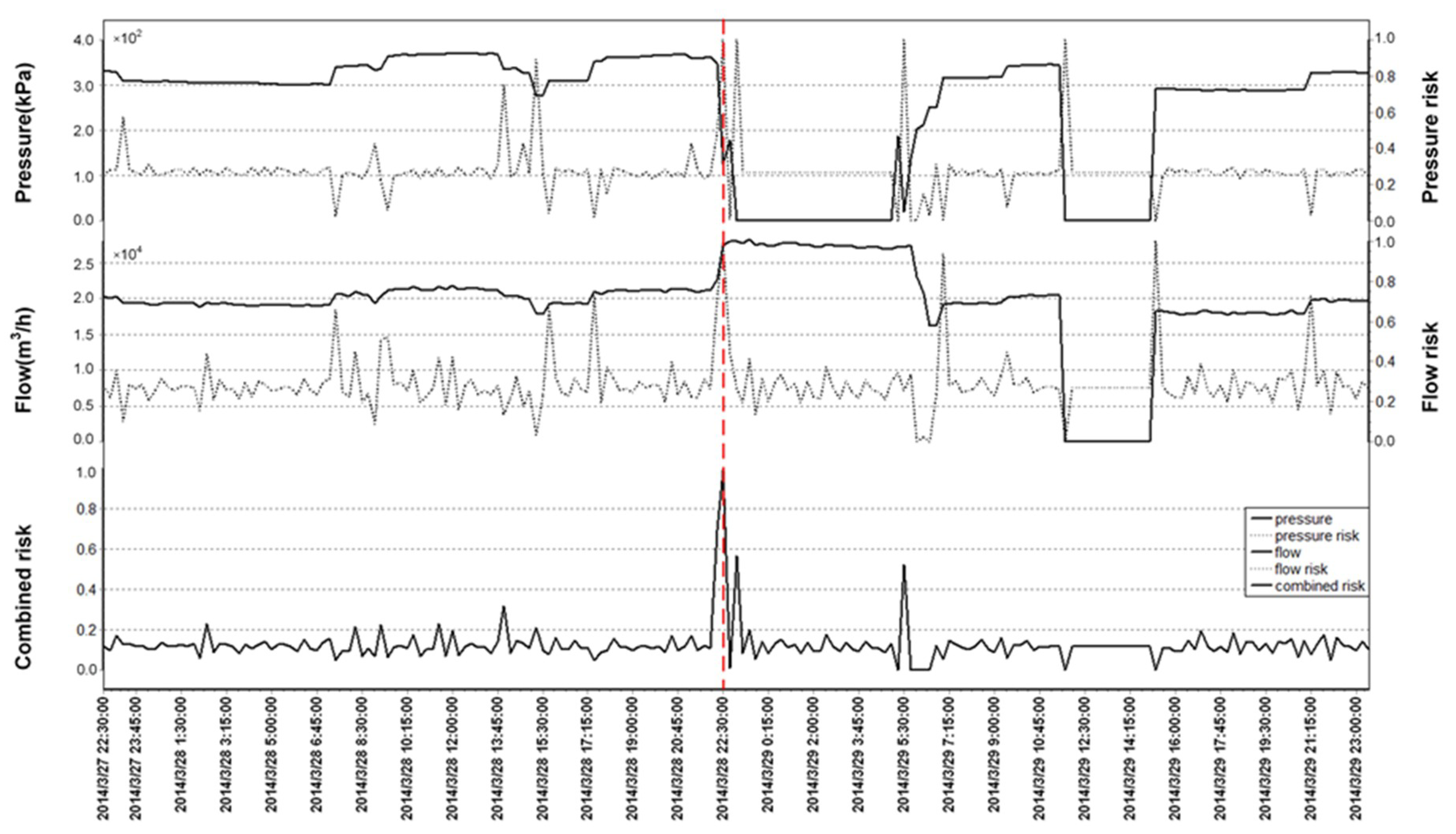
4.1. Pipe Burst Detection
4.1.1. Risk Threshold
4.1.2. Two Burst Events
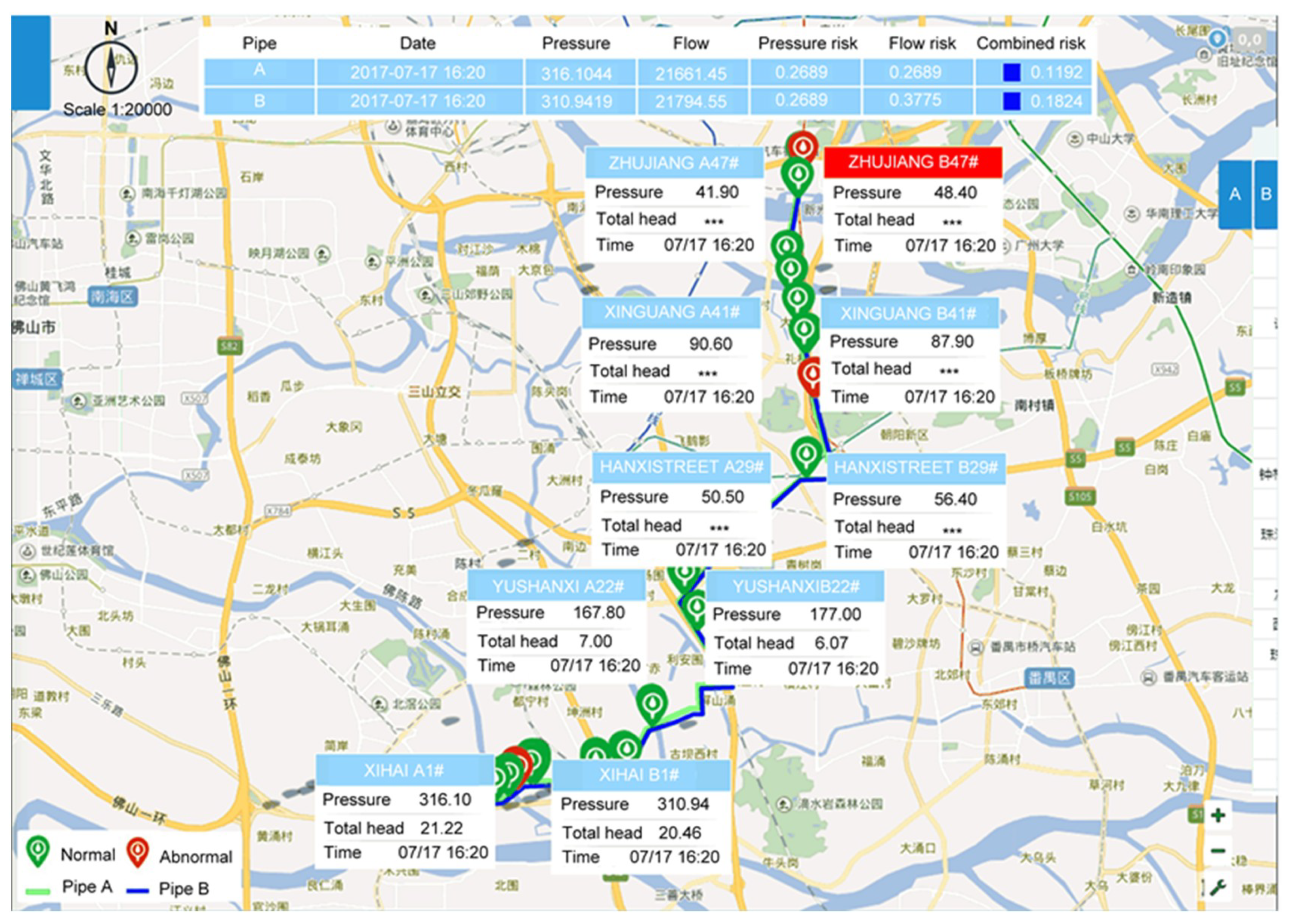
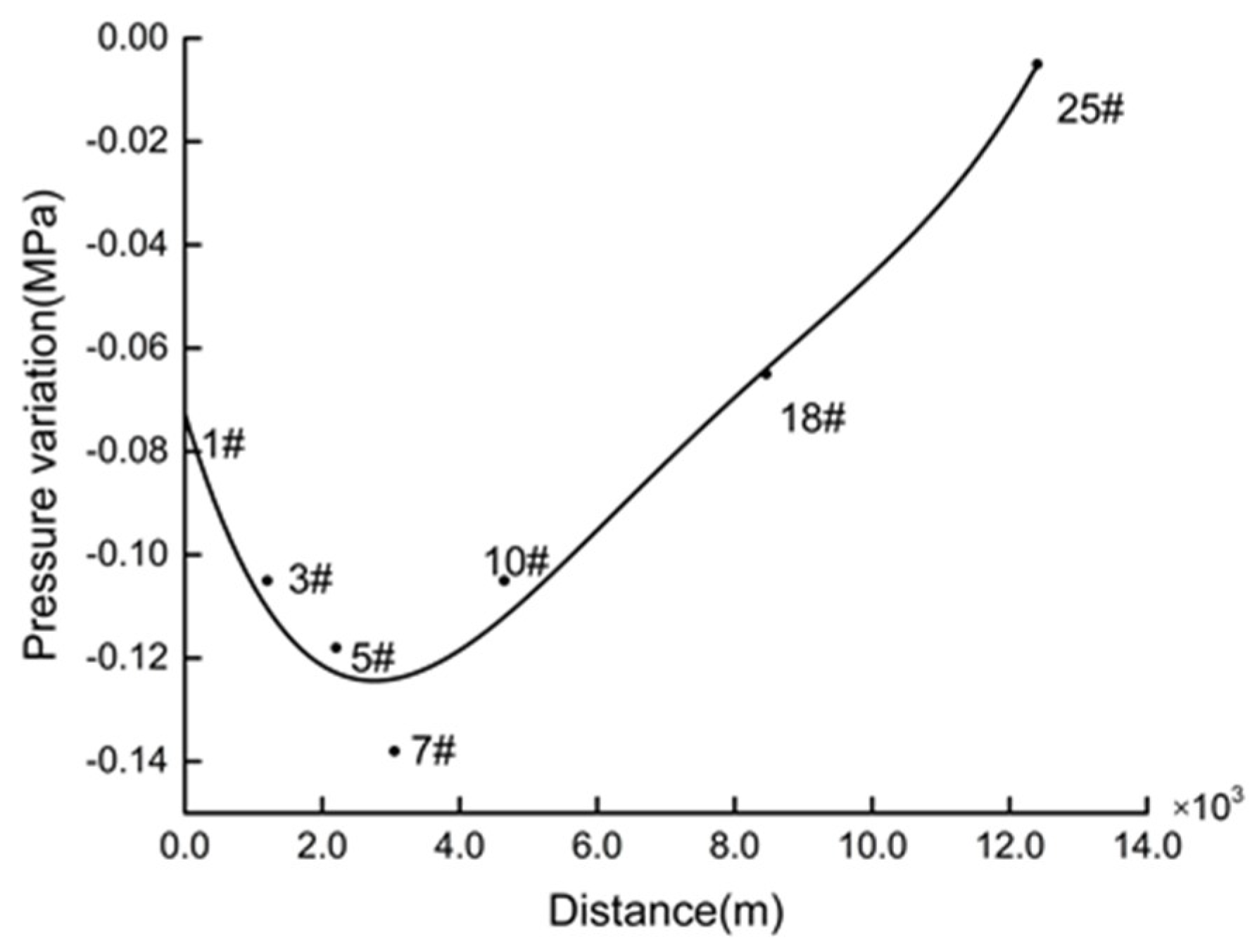
4.2. Pipe Burst Location
4.3. Parameter Sensitivity Analysis
5. Discussion and Conclusions
- The pressure sensors that are used for burst detection in a long-distance water transportation pipeline should be evenly distributed, and the distance between sensors should not exceed 5000 m. It is not necessary to increase the density of sensors because there would be little improvement in the results but the management costs would greatly increase.
- The sampling return period of the pressure sensors should not exceed 5 min. If the sampling time is too long, the backflow of water in the pipe after the burst point will affect the sensor readings, which will lead to large deviations in the calculations. More frequent sampling results will require more power, but will not greatly increase precision. A reasonable sampling frequency is necessary to ensure the feasibility and effectiveness of the monitoring system.
- The data fluctuations observed in a long-distance water pipeline are consistent with the behavior of a water distribution system. In practice, the accuracy of instrumental monitoring can be improved by taking account of the statistical characteristics of monitored data during normal operation of the system.
Author Contributions
Funding
Conflicts of Interest
References
- Li, R.; Huang, H.D.; Xin, K.L.; Tao, T. A review of methods for burst/leakage detection and location in water distribution systems. Water Sci. Technol.-Water Supply 2015, 15, 429–441. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Vibroacoustic Measurements for Detecting Water Leaks in Buried Small-Diameter Plastic Pipes. J. Pipeline Syst. Eng. Pract. 2017, 8, 10. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A.; Nascetti, D. Preliminary Investigations on Automatic Detection of Leaks in Water Distribution Networks by Means of Vibration Monitoring. Adv. Cond. Monit. Mach. Non-Station. Oper. 2014, 535–544. [Google Scholar] [CrossRef]
- Yazdekhasti, S.; Piratla, K.R.; Atamturktur, S.; Khan, A.A. Novel vibration-based technique for detecting water pipeline leakage. Struct. Infrastruct. Eng. 2016, 13, 731–742. [Google Scholar] [CrossRef]
- Yazdekhasti, S.; Piratla, K.R.; Atamturktur, S.; Khan, A. Experimental evaluation of a vibration-based leak detection technique for water pipelines. Struct. Infrastruct. Eng. 2018, 14, 46–55. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Leak Detection in Water-Filled Small-Diameter Polyethylene Pipes by Means of Acoustic Emission Measurements. Appl. Sci.-Basel 2017, 7, 13. [Google Scholar] [CrossRef]
- Baghdadi, A.H.A.; Mansy, H.A. A mathematical-model for leak location in pipelines. Appl. Math. Model. 1988, 12, 25–30. [Google Scholar] [CrossRef]
- Pudar, R.S.; Liggett, J.A. Leaks in pipe networks. J. Hydraul. Eng. 1992, 118, 1031–1046. [Google Scholar] [CrossRef]
- Misiunas, D.; Lambert, M.; Simpson, A.; Olsson, G. Burst detection and location in water distribution networks. Effic. Use Manag. Urban Water Supply 2005, 5, 71–80. [Google Scholar] [CrossRef]
- Lee, P.J.; Vitkovsky, J.P.; Lambert, M.F.; Simpson, A.R.; Liggett, J.A. Leak location using the pattern of the frequency response diagram in pipelines: A numerical study. J. Sound Vib. 2005, 284, 1051–1073. [Google Scholar] [CrossRef]
- Bicik, J.; Kapelan, Z.; Makropoulos, C.; Savic, D.A. Pipe burst diagnostics using evidence theory. J. Hydroinform. 2011, 13, 596–608. [Google Scholar] [CrossRef]
- Srirangarajan, S.; Allen, M.; Preis, A.; Iqbal, M.; Lim, H.B.; Whittle, A.J. Wavelet-based burst event detection and localization in water distribution systems. J. Signal Process. Syst. Signal Image Video Technol. 2013, 72, 1–16. [Google Scholar] [CrossRef]
- Mounce, S.R.; Machell, J. Burst detection using hydraulic data from water distribution systems with artificial neural networks. Urban Water J. 2006, 3, 21–31. [Google Scholar] [CrossRef]
- Farley, B.; Mounce, S.R.; Boxall, J.B. Development and field validation of a burst localization methodology. J. Water Resour. Plan. Manag. 2013, 139, 604–613. [Google Scholar] [CrossRef]
- Mounce, S.R.; Boxall, J.B.; Machell, J. Development and verification of an online artificial intelligence system for detection of bursts and other abnormal flows. J. Water Resour. Plan. Manag.-ASCE 2010, 136, 309–318. [Google Scholar] [CrossRef]
- Ye, G.L.; Fenner, R.A. Kalman filtering of hydraulic measurements for burst detection in water distribution systems. J. Pipel. Syst. Eng. Pract. 2011, 2, 14–22. [Google Scholar] [CrossRef]
- Choi, D.Y.; Kim, S.W.; Choi, M.A.; Geem, Z.W. Adaptive Kalman filter based on adjustable sampling interval in burst detection for water distribution system. Water 2016, 8, 142. [Google Scholar] [CrossRef]
- Ye, G.; Fenner, R.A. Weighted least squares with expectation-maximization algorithm for burst detection in U.K. water distribution systems. J. Water Resour. Plan. Manag. 2014, 140, 417–424. [Google Scholar] [CrossRef]
- Lin, C.C. A hybrid heuristic optimization approach for leak detection in pipe networks using ordinal optimization approach and the symbiotic organism search. Water 2017, 9, 812. [Google Scholar] [CrossRef]
- Wu, Y.P.; Liu, S.M.; Wu, X.; Liu, Y.F.; Guan, Y.S. Burst detection in district metering areas using a data driven clustering algorithm. Water Res. 2016, 100, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.P.; Liu, S.M. A review of data-driven approaches for burst detection in water distribution systems. Urban Water J. 2017, 14, 972–983. [Google Scholar] [CrossRef]
- Zhao, D.D.; Cheng, W.P. Study on minimum detectable pipe diameter for pipe burst in water distribution system. China Water Wastewater 2014, 30, 117–122. (in Chinese). [Google Scholar]
- Shafer, G.A. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]

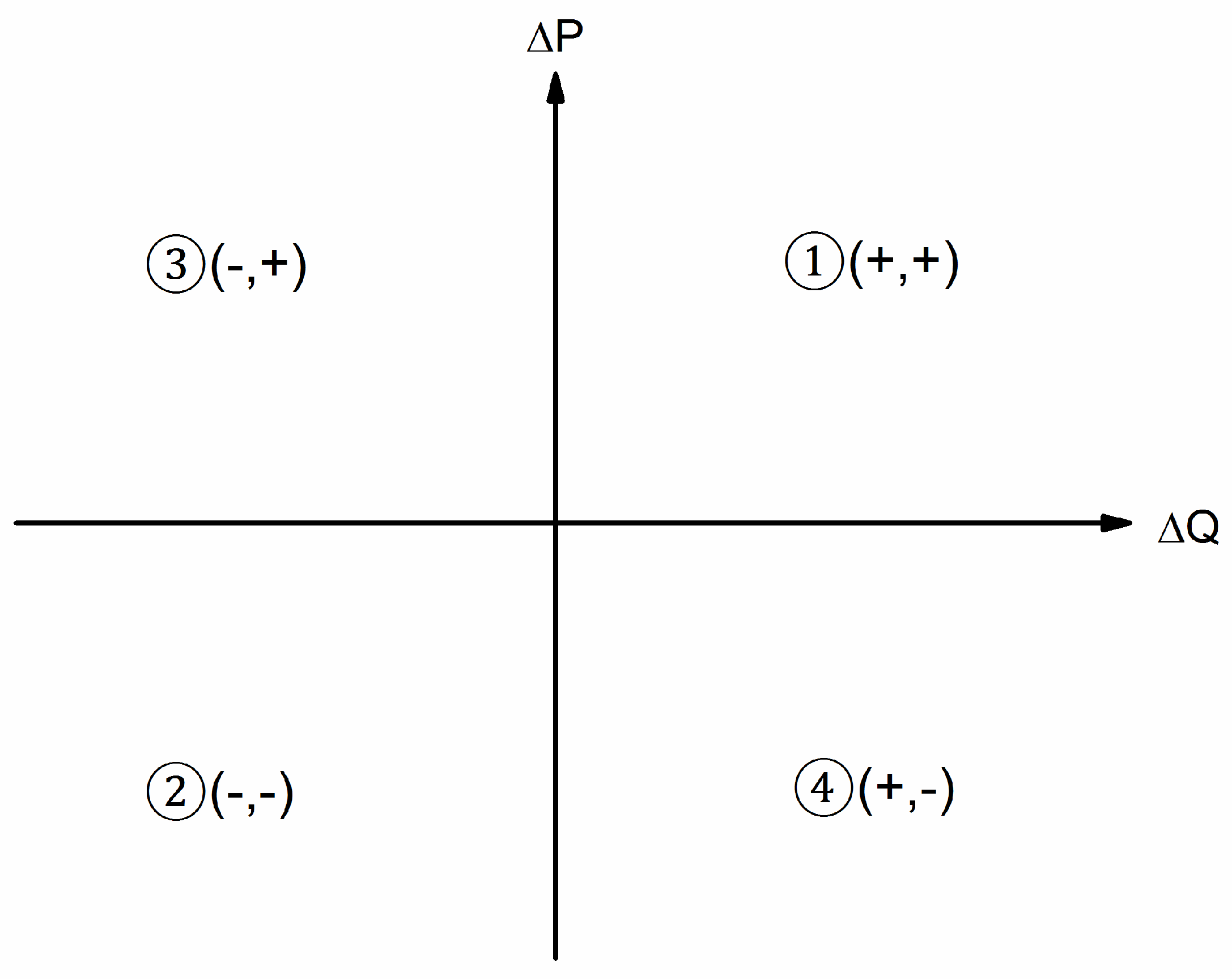


| Pressure Risk | Flow Risk | Combined Risk | ||||||
|---|---|---|---|---|---|---|---|---|
| Risk | Counts | Proportion | Risk | Counts | Proportion | Risk | Counts | Proportion |
| 0.0–0.1 | 813 | 2.32% | 0.0–0.1 | 615 | 1.75% | 0.0–0.1 | 7901 | 22.55% |
| 0.1–0.2 | 123 | 0.35% | 0.1–0.2 | 1677 | 4.78% | 0.1–0.2 | 26,525 | 75.70% |
| 0.2–0.3 | 31,608 | 90.21% | 0.2–0.3 | 24,359 | 69.51% | 0.2–0.3 | 403 | 1.15% |
| 0.3–0.6 | 1807 | 5.15% | 0.3–0.6 | 7848 | 22.39% | 0.3–0.6 | 116 | 0.33% |
| 0.6–0.9 | 380 | 1.08% | 0.6–0.9 | 362 | 1.03% | 0.6–0.9 | 71 | 0.20% |
| 0.9–1.0 | 309 | 0.88% | 0.9–1.0 | 179 | 0.51% | 0.9–1.0 | 24 | 0.07% |
| Sensor | 1# | 3# | 5# | 7# | 10# | 18# | 25# |
|---|---|---|---|---|---|---|---|
| Pb (MPa) | 0.330 | 0.332 | 0.314 | 0.303 | 0.281 | 0.203 | 0.121 |
| Pa (MPa) | 0.255 | 0.227 | 0.197 | 0.165 | 0.177 | 0.138 | 0.116 |
| Pb − Pa (MPa) | −0.075 | −0.105 | −0.118 | −0.138 | −0.105 | −0.065 | −0.005 |
| Distance from pumping station (m) | 0 | 1200 | 2200 | 3050 | 4646 | 8459 | 12403 |
| Pipe Section | 1–10 | 3–10 | 5–10 | 7–10 |
|---|---|---|---|---|
| S × 1011 (kPa·h2/m7) | 3.49 | 3.80 | 3.15 | 3.73 |
| C (kPa) | −27.70 | 4.00 | −2.67 | −3.53 |
| X (m) | 2683.06 | 2365.52 | 1181.89 | −1362.80 |
| Distance from pumping station (m) | 2683.06 | 3565.52 | 3381.89 | 1687.20 |
| Pipe Section | Items | S | S − 20% | S − 10% | S + 10% | S + 20% |
|---|---|---|---|---|---|---|
| 1–10 | S | 3.49 | 2.79 | 3.14 | 3.84 | 4.19 |
| x (m) | 2682.519 | 3355.552 | 2981.526 | 2438.018 | 2234.365 | |
| Location (m) | 2682.519 | 3355.552 | 2981.526 | 2438.018 | 2234.365 | |
| Deviation (m) | 0 | 673.033 | 299.007 | −244.501 | −448.154 | |
| 3–10 | S | 3.80 | 3.04 | 3.42 | 4.18 | 4.56 |
| x (m) | 2365.520 | 3042.988 | 2666.617 | 2119.168 | 1913.874 | |
| Location (m) | 3565.520 | 4242.988 | 3866.617 | 3319.168 | 3113.874 | |
| Deviation (m) | 0 | 677.468 | 301.097 | −246.352 | −451.646 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Fang, H.; Xu, G.; Chen, M. Using SCADA to Detect and Locate Bursts in a Long-Distance Water Pipeline. Water 2018, 10, 1727. https://doi.org/10.3390/w10121727
Cheng W, Fang H, Xu G, Chen M. Using SCADA to Detect and Locate Bursts in a Long-Distance Water Pipeline. Water. 2018; 10(12):1727. https://doi.org/10.3390/w10121727
Chicago/Turabian StyleCheng, Weiping, Hongji Fang, Gang Xu, and Meijun Chen. 2018. "Using SCADA to Detect and Locate Bursts in a Long-Distance Water Pipeline" Water 10, no. 12: 1727. https://doi.org/10.3390/w10121727
APA StyleCheng, W., Fang, H., Xu, G., & Chen, M. (2018). Using SCADA to Detect and Locate Bursts in a Long-Distance Water Pipeline. Water, 10(12), 1727. https://doi.org/10.3390/w10121727




