Effects of Geometry and Hydraulic Characteristics of Shallow Reservoirs on Sediment Entrapment
Abstract
1. Introduction
2. Governing Equations
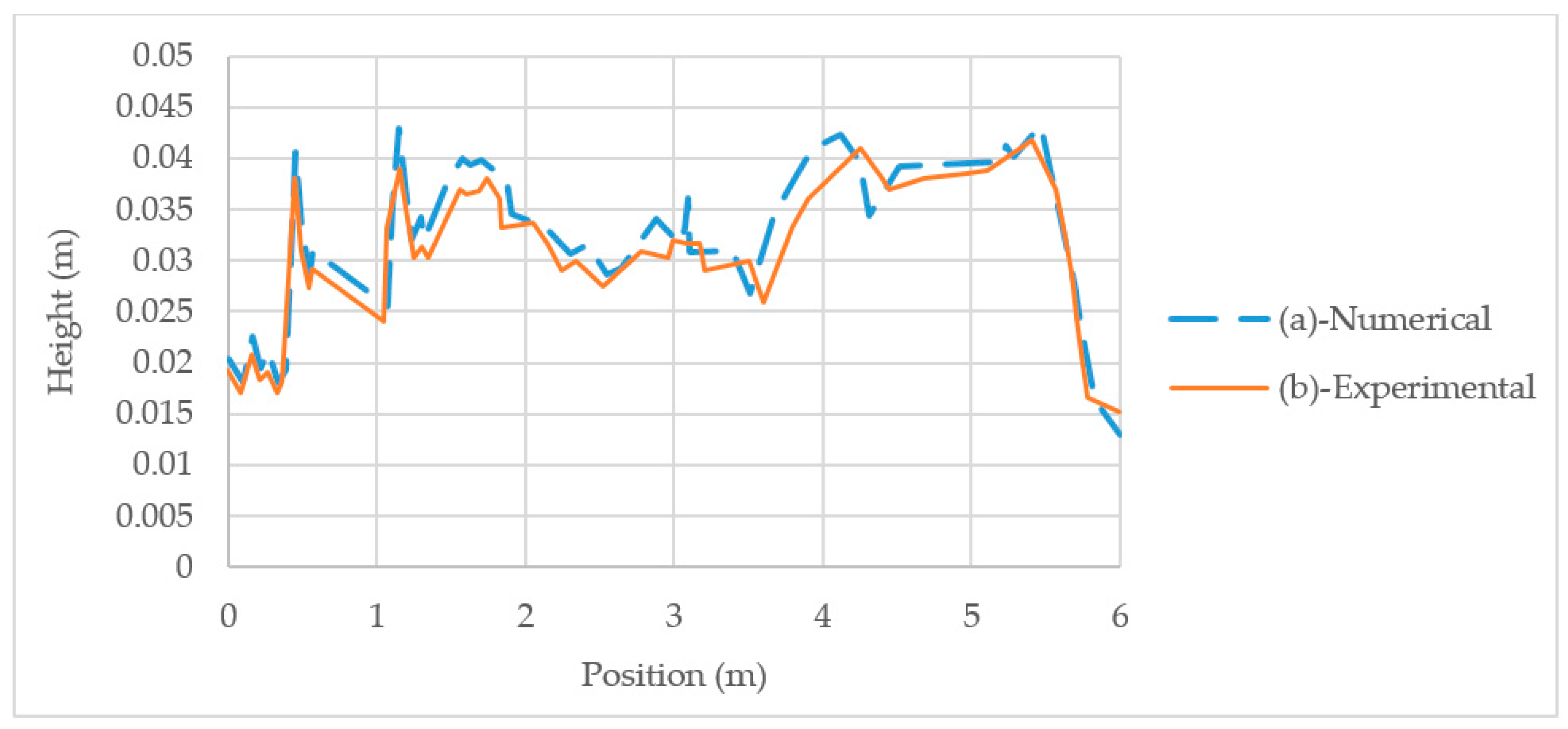
3. Numerical Modeling
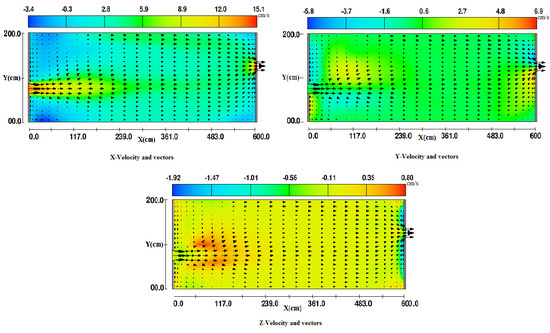
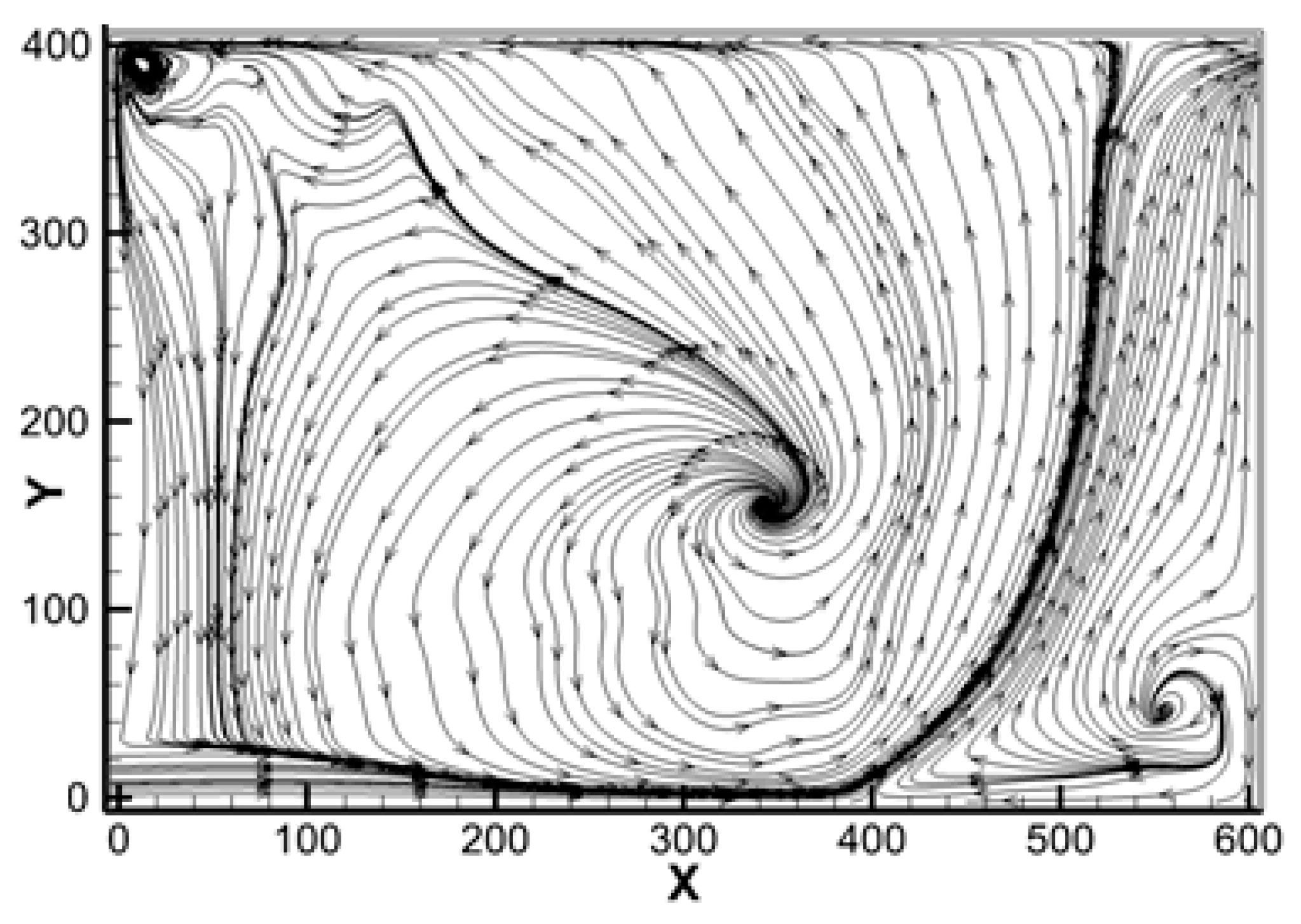
4. Results and Discussion
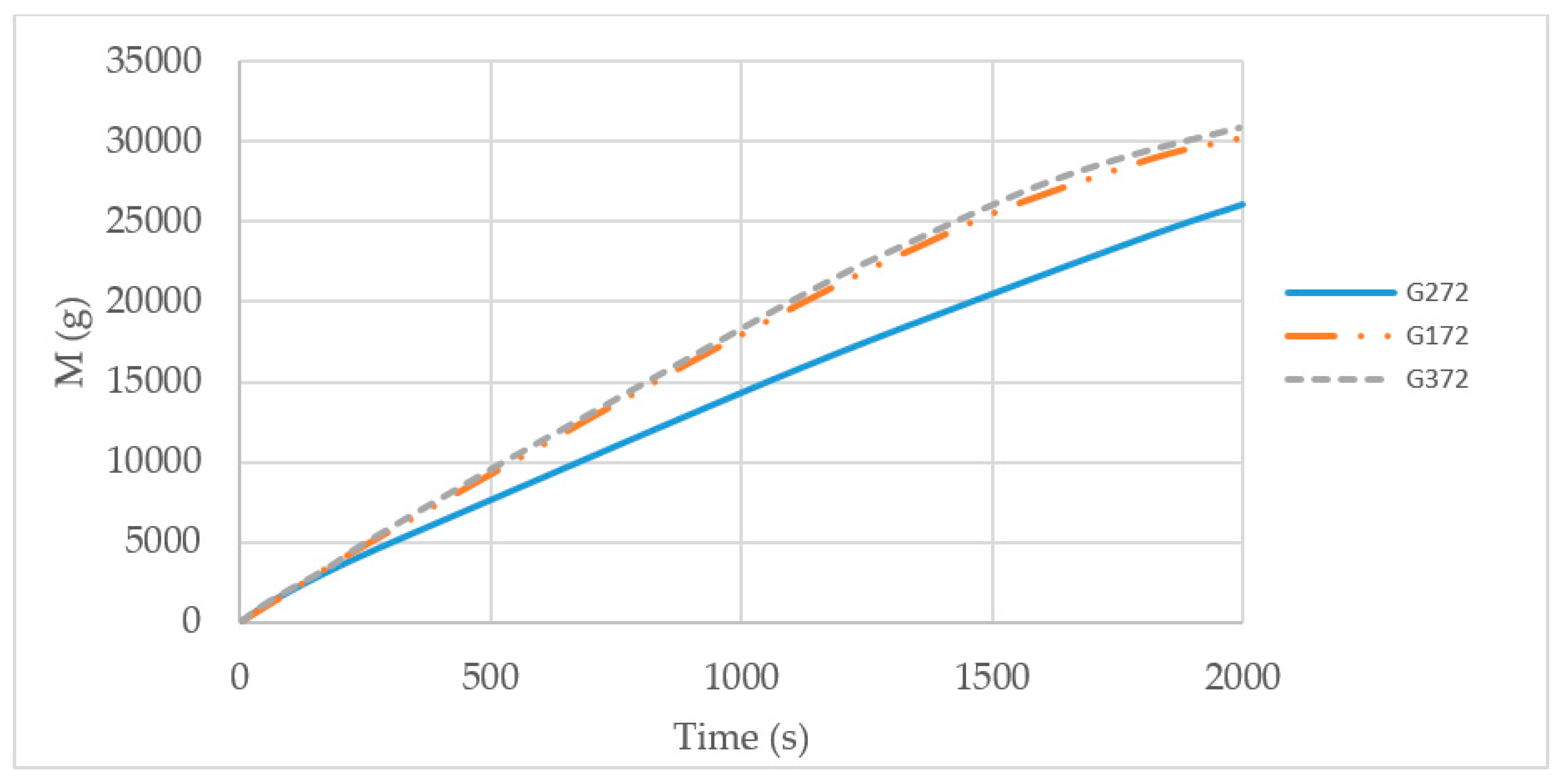
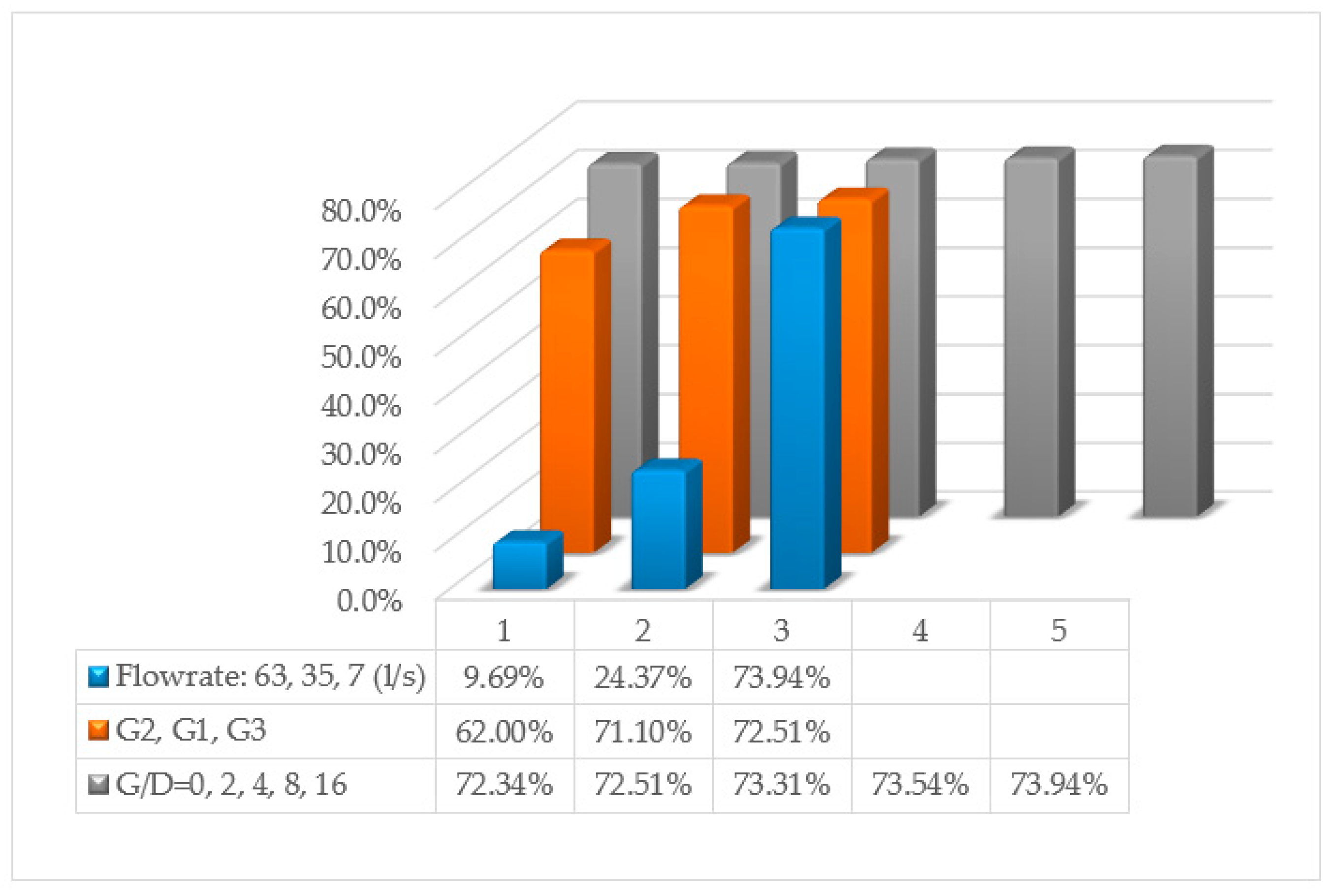
4.1. Dimensional Ratio
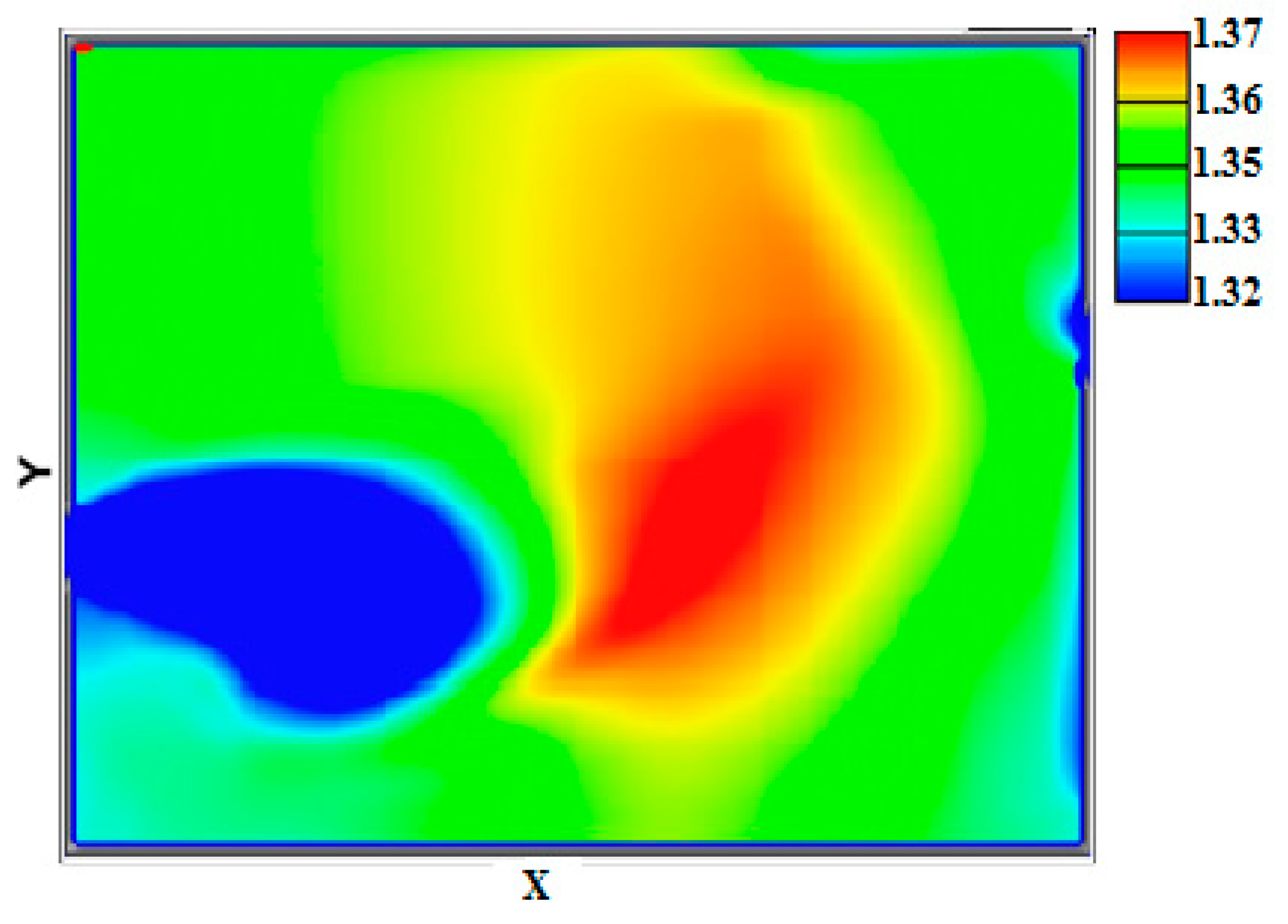
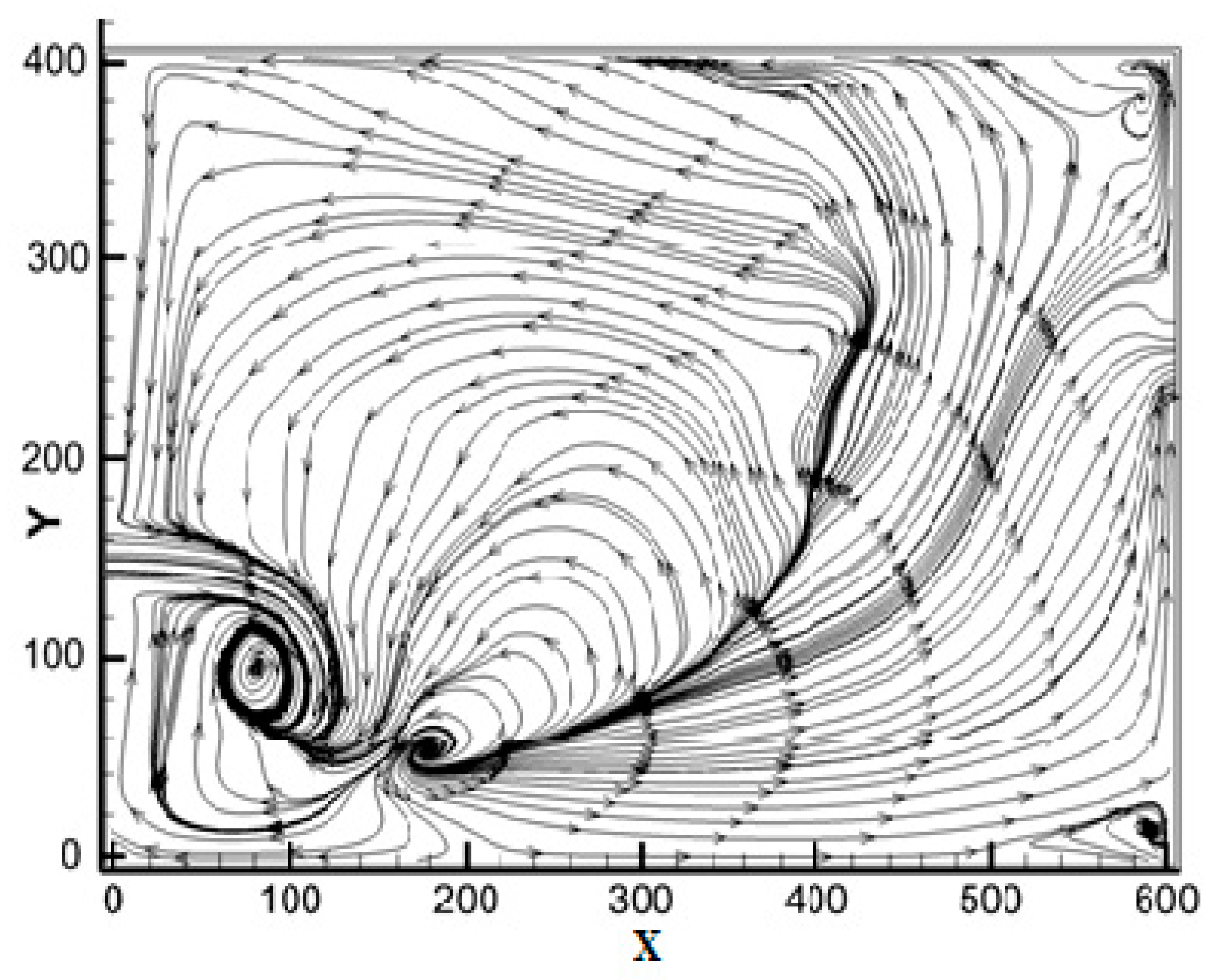
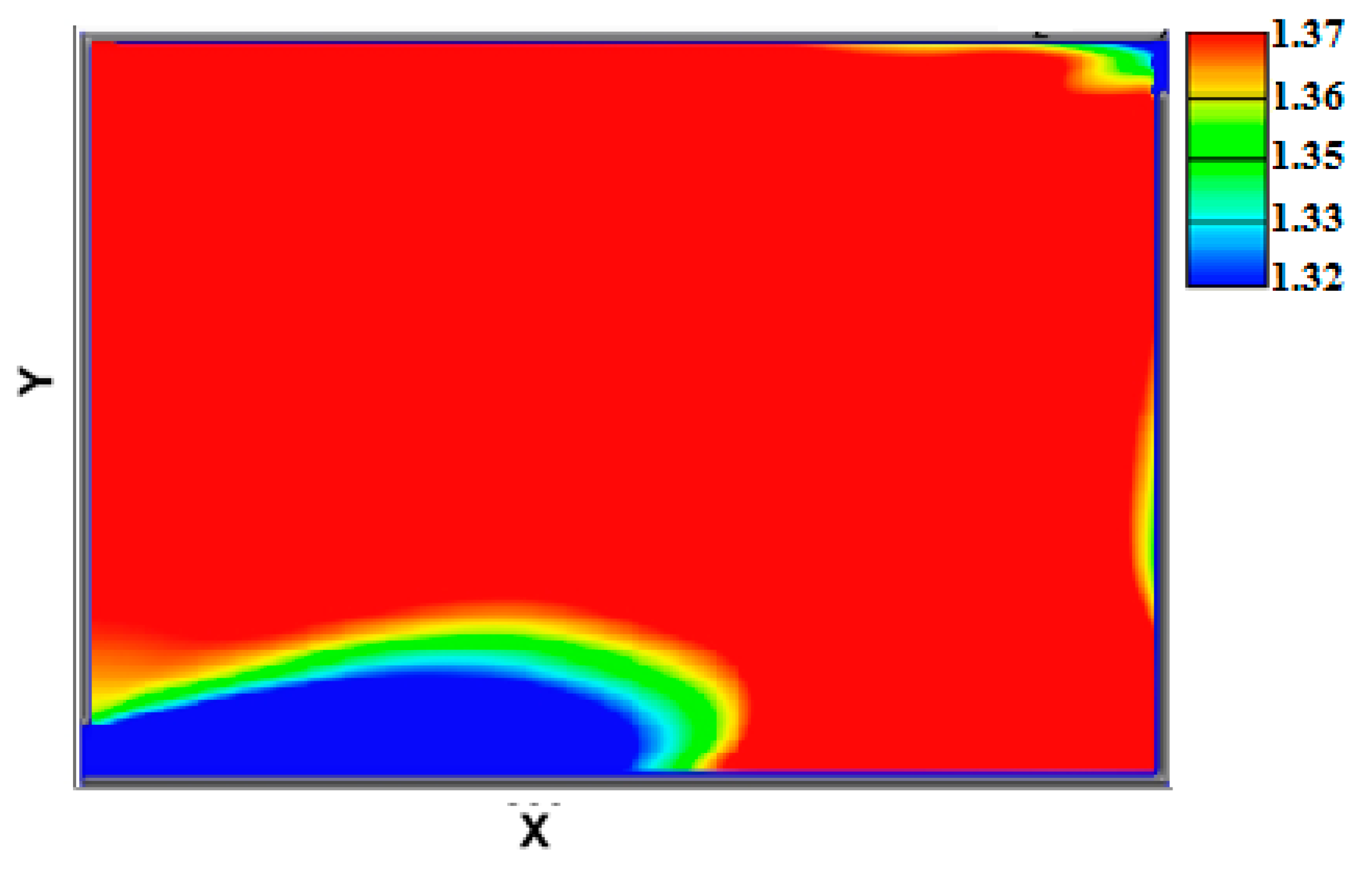
4.2. Effect of the G/D Ratio
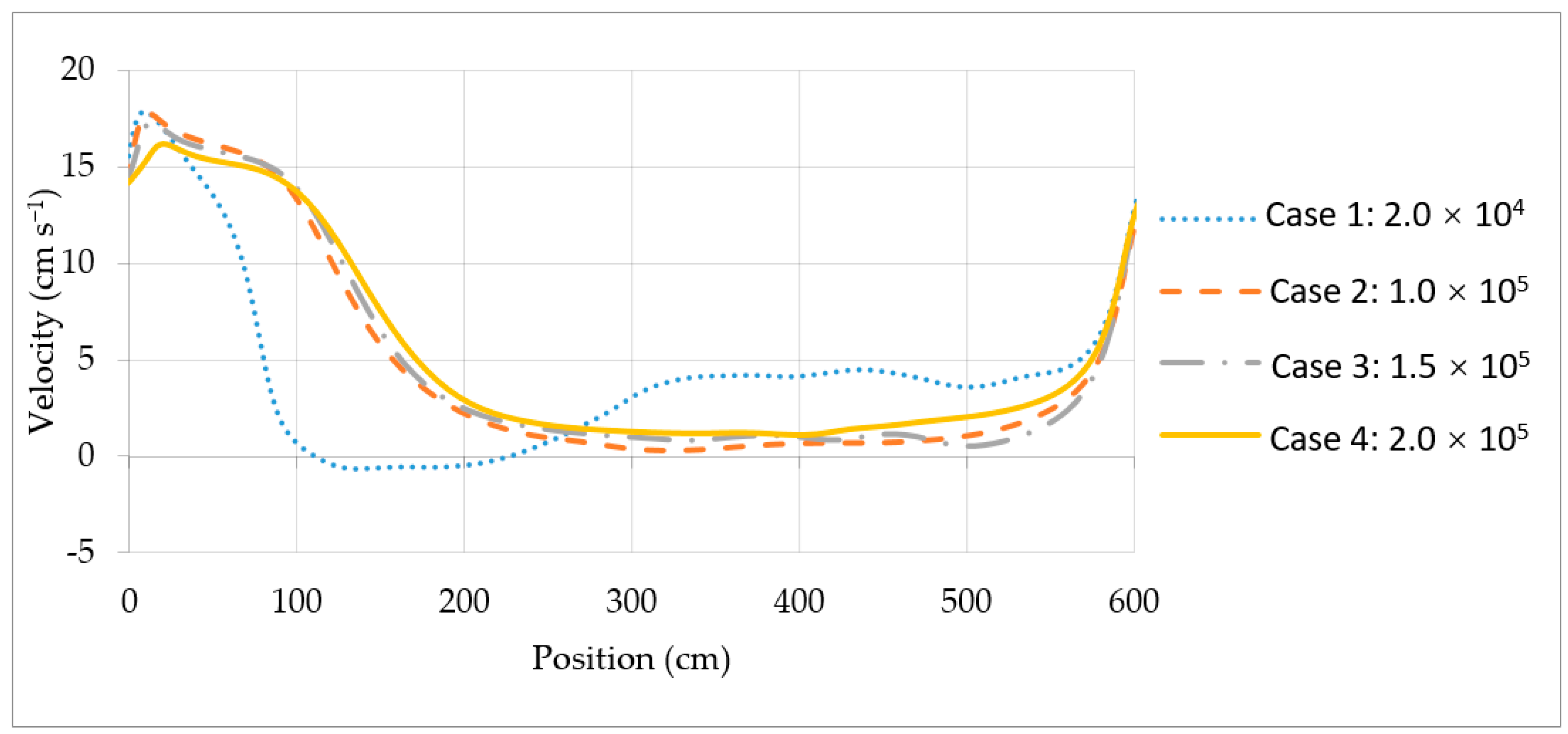
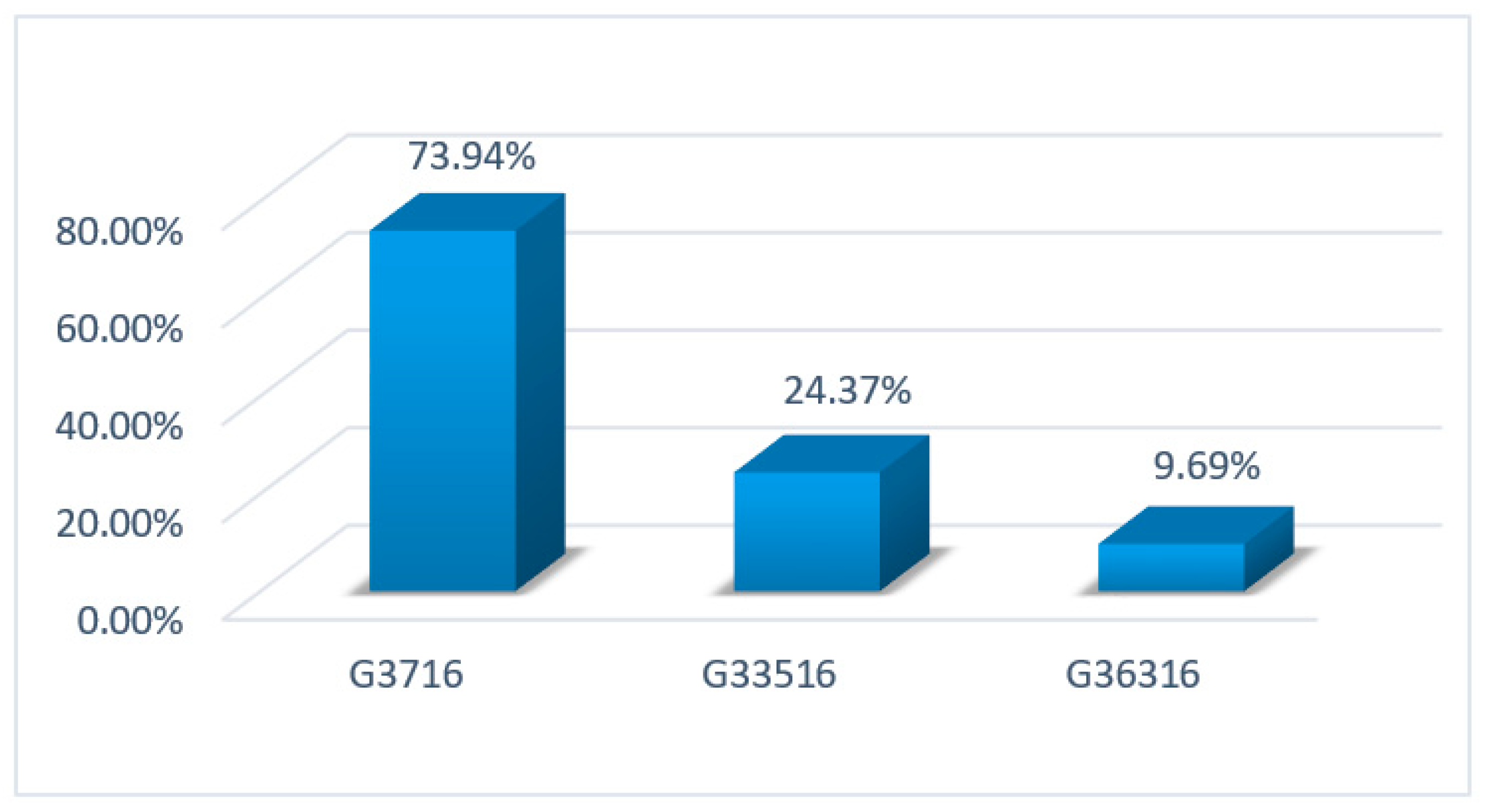
4.3. Changing the Flow Rate of the Inflow
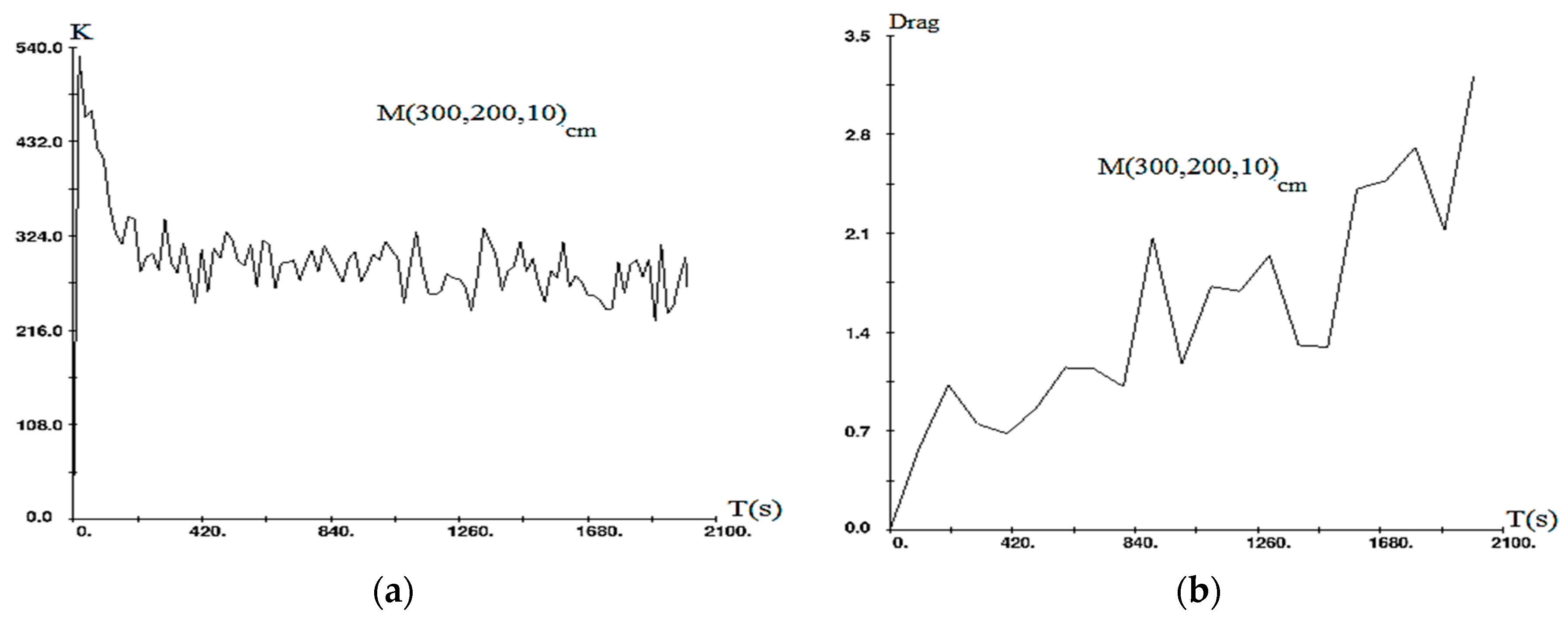
4.4. Sensitivity of Variables
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Kinematic viscosity (m2/s) | |
| Velocity (m/s) | |
| B | Width (m) |
| L | Length (m) |
| Filtered velocity (m/s) | |
| Filtered pressure (Pa) | |
| Diffusion coefficient (m2/s) | |
| Filtered rate-of-strain tensor | |
| Cs | Smagorinsky coefficient |
| Δg | Grid size (m3) |
| Cs,n | Suspended sediment mass concentration (kg/m3) |
| us,n | Sediment velocity (m/s) |
| Standard deviation | |
| Number of data | |
| Average of data | |
| G/D | Eccentricity |
| Q | Flow rate (L/s) |
| Density (kg/m3) | |
| Time (s) | |
| Scalar | |
| Unit in x direction | |
| Unit in y direction | |
| Direction |
References
- Abbasi, A.; Annor, F.O.; van de Giesen, N. Investigation of temperature dynamics in small and shallow reservoirs, case study: Lake Binaba, Upper East Region of Ghana. Water 2016, 8, 84. [Google Scholar] [CrossRef]
- Jamalabadi, M.; Ho-Huu, V.; Nguyen, T. Optimal design of circular baffles on sloshing in a rectangular tank horizontally coupled by structure. Water 2018, 10, 1504. [Google Scholar] [CrossRef]
- Ebnjalal, R.; Bajestan, S. Theoretical and Practical Principles of Soil Mechanics, 4th ed.; Shahid Chamran University Press: Ahvaz, Iran, 2004. [Google Scholar]
- Kuksina, L. Variations of water runoff and suspended sediment yield in the Kamchatsky Krai, Russia. Water 2018, 10, 1451. [Google Scholar] [CrossRef]
- Dominic, J.A.; Aris, A.Z.; Sulaiman, W.N.A.; Tahir, W.Z.W.M. Discriminant analysis for the prediction of sand mass distribution in an urban stormwater holding pond using simulated depth average flow velocity data. Environ. Monit. Assess. 2016, 188, 191. [Google Scholar] [CrossRef] [PubMed]
- Sebastian, C.; Becouze-Lareure, C.; Kouyi, C.L.; Barraud, S. Event-based quantification of emerging pollutant removal for an open stormwater retention basin–Loads, efficiency and importance of uncertainties. Water Res. 2015, 72, 239–250. [Google Scholar] [CrossRef] [PubMed]
- Adamsson, Å.; Stovin, V.; Bergdahl, L. Bed shear stress boundary condition for storage tank sedimentation. J. Environ. Eng. 2003, 129, 651–658. [Google Scholar] [CrossRef]
- Michalec, B. Evaluation of an empirical reservoir shape function to define sediment distributions in small reservoirs. Water 2015, 7, 4409–4426. [Google Scholar] [CrossRef]
- Tsavdaris, A.; Mitchell, S.; Williams, J.B. Computational fluid dynamics modelling of different detention pond configurations in the interest of sustainable flow regimes and gravity sedimentation potential. Water Environ. J. 2015, 29, 129–139. [Google Scholar] [CrossRef]
- Michalec, B. The use of modified Annandale’s method in the estimation of the sediment distribution in small reservoirs—A case study. Water 2014, 6, 2993–3011. [Google Scholar] [CrossRef]
- Liu, X.; Xue, H.; Hua, Z.; Yao, Q. Inverse calculation model for optimal design of rectangular sedimentation tanks. J. Environ. Eng. 2012, 139, 455–459. [Google Scholar] [CrossRef]
- Tarpagkou, R.; Pantokratoras, A. CFD methodology for sedimentation tanks: The effect of secondary phase on fluid phase using DPM coupled calculations. Appl. Math. Model. 2013, 37, 3478–3494. [Google Scholar] [CrossRef]
- Zhang, J.M.; Lee, H.P.; Khoo, B.C.; Peng, K.Q.; Zhong, L.; Kang, C.W. Shape effect on mixing and age distributions in service reservoirs. J. Am. Water Work. Assoc. 2014, 106, E481–E491. [Google Scholar] [CrossRef]
- Ferrara, V.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Dewals, B. Flow field in shallow reservoir with varying inlet and outlet position. J. Hydraul. Res. 2018, 56, 689–696. [Google Scholar] [CrossRef]
- Dufresne, M.; Dewals, B.; Erpicum, S.; Archambeau, P.; Pirotton, M. Numerical investigation of flow patterns in rectangular shallow reservoirs. Eng. Appl. Comput. Fluid Mech. 2011, 5, 247–258. [Google Scholar] [CrossRef]
- Camnasio, E.; Orsi, E.; Schleiss, A.J. Experimental study of velocity fields in rectangular shallow reservoirs. J. Hydraul. Res. 2011, 49, 352–358. [Google Scholar] [CrossRef]
- Wu, W. CCHE2D Sediment Transport Model (Version 2.1); Technical Rep. of National Center for Computational Hydroscience and Engineering NCCHE-TR-2001-03; University of Mississippi: Oxford, MS, USA, 2001. [Google Scholar]
- Shadloo, M.S.; Weiss, R.; Yildiz, M.; Dalrymple, R.A. Numerical simulation of long wave runup for breaking and nonbreaking waves. Int. J. Offshore Polar Eng. 2015, 25, 1–7. [Google Scholar]
- Kantoush, S.; Bollaert, E.; Schleiss, A. Influence of the width of a rectangular shallow reservoir on sedimentation behaviour and trap efficiency. In Proceedings of the 32nd Congress of IAHR, Special Session 06 (SS06-07-0), Venice, Italy, 1–6 July 2007. [Google Scholar]
- Dewals, B.J.; Kantoush, S.A.; Erpicum, S.; Pirotton, M.; Schleiss, A.J. Experimental and numerical analysis of flow instabilities in rectangular shallow basins. Environ. Fluid Mech. 2008, 8, 31–54. [Google Scholar] [CrossRef]
- Janssen, R.H. Efficiency of Sediment Settling Basins, in Advances in Water Resources and Hydraulic Engineering; Springer: Berlin, Germany, 2009; pp. 2025–2030. [Google Scholar]
- Toniolo, H. Numerical simulation of sedimentation processes in reservoirs as a function of outlet location. Int. J. Sediment Res. 2009, 24, 339–351. [Google Scholar] [CrossRef]
- Camnasio, E.; de Cesare, G.; Kantoush, S.A. Flow field and sediment deposition in a rectangular shallow reservoir with non symmetric inlet and outlet configuration. In Proceedings of the Seventh International Symposium on Ultrasonic Doppler Methods for Fluid Mechanics and Fluid Engineering, Gothenburg, Sweden, 7–9 April 2010. [Google Scholar]
- Bouisfi, F.; Bouisfi, A.; Che, H.O.; Bouhali, M.E.; Chaoui, M. The effect of inlet and outlet position and sediments concentration on sedimentation tank efficiency. In Proceedings of the 2018 4th International Conference on Optimization and Applications (ICOA), Morocco, Morocco, 26–27 April 2018. [Google Scholar]
- Majdzadeh, T.M.R.; Pirestani, M.R.; Alimohamadi, S. Investigating the effect of inlet and outlet location on flow field and sedimentation pattern of a rectangular settling basin Using CCHE2D. J. Water Sci. Res. 2013, 5, 55–63. [Google Scholar]
- Westhoff, M.C.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Dewals, B. Maximum energy dissipation to explain velocity fields in shallow reservoirs. J. Hydraul. Res. 2018, 56, 221–230. [Google Scholar] [CrossRef]
- Torabi, M.A.; Shafieefar, M. An experimental investigation on the stability of foundation of composite vertical breakwaters. J. Mar. Sci. Appl. 2015, 14, 175–182. [Google Scholar] [CrossRef]
- Hadjadj, A.; Ben-Nasr, O.; Shadloo, M.S.; Chaudhuri, A. Effect of wall temperature in supersonic turbulent boundary layers: A numerical study. Int. J. Heat Mass Transf. 2015, 81, 426–438. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Ben-Nasr, O.; Hadjadj, A.; Chaudhuri, A.; Shadloo, M.S. Assessment of subgrid-scale modeling for large-eddy simulation of a spatially-evolving compressible turbulent boundary layer. Comput. Fluids 2017, 151, 144–158. [Google Scholar] [CrossRef]
- Shojaeizadeh, A.; Reza Safaei, M.; Abdullah AA, A.A.; Ghodsian, M.; Geza, M.; Ammar Abbassi, M. Bed roughness effects on characteristics of turbulent confined wall jets. Measurement 2018, 122, 325–338. [Google Scholar] [CrossRef]
- Shadloo, M.; Hadjadj, A.; Chaudhuri, A.; Ben-Nasr, O. Large-eddy simulation of a spatially-evolving supersonic turbulent boundary layer at M∞ = 2. Eur. J. Mech. B Fluids 2018, 67, 185–197. [Google Scholar] [CrossRef]
- Wong, M.; Parker, G. Reanalysis and correction of bed-load relation of Meyer-Peter and Müller using their own database. J. Hydraul. Eng. 2006, 132, 1159–1168. [Google Scholar] [CrossRef]
- Sangsefidi, Y.; Mehraein, M.; Ghodsian, M. Experimental study on flow over in-reservoir arced labyrinth weirs. Flow Meas. Instrum. 2018, 59, 215–224. [Google Scholar] [CrossRef]
- Kantoush, S.A. Experimental Study on the Influence of the Geometry of Shallow Reservoirs on Flow Patterns and Sedimentation by Suspended Sediments. Ph.D. Thesis, Laboratoire de Constructions Hydrauliques, Lausanne, Switzerland, 2008. [Google Scholar]
- Holdich, R.; Butt, G. Experimental and numerical analysis of a sedimentation forming compressible compacts. Sep. Sci. Technol. 1997, 32, 2149–2171. [Google Scholar] [CrossRef]
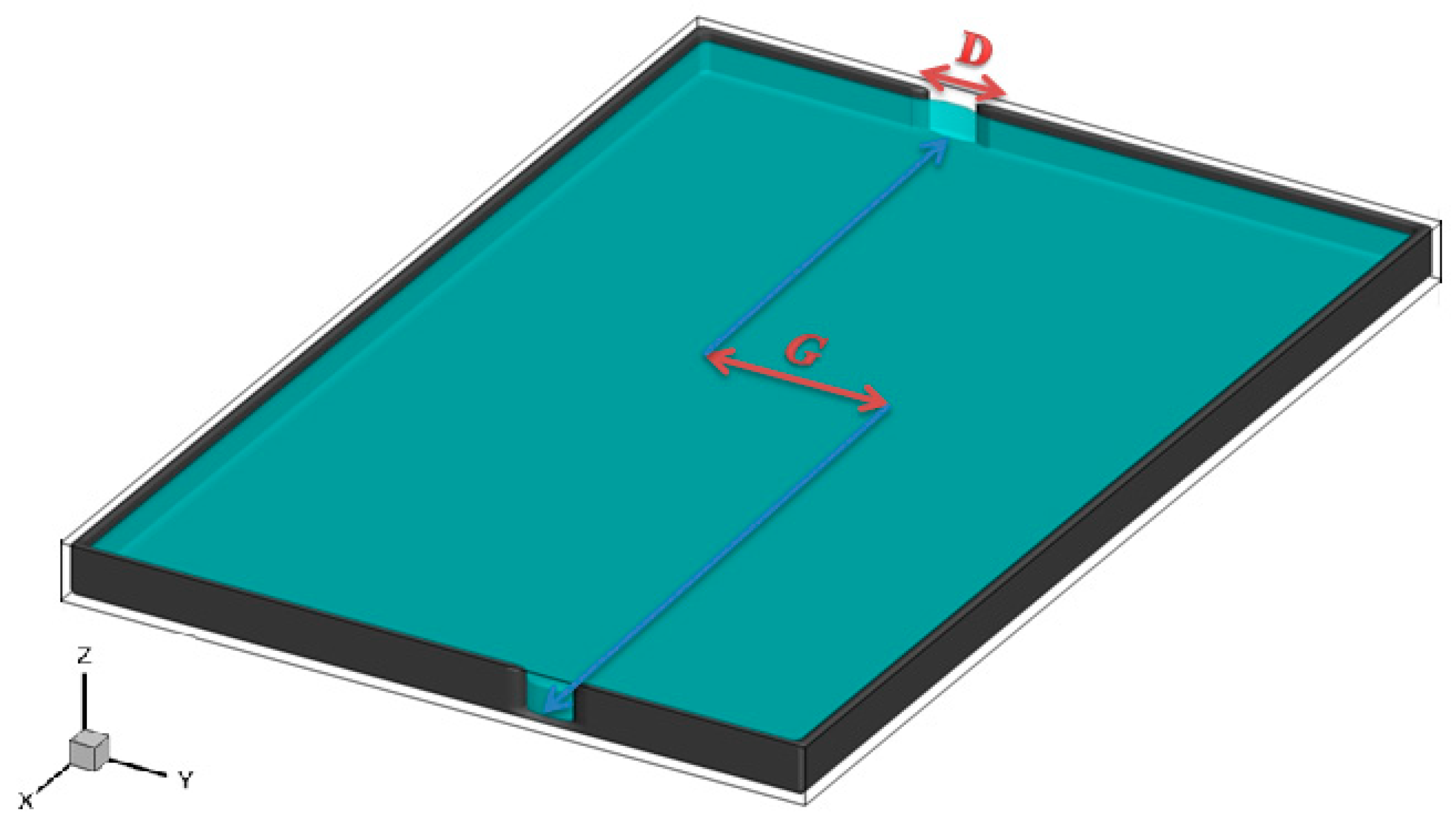
| Geometry | Width (B) (m) | Length (L) (m) | Ratio |
|---|---|---|---|
| G1 | 2 | 6 | 1/3 |
| G2 | 4 | 3 | 4/3 |
| G3 | 4 | 6 | 2/3 |
| Property | Density (kg/m3) | Diameter (µm) |
|---|---|---|
| Value | 1500 | 50 |
| Geometry | G/D | Q (L/s) |
|---|---|---|
| G1 | 0, 2, 4, 8 | 7, 35, 63 |
| G2 | 0, 2, 4, 8, 16 | 7, 35, 63 |
| G3 | 0, 2, 4, 8, 16 | 7, 35, 63 |
| Reservoir | G370 | G372 | G374 | G378 | G3716 |
| Amount of Sediment | 72.34% | 72.51% | 73.31% | 73.54% | 73.94% |
| Variables | Margin of Error |
|---|---|
| Flow rate | 0.381 |
| Dimensional ratio | 0.064 |
| Eccentricity (G/D) | 0.005 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zahabi, H.; Torabi, M.; Alamatian, E.; Bahiraei, M.; Goodarzi, M. Effects of Geometry and Hydraulic Characteristics of Shallow Reservoirs on Sediment Entrapment. Water 2018, 10, 1725. https://doi.org/10.3390/w10121725
Zahabi H, Torabi M, Alamatian E, Bahiraei M, Goodarzi M. Effects of Geometry and Hydraulic Characteristics of Shallow Reservoirs on Sediment Entrapment. Water. 2018; 10(12):1725. https://doi.org/10.3390/w10121725
Chicago/Turabian StyleZahabi, Hamidreza, Mohammadamin Torabi, Ebrahim Alamatian, Mehdi Bahiraei, and Marjan Goodarzi. 2018. "Effects of Geometry and Hydraulic Characteristics of Shallow Reservoirs on Sediment Entrapment" Water 10, no. 12: 1725. https://doi.org/10.3390/w10121725
APA StyleZahabi, H., Torabi, M., Alamatian, E., Bahiraei, M., & Goodarzi, M. (2018). Effects of Geometry and Hydraulic Characteristics of Shallow Reservoirs on Sediment Entrapment. Water, 10(12), 1725. https://doi.org/10.3390/w10121725