Evolution of Velocity Field and Vortex Structure during Run-Down of Solitary Wave over Very Steep Beach
Abstract
1. Introduction
2. Experiment Set-Ups and Instrumentations
2.1. Wave Flume, Model of Sloping Bottom and Coordinate Systems
2.2. Flow Field Observations Using Flow Visualization Techniques (FVT)
2.3. Velocity Measurements by HSPIV
2.4. Experimental Conditions
3. Preliminary Tests
3.1. Verification for Free Surface Elevation over Horizontal Bottom
3.2. Test for Viscous Effect of Two Sidewalls on Attenuation of Incident Wave Height
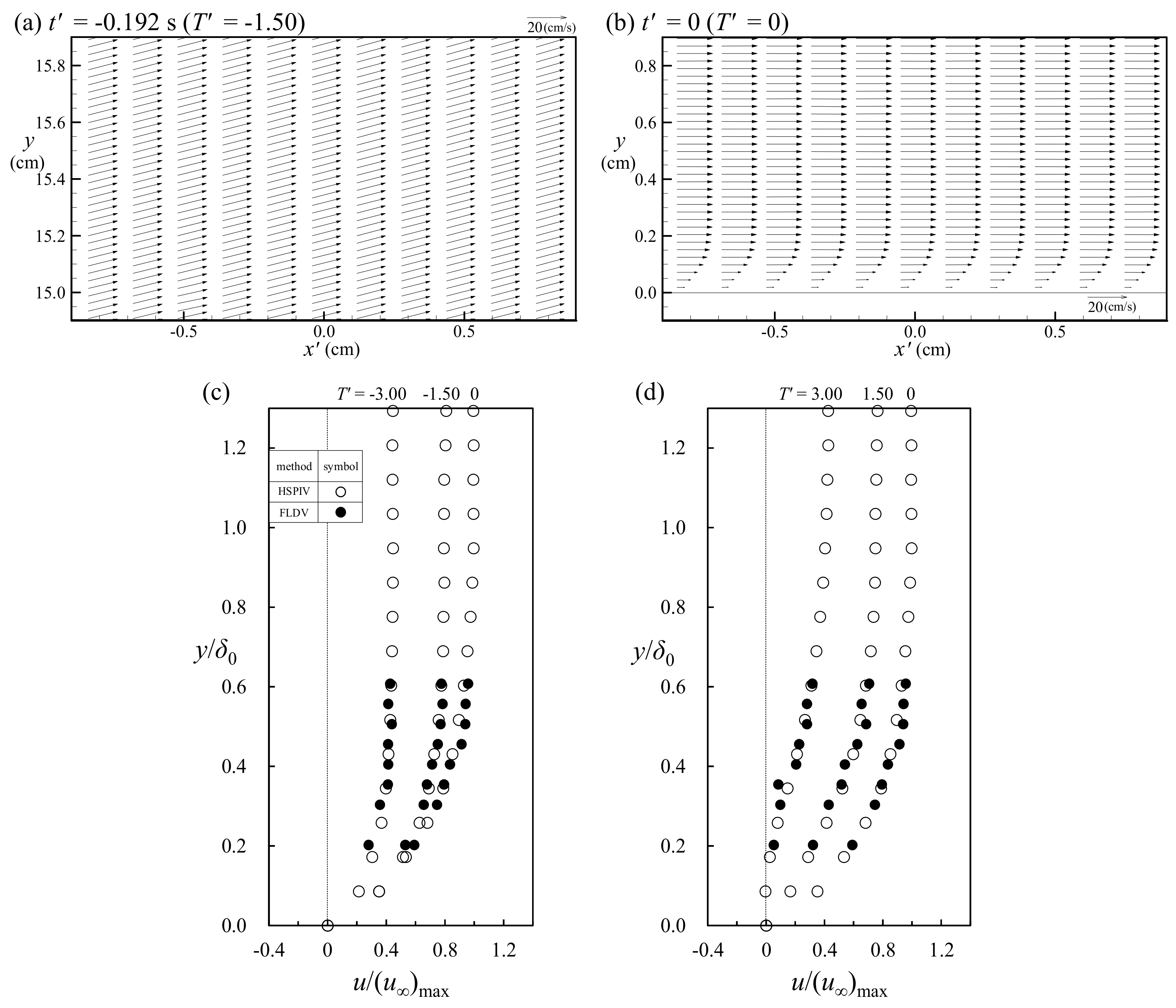
3.3. Verifications for Velocity Fields/Profiles Measured over Horizontal Bottom
3.4. Identification for Flow Pattern in Boundary Layer over Horizontal Bottom
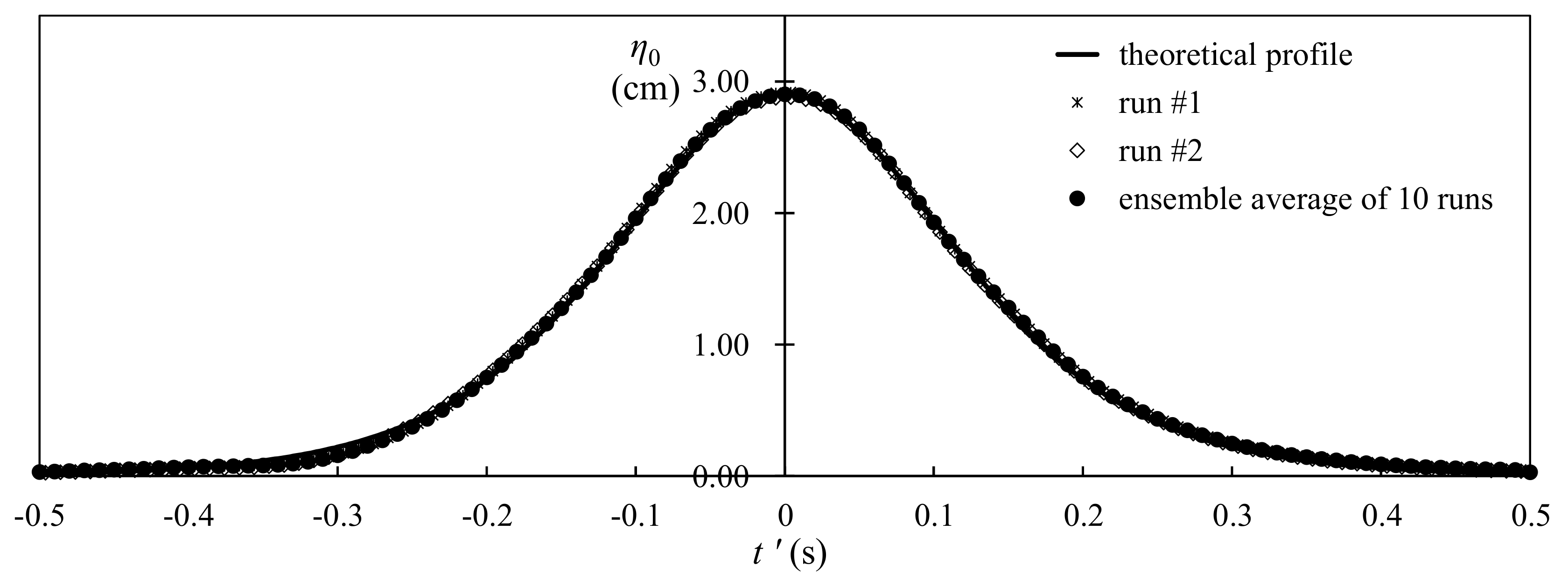
3.5. Repeatability Test for Instantaneous Free Surface Profile and Velocity Field over Sloping Bottom
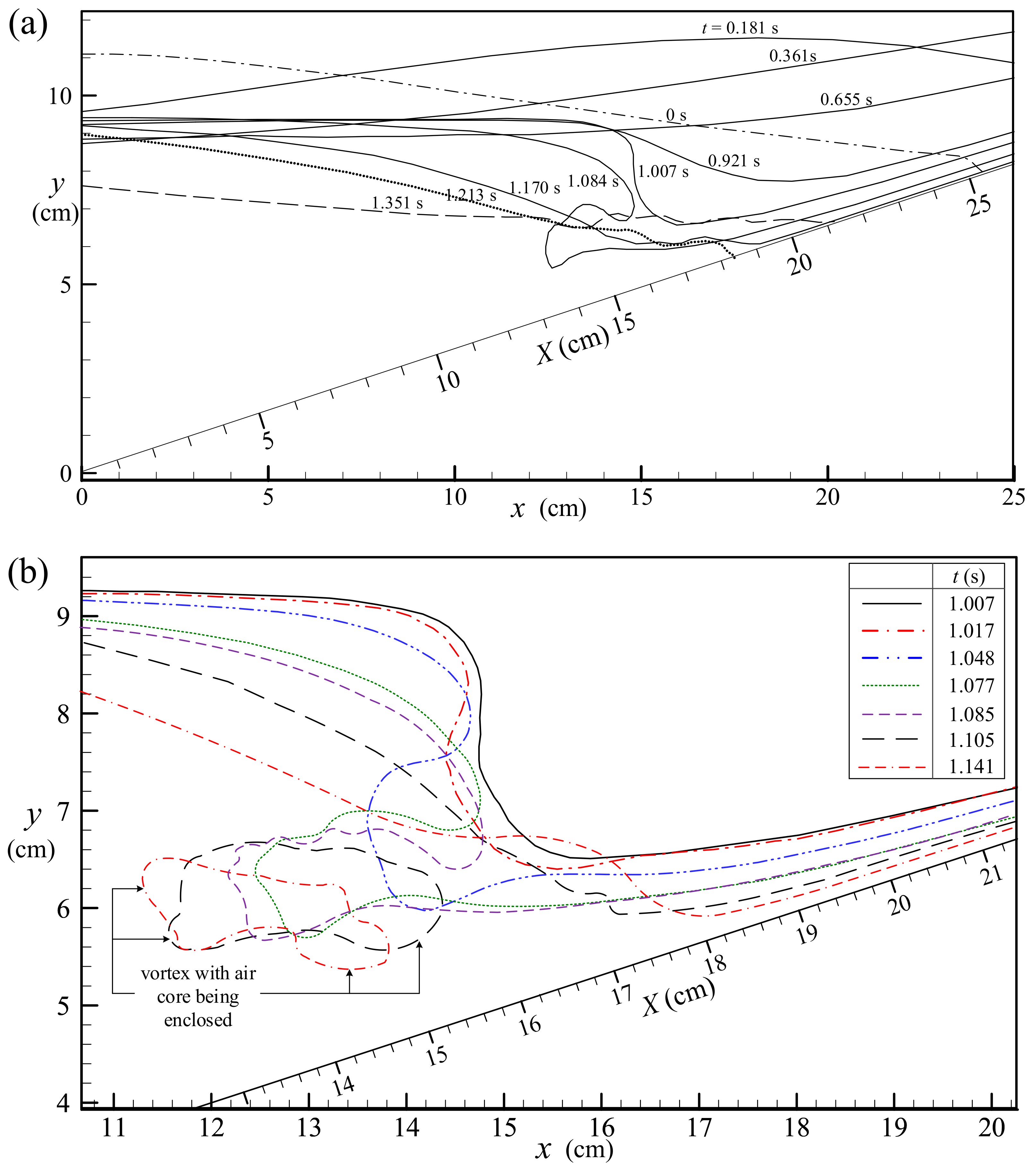
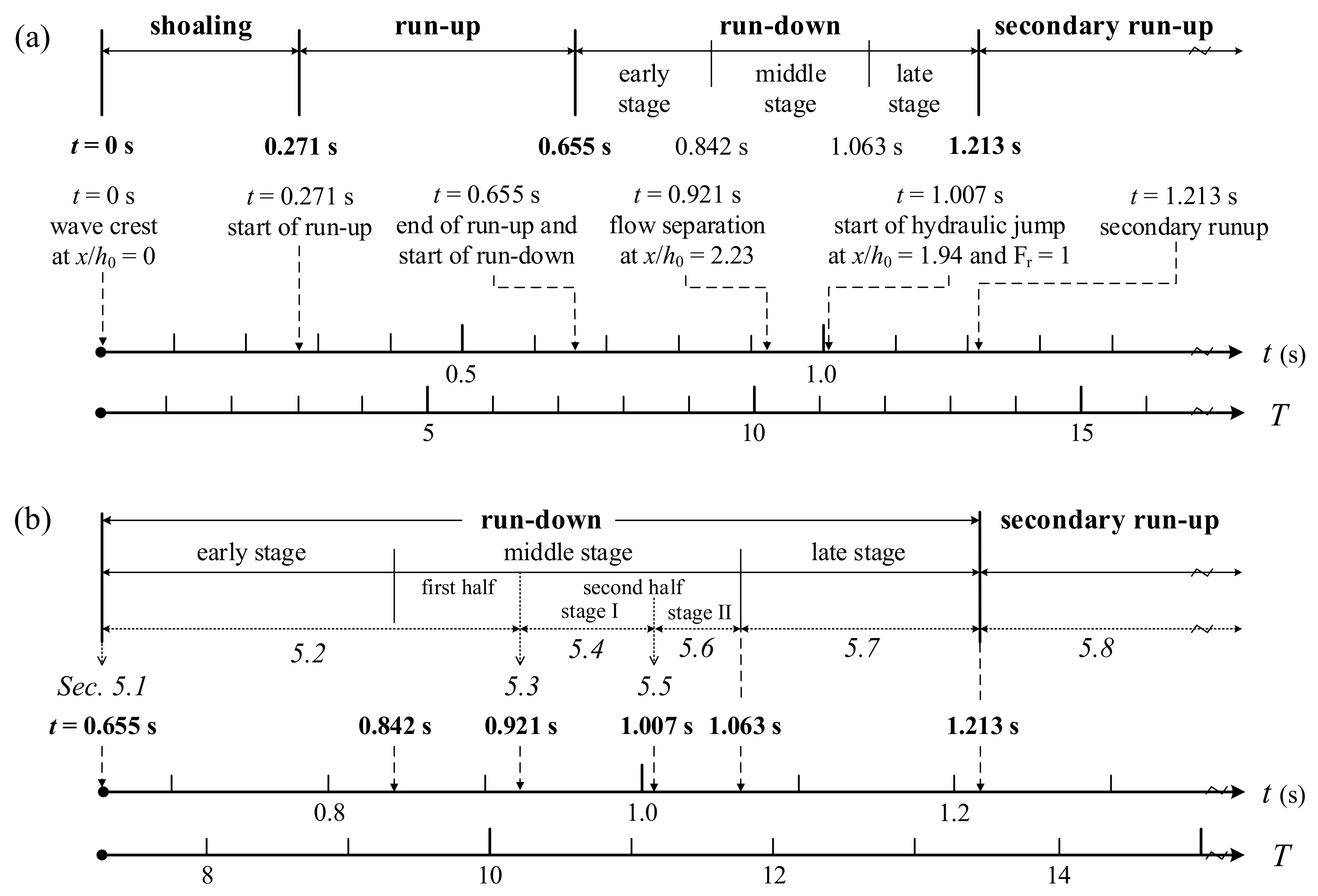
4. General Description of Run-Up and Run-Down Process of Solitary Wave
5. Results and Discussion for Complete Evolution of Run-Down (Case 1)
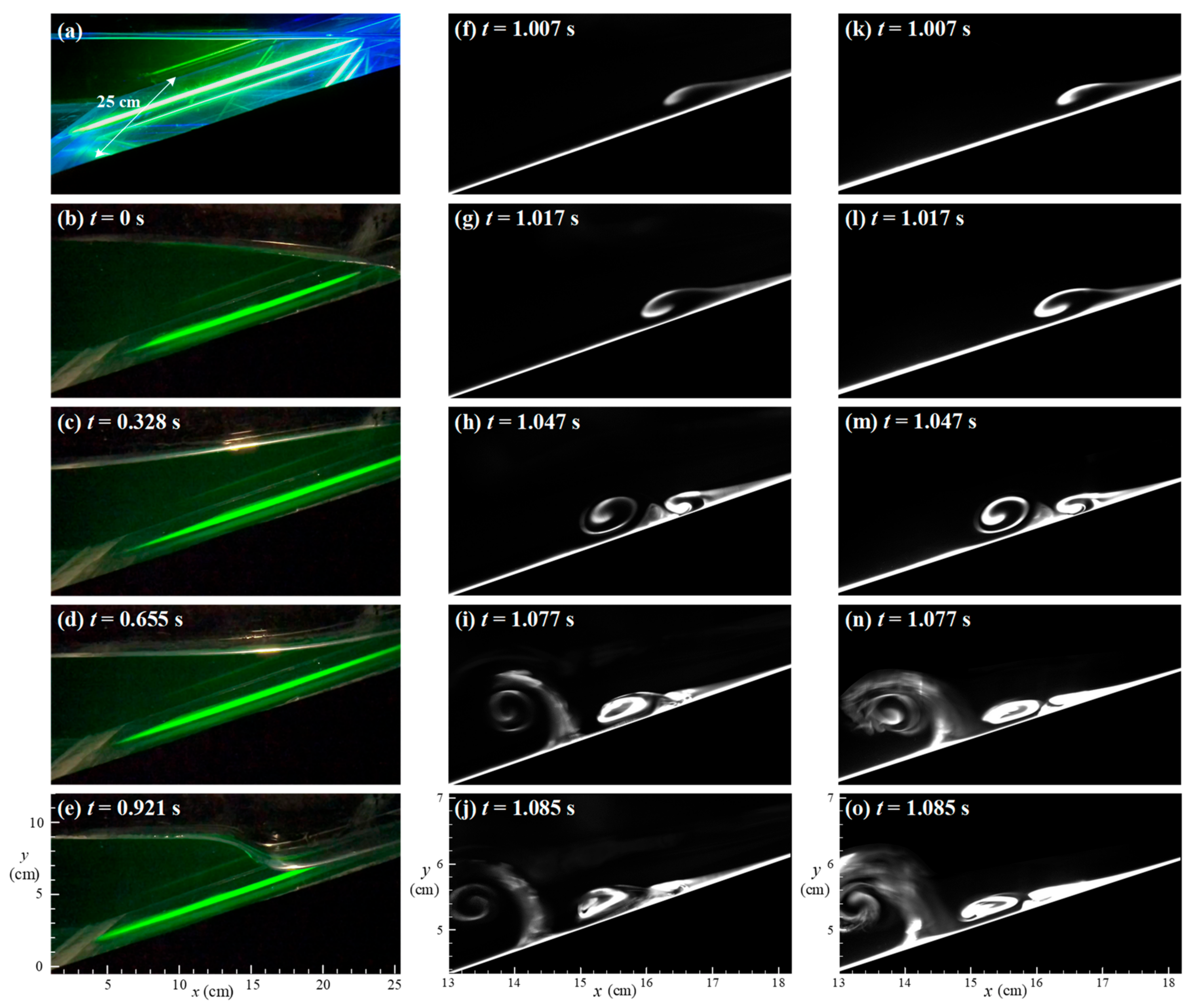
5.1. Start of Run-Down at t = 0.655 s
5.2. Early and First-Half Middle Stages of Run-Down for 0.655 s < t < 0.921 s
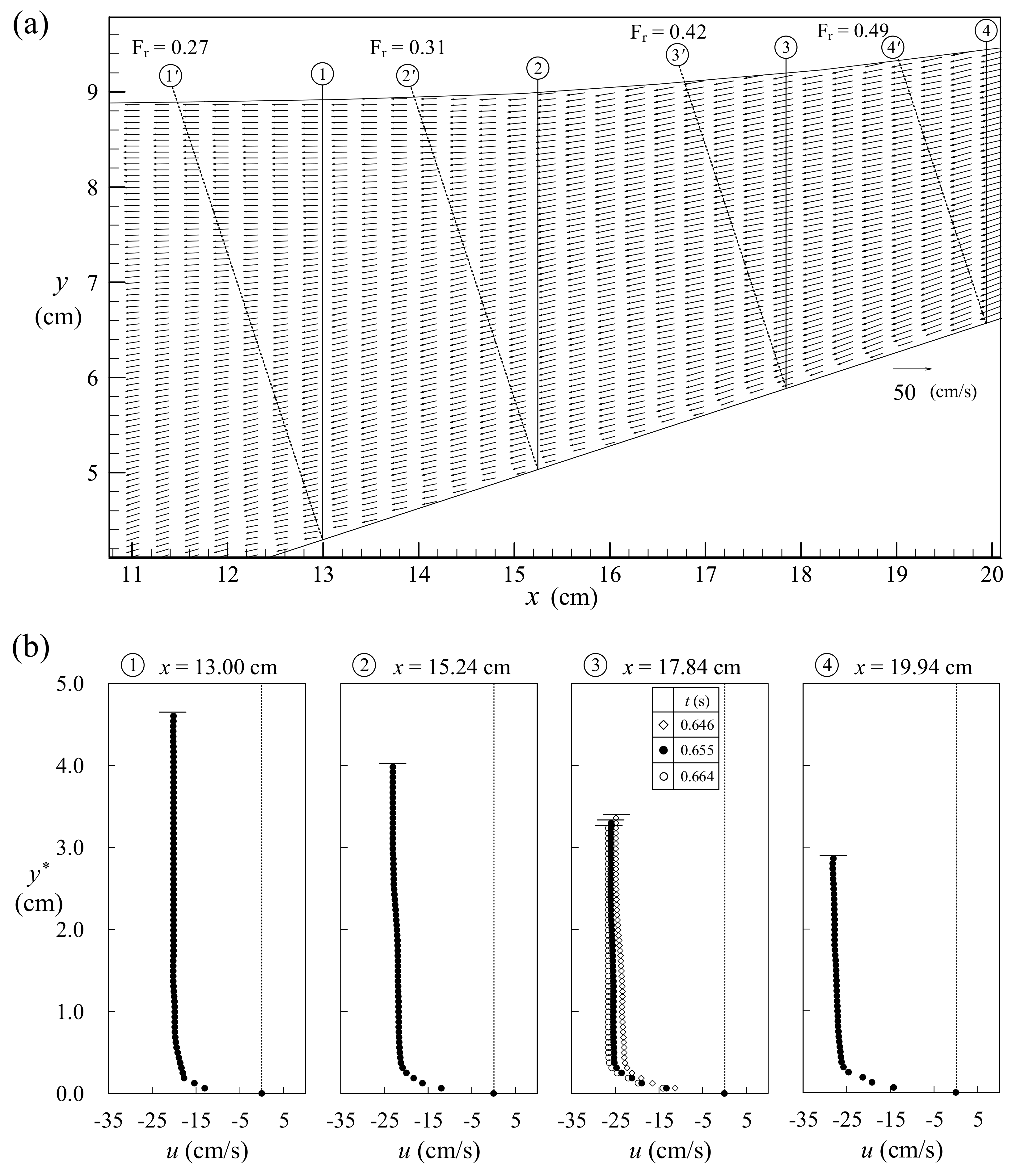
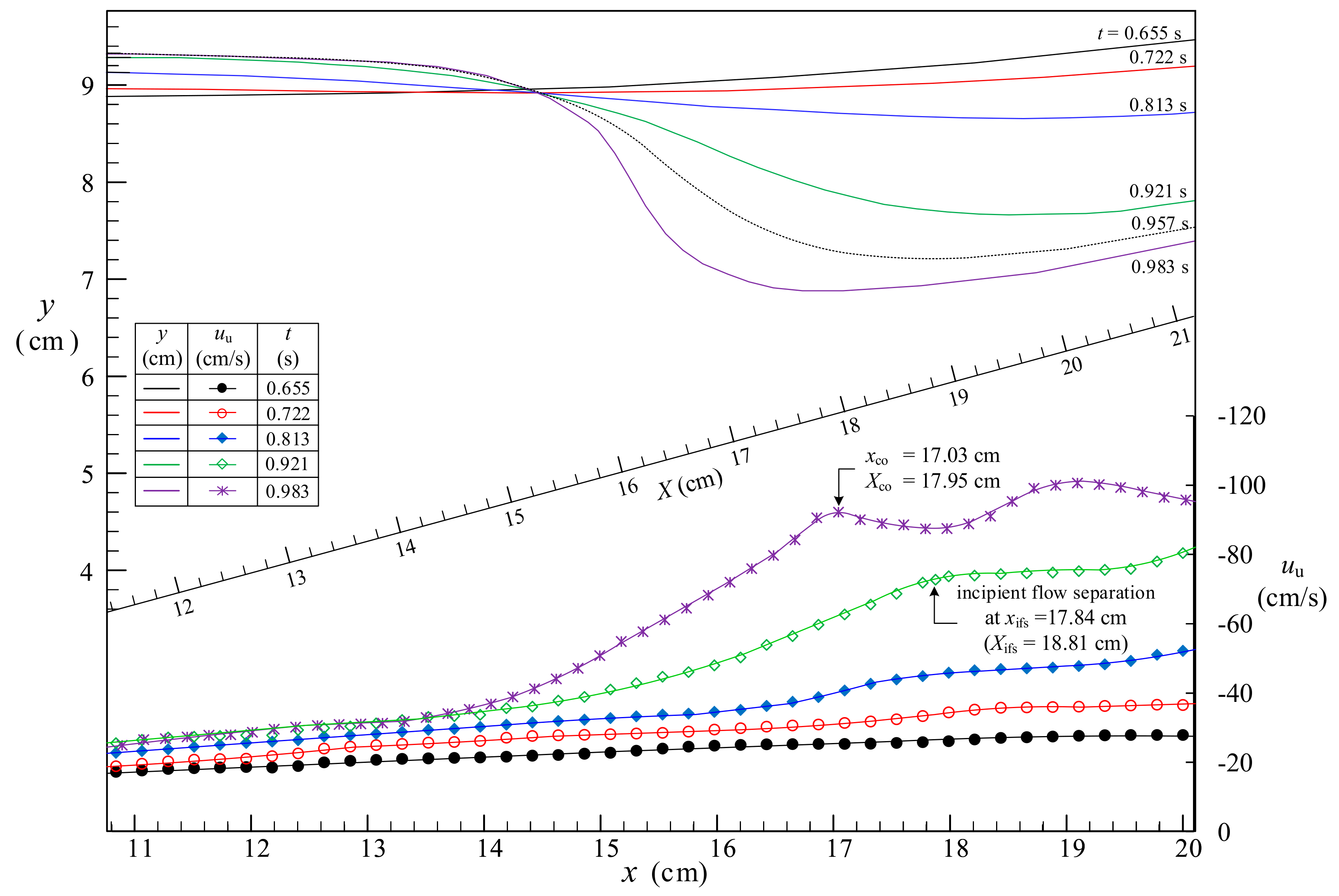
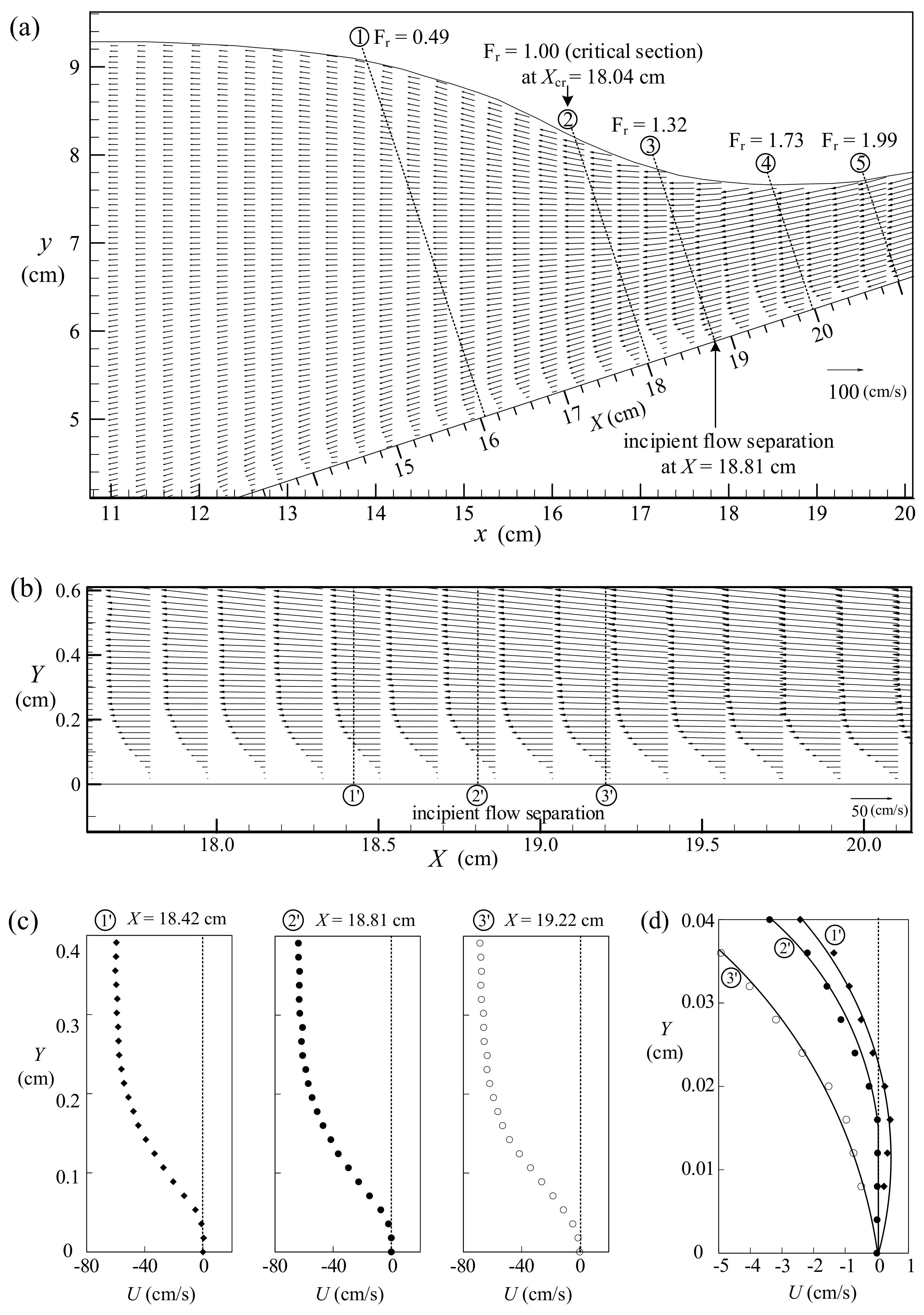
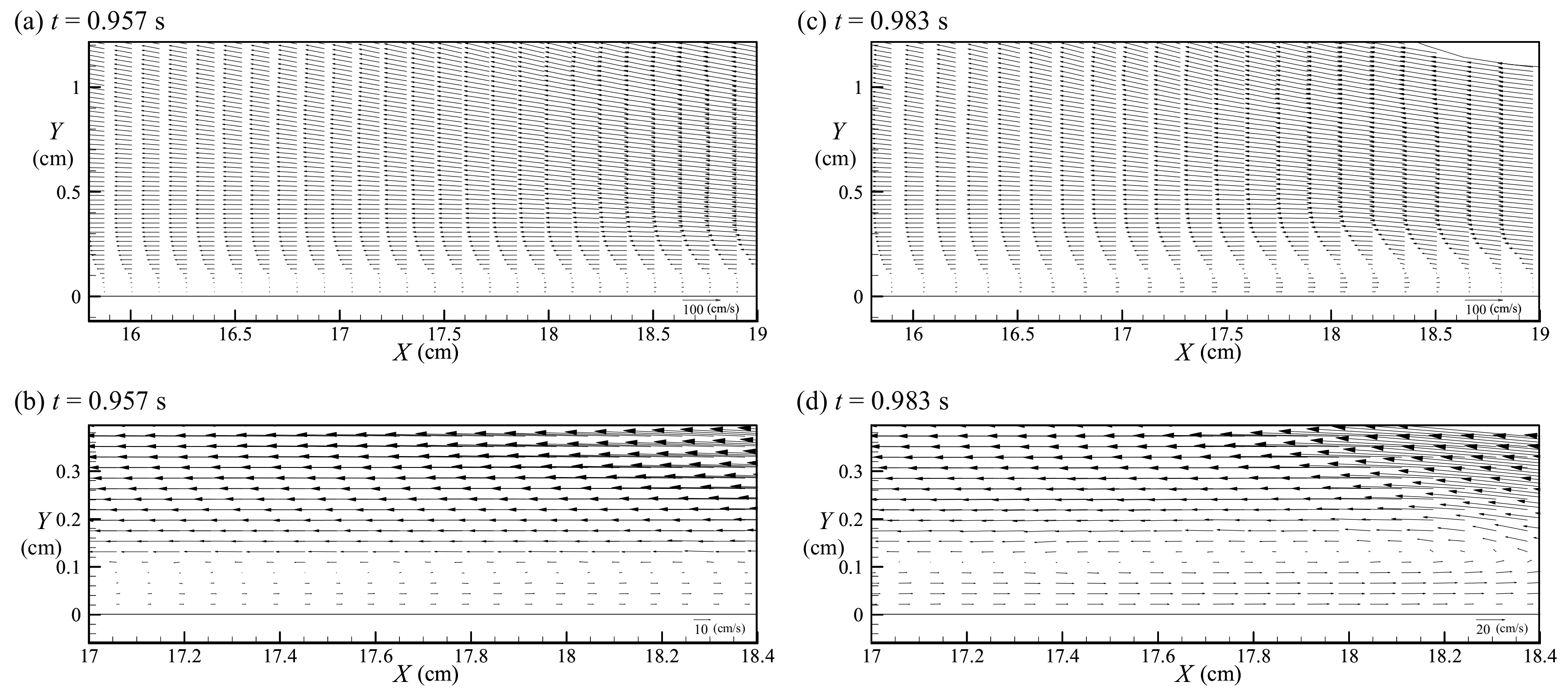
5.3. Incipient Flow Separation from Beach Surface at t = 0.921 s
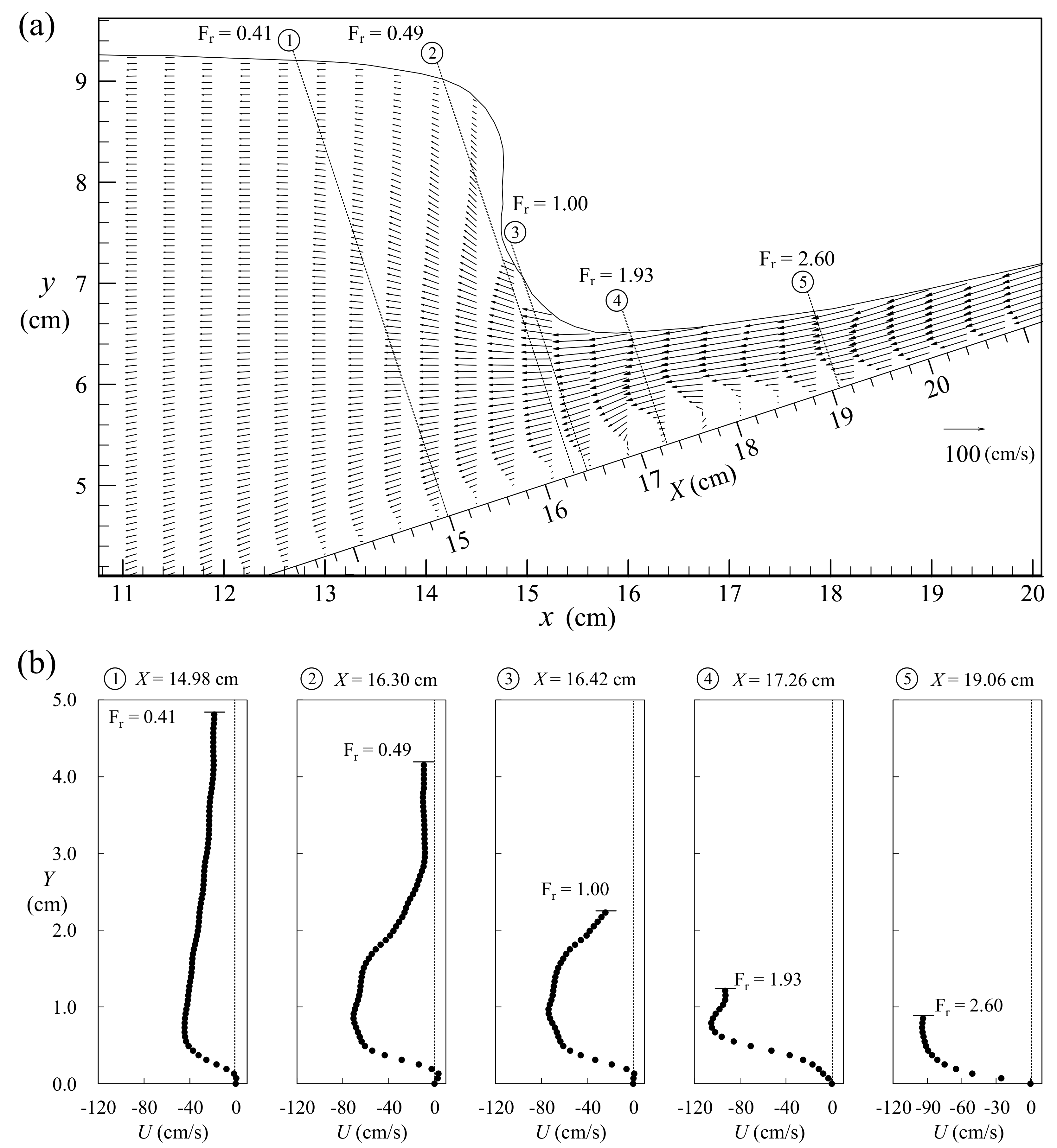
5.4. Second-Half Middle Stage I of Run-Down for 0.921 s < t < 1.007 s
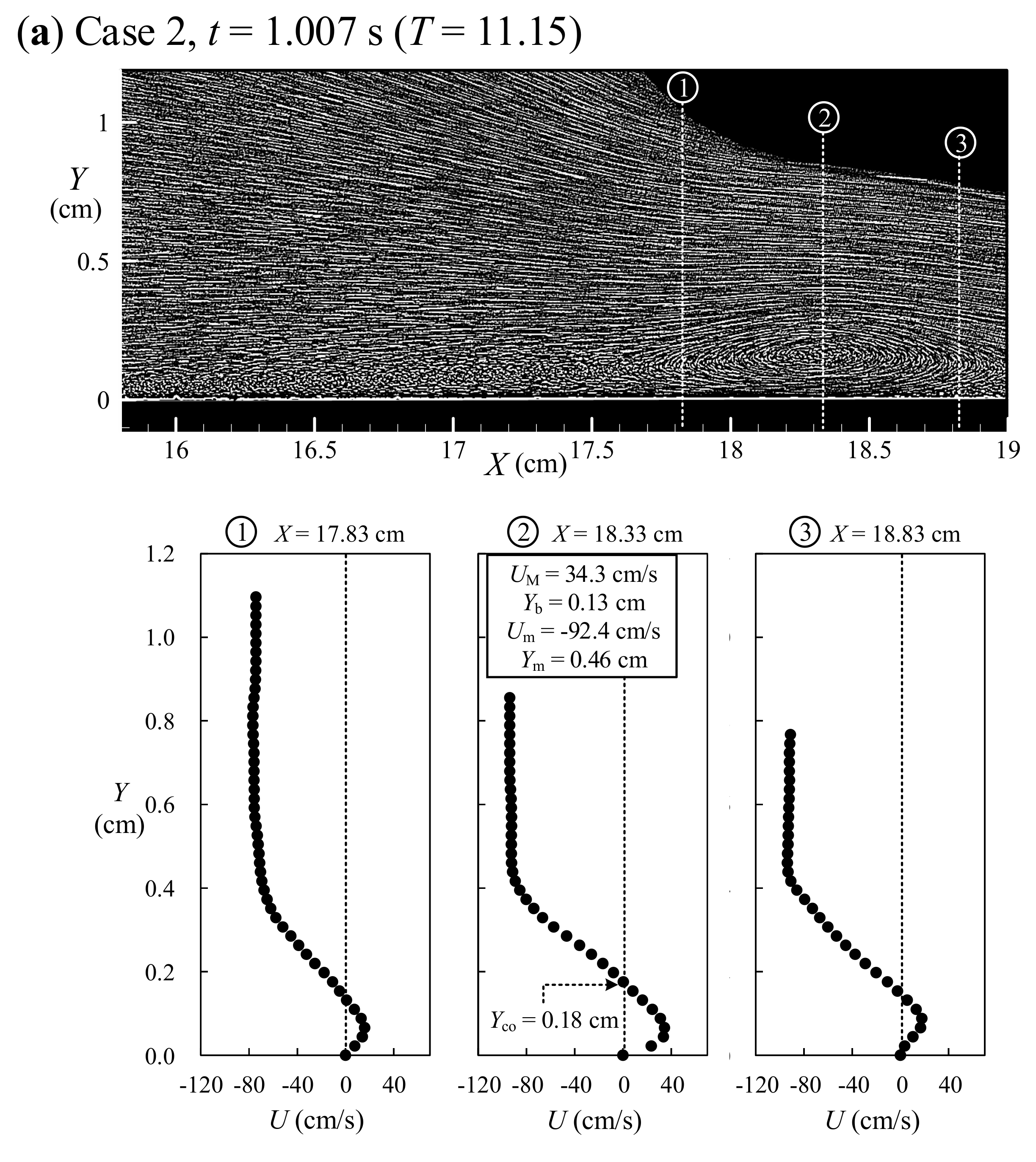
5.5. Incipient Hydraulic Jump at t = 1.007 s
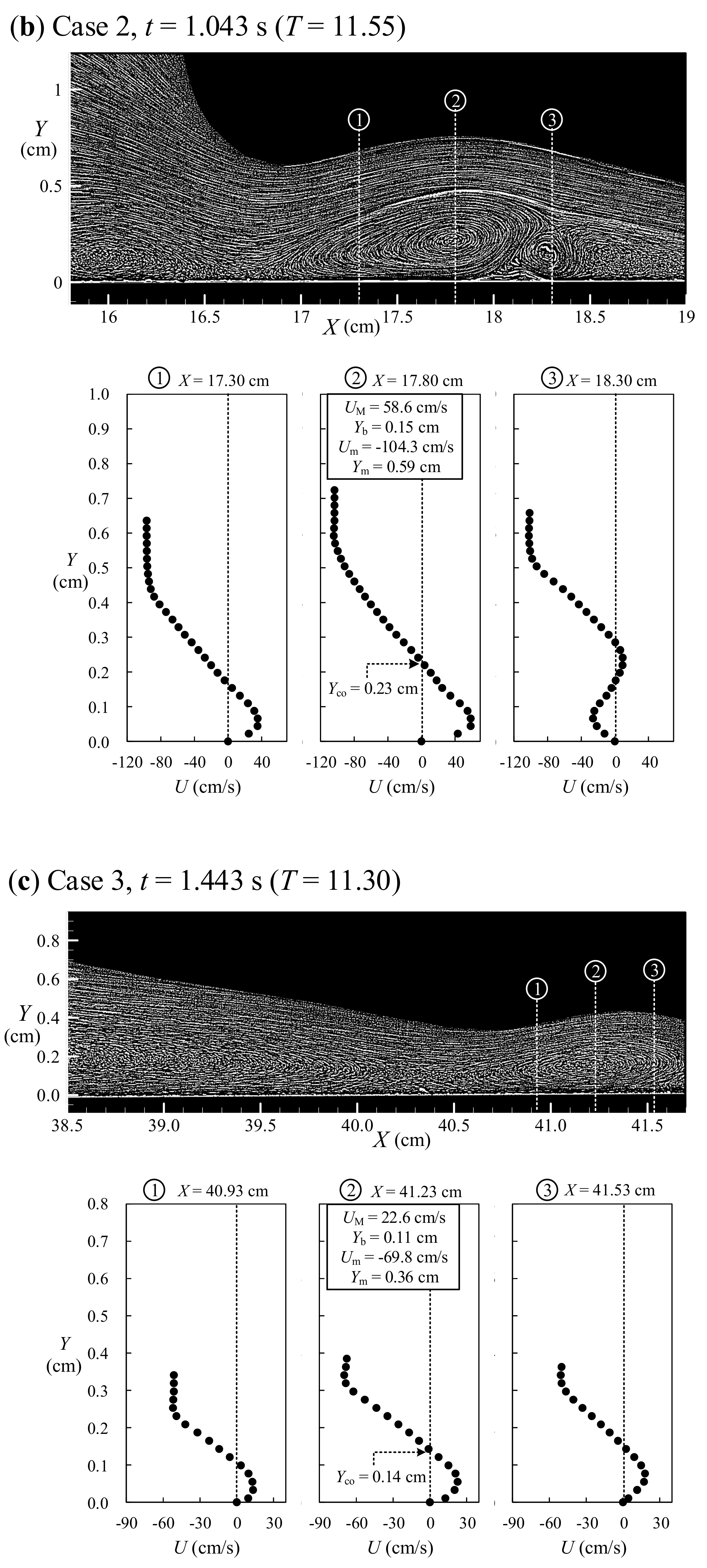
5.6. Second-Half Middle Stage II of Run-Down for 1.007 s < t ≤ 1.063 s
5.7. Late Stage of Run-Down for 1.063 s < t < 1.213 s
5.8. Second Run-Up for t ≥ 1.213 s
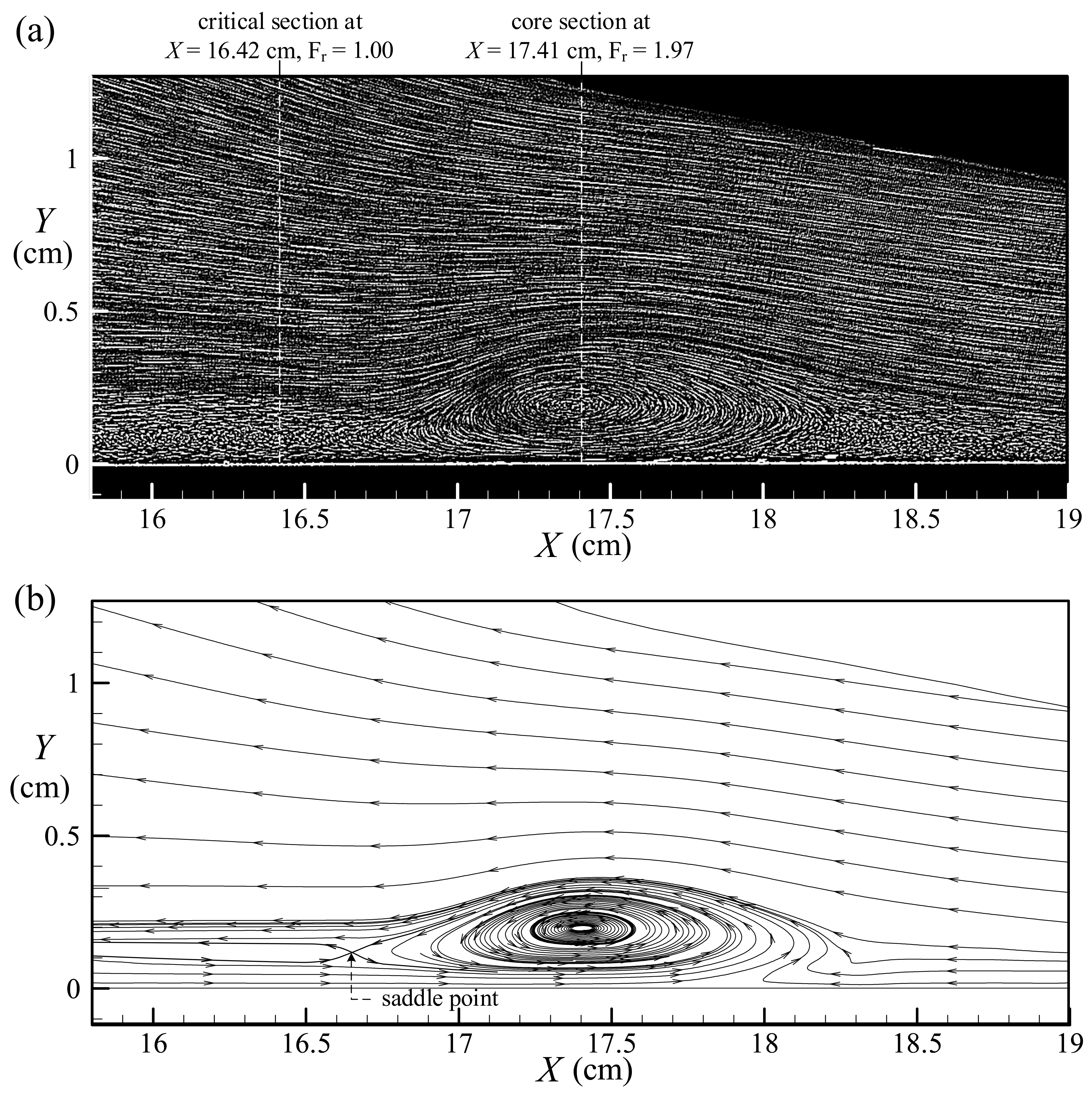
6. Discussion on Characteristics of Primary Vortex Structure
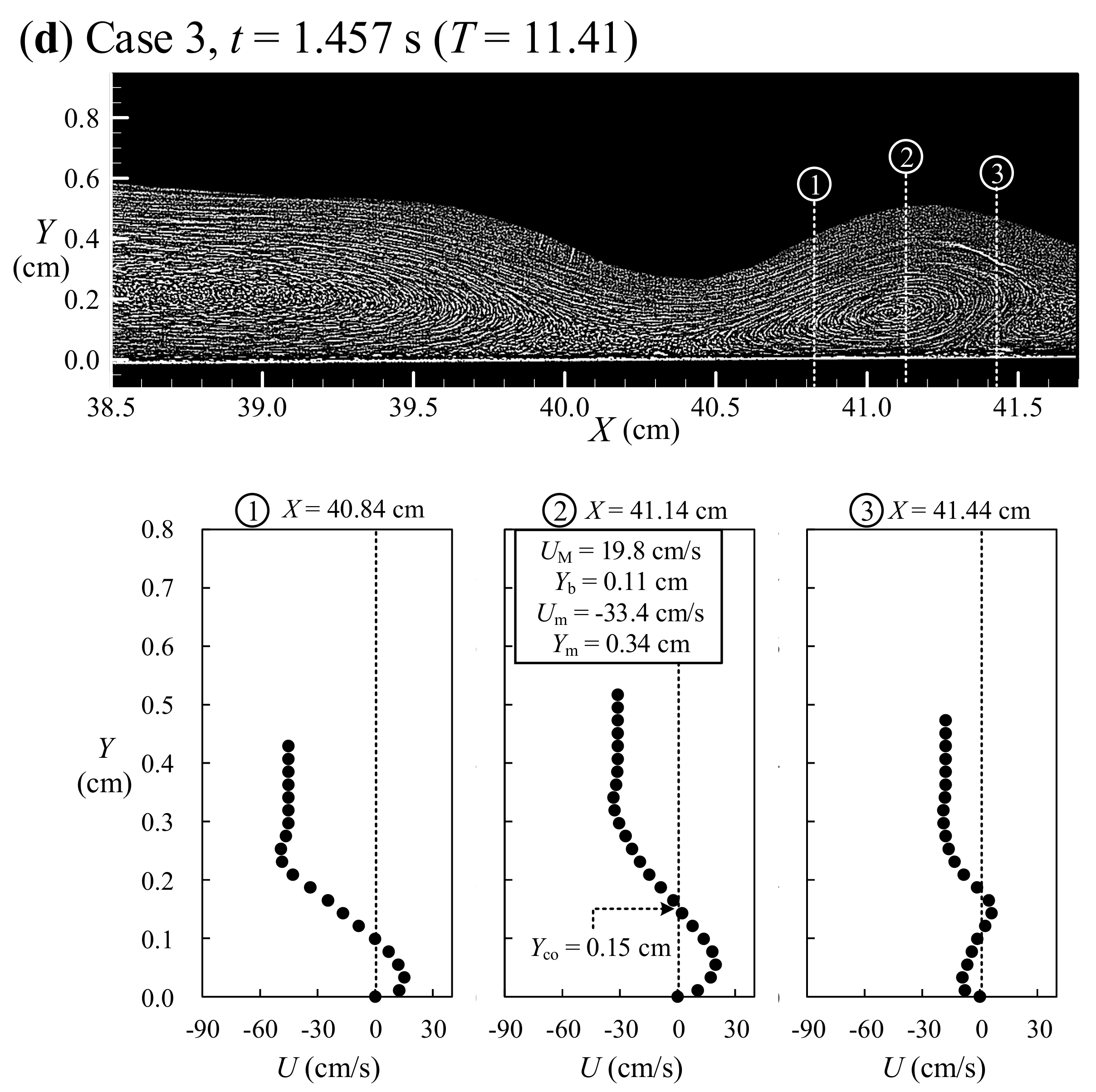
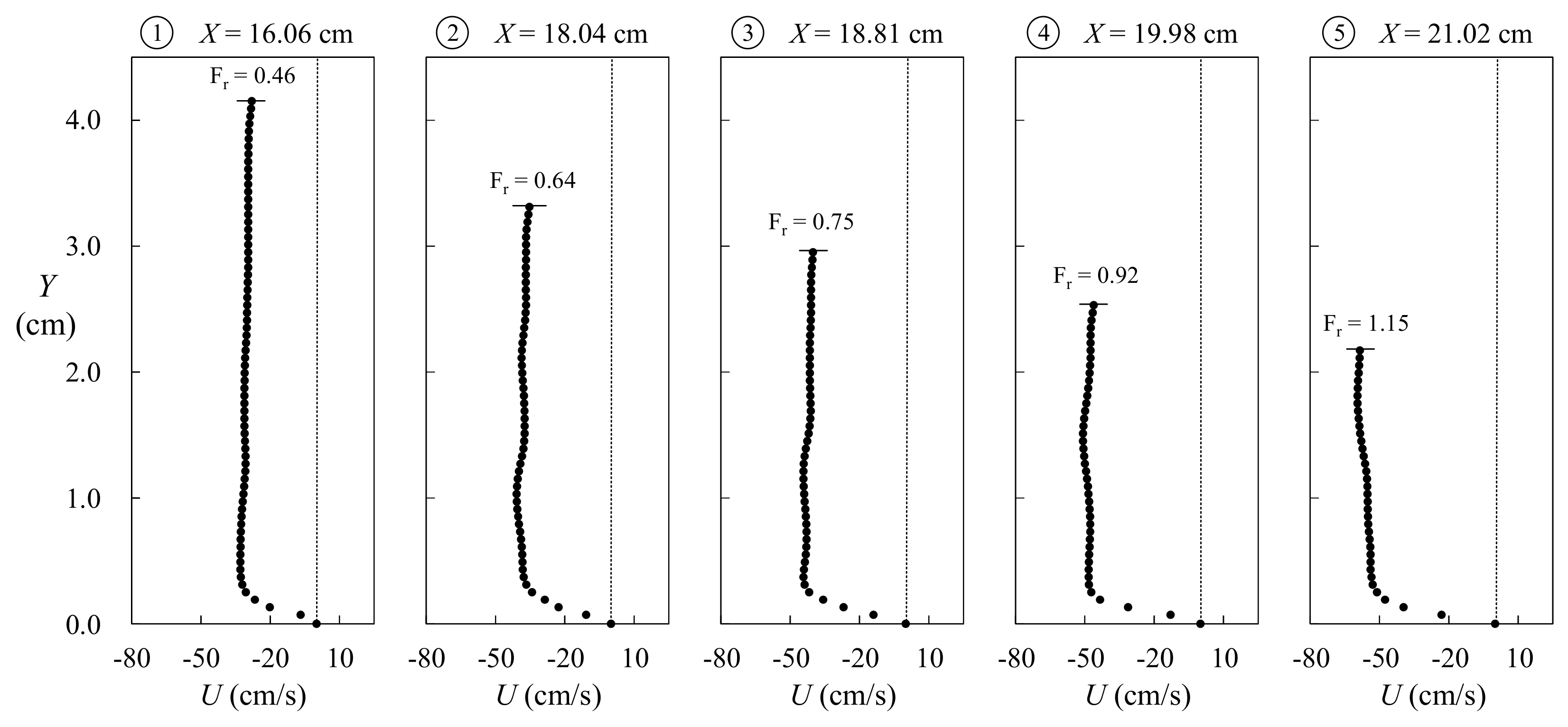
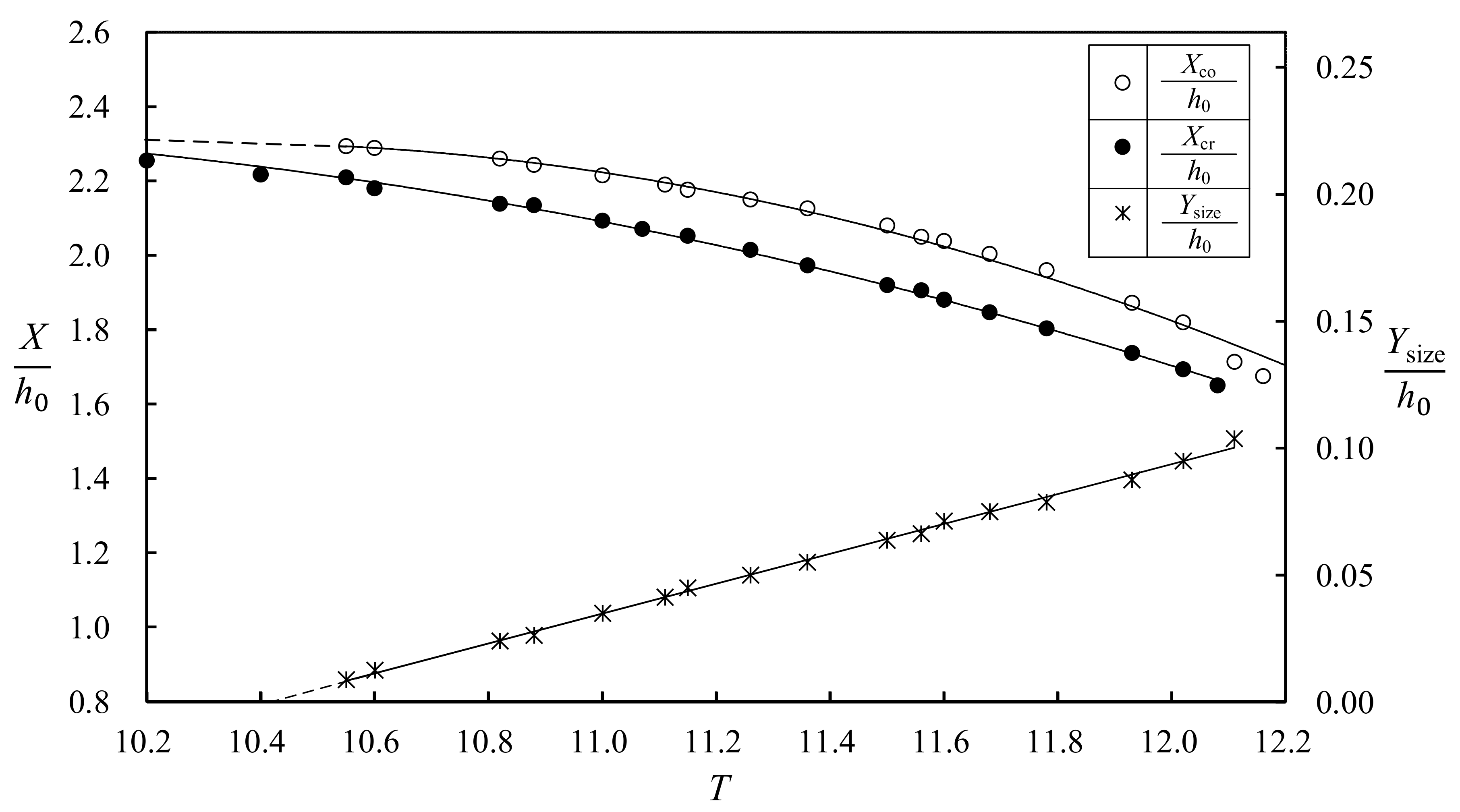
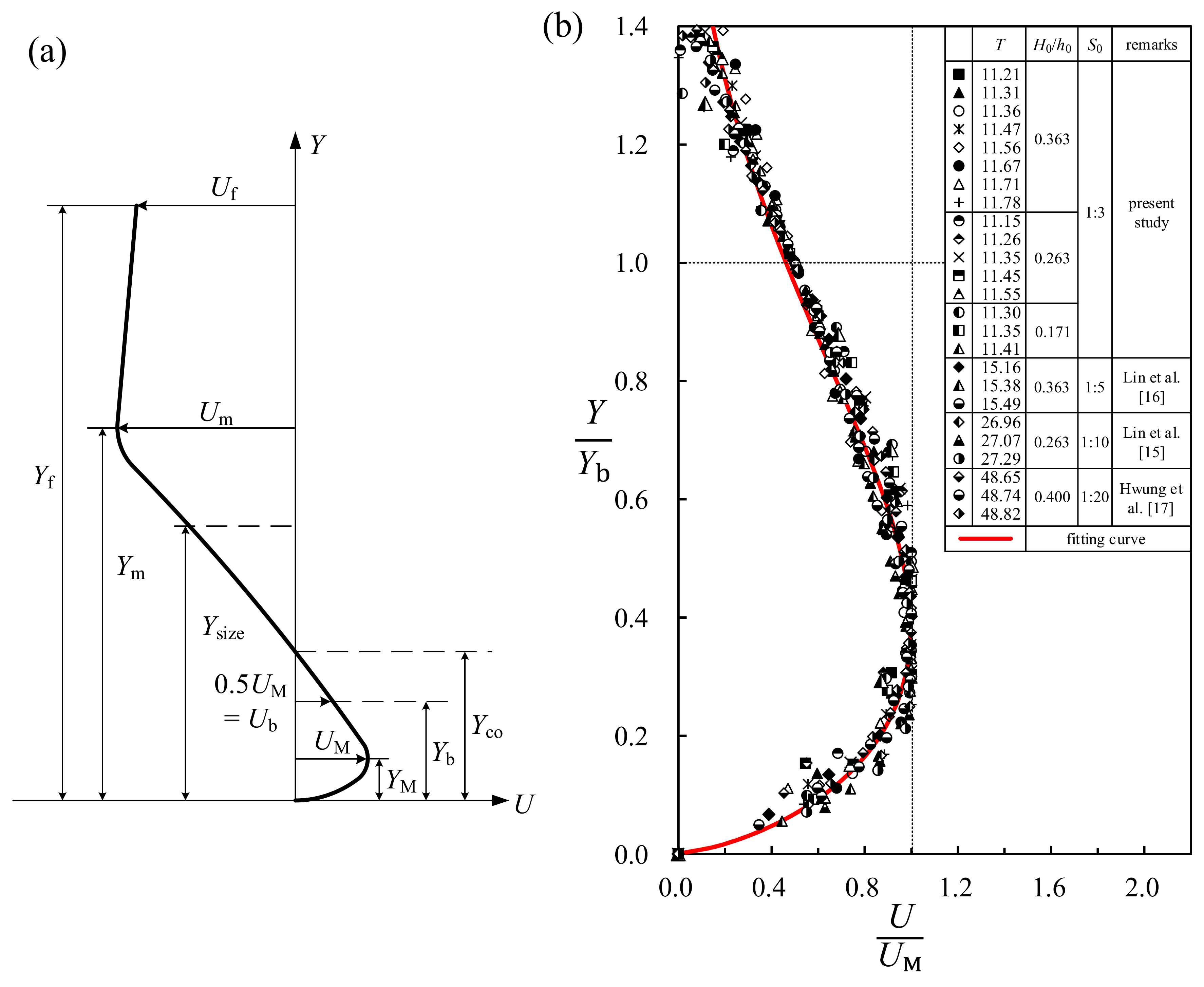
6.1. Variations of Critical and Core Sections as Well as Size Height for 10.20 ≤ T ≤ 12.11
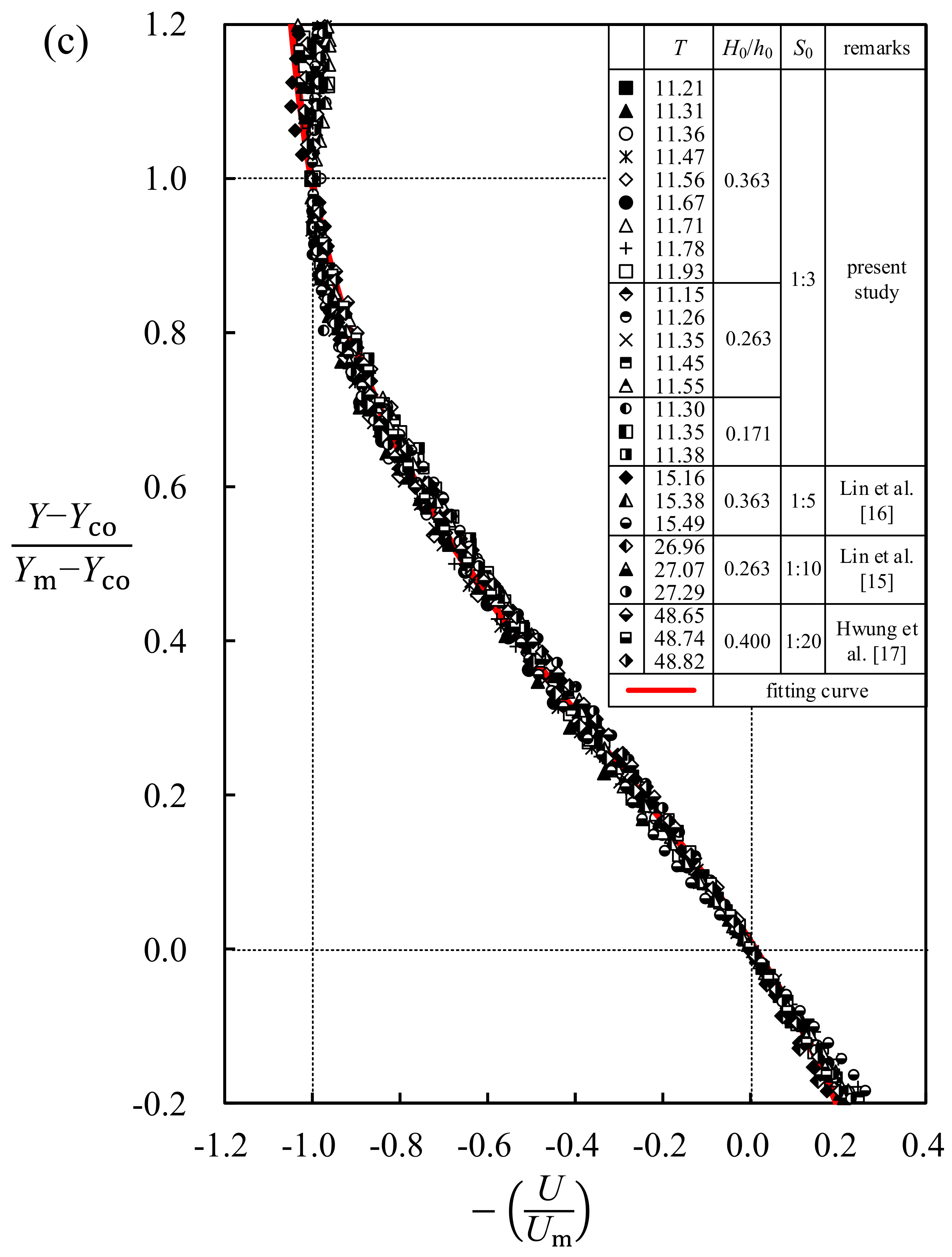
6.2. Similarity Profiles for Velocity Distributions at Core Sections for 11.00 < T < 12.11
7. Conclusions
- The run-down process of the solitary wave for 7.25 ≤ T < 13.43 can be divided into the early, middle, and late stages. In the early and first-half middle stage for about 7.25 ≤ T < 10.20, formation of the very streamlined free surface characterizes the flow event, highlighting the flow being decelerated in the offshore direction and subjected to adverse pressure gradient. The section of occurrence of the critical Froude number moves offshore as T increases for T > 9.00.
- In the second-half middle stage of the run-down process for 10.20 ≤ T < 11.60, the incipient flow separation, evolution of the primary vortex structure, hydraulic jump with sudden rising of the free surface in the retreated flow, and formation of curling jet on the upper portion of free surface take place sequentially.
- As regards the late stage of run-down process with 11.60 ≤ T < 13.43, transformation of the curled free surface into the impinging jet impacting on the free surface of the retreated flow at T = 12.11, and the two-phase flow with air core and/or subsequent air bubbles being entrained into vortex occur. Right at T = 13.43, the free surface of the retreated flow reaching its offshore-most position identifies the end of the run-down process.
- The non-dimensional shoreward distance of the critical/core section moves offshore as T increases for 10.2/10.55 ≤ T ≤ 12.11, with the latter taking place on the onshore side of the former for the identical T. The magnitudes of the non-dimensional size height of the primary vortex increases linearly with increasing T for 10.55 ≤ T ≤ 12.16. As a result of entrainment of air core within vortex, the two-phase flow field develops with a larger water depth for T ≥ 12.11, and consequently the critical section no longer exists.
- A unique similarity profile for the onshore velocity U(Y) measured through the primary vortex core and obtained very close to beach surface for 0 ≤ Y ≤ Yco has been achieved by selecting the positive maximum velocity UM and the specified half thickness Yb as the characteristic velocity and length scales, respectively. This profile, with Equation (4), is very similar to Verhoff’s velocity distribution equation for the traditional plane wall jet, demonstrating existence of the wall jet flow right beyond the beach surface.
- Further, a similarity profile for the offshore velocity U(Y) in the shear layer, obtained between the core height of the primary vortex Yco and the specified height Ym, has been realized by selecting the negative maximum velocity Um and the representative thickness of the shear layer (Ym − Yco) as the characteristic velocity and length scales, respectively. This profile, with Equation (5), identifies the feature of the shear layer flow, similar to those of traditional velocity distributions in the free and cavity shear layer flows.
- The two similarity profiles obtained for wall jet flow very close to the beach surface (0 ≤ Y ≤ Yco) and for shear layer flow between the core height of the primary vortex Yco and the specified height Ym are obtained considering all of the three cases of the present study (H0/h0 = 0.171, 0.263, and 0.363) as well as data of Lin et al. [15,16] for S0 = 1:10 and 1:5 and Hwung et al. [17] for S0 = 1:20. This is evidence that neither the wave-height to water-depth ratio H0/h0 nor the beach slope S0 has effects on both the wall jet and shear layer similarity profiles, strongly highlighting their universal feature.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- British Association for the Advancement of Science. Committee on Waves. In Report of the Committee on Waves: Appointed by the British Association at Bristol in 1836 [and Consisting of Sir John Robison and John Scott Russell]; R. and J.E. Taylor: London, UK, 1838; pp. 417–496. [Google Scholar]
- United States. Beach Erosion Board. Laboratory Investigation of the Vertical Rise of Solitary Waves on Impermeable Slopes; U.S. Beach Erosion Board: Washington, DC, USA, 1953.
- Synolakis, C.E. The runup of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Zelt, J.A. The run-up of nonbreaking and breaking solitary waves. Coast. Eng. 1991, 15, 205–246. [Google Scholar] [CrossRef]
- Grilli, S.T.; Subramanya, R.; Svendsen, I.A.; Veeramony, J. Shoaling of solitary waves on plane beaches. J. Waterw. Port Coast. Ocean Eng. 1994, 120, 609–628. [Google Scholar] [CrossRef]
- Grilli, S.T.; Svendsen, I.A.; Subramanya, R. Breaking criterion and characteristics for solitary waves on slopes. J. Waterw. Port Coast. Ocean Eng. 1997, 123, 102–112. [Google Scholar] [CrossRef]
- Lin, P.; Chang, K.A.; Liu, P.L.F. Runup and rundown of solitary waves on sloping beaches. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 247–255. [Google Scholar] [CrossRef]
- Li, Y.; Raichlen, F. Energy balance model for breaking solitary wave runup. J. Waterw. Port Coast. Ocean Eng. 2003, 129, 47–59. [Google Scholar] [CrossRef]
- Jensen, A.; Pedersen, G.K.; Wood, D.J. An experimental study of wave run-up at a steep beach. J. Fluid Mech. 2003, 486, 161–188. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Hsu, T.W.; Lin, T.C.; Chang, Y.H. On the evolution and run-up of breaking solitary waves on a mild sloping beach. Coast. Eng. 2008, 55, 975–988. [Google Scholar] [CrossRef]
- Sumer, B.M.; Sen, M.B.; Karagali, I.; Ceren, B.; Fredsøe, J.; Sottile, M.; Zilioli, L.; Fuhrman, D.R. Flow and sediment transport induced by a plunging solitary wave. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Lo, H.Y.; Park, Y.S.; Liu, P.L.F. On the run-up and back-wash processes of single and double solitary waves—An experimental study. Coast. Eng. 2013, 80, 1–14. [Google Scholar] [CrossRef]
- Pedersen, G.; Lindstrom, E.; Bertelsen, A.F.; Jensen, A.; Laskovski, D. Runup and boundary layers on sloping beaches. Phys. Fluids 2013, 25, 012102. [Google Scholar] [CrossRef]
- Lin, C.; Yeh, P.H.; Hseih, S.C.; Shih, Y.N.; Lo, L.F.; Tsai, C.P. Pre-breaking internal velocity field induced by a solitary wave propagating over a 1:10 slope. Ocean Eng. 2014, 80, 1–12. [Google Scholar] [CrossRef]
- Lin, C.; Yeh, P.H.; Kao, M.J.; Yu, M.H.; Hseih, S.C.; Chang, S.C.; Wu, T.R.; Tsai, C.P. Velocity fields in near-bottom and boundary layer flows in pre-breaking zone of solitary wave propagating over a 1:10 slope. J. Waterw. Port Coast. Ocean Eng. 2015, 141, 04014038. [Google Scholar] [CrossRef]
- Lin, C.; Kao, M.J.; Tzeng, G.W.; Wong, W.Y.; Yang, J.; Raikar, R.V.; Wu, T.R.; Liu, P.L.F. Study on flow fields of boundary-layer separation and hydraulic jump during rundown motion of shoaling solitary wave. J. Earthq. Tsunami 2015, 9, 154002. [Google Scholar] [CrossRef]
- Hwung, H.H.; Wu, Y.T.; Lin, C. Tsunami propagation and related new approach of mitigation. In Proceedings of the 8th Taiwan-Japan Joint Seminar on Natural Hazard Mitigation, Kyoto, Japan, 7 December 2015. [Google Scholar]
- Skene, D.M.; Bennetts, L.G.; Wright, M.; Meylan, M.H.; Maki, K.J. Water wave overwash of a step. J. Fluid Mech. 2018, 839, 293–312. [Google Scholar] [CrossRef]
- Higuera, P.; Liu, P.L.F.; Lin, C.; Wong, W.Y.; Kao, M.J. Laboratory-scale swash flows generated by a non-breaking solitary wave on a steep slope. J. Fluid Mech. 2018, 847, 186–227. [Google Scholar] [CrossRef]
- Lin, C.; Hwung, H.H. Observation and measurement of the bottom boundary layer flow in the prebreaking zone of shoaling waves. Ocean Eng. 2002, 29, 1479–1502. [Google Scholar] [CrossRef]
- Goring, D.G. Tsunami: The Propagation of Long Waves onto a Shelf; Technical Report No. KH-R-38; W. M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology: Pasadena, CA, USA, 1978. [Google Scholar]
- Adrian, R.J.; Westerweel, J. Particle Image Velocimetry; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Cowen, E.A.; Monismith, S.G. A hybrid digital particle tracking velocimetry technique. Exp. Fluids 1997, 22, 199–211. [Google Scholar] [CrossRef]
- Mori, N.; Chang, K.A. Introduction to MPIV-PIV Toolbox in Matlab. User Reference Manual. 2009, pp. 1–15. Available online: http://www.oceanwave.jp/softwares/mpiv/index.php?Download (accessed on 1 November 2018).
- Adrian, R.J. Particle imaging techniques for experimental fluid mechanics. Annu. Rev. Fluid Mech. 1991, 23, 261–304. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 1995. [Google Scholar]
- Lin, C.; Yu, S.M.; Wong, W.Y.; Tzeng, G.W.; Kao, M.J.; Yeh, P.H.; Raikar, R.V.; Yang, J.; Tsai, C.P. Velocity characteristics in boundary layer flow caused by solitary wave traveling over horizontal bottom. Exp. Therm. Fluid Sci. 2016, 76, 238–252. [Google Scholar] [CrossRef]
- Keulegan, G.H. Gradual damping of solitary waves. J. Res. Nat. Bur. Stand. 1948, 40, 487–498. [Google Scholar] [CrossRef]
- Mei, C.C. The Applied Dynamics of Ocean Surface Waves; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1989. [Google Scholar]
- Lin, C.; Kao, M.J.; Wong, W.Y.; Shao, Y.P.; Fu, C.F.; Yuan, J.M.; Raikar, R.V. Effect of leading waves on velocity distribution of undular bore traveling over sloping bottom. Eur. J. Mech. Ser. B Fluids 2018. [Google Scholar] [CrossRef]
- Chang, K.A.; Liu, P.L.F. Pseudo turbulence in PIV breaking wave measurements. Exp. Fluids 2000, 29, 331–338. [Google Scholar] [CrossRef]
- Ho, T.C. Characteristics of Vortical Flow Fields Induced by Solitary Waves Propagating over Submerged Structures with Different Aspect Ratios. Ph.D. Thesis, Department of Civil Engineering, National Chung Hsing University, Taichung City, Taiwan, 2009. [Google Scholar]
- Sumer, B.M.; Jensen, P.M.; Sørensen, L.B.; Fredsøe, J.; Liu, P.L.F.; Carstensen, S. Coherent structures in wave boundary layers. Part 2. Solitary motion. J. Fluid Mech. 2010, 646, 207–231. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Albohr, O.; Tartaglino, U.; Volokitin, A.I.; Tossatti, E. On the nature of surface roughness with application to contact mechanics, sealing, rubber friction and adhesion. J. Phys. Condens. Matter 2005, 17, 82. [Google Scholar] [CrossRef] [PubMed]
- Engineering Tool Box. Available online: http://www.engineeringtoolbox.com/surface-roughness-ventilation-ducts-d_209.html (accessed on 1 November 2018).
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; the MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Daily, J.W.; Harleman, D.R.F. Fluid Dynamics; Addison-Wesley Publishing Company, Inc.: Boston, MA, USA, 1966. [Google Scholar]
- Henderson, F.M. Open Channel Flow; Macmillan Publishing Company Inc.: New York, NY, USA, 1966; pp. 218–219. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Book Company: Singapore, 1973; pp. 425–428. [Google Scholar]
- Subramanya, K. Flow in Open Channels; McGraw-Hill Book Company: New York, NY, USA, 1986; pp. 204–206. [Google Scholar]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill Book Company: New York, NY, USA, 1979. [Google Scholar]
- Lin, C.; Chiu, P.H.; Hsieh, S.J. Characteristics of horseshoe vortex system near a vertical plate-base plate juncture. Exp. Therm. Fluid Sci. 2002, 27, 25–46. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Abell, C.J.; Peterka, J.A.; Woo, H.J. Kinematical studies of the flows around free or surface-mounted obstacles—Applying topology to flow visualization. J. Fluid Mech. 1978, 86, 179–200. [Google Scholar] [CrossRef]
- Lin, C.; Hsieh, S.C.; Lin, I.J.; Chang, K.A.; Raikar, V.R. Flow property and self-similarity in steady hydraulic jump. Exp. Fluids 2012, 53, 1591–1616. [Google Scholar] [CrossRef]
- Rajaratnam, N. Turbulent Jet; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Verhoff, A. The Two-Dimensional Turbulent Wall Jet without an External Free Stream; Report No. 626; Princeton University: Princeton, NJ, USA, 1963. [Google Scholar]
- Michalke, A. The instability of free shear layers. Prog. Aerosp. Sci. 1972, 12, 213–239. [Google Scholar] [CrossRef]
- Kuo, C.H.; Huang, S.H.; Chang, C.W. Self-sustained oscillation induced by horizontal cover plate above cavity. J. Fluids Struct. 2000, 14, 25–48. [Google Scholar] [CrossRef]
- Lin, C.; Ho, T.C.; Chang, S.C.; Hsieh, S.C.; Chang, K.A. Vortex shedding induced by a solitary wave propagating over a submerged vertical plate. Int. J. Heat Fluid Flow 2005, 26, 894–904. [Google Scholar] [CrossRef]
- Lin, C.; Chang, S.C.; Chang, K.A. Laboratory observation of a solitary wave propagating over a submerged rectangular dike. J. Eng. Mech. 2006, 132, 545–554. [Google Scholar] [CrossRef]
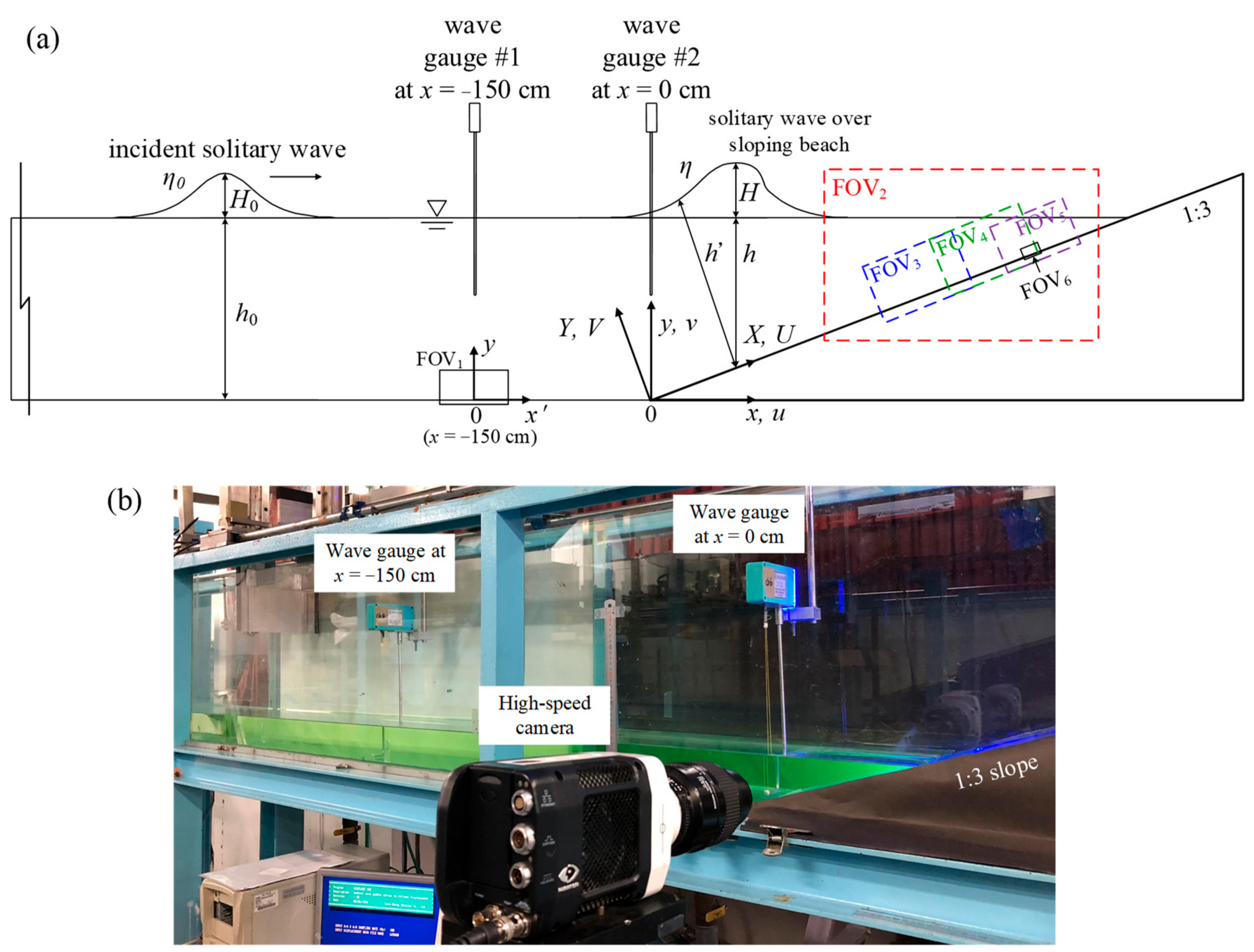


| FOVi | Dimension | Range | Pixel Resolution |
|---|---|---|---|
| FOV1 | 2.00 cm × 1.00 cm | −1.00 cm ≤ x’ ≤ 1.00 cm | 1280 × 640 |
| FOV2 | 9.95 cm × 6.22 cm | 10.80 cm ≤ x ≤ 20.08 cm | 1280 × 800 |
| FOV3 | 3.50 cm × 2.19 cm | 13.15 cm ≤ X ≤ 16.65 cm | 1280 × 800 |
| FOV4 | 3.50 cm × 2.19 cm | 15.75 cm ≤ X ≤ 19.25 cm | 1280 × 800 |
| FOV5 | 2.85 cm × 1.78 cm | 17.55 cm ≤ X ≤ 20.40 cm | 1280 × 800 |
| FOV6 | 0.65 cm × 0.41 cm | 18.50 cm ≤ X ≤ 19.15 cm | 1280 × 800 |
| Case | H0 (cm) | h0 (cm) | H0/h0 | Breaker Type |
|---|---|---|---|---|
| 1 | 2.90 | 8.0 | 0.363 | Non-breaking |
| 2 | 2.10 | 8.0 | 0.263 | Non-breaking |
| 3 | 2.74 | 16.0 | 0.171 | Non-breaking |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Wong, W.-Y.; Kao, M.-J.; Tsai, C.-P.; Hwung, H.-H.; Wu, Y.-T.; Raikar, R.V. Evolution of Velocity Field and Vortex Structure during Run-Down of Solitary Wave over Very Steep Beach. Water 2018, 10, 1713. https://doi.org/10.3390/w10121713
Lin C, Wong W-Y, Kao M-J, Tsai C-P, Hwung H-H, Wu Y-T, Raikar RV. Evolution of Velocity Field and Vortex Structure during Run-Down of Solitary Wave over Very Steep Beach. Water. 2018; 10(12):1713. https://doi.org/10.3390/w10121713
Chicago/Turabian StyleLin, Chang, Wei-Ying Wong, Ming-Jer Kao, Ching-Piao Tsai, Hwung-Hweng Hwung, Yun-Ta Wu, and Rajkumar V. Raikar. 2018. "Evolution of Velocity Field and Vortex Structure during Run-Down of Solitary Wave over Very Steep Beach" Water 10, no. 12: 1713. https://doi.org/10.3390/w10121713
APA StyleLin, C., Wong, W.-Y., Kao, M.-J., Tsai, C.-P., Hwung, H.-H., Wu, Y.-T., & Raikar, R. V. (2018). Evolution of Velocity Field and Vortex Structure during Run-Down of Solitary Wave over Very Steep Beach. Water, 10(12), 1713. https://doi.org/10.3390/w10121713









