Potential of Rainwater Utilization in Households Based on the Distributions of Catchment Area and End-Use Water Demand
Abstract
:1. Introduction
2. Methods
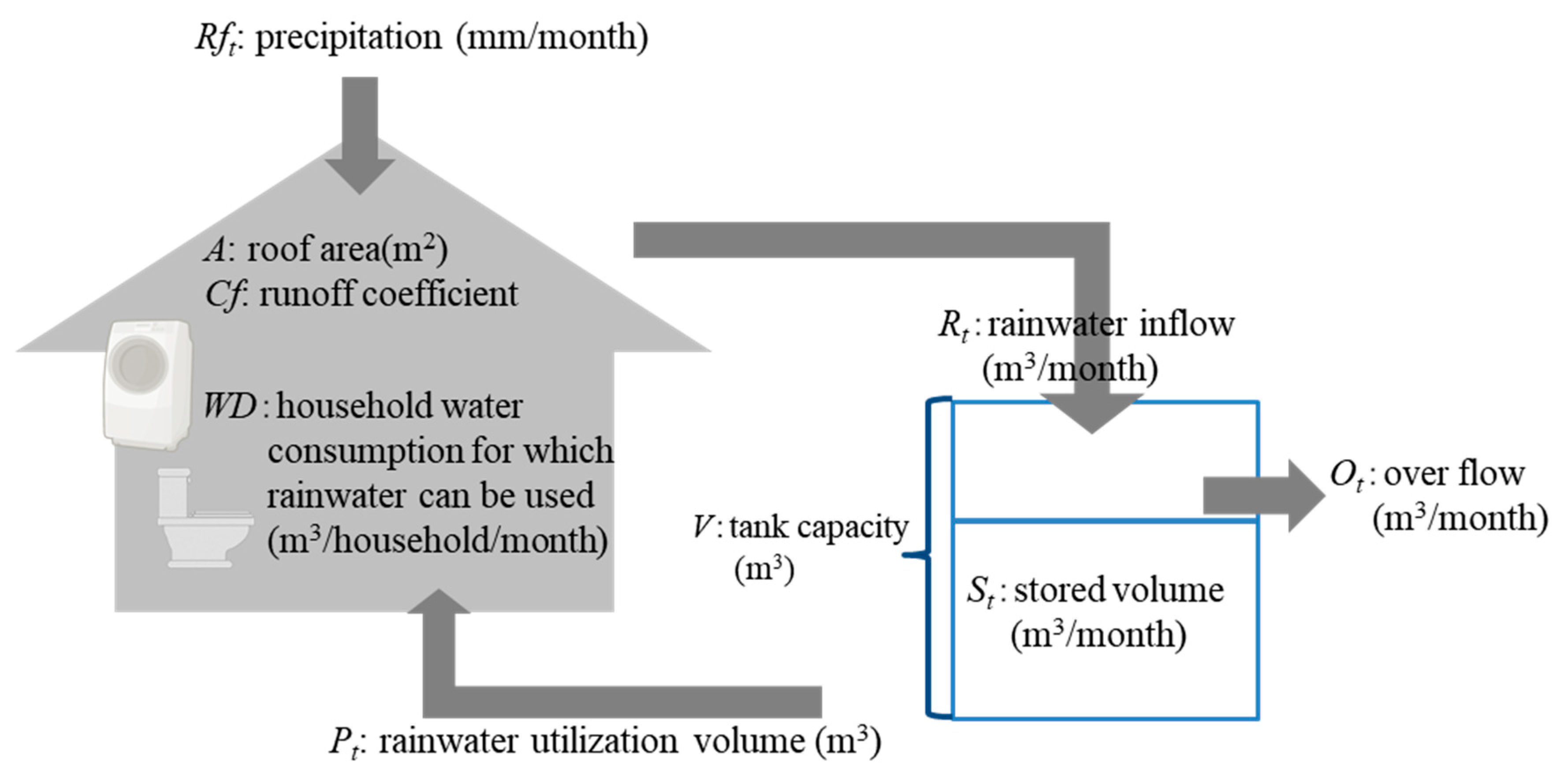
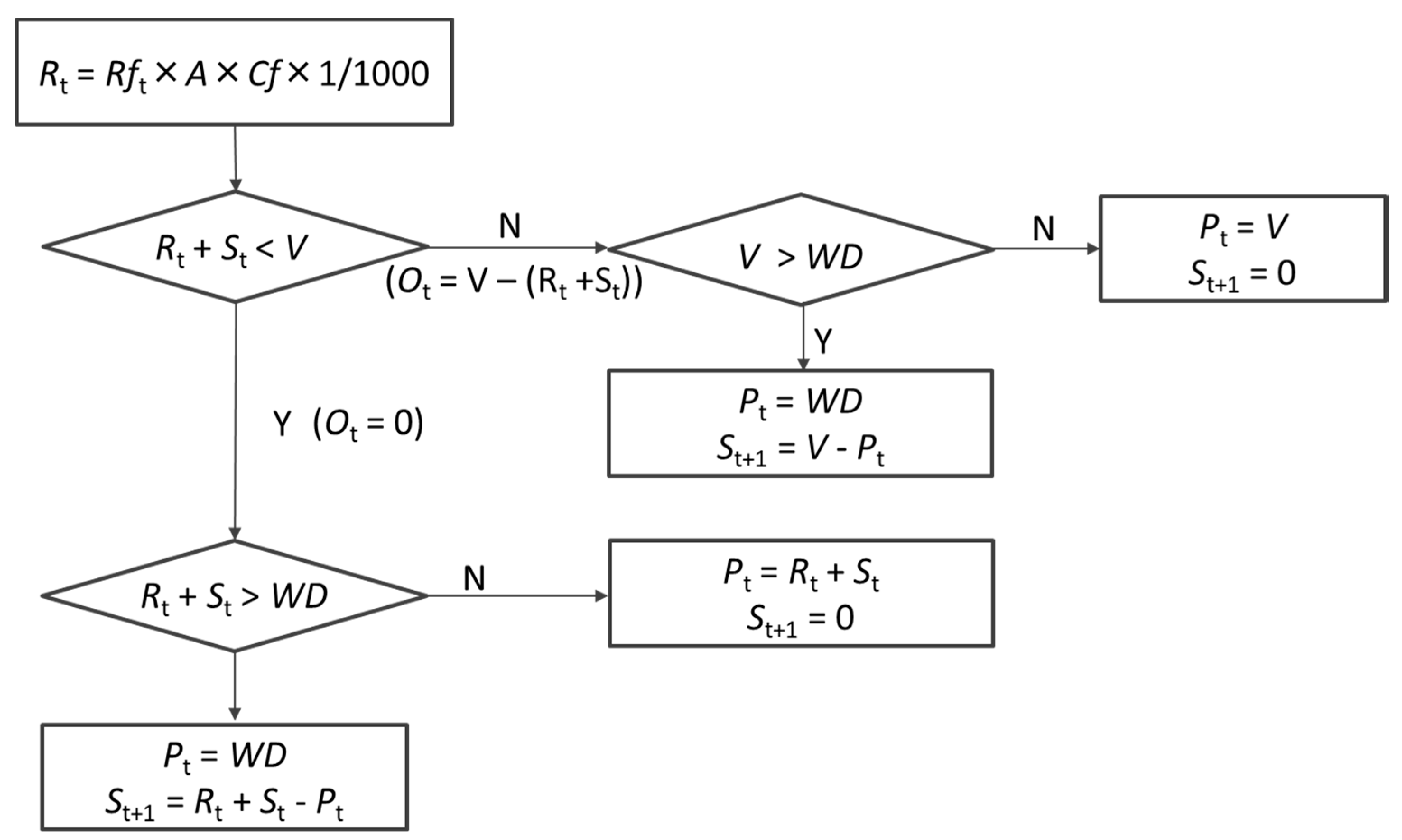
2.1. Simulation Model
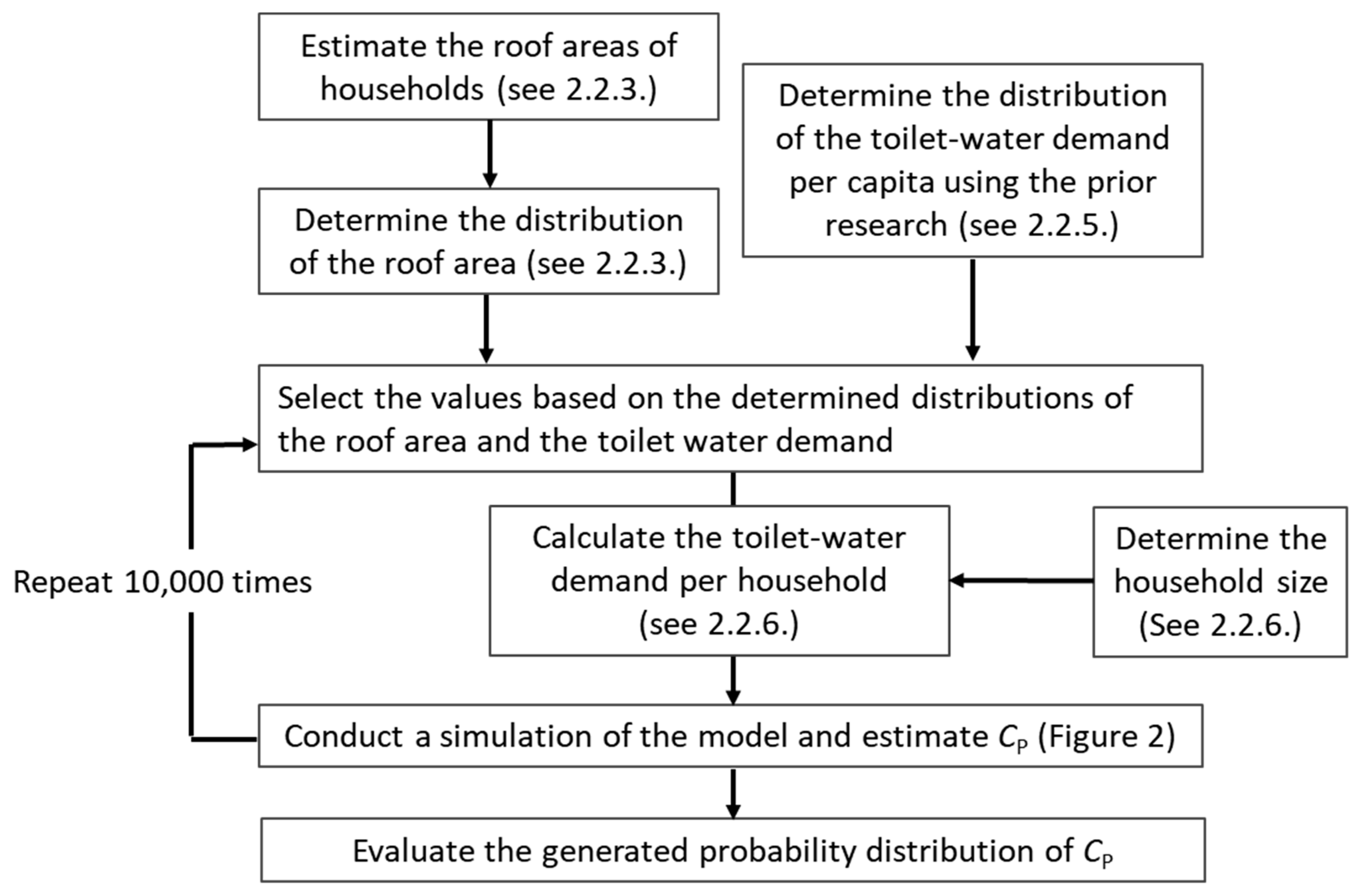
2.1.1. Probabilistic Approach
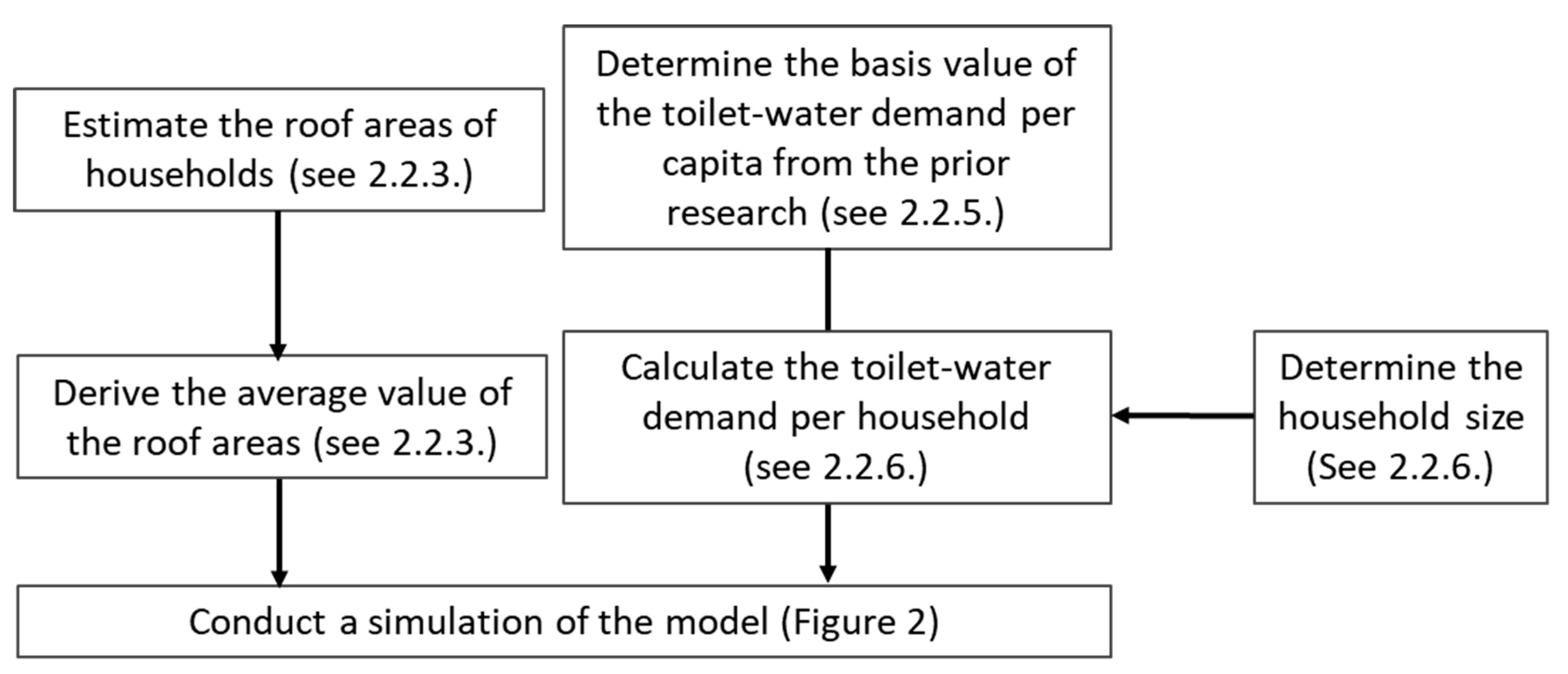
2.1.2. Conventional Approach
2.2. Data Utilized for Simulations
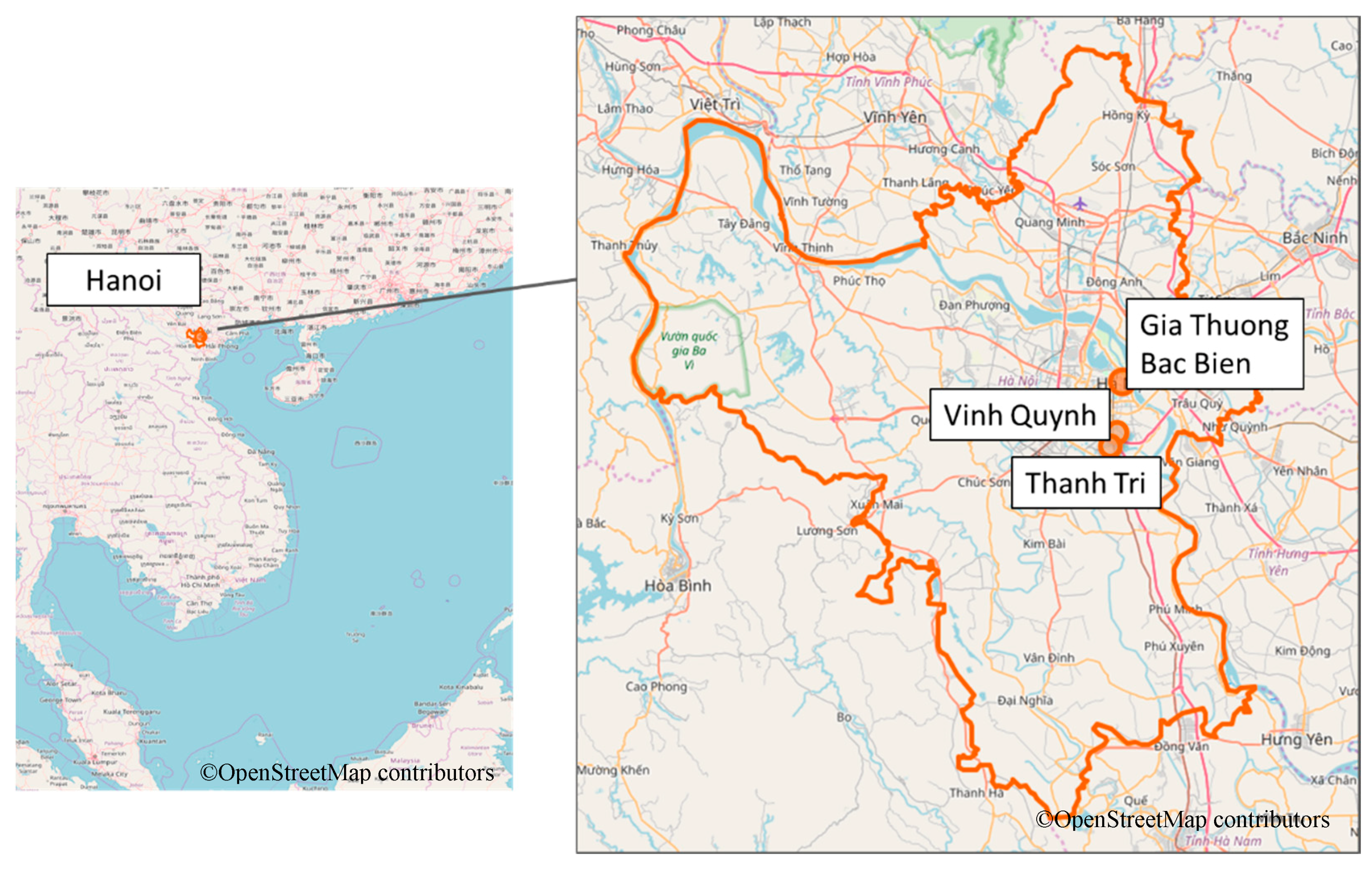
2.2.1. Targeted Area
2.2.2. Precipitation
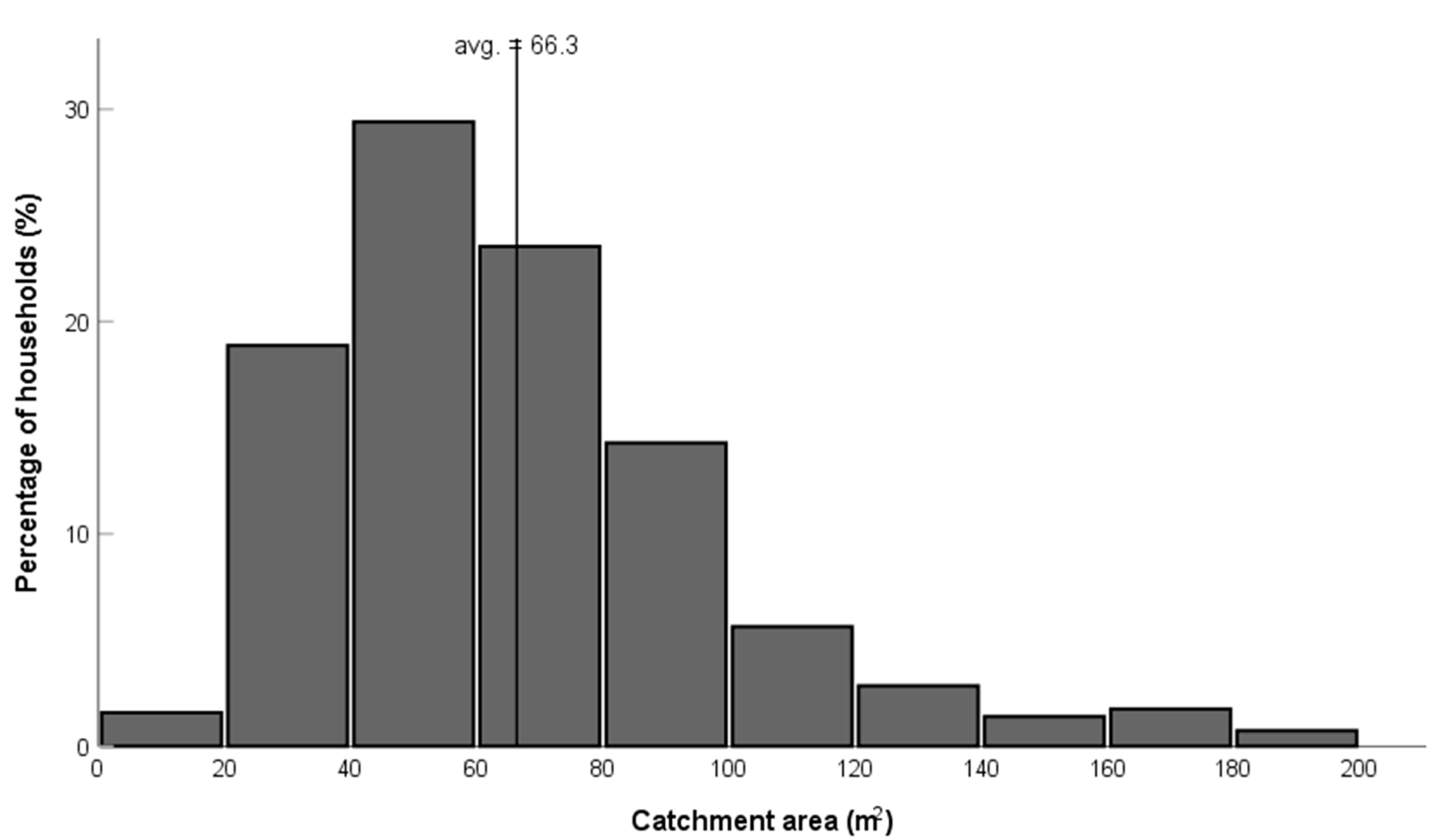
2.2.3. Distribution of the Catchment Areas
2.2.4. Rainwater Tank Size
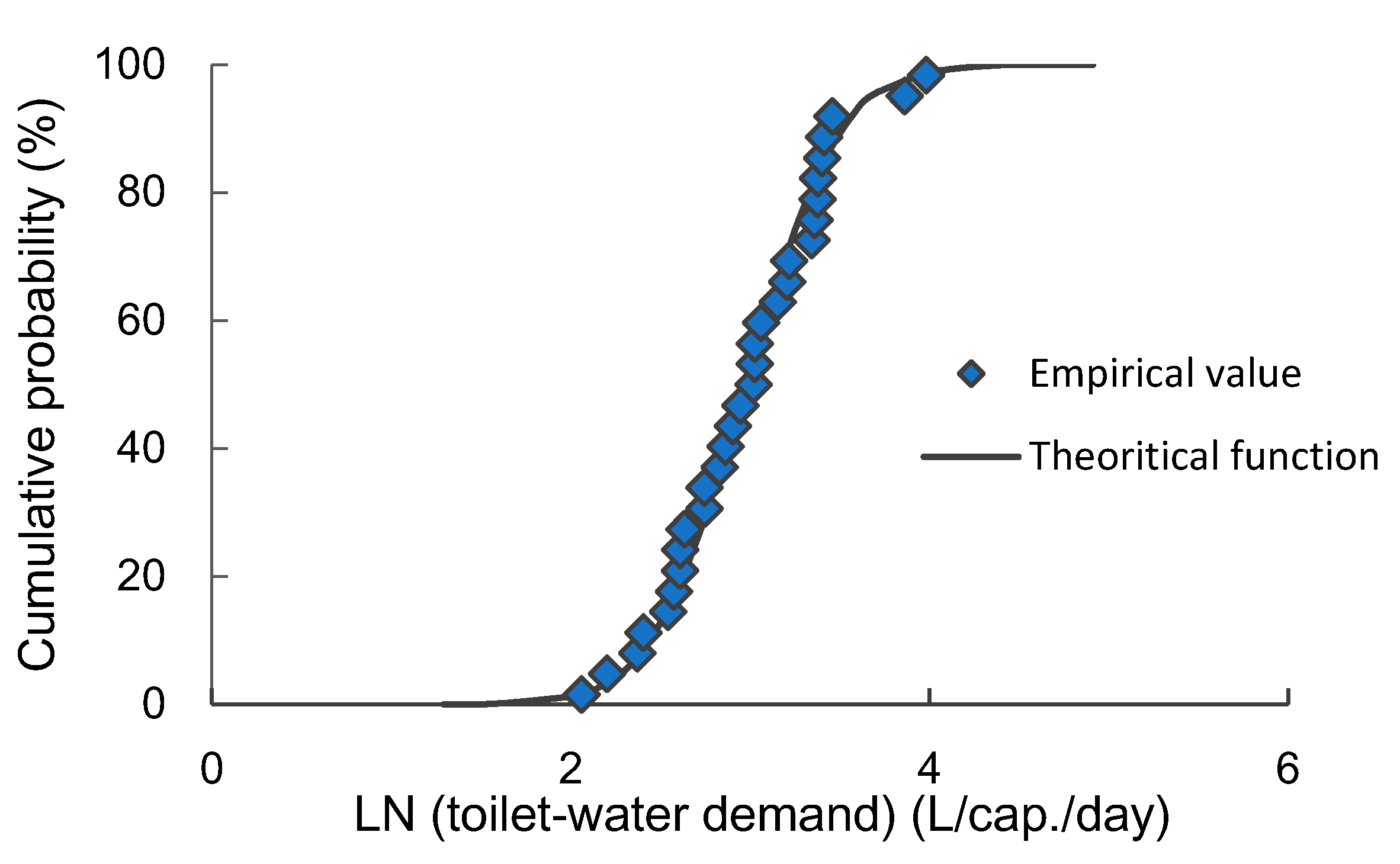
2.2.5. Distribution of Toilet-Water Demand Per Capita
2.2.6. Household Size
3. Results
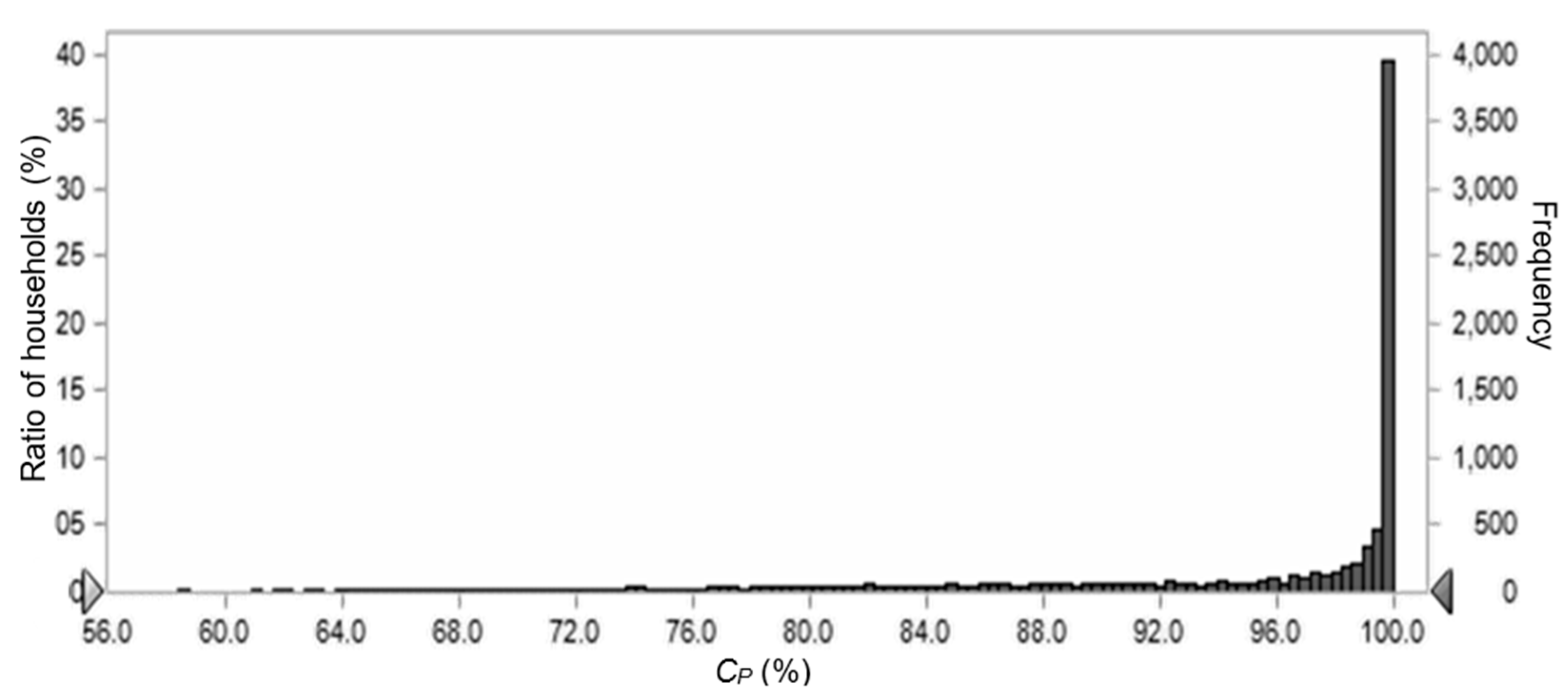
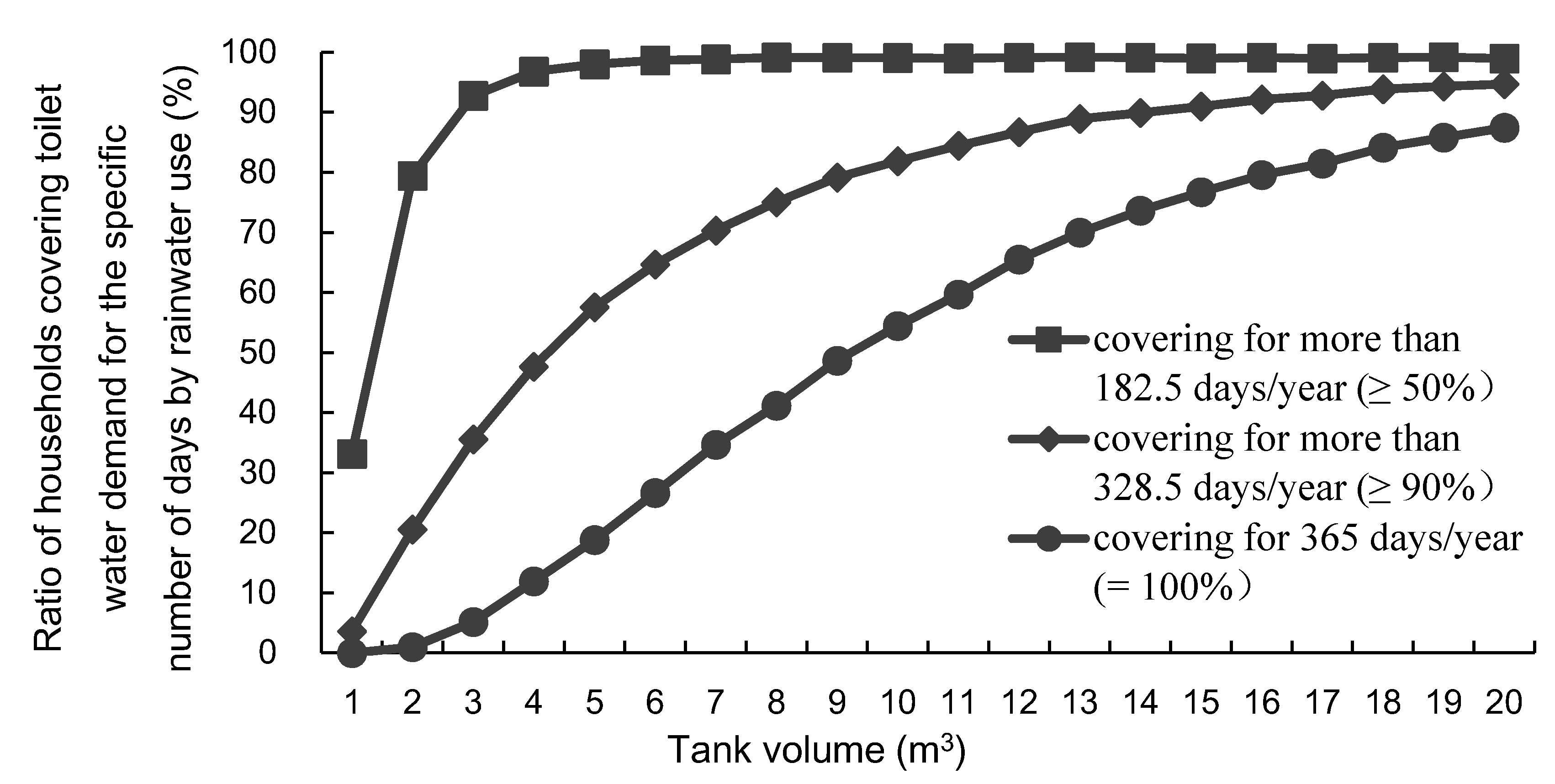
3.1. Estimated Potential of Rainwater Utilization
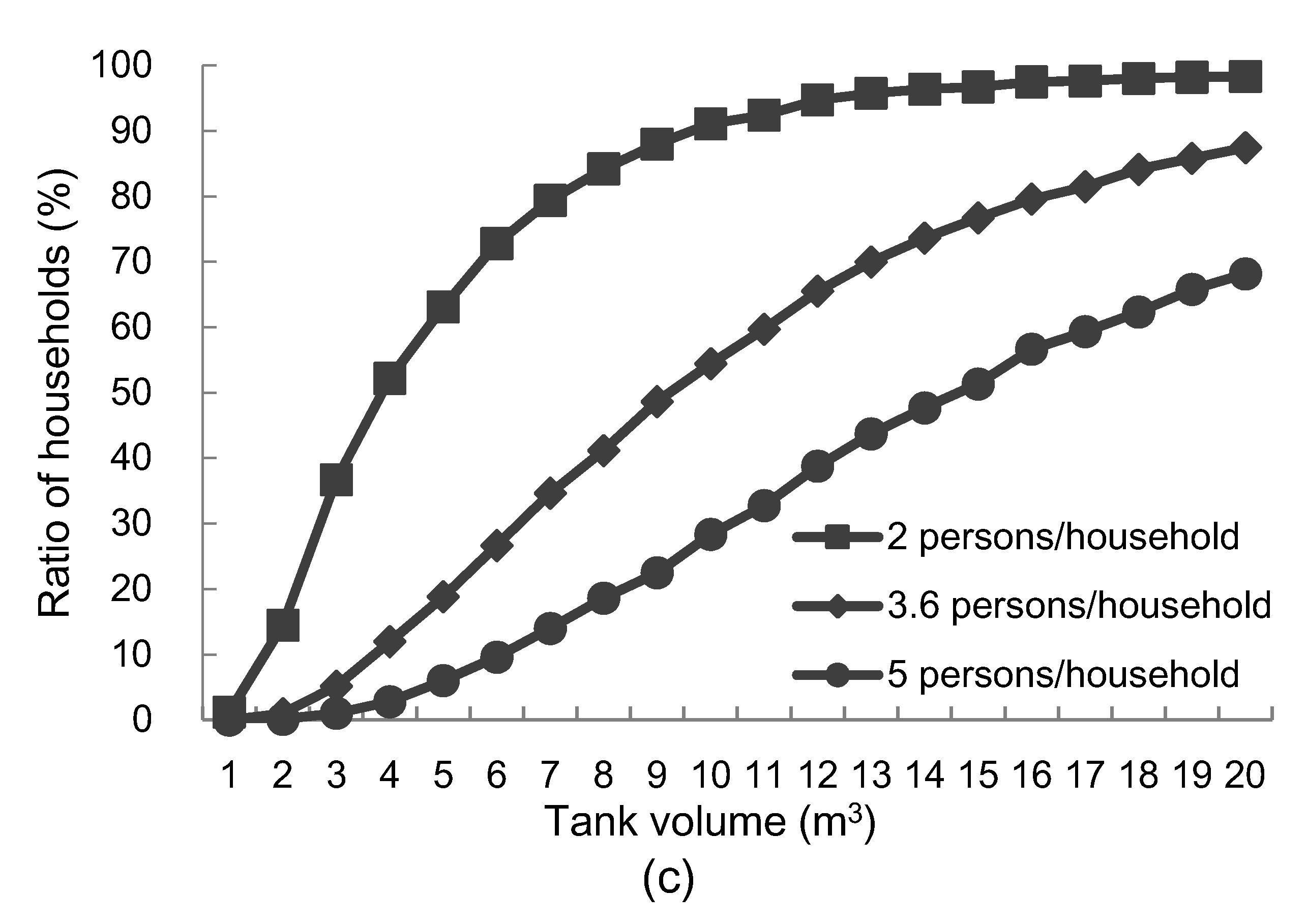
3.2. Potential of Rainwater Utilization for Toilet-Water in Households of Different Sizes
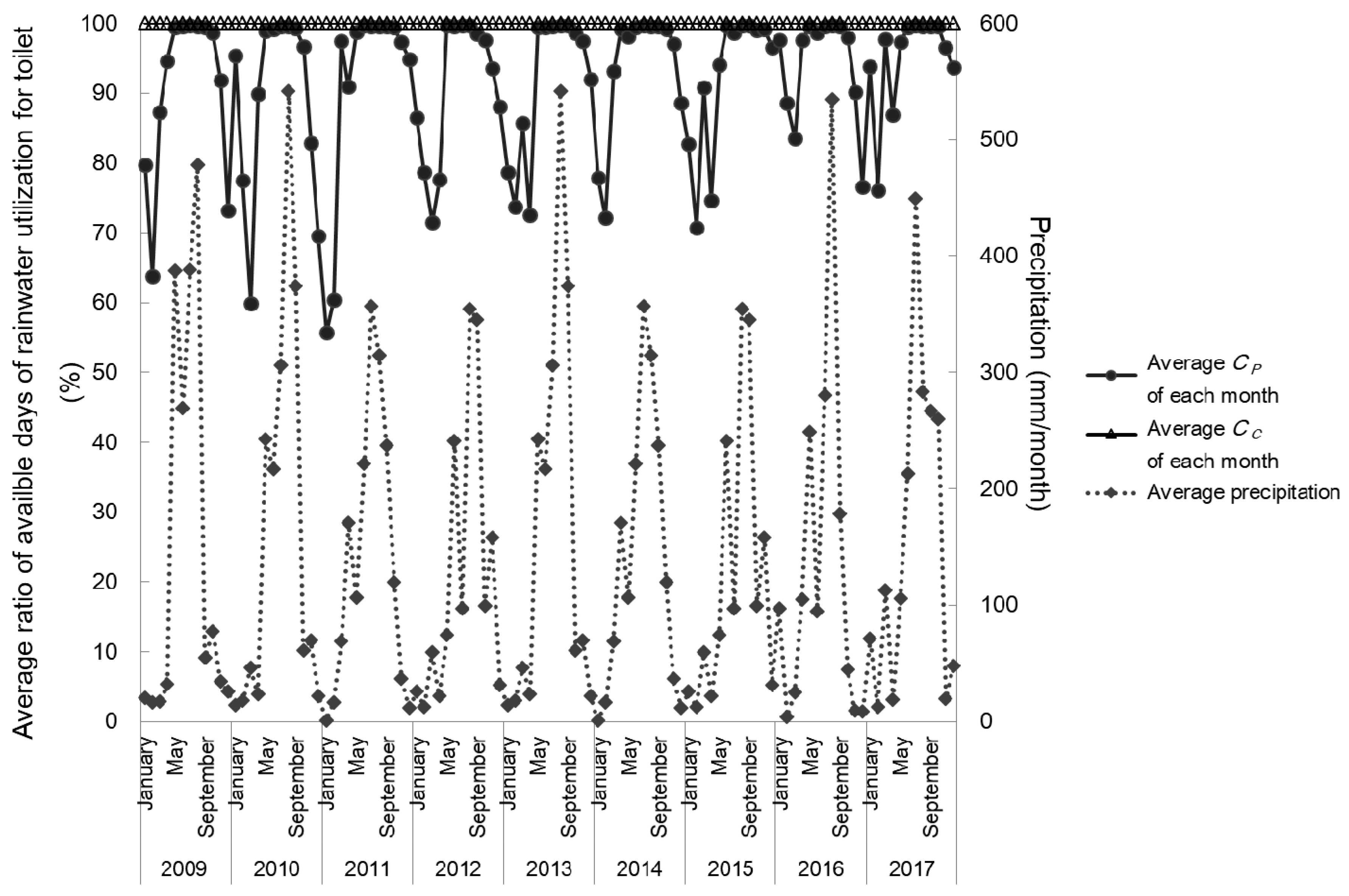
3.3. Seasonal Change in the Potential of Rainwater Utilization for Toilet Requirements
4. Discussion
5. Limitation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stavenhagen, M.; Buurman, J.; Tortajada, C. Saving water in cities: Assessing policies for residential water demand management in four cities in Europe. Cities 2018, 79, 187–195. [Google Scholar] [CrossRef]
- Kummu, M.; Guillaume, J.H.A.; De Moel, H.; Eisner, S.; Flörke, M.; Porkka, M.; Siebert, S.; Veldkamp, T.I.E.; Ward, P.J. The world’s road to water scarcity: Shortage and stress in the 20th century and pathways towards sustainability. Sci. Rep. 2016, 6, 1–16. [Google Scholar] [CrossRef] [PubMed]
- OECD. OECD Environmental Outlook to 2050; OECD Publishing: Paris, France, 2012; Volume 2030, ISBN 9789264122246. [Google Scholar]
- Xiong, W.; Li, Y.; Zhang, W.; Ye, Q.; Zhang, S.; Hou, X. Integrated multi-objective optimization framework for urban water supply systems under alternative climates and future policy. J. Clean. Prod. 2018, 195, 640–650. [Google Scholar] [CrossRef]
- Charles, K.; Pond, K.; Pedley, S.; Hossain, R.; Guillarmod, F.J. Vision 2030: The Resilience of Water Supply and Sanitation in the Face of Climate Change, Technology Projection Study; University of Surrey: Guildford, UK, 2010; p. 81. [Google Scholar]
- Fielding, K.S.; Spinks, A.; Russell, S.; McCrea, R.; Stewart, R.; Gardner, J. An experimental test of voluntary strategies to promote urban water demand management. J. Environ. Manag. 2012, 114, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Arbués, F.; García-Valiñas, M.Á.; Martínez-Espiñeira, R. Estimation of residential water demand: A state-of-the-art review. J. Socio-Econ. 2003, 32, 81–102. [Google Scholar] [CrossRef]
- Friedman, K.; Heaney, J.P.; Morales, M.; Palenchar, J. Water demand management optimization methodology. J. Am. Water Works Assoc. 2011, 103, 74–84. [Google Scholar] [CrossRef]
- Beal, C.D.; Gurung, T.R.; Stewart, R.A. Demand-side management for supply-side efficiency: Modeling tailored strategies for reducing peak residential water demand. Sustain. Prod. Consum. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Baki, S.; Rozos, E.; Makropoulos, C. Designing water demand management schemes using a socio-technical modelling approach. Sci. Total Environ. 2018, 622–623, 1590–1602. [Google Scholar] [CrossRef] [PubMed]
- Renwick, M.E.; Green, R.D. Do residential water demand side management policies measure up? An analysis of eight California water agencies. J. Environ. Econ. Manag. 2000, 40, 37–55. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Adeboye, O.B.; Rayburg, S.; Shanableh, A. Rainwater harvesting potential for southwest Nigeria using daily water balance model. Resour. Conserv. Recycl. 2012, 62, 51–55. [Google Scholar] [CrossRef]
- Hurlimann, A. Household use of and satisfaction with alternative water sources in Victoria Australia. J. Environ. Manag. 2011, 92, 2691–2697. [Google Scholar] [CrossRef] [PubMed]
- Dolnicar, S.; Hurlimann, A.; Nghiem, L.D. The effect of information on public acceptance—The case of water from alternative sources. J. Environ. Manag. 2010, 91, 1288–1293. [Google Scholar] [CrossRef] [PubMed]
- National Research Council of the National Academies. Desalination: A National Perspective, Environmental Protection; The National Academies Press: Washington, DC, USA, 2008. [Google Scholar] [CrossRef]
- Domenech, L. Rethinking water management: From centralised to decentralised water supply and sanitation models. Doc. Anàl. Geogr. 2011, 57, 293–310. [Google Scholar] [CrossRef]
- UNEP. Rainwater Harvesting: A Lifeline for Human Well-Being; Stockholm Environment Institute: Stockholm, Sweden, 2009; Volume 41, p. 69. [Google Scholar] [CrossRef]
- Australian Bureau of Statistics 4610.0—Water Account, Australia, 2013–14. Available online: http://www.abs.gov.au/AUSSTATS/abs@.nsf/Previousproducts/4610.0Main Features32013-14?opendocument&tabname=Summary&prodno=4610.0&issue=2013-14&num=&view= (accessed on 11 June 2018).
- Luong, T.V.; Luckmuang, P. Household rainwater harvesting—Thailand. In Proceedings of the 28th WEDC Conference, Sustainable Environmental Sanitation and Water Services, Kolkata, India, 18–22 November 2002; pp. 1–4. [Google Scholar]
- Lee, K.E.; Mokhtar, M.; Hanafiah, M.M.; Halim, A.A.; Badusah, J. Rainwater harvesting as an alternative water resource in Malaysis: Potential, policies and development. J. Clean. Prod. 2016, 126, 218–222. [Google Scholar] [CrossRef]
- Aladenola, O.O.; Adeboye, O.B. Assessing the potential for rainwater harvesting. Water Res. Manag. 2010, 24, 2129–2137. [Google Scholar] [CrossRef]
- Ghisi, E.; Mengotti de Oliveira, S. Potential for potable water savings by combining the use of rainwater and greywater in houses in southern Brazil. Build. Environ. 2007, 42, 1731–1742. [Google Scholar] [CrossRef]
- Silva, A.S.; Ghisi, E. Uncertainty analysis of daily potable water demand on the performance evaluation of rainwater harvesting systems in residential buildings. J. Environ. Manag. 2016, 180, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Fewkes, A. Modelling the performance of rainwater collection systems: Towards a generalised approach. Urban Water 1999, 1, 323–333. [Google Scholar] [CrossRef]
- Liaw, C.H.; Chiang, Y.C. Dimensionless analysis for designing domestic rainwater harvesting systems at the regional level in Northern Taiwan. Water 2014, 6, 3913–3933. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C. Selecting time scale resolution to evaluate water saving and retention potential of rainwater harvesting tanks. Procedia Eng. 2014, 70, 218–227. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C. Regional scale analysis for the design of storage tanks for domestic rainwater harvesting systems. Water Sci. Technol. 2012, 66, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Otaki, Y.; Otaki, M.; Bao, P.N.; Nga, T.T.V.; Aramaki, T. Micro-component survey of residential water consumption in Hanoi. Water Sci. Technol. Water Supply 2013, 13, 469–478. [Google Scholar] [CrossRef]
- Villarreal, E.L.; Dixon, A. Analysis of a rainwater collection system for domestic water supply in Ringdansen, Norrköping, Sweden. Build. Environ. 2005, 40, 1174–1184. [Google Scholar] [CrossRef]
- General Statistics Office of Viet Nam Area, Population and Population Density by Province. Available online: http://www.gso.gov.vn/default_en.aspx?tabid=774 (accessed on 15 October 2018).
- Mitchell, V.G.; Mccarthy, D.T.; Deletic, A.; Fletcher, T.D. Urban stormwater harvesting—Sensitivity of a storage behaviour model. Environ. Model. Softw. 2008, 23, 782–793. [Google Scholar] [CrossRef]
- Geraldi, M.S.; Ghisi, E. Influence of the length of rainfall time series on rainwater harvesting systems: A case study in Berlin. Res. Conserv. Recycl. 2017, 125, 169–180. [Google Scholar] [CrossRef]
- General Statistics Office of Viet Nam Monthly Rainfall at Some Stations. Available online: http://www.gso.gov.vn/default_en.aspx?tabid=773 (accessed on 11 June 2018).
- Ndiritu, J.; Moodley, Y.; Guliwe, M. Generalized storage-yield-reliability relationships for analysing shopping centre rainwater harvesting systems. Water 2017, 9, 771. [Google Scholar] [CrossRef]
- Ward, S.; Memon, F.A.; Butler, D. Rainwater harvesting: Model-based design evaluation. Water Sci. Technol. 2010, 61, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Osaka Prefectural Government Daredemodekiru! Tanoshii Amamizu Riyou! (Everione Can Do It! Happy Utilisation of Rainwater!). Available online: http://www.pref.osaka.lg.jp/attach/4725/00112927/jirei.pdf (accessed on 11 June 2018).
- The International Benchmarking Network, The International Benchmarking Network for Water and Sanitation Utilities (IBNET). Available online: https://www.ib-net.org/ (accessed on 19 October 2018).
- General Statistics Office of Viet Nam, The 2009 Vietnam Population and Housing Census: Major Findings. Available online: https://www.gso.gov.vn/default_en.aspx?tabid=515&idmid=5&ItemID=9813 (accessed on 11 June 2018).
- Otaki, Y.; Otaki, M.; Pengchai, P.; Ohta, Y.; Aramaki, T. Micro-components survey of residential indoor water consumption in Chiang Mai. Drink. Water Eng. Sci. Discuss. 2008, 1, 45–70. [Google Scholar] [CrossRef]
- Otaki, Y.; Otaki, M.; Aramaki, T. Potential of efficient toilets in Hanoi, Vietnam. Water Pract. Technol. 2018, 13, 621–628. [Google Scholar] [CrossRef]
- Rosenberg, D.E. Probabilistic estimation of water conservation effectiveness. J. Water Res. Plan. Manag. 2007, 133, 39–49. [Google Scholar] [CrossRef]
- Santos, C.; Taveira-Pinto, F. Analysis of different criteria to size rainwater storage tanks using detailed methods. Res. Conserv. Recycl. 2013, 71, 1–6. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takagi, K.; Otaki, M.; Otaki, Y. Potential of Rainwater Utilization in Households Based on the Distributions of Catchment Area and End-Use Water Demand. Water 2018, 10, 1706. https://doi.org/10.3390/w10121706
Takagi K, Otaki M, Otaki Y. Potential of Rainwater Utilization in Households Based on the Distributions of Catchment Area and End-Use Water Demand. Water. 2018; 10(12):1706. https://doi.org/10.3390/w10121706
Chicago/Turabian StyleTakagi, Kaori, Masahiro Otaki, and Yurina Otaki. 2018. "Potential of Rainwater Utilization in Households Based on the Distributions of Catchment Area and End-Use Water Demand" Water 10, no. 12: 1706. https://doi.org/10.3390/w10121706
APA StyleTakagi, K., Otaki, M., & Otaki, Y. (2018). Potential of Rainwater Utilization in Households Based on the Distributions of Catchment Area and End-Use Water Demand. Water, 10(12), 1706. https://doi.org/10.3390/w10121706



