1. Introduction
Future river discharge predictions have been widely used for flood control, drought protection, reservoir management, and water allocation. However, it is difficult to develop an exact physically based mathematical model to express the relationship between flow discharge and future forecasted precipitations, due to various uncertainties. Owing to a lack of adequate knowledge regarding the physical processes in the hydrologic cycle, traditional statistical models, such as the auto regressive moving average (ARMA) and auto regressive integrated moving average (ARIMA) models [
1], have been developed to predict and generate synthetic data. Nevertheless, such models do not attempt to represent the nonlinear dynamics inherent to the hydrological process, and may not always perform well [
2]. During the past few decades, artificial neural networks have gained considerable attention for time series predictions [
3]. ANNs have been successfully applied to river level predictions and flood forecasting [
4,
5], daily flow forecasting [
6], rainfall-runoff modeling and short-term forecasting [
7], and monthly flow predictions [
8]. The main advantage of using an ANN instead of a conventional statistical approach is that an ANN does not require information on the complex nature of the hydrological process under consideration to be explicitly described in a mathematical form. However, ANN models suffer from overfitting or overtraining, which decreases the capability of the prediction for data far from the training samples.
Another machine learning algorithm that appears to be successful in hydrological predictions is support vector machine (SVM), which is also called support vector regression (SVR) when applied to function approximation or time series predictions. SVMs have been successfully applied to time series forecasting [
9], the stock market [
10] and in particular, water-related applications for the prediction of wave height [
11]), the generation of operating rules for reservoirs [
12], drought monitoring [
13], water level prediction [
14], and short- and long-term flow forecasting [
15], among others. Overfitting and local optimal solution are unlikely to occur with an SVM, and this enhances the performance of SVM for the prediction. A major challenge in the application of the SVM method is the tuning of the parameters of the model and kernels, which severely affects the accuracy of the results [
16]. Applying SVR model in combination with other machine learning models can lead to more accurate predictions [
16,
17] or discharge estimations at ungauged sites [
18]. For this study, a grasshopper optimization algorithm (GOA) [
19] is used and combined with the SVM to enhance the ability of the machine for river-flow predictions.
KNN is another data-driven method, a simple, but efficient, method to model monthly flow [
20] and daily inflow [
21].
The main contribution of this paper is the assessment of different soft-computing methods in a unified platform along with applying Gaussian process regression (GPR) and GOA-SVR models for predicting monthly river discharge as the basis of reservoir management. To evaluate the efficiency of the proposed models, two study area with different input variables are chosen. In the first study area, the input data set involves monthly discharge and temperature, each with three temporal lags, which belong to a period of 18-years (from 1983 to 2004) and in another case study, there are three input variables, including river discharge of three temporal lags which have been observed monthly during 40 years (from 1962 to 1990). The results obtained were compared with those found by different types of artificial neural networks, including feedforward neural networks (FFNNs), time delay neural networks (TDNNs), radial basis neural networks (RBFNNs), recurrent neural networks (RNNs), and a KNN model. The remainder of this paper is organized as follows. In
Section 2, a brief description of the models and their concepts, including the GPR, SVR, GOA, ANN configurations, and KNN, are represented. The case studies used, and their characteristics, are then illustrated in
Section 3. In
Section 4, the models are applied to time series predictions for the two case studies, and the performance of the models is compared in terms of statistical metrics. Finally,
Section 5 offers some concluding remarks and future research issues.
2. Materials and Methods
There are many textbooks and scientific papers in the literature that provide a detailed description of GPR [
22], SVM [
23,
24], neural networks, and their variants [
25] in terms of both theory and application. Hence, in this paper, only a brief description of the applied techniques is given.
2.1. Gaussian Process Regression
Gaussian process regression (GPR) as a statistical method, is a generalization of the Gaussian probability distribution. This method is described as follows:
Consider a training dataset with
n observations
where
is the input variable and
is the target. The principal goal is the estimation of output value
corresponding to the new (test) input
. In the Gaussian process regression, it is assumed that the observations are noisy as
where
is a regression function approximated by a Gaussian process with the corresponding mean
that is often null and the covariance (or kernel) function
. Also,
is the noise that follows a Gaussian distribution
. Thus, the form of GPR model is as follows:
Considering the properties of Gaussian distribution, the marginal distribution of
can be defined as:
where,
is the input data set,
is the set of target values and
is the value of the stochastic function
f calculated for each input variable. There is a joint distribution between outputs
and
as below:
where
,
, and
are the test data set, testing outputs, and identity matrix, respectively. In addition,
,
and
are covariance matrices. The covariance function plays an important role in a Gaussian process regression to specify the similarity among data. There are several types of covariance functions; some of the most useful ones are written in the following:
Squared exponential: ;
Exponential: ;
-exponential: ;
Rational quadratic: ;
Matern 3/2: ;
Matern 5/2: .
where
is the noise variance;
(the length scale parameter),
(the signal standard deviation),
and
are the parameters to be learned. The marginal likelihood is defined according to the Equation (7), where
is the prior and
is the likelihood. The log prior is defined as Equation (8), and the final log marginal likelihood is obtained as Equation (9):
According to the conditional distribution, the prediction process in GP regression for a given test data can be stated as:
where
and
are considered as posterior mean and covariance functions, respectively and defined as:
For more details on GPR algorithm, the reader is referred to [
22].
2.2. SVR
Support Vector Machine is employed as a regression method in which a function is applied to discover the relationship between input and output variables,
and
, respectively.
where mapping the input vector into a high dimensional space is performed by non-linear transfer functions,
ϕ(
x). The most important feature of this space is the possibility of using a simple linear regression function.
W is a coefficient vector and
b represents a bias term.
A set of training data are employed to determine
f(
x) by calculating
W and
b. Then, the obtained coefficients are used to minimize the error function as below equations:
Subject to:
In the training process, the occurrence of the training error is inevitable. Therefore, a penalty term must be considered which is demonstrated by C. and N are the kernel function, and the number of samples, respectively. Moreover, are two indices of slack variables. stands for loss function related to the accuracy of the training process.
Finally, the SVR function can be rewritten as:
where
are Lagrangian coefficients,
is the kernel function. In the following, there is a number of these functions
linear,
polynomial,
radial basis function (RBF) or Gaussian,
sigmoid,
quadratic,
The best SVR parameter values are often selected through a grid search with exponentially growing sequences of parameter values [
23]. Another approach is applying an optimization algorithm. In this paper, GOA is applied to identify optimal values for the SVR parameters. The main steps of this algorithm are briefly described in the following section. The details of the SVR algorithm can be found in [
23,
24].
It is worth noting that there is a relationship between GPR and SVR algorithms. In order to obtain the maximum a posteriori margin (MAP) value of
, presented in Equation (8), the below equation must be minimized:
On the other hand, by kernelizing Equation (13), the objective function can be stated as:
As can be seen, these two optimization problems are similar and by using a particular kernel and likelihood function in GPR model, the SVR model can be derived [
22].
GOA Algorithm
The grasshopper optimization algorithm developed by Saremi et al. [
19] is one of the recent algorithms inspired by grasshopper swarm behavior in nature. Grasshoppers, the insects moving in a network to find food, have a social interaction that leads to one of two type forces: Opposite forces and attraction forces that make possible global and local search, respectively. There is an area called comfort zone, where there is a balanced state between these forces such that they neutralize each other.
To reach the network target, in each step, grasshoppers move in the way so that their position is at the least spatial distance from the target while there must be a balance between local search and global search. Ultimately, after repeating the search steps, grasshoppers meet the optimum position. The mathematical structure of the grasshopper optimization algorithm is as follows:
where:
: the d-dimensional position of the ith grasshopper in the iteration t;
G: the number of grasshoppers;
s: an evaluation function of social interactions;
l: the attractive length scale;
: the upper bound in the d-dimensional functions;
: the lower bound in the d-dimensional functions;
: the distance between the ith and jth grasshoppers;
: is the d-dimensional position of the optimum solution found;
c: the reduction factor to decrease the comfort zone;
In this algorithm, three agents have influences on the new place of each grasshopper: Its current location, the target point, and the situation of other grasshoppers.
2.3. Artificial Neural Networks
Artificial Neural Networks (ANNs) are highly flexible tools commonly used for function approximation and time series predictions. ANNs are typically a collection of neurons with a specific architecture constructed based on the relationship among neurons at different layers. This relatively complex architecture provides a nonlinear mapping from the input to the output space that can be used for a time series prediction. A typical problem of neural networks is overfitting or overtraining of the network arising from the “conformability” of the model structure with the shape of the available data. Overfitting decreases the generalization ability of ANN and degrades the accuracy level of the approximation model for data away from the training data. In this study, the early stopping approach [
26] is used to avoid overtraining of ANN models. It is worth pointing out that this approach requires consistent data availability, and its application is not suggested in cases with sparse data where some alternative methods have better performance. In this technique, the available data are divided into three subsets. The first subset is the training set, which is used for computing the gradient and updating the network weights and biases. The second subset is the validation set. The error in the validation set is monitored during the training process. The validation error normally decreases during the initial phase of training, as does the training set error. However, when the network begins to overfit the data, the error in the validation set typically begins to increase. When the validation error increases for a specified number of iterations, the training is stopped, and the weights and biases at the minimum of the validation error are returned. The test set error is not used during training but is used to verify the generalization capability of the ANN model after training.
Based on the configuration of the network elements, different types of neural networks have been developed, and in this study, three commonly used ANNs, i.e., feedforward NNs, time delay NNs, and radial base NNs were chosen for monthly flow predictions. These networks are briefly described in the following section.
2.3.1. Feedforward Neural Networks
Feedforward neural networks (FFNNs) in this paper refer to multilayer perceptrons (NN-MLPs), which are by far the most popular type of neural networks [
27].
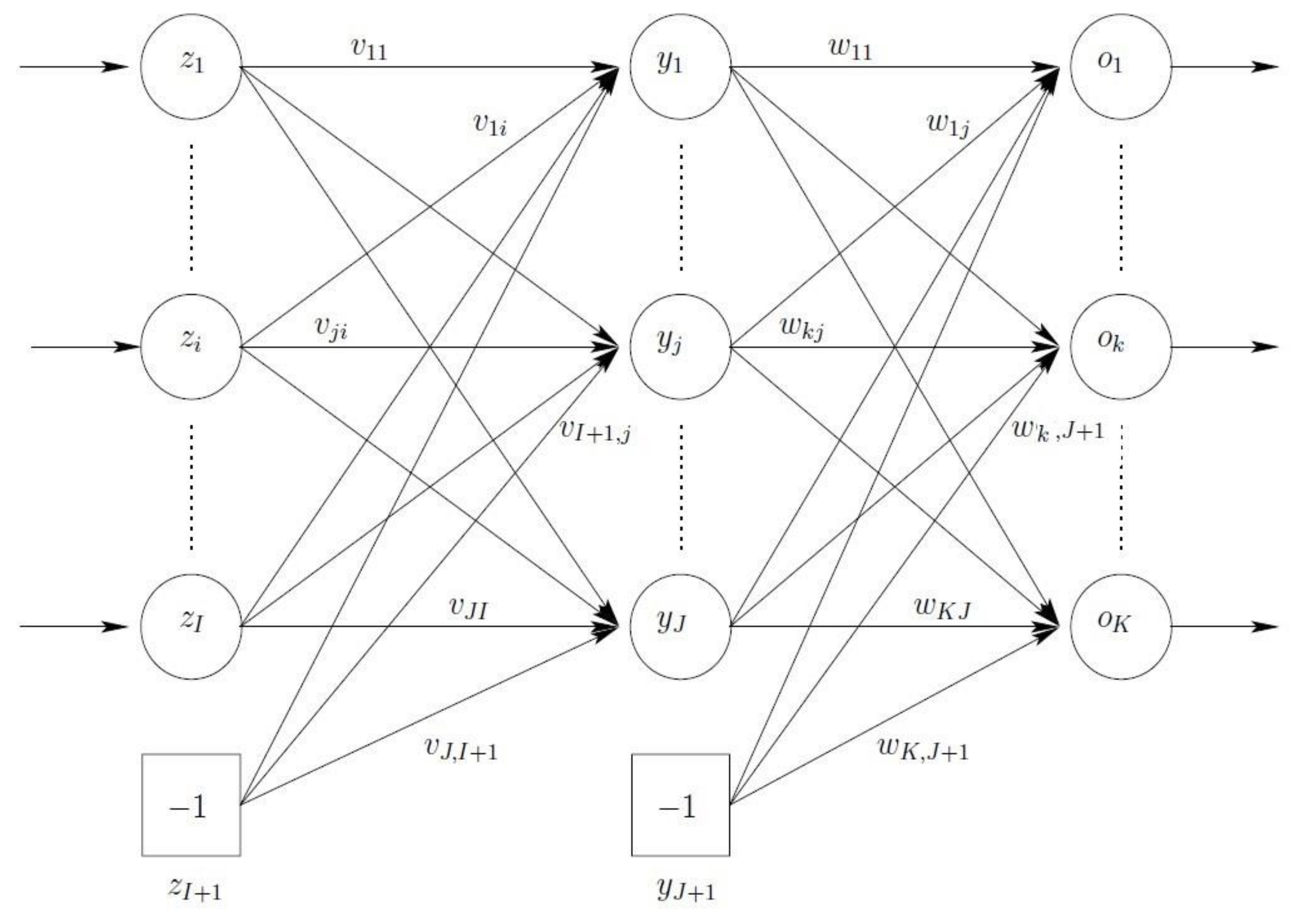
Figure 1 illustrates a standard FFNN consisting of three layers: An input layer (note that sometimes an input layer is not counted as a layer), a hidden layer, and an output layer.
As shown in this figure, the output of an FFNN for any given input pattern
zp is calculated with a single forward pass through the network. For each output unit
ok, we have
where
and
are the activation function for output unit
ok and hidden unit
yj, respectively,
wkj is the weight between output unit
ok and hidden unit
yj, and
zi,p is the value of input unit
zi of input pattern
zp. In addition, the (
I + 1)-th input unit and the (
J + 1)-th hidden unit are bias units, representing the threshold values of neurons in the next layer.
FFNNs with one sigmoidal hidden layer and a linear output layer have been proven capable of approximating any function with any desired accuracy if the associated conditions are satisfied [
28].
In this study, a two-layer feedforward neural network (one hidden layer and one output layer) is used for predicting monthly flows. The number of neurons in the hidden layer, along with the weights and biases, are obtained, based on the errors in the predicted values. Sigmoid and linear activation functions are used for the hidden layer and output layer, respectively. The weights and biases of the network are obtained using a back propagation Levenberg-Marquardt algorithm. After tuning the weights and testing the network, it is used for the prediction.
2.3.2. Radial Basis Neural Network
Radial basis neural networks are referred to as networks that, in contrast to conventional neural networks use regression-based methods and are not inspired by the biological neural system [
29]. They work best when many training vectors are available [
30]. A radial basis function (RBF) neural network (RBFNN) is an FFNN in which hidden units do not implement an activation function, but represent a radial basis function. An RBFNN approximates the desired function through the superposition of non-orthogonal, radially symmetric functions. An RBF is a three-layer network, with only one hidden layer. The output of each hidden unit is calculated as follows:
where
represents the center of the basis function, and
is the Euclidean norm. The output of an RBFNN is calculated as
2.3.3. Time Delay Neural Networks
MLP neural networks only process input patterns that are spatial in nature, i.e., input patterns that can be arranged along one or more spatial axes, such as a vector or an array [
30]. In many tasks, such as a time series prediction, the input pattern comprises one or more temporal signals. Time-delay neural networks (TDNNs) are of the dynamic neural network configurations that can handle temporal patterns of data. A TDNN [
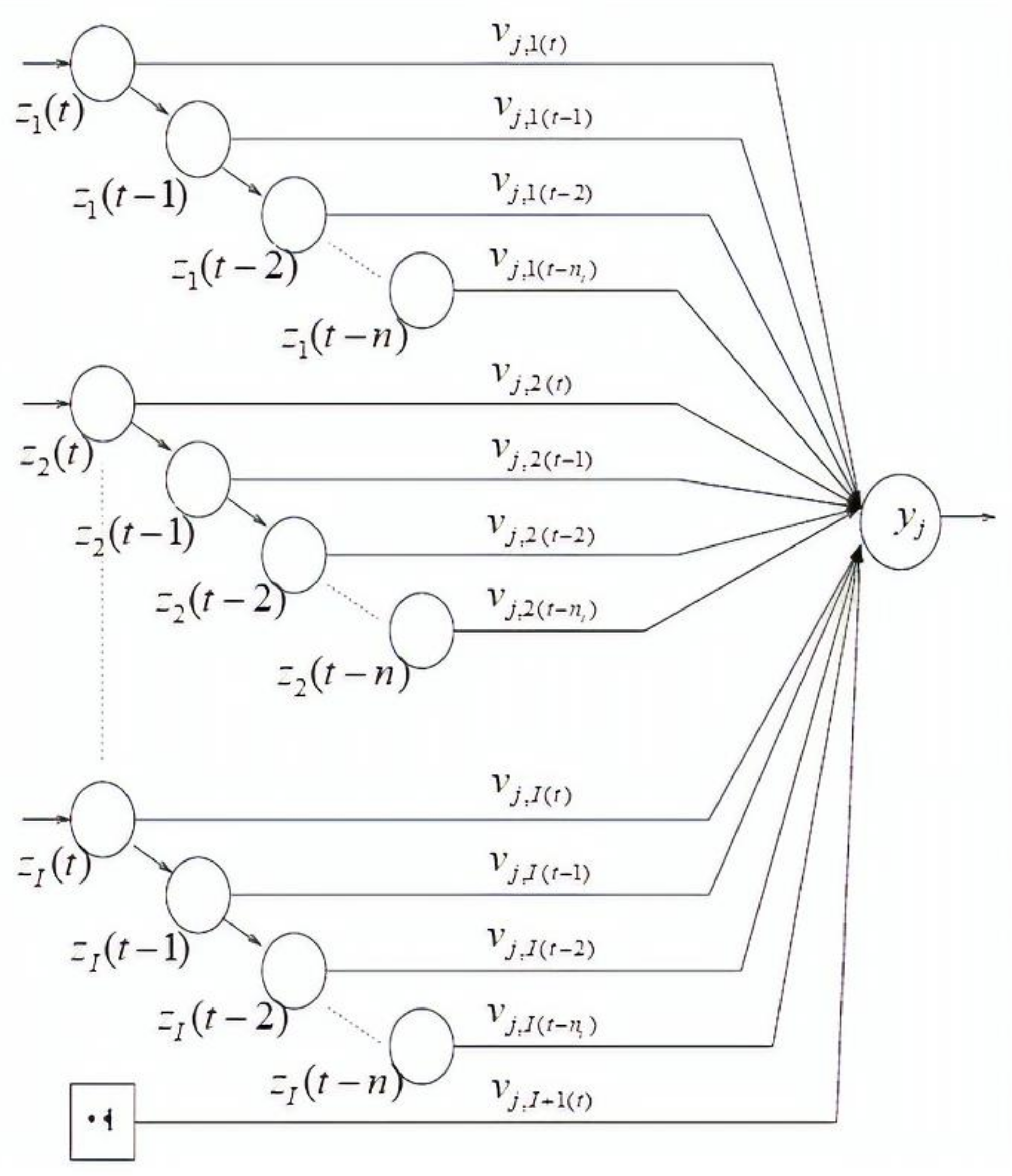
31] is a temporal network in that its input patterns are successively delayed over time. A single neuron with
nt time delays for each input unit is illustrated in
Figure 2. The output of a TDNN is calculated as follows:
2.3.4. Recurrent Neural Network
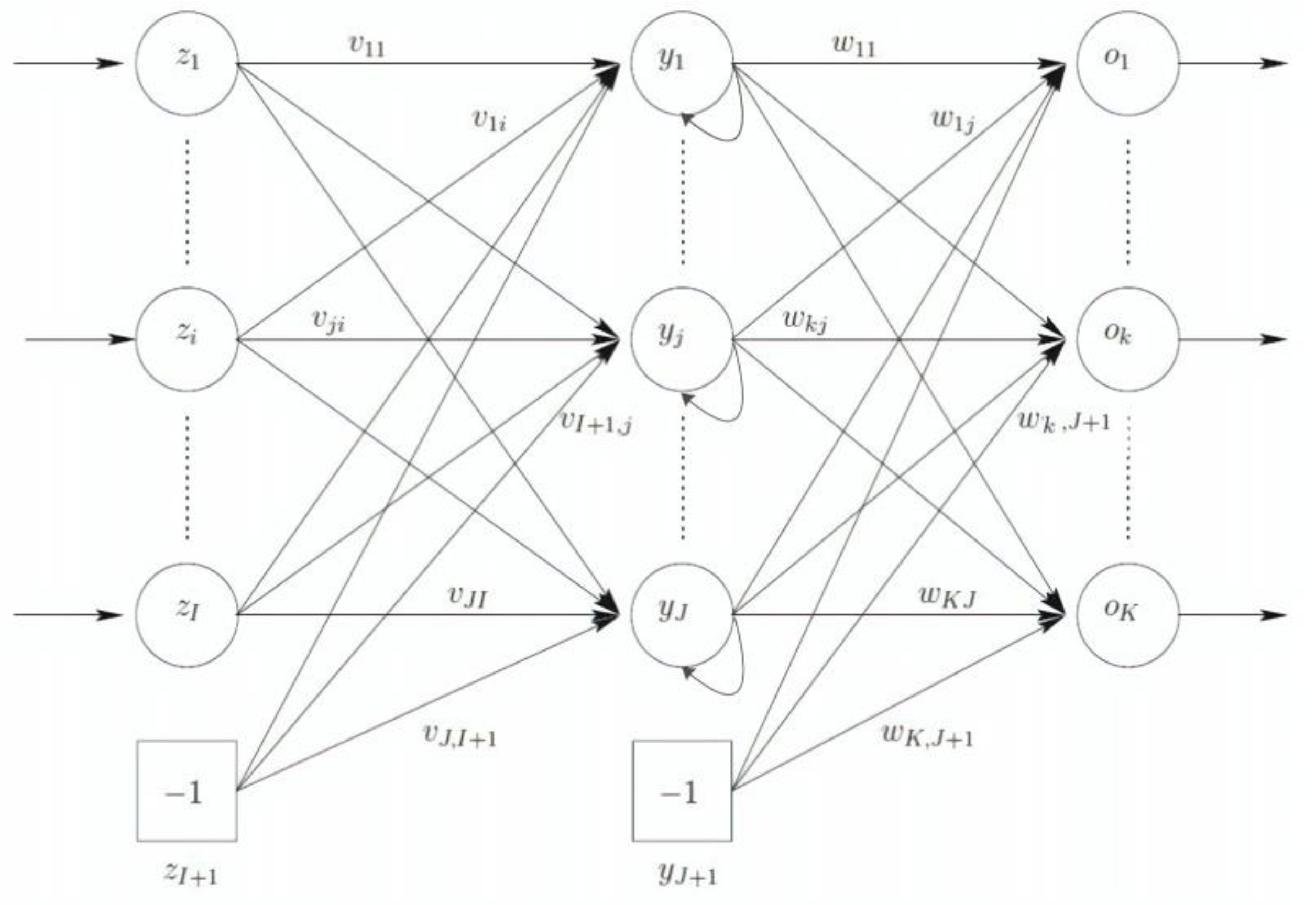
This section is intended for recurrent neural network (RNN) description. RNNs have a feedback loop to enhance the ability to learn from data sets. A simple type of these networks is schematized in
Figure 3. As shown, outputs of the hidden layer, before entering to the output layer, are considered as new inputs with weights equal 1, to the (first) hidden layer. The input vector is therefore [
25]:
Context units
zI+2,…,
zI+1+J are connected to all hidden units
yj (for
j = 1, · · ·,
J) with a weight equal to 1. Thus, the activation value
yj is simply copied to
zI+1+j. Each output unit’s activation is then calculated as [
25]:
where (
zI+2,p, …,
zI+1+J,p) = (
y1,p(t−1), …,
yJ,p(t−1)).
2.4. KNN Model
K-nearest neighbor (KNN) method, one of the nonparametric regression methods, utilizes the own data set to estimate the unknown variables applying the data in the nearest neighbor. Each of the close neighbors, the participants in the estimation process, has own weight which is determined based on its Euclidean distance from the unknown variable. The KNN formulation is presented as:
where
is the amount of the unknown variable,
is the neighbors’ values in the estimation process,
is the Euclidean distance between known and unknown variables, and
is the weight of each neighbor in the estimation process determined as follows:
Since, the number of diverse neighbors, leads to different results, it is important to find the best number of neighbors. Here, the choice of the various number of neighbors leads to relatively similar accuracy and the optimal value of K, considered as 7, has been obtained through a trial and error process with an accuracy of in terms of the correlation coefficient.
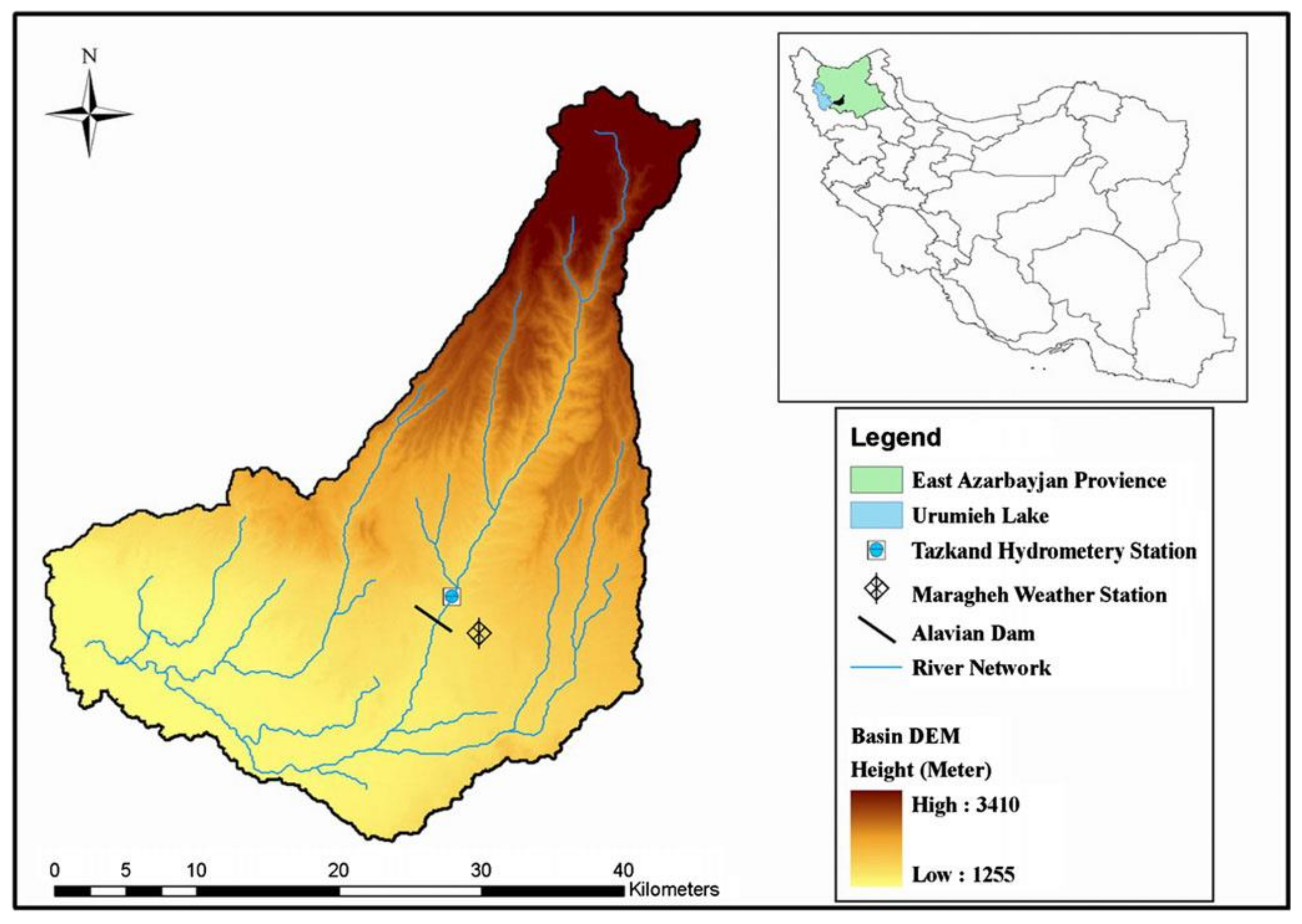
For the Alavian Basin, both the temperature and discharge data are available from the recorded data from Maragheh Station. Therefore, the monthly discharges and temperatures with three temporal lags, i.e., Q(t − 2), Q(t − 1), Q(t), T(t − 2), T(t − 1), and T(t), are considered as input variables to predict the next month’s discharge of the river, Q(t + 1), as the output variable. To assess the performance of the models, the observed time series datasets were divided into two independent subsets, namely, training and verification subsets. The training sets were used to learn the GPR, the SVR, and ANNs for prediction, whereas the verification sets were used to verify the ability of the models for prediction. The dataset from June 1983 to November 1996 (75% of the data) was selected for training, whereas that from December 1996 to June 2001 (the remaining 25%) was used for verification.
4. Results and Discussion
To employ the GPR for monthly flow prediction, a rational quadratic function was chosen as the appropriate kernel function and the basis function was considered as constant. The related parameters for the rational quadratic kernel were acquired as
,
, and
. To use the SVR for prediction, the SVR algorithm was coded in MATLAB, and a GOA algorithm was then utilized to identify the best values for the SVR parameters.
Table 1 shows the suitable parameter values of the GOA algorithm.
Support vector regression with quadratic kernel function was considered for prediction process. The optimal parameters for the quadratic kernel were obtained as and .
For the training of neural networks, as mentioned, the observed data were divided into three subsets: Training, validation, and test datasets. The previous verification data (from December 1996 to June 2001) used for the evaluation of the SVR are considered the test data of the ANNs. A portion of the remaining data (20%) is randomly selected as the validation dataset, and the other portion is used for training the networks (tuning the weights and biases). In order to avoid overfitting, K-fold cross-validation with k = 5 is used in all methods.
To select a suitable architecture, different architectures are checked; however, when considering different architectures, the arrangement of the training, validation, and testing data are not changed. Furthermore, the training of all architectures is started with the same initial weights and biases. The candidate architecture is constructed by only one hidden layer, and the network is allowed to incrementally increase the numbers of its neurons within a suitable range. This range depends on the amount of data available for training, and five to 20 neurons are considered herein. After stopping the training process, errors in the network, including (training + validation) the dataset and test dataset (also referred to as verification data), are checked and the network with the minimum level of error is chosen for a time series prediction.
For both the FFNN and TDNN, the best architecture was obtained as a network with 14 neurons in the hidden layer. For the RBFNN, the number of neurons was equal to the number of experimental pairs of training data, and the Gaussian function parameter was determined by the user through trial and error. Moreover, for the RNN, the best network contains 9 hidden neurons.
To compare the performance of the described techniques for a monthly flow prediction, several statistical metrics, including
R, MRAE, MAE, AME, MSE, RMSE, and E, were considered. These metrics and their values are tabulated in
Table 2 and
Table 3 for the training and verification datasets, respectively. All metrics have an ideal value equal to zero except for
R and E metrics, whose ideal value is 1.
In the first case study, the KNN model has the best performance according to the residual criteria for the results of verification data, including R, MSE, RMSE and E. Among the neural network models, RNN model has the highest correlation coefficient and the other predictors, i.e., FFNN, TDNN, and RFBNNs, showed almost the same level of performance in this case and SVR-Quadratic with optimal parameters, could not improve the prediction accuracy. In the models, such as ANNs, SVR, and GPR where there is a training step, as the number of noisy input variables increases, the prediction accuracy decreases. The KNN model, unlike other techniques, has no training process.
Figure 6 shows scatter plots of the observed discharges versus the predicted discharges during the training (left) and verification (right) periods for the five prediction models. This figure also confirms the KNN forecasting method has the desired performance based on the value of the correlation coefficient. In order to provide a visual comparison between the applied models, the results of the correlation coefficient (R), the most important criterion in the process of choosing the best model, are reported in the form of a bar histogram in
Figure 7.
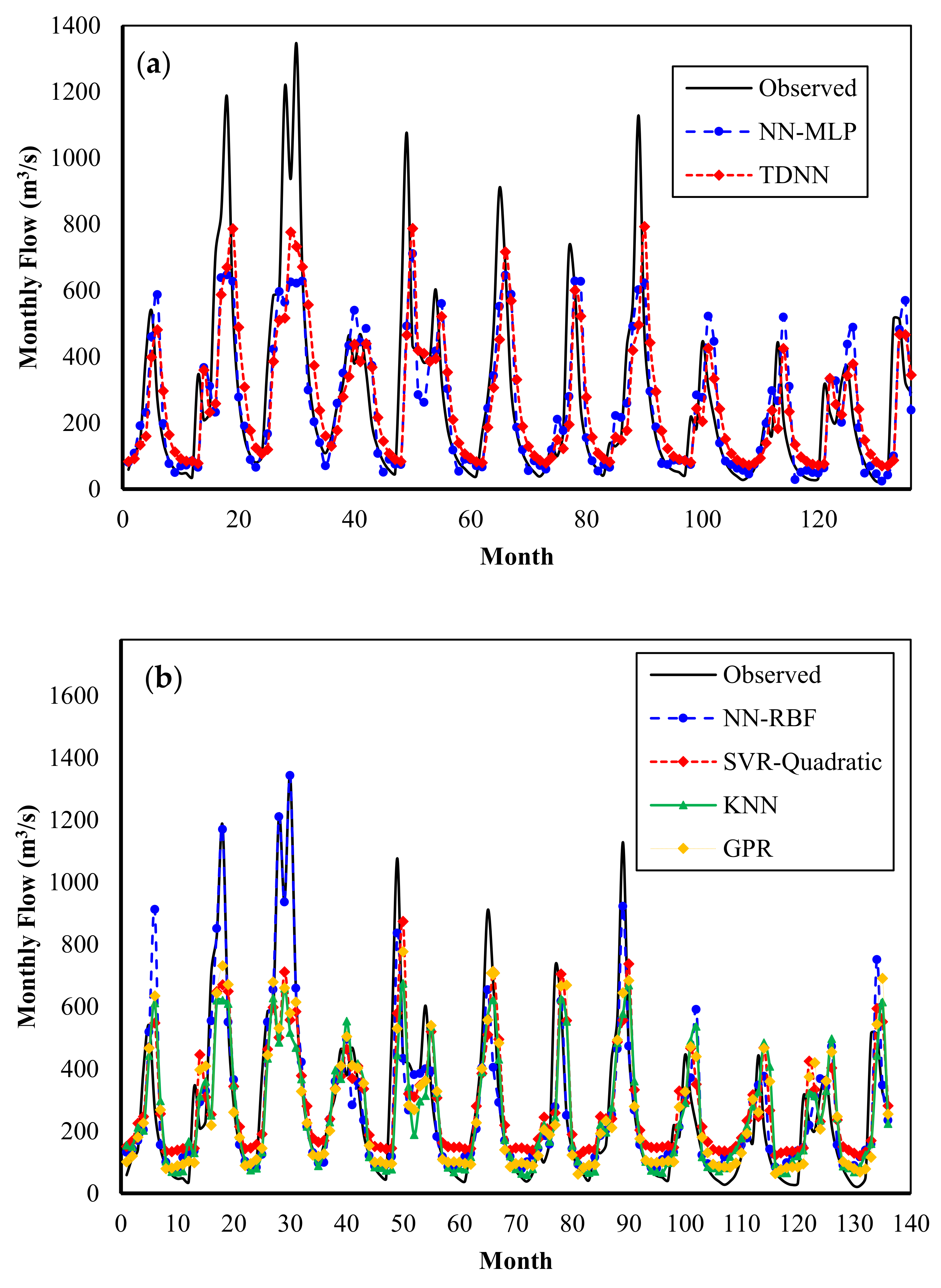
Figure 8 compares the flows predicted by the models with the flows observed during the verification periods. It can be seen that the RNN and RBFNN models produce mostly the same results, whereas the TDNN model has slightly worse prediction for low flows. Again, the KNN model shows highly accurate predictions, whereas less accurate results are obtained by the SVR with quadratic kernel.
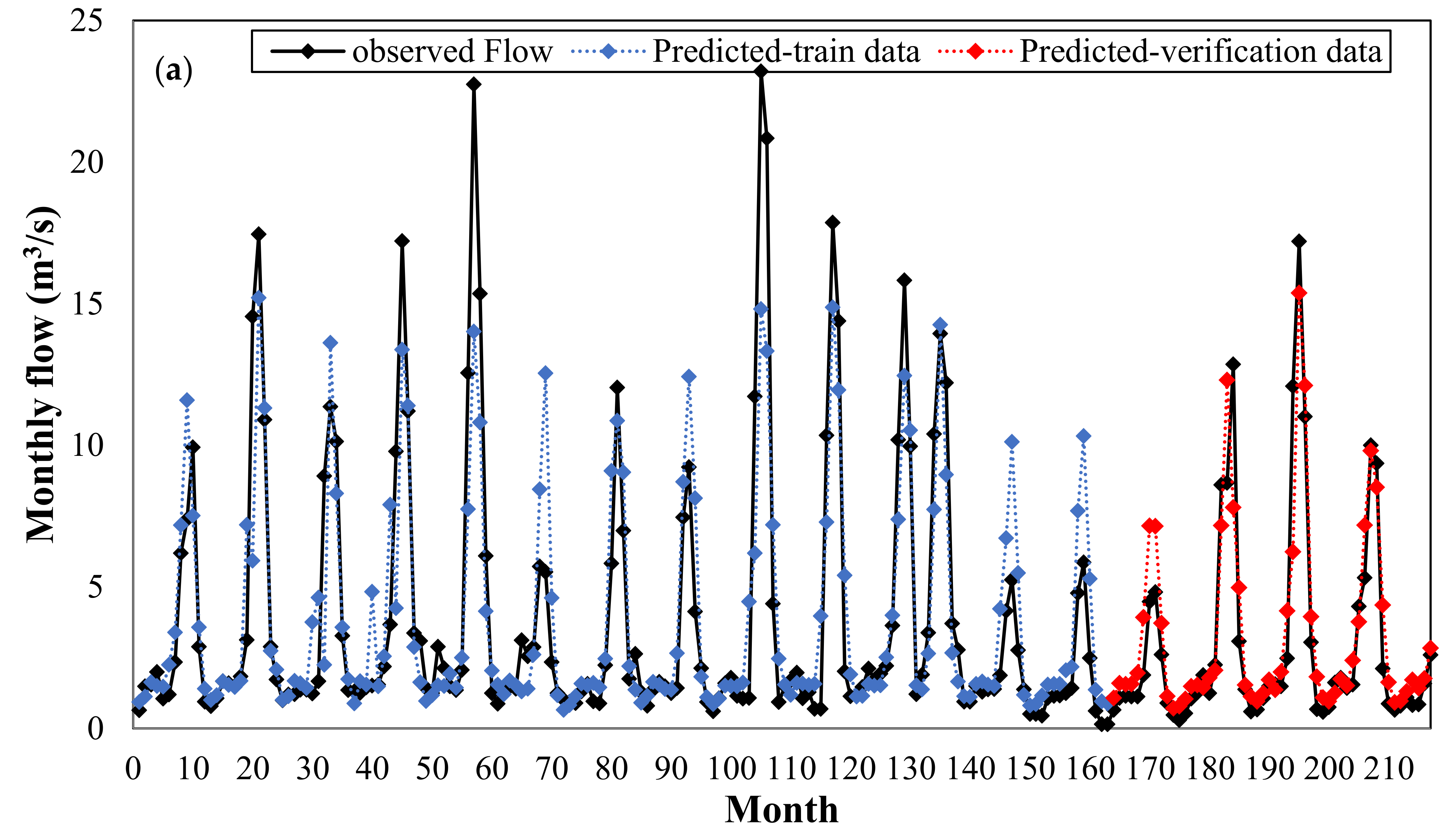
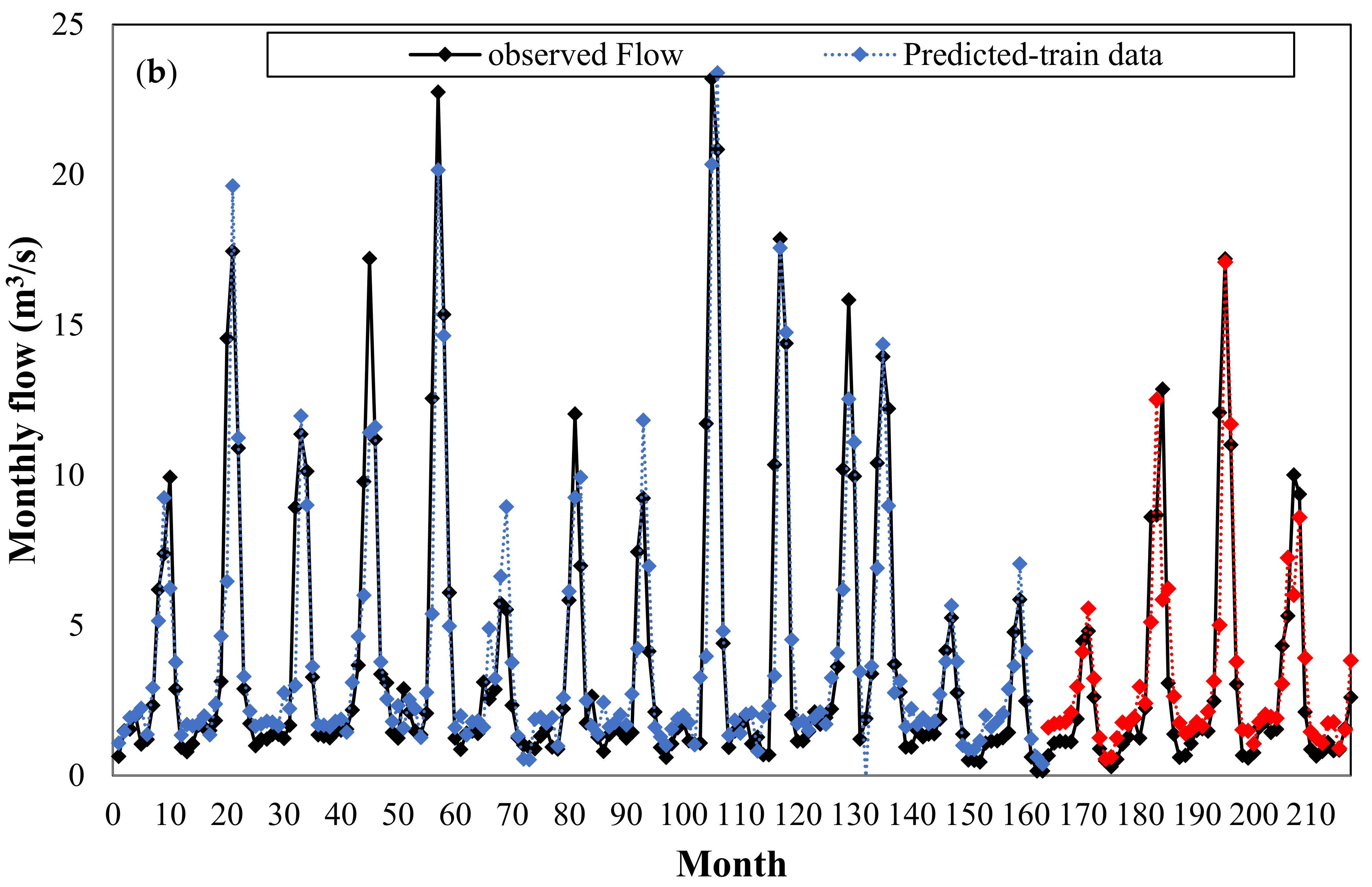
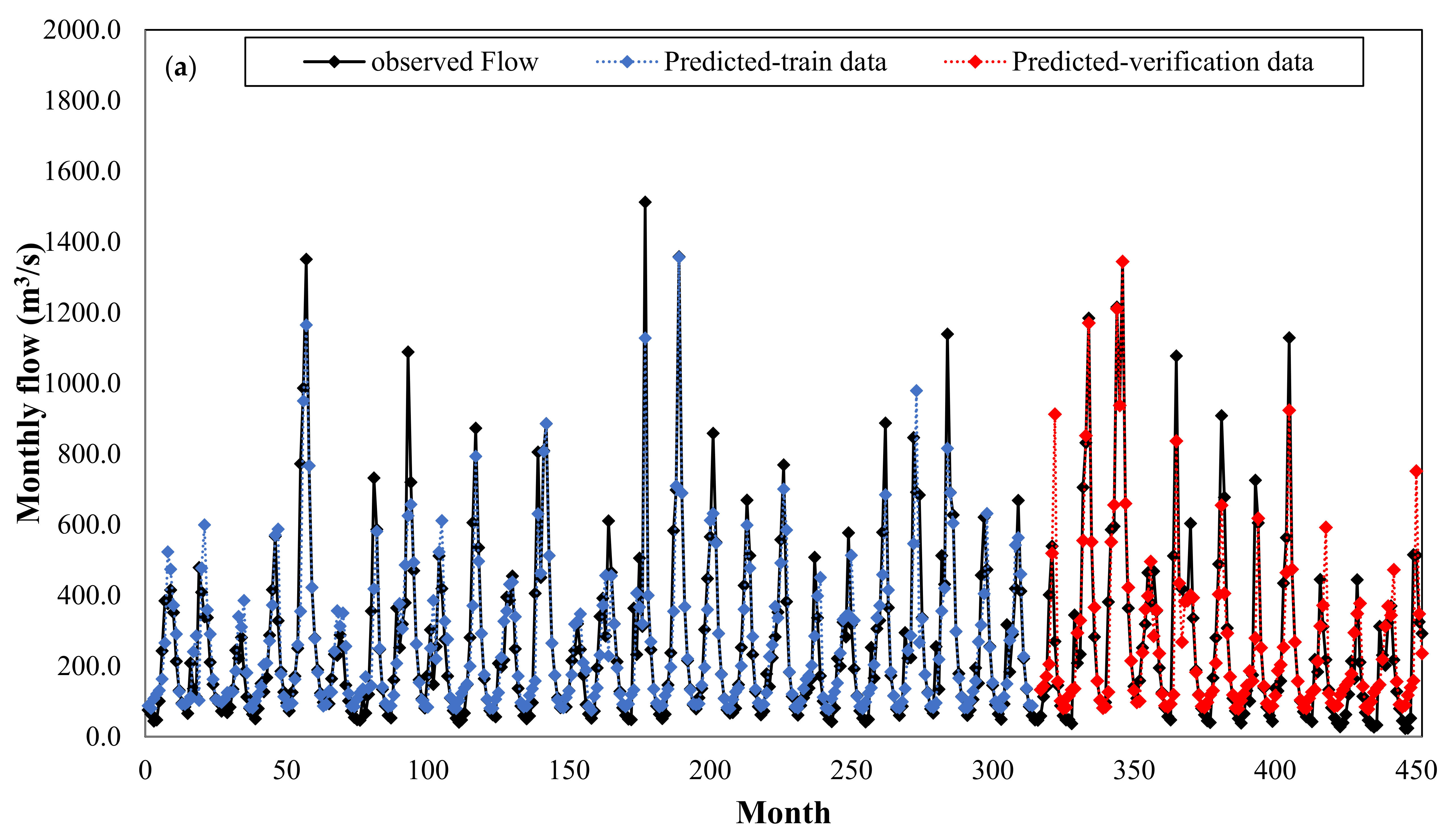
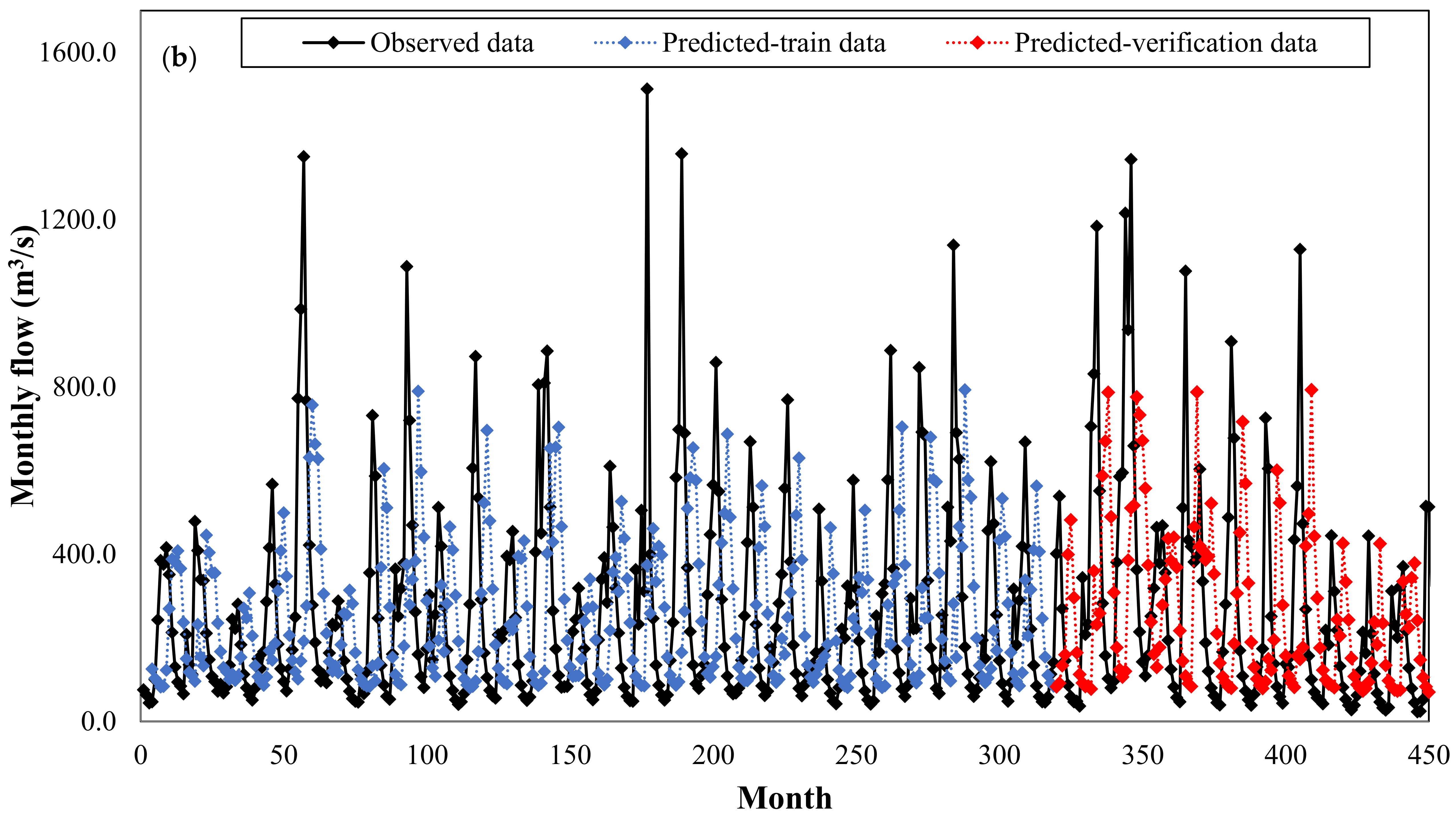
Figure 9 plots the observed and predicted flows by KNN model versus the whole time series period for June 1983 to June 2001 (during both the training and verification periods). This figure clearly demonstrates the high capability of the KNN model for predicting a monthly discharge.
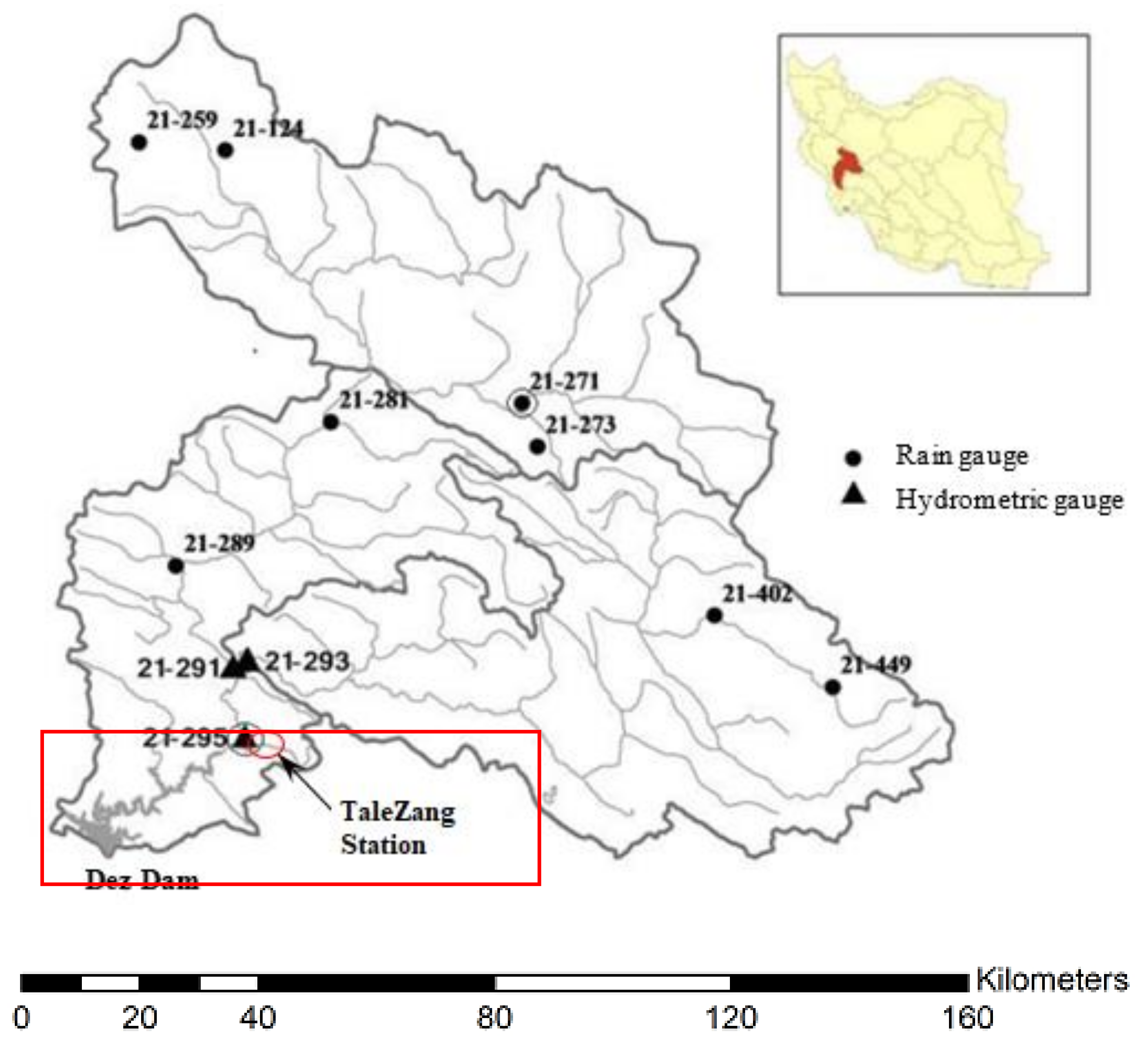
The second case study was conducted on the Dez River Basin, which has considerably higher flow regimes and longer periods of observed data than the previous area. For this case, the only type of data available was on the monthly discharge, and thus monthly discharges with three temporal lags, i.e., Q(t − 2), Q(t − 1), and Q(t), were used as the input variables to predict the next month’s river discharge, Q(t + 1), as the output variable. In this case, the dataset from April 1962 to August 1988 (70% of the data) was selected for training, whereas the dataset from September 1988 to November 1999 (the remaining 30%) was used for verification.
To apply the GPR for monthly discharge prediction, the model with a squared exponential kernel function and a constant basis function was selected as the proper regression model. The related parameters for the rational quadratic kernel were acquired as and .
The optimal parameters for the SVR with a quadratic kernel were obtained as and . The best architecture for the FFNN, TDNN, and RNN models was obtained for networks with 14, 10, and 37 neurons in the hidden layer, respectively.
The results of training and verification based on residual metrics are shown in
Table 4 and
Table 5, respectively. Here, the best performance is by the RBFNN model based on
R, AME, MSE, RMSE and E criteria. The RBFNN model showed the better performance because in this case study there were more observed data, and RBF networks perform better than other NNs as there is a large number of training vectors available [
30].
Comparing other neural network models, it is evident that RBFNN has the best performance according to the and E criteria. Furthermore, the results of R, MSE, RMSE and E criteria from these two case studies also show that the FFNN outperforms the TDNN. This means that establishing a static neural network (or FFNN) with independent input variables of the time lags is more successful for time series prediction than time delay network configurations, which have a smaller number of input variables, but with delay signals.
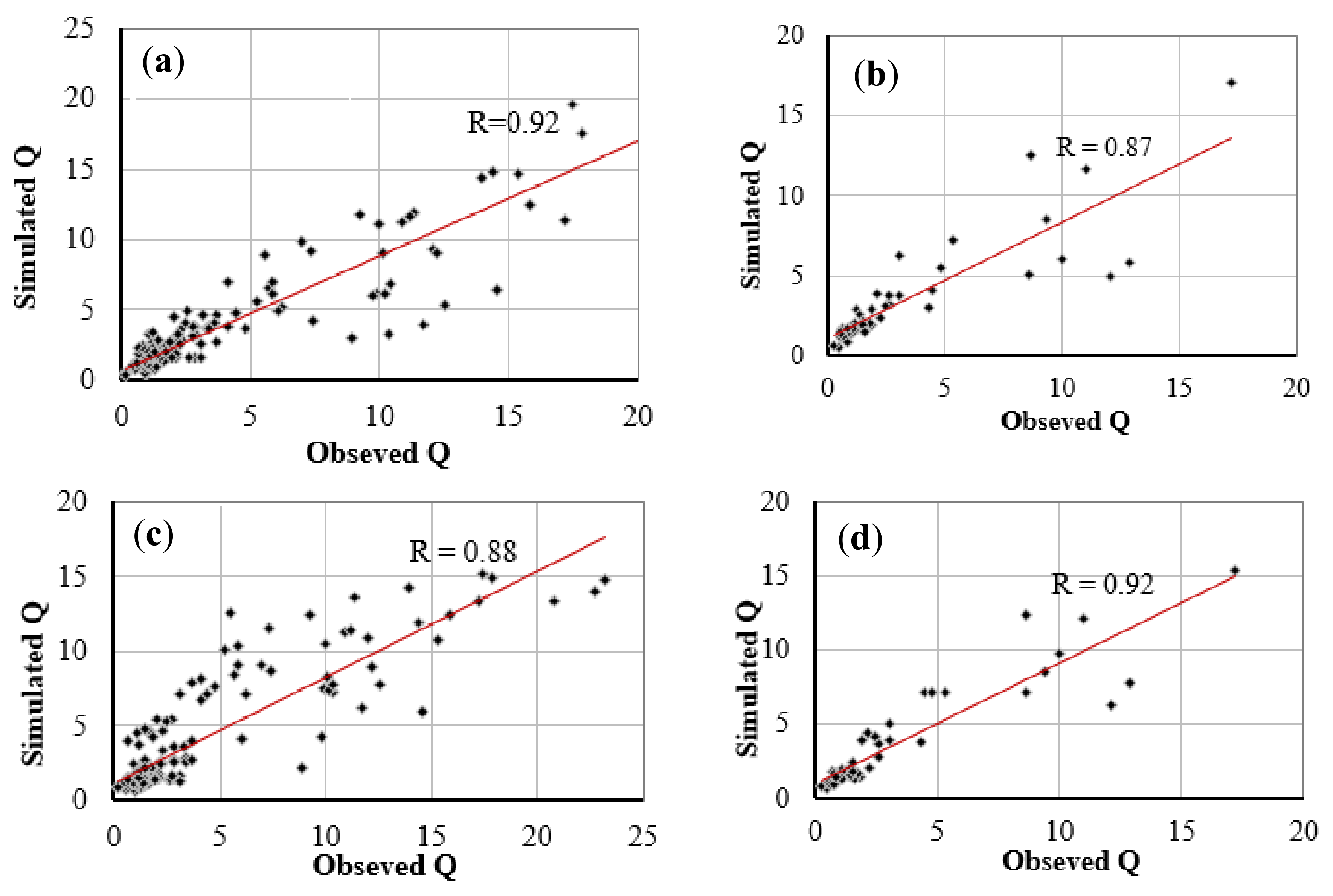
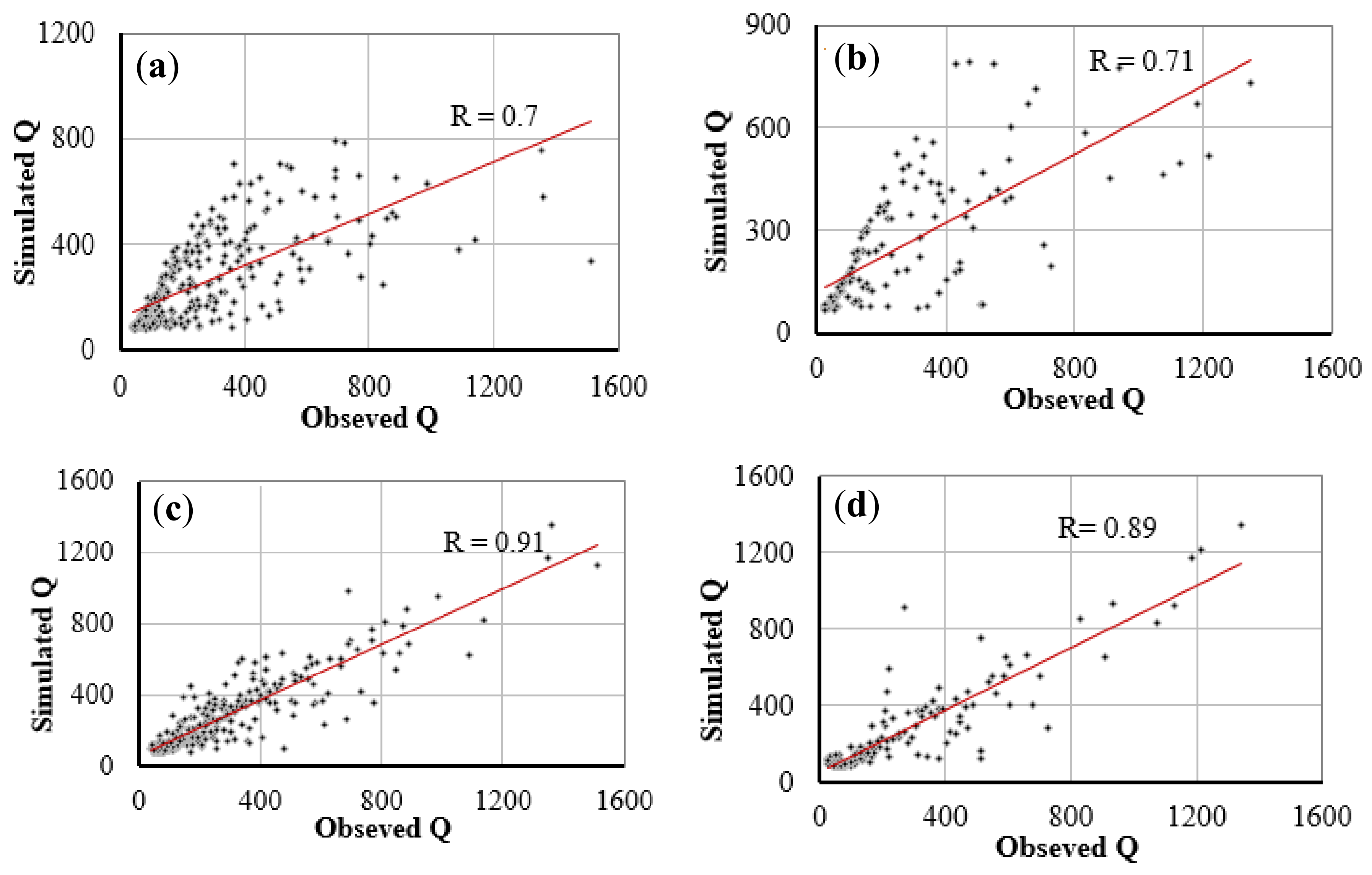
Figure 10 shows the scatter plots of observed discharges versus the predicted discharges during the training (left) and verification periods (right), and the correlation coefficient for the best and the worst prediction models. The RBFNN method is also more accurate in terms of the correlation coefficient. As displayed in
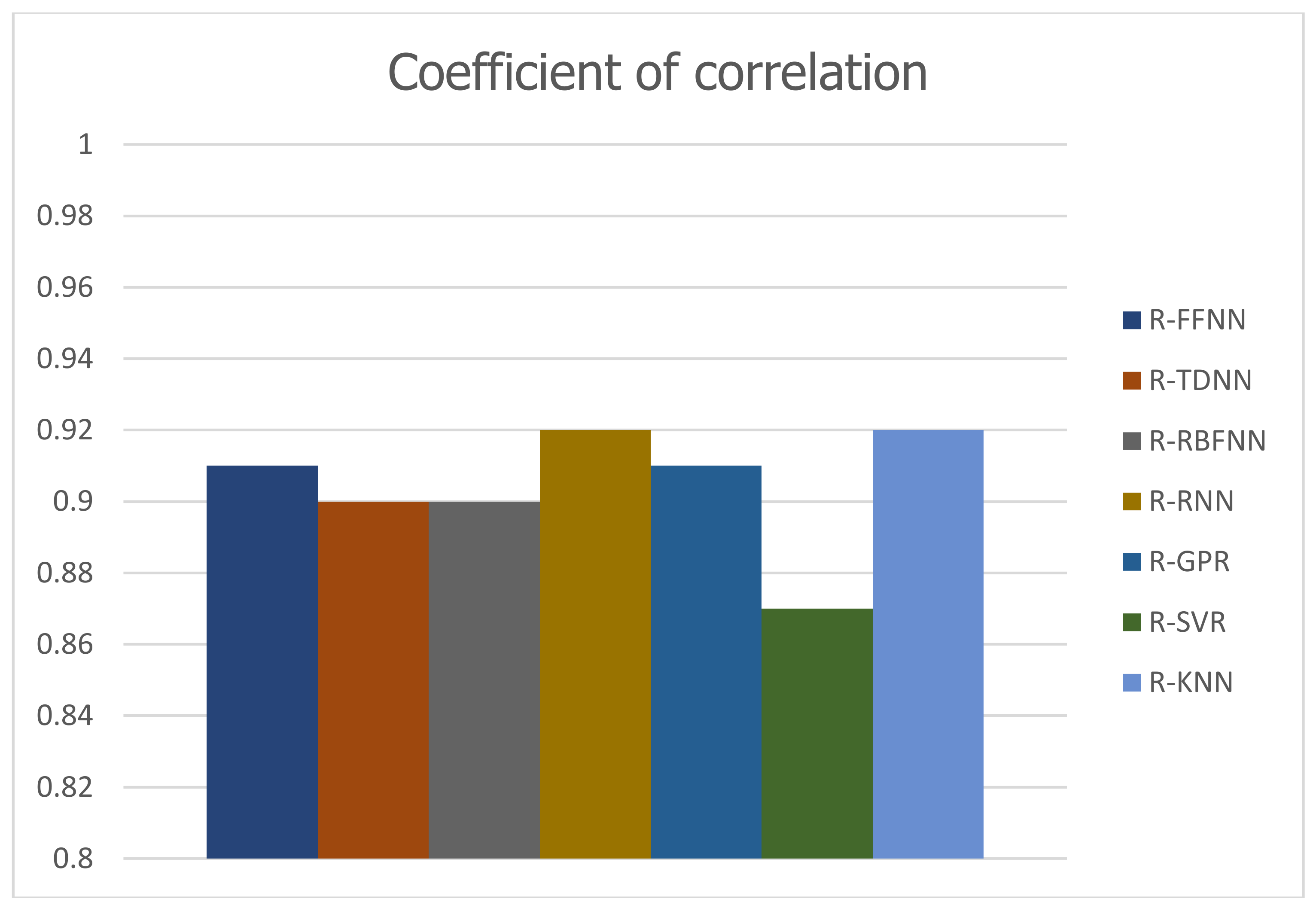
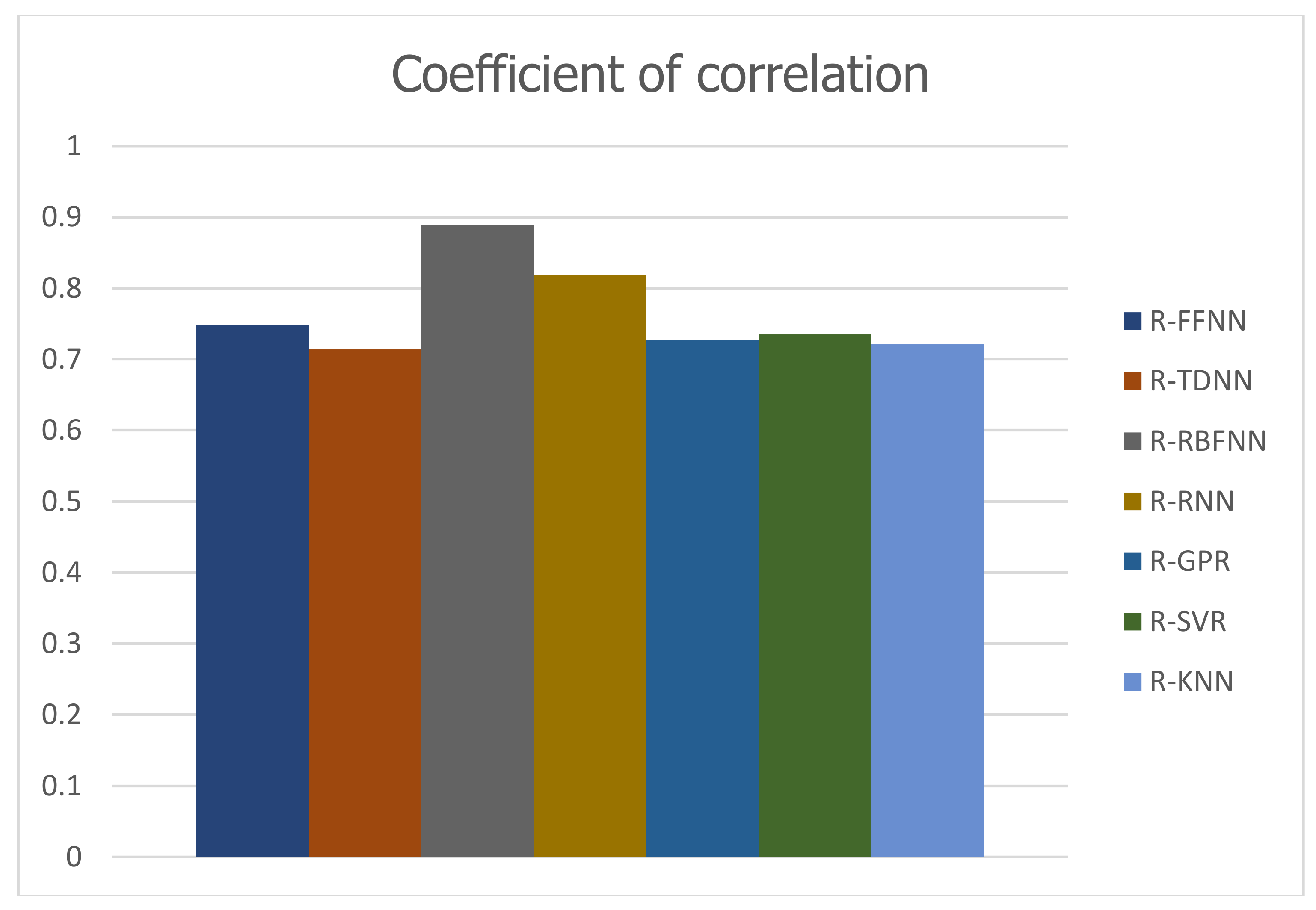
Figure 11, the bar histogram of correlation coefficient values acquired from various models shows the best performance of NNRBF model.
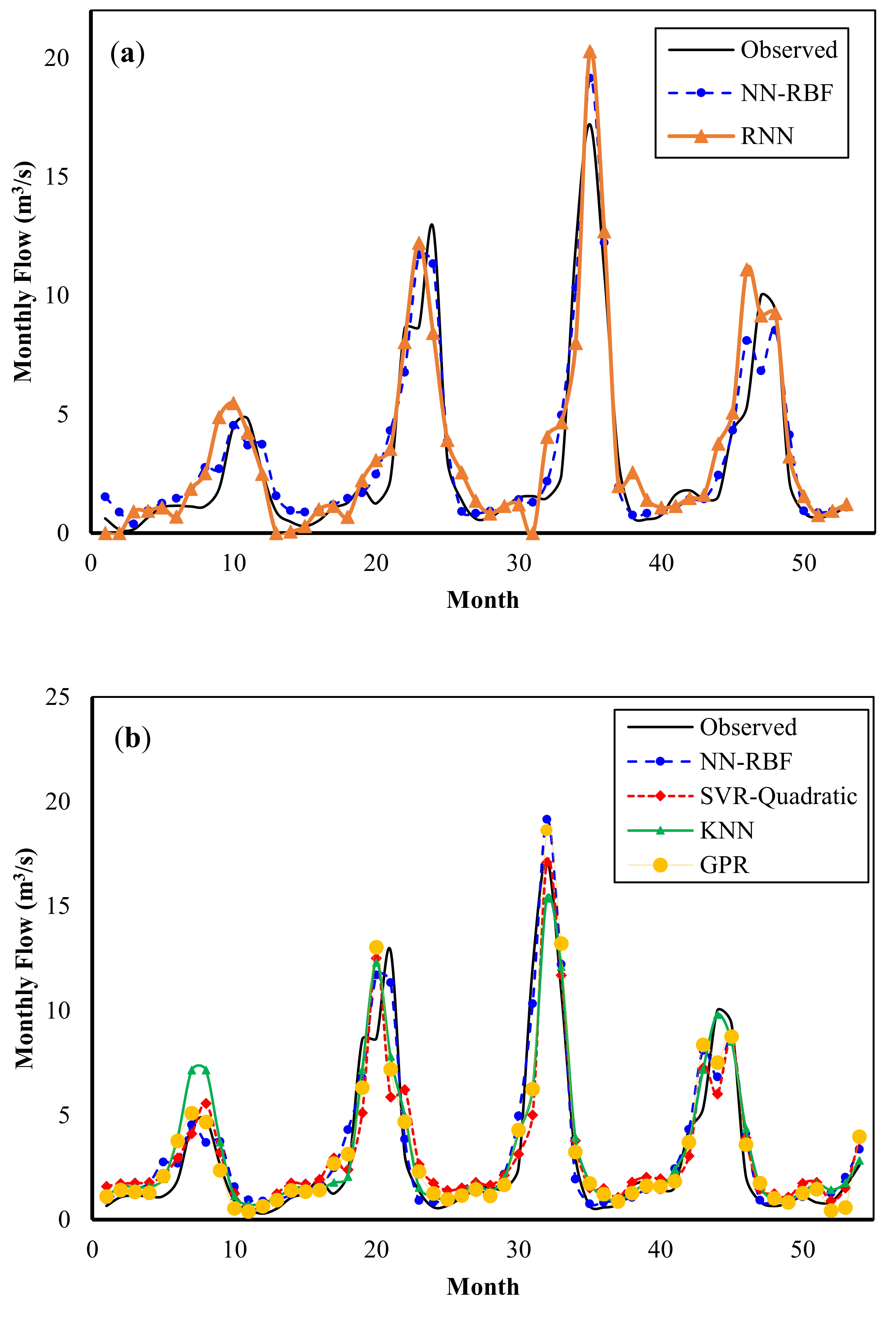
Figure 12 shows a graphical comparison of the observed data and the results of the prediction models for the verification period in Dez Basin. The FFNN and TDNN models show a relatively suitable prediction for median and low flows, but their prediction capability for extreme flows is poor. The RBFNN model predicts extreme flows slightly better than the two previous models. Although the GPR, SVR-Quadratic, and KNN models have the relatively same prediction quality, their prediction performance is weaker than the RBFNN, FFNN, and RNN models.
Figure 13 shows the observed and predicted discharges of the RBFNN model for the whole time series, from April 1962 to November 1999.
5. Conclusions
In this study, GPR and GOA based SVR models were applied to predict long-term river flows in Alavian and Dez Basins based on historical records. Five other machine learning algorithms, i.e., feedforward neural network, time delay neural network, radial basis neural network, recurrent neural network, and KNN were also established to verify the capability of these algorithms for discharge prediction. Through a comparison of the results based on the value of the coefficient of correlation, it was found that the KNN model, without any training process in which a part of noisy data is used to train the model, and RBFNN model can provide more accurate predictions for Alavian and Dez Basins, respectively. In the first study area, Alavian Basin, where there were six predictor variables, the KNN and RNN models have the maximum correlation coefficient in comparison to other models. Based on MRAE criterion for the verification data, the FFNN model is the most accurate prediction model and the GPR has a better performance than the SVR-Quadratic and KNN models. In the first study area, KNN has the lowest prediction error in terms of MAE and MSE criteria. In addition, FFNN with a lower value of MAE and MSE criteria than TDNN, RBFNN, RNN, GPR, and SVR-Quadratic, provides more accurate predictions. Also, the RNN model has less predictive accuracy in terms of MRAE, MAE, and RMSE than FFNN and RBFNN models in Alavian Basin. In the second case study, Dez Basin with more observations, but fewer features, in comparison to the first study area, the RBFNN model has been selected as the best predictor model based on correlation coefficient (R) criterion for the verification data. Although, the SVR model linked with a powerful optimizer, i.e., the GOA algorithm to identify the SVR parameters, leads to more accurate predictions than the GPR and KNN models in terms of R criterion, but it was not precise enough for extreme point predictions and based on MAE criterion, it has undesirable performance in comparison to other prediction models. In the study area according to MAE, AME and MSE criteria, RBFNN has more accurate predictions than FFNN, TDNN, RNN, GPR, SVR-Quadratic, and KNN. Furthermore, the RNN model has a higher prediction error in terms of MRAE, MAE, AME, and MSE in comparison to FFNN and RBFNN models in Dez Basin. Considering AME, and RMSE, the GPR model has a more accurate prediction than the SVR-Quadratic and KNN models.
As a result, comparing the results of the current study, developing a GOA-SVR model, with many of previous ones indicated that the GPR and SVR models are not always the best estimators in time series prediction.
Applying other optimization algorithms, suggested for future researches, can affect the model efficiency. Furthermore, changing the time step of observations (e.g., using daily data instead of monthly ones) is proposed as another suggestion for future studies that may vary the derived results from various models.