Abstract
Seasonal forecasting is a fast-growing climate prediction application that puts into practice the latest improvements in the climate modeling research. Skillful seasonal forecasts can drastically aid practical applications and productive sectors by reducing weather-related risks such as water availability. In this study two operational seasonal forecasting systems are tested in a water resource important watershed on the island of Crete. Hindcast precipitation and temperature data from the European Centre for Medium-Range Weather Forecasts (ECMWF) System 4 and Met Office GloSea5 systems are tested for their forecast skill up to seven months ahead. Data of both systems are downscaled and corrected for biases towards the observations. Different correction methods are applied and evaluated. Post-processed data from these methods are used as an input to the hydrological model HYPE, to provide streamflow forecasts. Results show that a prior adjustment of the two systems’ precipitation and temperature may improve their forecast skill. Adjusted GloSea5 forecasts are slightly better estimates than the corresponding forecasts based on System 4. The results show that both systems provide a skillful ensemble streamflow prediction for one month ahead, with the skill decreasing rapidly beyond that. Update of the initial state of HYPE results in the reduction of the variability of the ensemble flow predictions and improves the skill but only as far as two months of forecast. Finally, the two systems were tested for their ability to capture a limited number of historical streamflow drought events, with indications that GloSea5 has a slightly better skill.
1. Introduction
Seasonal forecasting has advanced in the last decade. With improved skill, seasonal forecasting is able to provide valuable information to management authorities. Exploiting forecasts can result in better anticipation of water- and climate-related risks in the near future and improved preparedness. At a regional scale, examples can be found in the management of European hydrological extremes [1,2] and the European Forest Fire Information System (EFFIS) [3], as well as in triggering risk reduction and relief actions in flood prone areas [4]. Along with these advances, there is a growing pool of recent research that assesses forecast skill at regional or watershed level [5,6,7,8]. Seasonal streamflow forecasting is a challenging task for climate forecast systems, but also for pre-hydrological simulation processing methods. Marco et al. [9] assess seasonal forecasts of the inflow and outflow of a reservoir in northeastern Spain, finding that the skill in inflow prediction is limited to the first month of the forecast. In a pan-European work, Pechlivanidis et al. [7] analyzed the skill of streamflow forecasts across a large number of sub-basins in Europe using the E-HYPE hydrological model. They found that the forecasting system exhibits good performance in water volume estimation in the majority of the tested basins, with the skill to deteriorate with increasing lead-time, especially in central Europe and Mediterranean regions. The majority of the aforementioned studies consider a prior downscaling and adjustment of the climatological biases for the forecasted variables prior to their use in the impact models. These biases are a result of the incomplete representation of the physical processes of the climate system into the forecast models, as well as scale mismatch between the forecasting system and the region of interest. As an indicative example, the operational forecasting system of the European Centre for Medium-Range Weather Forecasts (ECMWF) System 4 (S4) [10], operates on a ~0.7° × 0.7° grid, while Crete, the fifth largest island in the Mediterranean Sea that consists of more than 100 small and very small watersheds, has an approximate size of 0.5° × 3°. Added to that, the elevation of the Cretan watersheds varies between sea level and 2500 m, generating orographic precipitation [11,12,13]. Furthermore, the raw climate (and consecutively seasonal) model data cannot be used in hydrological applications due to scaling effects resulting in unrealistic results [14]. A variety of adjustment methods have been presented and assessed in the literature for seasonal forecast applications [5,6,15]. Among them is quantile mapping, which has been primarily used for processing climate model output. From a climate perspective, quantile mapping has been found to outperform other methods for hydrologic impact studies [16]. Tian et al. and Zhao et al. [17,18] discuss the effectiveness of quantile mapping in forecast applications of precipitation and temperature. They conclude that while they are highly effective in bias removal, they exhibit limitations in adjusting forecast-related issues. Furthermore, quantile mapping, as well as additive/multiplicative bias correction methods, have been found to be ineffective in cases in which a forecast system is unskillful [18,19].
Beyond post-processing of climate data, a critical element in the hydrological predictability at the seasonal time scale is the initial land surface conditions (ICs) for water storage, i.e., snow and soil moisture [20,21]. Surface soil moisture, in particular, affects the percolation rate of precipitation, and hence runoff generation is a significant element of the initial conditions [22,23,24]. A number of studies [25,26,27] have analyzed the initial conditions effect on a global scale, finding that their role is very important. However, this impact varies with the region, the season and the lead time.
Hydrological forecast skill is estimated by comparison between the discharge of the forecast data simulation and the observed discharge or, alternatively, by comparison of the former to hydrological simulation using observed climate forcings. The former approach derives the real skill of the weather forecast and hydrological simulation modelling chain. In the latter approach, the theoretical skill of the forecast is estimated [28,29,30], precluding the hydrological model deficiency from capturing the actual hydrological regime.
There are two major techniques for modelling and forecasting of hydrological systems. These are the process-based and data-driven models. The major difference in these approaches is that process-based techniques conceptualize the hydrological processes while data-driven techniques describe the behavior of hydrological processes by considering limited assumptions about the underlying physics of the system being modelled [31]. Data-driven models have been applied in the literature with great success, and multiple linear regression and autoregressive models, in particular [32,33]. Process-based models have been shown to be powerful tools to reproduce and understand system fluxes and state dynamics [34]. This is particularly true for understanding and assessing the impact of initial conditions to the model performance.
Many studies [35,36,37,38] have outlined the outlook of negative climate change impacts in the water resources of the eastern Mediterranean regions, identifying potential negative effects on key economic activities, such as agriculture [39,40], tourism [41,42,43] and energy [44], as well as noteworthy increases in water-related vulnerability [45,46,47]. In this context, skillful seasonal forecasting is becoming an indispensable tool to mitigate the forthcoming climate change effects on water resources management of the Mediterranean region. To this end, this study aims to assess the forecast skills of two seasonal forecast systems for estimating the 1 to 7 months lead-time runoff on a small Mediterranean catchment on the island of Crete. Predictive skill is assessed through the analysis of the hindcast simulations of the two systems. Potential improvements from the pre-processing of the meteorological data are evaluated, as well as the effect of the initialization of the hydrological model state. Finally, the results are assessed for their skill to predict the streamflow drought state and a small number of historical streamflow drought events.
2. Materials and Methods
2.1. Hindcast Data
Daily precipitation and temperature hindcast data from the ECMWF S4 [10] and the UK Met Office’ system GloSea5 [48] were utilized for this study. The data were available from between 1981 and 2015 for ECMWF S4 and 1996–2010 for GloSea5. The data were bilinearly interpolated at sub-basin level, as this is considered a straight-forward methodology that does not add redundant information to the results [49], while it considers information from the surrounding grid-cells that reinforces the robustness of the forecast. The skill of the forecast data is evaluated by comparing observations prior and after the adjustment of the biases. The forecast data are rearranged according to Figure 1, to create seamless lagged ensemble time series with similar lead time characteristics [48]. This pre-processing step serves two different purposes. First, to determine the forecast skill at different lead times, which is one of the objectives of this study. Second, to apply bias adjustment at the different lead-times between one and seven months (LT1 to LT7), as different lead-times of the forecast exhibit different bias characteristics. Figure 2 exhibits the average bias of the raw forecast data per lead time, comparing the basin average observations. For the adjustment, two different strategies were applied. The first considers the adjustment to the different forecast realizations individually, while in the second, all the forecast realizations are adjusted together. The former approach considers that the potential biases are realization-dependent and, hence, each one is treated independently (hereby referred to as independent realization correction—IRC). This provides the flexibility to the adjustment method to correct potentially unrealistic values in a single member, without tampering the correction of the other ensemble members. On the other hand, since it can be argued that while the forecast systems biases are time dependent (Figure 2), they are ensemble independent. In this approach, the ensemble members that exhibit special characteristics, e.g., wetter conditions, will retain their relative difference compared to the rest of the members. Nonetheless, this may trigger more false alarms in the case of a risk-averse decision maker. In this study, tests were conducted in the case study watershed to assess each strategy’s performance for the adjustment of precipitation and temperature variable biases.
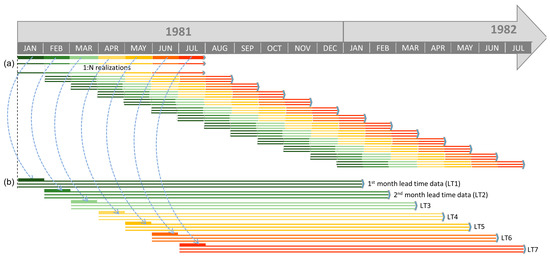
Figure 1.
Conversion of the forecast data (a) to the lagged ensemble time series of different lead times (b).
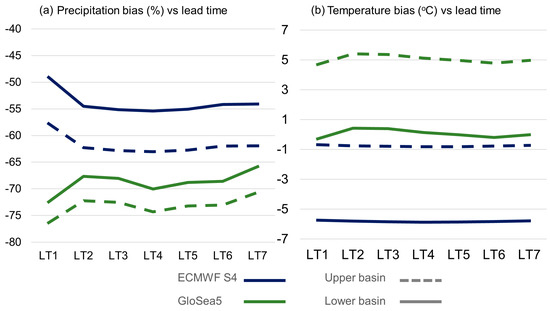
Figure 2.
Differences between the observed and raw forecast data of precipitation and temperature for ECMWF S4 and GloSea5 and the two (upper and lower) sub-basins: (a) Precipitation bias (%) vs. lead time; (b) Temperature bias (°C) vs. lead time.
2.2. Bias Adjustment
A quantile mapping (QM) and a simpler multiplicative/additive bias correction methodology were used to adjust the biases of the precipitation and temperature forecasts. The QM is based on the well-established multi-segment statistical bias correction of daily Global Climate Model (GCM) and Regional Climate Model (RCM) precipitation and temperature parameters. Technical details of those methodologies can be found in [50,51]. These methodologies have been used mainly in a series of climate change impact studies [52,53,54,55,56,57,58]. Additionally, less intrusive multiplicative/additive corrections for precipitation and temperature data were tested: the temperature average was scaled by adding the difference between the forecast and the observed data and, accordingly, the precipitation was multiplied by a factor equal to the fraction of the average observed over the forecast average precipitation. Equations (1) and (2) describe the methodology.
where and are the daily corrected values, and are the raw forecast data, and are the mean of the calendar month to which day i belongs, and and are the respective raw values of the calendar month.
The methodology can be found in [59] who refers to it as a “simple unbiasing” method (SU). Both methodologies are applied explicitly for each calendar month. The two different adjustment methods (QM and SU) and the two different adjustment strategies (individual or joint member correction) were combined and applied to the daily data as shown in Figure 3.
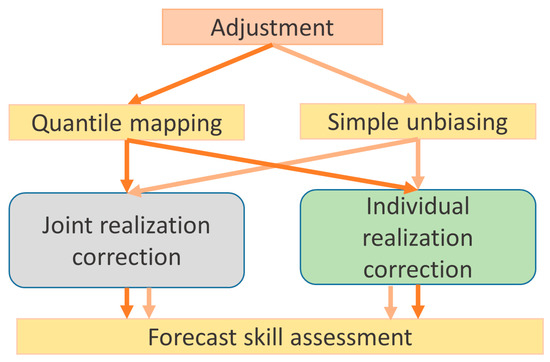
Figure 3.
Skill assessment scheme followed.
2.3. Hydrological Model HYPE
The hydrological simulations were performed by hydrological model HYPE [60]. The model simulates water flow from precipitation through soil to the river outlet. The HYPE model has been assessed in seasonal forecast applications in basin scale Sweden [61], the Niger River basin [62] and at pan-European scale [63]. The HYPE model (version 5.2) was calibrated and validated by using observed precipitation and temperature data. The model considers different hydrological response units (HRUs) that are lump treated within the model.
2.4. Performance Estimation
The hydrological model calibration and validation was performed by using the Nash-Sutcliffe efficiency coefficient (NSE) [64] and the Kling-Gupta efficiency (KGE) [65]. Both aforementioned metrics have a perfect value of 1 while values below zero indicate that the simulation has no skill. The forecast results of the hydrological simulations were assessed using the KGE, and continuous ranked probability skill score (CRPSS) [66]. The latter metric evaluates the probabilistic skill of the forecast by measuring the weighted average skill over a range of discrete threshold levels for which exceedance probabilities are computed [67]. The skill score estimation is based on CRPSS values. A perfect score equals 1, while negative values indicate no skill. The evaluation is performed at daily and monthly timescales, to exhibit dependencies of the skill in the timescale.
2.5. Case Study Area
The island of Crete covers more than 6% of the area of Greece and is the fifth largest Mediterranean island. The island’s climate is dry sub-humid Mediterranean, with warm dry summers and cold humid winters. More than 40% of annual precipitation occurs in the winter months. The average precipitation of the island ranges between 440 mm/year on the eastern part of the island to more than 2000 mm/year on the western mountainous areas. Moreover, orographic precipitation effects tend to increase both frequency and intensity of winter precipitation [11,55,68,69]. The Messara valley is located in the central-south area of Crete and encompasses an area of 400 km2 (Figure 3). About 250 km2 of the total valley area is cultivated while the remaining area (higher ground) is used for livestock. Agriculture on the Messara plain has a significant impact on water resources and ecosystem services of the area by substantially increasing water demand. The economy of the region is based on agriculture, with intensive cultivation of mainly olive trees, grapes, citrus, and vegetables in greenhouses. The overexploitation of the aquifer has reduced water availability, as groundwater is a major resource for irrigation. Nonetheless, Faneromeni dam located in the northeast part of the valley stores the runoff water of the Koutsoulidis watershed for irrigation. Since its construction, the dam has served as a major water resource for the summer period. Also, as Messara valley often experiences dry years, dam-stored water mitigates the water deficit. The dry hydrological year 2016–2017 (1 September 2016–31 August 2017) for the Messara region, in combination with the ineffectiveness of water management policy, led to a major reduction of the water stored in the Faneromeni dam (Figure 4).
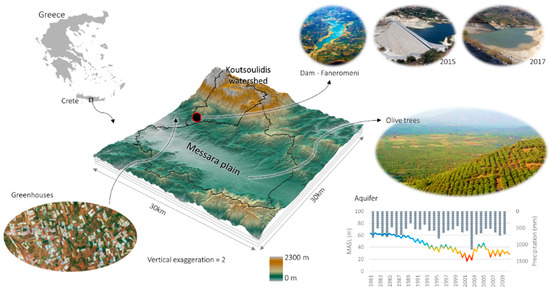
Figure 4.
Location of Messara case study area with the location of the Faneromeni Dam and the long-term trend of the aquifer water table depth.
In this work, Koutsoulidis catchment was divided into two sub-basins, one for the higher grounds of the watershed (1200 m a.s.l.) for the better representation of the snow accumulation and snowmelt, and one for the lower grounds (440 m a.s.l.). The different hydrological response units (HRUs) were determined by the nine most common land use classes of the Corine Land Cover 2000 (Table 1). Observed precipitation, temperature and discharge data for the hydrological years 1973 and 1993 were split into two independent 10-year long sets for the calibration and the validation periods. The HYPE model was calibrated by using its built-in differential evolution Markov chain method. A thorough description of the HYPE model can be found at the SMHI site (http://www.smhi.net/hype/wiki/doku.php?id=start:hype_model_description).

Table 1.
Land use classes.
3. Results
3.1. Forecast Precipitation and Temperature Performance
First, the two forecast systems’ skill was assessed. The CRPSS score was evaluated for the two sub-basins for the skill assessment of the forecasting parameters with and without the data adjustment. In Figure 5, the daily CRPSS is shown before and after the different adjustments. In the case of ECMWF precipitation, the QM methods perform better, increasing the CRPSS at least to the lead-time of the first month (LT1), while the SU degraded the skill for LT2 and higher. In both cases and sub-basins, the corrected forecasts remained unskillful. In the case of GloSea5, the QM methods were found to provide a significant improvement of the skill for the first three LTs, but in LT5 to LT7, the SU methods slightly outperformed the former. Moreover, an increase in the skill with the lead time was observed, in both SU and QM methods, following the behaviour of the raw data. After these improvements, the skill remained low (CRPSS below 0.1). For the ECMWF temperature skill, the results are comparable with those for precipitation. A deterioration of the skill is observed by all tested methods compared to the raw data skill, especially beyond LT1. As an exception, the SU IRC of the lower sub-basin showed less deterioration. In the case of GloSea5 temperature, all methods provided an increase similar to the skill of the temperature for all LTs. In all the above cases, the individual realization adjustment provided similar results to the joint realization adjustment.
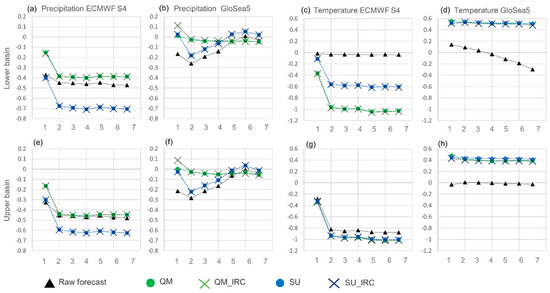
Figure 5.
Continuous ranked probability skill score (CRPSS) for the daily forecast data before and after the application of the different adjustment procedures. QM-quantile mapping treated data; SU-simple unbiasing adjustment; IRC-individual realization correction of the observations. X-axis refer to the lead time of the forecast data. (a,e) Precipitation ECMWF S4; (b,f) Precipitation GloSea5; (c,g) Temperature ECMWF S4; (d,h) Temperature GloSea5.
Additionally, the CRPSS was assessed on the monthly precipitation and temperature aggregates (Figure 6). The aggregation was performed after the adjustment in daily time-step data. The results are diverse among the two systems and the different data treatment methods. For most of the treatments of the ECMWF data and both variables, the skill decreases relative to the raw data skill. As an exception, S4 temperature for the lower basin was slightly improved by the SU methods. On the other hand, the GloSea5 forecast data largely benefit from the correction procedures, especially QM, which outperformed in the first and second month LTs. Finally, the results of the individual realization adjustment showed almost no difference to those from the joint realization adjustment.
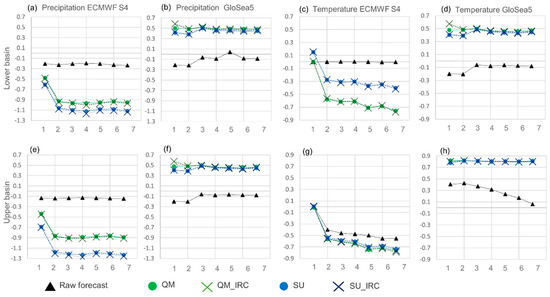
Figure 6.
Same as Figure 5 but for the monthly precipitation and temperature average. (a,e) Precipitation ECMWF S4; (b,f) Precipitation GloSea5; (c,g) Temperature ECMWF S4; (d,h) Temperature GloSea5.
3.2. Calibration of the Hydrological Model
The model calibration and validation showed good results with the seven-day KGE at 0.851 and 0.795 and the seven-day NSE at 0.903 and 0.736 for the calibration (1973–1982) and validation (1983–1993) period. The percent of bias (Pbias) was estimated at −4.4% and 1.8% respectively. A graphical representation of the observed and simulated discharge is shown in Figure 7.The calibrated model was then used to extend the simulated discharge to 2004. This time series was used as the reference to estimate the theoretical skill of the forecasts.
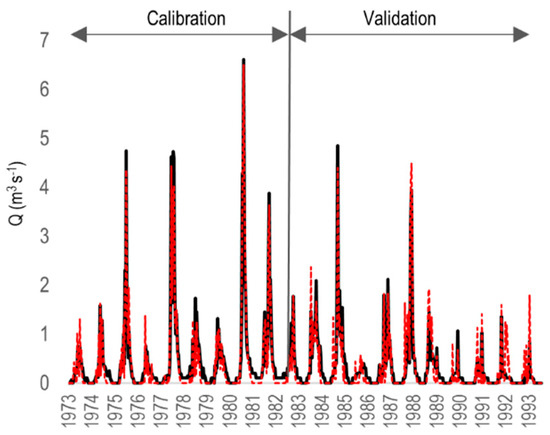
Figure 7.
Observed (black) and model simulated (red) hydrograph for the calibration and validation periods.
3.3. Hydrological Skill of the Forecast Systems
The S4 and GloSea5 data between 1981–2004 and 1996–2004 were used as an input to the calibrated HYPE model. Two types of hydrological simulations were performed. The first considered the continuous simulation of the lagged ensemble time series of different lead times, while the second considered the initial hydrological conditions update of the model towards the reference run and then the hydrological simulation of the seven-month-long forecasts. The initial conditions updated were snow water, soil water and water in the river. The former approach unveils the theoretical skill of the modelling cascade of the climatic forecast, post processing and hydrological simulation, while the latter approach unveils the potential skill of the hydrological forecast in an operational system. The difference of the skill obtained by the two approaches shows the effect of the initial conditions to the hydrological forecast system.
First, the CRPSS was estimated for the monthly aggregated runoff. S4 and GloSea5 provided similar results, with the first month lead time having the highest CRPSS and a skill reduction from the second month onwards (Figure 8). QM methods were shown to provide marginally better results for S4, while SU performed better in the case of GloSea5. Nevertheless, CRPSS had negative values in all the lead times of both systems in the continuous simulations. The initial condition update provided a noteworthy improvement in the first three lead time months of the forecast in the case of S4 and the first two lead time months in the case of GloSea5.
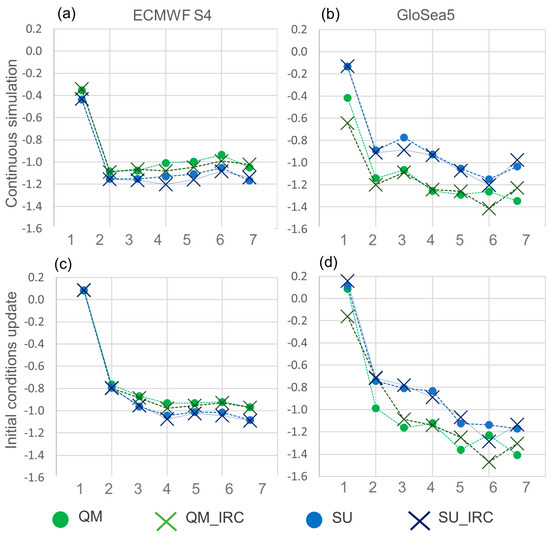
Figure 8.
CRPSS on the forecast data flow simulations (monthly aggregates): (a,c) ECMWF S4; (b,d) GloSea5.
The hydrological results were also assessed in terms of KGE relative to the reference run. The seven days runoff was used, and the results showed that in the first month of the forecast the skill is significant with the KGE ranging between 0.4 and 0.6 for S4 and 0.3 to 0.6 for GloSea5. After the first month, the KGE for both systems reduced to 0.2–0.4 (Figure 9). Regarding the different adjustment methodologies, S4 results of the four different treatments showed consistent results with SU methods, exhibiting a slightly better performance. Moreover, the IRC methods show less spread in the results. On the other hand, the GloSea5-based simulation results showed a large uniformity among the different adjustment treatments, with a slightly better performance of QM methods.
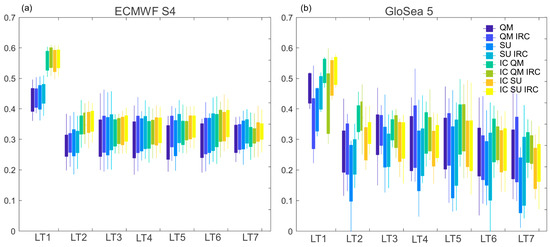
Figure 9.
Kling-Gupta efficiency (KGE) theoretical skill for each adjustment type and lead time. The performance was assessed against the reference run: (a) ECMWF S4; (b) GloSea5.
The initial conditions update provided significant improvements in the forecast ability of the two systems, especially in the first and second lead time months, with a simultaneous reduction of the variability for the entire forecast span.
Beyond the performance of the hydrological simulation, the results were assessed for their skill to reproduce the historical dry hydrological years. The reference runoff simulation was aggregated in a hydrological year basis into three categories based on the 33th and 66th percentile of the hydrological year runoff (wet–normal–dry). The same percentiles were also used to categorize the forecast-based hydrological simulations. Then, the ratio of correctly forecasted drought (or wetness) categorization was estimated. In Figure 10a–d, the correct state detection rate was estimated for S4 and GloSea5. The shaded area represents 33%, which is the ratio of random correctly selected drought states if there was no skill to the systems. S4 exhibits a marginal ability to capture drought state, when the simulation does not include the initial state update (Figure 10, blue bar graphs), with GloSea5 providing a better drought state detection ability for the first lead time month. The skill of both systems is highly enhanced by the initial state updating, with the forecast reaching 60% for the first lead time month. Beyond the first month, S4 skill reduces significantly, while GloSea5 has a good skill (~45%) until the fourth month of the forecast. Moreover, the skill of the systems to forecast a drought state that was at least more severe than what really occurred was assessed, as this information is helpful for risk averse decision making (Figure 10e–h). It is shown that both systems have a limited skill without the initial conditions updating (about 70–75% for S4 and about 60–65% for GloSea5). However similarly to the previous results, initial condition updated hydrological forecasts largely enhance results for the first two months lead time for S4 and five months for GloSea5.
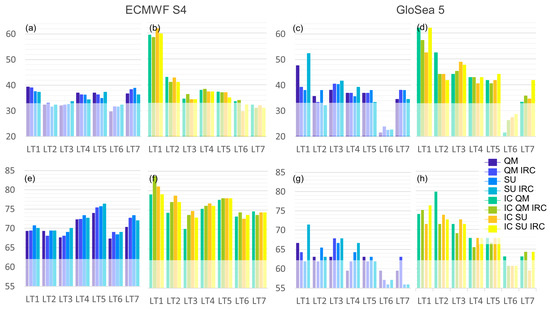
Figure 10.
Drought state detection rate (%) in hydrological year basis. (a–d): Forecast detection of the exact drought condition. (e–h): Forecast detected conditions at least as wet as the reference. Shaded areas indicate the fraction of “random” drought condition selection, over which the forecast exhibits skill.
As a last stage of assessment, the ability of the hydrological simulations to forecast specific historical streamflow drought events was estimated. Four drought events for the hydrological years 1985–1986, 1989–1990, 1990–1991 and 1999–2000 were considered (Figure 11). All four droughts were covered by the S4 forecast, while GloSea5 included only the latter event. The results show that S4 has a significant skill for one month ahead in all cases, however, it did not perform well in larger lead times. The variability among the type of the forecast data pre-processing was found to be increased, missing a clear pattern about which combination of adjustment and treatment methods would provide the best forecast. As an example, the 1985–1986 event was better predicted when the initial conditions of the hydrological model were updated; however in the 1989–1990 case, hydrological prediction without the initial conditions update provided better results. Also, in many lead times of all the drought events, the prediction was not accurate. The drought event of 1999–2000, which was forecasted by both systems, served as a benchmark. The GloSea5 was found to predict the drought event well, especially using the QM methods, where the successful forecast reached as far as five months ahead. On the other hand, S4 exhibited a poor skill, with the successful prediction limited mainly to the first month.
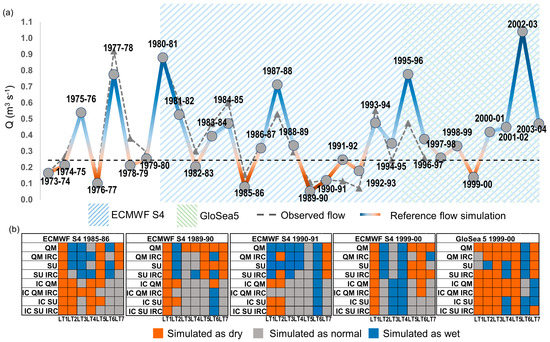
Figure 11.
Historical runoff droughts (a) as simulated by the reference simulation. S4 and GloSea5 ability to capture major drought events of hydrological years 1985–1986, 1989–1990, 1990–1991 and 1999–2000 (b) at different lead times.
4. Discussion
This study investigates the current skill of two operational seasonal forecast systems to provide valuable seasonal discharge forecasting information for a typical Mediterranean watershed. Different types of downscaling and bias adjustment were assessed, i.e., a quantile mapping and a simple additive/multiplicative approach. Moreover, different approaches of adjustment were tested, with the first to consider each forecast realization run individually and the second to consider the joint adjustment of all realizations. Additionally, the effect of the initial hydrological model state was assessed for its effect on the forecast skill. The adjusted data were used to simulate the watershed surface runoff by using the HYPE hydrological model. The forecast skill was assessed for the climatic parameters of precipitation and temperature and for the flow simulations.
Regarding the precipitation and temperate adjustment operations, a key finding is that the adjustment does not necessarily improve the forecast skill, despite the improvement of the climatological statistical parameters such as the mean and variability. This is explained by the type of adjustment methods, which do not alter the forecast skill, but rather adjust the climatological statistics towards the observations. In the cases that the skill of precipitation and temperature was increased, the QM methods perform better or equal to the SU method. Another important outcome is that the joint realization adjustment provided similar skill to the individual realization adjustment in the vast majority of the experiments considered, for precipitation and temperature, as well as for discharge. Upper and lower basin results showed similar results in the skill, which was partly expected due to the similarity of the forecast data in the two sub-basins.
The discharge forecast skill of the two systems was also assessed compared to the reference simulation. Results show that the first and second months of the forecast exhibited noteworthy skill, which thereafter decreased rapidly as lead time increased. Nonetheless, ECMWF showed greater consistency among the results of the different adjustment methodologies, while GloSea5 showed slightly better results up to five months ahead.
Furthermore, the ability of the two systems to forecast the streamflow drought state was assessed, revealing that GloSea5 showed a slightly better skill. Additionally, it was shown that initial hydrological state updating provides a large improvement to the drought state forecast. Regarding the skill of the two systems to predict four past runoff drought events, results showed that ECMWF had a limited predictability, while GloSea5 had better skill in the single event for which it was evaluated.
Attribution of the two systems’ skill differences is difficult due to the local extent of the study region. Nonetheless, GloSea5 has been found to be skillful in the prediction of large scale events, such as the winter North Atlantic Oscillation, Arctic Oscillation and El Niño–Southern Oscillation, which have strong correlations with year-to-year precipitation and temperature variations [48,70,71]. Both forecast systems are continuously under development, delivering more skillful predictions. S4 has already been upgraded to System 5, with upgrades including an increase in spatial resolution, which has a proven positive correlation to the simulation performance in climate simulations [72].
Seasonal forecasting has a great potential to provide valuable water resource information that will aid in climate change mitigation plans. The results of this study confirm the potential usefulness of the seasonal forecast in the decision-making chain. Nonetheless, there is still need to increase the forecast skill, especially for the longer lead times. In the Mediterranean environment, in particular, where precipitation is highly seasonal, forecasting would be more useful if it could provide skillful predictions for the forthcoming wet season conditions from the beginning of the dry season (7–9 months earlier). This would allow for a more effective reaction time to adopt water-saving measurements. Finally, it has to be noted that this study does not aim to advocate a specific prediction system or pre-processing methodology, as each has its strengths and weaknesses. Due to the limited extent of the case study region, the findings of this study cannot be widely extrapolated beyond the region of study. Nonetheless, they indicate the current level of skill in the seasonal forecast at a local decision-making level for an eastern Mediterranean island.
Author Contributions
Conceptualization, M.G. and A.K.; Methodology, M.G. and A.K.; Validation, M.G. and A.K.; Writing—Original Draft Preparation, M.G.; Writing—Review and Editing, A.K.; Visualization, M.G. and A.K.; Supervision, I.T.; Project Administration, I.T.; Funding Acquisition, I.T.
Funding
This research is funded by the Horizon 2020 Framework programme through the project IMPREX (grant agreement no. 641811).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van den Hurk, B.J.J.M.; Bouwer, L.M.; Buontempo, C.; Döscher, R.; Ercin, E.; Hananel, C.; Hunink, J.E.; Kjellström, E.; Klein, B.; Manez, M.; et al. Improving predictions and management of hydrological extremes through climate services: www.imprex.eu. Clim. Serv. 2016, 1, 6–11. [Google Scholar] [CrossRef]
- Pappenberger, F.; Cloke, H.L.; Parker, D.J.; Wetterhall, F.; Richardson, D.S.; Thielen, J. The monetary benefit of early flood warnings in Europe. Environ. Sci. Policy 2015, 51, 278–291. [Google Scholar] [CrossRef]
- Di Giuseppe, F.; Pappenberger, F.; Wetterhall, F.; Krzeminski, B.; Camia, A.; Libertá, G.; San Miguel, J. The potential predictability of fire danger provided by numerical weather prediction. J. Appl. Meteorol. Climatol. 2016, 55, 2469–2491. [Google Scholar] [CrossRef]
- Coughlan De Perez, E.; Stephens, E.; Bischiniotis, K.; Van Aalst, M.; Van Den Hurk, B.; Mason, S.; Nissan, H.; Pappenberger, F. Should seasonal rainfall forecasts be used for flood preparedness? Hydrol. Earth Syst. Sci. 2017, 21, 4517–4524. [Google Scholar] [CrossRef]
- Marcos, R.; Llasat, M.C.; Quintana-Seguí, P.; Turco, M. Use of bias correction techniques to improve seasonal forecasts for reservoirs—A case-study in northwestern Mediterranean. Sci. Total Environ. 2018, 610–611, 64–74. [Google Scholar] [CrossRef] [PubMed]
- Crochemore, L.; Ramos, M.-H.; Pappenberger, F. Bias correcting precipitation forecasts to improve the skill of seasonal streamflow forecasts. Hydrol. Earth Syst. Sci. 2016, 20, 3601–3618. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Crochemore, L.; Bosshard, A. Seasonal hydrological forecasting in Europe: Analysis of skill and its key driving factors. In Proceedings of the 15th International Conference on Environmental Science and Technology, Rhodes, Greece, 31 August–2 September 2017. [Google Scholar]
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. The skill of seasonal ensemble low-flow forecasts in the Moselle River for three different hydrological models. Hydrol. Earth Syst. Sci. 2015, 19, 275–291. [Google Scholar] [CrossRef]
- Marcos, R.; Llasat, M.C.; Quintana-Seguí, P.; Turco, M. Seasonal predictability of water resources in a Mediterranean freshwater reservoir and assessment of its utility for end-users. Sci. Total Environ. 2017, 575, 681–691. [Google Scholar] [CrossRef] [PubMed]
- Molteni, F.; Stockdale, T.; Balmaseda, M.; Balsamo, G.; Buizza, R.; Ferranti, L.; Magnusson, L.; Mogensen, K.; Palmer, T.; Vitart, F. The New ECMWF Seasonal Forecast System (System 4); European Centre for Medium-Range Weather Forecasts: Reading, UK, 2011. [Google Scholar]
- Koutroulis, A.G.; Tsanis, I.K.; Daliakopoulos, I.N. Seasonality of floods and their hydrometeorologic characteristics in the island of Crete. J. Hydrol. 2010, 394, 90–100. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Tsanis, I.K. A method for estimating flash flood peak discharge in a poorly gauged basin: Case study for the 13–14 January 1994 flood, Giofiros basin, Crete, Greece. J. Hydrol. 2010, 385, 150–164. [Google Scholar] [CrossRef]
- Iordanidou, V.; Koutroulis, A.G.; Tsanis, I.K. Mediterranean cyclone characteristics related to precipitation occurrence in Crete, Greece. Nat. Hazards Earth Syst. Sci. 2015, 15, 1807–1819. [Google Scholar] [CrossRef]
- Harding, R.J.; Weedon, G.P.; van Lanen, H.A.J.; Clark, D.B. The future for global water assessment. J. Hydrol. 2014, 518, 186–193. [Google Scholar] [CrossRef]
- Kang, T.H.; Kim, Y.O.; Hong, I.P. Comparison of pre- and post-processors for ensemble streamflow prediction. Atmos. Sci. Lett. 2010, 11, 153–159. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Tian, D.; Martinez, C.J.; Graham, W.D.; Hwang, S.; Tian, D.; Martinez, C.J.; Graham, W.D.; Hwang, S. Statistical downscaling multimodel forecasts for seasonal precipitation and surface temperature over the Southeastern United States. J. Clim. 2014, 27, 8384–8411. [Google Scholar] [CrossRef]
- Zhao, T.; Bennett, J.C.; Wang, Q.J.; Schepen, A.; Wood, A.W.; Robertson, D.E.; Ramos, M.-H. How suitable is quantile mapping for postprocessing GCM precipitation forecasts? J. Clim. 2017, 30, 3185–3196. [Google Scholar] [CrossRef]
- Schepen, A.; Zhao, T.; Wang, Q.J.; Robertson, D.E. A Bayesian modelling method for post-processing daily sub-seasonal to seasonal rainfall forecasts from global climate models and evaluation for 12 Australian catchments. Earth Syst. Sci. 2018, 225194, 1615–1628. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.P.; Livneh, B.; Lettenmaier, D.P.; Reichle, R.H. Skill in streamflow forecasts derived from large-scale estimates of soil moisture and snow. Nat. Geosci. 2010, 3, 613–616. [Google Scholar] [CrossRef]
- Hamill, T.M.; Hagedorn, R.; Whitaker, J.S. Probabilistic forecast calibration using ECMWF and GFS ensemble reforecasts. Part II: Precipitation. Mon. Weather Rev. 2008, 136, 2620–2632. [Google Scholar] [CrossRef]
- Li, H.; Luo, L.; Wood, E.F.; Schaake, J. The role of initial conditions and forcing uncertainties in seasonal hydrologic forecasting. J. Geophys. Res. 2009, 114, D04114. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Komma, J.; Tsanis, I.K.; Wagner, W.; Blöschl, G. Initial soil moisture effects on flash flood generation—A comparison between basins of contrasting hydro-climatic conditions. J. Hydrol. 2016. [Google Scholar] [CrossRef]
- Bischiniotis, K.; Van Den Hurk, B.; Jongman, B.; Coughlan De Perez, E.; Veldkamp, T.; De Moel, H.; Aerts, J. The influence of antecedent conditions on flood risk in sub-Saharan Africa. Hazards Earth Syst. Sci. 2018, 18, 271–285. [Google Scholar] [CrossRef]
- Bierkens, M.F.P.; van den Hurk, B.J.J.M. Groundwater convergence as a possible mechanism for multi-year persistence in rainfall. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Shukla, S.; Lettenmaier, D.P. Seasonal hydrologic prediction in the United States: Understanding the role of initial hydrologic conditions and seasonal climate forecast skill. Hydrol. Earth Syst. Sci. 2011, 15, 3529–3538. [Google Scholar] [CrossRef]
- Yossef, N.C.; Winsemius, H.; Weerts, A.; van Beek, R.; Bierkens, M.F.P. Skill of a global seasonal streamflow forecasting system, relative roles of initial conditions and meteorological forcing. Water Resour. Res. 2013, 49, 4687–4699. [Google Scholar] [CrossRef]
- Candogan Yossef, N.; Van Beek, R.; Weerts, A.; Winsemius, H.; Bierkens, M.F.P. Skill of a global forecasting system in seasonal ensemble streamflow prediction. Hydrol. Earth Syst. Sci. 2017, 21, 4103–4114. [Google Scholar] [CrossRef]
- Alfieri, L.; Pappenberger, F.; Wetterhall, F.; Haiden, T.; Richardson, D.; Salamon, P. Evaluation of ensemble streamflow predictions in Europe. J. Hydrol. 2014, 517, 913–922. [Google Scholar] [CrossRef]
- Thiemig, V.; Pappenberger, F.; Thielen, J.; Gadain, H.; de Roo, A.; Bodis, K.; Del Medico, M.; Muthusi, F. Ensemble flood forecasting in Africa: A feasibility study in the Juba-Shabelle river basin. Atmos. Sci. Lett. 2010, 11, 123–131. [Google Scholar] [CrossRef]
- Oyebode, O.; Otieno, F.; Adeyemo, J. Review of three data-driven modelling techniques for hydrological modelling and forecasting. Fresenius Environ. Bull. 2014, 23, 1443–1454. [Google Scholar]
- Liu, Z.; Zhou, P.; Chen, X.; Guan, Y. A multivariate conditional model for streamflow prediction and spatial precipitation refinement. J. Geophys. Res. Atmos. 2015, 120, 10116–10129. [Google Scholar] [CrossRef]
- Pokhrel, P.; Wang, Q.J.; Robertson, D.E. The value of model averaging and dynamical climate model predictions for improving statistical seasonal streamflow forecasts over Australia. Water Resour. Res. 2013, 49, 6671–6687. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Clark, M.P. HESS Opinions: The complementary merits of competing modelling philosophies in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3953–3973. [Google Scholar] [CrossRef]
- Gao, X.; Giorgi, F. Increased aridity in the Mediterranean region under greenhouse gas forcing estimated from high resolution simulations with a regional climate model. Glob. Planet. Chang. 2008, 62, 195–209. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Grillakis, M.G.; Daliakopoulos, I.N.; Tsanis, I.K.; Jacob, D. Cross sectoral impacts on water availability at +2 °C and +3 °C for east Mediterranean island states: The case of Crete. J. Hydrol. 2016, 532, 16–28. [Google Scholar] [CrossRef]
- Tsanis, I.K.; Koutroulis, A.G.; Daliakopoulos, I.N.; Jacob, D. Severe climate-induced water shortage and extremes in Crete. Clim. Chang. 2011, 106, 667–677. [Google Scholar] [CrossRef]
- Apostolakis, A.; Wagner, K.; Daliakopoulos, I.N.; Kourgialas, N.N.; Tsanis, I.K. Greenhouse soil moisture deficit under saline irrigation and climate change. Procedia Eng. 2016, 162, 537–544. [Google Scholar] [CrossRef]
- Daliakopoulos, I.N.; Pappa, P.; Grillakis, M.G.; Varouchakis, E.A.; Tsanis, I.K. Modeling soil salinity in greenhouse cultivations under a changing climate with SALTMED. Soil Sci. 2016, 181, 241–251. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Seiradakis, K.D.; Tsanis, I.K. Implications of 2 °C global warming in European summer tourism. Clim. Serv. 2016. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Tsanis, I.K. The 2 °C global warming effect on summer European tourism through different indices. Int. J. Biometeorol. 2016, 60. [Google Scholar] [CrossRef] [PubMed]
- Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Jacob, D. Mapping the vulnerability of European summer tourism under 2 °C global warming. Clim. Chang. 2018, 1–15. [Google Scholar] [CrossRef]
- Panagea, I.S.; Tsanis, I.K.; Koutroulis, A.G.; Grillakis, M.G. Climate change impact on photovoltaic energy output: The case of Greece. Adv. Meteorol. 2014, 2014. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Papadimitriou, L.V.; Grillakis, M.G.; Tsanis, I.K.; Wyser, K.; Betts, R.A. Freshwater vulnerability under high end climate change. A pan-European assessment. Sci. Total Environ. 2018, 613–614. [Google Scholar] [CrossRef] [PubMed]
- Betts, R.A.; Alfieri, L.; Bradshaw, C.; Caesar, J.; Feyen, L.; Friedlingstein, P.; Gohar, L.; Koutroulis, A.; Lewis, K.; Morfopoulos, C.; et al. Changes in climate extremes, fresh water availability and vulnerability to food insecurity projected at 1.5 °C and 2 °C global warming with a higher-resolution global climate model. Philos. Trans. R. Soc. A 2018, 376, 20160452. [Google Scholar] [CrossRef] [PubMed]
- Jacob, D.; Kotova, L.; Teichmann, C.; Sobolowski, S.P.; Vautard, R.; Donnelly, C.; Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Damm, A.; et al. Climate impacts in Europe under +1.5 °C global warming. Earth’s Future 2018. [Google Scholar] [CrossRef]
- MacLachlan, C.; Arribas, A.; Peterson, K.A.; Maidens, A.; Fereday, D.; Scaife, A.A.; Gordon, M.; Vellinga, M.; Williams, A.; Comer, R.E.; et al. Global seasonal forecast system version 5 (GloSea5): A high-resolution seasonal forecast system. Q. J. R. Meteorol. Soc. 2015, 141, 1072–1084. [Google Scholar] [CrossRef]
- Accadia, C.; Mariani, S.; Casaioli, M.; Lavagnini, A.; Speranza, A.; Accadia, C.; Mariani, S.; Casaioli, M.; Lavagnini, A.; Speranza, A. Sensitivity of precipitation forecast skill scores to bilinear interpolation and a simple nearest-neighbor average method on high-resolution verification grids. Weather Forecast. 2003, 18, 918–932. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Tsanis, I.K. Multisegment statistical bias correction of daily GCM precipitation output. J. Geophys. Res. Atmos. 2013, 118, 3150–3162. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Daliakopoulos, I.N.; Tsanis, I.K. A method to preserve trends in quantile mapping bias correction of climate modeled temperature. Earth Syst. Dyn. Discuss. 2017, 1–26. [Google Scholar] [CrossRef]
- Papadimitriou, L.V.; Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K. High-end climate change impact on European runoff and low flows—Exploring the effects of forcing biases. Hydrol. Earth Syst. Sci. 2016, 20, 1785–1808. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Papadimitriou, L.V.; Daliakopoulos, I.N.; Tsanis, I.K. Climate-induced shifts in global soil temperature regimes. Soil Sci. 2016, 181, 264–272. [Google Scholar] [CrossRef]
- Daliakopoulos, I.N.; Tsanis, I.K.; Koutroulis, A.G.; Kourgialas, N.N.; Varouchakis, E.A.; Karatzas, G.P.; Ritsema, C.J. The threat of soil salinity: A European scale review. Sci. Total Environ. 2016, 573, 727–739. [Google Scholar] [CrossRef] [PubMed]
- Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Jacob, D. Exploring the ability of current climate information to facilitate local climate services for the water sector. Earth Perspect. 2015, 2, 6. [Google Scholar] [CrossRef]
- Papadimitriou, L.V.; Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K. The effect of GCM biases on global runoff simulations of a land surface model. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–43. [Google Scholar] [CrossRef]
- Nikulin, G.; Bosshard, T.; Yang, W.; Bärring, L.; Wilcke, R.; Vrac, M.; Vautard, R.; Noel, T.; Gutiérrez, J.; Herrera, S.; et al. Bias Correction Intercomparison Project (BCIP): An introduction and the first results. In Proceedings of the EGU 2015, Vienna, Austria, 12–17 April 2015. [Google Scholar]
- Koutroulis, A.; Papadimitriou, L.; Grillakis, M.; Tsanis, I.; Wyser, K.; Caesar, J.; Betts, R. Simulating hydrological impacts under climate change: Implications from methodological differences of a Pan European Assessment. Water 2018, 10, 1331. [Google Scholar] [CrossRef]
- Déqué, M. Frequency of precipitation and temperature extremes over France in an anthropogenic scenario: model results and statistical correction according to observed values. Glob. Planet. Chang. 2007, 57, 16–26. [Google Scholar] [CrossRef]
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Bosshard, T.; Spångmyr, H.; Lindström, G.; Gustafsson, D.; Arheimer, B. Uncertainty in the Swedish Operational Hydrological Forecasting Systems. In Vulnerability, Uncertainty, and Risk; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 253–262. [Google Scholar]
- Andersson, J.C.M.; Ali, A.; Arheimer, B.; Gustafsson, D.; Minoungou, B. Providing peak river flow statistics and forecasting in the Niger River basin. Phys. Chem. Earth Parts A/B/C 2017, 100, 3–12. [Google Scholar] [CrossRef]
- Pechlivanidis, I.; Spångmyr, H.; Bosshard, T. Identification of the drivers controlling the seasonal hydrological forecasting skill in Europe. In Proceedings of the EGU General Assembly 2016, Vienna, Austria, 17–22 April 2016; Volume 18. ID. EPSC2016-1724. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Hersbach, H. Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather Forecast. 2000, 15, 559–570. [Google Scholar] [CrossRef]
- Bradley, A.A.; Schwartz, S.S. Summary verification measures and their interpretation for ensemble forecasts. Mon. Weather Rev. 2011, 139, 3075–3089. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Kotroni, V.; Lagouvardos, K. Lightning activity, rainfall and flash flooding-occasional or interrelated events? A case study in the island of Crete. Nat. Hazards Earth Syst. Sci. 2012, 12. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Vrohidou, A.-E.K.; Tsanis, I.K. Spatiotemporal characteristics of meteorological drought for the Island of Crete. J. Hydrometeorol. 2011, 12, 206–226. [Google Scholar] [CrossRef]
- Siegert, S.; Stephenson, D.B.; Sansom, P.G.; Scaife, A.A.; Eade, R.; Arribas, A. A Bayesian framework for verification and recalibration of ensemble forecasts: How uncertain is NAO predictability? J. Clim. 2016, 29, 995–1012. [Google Scholar] [CrossRef]
- Scaife, A.A.; Arribas, A.; Blockey, E.; Brookshaw, A.; Clark, R.T.; Dunstone, N.; Eade, R.; Fereday, D.; Folland, C.K.; Gordon, M.; et al. Skillful long range prediction of European and North American winters. Geophys. Res. Lett. 2014, 5, 2514–2519. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Papadimitriou, L. Evaluation of precipitation and temperature simulation performance of the CMIP3 and CMIP5 historical experiments. Clim. Dyn. 2016, 47. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).