Case Study of Heat Transfer during Artificial Ground Freezing with Groundwater Flow
Abstract
:1. Introduction
2. Methods
- the ice is immobile and the medium is non-deformable;
- the aquifer is fully saturated and its total porosity remains constant; and,
- the freezing point depression due to solute concentrations is negligible.
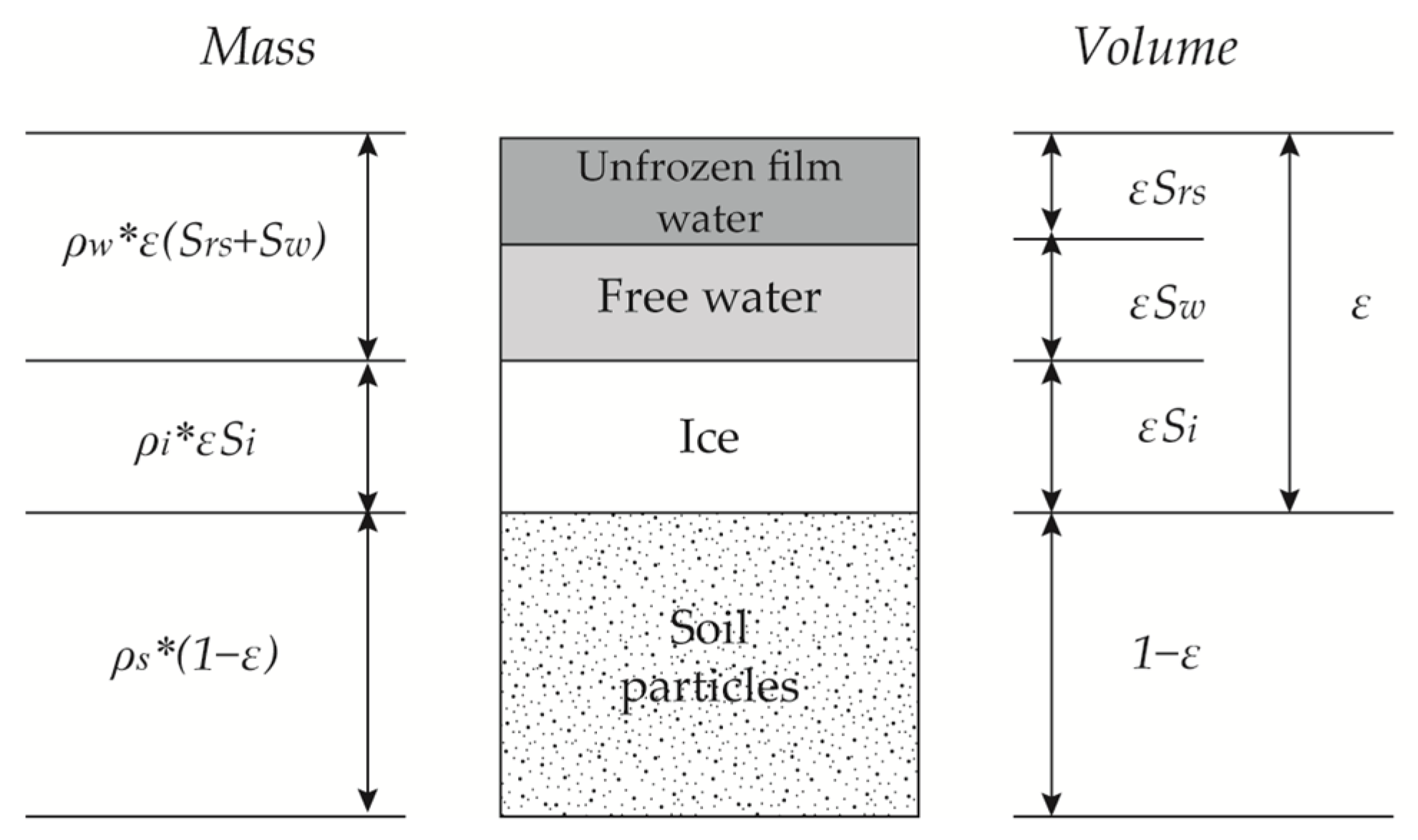
2.1. Water Mass Conservation Equation
2.2. Energy Conversation Equation
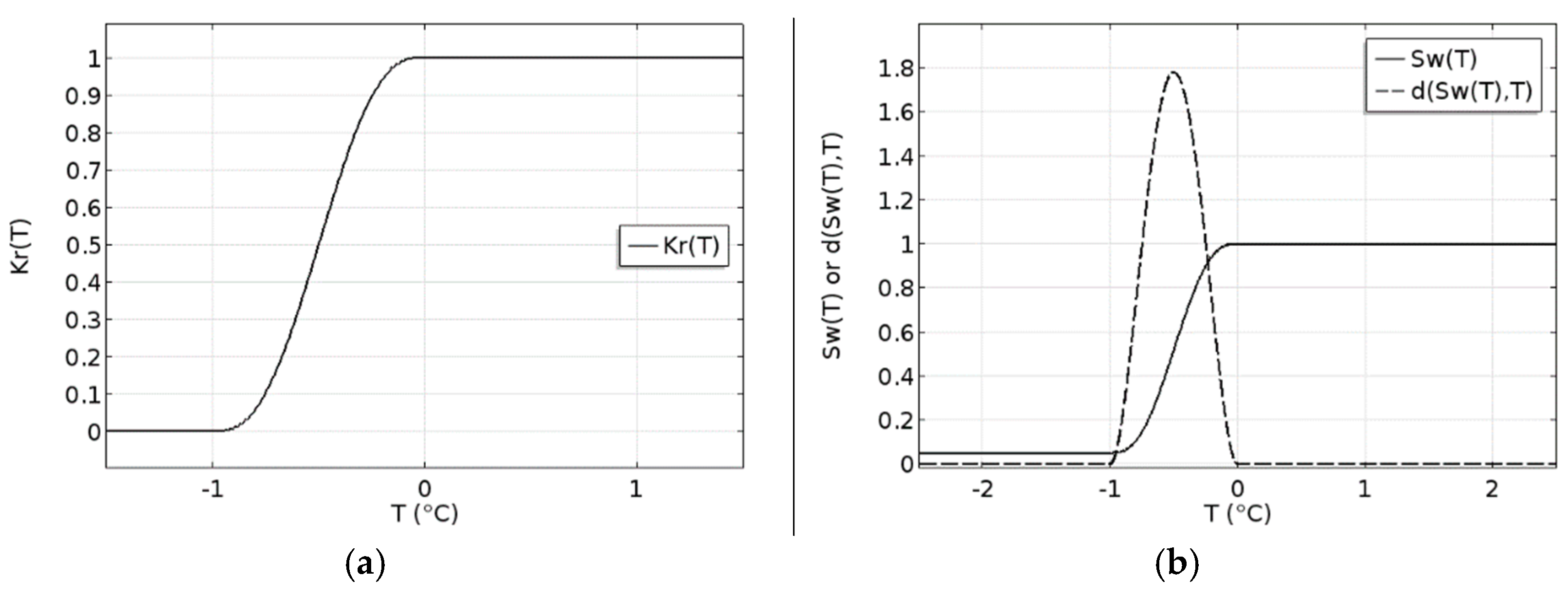
2.3. TH Coupling Parameters Description
2.3.1. Effective Hydraulic Conductivity
2.3.2. The Function of Water Saturation and Freezing
2.4. Numerical Implementation
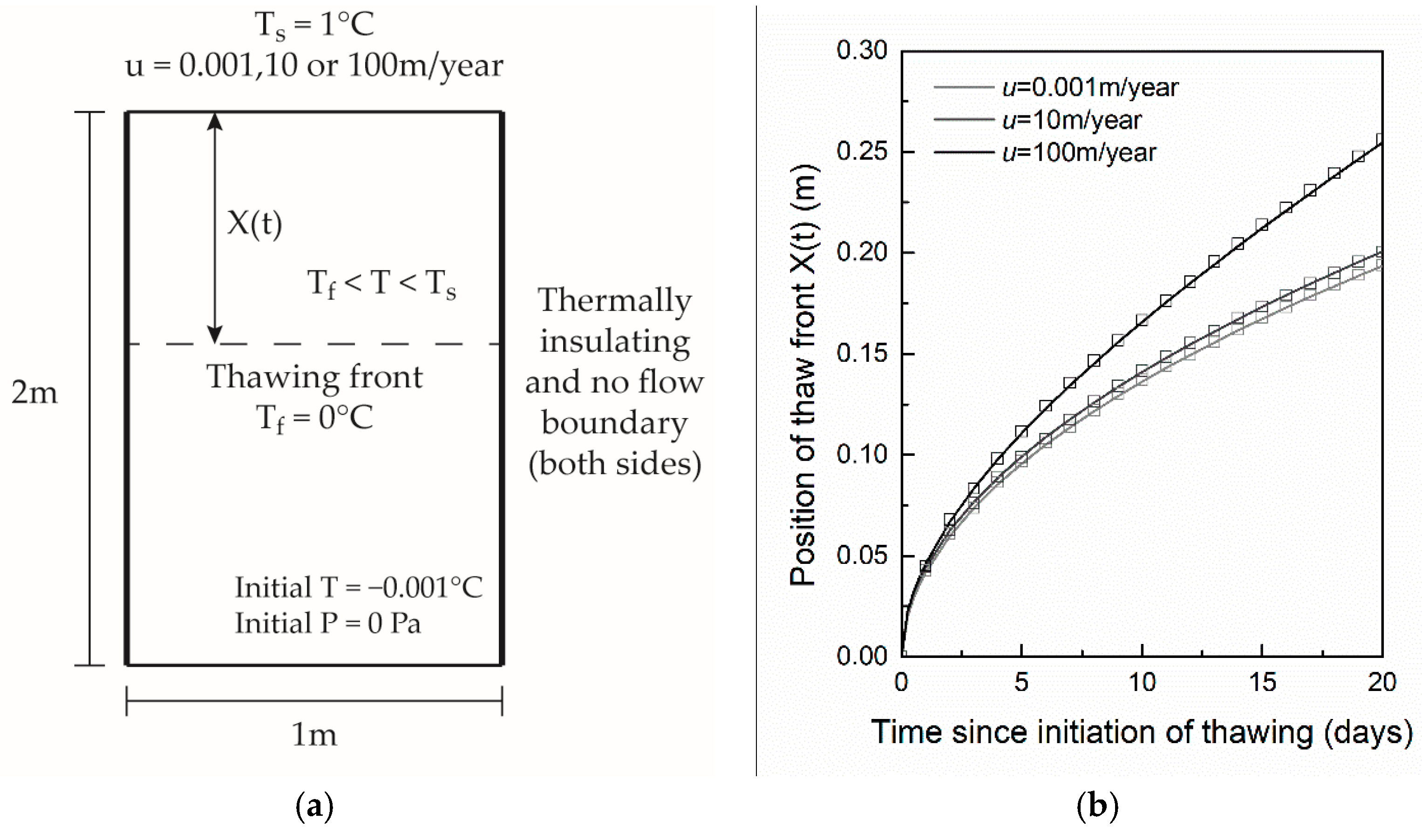
3. Validation and Simulation Studies
3.1. Comparison with Analytical Solution Based Results
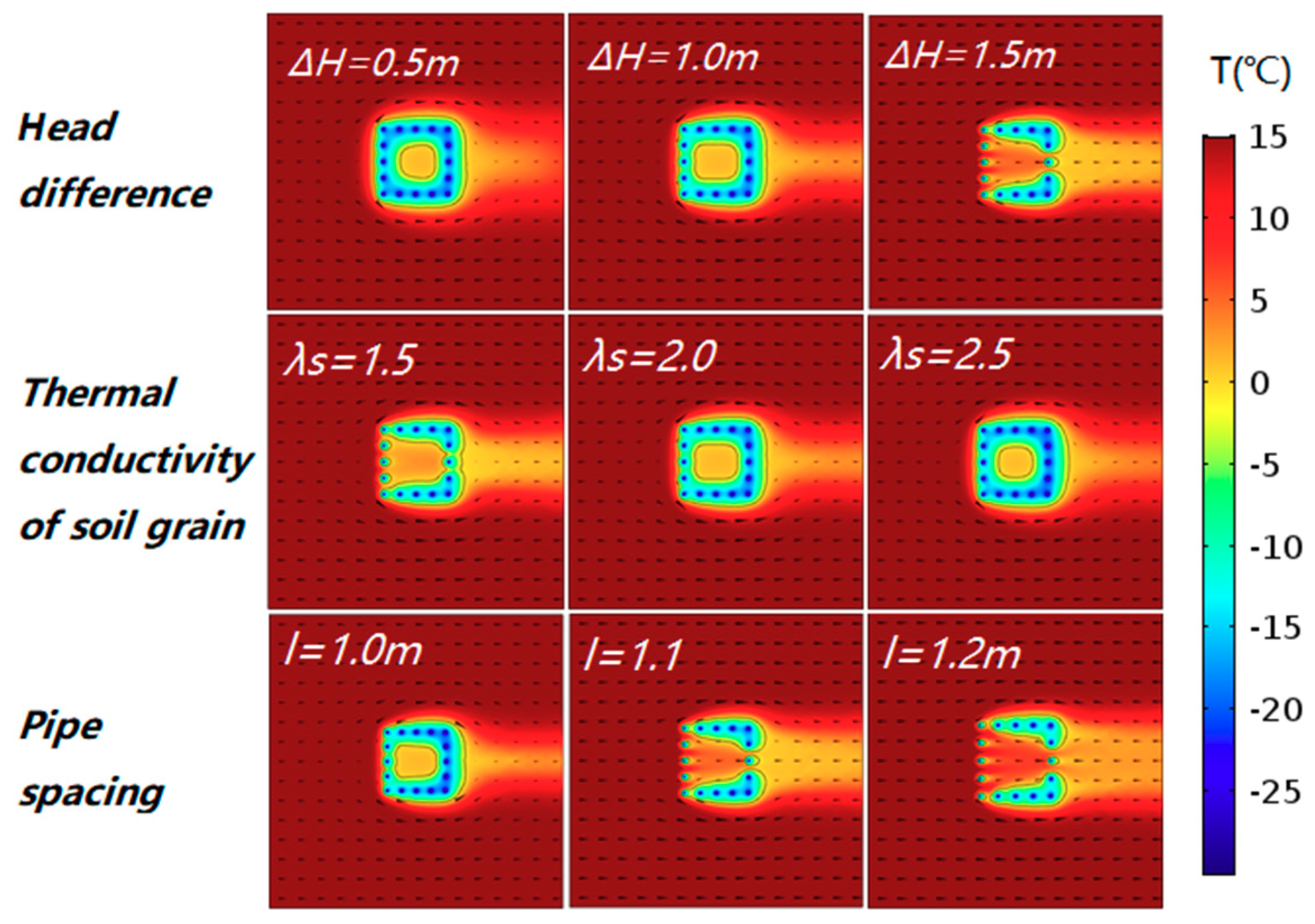
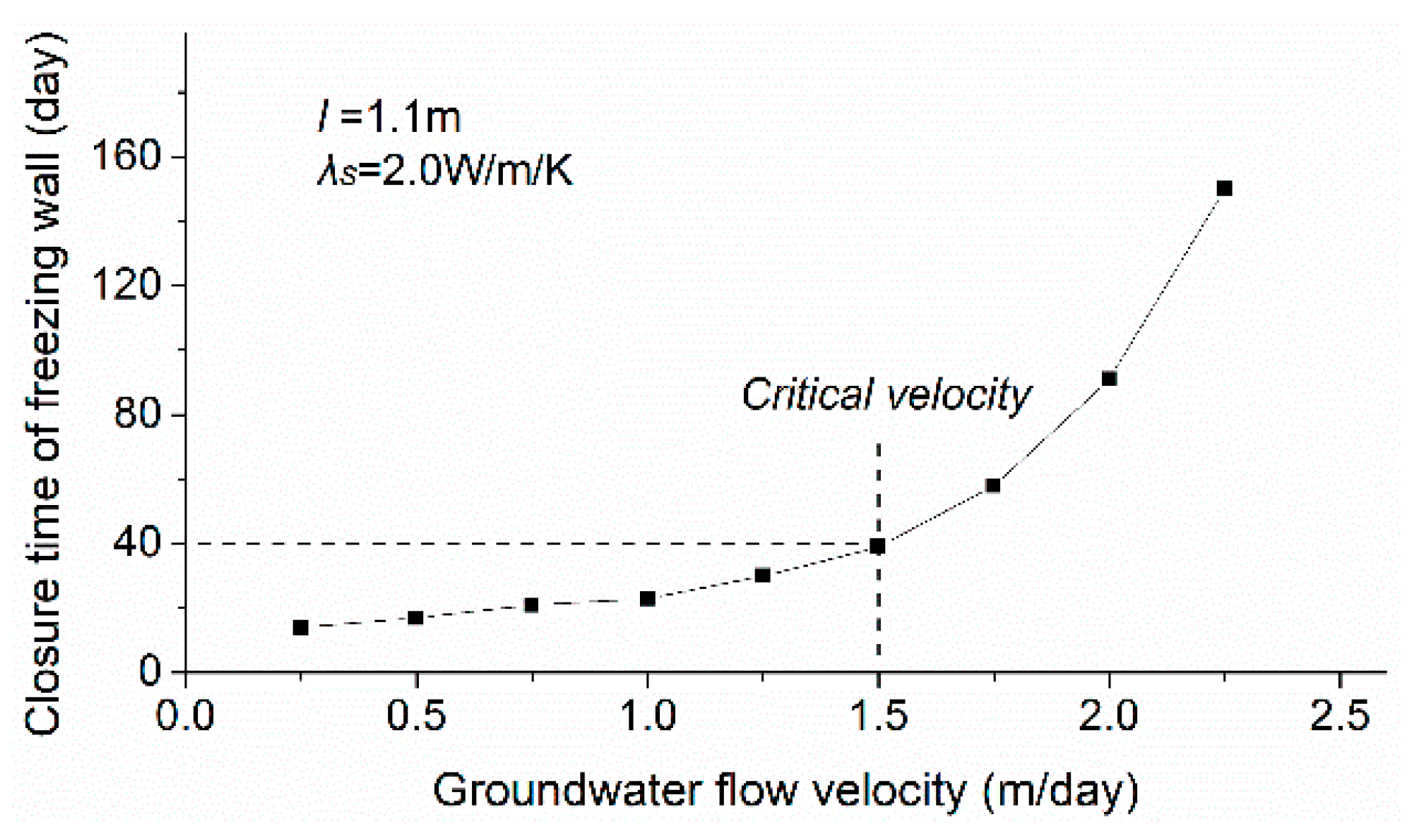
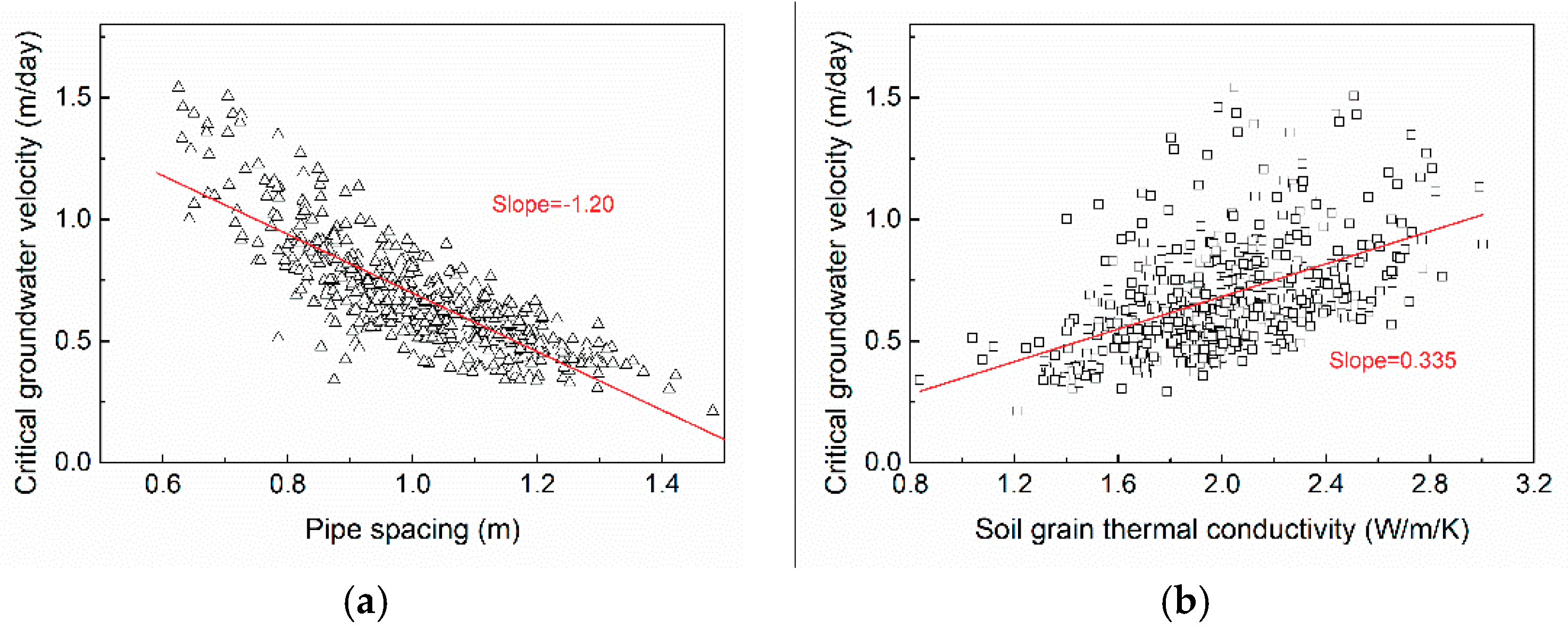
3.2. Simulation Studies
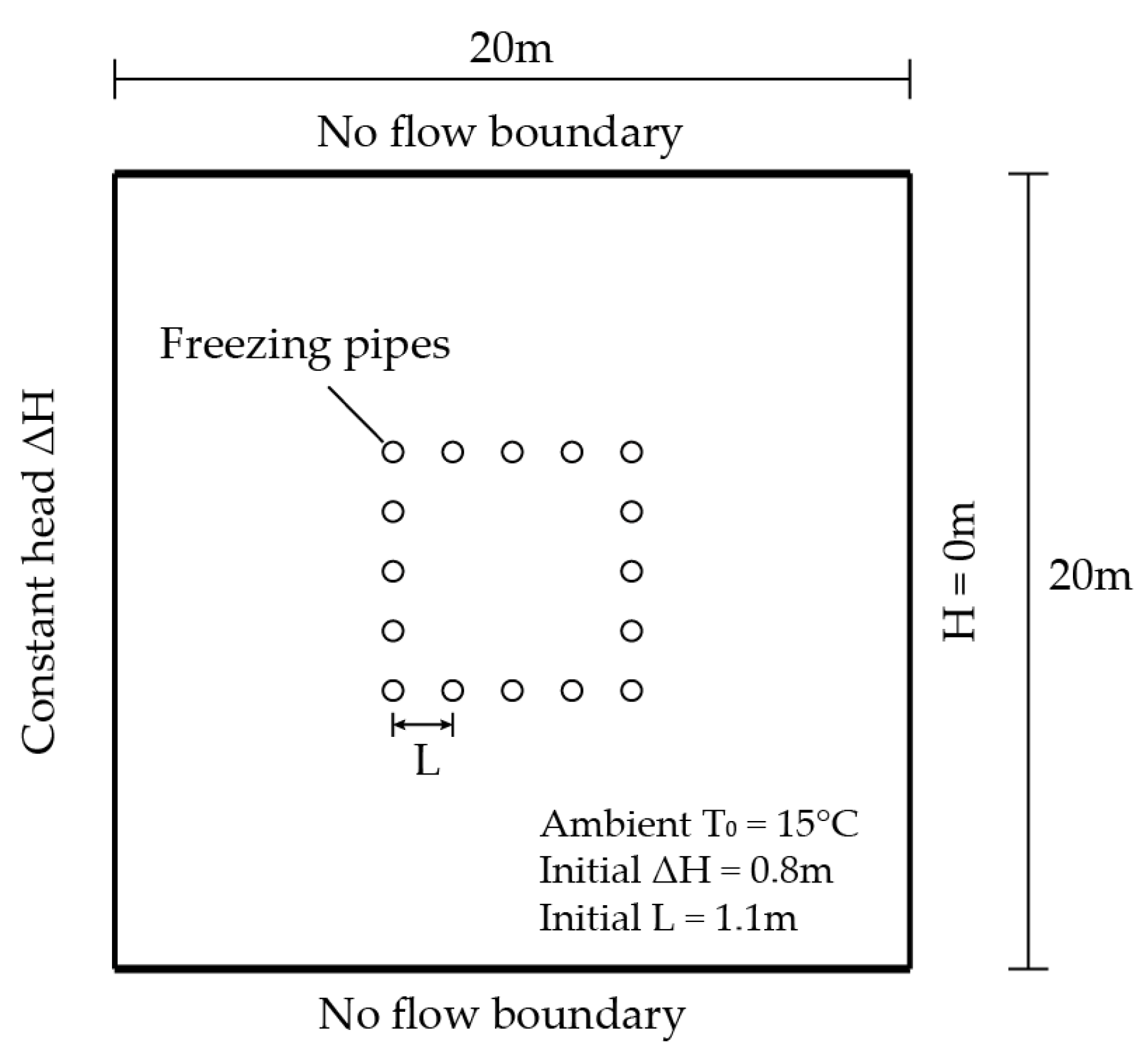
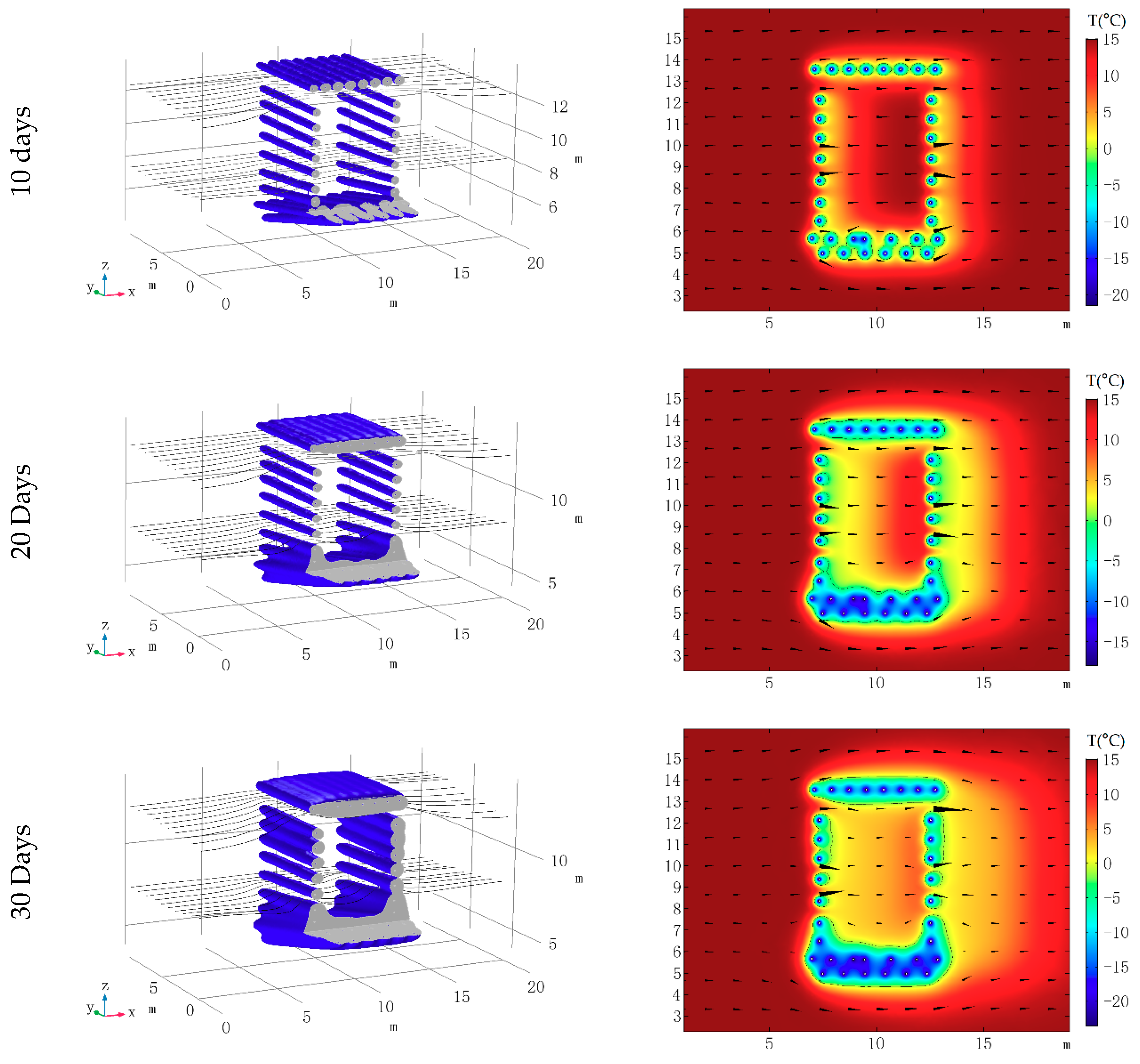
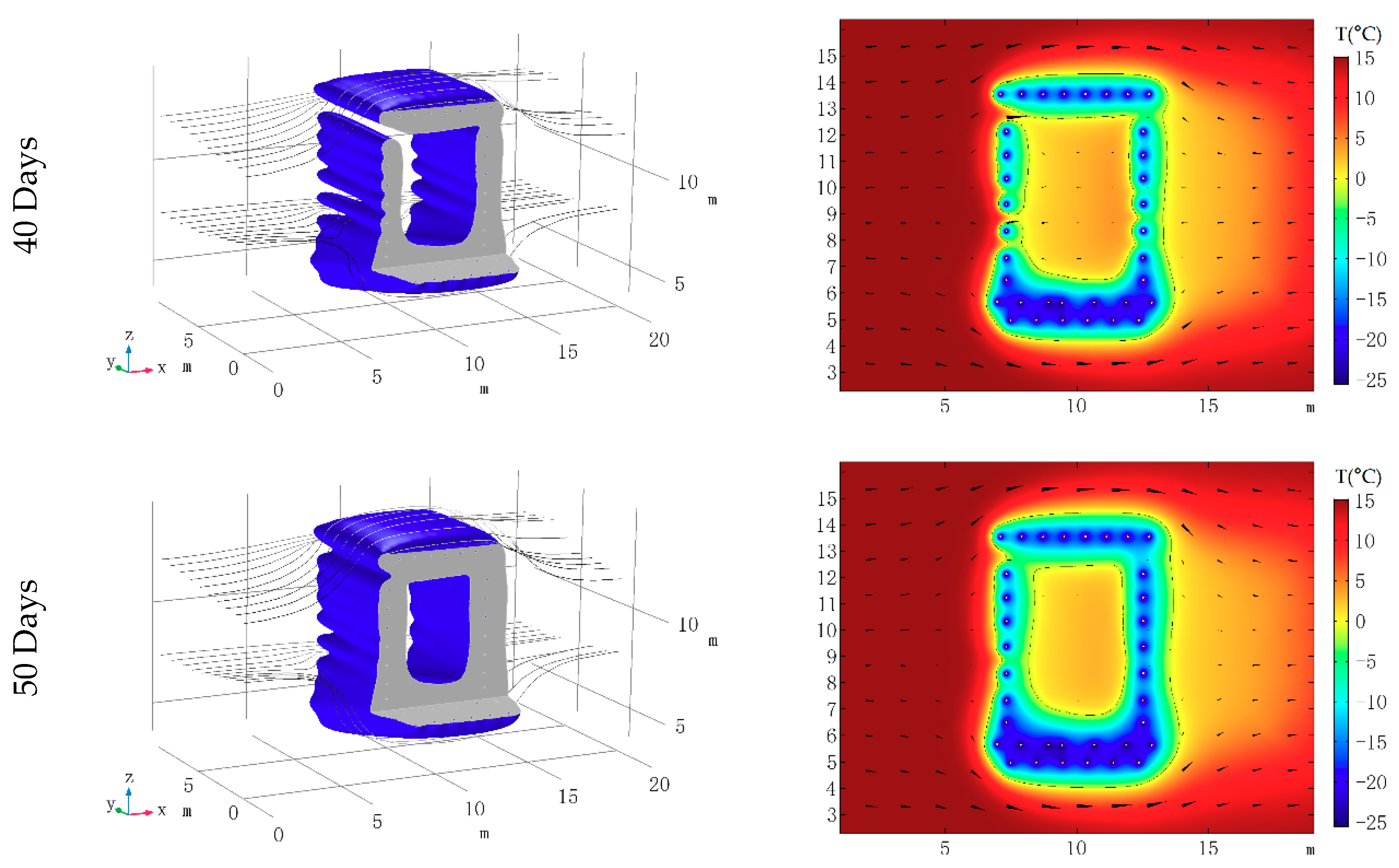
4. Engineering Application
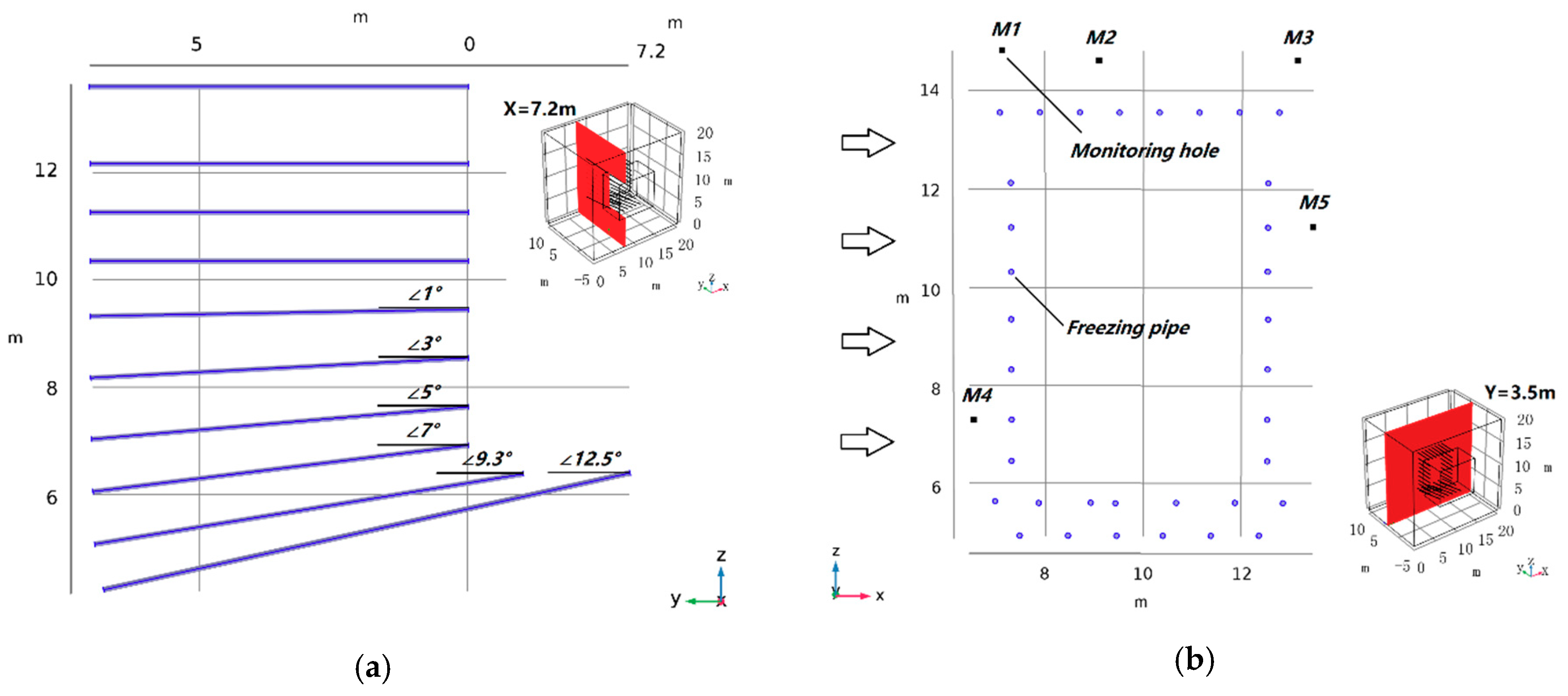
4.1. Engineering Background and the 3D Model
4.2. Boundary and Intial Conditions
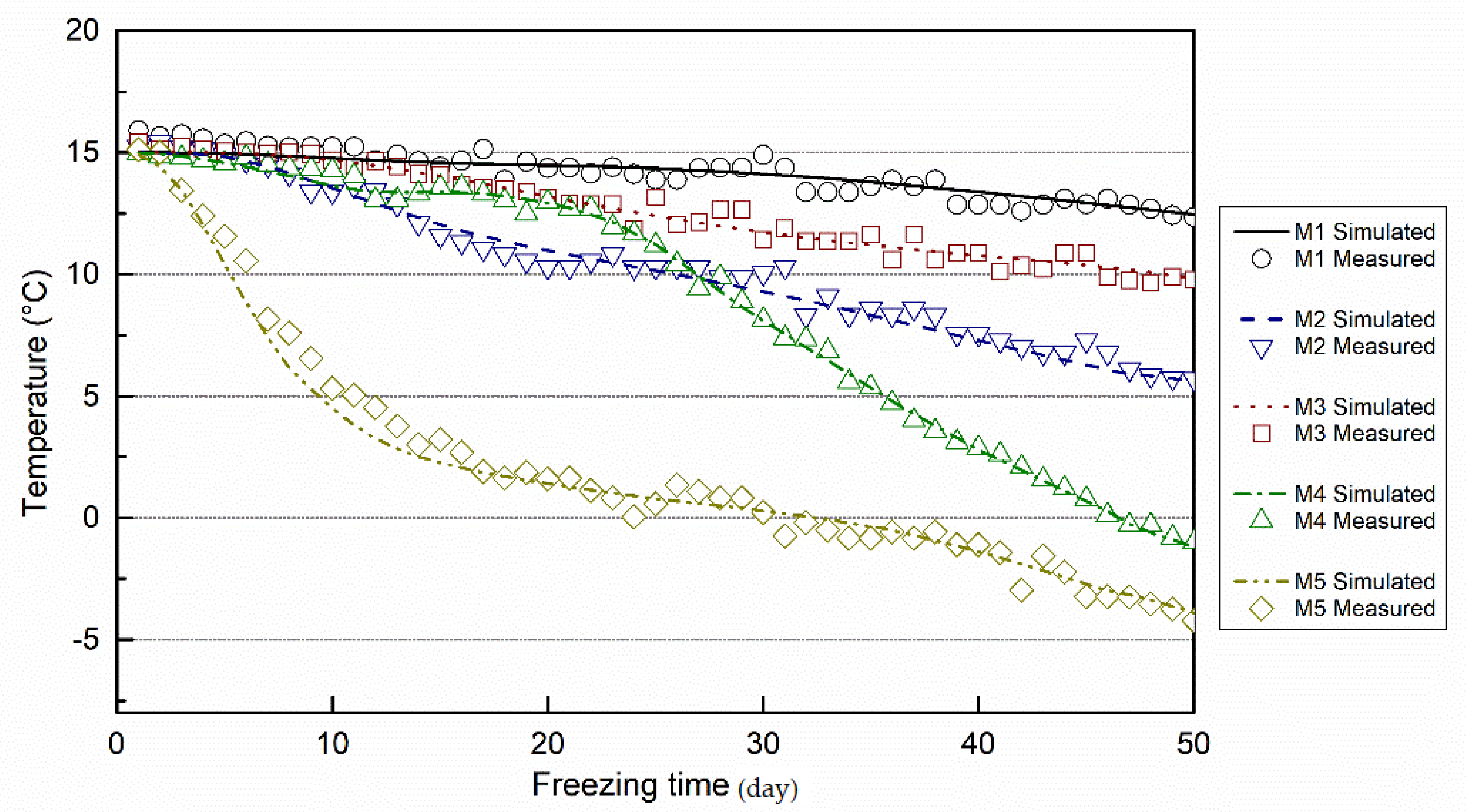
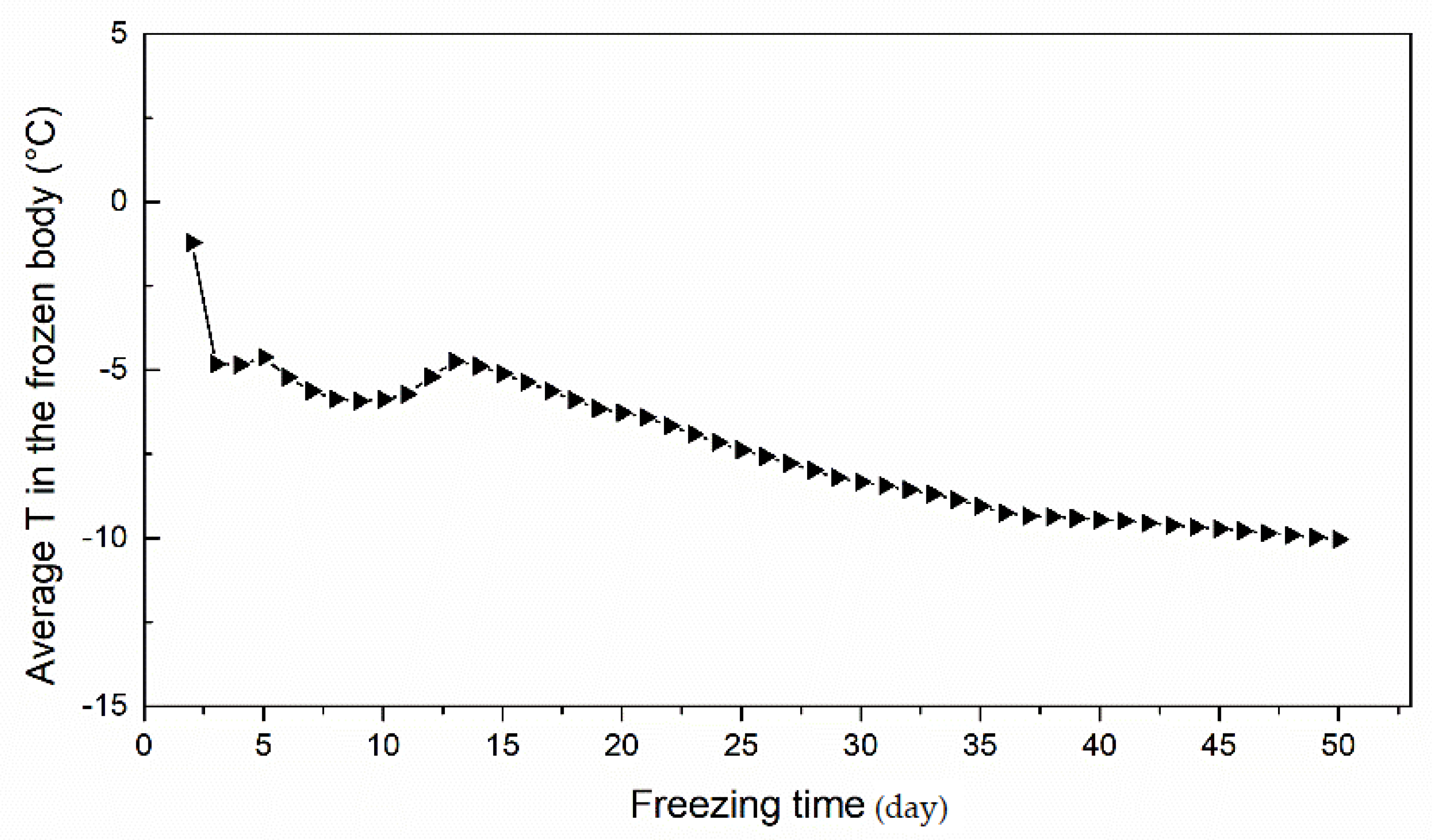
4.3. Simulation Results, Verification and Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gallardo, A.H.; Marui, A. The aftermath of the Fukushima nuclear accident: Measures to contain groundwater contamination. Sci. Total Environ. 2016, 547, 261–268. [Google Scholar] [CrossRef] [PubMed]
- Dash, J. Ground freezing technology for environmental. Ice Phys. Nat. Environ. 2013, 56, 241. [Google Scholar]
- Wallis, S. Freezing under the sea rescues oslofjord highway tunnel. Tunnel 1999, 8, 19–26. [Google Scholar]
- Hu, X.D.; Zhang, L.Y. Artificial Ground Freezing for Rehabilitation of Tunneling Shield in Subsea Environment; Advanced Materials Research; Trans Tech Publications: Zurich, Switzerland, 2013; pp. 517–521. [Google Scholar]
- Papakonstantinou, S.; Anagnostou, G.; Pimentel, E. Evaluation of ground freezing data from the Naples subway. Proc. Inst. Civ. Eng. Geotech. Eng. 2013, 166, 280–298. [Google Scholar] [CrossRef]
- Marwan, A.; Zhou, M.-M.; Abdelrehim, M.Z.; Meschke, G. Optimization of artificial ground freezing in tunneling in the presence of seepage flow. Comput. Geotech. 2016, 75, 112–125. [Google Scholar] [CrossRef]
- Russo, G.; Corbo, A.; Cavuoto, F.; Autuori, S. Artificial ground freezing to excavate a tunnel in sandy soil. Measurements and back analysis. Tunnelling Underground Space Technol. 2015, 50, 226–238. [Google Scholar] [CrossRef]
- Haß, H.; Schäfers, P. International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground. In Application of Ground Freezing for Underground Construction in Soft Ground; Taylor & Francis London: Oxfordshire, UK, 2005; pp. 405–412. [Google Scholar]
- Colombo, G.; Lunardi, P.; Cavagna, B.; Cassani, G.; Manassero, V. The artificial Ground Freezing Technique Application for the Naples Underground. In Proceedings of the Word Tunnel Congress, Agra, India, 22–24 September 2008. [Google Scholar]
- Vitel, M.; Rouabhi, A.; Tijani, M.; Guérin, F. Thermo-hydraulic modeling of artificial ground freezing: Application to an underground mine in fractured sandstone. Comput. Geotech. 2016, 75, 80–92. [Google Scholar] [CrossRef]
- Pimentel, E.; Sres, A.; Anagnostou, G. Large-scale laboratory tests on artificial ground freezing under seepage-flow conditions. Géotechnique 2012, 62, 227. [Google Scholar] [CrossRef]
- Arenson, L.U.; Sego, D.C. Freezing Processes for a Coarse sand with Varying Salinities. In Proceedings of the Cold Regions Engineering & Construction Conference, Edmonton, Alta, 16–19 May 2004. [Google Scholar]
- Bing, H.; Ma, W. Laboratory investigation of the freezing point of saline soil. Cold Reg. Sci. Technol. 2011, 67, 79–88. [Google Scholar] [CrossRef]
- Frivik, P.; Comini, G. Seepage and heat flow in soil freezing. J. Heat Transf. 1982, 104, 323–328. [Google Scholar] [CrossRef]
- Nishimura, S.; Gens, A.; Olivella, S.; Jardine, R. THM-coupled finite element analysis of frozen soil: Formulation and application. Géotechnique 2006. [Google Scholar] [CrossRef]
- Lai, Y.; Pei, W.; Zhang, M.; Zhou, J. Study on theory model of hydro-thermal–mechanical interaction process in saturated freezing silty soil. Int. J. Heat Mass Transf. 2014, 78, 805–819. [Google Scholar] [CrossRef]
- Yang, P.; Ke, J.-M.; Wang, J.; Chow, Y.; Zhu, F.-B. Numerical simulation of frost heave with coupled water freezing, temperature and stress fields in tunnel excavation. Comput. Geotech. 2006, 33, 330–340. [Google Scholar] [CrossRef]
- Wu, D.; Lai, Y.; Zhang, M. Heat and mass transfer effects of ice growth mechanisms in a fully saturated soil. Int. J. Heat Mass Transf. 2015, 86, 699–709. [Google Scholar] [CrossRef]
- Gao, J.; Feng, M.; Yang, W.-H. Research on distribution law of frozen temperature field of fractured rock mass with groundwater seepage. J. Min. Saf. Eng. 2013, 1, 013. [Google Scholar]
- Vitel, M.; Rouabhi, A.; Tijani, M.; Guérin, F. Modeling heat transfer between a freeze pipe and the surrounding ground during artificial ground freezing activities. Comput. Geotech. 2015, 63, 99–111. [Google Scholar] [CrossRef]
- Vitel, M.; Rouabhi, A.; Tijani, M.; Guérin, F. Modeling heat and mass transfer during ground freezing subjected to high seepage velocities. Comput. Geotech. 2016, 73, 1–15. [Google Scholar] [CrossRef]
- Grenier, C.; Anbergen, H.; Bense, V.; Chanzy, Q.; Coon, E.; Collier, N.; Costard, F.; Ferry, M.; Frampton, A.; Frederick, J.; et al. Groundwater flow and heat transport for systems undergoing freeze-thaw: Intercomparison of numerical simulators for 2d test cases. Adv. Water Resour. 2018, 114, 196–218. [Google Scholar] [CrossRef]
- Harlan, R. Analysis of coupled heat-fluid transport in partially frozen soil. Adv. Water Resour. 1973, 9, 1314–1323. [Google Scholar] [CrossRef]
- Guymon, G.L.; Luthin, J.N. A coupled heat and moisture transport model for arctic soils. Water Resour. Res. 1974, 10, 995–1001. [Google Scholar] [CrossRef]
- Hansson, K.; Šimůnek, J.; Mizoguchi, M.; Lundin, L.-C.; Van Genuchten, M.T. Water flow and heat transport in frozen soil. Vadose Zone J. 2004, 3, 693–704. [Google Scholar] [CrossRef]
- McKenzie, J.M.; Voss, C.I.; Siegel, D.I. Groundwater flow with energy transport and water–ice phase change: Numerical simulations, benchmarks, and application to freezing in peat bogs. Adv. Water Resour. 2007, 30, 966–983. [Google Scholar] [CrossRef]
- Lunardini, V. Freezing of soil with phase change occurring over a finite temperature difference. In Proceedings of the 4th International Offshore Mechanics and Arctic Engineering Symposium, Dallas, TX, USA, 17–21 February 1985. [Google Scholar]
- Kurylyk, B.L.; McKenzie, J.M.; MacQuarrie, K.T.; Voss, C.I. Analytical solutions for benchmarking cold regions subsurface water flow and energy transport models: One-dimensional soil thaw with conduction and advection. Adv. Water Resour. 2014, 70, 172–184. [Google Scholar] [CrossRef]
- British Geological Survey Commissioned Report: 2017: Coupled Modelling of Permafrost and Groundwater. A Case Study Approach; British Geological Survey: Keyworth, Nottingham, UK, 2017; p. 157.
- Tan, X.; Chen, W.; Tian, H.; Cao, J. Water flow and heat transport including ice/water phase change in porous media: Numerical simulation and application. Cold Reg. Sci. Technol. 2011, 68, 74–84. [Google Scholar] [CrossRef]
- Mizoguchi, M. Water, Heat and Salt Transport in Freezing Soil. Ph.D. Thesis, University of Tokyo, Tokyo, Japan, 1990. [Google Scholar]
- Sres, A. Theoretische und Experimentelle Untersuchungen zur Künstlichen Bodenvereisung im Strömenden Grundwasser; vdf Hochschulverlag AG: Zurich, Switzerland, 2010; p. 18378. [Google Scholar]
- Ständer, W. Mathematische Ansätze zur Berechnung der Frostausbreitung in Ruhendem Grundwasser im Vergleich zu Modelluntersuchungen für Verschiedene Gefrierrohranordnungen im Schactund Grundbau; Technische Hochschule Fridericiana, Institut für Bodenmechanik und Felsmechanik: Karlsruhe, Germany, 1967. [Google Scholar]
- Victor, H. Die Frostausbreitung beim Künstlichen Gefrieren von Böden unter dem Einfluss Strömenden Grundwassers; Univ. Inst. f. Bodenmechanik u. Felsmechanik: Karlsruhe, Germany, 1969; p. 42. [Google Scholar]
- Sanger, F.; Sayles, F. Thermal and rheological computations for artificially frozen ground construction. Eng. Geol. 1979, 13, 311–337. [Google Scholar] [CrossRef]
- Huang, R.; Chang, M.; Tsai, Y.; Lu, S.; Wu, P. Influence of seepage flow on temperature field around an artificial frozen soil through model testing and numerical simulations. In Proceedings of the 18th Southeast Asian Geotechnical Conference, Singapore, 29–31 May 2013; Leung; Leung, C.F., Goh, S.H., Shen, R.F., Eds.; Geotechnical Society of Singapore, Research Publishing Services: Singapore, 2013. [Google Scholar]
- Jessberger, H.; Jagow-Klaff, R. Bodenvereisung. Grundbau-Taschenbuch, Teil 2: Geotechnische Verfahren; Country Ernst & Sohn: Berlin, Germany, 2001; pp. 121–166. [Google Scholar]
- Andersland, O.B.; Ladanyi, B. Frozen Ground Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Endo, K. Artificial Soil Freezing Method for Subway Construction; Japan Society of Civil Engineers: Tokyo, Japan, 1969. [Google Scholar]
- Zhou, X.; Wang, M.; Zhang, X. Model test research on the formation of freezing wall in seepage ground. J. Chin. Coal Soc. 2005, 30, 196–201. [Google Scholar]
- Williams, P.; Burt, T. Measurement of hydraulic conductivity of frozen soils. Can. Geotech. J. 1974, 11, 647–650. [Google Scholar] [CrossRef]
- Burt, T.; Williams, P.J. Hydraulic conductivity in frozen soils. Earth Surf. Process. Landf. 1976, 1, 349–360. [Google Scholar] [CrossRef]
- Horiguchi, K.; Miller, R. Experimental studies with frozen soil in an “ice sandwich” permeameter. Cold Reg. Sci. Technol. 1980, 3, 177–183. [Google Scholar] [CrossRef]
- Jame, Y.W.; Norum, D.I. Heat and mass transfer in a freezing unsaturated porous medium. Water Resour. Res. 1980, 16, 811–819. [Google Scholar] [CrossRef]
- Heat and Mass Transfer Modeling with GeoStudio 2018, 2nd ed.; GEOSLOPE International Ltd.: Calgary, AB, Canada, 2017.
- Embleton, C. The Frozen Earth: Fundamentals of Geocryology; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Ziegler, M.; Baier, C.; Aulbach, B. Optimization of artificial ground freezing application of tunneling subject to water seepage. In Proceedings of the 17th Internal Conference on Soil Mechanics and Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009. [Google Scholar]
- Zhou, M.; Meschke, G. A three-phase thermo-hydro-mechanical finite element model for freezing soils. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 3173–3193. [Google Scholar] [CrossRef]
- Shen, C.; McKinzie, B.; Arbabi, S. A reservoir simulation model for ground freezing process. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Lackner, R.; Amon, A.; Lagger, H. Artificial ground freezing of fully saturated soil: Thermal problem. J. Eng. Mech. 2005, 131, 211–220. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Density of Soil (kg/m3) | 2600 |
| Density of Water (kg/m3) | 1000 |
| Density of Ice (kg/m3) | 920 |
| Pipe Spacing (m) | 1.0, 1.1, 1.2 1 |
| Head Difference (m) | 0.5, 1.0, 1.5 1 |
| Thermal Conductivity of Soil Grain (W/(m·K)) | 1.5, 2.0, 2.5 1 |
| Thermal Conductivity of Water (W/(m·K)) | 0.6 |
| Thermal Conductivity of Ice (W/(m·K)) | 2.14 |
| Heat Capacity of Soil (J/(kg·K)) | 840 |
| Heat Capacity of Water (J/(kg·K)) | 4200 |
| Heat Capacity of Ice (J/(kg·K)) | 2100 |
| Porosity | 0.3 |
| Permeability Coefficient (m/day) | 20 |
| Latent Heat of Formation (J/kg) | 334,720 |
| Parameters | Value |
|---|---|
| Density of Soil (kg/m3) | 1800 |
| Density of Water (kg/m3) | 1000 |
| Density of Ice (kg/m3) | 920 |
| Head Difference (m) | 0.8 |
| Thermal Conductivity of Soil Grain (W/(m·K)) | 0.73 |
| Thermal Conductivity of Water (W/(m·K)) | 0.6 |
| Thermal Conductivity of Ice (W/(m·K)) | 2.14 |
| Heat Capacity of Soil (J/(kg·K)) | 1020 |
| Heat Capacity of Water (J/(kg·K)) | 4200 |
| Heat Capacity of Ice (J/(kg·K)) | 2100 |
| Porosity | 0.4 |
| Permeability Coefficient (m/day) | 5 |
| Latent Heat of Formation (J/kg) | 334,720 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, R.; Liu, Q.; Xing, Y. Case Study of Heat Transfer during Artificial Ground Freezing with Groundwater Flow. Water 2018, 10, 1322. https://doi.org/10.3390/w10101322
Hu R, Liu Q, Xing Y. Case Study of Heat Transfer during Artificial Ground Freezing with Groundwater Flow. Water. 2018; 10(10):1322. https://doi.org/10.3390/w10101322
Chicago/Turabian StyleHu, Rui, Quan Liu, and Yixuan Xing. 2018. "Case Study of Heat Transfer during Artificial Ground Freezing with Groundwater Flow" Water 10, no. 10: 1322. https://doi.org/10.3390/w10101322
APA StyleHu, R., Liu, Q., & Xing, Y. (2018). Case Study of Heat Transfer during Artificial Ground Freezing with Groundwater Flow. Water, 10(10), 1322. https://doi.org/10.3390/w10101322






