Characteristics of Positive Surges in a Rectangular Channel
Abstract
1. Introduction
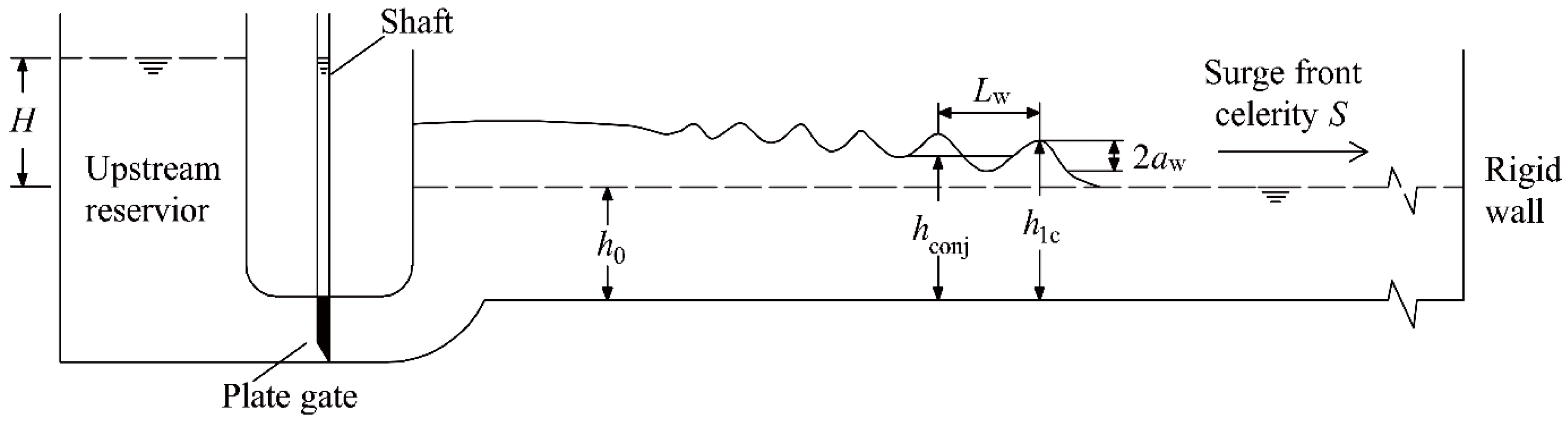
2. Experimental Setup and Experiment
3. Results and Discussion
3.1. Basic Flow Patterns
- In Stage 1, the front of the positive wave is rather smooth.
- Stage 2 corresponds to the generating process of the undular surges, and can be divided into two sub-stages: Stage2a and Stage2b. In Stage 2a, the front head of the positive wave gradually becomes “rough” and develops into a series of cascading steps at the end of this stage; in Stage 2b, the cascading steps develop into a train of well-formed undulations (i.e., non-breaking undular surges) (Figure 2). Additionally, some sidewall shock waves can be observed in this stage that develop upstream of the first wave crest and intersect next to the first crest. This stage ends when some small waves break at the first wave crest (i.e., breaking undular surges) (Figure 3).
- In Stage 3, the wave amplitude decreases and the free-surface undulations become flatter. This stage ends with the disappearance of fluctuating characteristics of water depth at the surge front.
- During Stage 4, the surge front behaves as a nearly vertical water wall (i.e., breaking surges) (Figure 4).
3.2. Free-Surface Properties
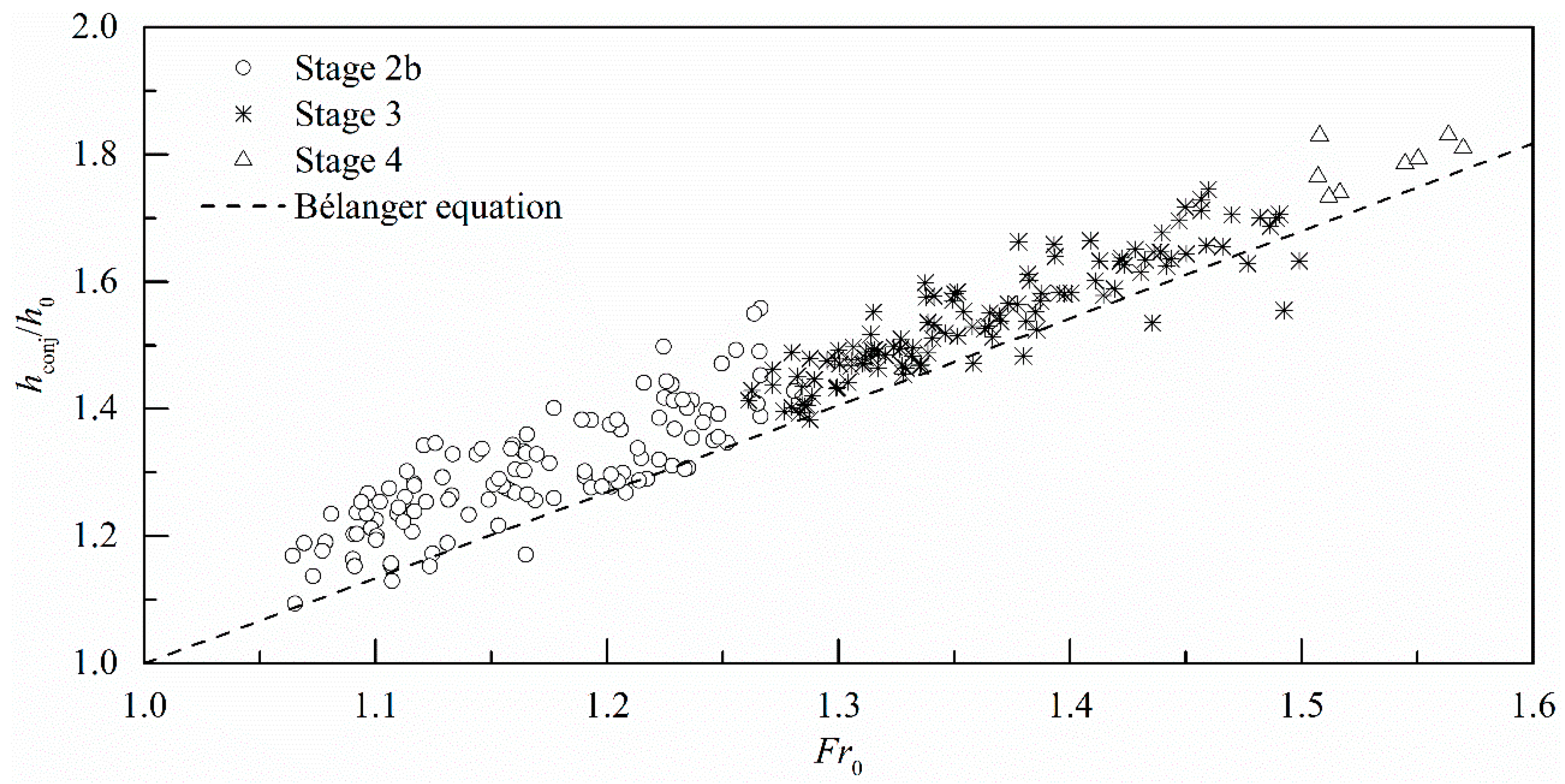
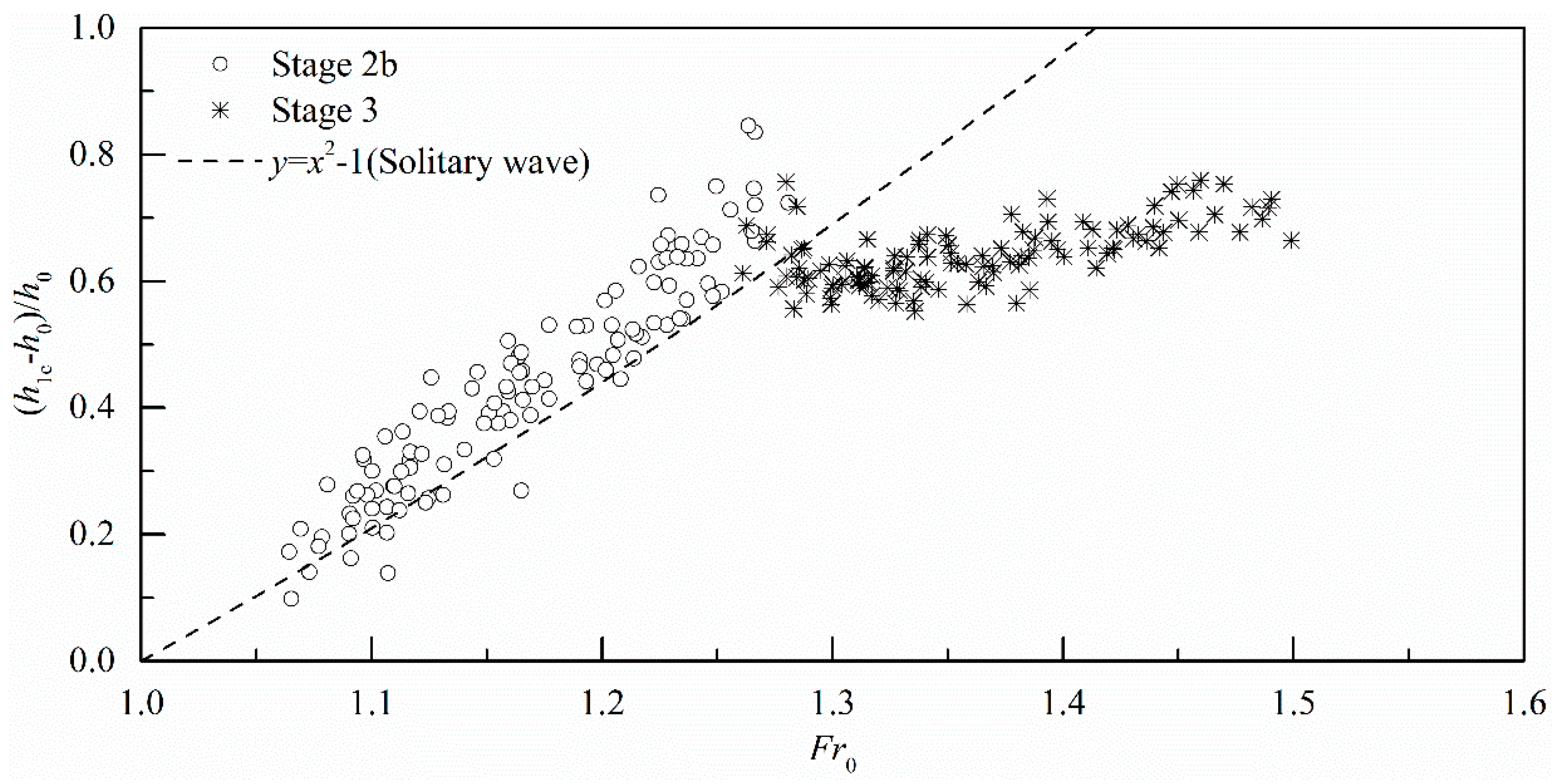
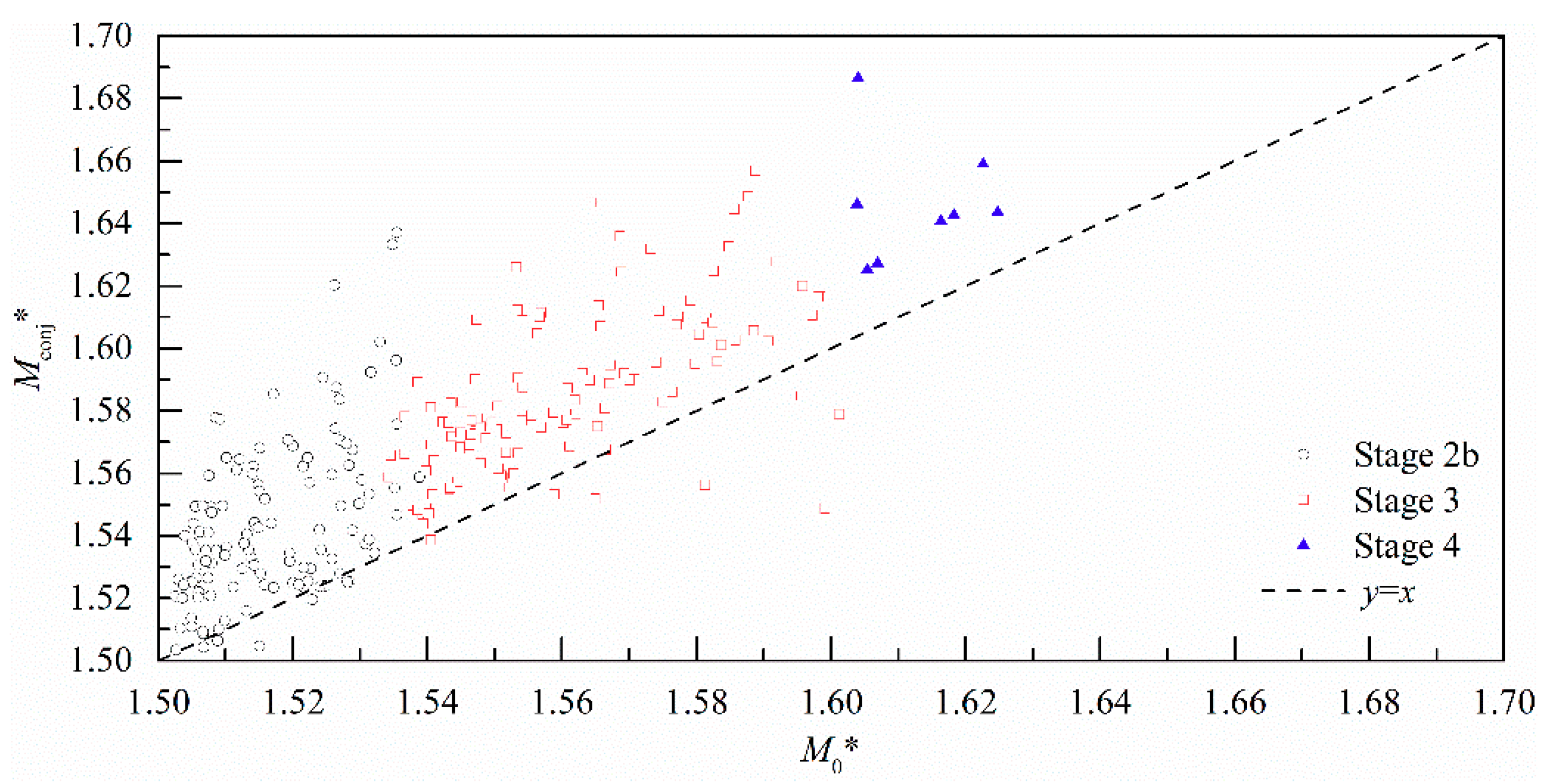
3.2.1. Ratio of Conjugate Depths
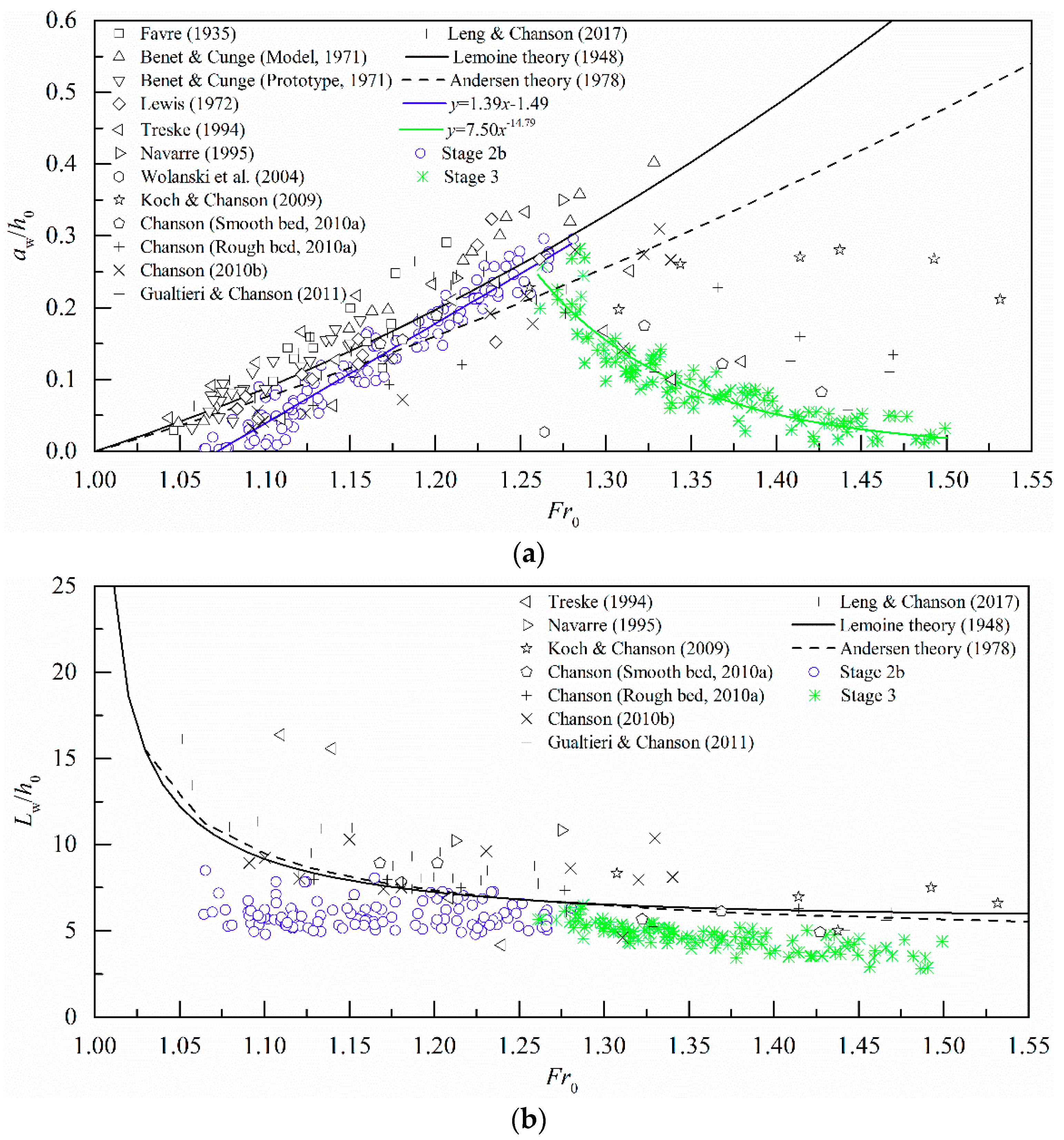
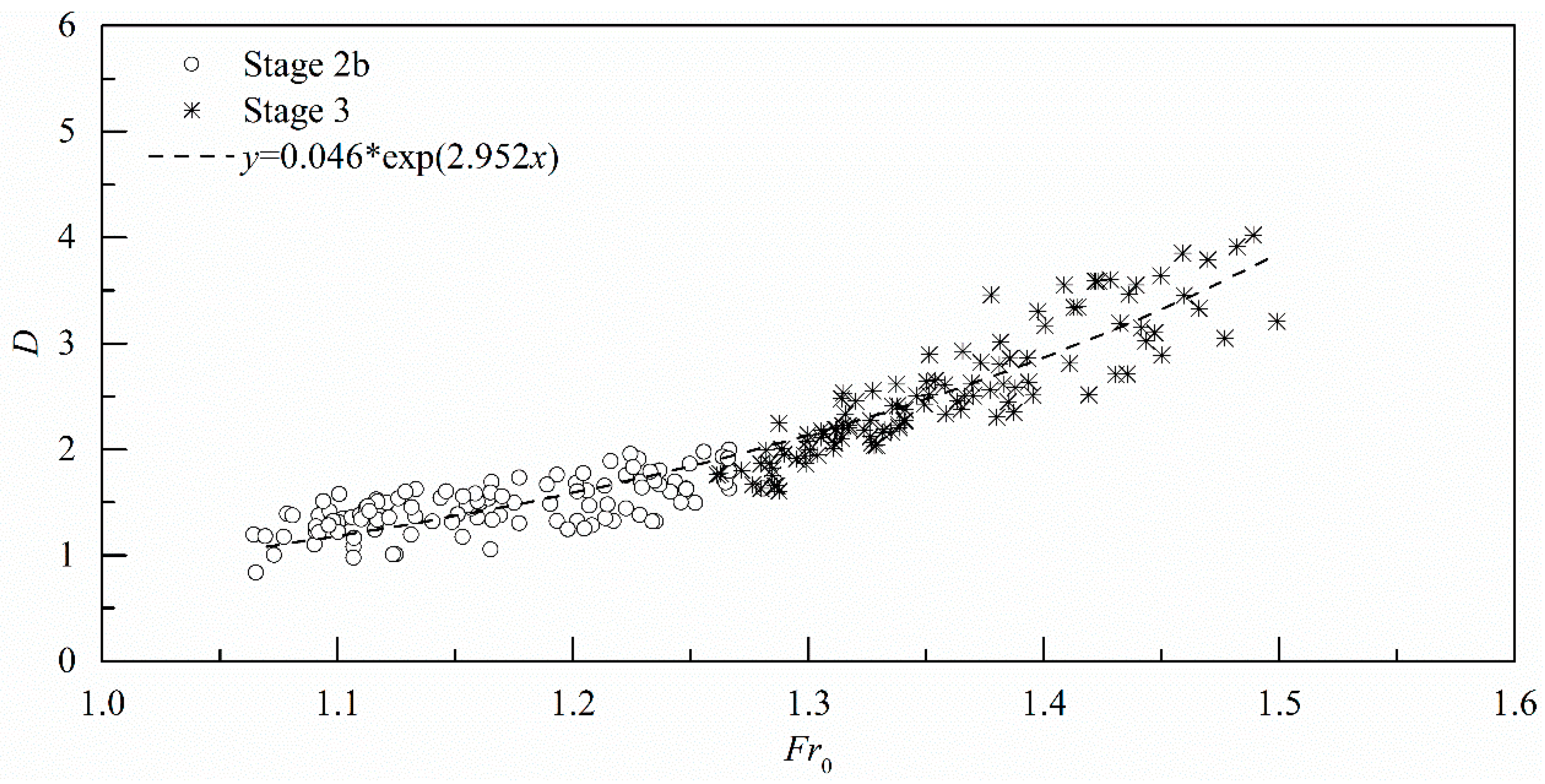
3.2.2. Free-Surface Undulation Characteristics
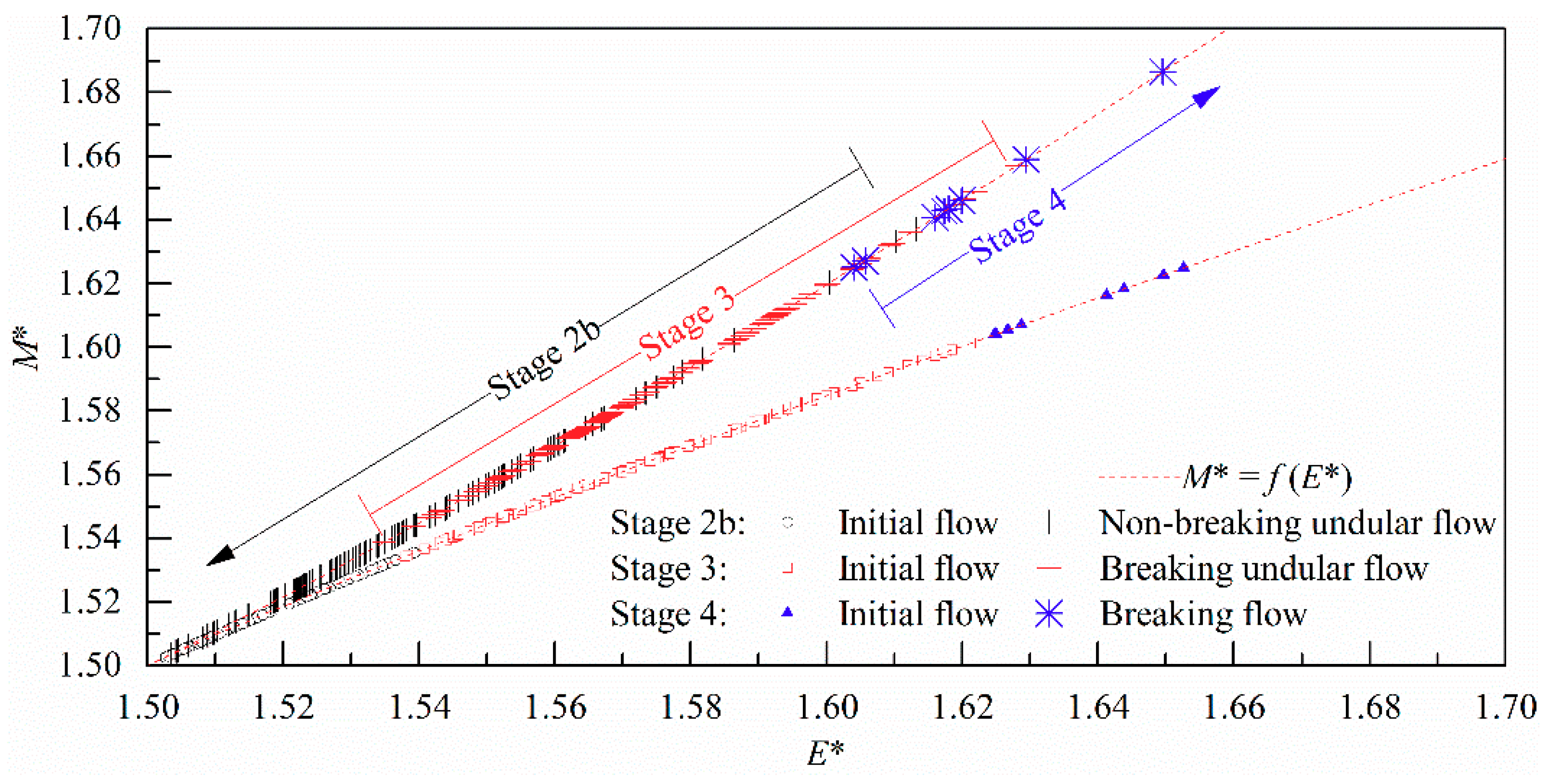
3.2.3. Energy and Momentum Fluxes Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Henderson, F.M. Open-Channel Flow; McMillan Publishing Co.: New York, NY, USA, 1966. [Google Scholar]
- Maeck, A.; Lorke, A. Ship-lock induced surges in an im-pounded river and their impact on subdaily flow velocity variation. River Res. Appl. 2013, 30, 494–507. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Open Channel Flows: An Introduction; Butterworth-Heinemann: Oxford, UK, 2004; p. 630. [Google Scholar]
- Chen, C.L. Unified Theory on Power Laws for Flow Resistance. J. Hydraul. Eng. ASCE 1990, 117, 371–389. [Google Scholar] [CrossRef]
- Kjerfve, B.; Ferreira, H.O. Tidal Bores: First Ever Measurements. Ciência e Cultura (J. Braz. Assoc. Adv. Sci.) 1993, 45, 135–138. [Google Scholar]
- Treske, A. Undular bores (Favre-waves) in open channels—Experimental studies. J. Hydraul. Res. 1994, 32, 355–370. [Google Scholar] [CrossRef]
- Favre, H. Etude Théoretique et Expérimentale des Ondes de Translation Dans les Canaux Découverts (Theoretical and Experimental Study of Travelling Surges in Open Channels); Dunod: Paris, France, 1935. [Google Scholar]
- Benet, F.; Cunge, J.A. Analysis of experiments on secondary undulations caused by surge waves in trapezoidal channels. J. Hydraul. Res. 1971, 9, 11–33. [Google Scholar] [CrossRef]
- Soares-Frazão, S.; Zech, Y. Undular bores and secondary waves—Experiments and hybrid finite-volume modeling. J. Hydraul. Res. 2002, 40, 33–43. [Google Scholar] [CrossRef]
- Koch, C.; Chanson, H. Turbulence measurements in positive surges and bores. J. Hydraul. Res. 2009, 47, 29–40. [Google Scholar] [CrossRef]
- Chanson, H. Unsteady turbulence in tidal bores: Effects of bed roughness. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 247–256. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Experimental study of a positive surge. Part 1: Basic flow patterns and wave attenuation. Environ. Fluid Mech. 2012, 12, 145–159. [Google Scholar] [CrossRef]
- Chanson, H. Undular Tidal Bores: Basic Theory and Free-surface Characteristics. J. Hydraul. Eng. ASCE 2010b, 136, 940–944. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Experimental study of a positive surge. Part 2: Comparison with literature theories and unsteady flow field analysis. Environ. Fluid Mech. 2011, 11, 641–651. [Google Scholar] [CrossRef]
- Leng, X.; Chanson, H. Upstream Propagation of Surges and Bores: Free-Surface Observations. Coast. Eng. J. 2017, 59, 1750003. [Google Scholar] [CrossRef]
- Lemoine, R. Sur les ondes positives de translation dans les canaux et sur le ressaut ondulé de faible amplitude (On the Positive Surges in Channels and on the Undular Jumps of Low Wave Height). Jl La Houille Blanche 1948, 2, 183–185. (In French) [Google Scholar]
- Andersen, V.M. Undular Hydraulic Jump. J. Hydraul. Div. ASCE 1978, 104, 1185–1188. [Google Scholar]
- Viero, D.P.; Peruzzo, P.; Defina, A. Positive Surge Propagation in Sloping Channels. Water 2017, 9, 518–530. [Google Scholar] [CrossRef]
- Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar] [CrossRef]
- McCowan, J. On the solitary wave. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1891, 32, 45–58. [Google Scholar] [CrossRef]
- Lewis, A.W. Field Studies of a Tidal Bore in the River Dee. Master’s Thesis, University College of North Wales, Bangor, UK, 1972. [Google Scholar]
- Navarre, P. Aspects Physiques du Caracteres Ondulatoire duMacaret en Dordogne (Physical Features of the Undulations of the Dordogne River Tidal Bore). Ph.D. Thesis, University of Bordeaux, Bordeaux, France, 1995. [Google Scholar]
- Wolanski, E.; Williams, D.; Spagnol, S.; Chanson, H. Undular tidal bore dynamics in the Daly Estuary, Northern Australia. Estuar. Coast. Shelf Sci. 2004, 60, 629–636. [Google Scholar] [CrossRef]
- Montes, J.S.; Chanson, H. Characteristics of undular hydraulic jumps. Results and calculations. J. Hydraul. Eng. ASCE 1998, 124, 192–205. [Google Scholar] [CrossRef]
- Chanson, H. Physical modelling of the flow field in an undular tidal bore. J. Hydraul. Res. 2005, 43, 234–244. [Google Scholar] [CrossRef]
- Montes, J.S. Hydraulics of Open Channel Flow; ASCE Press: New York, NY, USA, 1998. [Google Scholar]
- Benjamin, T.B.; Lighthill, M.J. On cnoidal waves and bores. Proc. R. Soc. Lond. Ser. A 1954, 224, 448–460. [Google Scholar] [CrossRef]






| Series | h0 (m) | tv (s) | H (m) |
|---|---|---|---|
| A | 0.08 | 20 | 0.1, 0.2, 0.3, 0.4 |
| B | 0.08 | 25 | 0.1, 0.2, 0.3, 0.4 |
| C | 0.08 | 30 | 0.1, 0.2, 0.3, 0.4 |
| D | 0.08 | 40 | 0.1, 0.2, 0.3, 0.4 |
| Flow Stage Transition | Surge Froude Number Fr0 |
|---|---|
| 1–2a | ≈1.03 |
| 2a–2b | 1.07–1.10 |
| 2b–3 | 1.26–1.28 |
| 3–4 | 1.45–1.50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, F.; Li, Y.; Xuan, G.; Li, Z.; Zhu, L. Characteristics of Positive Surges in a Rectangular Channel. Water 2018, 10, 1473. https://doi.org/10.3390/w10101473
Zheng F, Li Y, Xuan G, Li Z, Zhu L. Characteristics of Positive Surges in a Rectangular Channel. Water. 2018; 10(10):1473. https://doi.org/10.3390/w10101473
Chicago/Turabian StyleZheng, Feidong, Yun Li, Guoxiang Xuan, Zhonghua Li, and Long Zhu. 2018. "Characteristics of Positive Surges in a Rectangular Channel" Water 10, no. 10: 1473. https://doi.org/10.3390/w10101473
APA StyleZheng, F., Li, Y., Xuan, G., Li, Z., & Zhu, L. (2018). Characteristics of Positive Surges in a Rectangular Channel. Water, 10(10), 1473. https://doi.org/10.3390/w10101473





