Communication Optimization for Multiphase Flow Solver in the Library of OpenFOAM

Abstract

Multiphase flow solvers are widely-used applications in OpenFOAM, whose scalability suffers from the costly communication overhead. Therefore, we establish communication-optimized multiphase flow solvers in OpenFOAM. In this paper, we first deliver a scalability bottleneck test on the typical multiphase flow case damBreak and reveal that the Message Passing Interface (MPI) communication in a Multidimensional Universal Limiter for Explicit Solution (MULES) and a Preconditioned Conjugate Gradient (PCG) algorithm is the short slab of multiphase flow solvers. Furthermore, an analysis of the communication behavior is carried out. We find that the redundant communication in MULES and the global synchronization in PCG are the performance limiting factors. Based on the analysis, we propose our communication optimization algorithm. For MULES, we remove the redundant communication and obtain optMULES. For PCG, we import several intermediate variables and rearrange PCG to reduce the global communication. We also overlap the computation of matrix-vector multiply and vector update with the non-blocking computation. The resulting algorithms are respectively referred to as OFPiPePCG and OFRePiPePCG. Extensive experiments show that our proposed method could dramatically increase the parallel scalability and solving speed of multiphase flow solvers in OpenFOAM approximately without the loss of accuracy.

1. Introduction

OpenFOAM [1] is an open source library written in object-oriented C++ for Computational Fluid Dynamics (CFD) and is extensively applied in a wide range of engineering fields, such as aerospace, shipbuilding, oil exploration, and so on. Multiphase flow is generally used for referring to fluid flow composed of a material with different phases or different components [2]. The accurate representation and solution of this flow is a key part in the ship engineering, chemistry, hydraulics and other industries [3]. As a result, OpenFOAM develops a series of multiphase flow solvers like interFoam, interphaseChangeFoam, and compressibleInterFoam to help users study multiphase flow. Until now, the scalability and solving speed of multiphase flow solvers in the OpenFOAM library is relatively smaller and slower [4], in comparison with the commercial CFD software, e.g., ANSYS Fluent [5], ANSYS CFX [6]. According to the scalability and efficiency test of OpenFOAM [4,7,8,9], there is a great part of the room for scalability improvement of multiphase flow solvers in OpenFOAM (This paper is an extended version of our previous conference publication [10]).

Up to now, there have been some studies investigating the bottleneck in scalability and efficiency of solvers in OpenFOAM. Culpo et al. [4] have found that the communication is the main bottleneck in the large-scale simulation of OpenFOAM after strong and weak scaling tests. Scalability tests on some multiphase flow solvers have been carried out by Rivera et al. [11], Duran et al. [8], and Dagnaa et al. [9], all of which reveal that the bottleneck in the scalability of multiphase flow solvers is communication. So far, there are various attempts to decrease the communication overhead and increase the scalability of solvers. One of the most popular approaches is to take the advantage of thread parallelism on multi-core architectures to reduce MPI communication [9,12]. Besides the thread-level parallelism, another methods is to make full use of the heterogeneous high performance computing (HPC) platforms or public external library PETSc [13] to directly improve the performance of OpenFOAM [14,15]. These methods obtain impressive enhancement in parallel performance. However, they retain some feeble design in MPI communication of multiphase flow solvers and lead to deficient exploitation of the cluster.

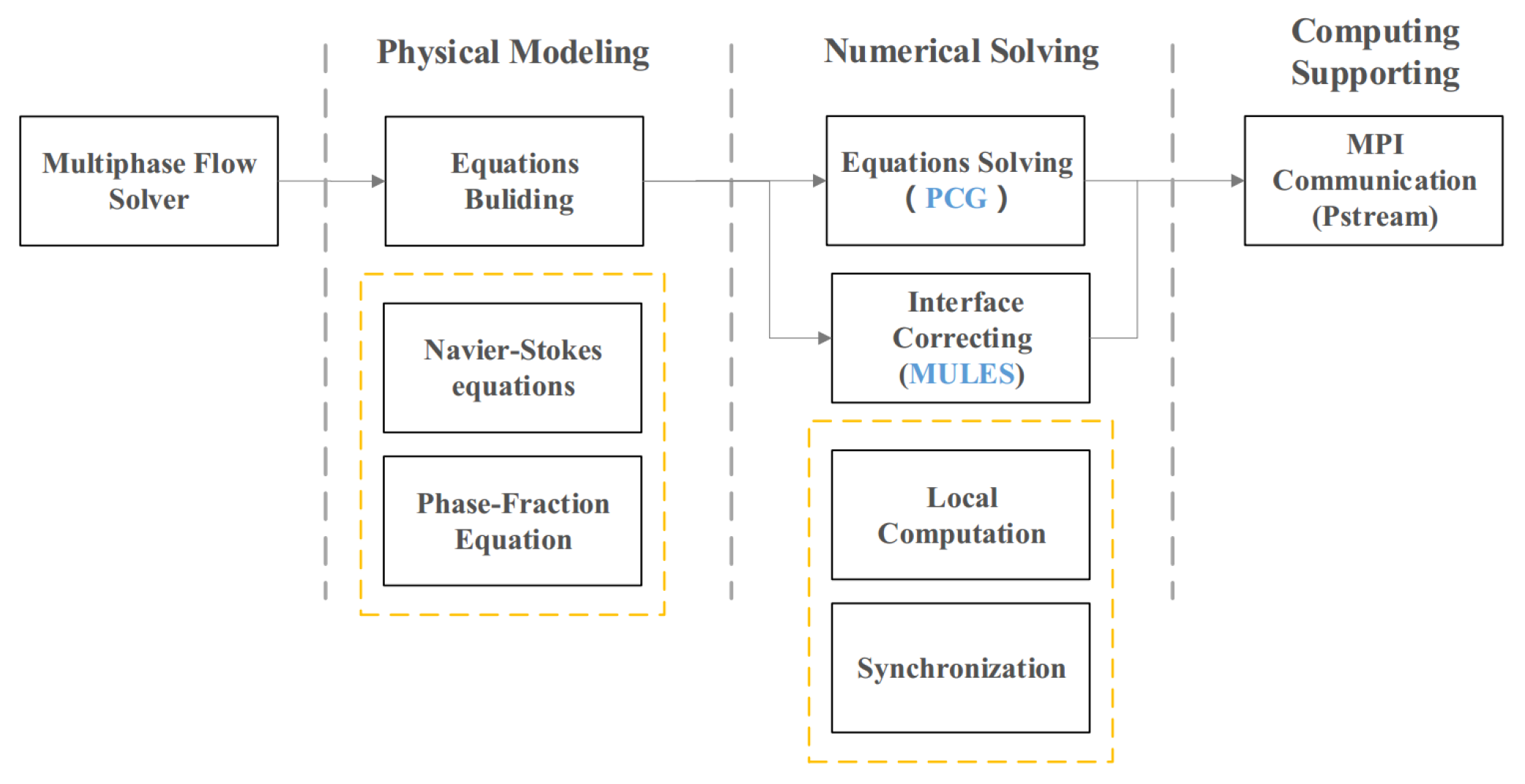
The multiphase flow solvers in OpenFOAM are mainly based on the volume-of-fluid (VOF) method [16]. VOF method has been proven to be an efficient and successful approach to simulate the fluid–fluid interface without complex mesh motion and topology changes. The core work of multiphase flow solvers is to solve the Navier–Stokes equations and phase-fraction equation [17]. The framework of multiphase flow solvers in OpenFOAM is illustrated in Figure 1. During the process of physical modeling, users are required to build the equations of different models in multiphase flow, all of which will be solved in the next numerical solving procedure. In the second stage is not only the solution of linear system obtained by the finite volume method (FVM) methods [18], but also the limitation of Zalesak’s weighting factor, which originates from the Flux Corrected Transport (FCT) and can combine transportive flux given by some low order scheme and high order scheme to avoid interface dispersing [19]. The limitation is realized by MULES and the linear system is solved by some iterative solvers like PCG solver. It is noted that the communication mechanism in OpenFOAM is used to interchange field values among sub domain [20]. There are two parts in the process of numerical solving: local computation and synchronization. For the sake of parallel computing, there is a communication shared library like Psteam, providing parallel support at the computing supporting layer.

Both MULES and PCG are key modules in multiphase flow simulation. In OpenFOAM, Multidimensional Universal Limiter for Explicit Solution (MULES) is the dominant technique for the limitation of Zalesak’s weighting factor to guarantee the boundedness of interface [16] and a Preconditioned Conjugate Gradient (PCG) algorithm is one of the most effective iterative methods for solving large sparse symmetric positive definite linear equations [21]. As for the bottleneck in MULES, our experiment result shows that the redundant communication is a major bottleneck in the large scale computing of MULES. When it comes to the bottleneck of PCG, as early as the 1980s and 1990s, Duff I [22] and Dt Sturler [23] have proved that the global communication is the main bottleneck of the development of parallel PCG method from the perspective of experimental test analysis and performance model analysis.

In this paper, we propose a communication optimization method based on the framework of multiphase flow solvers. We first present an analysis of communication bottleneck on multiphase flow solvers, which show that the communication overhead in MULES and PCG is the hindrance to high-efficient multiphase solvers. After this, we then show our communication optimization for MULES and PCG in multiphase flow solvers. The C++ code of our work will be publicly available at https://github.com/cosoldier/OF231-Comm-opt. Experiments prove that the optimized OpenFOAM significantly enhances the scalability and solving speed of multiphase flow simulation.

The main contributions of this paper are:

• We deliver a scalability bottleneck test of multiphase solvers and reveal that the Message Passing Interface (MPI) communication in MULES and PCG is the short slab of these solvers.
• To address the bottleneck, we analyze Reviewer 4 the communication mechanism of MULES and PCG in OpenFOAM and find the redundant communication in MULES and the key synchronization in PCG. To the best of our knowledge, this is the first study to find the redundant communication of MULES in OpenFOAM.
• We propose our communication optimization algorithm. To begin with, we design OFPiPePCG and OFRePiPePCG solvers to reduce and hide global communication. We then design optMULES which eliminates redundant communication in MULES.
• We evaluate our method based on three typical cases in multiphase flow simulation. Tests show that our method dramatically increases the strong scalability by three times and cut execution time down by up to 63.87% in test cases. A real-life application case dam break flood is also designed and tested for the verification of our method in real application.

The extension of our journal paper to our previous conference publication [10] is as follows. In this journal article, for the completeness of the theory behind this optimization, we give the theoretical analysis and proof of our proposed method (Section 2.2 and Section 2.3; Section 3.2) to make our optimization theory more solid. In addition, we carry out more experiments to illustrate the effectiveness of our communication optimization method, ranging from a verification test for redundant communication (Section 2.2; Figure 2) to a complex real-life 3D multiphase flow simulation (Section 5.8; Figure 3;

Table 1. Results of tests on a head-form case. The OF-opt means optimized OpenFOAM

Runtime in Head-Form Case (s).
cores	12	24	48	96	192	384	768	1152
OF-opt	7140.80	2957.81	994.63	277.82	193.08	167.74	576.17	2476.82
OF-ori	7330.81	3207.62	1289.28	464.27	847.88	2634.08	11,895.50	77,486.78

). Finally, we provide key details of the implementation of our optimization (e.g.,

Table 2. Some descriptions of notations.

Notations	Descriptions
$\alpha$	Volume fraction
U	Velocity
P	Number of processors
$t_s$	Start-up time of inter-processor communications
$t_w$	Word transmission time of inter-processor communications
$n_z$	Average number of non-zero elements in a row of a matrix
len	Length of a vector
MULES	Multidimensional Universal Limiter for Explicit Solution
PCG	Preconditioned Conjugate Gradient
Pstream	An OpenFOAM library for inter-processor communications stream
syncTools	An OpenFOAM tool to aid synchronizing lists across coupled patches
Field Function	OpenFOAM high performance macro functions for Field algebra

and 

Table 3. Comparison of the PCG algorithm.

Method	Vec	MV	Pre	All	Overlap	Init
PCG	3	1	1	2All	None	1Pre,1MV
OFPiPePCG	8	1	1	1Iall	1Pre,1MV	2Pre,3MV
OFRe- PiPePCG	8	1	1	1Iall	1Pre,1MV, 2Vec	2Pre,3MV

, and Section 4).

The remainder of our work is organized as follows: we present a bottleneck test and analysis in Section 2. Section 3 shows the communication optimization algorithm. Subsequently, Section 4 shows the implementation in details, followed by experimental analysis in Section 5. Section 6 shows the conclusion.

2. Bottleneck Test and Analysis

2.1. Key Modules and MPI Communications

To help analyze bottleneck and optimize performance, it is necessary to detect the runtime and MPI communications in different modules. Integrated Performance Monitoring(IPM) is a lightweight profiling infrastructure for parallel codes [24], which provides a low-overhead performance profile in a parallel program. We use the IPM toolkit to track the damBreak case. The details of damBreak will be shown in Section 5.1. The overhead of modules and key MPI operations are shown in Figure 4 and Figure 5.

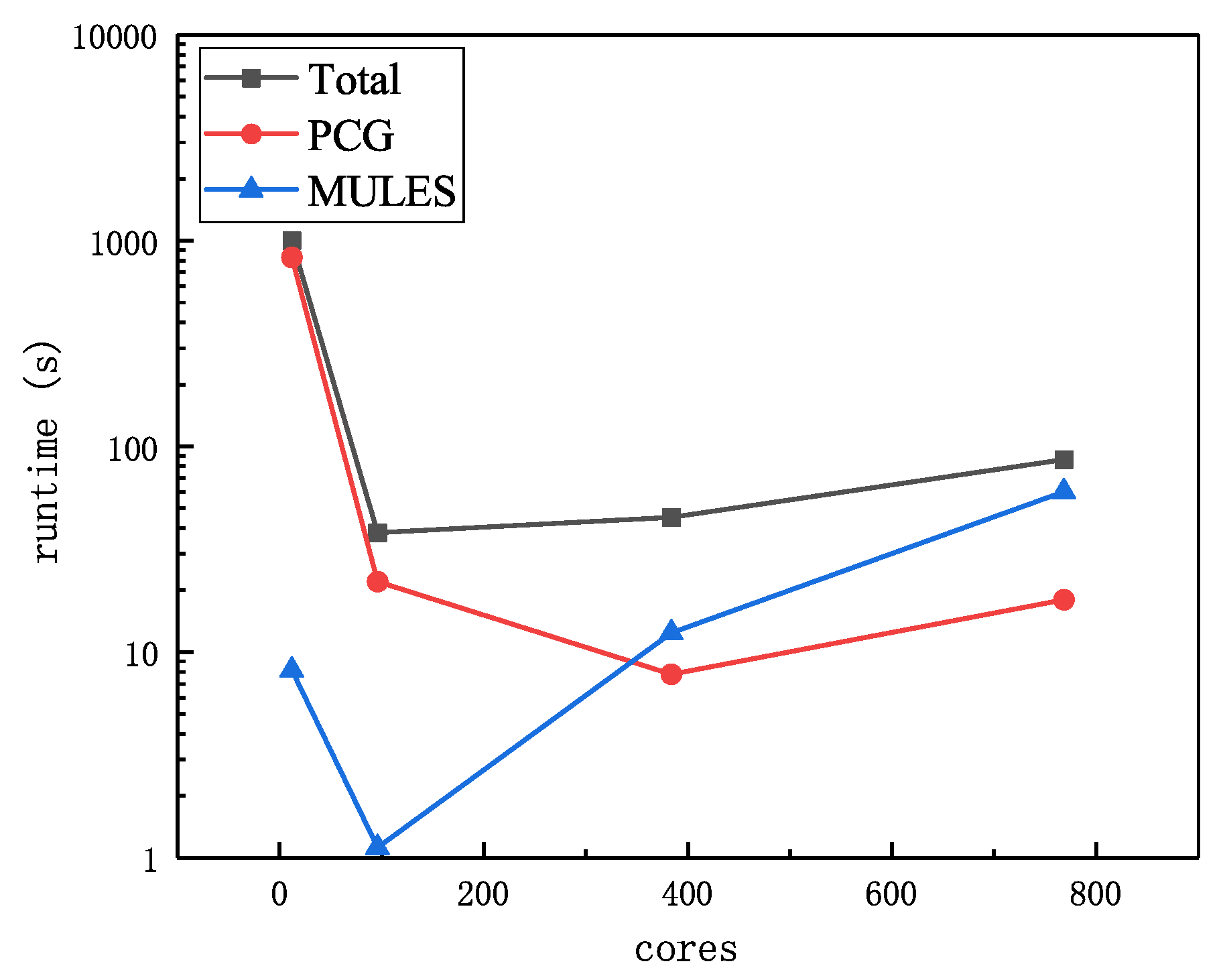
From Figure 4, we can find that the total runtime rapidly hits bottom at the number of 96 cores before a monotonous rise between 96 and 768. The upward trend is caused by the rapid increase of the overload in MULES and PCG. Both of which take more cost, as the degree of parallelism going up. Compared with PCG, MULES suffers more from the large-scale parallel computation. Remarkably, MULES and PCG cost about 69.8% and 20.8% of the total execution time in the 768 degrees of parallelism. Thus, it is clear that MULES and PCG are the hotspots of multiphase flow simulation. When maintaining the momentum of the decrease in MULES and PCG or even making the sharp increase gentle, the downward trend in total runtime will be sustained and the solving speed of multiphase flow solver will benefit.

During the execution process of MULES and PCG, the local process has frequent communication with other processes. For the sake of simplicity and efficiency, a dedicated communication library Pstream is designed to manage the communication in OpenFOAM. Pstream mainly uses MPI protocol for the communication in parallel computation.

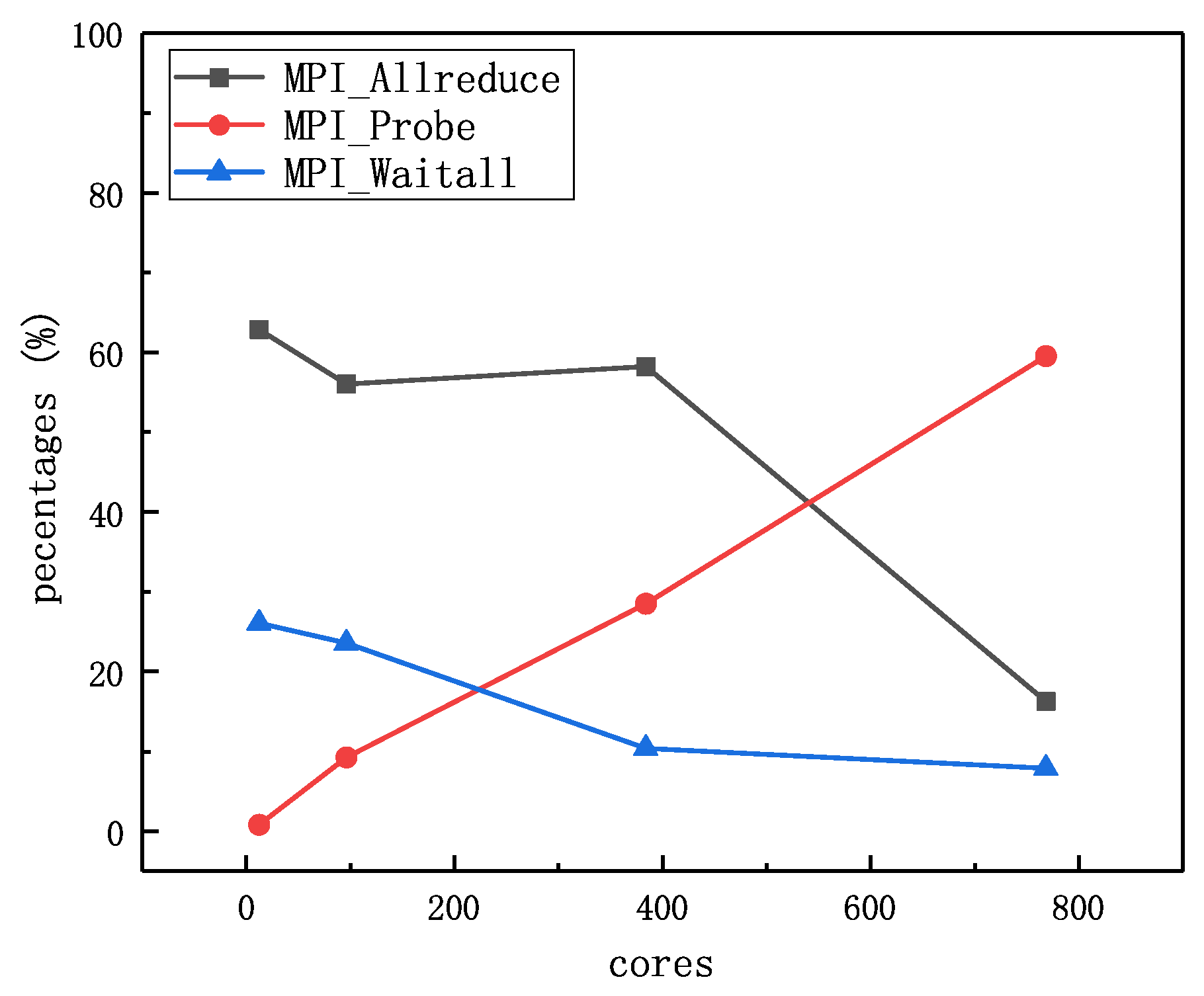
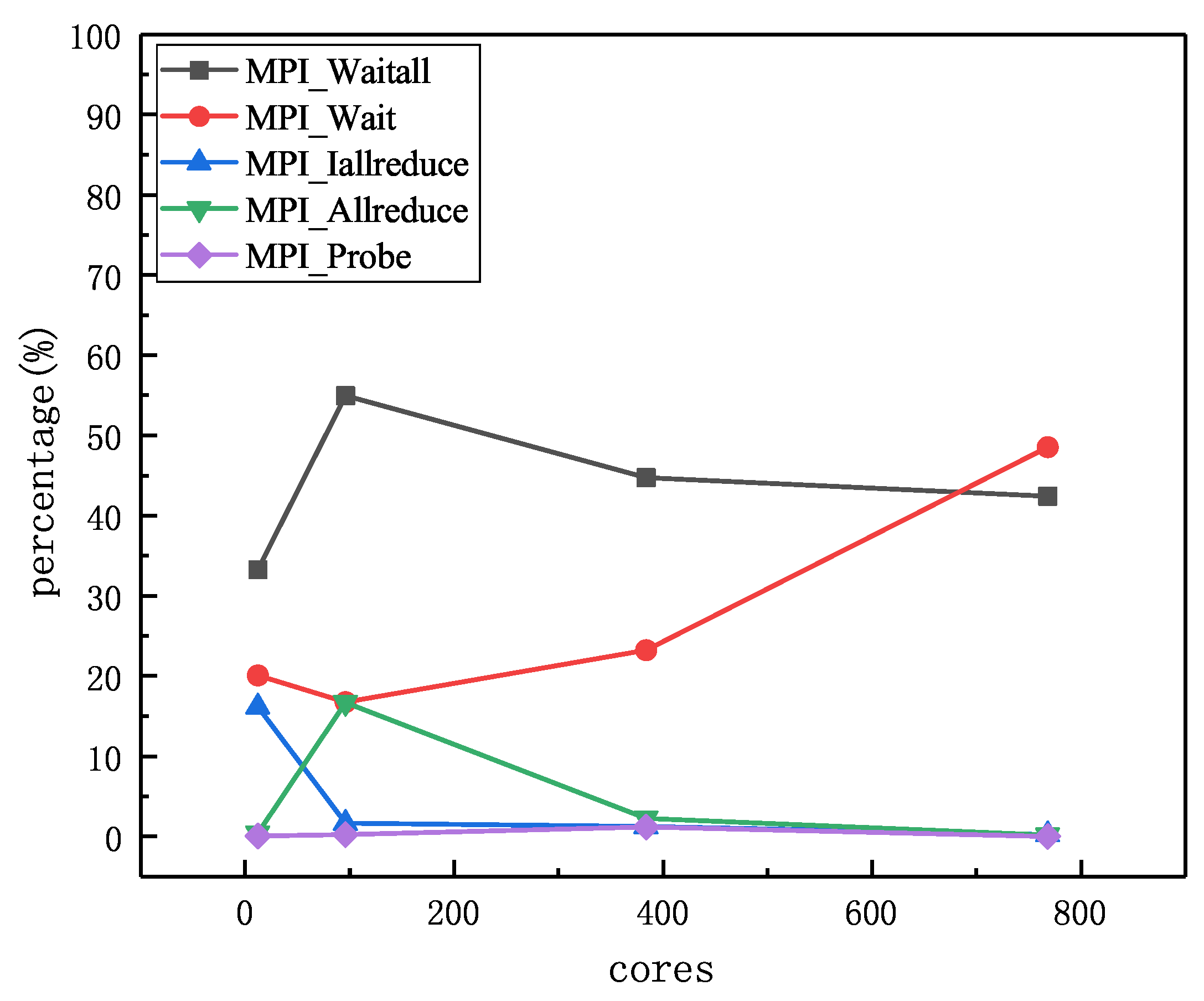
The percentages of key MPI communication overhead relative to total communication time is illustrated in Figure 5. There are three key MPI communications, the sum of which could occupy almost 90 percent of total runtime. As the number of cores increases, the execution time of key MPI operations goes up. Note that the decline of MPI_Allreduce() and MPI_Waitall() is the result of a dramatic increase in MPI_Probe(). At a small-scale parallel computing stage (cores < 384), the MPI_Allreduce() is the dominant MPI communication, while the MPI_Probe() becomes a major operation when the number of cores rises. We can figure out that the MPI_Probe() takes up to 59.6% of the total execution time at 768 cores and the MPI_Allreduce() accounts for 62.7% at 12 cores. Therefore, MPI_Probe() and MPI_Allreduce() is the communication bottleneck of multiphase flow solver.

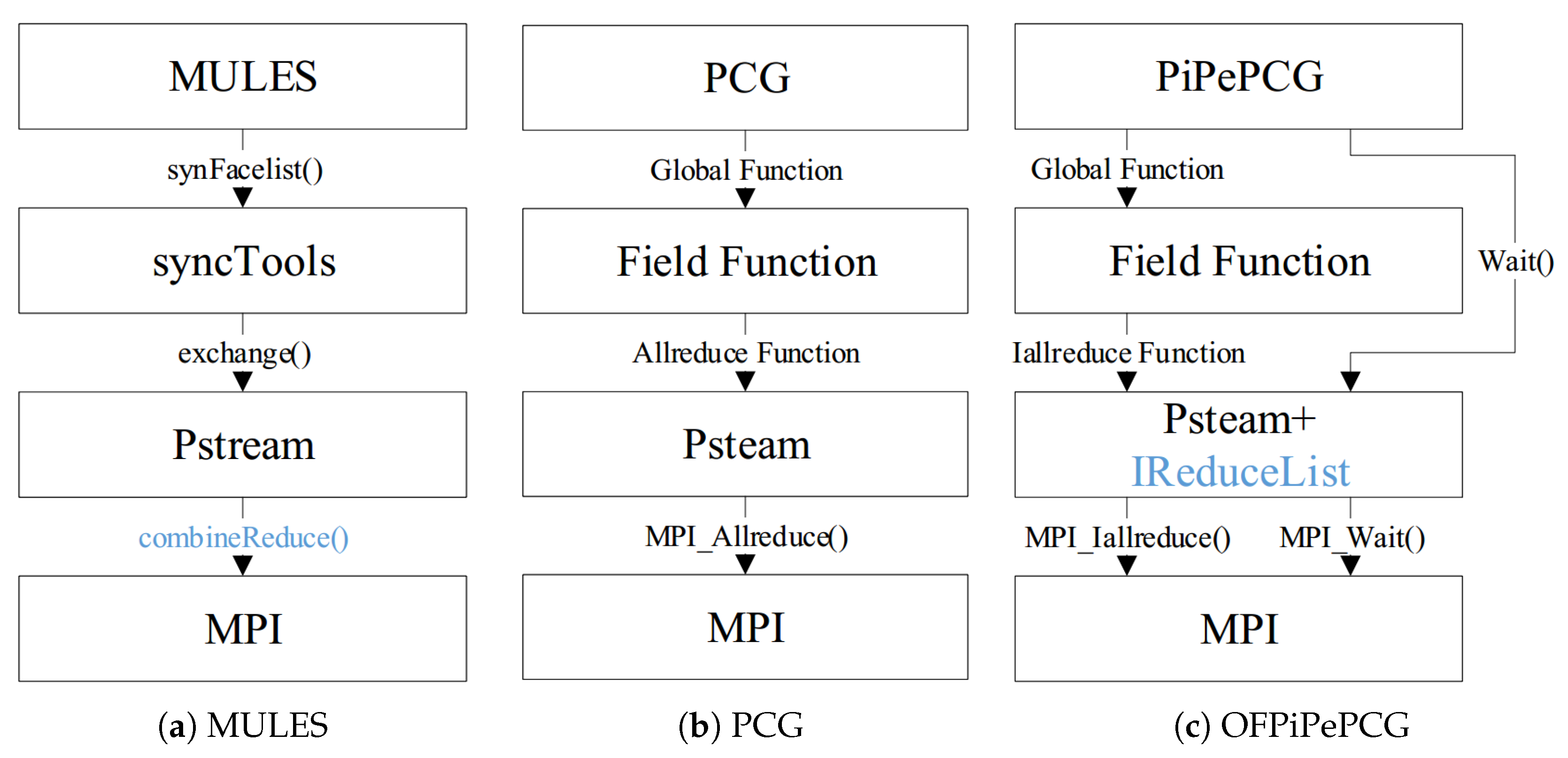
The MPI_Probe() is mainly called by MULES and MPI_Allrduce() by PCG. The graph of MULES and PCG invoking the MPI library is demonstrated in Figure 6a,b. Based on the bottleneck test, we can safely conclude that: (1) MULES and PCG are the key modules in multiphase flow solvers; (2) MPI_Probe() in MULES and MPI_Allreduce() in PCG are the short slabs of solvers.

2.2. Redundant Communications in MULES

In this section, we analyze the communication mechanism of MULES and point out the redundant communications in MULES. We also make a test for the verification.

In the Volume-of-Fluid (VOF) method, the gas-water interface is indirectly described by a numerical field that records the volume fraction of water in each grid. In order to make the air–water interface more accurate and sharper, during solving the phase equation, it is necessary to further correct the volume fraction field [25], which is primarily done by a Multidimensional Universal Limiter for Explicit Solution (MULES) in OpenFOAM. The volume fraction equation for the incompressible flow is shown in Equation (1):

$$\frac{D\alpha }{Dt}=\frac{\partial \alpha }{\partial t}+\nabla ·\left(\alpha \mathbf{U}\right),$$

(1)

where $\alpha$ is the volume fraction and $\mathit{U}$ is the velocity.

In MULES, Zalesak’s weight is a key to combine the low order scheme and high order scheme. The algorithm to calculate the Zalesak’s weight is shown in Algorithm 1. Generally, the calculation is divided into three steps. The first step is to calculate corrected local extrema for each cell, followed by the second step to sum up the inflow and outflows for each cell. The last part is the core of MULES, which will be executed nLimiterIter times. In the last step, MULES calculates the weight of each cell and face. Due to the design of OpenFOAM, the same face may have a different weight for the neighbor cells. Thus, MULES requires a communication operation to get the minimum of the weight of one face.

Algorithm 1: Multi-dimensionsal Limiter for Explicit Solution

Input: $\lambda$: initial Zalesak’s weight, nLimiterIter: iteration     $\psi$: volume fraction field, $\Delta t$: time step, $\rho$: density,     ${\varphi }^{BD}$: upwind flux, $s_u$: explicit cavitation source term     $\varphi$: high-order flux, $s_p$: implicit cavitation source term     ${\psi }^{max}$ and ${\psi }^{min}$: user defined maximum and minimum  Output: the corrected Zalesak’s weight ${\lambda }_f$ for faces 1: Calculate corrected local extrema for each cell as ${\psi }_i^{+}=max({\psi }^{min},{\psi }_i,{\psi }_{nei})$ ${\psi }_i^{-}=min({\psi }^{max},{\psi }_i,{\psi }_{nei})$ ${\psi }_i^{+}=V\times \left(\left(\rho /\Delta t-s_p\right)\times {\psi }_i^{+}-s_u-\left(\rho /\Delta t\right)\times {\psi }_i\right)+{\displaystyle \sum _f}{\varphi }_f^{BD}$ ${\psi }_i^{-}=V\times \left(s_u-\left(\rho /\Delta t-s_p\right)\times {\psi }_i^{-}+\left(\rho /\Delta t\right)\times {\psi }_i\right)-{\displaystyle \sum _f}{\varphi }_f^{BD}$ 2: Calculate the inflow and outflows for each cell as ${\Phi }_i^{+}=-{\sum }_f{\varphi }_f^{-}$ ${\Phi }_i^{-}={\sum }_f{\varphi }_f^{+}$ 3: Do the following loop nLimiterIter times $${\lambda }_i^{\mp }=max\left[min\left(\frac{\pm {\sum }_f{\lambda }_f{\varphi }_f^{\pm }+{\psi }_i^{\pm }}{{\Phi }_i^{\pm }},1\right),0\right]$$ $${\lambda }_f=\left\{\begin{array}{c}min({\lambda }_{own}^{+},{\lambda }_{nei}^{-}),\hspace{1em}{\varphi }_{i+1/2}\ge 0\hfill \\ min({\lambda }_{own}^{-},{\lambda }_{nei}^{+}),\hspace{1em}{\varphi }_{i+1/2}<0\hfill \end{array}\right.$$ 4: return${\lambda }_f$

The communication of MULES is presented in Figure 6a, which shows that the synFacelist() in syncTools will be called by MULES to finish the minimize operation. Furthermore, the exchange() will be executed to finish communication across processors. For allocating adequate memory to the receiving buffer of sync message, the local process will execute a function called combineReduce() to receive another message, namely, sizes, which implies the size of sync message and its size is determined already (a $P\times P$ array, where P is the number of processors). Each call to the combineReduce() takes small but nontrivial time, which will have a rapid expansion with the increase of the degree of parallelism and become the major scalability bottleneck of MULES. In summary, the third step in Algorithm 1 is where the costly combineReduce() occurs.

We find that the sizes message is an invariant in the iterative solving process for static-mesh multiphase flow simulation. Specifically, a great number of multiphase flow solver in OpenFOAM are simulated based on the static mesh, like inetrFoam, driftFluxFoam, compressibleInterFoam, and interphaseChangeFoam. When the multiphase flow is simulated on the static mesh, the topological structure, boundary type, and numerical scheme across subdomains keep constant, which ensure that the message of sizes array are invariant. Therefore, the whole function of combineReduce() is needless and redundant. If we can memory the sizes array and eliminate the redundant use of combineReduce(), we can dramatically decrease communication cost and increase the parallel scalability of MULES.

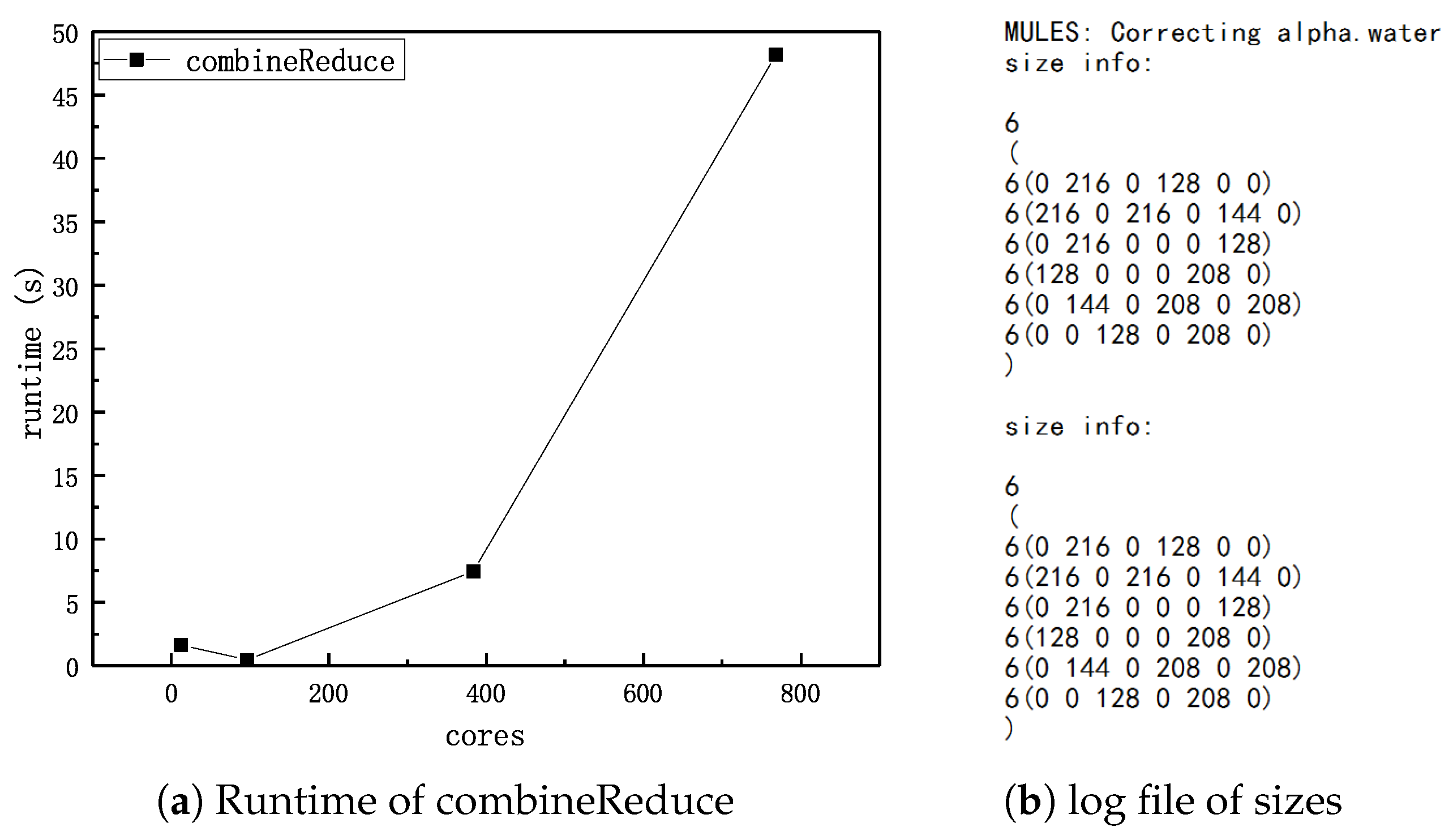
To verify the redundancy and rapid growth of combineReduce(), we carried out a test to record the information of sizes in a small scale simulation (6 cores, damBreak) and use IPM to track the overhead of combineReduce() in the damBreak case. The results are shown in Figure 2a,b. The sizes is a matrix $M\in {\mathbb{R}}^{p\times p}$ and the element $M_{i,j}$ is the size of message sent from the i-th processor to j-th processor. Note that diagonal elements are always zero. Obviously, the communication of sizes is an all-to-all communication, which means each processor needs to send a message to other processors but also receives a message from other processors and the total number of messages will have a significantly positive correlation with the number of processors. Owing to the effect of network congestion, the communication overhead of sizes message will dramatically increase as the degree of parallelism goes up. The strong scaling tests of the cost of combineReduce() on the damBreak case also confirm our analysis. From the line chart, we can find that the cost of combineReduce() will have a sharp increase as the number of cores goes up.

2.3. Global Communications in PCG

In this section, we want to make an analysis on the communication of PCG and deliver a performance model for runtime. We also give a research on the communication optimization of the PCG.

As shown in Algorithm 2, the preconditioned conjugate gradient method (PCG) [26], which could be divided into two parts: initialization (1–3) and iteration (4–16), containing four kinds of key operations: sparse matrix-vector multiply (MV), preconditioner process (Pre), allreduce (All), and vector multiply-add (Vec). Table 3 shows an overview of key operations of PCG and other variant PCG methods, which will be induced in Section 3. In the parallel computing of PCG, the matrix-vector multiply and most preconditioners require peer-to-peer communication (like MPI_Send() and MPI_Recv()) with neighbor processes to construct the local linear system, and the allreduce requires global communication (like MPI_Allreduce()) to calculate the global dot product. In MPI3, MPI_Allreduce() is global (collective) communication used for the combination of values from all processes and the distribution of the results back to all processes.

In Section 2.1, we make a bottleneck test and confirm the execution of MPI_Allreduce() is the main bottleneck of the scalability of PCG. Following the work of Dt Sturler [23], we give our performance model in PCG. Here, we make a hypothesis that the PCG is run on square processor grids with P processors, which indicates that the distance from a vertex processor to the so-called central processor is $\sqrt{P}$. The side length value of the square processor grids is $\sqrt{P}$. On the square processor grids, a message is transmitted along the x- or the y-axis. Therefore, the distance from a vertex processor to the so-called central processor is $\sqrt{P}$.

We suppose the communication time of one double precision number across two neighboring processors is $t_s+3t_w$, where $t_s$ and $t_w$ are the start-up time and the word transmission time. Then, the communication time of one global double precision floating point dot product (including accumulation and broadcast) is $2\sqrt{P}\left(t_s+3t_w\right)$. Thus, the communication cost of three global dot product is given by:

$$\begin{array}{c}\hfill t_{comm}^{gdot}=6\sqrt{P}\left(t_s+3t_w\right).\end{array}$$

(2)

Algorithm 2: Preconditionded Conjugate Gradient

Input: A: $n\times n$ matrix, $x_0$: initial guess, b: $rhs$,M: $prec$  Output: x: approximate solution   1: $r_0\leftarrow b-A{x}_0{u}_0\leftarrow M{r}_0$   2: ${\gamma }_0\leftarrow (u_0,r_0)$   3: $nor{m}_0\leftarrow \sqrt{(u_0,u_0)}$   4: for$j=1,2,\dots ,$ until convergence do   5:  if $j>1$ then   6:   ${\beta }_j\leftarrow {\gamma }_{j-1}/{\gamma }_{j-2}$   7:  else   8:   ${\beta }_j\leftarrow 0.0$   9:  end if  10:  $p_j\leftarrow u_{j-1}+{\beta }_j{p}_{j-1}{s}_j\leftarrow A{p}_j$  11:  ${\sigma }_j\leftarrow (p_j,s_j)$  12:  ${\alpha }_j\leftarrow {\gamma }_{j-1}/\sigma j{x}_j\leftarrow x_{j-1}+{\alpha }_j{p}_j$  13:  $r_j\leftarrow r_{j-1}-{\alpha }_j{s}_j{u}_j\leftarrow M{r}_j$  14:  ${\gamma }_j\leftarrow (u_j,r_j)$  15:  $nor{m}_j\leftarrow \sqrt{(u_j,u_j)}$  16: end for  17: return$x_j$

When it comes to the communication time of matrix-vector multiply, it is necessary for local processors to send and receive the boundary elements from neighbor processors when executing the matrix-vector multiply. We first make basic assumptions that each processor needs to send and to receive $n_m$ messages, each of which takes d steps of communication between the neighborhood and the number of boundary elements that each processor has to exchange is $n_b$. Then, the total number of words to be communicated is $2(2n_b+n_m)$. Therefore, the communication time of one double precision floating point matrix-vector product(including sending and receiving) is given by:

$$\begin{array}{c}\hfill t_{comm}^{matvec}=2d{n}_m{t}_s+2d(n_b+n_m)t_w.\end{array}$$

(3)

In the parallel computing of OpenFOAM, the domain is divided into subdomain and the numerical value of different subdomains are stored in different processes (cores). In the modeling of computation cost, we will only focus on the local computational time. Suppose the computation time for a double precision number multiply is $t_{cal}$ and there are $N/P$ unknowns in each local processor. Then, the average computation time of a dot product or a vector update operation is $2t_{cal}N/P$ and the local computational overhead of a matrix-vector multiply or preconditioner is $2(n_z-1)t_{cal}N/P$, where $n_z$ is the average number of non-zero elements in a row of a matrix.

There are $3k$ dot products, $3k$ vector update, $k+1$ sparse matrix vector product and $k+1$ preconditioner in the computation of PCG with k iterations. Thus, the computation time of PCG with k iterations on P cores is given by:

$$\begin{array}{c}\hfill t_{comp}^{pcg}=4k(2n_z+1)t_{cal}N/P.\end{array}$$

(4)

The runtime of PCG with k iterations on P cores is given by:

$$\begin{array}{cc}\hfill t_{total}^{pcg}=& 4k(2n_z+1)t_{cal}N/P+6\sqrt{P}\left(t_s+3t_w\right)\hfill \\ \hfill & +2d{n}_m{t}_s+2d(n_b+n_m)t_w.\hfill \end{array}$$

(5)

Equation (5) indicates that the communication strongly affects the performance of PCG owing to the factor of $\sqrt{P}$. Apparently, the greater the number of processes, the greater the execution time of MPI_Allreduce() is.

In the current study, there are two main optimization ideas to settle the bottleneck of PCG global communication. One is to convert two separated data-dependent dot products into several consecutive dot products with no data dependency, reducing a synchronization point and thus decreasing the number of global communications [27,28,29]. The other, through the rearrangement of the original algorithm, is to overlap as much communication as possible with useful calculations, which can maintain the same stability with the original algorithm [29,30]. There is one special way to replace the inner product calculation with computations that do not require global communication, namely the multi-search direction conjugate gradient method (MSD-CG) [31].

So far, many variant PCG algorithms including NBPCG, SAPCG, PiPePCG, PiPePCG2, and PCG3 have been researched and analyzed. Eller et al. [32] conducted an in-depth analysis of the parallel performance of these algorithms on large-scale clusters. According to their modeling analysis and experiments, the PiPePCG algorithm is an algorithm that takes both scalability and precision into consideration, which can effectively reduce the time for solving linear systems.

3. Communication Optimization Algorithm

3.1. Communication Optimization in MULES

Based on the simplified call stack of communication in Figure 6a, we modify the exchange() function to avoid the redundant invocation of combineReduce() for multiphase flow solver. The new exchange function needs to meet three demands: (1) Determine whether the function is called by MULES during the calculation process; (2) Determine whether the size of the face list information has been memorized; (3) Record and read the sizes array.

For the three functions above, we add three static member variables as shown in

Table 4. Added static member variables.

Type	Static Member Variables	Location
bool	mulesFlag	FOAM:MULES
bool	memFlag	FOAM:Pstream
int	memArray	FOAM:Pstream

. To realize the first demand, we add the bool static variable mulesFlag in the namespace of MULES, which is initialized to true after entering MULES and is set to false after exiting MULES. As for the second demand, we add one bool static variable memFlag in the namespace of Pstream, where the exchange() is realized. The memflag is initialized to false while turns to true after the very first time MULES communicates the sizes message; The third demand is implemented by adding a static int array memArray to the Pstream. The n-th element of the array records the size of the message sent from the n-th process to the local processor.

The pseudo code for the new exchange() function is shown in Algorithm 3. The input and output of this new function are the same as that of the original exchange() function, avoiding other function modules to modify the code for calling the new exchange() function. During the initialization of the solver, memFlag is set to false. The statement before and after the implementation of the combineReduce() function is exactly the same as the original exchange() function. In the statement where the combineReduce() function was originally called, a new static judgment process is executed to remove the useless execution and obtain the memorized sizes message.

In the judgment process, for other functional modules, mulesFlag is false, and the original exchange() function is normally executed. For MULES, if it is the first time to call exchange, the combineReduce() function will be executed and the sizes message will be memorized in the array memArray. After this, the memFlag is turned to true and the exchange() function will skip the execution of combineReduce() and assign memArray to sizes.

In summary, we can see that the new exchange() function executes two more judgment statements than the original exchange function and adds two bool-type variables and one int-type array. Such lightweight modification will not occupy too much memory. In addition, with relatively minimal cost of just two simple judgment statements, the new exchange() function only executes the combineReduce() function one time, almost completely eliminating redundant communication of sizes during the synchronization of the minimization of Zalesak’s weighting factor.

Algorithm 3: New $exchange\left(\right)$ Function

Input: the same as original $exchange\left(\right)$ Function  Output: the same as original $exchange\left(\right)$ Function   1: process before $combineReduce\left(\right)$   2: // $SizesMessage$ = CombineReduce()   3: /*replace the $combineReduce\left(\right)$ with following judging process*/   4: if$mulesFlag$ and $memFlag$ then   5:  $SizesMessage$ = $memMessage$   6: else if$mulesFlag$ and !$memFlag$ then   7:  $memMessage$ = CombineReduce()   8:  $SizesMessage$ = $memMessage$   9:  $memFlag$ = true  10: else  11:  $SizesMessage$ = CombineReduce()  12: end if  13: process after $combineReduce\left(\right)$  14: return$OutputSet$

3.2. Communication Optimization in PCG

Due to the data dependency between the update of the $\sigma$ and $\gamma$, we can not directly combine these two dot products. Based on the classic PiPePCG [21] , which imports five intermediate variables to remove the dependency, we develop a new OFPiPePCG solver in OpenFOAM and optimize the original calculation of residual in Algorithm 4. Because the initial steps of PCG solver is different from the original PCG in mathematics, the OFPiPePCG solver is also different from the original PiPePCG in mathematics to make the initialization keeping the same as PCG solver in OpenFOAM. As for the iteration steps, we make the following optimization in the implementation. In OpenFOAM, the calculation of residual in PCG needs another separated global communication for the sum of residual in different subdomains, which has been combined with the communication of $\sigma$ and $\gamma$ in our new OFPiPePCG. Obviously, when waiting for the global communication, OFPiPePCG can execute some local computation through the non-blocking communication like MPI_Iallreduce(). Thus, we realize the interface for invoking MPI_Iallreduce(), which will be detailed in Section 3.3.

In this section, we prove concisely that the Algorithm 4 is mathematically equal to Algorithm 2 during iterations.

Lemma 1 (the quality of residual vector in conjugate gradient method [26]).

For the residual vector r and the search direction p in conjugate gradient methods, the following equality holds:

$$\begin{array}{c}\hfill \frac{(r_k,r_{k+1})}{(r_k,r_k)}\equiv \frac{(p_k,A{p}_k)}{(p_k,A{p}_k)}=0.\end{array}$$

(6)

Theorem 1.

Algorithm 4 is mathematically equal to Algorithm 2 during iteration.

Proof of Theorem 1.

Suppose that variables in Algorithms 2 and 4 respectively have a superscript of $pcg$ and $pipe$.

To begin with, we prove that ${\alpha }_k$ and ${\beta }_k$ is equal in the k iteration. Obviously, ${\beta }_k^{pcg}={\beta }_k^{pipe}$. For ${\alpha }_k$, we need to prove that ${\sigma }_k={\delta }_{k-1}-{\beta }_k\times {\gamma }_{k-1}/{\alpha }_{k-1}$, where ${\delta }_k=(u_k,w_k)=(u_k,A{u}_k)$.

According to Lemma 1, in the k-th iteration, we have:

$$\begin{array}{c}\hfill (u_k,r_{k-1})=(A{r}_k,r_{k-1})=0.\end{array}$$

(7)

According to Algorithm 2, in the k-th iteration, we have:

$$\begin{array}{ccc}\hfill p_k=& u_{k-1}+{\beta }_k{p}_{k-1}{r}_k=\hfill & \hfill r_{k-1}-{\alpha }_{k-1}{s}_{k-1},\end{array}$$

(8)

which indicates:

$$\begin{array}{cc}\hfill {\sigma }_k=& (p_k,s_k)=(p_{k-1},A{p}_k)=(u_{k-1}+{\beta }_k{p}_{k-1},A{u}_{k-1}+{\beta }_k{s}_{k-1})\hfill \\ \hfill =& (u_{k-1},A{u}_{k-1})+{\beta }_k(u_{k-1},s_{k-1})+{\beta }_k(p_{k-1},A{u}_{k-1})\hfill \\ \hfill & +{\beta }_k^2(p_{k-1},s_{k-1})\hfill \\ \hfill =& (u_{k-1},A{u}_{k-1})+2{\beta }_k(u_{k-1},s_{k-1})+{\beta }_k^2{\sigma }_{k-1}\hfill \end{array}$$

(9)

and

$$\begin{array}{cc}\hfill {\gamma }_k=& (r_k,u_k)=(u_k,r_{k-1})-{\alpha }_{k-1}(u_k,s_{k-1})\hfill \\ \hfill =& 0-{\alpha }_{k-1}(u_k,s_{k-1}).\hfill \end{array}$$

(10)

Combining Equations (9) and (10), we have:

$$\begin{array}{cc}\hfill {\sigma }_k=& (u_{k-1},A{u}_{k-1})+2{\beta }_k(-{\gamma }_k/{\alpha }_{k-1})+{\beta }_k^2{\sigma }_{k-1}\hfill \\ \hfill =& {\delta }_{k-1}-{\beta }_k\times {\gamma }_{k-1}/{\alpha }_{k-1}.\hfill \end{array}$$

(11)

Thus, we have ${\alpha }_k^{pcg}={\alpha }_k^{pipe}$. As for the update of intermediate variables, Combining $s_k=A{p}_k$, then we have the following equality:

$$\begin{array}{ccc}\hfill A{p}_k=& A{u}_{k-1}+{\beta }_{k}A{p}_{k-1}{s}_k=\hfill & \hfill w_{k-1}+{\beta }_k{s}_{k-1}.\end{array}$$

(12)

Due to $u_k=M{r}_k$, we have the following equation:

$$\begin{array}{cc}\hfill M{r}_k=& M{r}_{k-1}-{\alpha }_{k-1}M{s}_{k-1}M{s}_k=M{w}_{k-1},+{\beta }_{j}M{s}_k,\hfill \\ \hfill u_k=& u_{k-1}-{\alpha }_{k-1}{q}_{k-1},q_k=m_{k-1}+{\beta }_j{q}_k,\hfill \end{array}$$

(13)

where $q_k=M{s}_k$ and $m_{k-1}=M{w}_{k-1}$. In addition, according to $w_k=A{u}_k$, we have:

$$\begin{array}{cc}\hfill A{u}_k=& A{u}_{k-1}-{\alpha }_{k}A{q}_{k-1},A{q}_k=A{m}_{k-1}+{\beta }_{j}A{q}_k,\hfill \\ \hfill w_k=& w_{k-1}-{\alpha }_k{z}_{k-1},z_k=n_{k-1}+{\beta }_j{z}_k,\hfill \end{array}$$

(14)

where $z_k=A{q}_k$ and $n_{k-1}=A{m}_{k-1}$. ☐

By further analysis of the OFPiPePCG solver, we find that the OFPiPePCG solver can further overlap the communication by rearrangement. Since the updates of p and x have no data dependency on updates of other vectors, We can update p and x after the execution of MPI_Iallreduce(). By this arrangement, we obtain a OFRePiPePCG solver.

From Table 3, we can see that OFPiPePCG has five more vector operations per iteration step than the original PCG, but it not only reduces global communication but also overlaps matrix-vector multiplication and preconditioning with communication. Although OFPiPePCG introduces additional computational effort, as the number of cores increases, OFPiPePCG still maintains excellent scalability when global communication becomes a bottleneck, while OFRePiPePCG overlaps global communication with two vector operations at each iteration step, keeping the added extra computation invariant.

After the process executes the non-blocking global reduce operation MPI_Iallreduce(), the function immediately returns a request handle of type MPI_Request. The process does not have to wait for the communication to be completed and can perform subsequent calculations.

Algorithm 4: OFPiPePCG in OpenFOAM

Input: A: $n\times n$ matrix, $x_0$: initial guess, b: $rhs$,M: $prec$  Output: x: approximate solution   1: $r_0\leftarrow b-A{x}_0{u}_0\leftarrow M{r}_0{w}_0\leftarrow A{u}_0$   2: ${\delta }_0\leftarrow (w_0,u_0){\gamma }_0\leftarrow (r_0,u_0)$   3: $R_0\leftarrow \sum |r_0^{\left(i\right)}|X\leftarrow \sum |x_0^{\left(i\right)}|N\leftarrow n$   4: MPI_Iallreduce on ${\delta }_0$, ${\gamma }_0$, $R_0$, X, N   5: $a\leftarrow (X/N)\times A\times \overrightarrow{1}$   6: $norm\leftarrow |A{x}_0{-a|}_1+{|b-a|}_1$   7: MPI_Iallreduec on $norm$   8: $m_0\leftarrow M{w}_0{n}_0\leftarrow A{m}_0$   9: $residual=R_0/norm$  10:    11: for$j=1,residual>tolerance,j++$do  12:  if j > 1 then  13:   ${\beta }_j\leftarrow {\gamma }_{j-1}/{\gamma }_{j-2}$  14:   ${\alpha }_j\leftarrow {\gamma }_{j-1}/({\delta }_{j-1}-{\beta }_j\times {\gamma }_{j-1}/{\alpha }_{j-1})$  15:  else  16:   ${\beta }_j\leftarrow 0{\alpha }_j\leftarrow {\gamma }_{j-1}/{\delta }_{j-1}$  17:  end if  18:  $z_j\leftarrow n_{j-1}+{\beta }_j\times z_{j-1}{q}_j\leftarrow m_{j-1}+{\beta }_j\times q_{j-1}$  19:  $s_j\leftarrow w_{j-1}+{\beta }_j\times s_{j-1}{p}_j\leftarrow u_{j-1}+{\beta }_j\times p_{j-1}$  20:  $x_j\leftarrow x_{j-1}+{\alpha }_j\times p_{j-1}{r}_j\leftarrow r_{j-1}-{\alpha }_j\times s_{j-1}$  21:  $u_j\leftarrow u_{j-1}-{\alpha }_j\times q_{j-1}{w}_j\leftarrow w_{j-1}-{\alpha }_j\times z_{j-1}$  22:  ${\delta }_j\leftarrow (w_j,u_j){\gamma }_j\leftarrow (r_j,u_j)$  23:  $R_j\leftarrow \sum \left|r_j^{\left(i\right)}\right|$  24:  MPI_Iallreduce on ${\delta }_j$, ${\gamma }_j$, $R_j$  25:  $m_j\leftarrow M\times w_j{n}_j\leftarrow A\times m_j$  26:  $residual\leftarrow R_j/norm$  27: end for  28: return$x_j$

3.3. Communication Optimization in Pstream

In OpenFOAM, the MPI communication operation is abstracted and encapsulated from bottom to up. Specifically, the Pstream library supplies the interface to call MPI functions, based on which, Field Function implements all kinds of global functions like global summation and global minimum. However, OpenFOAM does not implement encapsulation and invocation of MPI_Iallreduce(). In order to keep code style and readability, we can not directly use non-blocking MPI communication and need to encapsulate MPI_Iallreduce() into the Pstream library and add different global functions according to the global operation of the OFPiPePCG and OFRePiPePCG solver.

In MPI3, a non-blocking communication first starts initialization for the operation but does not stop the transmission thread and will return before the message is copied out of the send buffer or stored into the receive buffer. Before the use of message, a separate call like MPI_Wait() is executed to complete the communication [33].

Based on the aforementioned mechanism, we augment the pstream library and Field Function with non-blocking global communication as illustrated in Figure 6c. To begin with, we encapsulate MPI_Iallreduce() into Iallreduce function. In order to manage all unfinished MPI_Iallreduce() request, we add a static list named IReduceList to record unfinished requests. The MPI_Iallreduce() will return a request handle, which will be inserted at the end of IReduceList. The return value of IReduceList is the corresponding index of MPI_Iallreduce() request handle in IReduceList. Then, we realize three non-blocking global functions in Field Function, whose return value is the very index. The functions are shown in

Table 5. Added global function.

Function Name	Operation
gAverageIReduce	average of a field
gSumProdVectorIReduce	dot product of two vectors
gSumIReduce	sum of a field

. The global sum, average, and dot product are all required in OFPiPePCG and OFRePiPePCG for the calculation of residual, $\sigma$ and $\gamma$. In the last one, we need to add Wait() to check the finish of non-blocking request. The input parameter of Wait() is the index of non-blocking request. When executing Wait(), the IReduceList will be queried to obtain the request handle. MPI_Wait() will finish the communication operation with the request handle.

Generally speaking, if with suitable hardware, the transfer of data between memory and buffer may proceed concurrently with computations done at the local process after the non-blocking operation is executed and before it is completed, which indicates that it is possible to overlap the communication with computation. In addition, the non-blocking receive function MPI_Irecv() may avoid the useless copying between system buffering and memory because the message has been provided early on the location of the receive buffer. However, when the hardware and network do not support the non-blocking communication, the benefit of non-blocking communication may be not so efficient as mentioned above. In Section 4, the implementation technique for such dilemma is detailed.

4. Implementation

Although MPI3 achieves non-blocking global communication, it may be not effective in global communication hiding when the hardware is not suitable for non-blocking communication [34,35,36]. Here, we give a simple example of this phenomena. If we want to overlap the communication with computation to get a high speedup, the code could be abstracted in Listing 1. However, without the support of adequate hardware, the non-blocking communication will have a similar performance to blocking communication, which indicates that the blocking code in Listing 2 is comparable with ideal non-blocking code in performance.

Aiming to alleviate this drawback, Eller et al. [32] propose an approach. The solution is to divide the computation into blocks, and, after each block of computation completed, execute MPI_Test(). The modified code is shown in Listing 3. By executing MPI_Test(), the control of the process is given to the MPI kernel from OpenFOAM, which makes progress on global communication. Note that the overhead of each call to MPI_Test() is small but not negligible, so the number of blocks is important. Besides adding an extra MPI_Test(), if there is frequent MPI communication in overlapping computational parts, the control of the process will also switch to the MPI kernel and without additional code modification.

Listing 1: Ideal non-blocking code.

1 MPI_Iallreduce();

2 computation();

3 MPI_Wait();

Listing 2: Blocking code.

1 computation();

2 MPI_Allreduce();

Listing 3: Modified code.

1 MPI_Iallreduce();

1 for(chunk){

3    chunk_computation();

4    MPI_Test();

5 }

6 MPI_Wait();

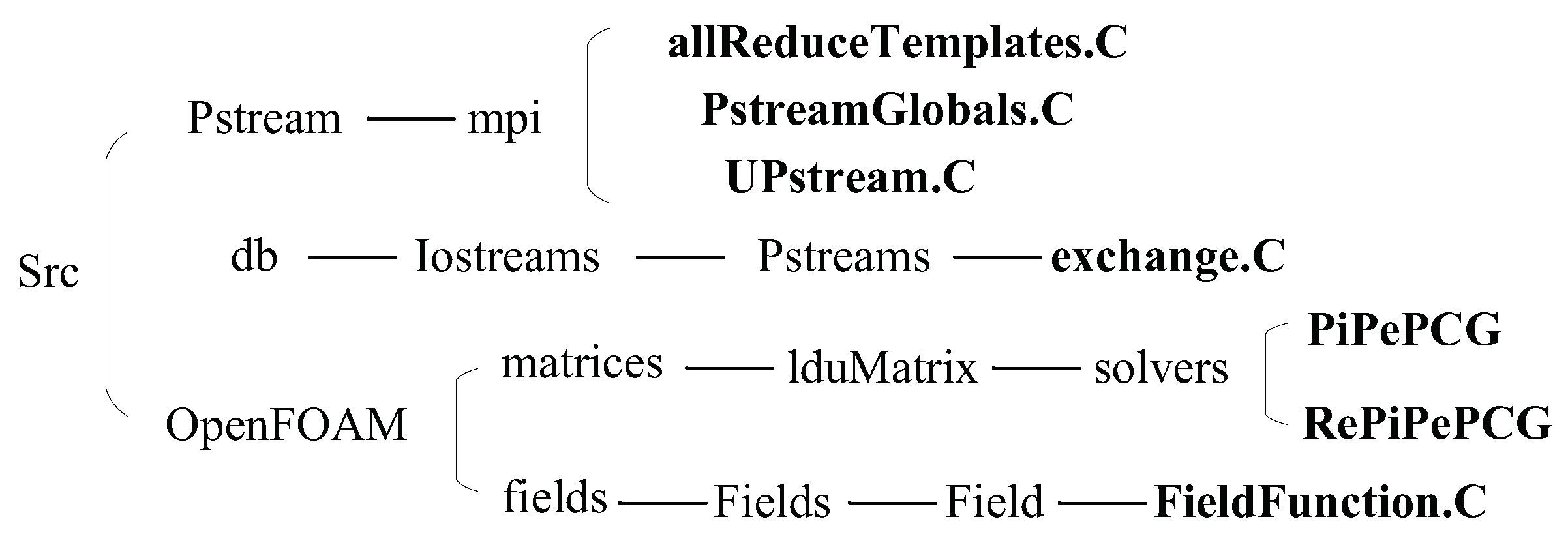
Inspired by the modified pattern, we modify the code of the OFRePiPePCG solver. We divide the two overlapped vector update operations of p and x into $2log\left(len\right)$ blocks, where $len$ is the length of the vector. After each update is completed, an MPI_Test () is executed. As for the OFPiPePCG solver, we find that the overlapping matrix-vector multiplication like $A\times m_j$ involves a large number of MPI communications, and non-blocking communications can obtain effective overlap without additional MPI_Test(). In addition, the key file we modified and added is listed in Figure 7. Our code is built on OpenFOAM and does not require any configuration of the computing environment or require additional hardware or toolkits.

5. Experiments

5.1. Platform and Test Cases

We conduct the experiment in the State Key Laboratory of High Performance Computing in China [15]. The cluster consists of 412 high-performance computing nodes: each node consists of two hexacore 2.1 GHz Intel Xeon E5-2620 CPUs (Changsha, China) and 16 GB memory, connected by an InfiniBand interconnect network (Changsha, China), with a total bandwidth of 40 Gb/s. The operating system on the cluster is a Red Hat Enterprise Linux Server 6.5 and the workload manager is slurm 14.03.10. However, the MPI implementation is MVAPICH2-2.3b and the OpenFOAM version is 2.3.1, and all its code is compiled by the corresponding mpicc and mpicxx compilers without any debug information. As shown in

Table 6. Configuration of OpenFOAM

Option	Value
WM_COMPILE_OPTION	OPT
commsType	nonBlocking
fileModificationSkew	timeStampMaster
floatTransfer	0
nProcsSimpleSum	0
writeNowSignal	−1
stopAtWriteNowSignal	−1
DebugSwitches	0

, OpenFOAM is on a performance configuration of non-blocking communication.

Our experiments benefit from the recent development of the OpenFOAM community on multiphase flow, which provides easy-to-use, customizable cases that represent diverse applications executed in the field of CFD. The cases chosen here depend primarily on the solution patterns that are expected to be run on OpenFOAM. We have tested three typical cases that represent and span a wide range of case design space in OpenFOAM.

Table 7. Configuration of the test case.

Case	nLimiterIter	Solver	Mesh
Head-form	5	interPhaseChangeFoam	636,000
cavity	none	icoFoam	4,000,000
damBreak	3	interFoam	2,041,200

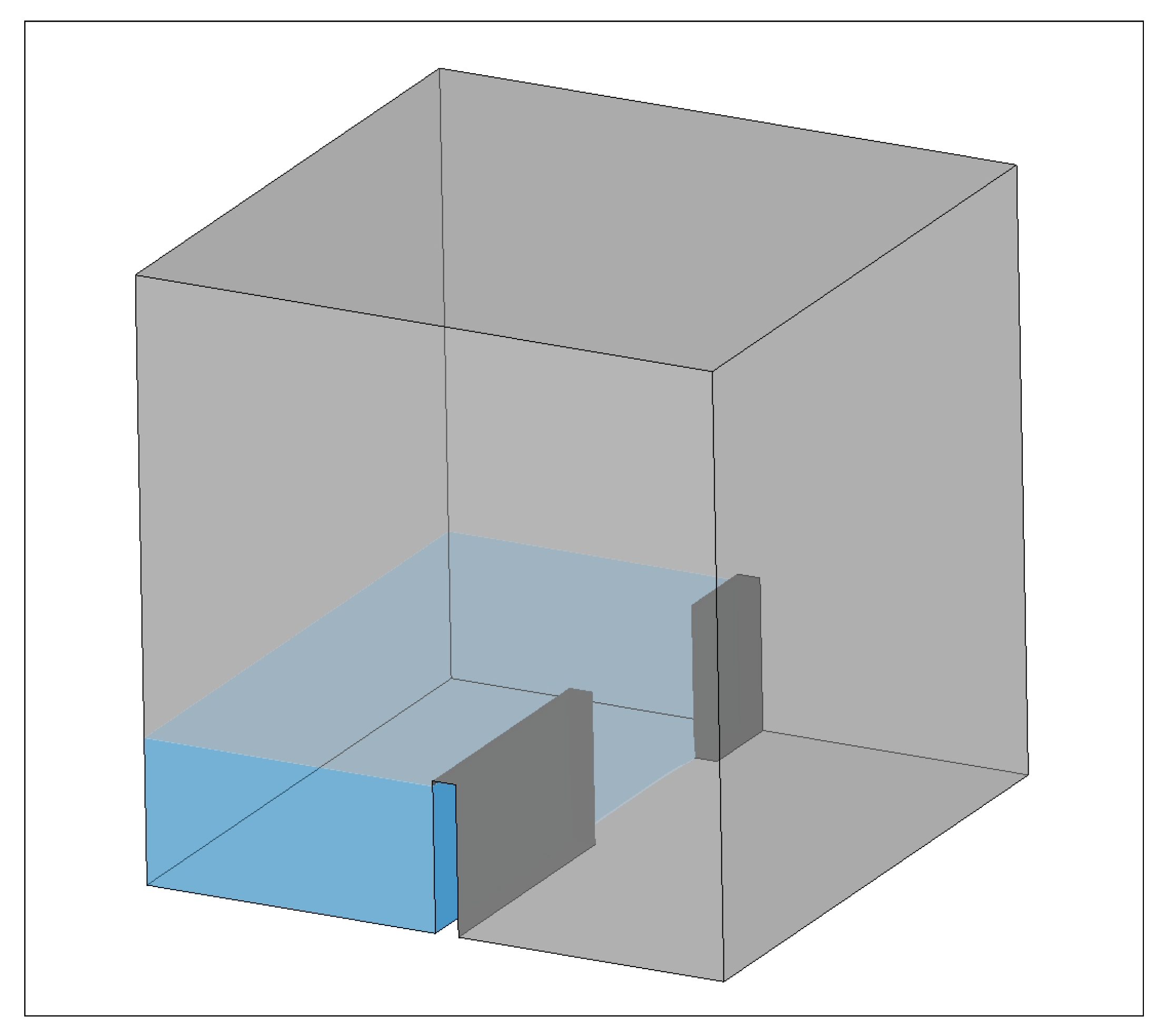
summarizes configurations that can be specified to these cases and Figure 8 illustrates the geometric schematization of respective cases. Using these cases, we test the performance optimization from a different solution pattern:

• cavity [37]: 2D case without MULES to test the performance of OFPiPePCG and OFRePiPePCG. It simulates the slipping process of the lid in three closed airtight boxes at 1 m/s speed. The solver is icoFoam. Although the solving process is relatively simple and does not involve the solution of phase equation, the lid-driven cavity flow is a classical case in computational fluid dynamics, which is of great significance to verify our PCG optimization algorithm.
• damBreak [38]: 2D case to verify the superiority of the whole communications (PCG + MULES). This case is another classic case in CFD, which simulates the process of a rectangular body of water rushing to a dam of 0.024 m × 0.048 m. We need to solve the complete Reynolds-Averaged Navier–Stokes (RANS) equations coupled to the Volume of Fluid method, using a solver called interFoam. This case can test the optimization effect of our optimization method.
• head-form [39]: 3D case to demonstrate the performance of solving complex 3D multiphase flow problem. The solver is interPhaseChangeFoam. The case simulated the cavitation process of the cylinder with a radius of 0.05 m in the flow of 8.27 m/s. This case is a classic case in the field of cavitation. It is important to verify the effect of the optimization method on the three-dimensional mesh.

5.2. Methodology

We follow a five-step methodology to demonstrate the performance of optimized OpenFOAM:

• To verify the correctness of the optimization method, we compared the relative error of final surface normal pressure field data in the head-form case shown in Figure 8c in different solvers.
• To analyze the parallel scalability of optimized OpenFOAM, we conducted strong and weak scaling tests based on the cavity and damBreak cases;
• To evaluate the effect of the optimized OpenFOAM on 3D simulation, we tested and analyzed the optimized OpenFOAM based on the 3D head-form case;
• To verify the effect of communication optimization on MULES and PCG, we tested and detected the MPI communication cost with the lightweight performance tool IPM.
• To study the performance of optimized OpenFOAM in the real-life application, we evaluate our optimization algorithm on interFoam based on the 3D dam-breaking flood problem, which is of widespread concern in academic circles and engineering fields [40,41]. If the dam fails, it will cause huge economic losses and great numbers of casualties.

5.3. Verification Tests

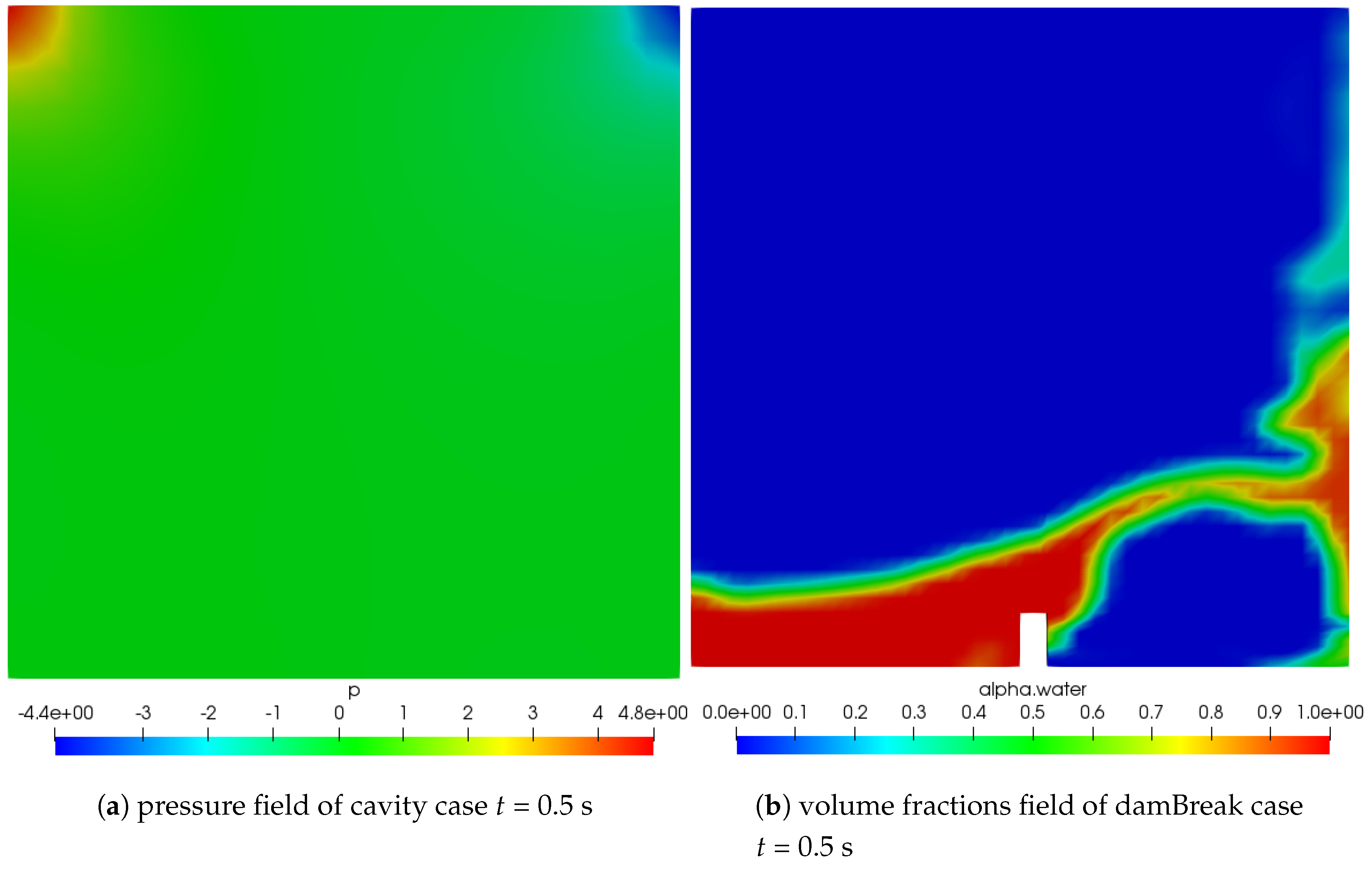
We validated the optimization method as follows. First, we delivered an intuitive comparison of the post-processed field data for the three cases. Figure 9a shows the pressure plot for the cavity case at t = 0.5 s, from which we can notice that the two corners above the cavity’s grid are respectively in the high and low pressure regions. Figure 9b shows the distribution of volume fractions of damBreak at t = 0.5 s. The red part is the liquid phase and the blue part is the gas phase. Figure 9c shows the shape of the cavitation of head-form at t = 0.5 s. Blue is the cavitation area. All post-processed result exhibited are exactly the same as the results running with the original OpenFOAM in identical configurations.

We then compared the field data on different solvers and found that the field data for these three cases in the optimized version tended to be the same as the original version of OpenFOAM. Furthermore, we compare the relative error of final surface normal pressure field data in the head-form case. Figure 10 shows the relative error of final surface normal pressure field data in the head-form case. The error is relative to the field data from the original OpenFOAM. It is clear that the test results using our OFPiPePCG and OFRePiPePCG is approximately equal to the result without optimization. As for the optMULES, due to we just reduce the redundant communication, the relative error is zero. Based on the verification tests, we can confirm that our communication optimization on MULES do not change the accuracy of original OpenFOAM, while the relative error caused by the communication optimization on PCG is quite small, less than almost 1%. Thus, the accuracy of our methods is basically equally to the original OpenFOAM.

5.4. Strong Scaling Tests

First, we performed strong scaling tests on the cavity case and the damBreak case with different parallel cores ranging from 12 to 1536 (12, 24, 48, 96, 192, 384, 768, 1152, 1536). For the cavity case, we focus on the comparison of different PCG solvers (PCG, OFPiPePCG, OFRePiPePCG), due to the icoFoam does not solve the volume fraction equation, while, in the damBreak case, we intend to combine the optMULES and variant PCG solvers, which helps to determine the best optimization combination for the improvement of strong scalability.

The results are shown in

Table 8. Results of strong scaling tests.

Case	Solution	Runtime With Different Cores Numbers (s)
		12	24	48	96	192	384	768	1152	1536
cavity	PCG	141,921.47	62,009.74	22,886.86	8440.26	1684.50	1036.79	806.14	85,990.41	88,625.36
	OFPiPePCG	157,132.26	26,658.99	46,154.35	14,703.69	3555.23	1062.62	682.04	35,060.98	36,814.02
	OFRePiPePCG	159,703.21	30,858.64	52,615.95	16,762.2066	3490.59	1056.41	738.37	36,638.72	44,176.82
damBreak	OF-ori	999.75	383.47	122.25	37.99	24.16	45.19	83.31	245.57	664.27
	optMULES+PCG	1000.89	385.19	123.65	40.17	21.01	18.98	17.98	49.68	120.55
	optMULES+OFPiPePCG	1291.725	565.533	227.826	64.368	22.33	16.77	14.94	48.44	113.25
	optMULES+OFRePiPePCG	1420.89	622.08	253.14	71.52	25.94	17.19	15.98	46.87	122.04

. We can figure out that, with the optimal core number, the shortest execution time of the optimized OpenFOAM is about 18.19% less than the original one for the cavity case and 38.16% for the damBreak case. For parallel scalability, the optimized OpenFOAM get the shortest run time for the damBreak case at 768 cores while the origin one reaches the inflection point at 192 cores, which means that the strong parallel scalability of optimized OpenFOAM in solving the damBreak case is greatly improved, about three times higher than that of the original OpenFOAM. The cavity case, which excludes the MULES and utilizes our optimization partly, gets the nearly identical parallel scalability for different PCG solver. The discrepancy in the strong scalability may be a result of the extra computation in OFPiPePCG and OFRePiPePCG solvers and removed redundant communication in MULES. In order to further compare the optimization algorithms for PCG and MULES, we calculate and compare the relative speedup.

The performance of three PCG solvers on the cavity case is shown in Figure 11. We can discover that the performance of non-blocking PCG solvers outperforms the blocking PCG algorithm at a large core number (>384) because non-blocking PCG solvers reduce global communications and overlap communications with the matrix-vector multiply and vector multiply-add. When the core number rises from 384 to 1152, the computation cost per core decreases rapidly and the cost of communication rises gently, which ensure the effect of optimized PCG solvers. However, at the core number of 1152, we can see a remarkable drop in the relative speedup line of OFPiPePCG and OFRePiPePCG, which is the result of the cost of global communication rising rapidly to more than 90%. Furthermore, in order to eliminate synchronization and create a pipeline, the variant PCG algorithm needs extra computation during the vector update, limiting the speedups at small cores. When the computation overhead is low (<384), they cannot fully overlap communication with extra computation and have a poor performance of speedup. In addition, the cavity case does not use optMULES and thus performs not as well as damBreak at small cores. OFPiPePCG scales better than the OFRePiPePCG due to the insertion of MPI_Test(). We will make a communication analysis for two variant PCG solvers in Section 5.7.

The results of strong scaling tests for solving damBreak case with original OpenFOAM($OF-ori$) and different optimized OpenFOAM($optMULES+PCG$, $optMULES+OFPiPePCG$, $optMULES+OFRePiPePCG$) are shown in Figure 12. Due to the elimination of redundant communications in MULES, three optimized OpenFOAM have a tremendous increase in strong scaling speedup and the knee point of run time increase dramatically from 192 to 768. The increment implies the strong scalability of OpenFOAM in multiphase flow simulation has a tremendous improvement. Note that the $optMULES+OFRePiPePCG$ has a better relative speedup than $optMULES+OFPiPePCG$ at 1152 cores, which is probably caused by the rearrangement in OFRePiPePCG. However, with fewer cores (<96), the optimization approach does not achieve ideal improvement from the 12 cores because there is less global communication in OpenFOAM when running on small scale cores, which causes a failure to keep a balance between additional computation and reduced communication. The optimization approach worked well when the original OpenFOAM reached its inflection point of execution time.

From the comparison of distinct combinations, we can find that the optimal run time of the three optimal combinations declines in turn, and $optMULES+PiPePCG$ is the most effective optimization combination.

5.5. Weak Scaling Tests

Next, we analyze parallel performance using weak scaling tests with grid scale changing from 62.5 k to 8000 k (62.5 k, 125 k, 250 k, 500 k, 1000 k, 2000 k, 4000 k, 8000 k) in cavity case and 127.2 k to 16,329.6 k (127.2 k, 254.4 k, 508.8 k, 1017.6 k, 2041.2 k, 4082.4 k, 8164.8 k, 16,329.6 k) in the damBreak case. The simulation of cavity case and damBreak case satisfy the convergence criteria on the smallest mesh (62.5 k and 127.2 k) and obtain more accurate results on large scale mesh. The number of cores increases from 12 to 1536 (12,24,48,96,192,384,768,1536), through which we can set the mesh size on each process constant. Besides the mesh size per core, the configuration on each case is the same as the setting in Table 7. Especially, the cavity case on 768 cores and the damBreak case on 192 cores have the same mesh size as the corresponding strong scaling cases, which could help us analyze the weak scalability.

Table 9. Results of weak scaling tests.

Case	Solution	Runtime With Different Cores Numbers (s)
		12	24	48	96	192	384	768	1536
cavity	OF-ori	123.32	182.43	262.48	388.86	630.90	718.82	806.14	1036.79
	OFPiPePCG	130.36	201.82	272.01	387.34	528.5	542.57	682.04	865.31
	OFRePiPePCG	136.22	210.9	284.25	404.77	552.28	566.98	738.37	904.24
damBreak	OF-ori	7.77	9.29	12.41	16.55	24.16	48.6	124.3	640.8
	optMULES+PCG	7.55	8.87	11.78	14.98	21.01	36.41	60.66	156.57
	optMULES+OFPiPePCG	7.92	9.31	12.52	15.87	22.33	34.28	55.94	150.88
	optMULES+OFRePiPePCG	8.15	9.58	13.21	16.54	25.94	35.3	57.61	153.96

records the run time of cavity and damBreak cases on different optimization methods. As shown in Table 9, in the cavity case, OFPiPePCG produces the best relative speedups of 1.324× at 384 cores among three PCG solvers, while the relative speedup of OFRePiPePCG at the same cores is 1.267×, due to the extra execution of MPI_Test() in OFRePiPePCG. Generally, Optimized PCG solvers outperform original PCG solvers at large scale core counts due to communication hiding and original PCG solvers consistently perform best at small scale core number due to lower cost in vector multiply-add. Tests on the damBreak case show optMULES + OFPiPePCG performing best with up to 4.274× speedups at 1536 cores. Remarkably, as the core number increases from 192 to 1536, we can find a distinguishable linear speedup in the weak scalability of optimized OpenFOAM in dambreak case, which implies the good weak scaling of our algorithm. However, the variant PCG solvers for optimized OpenFOAM does not show achieve obvious improvement in runtime, which may be caused by the PCG solution part in the damBreak case occupying a relatively small proportion of total solving process. In addition, at a small degree of parallelism, we do not observe the obvious superiority of the original PCG solver, which probably means that the extra computation in damBreak cases and the redundant communication are trivial.

Figure 13 and Figure 14 present the weak scalability of optimized OpenFOAM in the cavity and damBreak cases. In order to further analyze the weak scalability of different optimized algorithms, we focus on relative speedup at the key cores, which is 768 for cavity and 192 for damBreak. We make three key observations. First, when increasing the number of cores and the mesh size of cases, our method can also effectively reduce run time and communication cost. Especially in the damBreak case, our optimized OpenFOAM gets a distinct speedup line. After 192 core counts, we can also observe an approximately linear speedup line whose slope is about one. For the cavity case, from 192 to 384, we can also see a linear speedup, which turns to a drop from 384 to 768. The decrease indicates that communication cost has a superlinear growth even for only one non-blocking allreduce in OFPiPePCG and OFRePiPePCG. Second, speedup lines of two cases have a sharp contrast (see Figure 14) and point out that eliminating redundant communication in MULES is more effective than rearranging the PCG algorithm for improving weak scalability. Thirdly, among the three optimization pattern for damBreak case, the $optMULES+OFPiPePCG$ has the steepest speedup line, which means the $optMULES+OFPiPePCG$ is the most weakly scalable. As for a cavity case, the $OFPiPePCG$ is a more consistently weak scalable than $OFRePiPePCG$.

5.6. A Test on the 3D Case

Based on the previous tests, we use the $optMULES+OFPiPePCG$ solver as the optimization method for OpenFOAM and test the optimization effect in 3D multiphase flow simulation on the head-form case. The solver we used in this case is interPhaseChangeFoam, a solver for two in-compressible, isothermal immiscible fluids with phase-change. The volume of fluid phase-fraction is based on interface capturing approach [1]. The runtime on original OpenFOAM (OF-ori) and optimized OpenFOAM (OF-opt) are shown in Table 1. OF-opt starts to outperform OF-ori from the 12 cores due to removing the redundant communication costs and reducing the global communication overhead. In the head-form case, OF-opt does not have difficulty in keeping a balance between extra computation for vector multiply-add and reduced communication in OFPiPePCG and OFRePiPePCG, owing to the bigger nLimiterIter number of head-from case than that of a cavity case, which means that the head-form case executes more MULES than the cavity case.

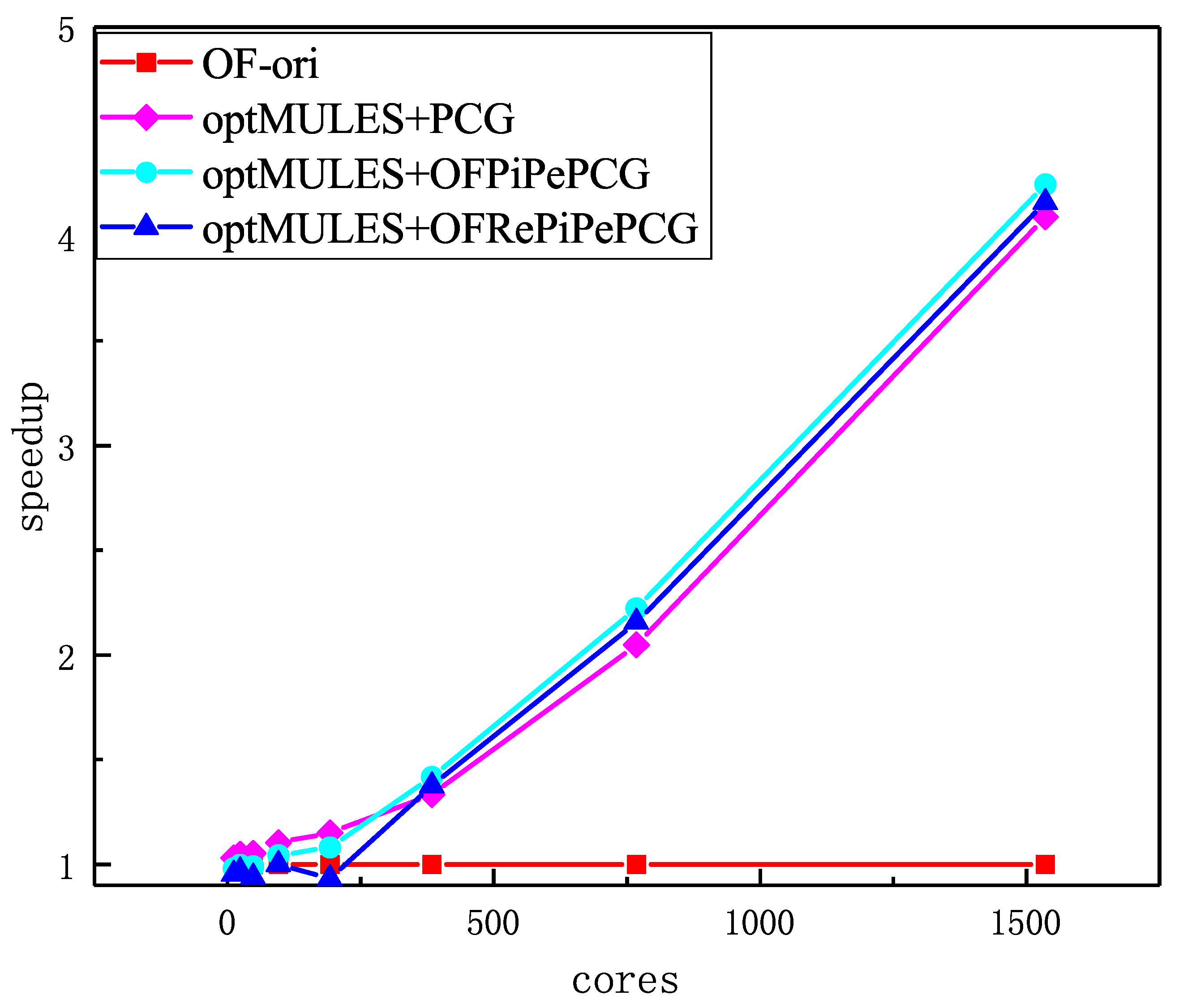
Figure 15 displays the lines of run time for solving the head-form case with original OpenFOAM and optimized OpenFOAM at different cores, ranging from 12 to 1152. We can analyze that the turning point of run time line is improved from 96 (OF-ori) to 384 (OF-opt), about three times higher than that of the original one, and there is a 63.87% decrease in the execution time of the optimized OpenFOAM, compared with the original OpenFOAM, respectively. From the graph, we can see that optimized OpenFOAM dramatically improves the performance of strong scalability and reduces execution time, which indicates that the OpenFOAM communication optimization method to remove redundant communication and reduce global communication has an obvious optimization effect in simulating the three-dimensional complex multiphase flow. Comparing the strong scaling result of damBreak case and head-form case, we can find that our algorithm could obtain a more efficient optimization when solving the case and having a more strict demand on the volume fraction field than the case with a low accuracy requirement.

5.7. MPI Communication Tests

To evaluate the communication optimization in detail, we probe the MPI communication cost in the damBreak case. The percentages of key MPI operations are shown in Figure 16. Because the optMULES has eliminated the redundant communication, there is little percentage of time spent in executing MPI_Probe(), almost 0%. Benefitting from communication optimization, the parallel performance in solving a multiphase flow problem has great improvement. According to our statistics, the OFPiPePCG can bring an up to almost 20% decrease in runtime when solving the linear system. We can find that MPI_Wait() and MPI_Waitall become the dominant MPI operation with the increasing core counts, while other MPI operations tend to be trivial. The increase in MPI_Waitall() is the result of the decline in the total communication time and the almost unchanged execution time in MPI_Waitall(). In addition, the increase in MPI_Wait() is probably caused by network congestion. Compared with Figure 5, we can find the dip in MPI_Allreduce(), the rise in MPI_Wait() and the appearance of MPI_Iallreduce() which is caused by the augmentation of non-blocking reduction in the implementation of OFPiPePCG. The decrease in MPI_Allreduce() and MPI_Probe() shows the effectiveness of our algorithm.

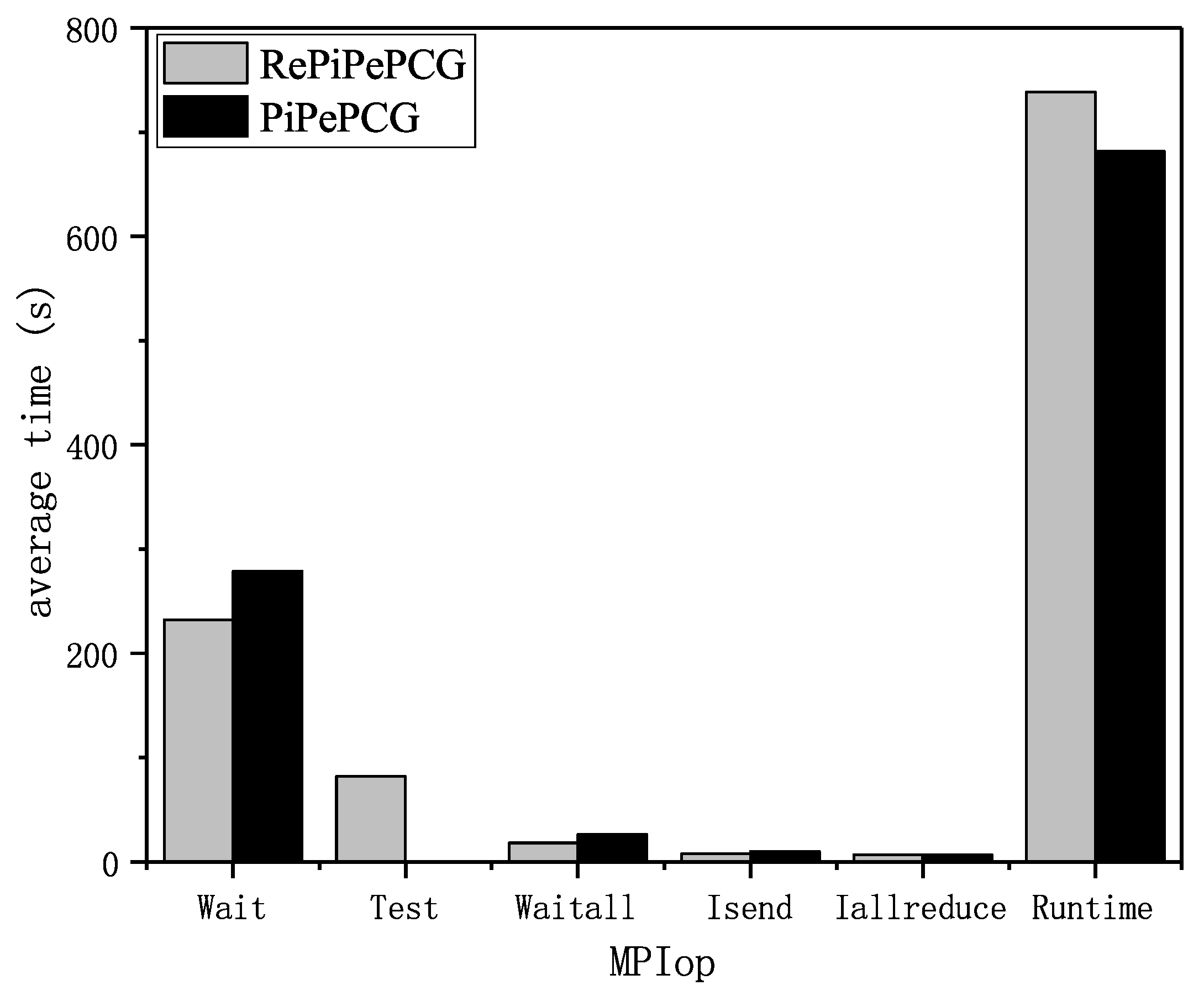
We also look at the effectiveness of the OFRePiPePCG. In order to avoid the impact of MULES, we choose a cavity case with 768 cores and detect the time spent in MPI_Test() compared to the OFPiPePCG implementation. Figure 17 profiles the average MPI communication cost of OFRePiPePCG and OFPiPePCG in solving the cavity case at 768 cores. We find that, in the OFRePiPePCG, approximately 8.4% of the total execution time (82.02 s) is executing MPI_Test(). After subtracting this MPI operation time, we obtain an estimate of the best execution time of OFRePiPePCG, which will drop to 656.35 s and is potentially 3.97% shorter than that of OFPiPePCG. This result suggests a 3 to 4% potential speedup in OFRePiPePCG.

The MPI communication tests give us insights into communication optimization. First, we can reduce the redundant communication in MULES, like MPI_Probe() to produce a new optMULES with more efficient communication at the cost of several extra simple judge statement. Second, we can rearrange the PCG solver to reduce global communication and produce a more efficient communication at the cost of extra vector operations. Furthermore, the non-blocking implementation of PCG solvers has a potential improvement in execution time.

5.8. A Test on a Real-Life Dam Break

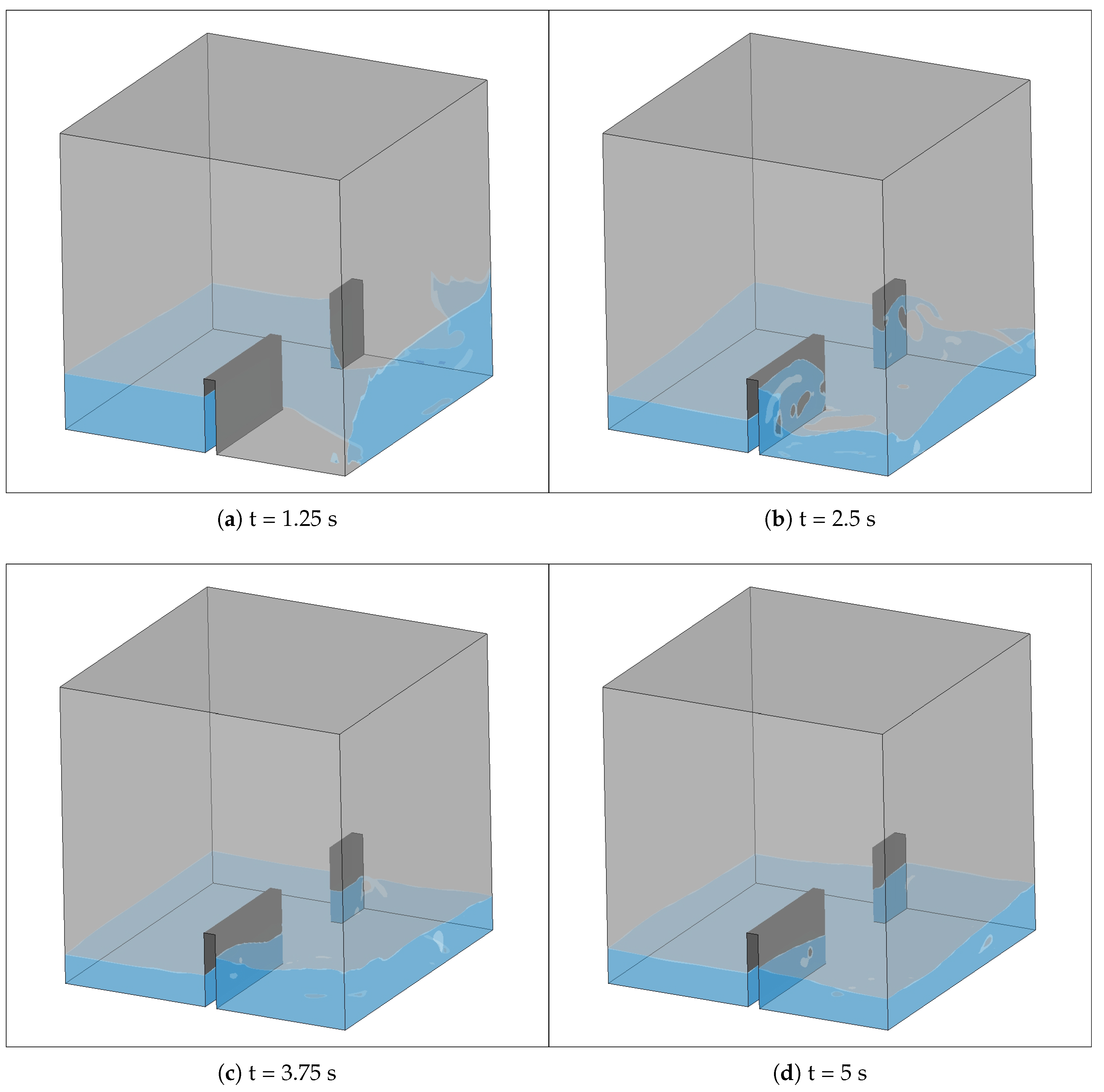
To verify the performance of optimized OpenFOAM in the real-life application, we modify a real-life 3D dam break case on OpenFOAM, which originates from the work of Fennema [42]. A dam break is the failure of a dam, which causes tons of water to be released. Owing to the damage of a resultant flood, the dam break is widely studied on engineering fields and academic cycles. As Figure 18 shows, the case simulates the downstream flood resulting from the release of the 4 m × 2 m × 1 m water body across a partial collapsing 4 m × 0.4 m × 1 m dam. The center of the 1.6 m gap of the dam is 1.6 meters from the back wall. The solver is interFOAM and the mesh size is 498,250. In order to keep a same solving configuration with a 2D damBreak case, we set nLimiterIter to 3, smaller than that of head-form case.

The post-processed visualization result of water surface on different times are shown in Figure 19. The water surface varies over time steps. The results are consistent with intuition. Furthermore, Biscarini and co-workers [43], who addresses a relevant problem on the selection of an appropriate model to undertake dam break flood routing, have simulated the 3D dam break case (partial instantaneous dam break over flat bed without friction). Because the geometric schematization of our 3D dam break case is different from the one of Biscarini, the visualization results have some differences. However, the general shape of water between two cases is similar. Comparing with the result of Biscarini [43], we make two key observations from these four graphs. First, we can find a saddle-like water surface downstream the gate and a sunken-like water surface upstream the gate. Second, although the wave celerity in our case is relatively smaller and the water levels outside the gate is relatively lower, the turbulence around the gate is in good agreement with the one obtained by Biscarini. In summary, our post-processed visualization result simulates the real-life 3D dam break properly.

The strong scaling tests results on original OpenFOAM (OF-ori) and optimized OpenFOAM (OF-opt) are shown in

Table 10. Results of tests on a 3D damBreak case.

Runtime in 3D damBreak Case (s)
cores	12	24	48	96	192	384	768	1152
OF-ori	2658.96	511.14	507.61	280.50	297.61	698.82	2986.92	13,180.70
OF-opt	2187.36	415.27	409.89	219.99	179.09	140.02	366.18	1435.24

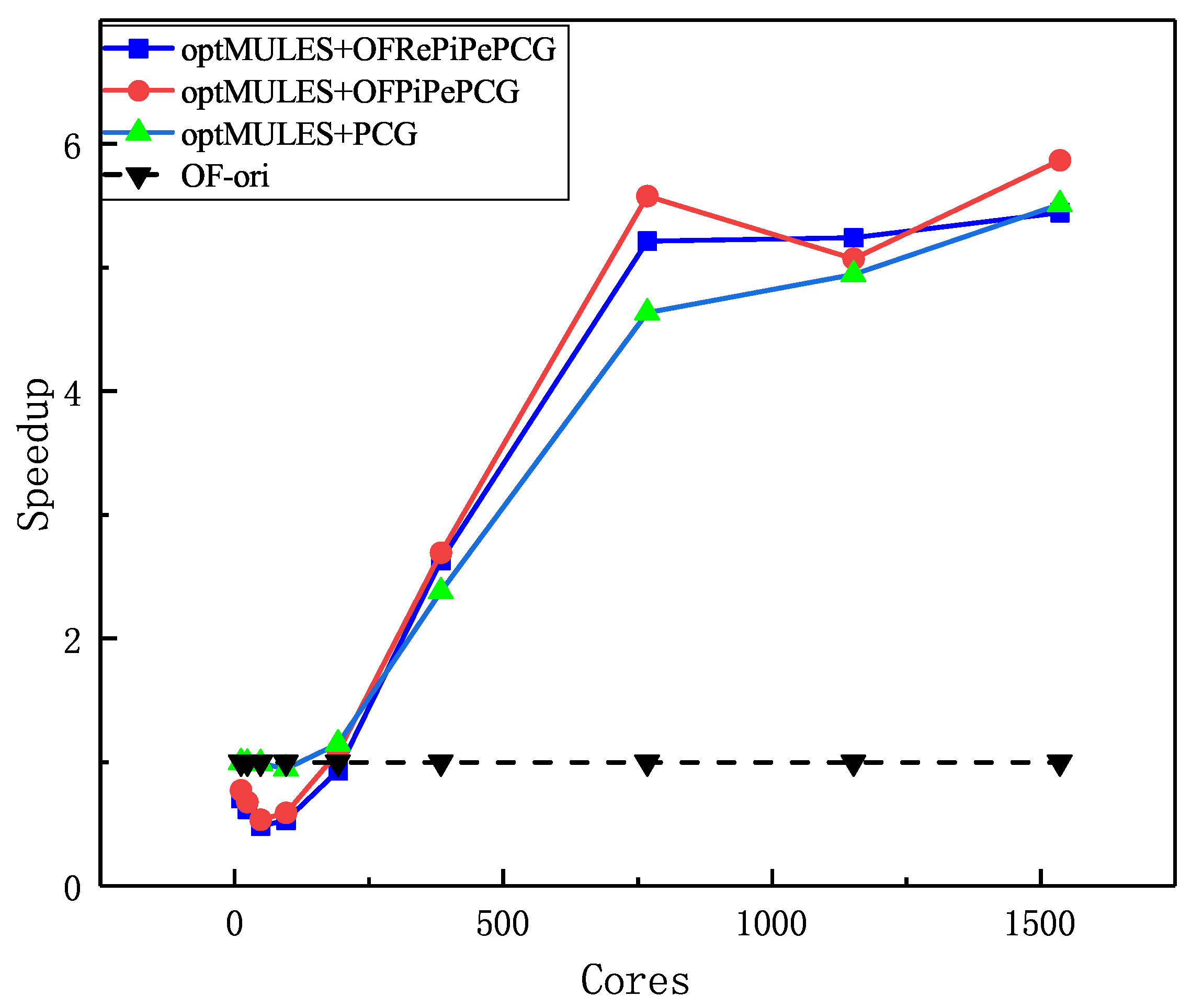
. Obviously, the communication optimization dramatically improves the strong scalability by about three times, cutting the optimal execution time from 280.50 s to 140.02 s, almost a fifty percent improvement. Figure 3 illustrates the lines of run time for 3D dam break case at different core counts from 12 to 1152.

Through a similar analysis to Figure 15, we can find that our communication optimization is an efficient method to improve the scalability of multiphase flow solver on OpenFOAM. Note that the scale of the y-axis is logarithmic. Therefore, we can find that the execution time of origin OpenFOAM has a more strong positive correlation with core counts than optimized OpenFOAM. The experimental results show that the elimination of redundant communication can greatly improve parallel scalability and reduce the execution time for a 3D real-life case. In addition, rearrangement of the PCG algorithm can also effectively reduce the communication cost and speed up the solution for a 3D real-life case. Comparing with Figure 15, we can find that our method can still keep a robust effect even with much smaller nLimiterIter, which implies the proportion of MULES in total solution.

6. Conclusions

In this paper, we propose a novel communication optimization method for multiphase flow solver in OpenFOAM. We carry out a detailed bottleneck test on multiphase flow solver to prove that redundant communication in the MULES of static mesh multiphase flow solvers like interFoam, interPhaseFoam, compressibleInterFoam and global communication in PCG are the hindrance to high-efficient multiphase solvers. In the optimized OpenFOAM, we not only eliminate redundant communications in MULES but also reduce and hide global communications in PCG solvers. The effects of redundant communications removing and global communications optimizing are two-fold. First, the redundant communications removing can guarantee a remarkable decline in the total runtime of multiphase flow solvers when on the same core counts and help improve the strong scalability for large scale parallel computing. Second, the global communications reducing and hiding can furthermore reduce the execution time for solving the linear system when the part of MULES in the total solution is relatively small. In summary, the optimization for MULES is only effective on OpenFOAM, but its idea may work on other similar VOF-based CFD software, while the optimization for a PCG linear solver could work on other C++ code with adequate modification. Experiments on high-performance computing platforms show that our optimization solvers outperform the original OpenFOAM multiphase flow solvers on the scalability and execution time approximately without the loss of accuracy. Our research shows that carrying out communication optimization is an effective way to improve the parallel scalability of CFD software.