Two-Dimensional Numerical Simulation Study on Bed-Load Transport in the Fluctuating Backwater Area: A Case-Study Reservoir in China

Abstract

Numerical modeling of sedimentation and erosion in reservoirs is an active field of reservoir research. However, simulation of the bed-load transport phenomena has rarely been applied to other water bodies, in particular, the fluctuating backwater area. This is because the complex morphological processes interacting between hydrodynamics and sediment transport are generally challenging to accurately predict. Most researchers assert that the shape of a river channel is mainly determined by the upstream water and sediment, and the physical boundary conditions of the river channel, rather than random events. In this study, the refinement and application of a two-dimensional shallow-water and bed-load transport model to the fluctuating backwater area is described. The model employs the finite volume method of the Godunov scheme and equilibrium sediment transport equations. The model was verified using experimental data produced by a scaled physical model, and the results indicated that the numerical model is believable. The numerical model was then applied to actual reservoir operations, including reservoir storage, reservoir drawdown, and the continuous flood process, to predict the morphology of reservoir sedimentation and sediment transport rates, and the changes in bed level in the fluctuating backwater area. It was found that the location and morphology of sedimentation affected by the downstream water level result in random evolution of the river bed, and bed-load sedimentation is moved from upstream to downstream as the slope of the longitudinal section of the river bed is reduced. Moreover, the research shows that the river channel sedimentation morphology is changed by the change water level of the downstream reach, causing the dislocation of the beach and channel and random events that will affect the river, which is of certain reference value for waterway regulation.

1. Introduction

The building of dams on rivers results in a disruption of the relative balance between river water and sediment condition. By trapping sediment in reservoirs, dams interrupt the continuity of sediment transport through rivers, resulting in the loss of reservoir storage and reduced reservoir life, and depriving downstream reaches of sediment essential for channel form and aquatic habitats. With the acceleration of new dam construction globally, these impacts are increasingly widespread [1]. Erosion and sedimentation in the fluctuating backwater area of a reservoir are important aspects of studying reservoir sedimentation, which have a considerable effect on the sedimentation of the entire reservoir and increase backwater elevation. These processes of erosion and sedimentation of sand in particular play an important role in waterway transport in the submerged and fluctuating backwater area [2,3]. The reservoir fluctuating backwater area is always defined as the river reach between the normal water level of a reservoir and the lowest end of the backwater tail, which has characteristics of both a reservoir and river. Due to the variability in water and sediment condition, sediment transport and river bed evolution in the fluctuating backwater area follow different laws compared with the perennial backwater and natural channel [3,4,5].

In certain past studies of reservoirs, sedimentation data were obtained based on numerical simulation. Many one-dimensional (1D) models have been developed and applied to many reservoirs in different countries, such as Italy and China. According to the Fourier law modified with the introduction of a derivative of fractional distributed orders as memory formalism, a 1D model was applied by Caputo to the Quarto Nuovo (Italy) reservoir, and the flux of sediment was estimated [6]. The HEC-RAS 1D model was also used to simulate the reservoir sedimentation of a 32 km reach of the Tenryu River between the Hiraoka and Sakuma dams in Japan, and the results showed that the Manning’s roughness coefficient has an effect on sedimentation, whereas water temperature has no effect [7]. Numerical simulations with a semi-2D sediment transport model, GSTARS4, were conducted using various methods for the determination of a recovery factor proposed by previous studies, and the simulated results of reservoir geometric change were sensitive to the selection of recovery factors [8]. In addition, dam-breaking flows referred to as the 2D shallow water equations were simulated by Xu and Zhong using a large time step based on the wave-propagation method proposed by LeVeque, and using an exact Riemann solver [9]. In addition to the development of 1D and 2D shallow water models, fully 3D models have been developed to study reservoirs. A fully 3D numerical model using the finite volume approach in combination with a wetting/drying algorithm was utilized to reproduce the flow velocity field in the Dashidaira reservoir [10]. In addition, a 3D computational fluid dynamics (CFD) model incorporating the Navier-Stokes equations using the k-epsilon turbulence closure and non-uniform sediment transport of Wu et al. was used to simulate the bed-load changes in a section of the river Danube, and the results were most sensitive to the Shields number for the critical movement of the sediment [11]. The effects of various intake and sluice gate configurations, as well as their operational schemes, on the flow and sediment transport processes into reservoirs, were also investigated by a 3D model [12]. A finite-volume non-hydrostatic and shock-capturing 3D model for the simulation of wave-structure interaction and hydrodynamic phenomena (wave refraction, diffraction, shoaling, and breaking) was proposed by Gallerano and Cannata [13]. Some studies based on field data have shown that changes in hydrodynamic conditions of the fluctuating backwater area are directly related to the peculiarities of morphology and dynamics of bottom topography forms, and are indirectly related to the variety of types of banks of reservoirs at the river section [14,15]. The study of physical models and field experiments of the fluctuating backwater area has been carried by many researchers. However, very few simulation models have been applied to simulate the fluctuating backwater area. Lu and Li [16] only calculated flow velocity and water levels distributed along a 609 km long dammed river reservoir by using a 1D hydrodynamics model to quantify the monthly fluctuations in response to changing hydraulic parameters and regional climatic factors. Meanwhile, few studies using simulation models have focused on the reservoir environment. Bao [4] has proposed that a series of unprecedented environmental problems are related to the fluctuating backwater area that influenced the life of the Three Gorges Reservoir (TGR). Based on a one-year field survey, the largest emissions of CH₄ from the water surface were detected in the fluctuating backwater area, likely due to a shallower water column and abundant organic matter [17]. The construction of hydro-junctions in the upper river will lead to variations of the incoming water and sediment conditions, and in turn, changes to the deposition and erosion processes operating in the fluctuating backwater reach of the downstream reservoir. Lu developed a 2D mathematical model using the boundary-fitting orthogonal curvilinear coordinate system, which was employed to predict the space-time changes of sedimentation in the Chongqing reach, part of the fluctuating backwater reach of the TGR [18].

In China, studies of the fluctuating backwater area of reservoirs have mainly focused on the Three Gorges, Gezhouba Dam, Danjiangkou reservoirs, and other large hydro-junctions. A large number of studies have been focused on sedimentation, and research on the regulation of the specific risk to the beach in the fluctuating backwater area of reservoirs is ongoing. Recent field experiments have benefited from the building of large reservoirs and have achieved good results. Han QW and He MM [19] studied sediment deposition in the variable backwater region of reservoirs based on the monitoring of eighteen reservoirs in south China in 1984. In addition, many useful insights have been achieved, including the decrease of the elevation difference between the river beach and channel and the evolution of the beach. Xie JH [20] showed that bed sedimentation mainly occurred in the lower-most water level of the variable backwater area, and that sedimentation in the tail of the convex bank was more serious. Xie BL [21] studied the changes of flow slope, flow velocity, and factors controlling the sediment-carrying capacity in the fluctuating backwater area based on experimental research on several physical models. In addition, Lu YJ [22,23] developed a 2D sediment mathematical model using the boundary fitting orthogonal curvilinear coordinate system based on the water-sediment characteristics and fluvial process of the backwater area of the TGP, and the rules of space-time changes of sediment deposition and erosion in the Chongqing reach were predicted for 100 years. A 2D model used by the MIKE21 software for simulating the fluctuating backwater zone of the Ankang Hydro-junction has been applied for research on waterway regulation and the variations of water level, surface slope, and flow velocity for managing the operation of a hydro-junction [24]. In addition to basic research, Wang suggested that flocculation had a significant influence on the sediment deposition rate in the fluctuating backwater area [25]. Tang illustrated how flow regulation can modulate sediment redistribution and explained how flow regulation controls sediment sorting in the water-level fluctuation area of the TGR [26].

A good understanding of the flow behavior and sediment transport process in reservoirs, especially near the fluctuating backwater area, is necessary to design appropriate operating strategies or for reducing the impact of dams on the environment, shipping, flood control, coastal industrial and agricultural development, and the lives of people, as considered herein. To date, numerical simulation studies of reservoirs have focused on computing sedimentation to predict reservoir storage. However, river-bed deformation of the fluctuating backwater area is more complicated, which has resulted in research on this topic being relatively limited. A study on the fluctuating backwater area is therefore of great significance. In the present work, a 2D shallow water hydrodynamic model calculated based on the finite volume method of a Godunov scheme and a sediment transport model using uncoupled equilibrium sediment transport equations are proposed and validated using a physical model. The Godunov scheme is one of the methods most widely used to solve the Riemann problem in the shallow water equations (SWEs) and an equilibrium sediment transport model was applied due to there being less sediment in mountain rivers. The model was used to simulate bed-load erosion and deposition in the fluctuating backwater area of a selected representative reach. In particular, the three actual conditions of the operation of the Zipingpu reservoir located in the northwest of Chengdu City in Sichuan Province, China, including reservoir storage, reservoir drawdown, and the continuous flood process in the fluctuating backwater area, were modeled with the variation of water and sediment. Furthermore, the application of the proposed numerical model was assessed according to academic and experimental benchmarks.

The present paper firstly summarizes the mathematical model for shallow-water flow and bed-load transport, and provides a review of the key elements of the underlying numerical scheme The paper then presents a proposed technique to deal with sediment transport. Next, validation tests of experimental results are shown and the three actual conditions are simulated and analyzed. Finally, key conclusions are presented.

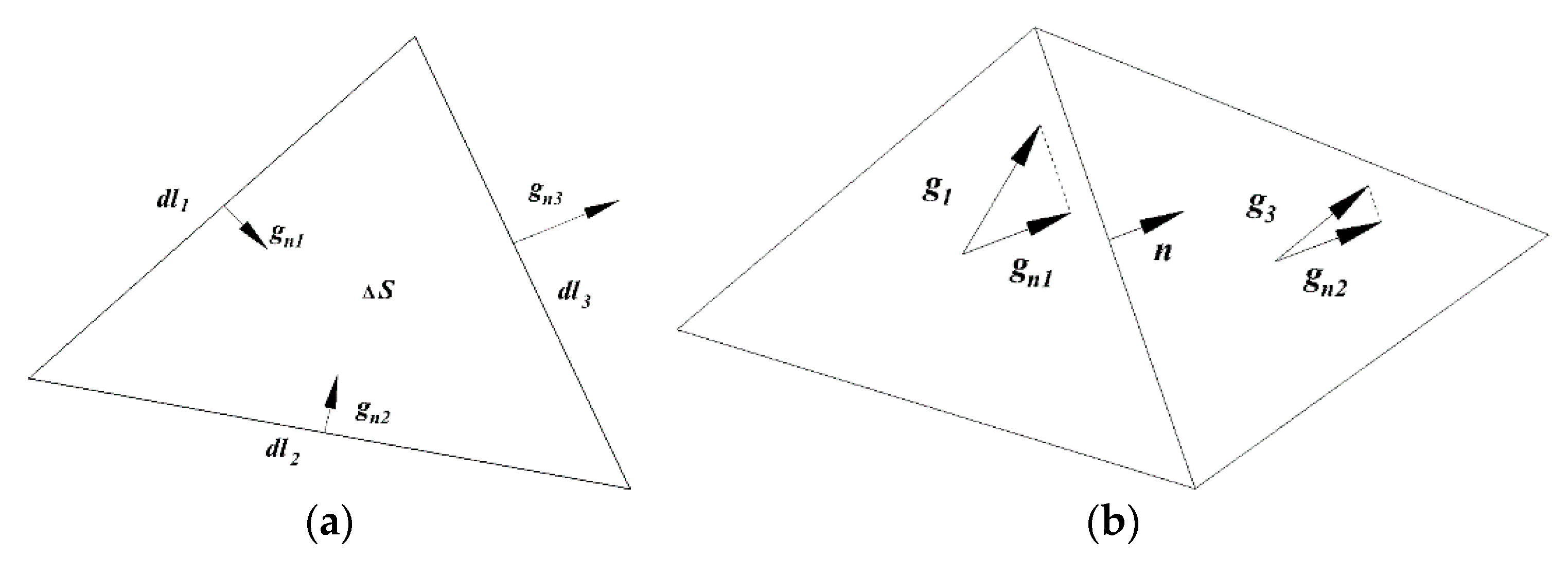
2. Mathematical Model

2.1. Shallow-Water Equations

The shallow-water equations in two dimensions are as follows:

$$\frac{\partial \mathit{U}}{\partial t}+\nabla \cdot \mathit{F}(\mathit{U})=\mathit{S}(\mathit{U})$$

(1)

where t = time; x = unit vector in the x-direction; U(x, t) = vector of conserved variables; and

$$\mathit{U}={\left[\begin{array}{ccc}h& hu& hv\end{array}\right]}^{\mathrm{T}}$$

(2)

where h = water depth; and u and v = components of the velocity vector u in the x-direction and y-direction, respectively.

The flux components $\mathit{F}(\mathit{U})=\left[\begin{array}{cc}\mathit{E}(\mathit{U})& \mathit{G}(\mathit{U})\end{array}\right]$ in Equation (1) are

$$\mathit{E}(\mathit{U})={\left[\begin{array}{ccc}hu& h{u}^2+\frac{1}{2}g{h}^2& huv\end{array}\right]}^{\mathrm{T}}\mathit{G}(\mathit{U})={\left[\begin{array}{ccc}hv& huv& h{v}^2+\frac{1}{2}g{h}^2\end{array}\right]}^{\mathrm{T}}$$

(3)

where g = gravitational acceleration.

The source term S(U) in Equation (1) can include several physical phenomena (i.e., wind, Coriolis force, outfall etc.). Here, only bed slope S_b(U) and fraction effects S_f(U) are considered. Therefore, the source term is

$$\mathit{S}(\mathit{U})={\mathit{S}}_{\mathit{b}}(\mathit{U})+{\mathit{S}}_{\mathit{f}}(\mathit{U})$$

(4)

where S_b(U) and S_f(U) can be expressed as

$${\mathit{S}}_{\mathit{b}}(\mathit{U})={\left[\begin{array}{ccc}0& -gh\frac{\partial z}{\partial x}& -gh\frac{\partial z}{\partial y}\end{array}\right]}^{\mathrm{T}}{\mathit{S}}_{\mathit{f}}(\mathit{U})={\left[\begin{array}{ccc}0& -\frac{1}{\rho }{\tau }_{fx}& -\frac{1}{\rho }{\tau }_{fy}\end{array}\right]}^{\mathrm{T}}$$

(5)

where z = bed elevation; ρ = density of water; and τ_fx and τ_fy = components of the shear stress τ of the river bed in the x-direction and y-direction, respectively, and according to the Manning formula:

$${\tau }_{fx}=\rho g{n}^{2}u\sqrt{u^2+v^2}\frac{1}{R^{1/3}}{\tau }_{fy}=\rho g{n}^{2}v\sqrt{u^2+v^2}\frac{1}{R^{1/3}}$$

(6)

where n = Gaucker-Manning roughness coefficient; and R = hydraulic radius, which is approximately h due to shallow water.

The coefficient n is dependent on the bed material. In the present study, the bed material is generally composed of non-uniform sediment and its non-uniformity coefficient is one of the main factors influencing resistance. Following Zhou GD and Liu QY [27], the quantificational relationship between non-uniformity and flow resistance was made on the basis of a large amount of laboratory test data and field measurements as:

$$n=1.38e^B\frac{\kappa R_b{}^{1/6}}{7.2\lg (12.27\frac{R_b}{K_s})}$$

(7)

where e = D₇₅/D₂₅, which is called the non-uniformity coefficient of river sediment distribution and has an effect on roughness; κ = 0.4, termed the Carmen coefficient; R_b = hydraulic radius corresponding to river bed resistance; K_s = comprehensive roughness of bed sediment, representing the average or median sediments; and B = the degree of influence of the non-uniformity coefficient, calculated by:

$$B=\{\begin{array}{cc}2.88e^3-17.97e^2+37.20e-25.19\hfill & \hfill 1<e\le 2\\ 0.025e^2-0.267e+0.799\hfill & \hfill 2<e\le 6\\ 0.077\hfill & \hfill e>6\end{array}$$

(8)

Finally, the system in Equation (1) requires appropriate initial conditions U(x, t = 0) and all boundary conditions to fully describe the fluctuating backwater area of the reservoir.

2.2. Movable Bed Model

The rate of change of bed elevation is key to determining the evolution of the river bed. The simulation equations of bed evolution are sufficient to calculate the rate of change of bed evolution, and are generally based on the Exner equation. The Exner equation assumes that the suspended sediment load is a function of the local conditions; consequently, the resulting equilibrium transport rates are described by empirical or semi-empirical expressions, which are introduced in the above equation so that sediment particles have time to reach a state of equilibrium under the local conditions. In recent years, the most advanced methodologies and those models which solve the suspended sediment concentration to yield the dynamic sediment load have been provided by Gallerano et al. [28]. Considering the slope of the river bed and sediment size, the evolution of a sediment-like movable bed can be modeled by the Exner equation:

$$(1-\lambda )\frac{\partial z}{\partial t}+\nabla {\mathit{g}}_{\mathit{b}}=0$$

(9)

where λ = the porosity factor of bed sediments, usually around 0.4; z = movable bed elevation for the SWE; and g_b = (g_bx, g_by) = non-uniform bed-load discharge. Bed-load discharge is often formulated semi-empirically, written as per Sharmov [29], in which velocity is the main variable.

$$g_b=9.31D^{1/2}{\left[\frac{U}{\frac{U_c}{1.2}}\right]}^3\left(U-\frac{U_c}{1.2}\right){\left(\frac{D}{h}\right)}^{1/4}$$

(10)

where U_c = incipient velocity, which is approximately equal to the point velocity acting directly on the sediment. Many formula for calculating the incipient velocity U_c ignoring viscous force exist. The basic form can be defined as

$$U_c=K\sqrt{\frac{{\gamma }_s-\gamma }{\gamma }gD}$$

(11)

where γ_s and γ = sediment and water densities, respectively; and K = several variations of the coefficient by different formulations, as illustrated in

Table 1. Incipient velocity formulas.

Name	Zhang RJ	Tang CB	Dou GR	Sha YQ	Sharmov	B.H.	Shields
K	1.53	1.789	1.314~1.343	1.277	1.33	1.58	1.272

[29]. In this work, K = 1.437 was adopted as the mean value of several incipient velocity formulas.

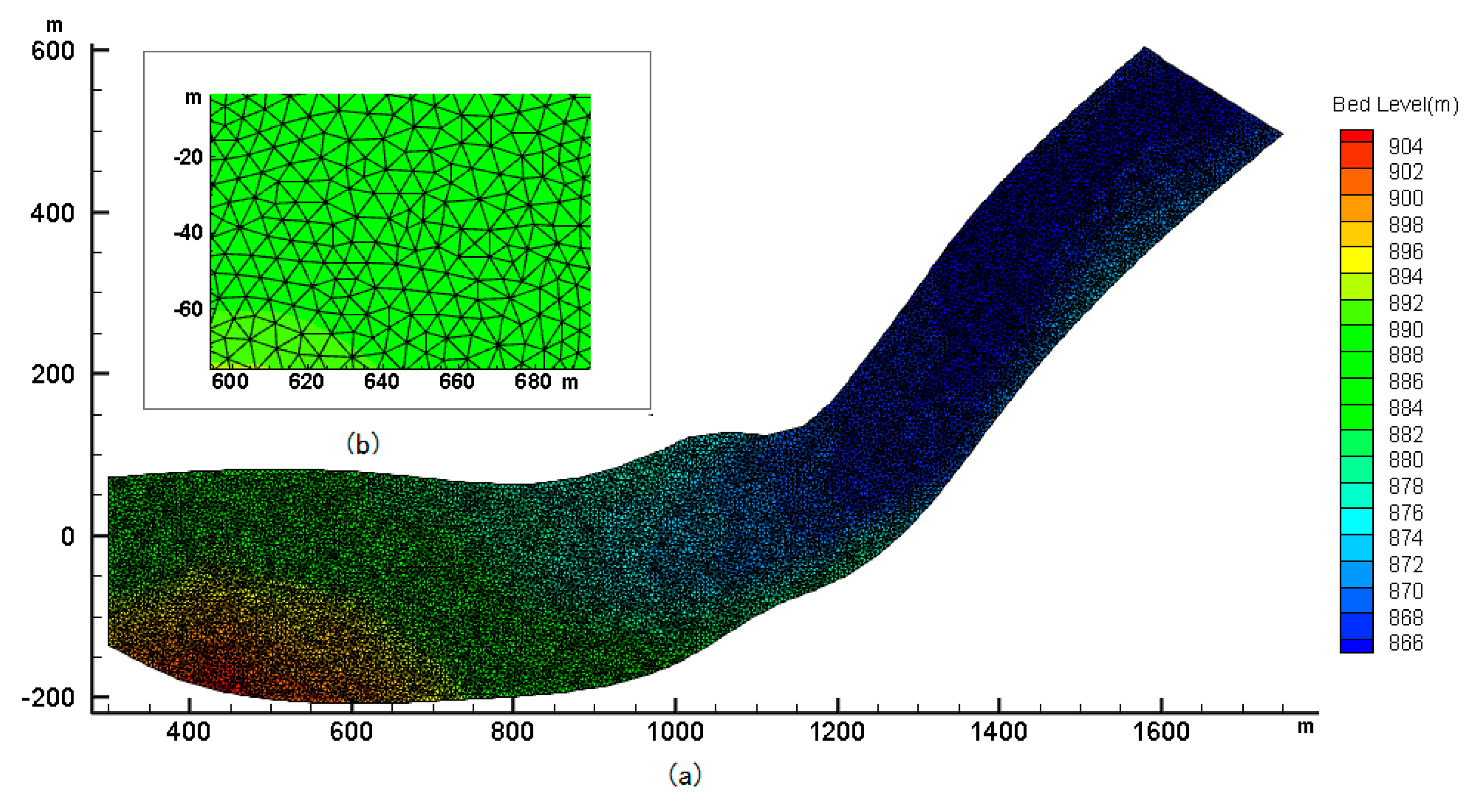
3. Numerical Model

The SWEs fall into a category of hyperbolic partial differential equations that develop discontinuous solutions, even if their initial conditions are continuous. The most famous numerical schemes of the shock-capturing method are based on Riemann problems, which are not only applied for smooth solutions, but also for large gradient and large deformation solutions. For instance, the Godunov scheme is one of the most popular approximate Riemann solvers developed for hyperbolic conservation equations. Similar computational schemes have been developed, such as the schemes of ENO, TVD, KFVS, BGK, and WENO, etc. [30]. In the present work, the SWEs are modeled by the finite volume method of the Godunov type. Arbitrary elements are used and all physical quantities are considered to be replaced by the mean value and act on the center of each element. Because of exiting of the source term, Equation (1) is a non-homogeneous partial differential equation. Consequently, Equations (12) and (13) are obtained after using the separation method within Equation (1):

$$\frac{\partial \mathit{U}}{\partial t}+\nabla \cdot \mathit{F}(\mathit{U})=0$$

(12)

$$\frac{d\mathit{U}}{\partial t}=\mathit{S}(\mathit{U})$$

(13)

Equation (14) represents pure convection and discretization of Equation (12) as follows:

$${\mathit{U}}_i^{n+1}={\mathit{U}}_i^n-\frac{\Delta t}{A_i}{\displaystyle \sum _{j=1}^m{\mathit{F}}_{\mathit{n}}{(\mathit{U})}_{ij}}$$

(14)

where Δt = the time step; i = the side number of the element i; m = total number of edges of the element i; j = number of edge; A_i = the area of element i; and ${\mathit{F}}_{\mathit{n}}(\mathit{U})=\mathit{E}(\mathit{U})\cos \theta +\mathit{G}(\mathit{U})\sin \theta$ = normal flux, which takes the normal direction outside the boundary as the positive direction and the angle between n and x as $\theta$.

Equation (13) adopts the explicit fourth-order Runge-Kutta, written as per Toro E.F. [31,32].

$$\{\begin{array}{l}{K}_1=\Delta t\mathit{S}({\mathit{U}}_i^n)\\ K_2=\Delta t\mathit{S}({\mathit{U}}_i^n+0.5K_1)\\ K_3=\Delta t\mathit{S}({\mathit{U}}_i^n+0.5K_2)\\ K_4=\Delta t\mathit{S}({\mathit{U}}_i^n+K_3)\\ {\mathit{U}}_i^{n+1}={\mathit{U}}_i^n+1/6(K_1+2K_2+2K_3+K_4)\end{array}$$

(15)

With all necessary information now at hand, the solutions of Equations (14) and (15) are expressed by using $A^{(\Delta t)}$ and $O^{(\Delta t)}$ as operators, respectively. The updating of the flow variables in an element at time tⁿ⁺¹ is expressed as

$${\mathit{U}}_i^{n+1}=0.5({\mathit{U}}_i^n+A^{(0.5\Delta t)}{O}^{(0.5\Delta t)}{A}^{(0.5\Delta t)}{O}^{(0.5\Delta t)}({\mathit{U}}_i^n))$$

(16)

The key procedure for solving Equation (16) is to calculate the numerical flux of the interface between elements (the normal numerical flux).

The approximate Riemann solver is used in the present work to calculate the normal numerical flux. $\mathit{E}(\mathit{U})$ and $\mathit{G}(\mathit{U})$ have rotational invariance as per Gallerano et al. and Cannata et al. [33,34], satisfied by:

$$\begin{array}{c}J(\theta )F_n(\mathit{U})=F[J(\theta )\mathit{U}]=F(\overline{\mathit{U}})\\ or\\ F_n(\mathit{U})=J{(\theta )}^{-1}F(\overline{\mathit{U}})\end{array}$$

(17)

where $J(\theta )$ = the transformation matrix from the Oxy coordinate to Onl coordinate and $J{(\theta )}^{-1}$ = inverse transformation matrix. The forms are:

$$J(\theta )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{con}\theta & \sin \theta \\ 0& -\sin \theta & \cos \theta \end{array}\right],J{(\theta )}^{-1}=\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{con}\theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right]$$

(18)

To solve ${\mathit{F}}_{\mathit{n}}(\mathit{U})$ in the n-direction of $\mathit{E}(\mathit{U})$ and $\mathit{F}(\mathit{U})$ within the Oxy coordinate, $F(\overline{\mathit{U}})$ within the Oxy coordinate is conversed at first, following which $F_n(\mathit{U})$ is inversed, which is transformed into a 1D Riemann problem (i.e., Equation (17)) from 2D along the normal direction of the surface of all circles in the element. The Riemann problem for Equation (1) can be expressed as

$$\{\begin{array}{l}\frac{\partial \overline{\mathit{U}}}{\partial t}+\frac{\partial F(\overline{\mathit{U}})}{\partial \overline{x}}=0\\ \overline{\mathit{U}}(\overline{x},0)=\{\begin{array}{l}{\overline{U}}_L,\overline{x}<0\\ {\overline{U}}_R,\overline{x}>0\end{array}\end{array}$$

(19)

where ${\overline{U}}_L$ and ${\overline{U}}_R$ = constants on the left and right of the interface of the element, respectively. Equation (17) exhibits the Riemann problem, the solution for which can be obtained by many methods. In the present work, the interface flux is calculated by the second-order WAF (Weighted Average Flux) TVD-type. The Riemann solver is used by the HLL solver.

In addition, the bed elevation is updated as follows:

$$z_i^{n+1}=z_i^n-\frac{\Delta t}{\Delta S}\frac{1}{1-\lambda }{\displaystyle \sum _1^m{g}_{ni}d{l}_i}$$

(20)

where g_ni = upwind bed-load transport contribution of each neighboring element, across each element edge. The schematic diagram of the element is shown (Figure 1a).

In the present work, the sediment transport rate of the model is estimated based on the center of the element. The weight format is introduced for application to the transport rate at the element interface. First, the upstream and downstream elements are identified by calculating the algebraic sum g_n of the sediment transport rate in the normal direction of the two neighboring elements.

$$\begin{array}{l}{g}_{bn}=g_{1n}+g_{2n}\\ g_{1n}={\overrightarrow{g}}_{b1}\overrightarrow{n}=g_{b1x}{n}_x+g_{b1y}{n}_y\\ g_{2n}={\overrightarrow{g}}_{b2}\overrightarrow{n}=+g_{b2x}{n}_x+g_{b2y}{n}_y\end{array}$$

(21)

If g_bn > 0, the upstream of element 1 is located upstream of element 2; If g_bn < 0, the result is the opposite Figure 1b. Secondly, after the upstream and downstream elements are identified, Equation (22) is used to calculate the sediment transport rate of the element interface (g_n):

$$g_n=\alpha g_{nup}+(1-\alpha )g_{ndown}$$

(22)

where α = weight coefficient, depending on g_1n/g_2n, calculated by:

$$\alpha =\tanh \left\{0.5493\max \left[{\left(\frac{g_{1n}}{g_{2n}}\right)}^2,{\left(\frac{g_{2n}}{g_{1n}}\right)}^2\right]\right\}$$

(23)

Because of the variation of the river-bed boundary and fluctuation of the water level, the wet and dry discontinuities problem can be encountered in the river-bank and beach. Two methods exist for dealing with the wet and dry discontinuities problem in the simulation. One is to track the exact position of the wet and dry discontinuities boundary, which poses a challenge to programing, whereas the other is to calculate the entire elements and adopt techniques for dry elements. The simulation used in the present paper introduces the latter method. It is assumed that all elements exist at least in minimal depth (it is taken to be 1 mm in actual simulation), which can also be regarded as soil moisture content, and the error of resulting water conservation may also be allowed. Hence, the method used to compute discontinuities can be adapted for other elements. If the water depth of an element and all adjacent elements are equal to the above minimal depth, it can be regarded as the land surface. Meanwhile the element at which the wet and dry discontinuities are located must be adjacent to a land element, and the specific location of the boundary need not be determined. The numerical solution is taken to represent the element average, and the singularity of the wet and dry discontinuities disappears due to integral processing.

4. Numerical Simulation

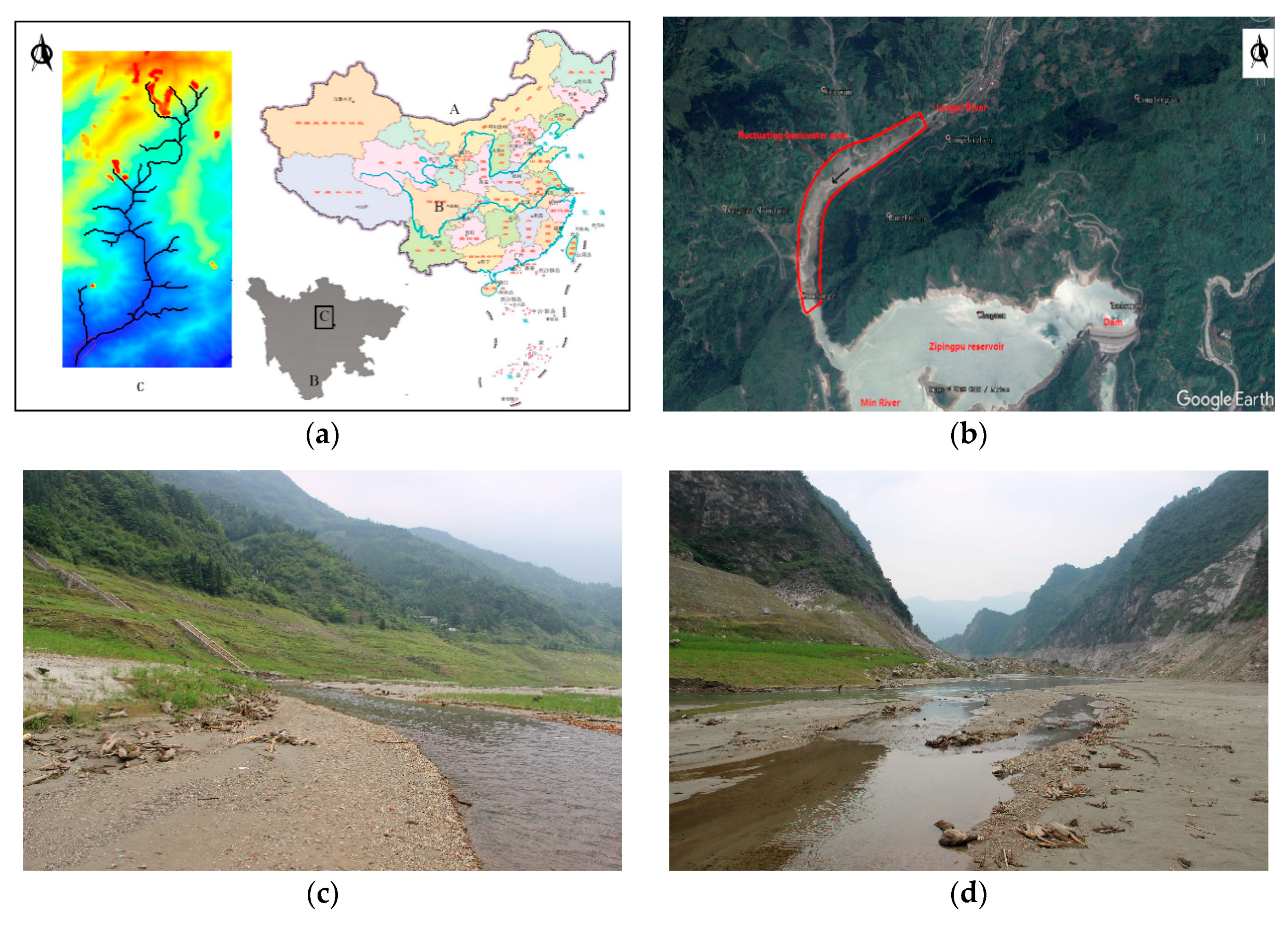
4.1. Study Case Description

The Longxi River originates from Longchi Mountain with an elevation of 2300 m, located in the northwest of Chengdu City in Sichuan Province, China (104°00′–104°10′ E, 28°50′–29°06′ N). Longxi River flows into Min River, which is a first grade tributary of the Yangzi River. Zipiingpu reservoir is a large hydro-junction, and the height of the dam is 156 m. The fluctuating backwater area of the reservoir is located downstream of Longchi River (Figure 2a,b). The Longchi River has a drainage area of 79 km², and the length of the river is 18.22 km [35]. The upstream bed has a steep slope with an average of 13.2% and the main channel of the upstream is narrower at approximately 8 m. The bed slope of the downstream reach is gentle, with an average of 4.5%. The main channel upstream is wider at approximately 25 m. The Longxi River basin experiences frequent seismic activity, which has resulted in large changes in topography, with the overall terrain showing higher elevations in the north moving to lower elevations in the south. After the Wenchuan earthquake, a large amount of loose material generated by the earthquake was accumulated in the basin. Due to the steepness of the ditch bed and huge variability in terrain between the hillsides, these loose sediments have large potential energy, which objectively increases the possibility of the movement of loose sediments and facilitates the transport of loose partials into the downstream river. The upstream and downstream reaches of the Longxi River experienced different morphological changes due to the earthquake [36]. The field investigation found more boulders and less sedimentation in the upstream reach with finer sediment particles, whereas a large degree of siltation occurred in the downstream reach of the Longxi River (Figure 2c,d). Therefore, it is of practical significance to study the Longxi River (Zipingpu Reservoir tail) for the study of the characteristics of bed-load sediment transport in the fluctuating backwater area.

There are few accurate hydrological data and grain size distribution data for the Longhe River (Zipingpu reservoir tail) because of the many natural disasters that have impacted the area. According to the relevant discharge estimates, the flood discharge values of 10-, 50-, and 100-year frequencies of Longxi River are approximately 386 m³ s⁻¹, 669 m³ s⁻¹, and 795 m³ s⁻¹, respectively. In the present work, the typical flood processes of 10- and 50-year frequencies were modeled (Figure 3a). In addition, the grain size distribution of the numerical simulation was scaled with the size of the physical model in Figure 3b. In addition, the average and median particle sizes were D_m = 37.01 mm and D₅₀ = 23.64 mm, respectively.

The point values of the variables at the element faces were reconstructed from the element averaged values on unstructured grids based on real measured topographic data of the Longhe River (Zipingpu reservoir tail) in 2016, and Equation (24) represents the computation of the above reconstruction:

$$x_i={\displaystyle \sum _{j=1}^3\frac{\frac{1}{3}{A}_{ij}}{{\displaystyle \sum _{j=1}^3\frac{1}{3}{A}_{ij}}}{x}_{ij}}$$

(24)

where i = the point number at element faces j; j = the element number; x_i = the point value i of physical variables at element faces j; x_ij = element averaged values i of physical variables at element faces j; and A_ij = the element j area. Both configurations are simulated on a 2D triangular unstructured mesh composed of 20,583 elements and 10,556 nodes. A detailed view of the mesh is shown in Figure 4.

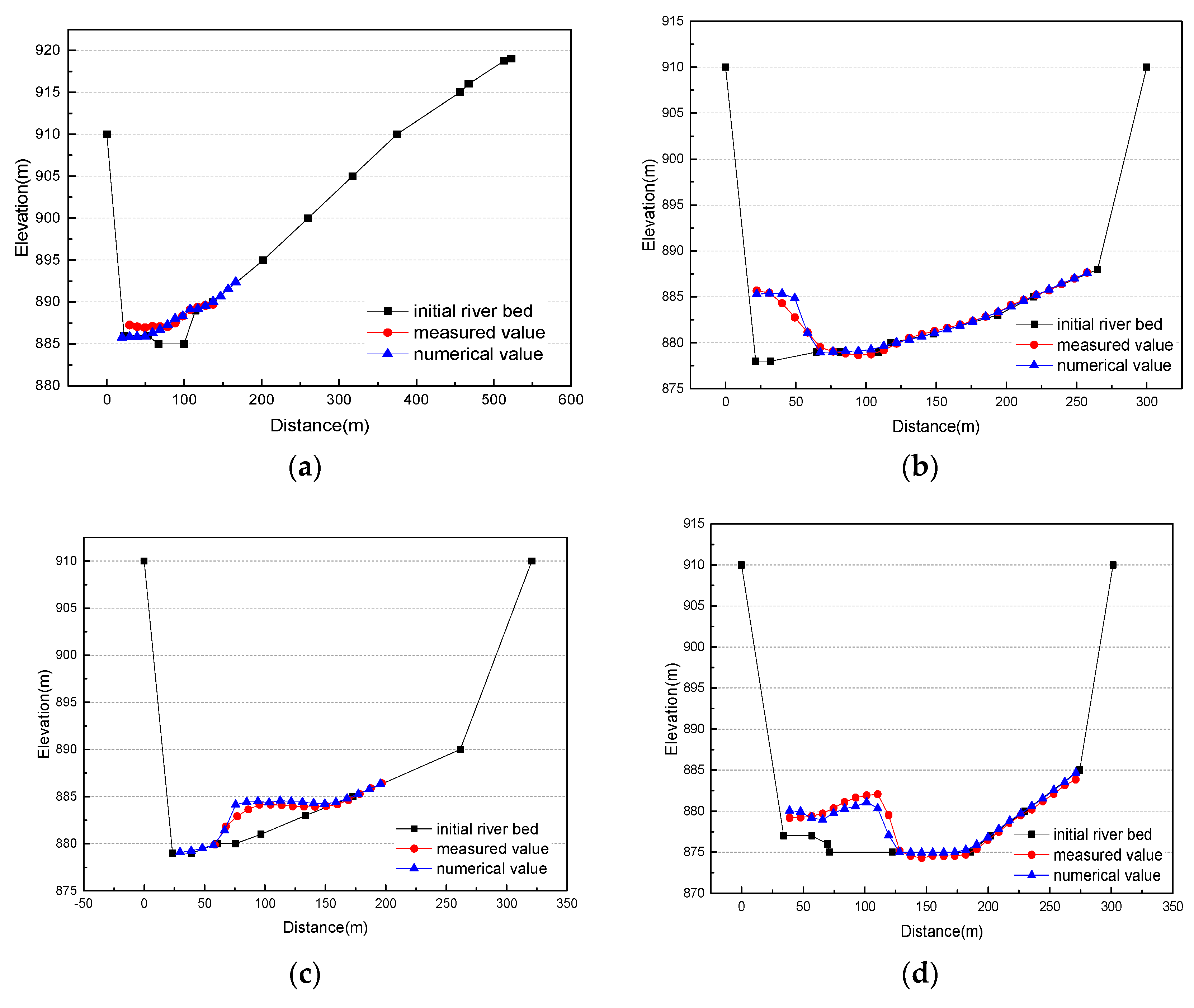
4.2. Validation Test

The physical model was built by the State Key Laboratory of Hydraulics and Mountain River Engineering (SKLH) at Sichuan University with a 1:50 scale, based on the actual topography measured in 2016 (Figure 5a). The simulation range of the physical model is from Suping Village in the downstream reach of Longhe River to the Zipingpu reservoir tail. The length of the physical model is 2150 m, including the numerical simulation calculation area. A numerical simulation was applied to the same sections of the fluctuating backwater area (Figure 5b).

Generally, the performance of the hydraulic numerical simulation was assessed by the consistency of the water level. The present work applied the water level assessed within the physical model to validate the results provided by the numerical simulation. A steady discharge of 707.1 m³ s⁻¹ was introduced into the system as the inlet boundary condition and two water levels of 890 m and 885 m were imposed as the outside boundaries. As illustrated in Figure 6, the average simulated water level was consistent with the measured value of the physical model, indicating that the hydraulic numerical model is believable.

A number of experiments of sediment transport were also conducted to improve the credibility of the results of the current study. The sediment transport was verified by a simulation of the above water flow boundaries, and the sediments were laid artificially between the CS36 and CS33 sections upstream of the physical model (Figure 5c,d). The total amount of simulated sediment in the middle and upper reaches was limited to 150,000 m³. During the test, all sediments laid in the upstream reach were transported downstream by water flow, and no sediment remained above section CS33 (Figure 5e). Figure 7 shows a comparison of the numerical simulation results and physical model measurement as the morphologies of two randomly-chosen cross sections of the sediment of the above two schemes. The comparison illustrates that the simulation results are consistent with the results of the experimental test and that a certain minor error of sedimentation thickness exists of an approximate average 0.15–0.24 m. The numerical sediment transport model can therefore be regarded as credibly validated by the physical model.

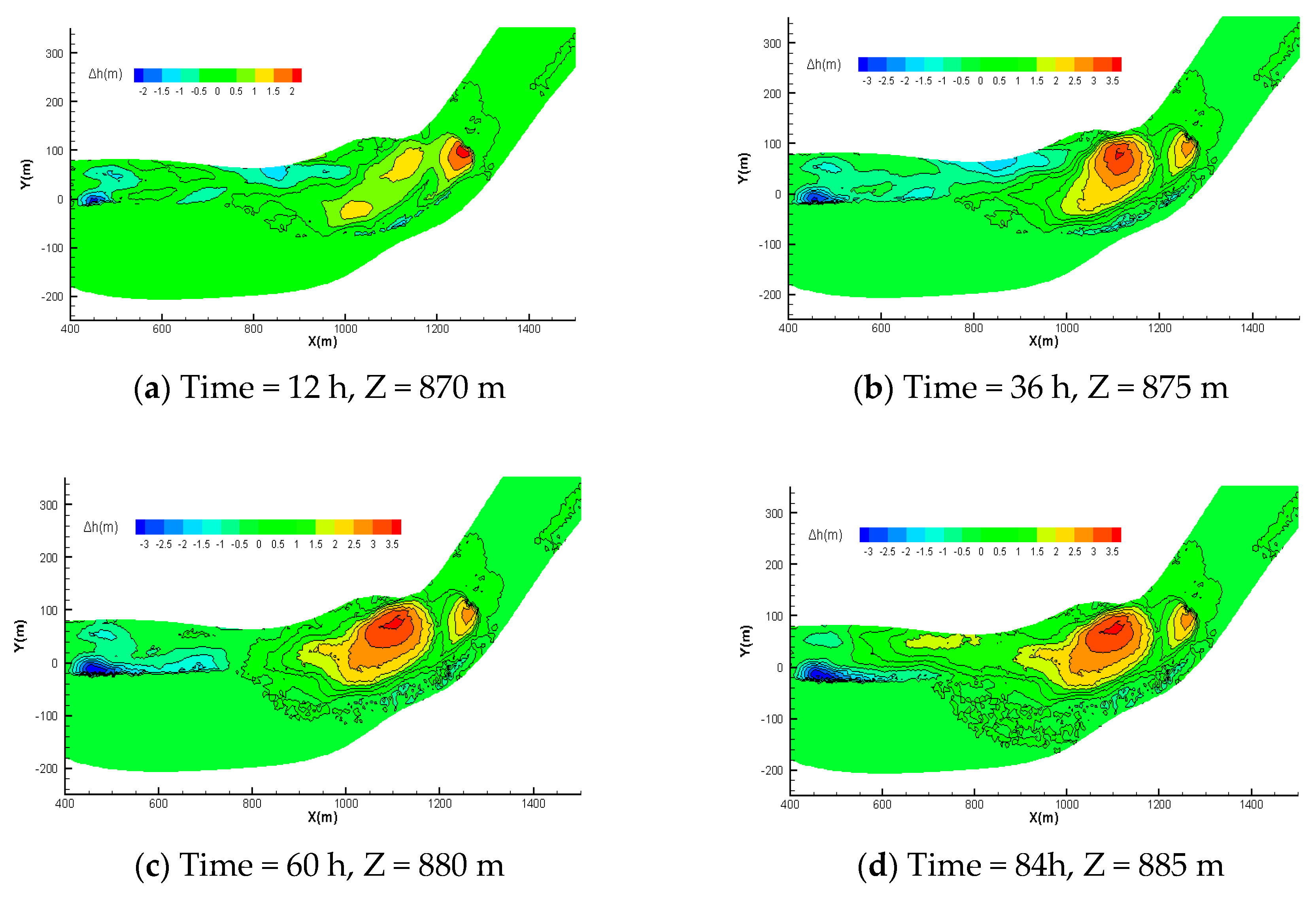
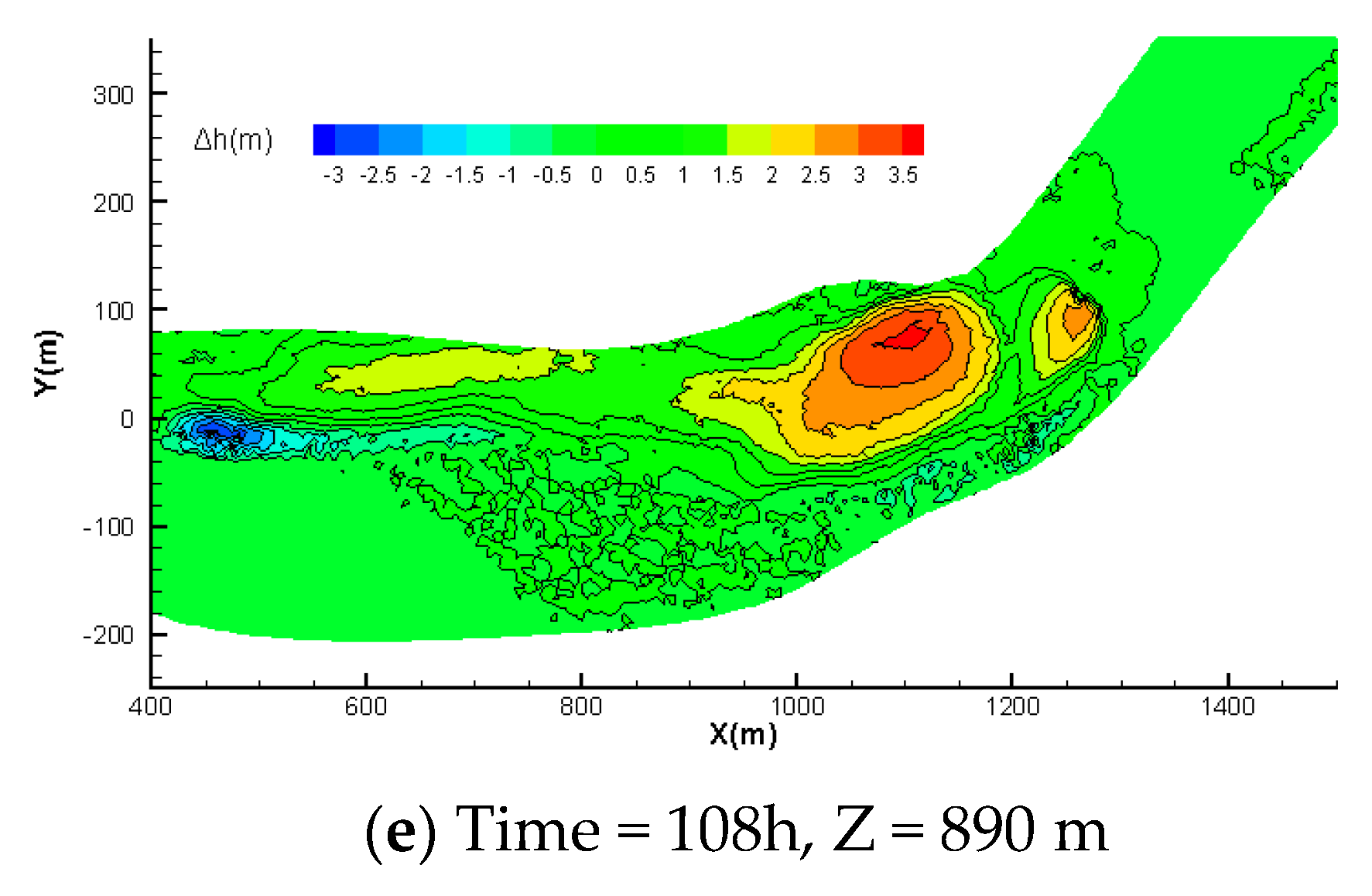
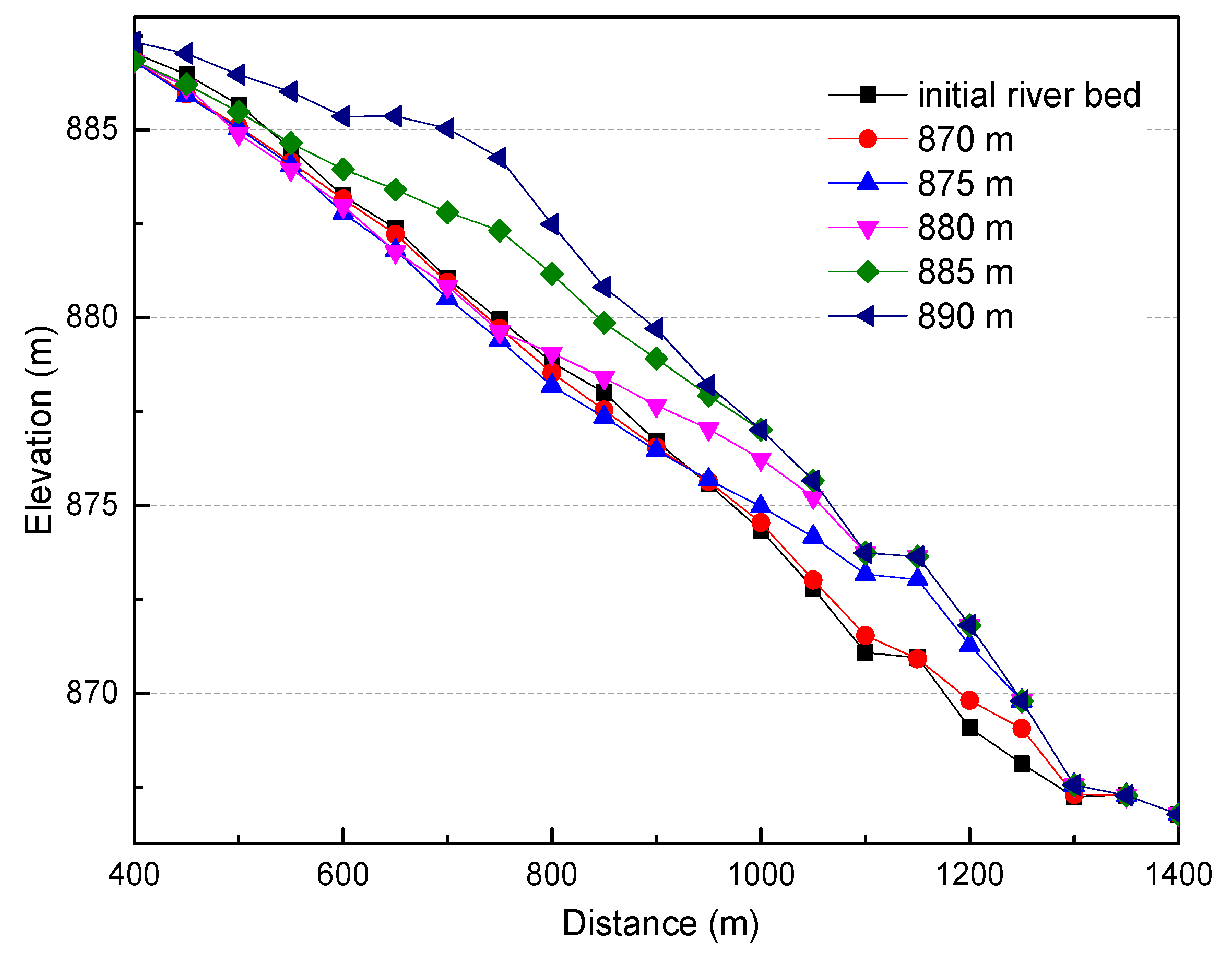
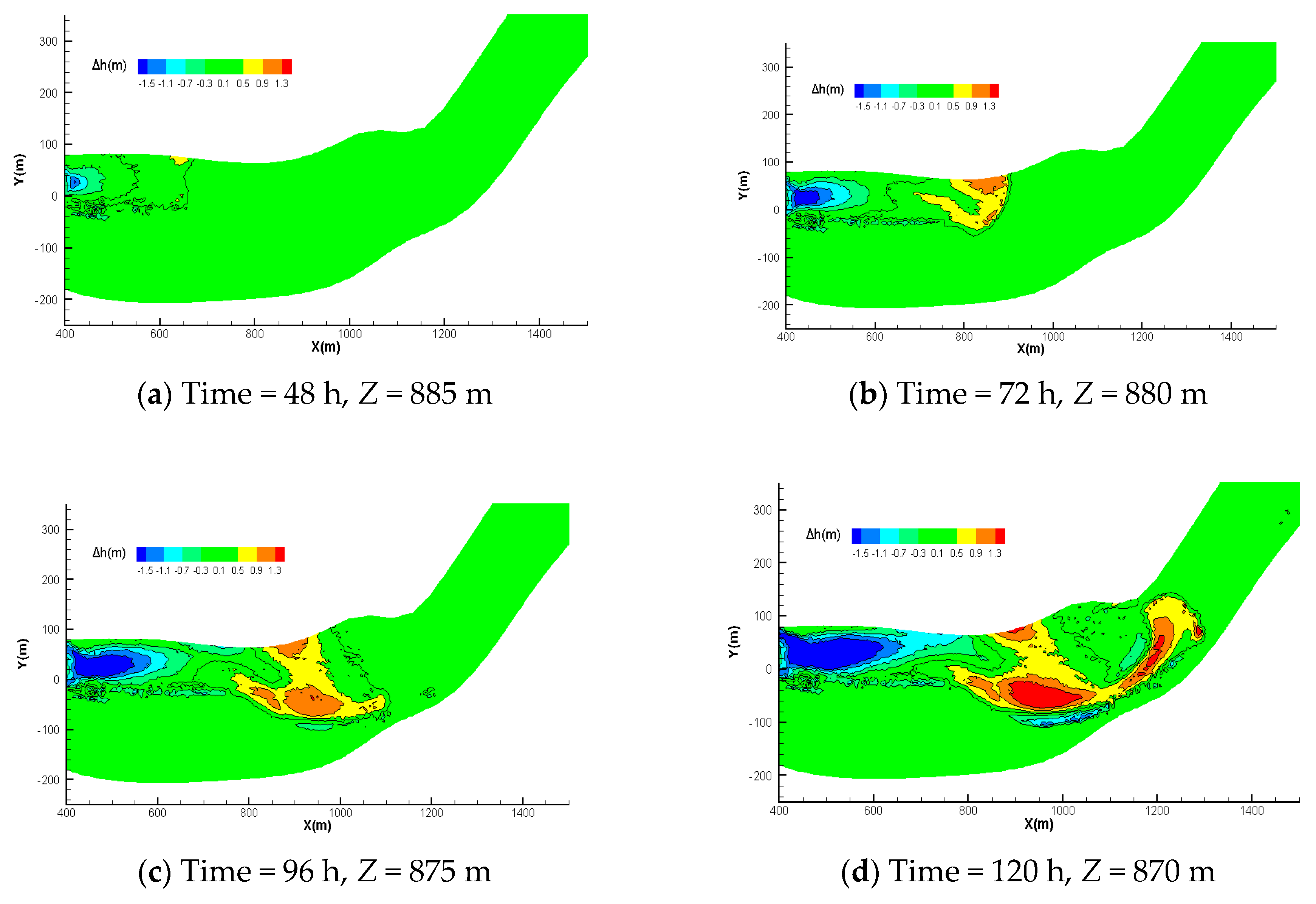
4.3. Evaluation of Morphological Bed Changes in the Fluctuating Backwater Area

According to the actual operation of reservoirs, this section presents three practical applications for which the numerical scheme presented by the current study is particularly relevant and suitable. The three applications concern the reservoir storage, the reservoir drawdown, and the continuous flood process, which reflect the regularity of the sedimentation transport in the fluctuating backwater area of the reservoir modeled by the 2D hydrodynamic and sediment transport numerical model with the variation of water and sediment.

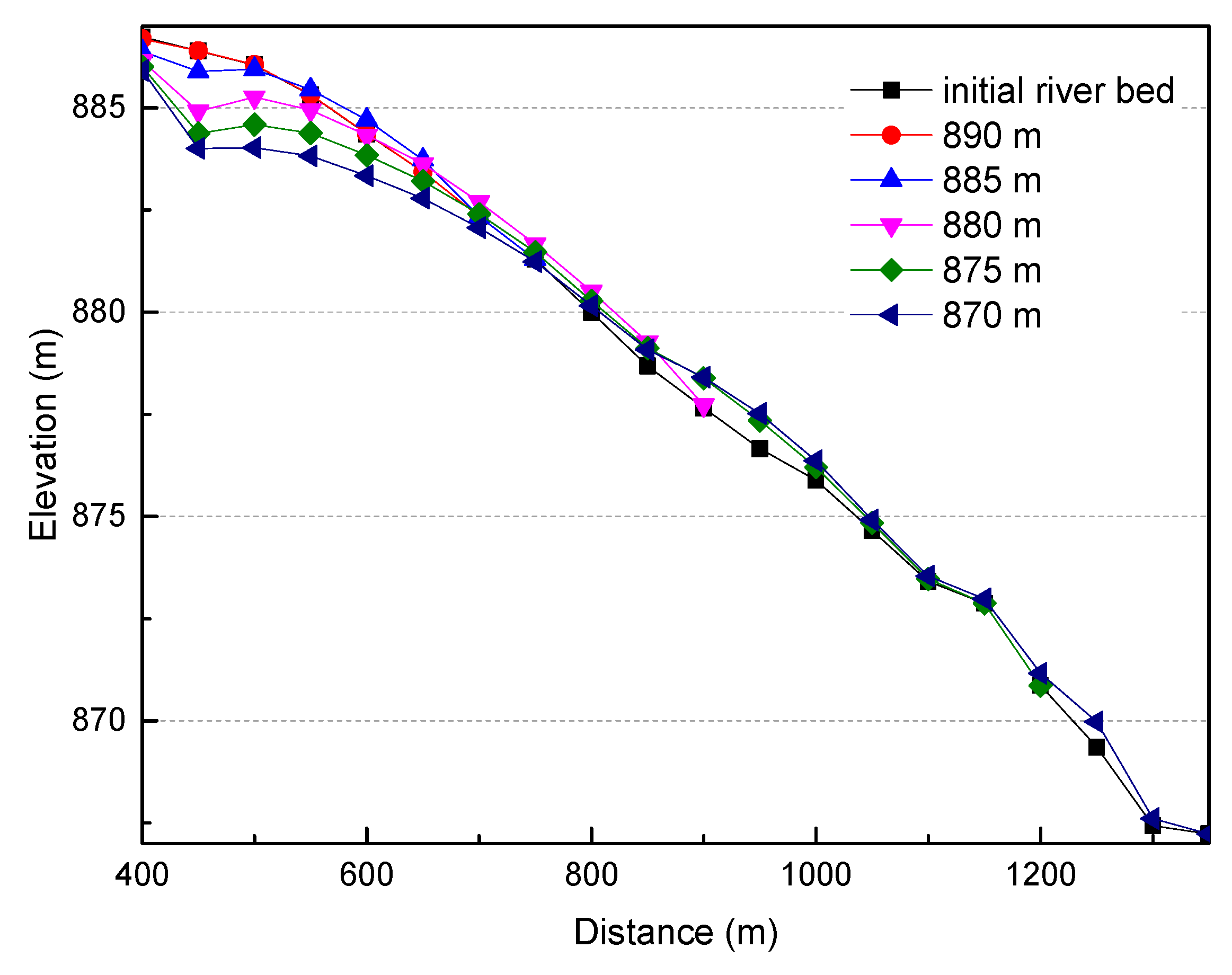
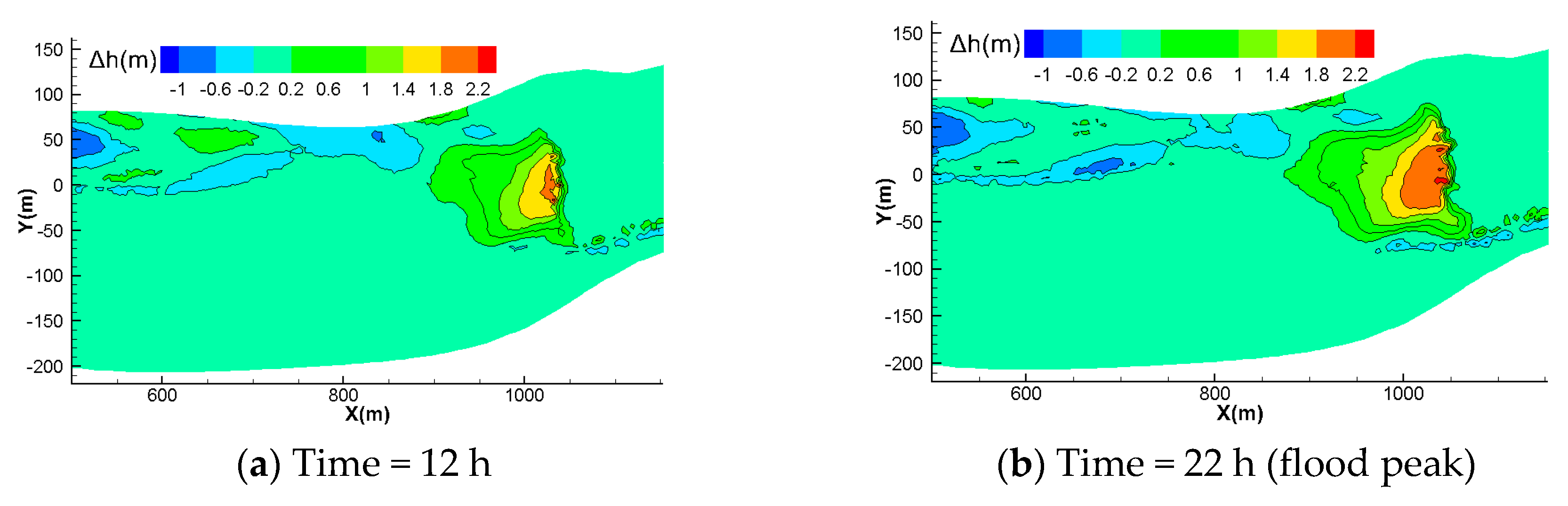
4.3.1. Type 1: Reservoir Storage

The reservoir storage is usually increased after flood conditions in which the discharge of flow is increased and sediment transport is elevated. In this type, the upstream is set to 386 m³ s⁻¹ as the steady flood discharge of a 10-year frequency in the Longxi River. The downstream elevation is set to vary uniformly with time within 870 m to 890 m. The upstream sediment is set as the discharge of bed-load. To show the overall trend and local characteristics, the reservoir sedimentation plane morphology is displayed with the variation in the contour of the bed elevation of the river-bed.

The variation in the contour of bed elevation of the river-bed is shown in Figure 8. Over time, dynamic sedimentation evolves into triangular sedimentation in the longitudinal direction. Under a low water level, the upstream river-bed is lightly scoured and sediment is deposited downstream. When the downstream water level is 870 m, dynamic sedimentation moves to CS12 and the bed-load mainly deposits at the convex bank (left). As the downstream water level rises uniformly, dynamic sedimentation gradually evolves to upstream and the tail of the dynamic sedimentation is kept back. Meanwhile, the tail of dynamic sedimentation retreats faster during the movement of the water level from 885 m to 890 m, during which the upstream river becomes contractive. New triangular sedimentation appears between CS23 and CS27 when the water level rises from 885 m to 890 m.

The morphology of reservoir sedimentation in the longitudinal direction is illustrated by the average of the river bed elevation of river talweg, which can reflect the balance of the main channel and is smoother along this direction. The averages of river bed elevation for every section at different times are shown in Figure 9. The sedimentation experienced by the river bed in the fluctuating backwater area gradually goes from sedimentation to erosion from downstream to upstream as the water level rises. In addition, this trend is the opposite to the increasing gradient of triangular sedimentation.

4.3.2. Type 2: Reservoir Drawdown

During the reservoir full flood period, the water level in front of the dam needs to gradually drop due to power generation, etc., which leads to erosion in the fluctuating backwater area. This process is simulated within this type 2. The final simulation results of reservoir storage were used as the initial topography in this simulation. The upstream flow was set as 189.6 m³ s⁻¹ as a steady mean flood discharge of Longxi River. The downstream elevation was set to uniformly vary with time within a range of an initial 890 m to 870 m. The upstream sediment load was set to zero.

The variation in the contours of bed elevation during reservoir drawdown are summarized by Figure 10. When the downstream water level is 885 m (Figure 10a), the upstream river bed is scoured and the river channel is reshaped, thereby establishing the river morphology for the non-flood period. However, erosive forces are concentrated, resulting in readily scouring of a deep channel. Ultimately, the river bed morphology takes the form of compound channels, including a beach and multiple channels. The sediment resulting from erosion is deposited in the neighboring downstream river section. Because the sediment-carrying capacity of flow is distributed along the horizontal direction, initial sedimentation mainly occurs on both sides of the main stream, which readily promotes the development of the beach. The growth of the left beach in the downstream bend is affected by the sedimentation of reservoir storage. After the water level drops to 875 m or 870 m, the conveyance capacity is reduced due to the influence of the left beach, during which the sediment-carrying flow is focused on the right channel and a large volume of sediment is deposited in the main channel, resulting in a decrease of the elevation difference between the beach and channel. This simulation result is consistent with the conclusions of a field investigation conducted by Han QW of eighteen reservoirs in South China in 1984 [17].

As illustrated by Figure 11 (the same as type 1), there is almost no scouring effect on the river bed by backwater when the downstream water level is 890 m. Scouring of the river bed between CS31 and CS39 begins when the downstream water level drops to 885 m, which produces a large amount of sediment in the backwater area and forms a triangular sedimentation pattern. The erosion of the river-bed gradually evolves as one passes downstream, and the triangular sedimentation also continues to move downstream as the downstream water level drops. Meanwhile, the triangular sedimentation pattern is stretched with the evolution of erosion and siltation. The slope of the longitudinal section of the river bed in the fluctuating backwater area is generally gradually reduced.

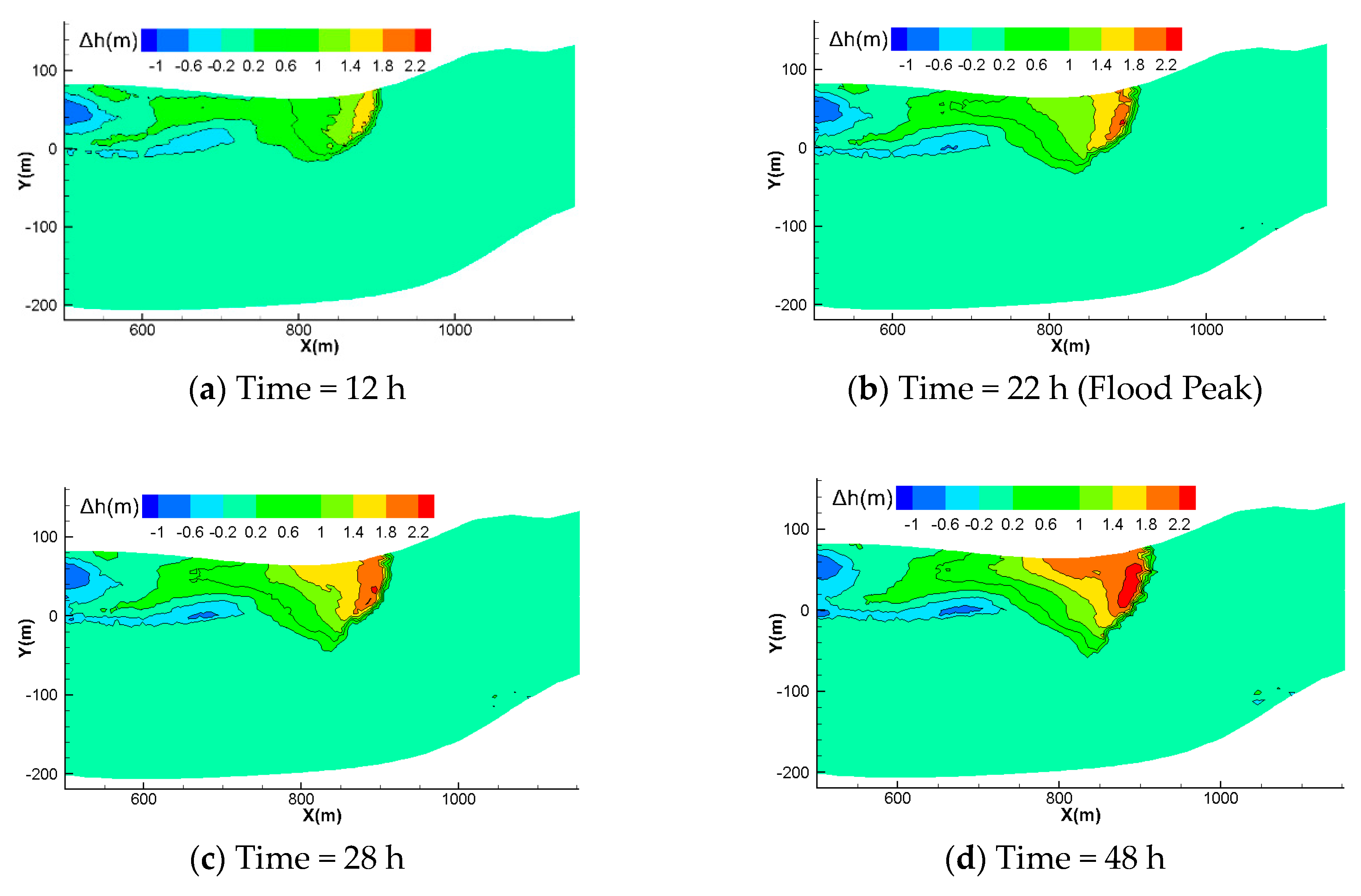
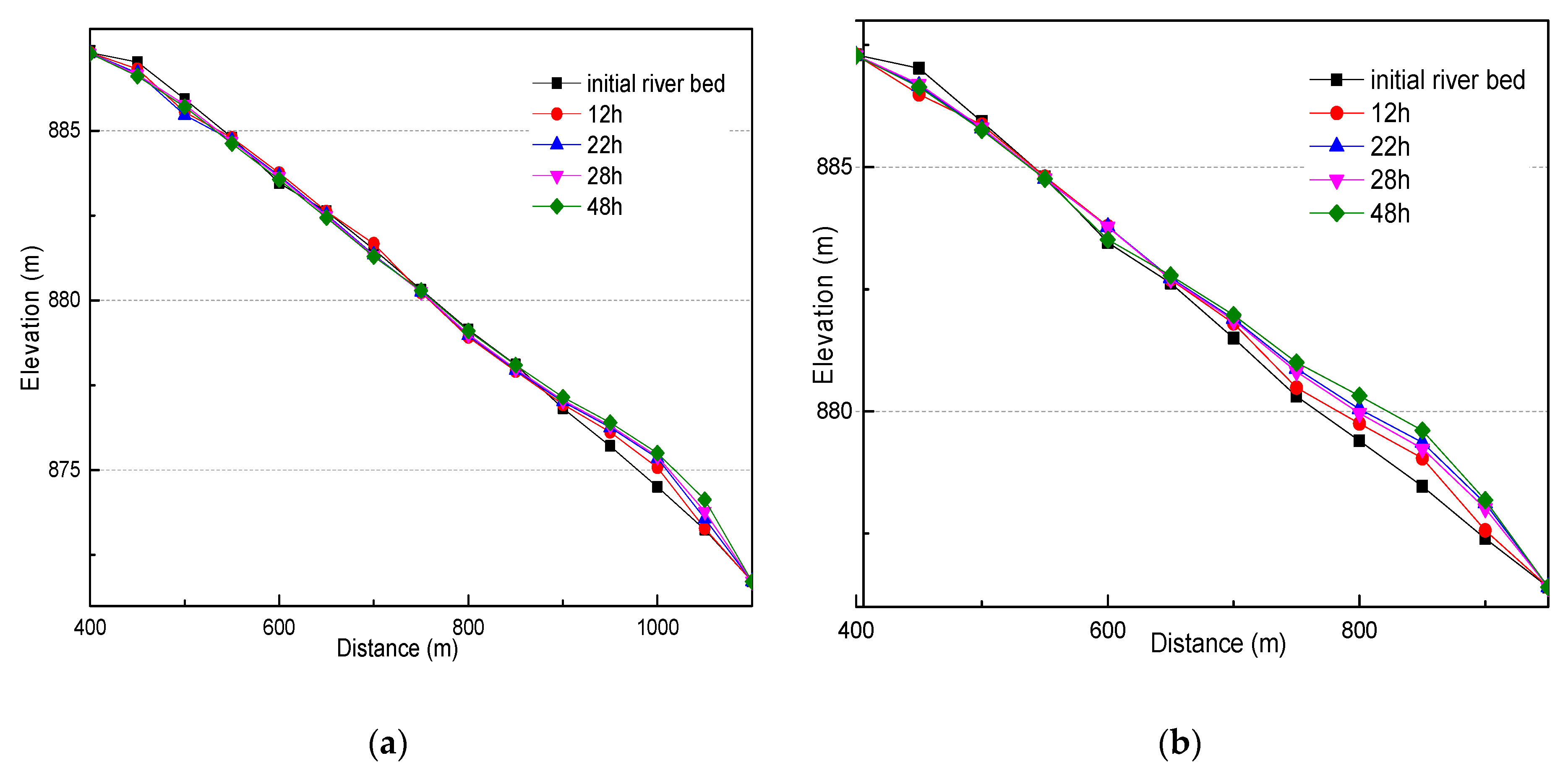
4.3.3. Type 3: Continuous Flood Process

This application simulates the typical continuous flood process, which conforms to the natural case. This application is useful to study bed-load transport in a fluctuating backwater area during a continuous flood process. In this type, the typical flood process of a 50-year frequency is modeled as the upstream discharge (Figure 3a). The downstream water level is set as 875 m for Case A and 880 m for Case B. The upstream sediment is employed in the discharge of bed-load. Figure 12 shows the reservoir sedimentation plane morphology with the variation in the contour of bed elevation. Numerical results are summarized in Figure 12 for Case A and Figure 13 for Case B. These figures include the results for variation in bed elevation at different times (Time = 12 h, 22 h, 28 h, 48 h).

Figure 12a of Case A shows that sedimentation appears near CS18 (x = 1000 m) and with scouring of the upstream river-bed. Because of the minimal discharge from upstream, some sediment carried by flow is deposited in CS26 (x = 650 m). It is clear that erosion occurs near CS23 (x = 800 m), where the channel is narrower and consequently the flow velocity is higher. As the simulation time progresses, erosion gradually moves downstream, and the sediment supplied by upstream gradually increases. A maximum discharge occurs at 22 h (flood peak) in Figure 12b, and the forward slope of sedimentation halts. The elevation of sedimentation rises and the tail is kept back. The triangular-shaped sediment body is deposited near CS21 (x = 800 m) when the downstream water level is 880 m. The elevation of sedimentation rises and the tail back is not obvious compared to that at 875 m up to 22 h (Figure 13 of Case B).

Figure 14 shows the river bed elevation of river talweg in the longitudinal section under a typical continuous flood process for all investigated times, including Figure 14a,b, corresponding to Case A and Case B, respectively. The figures show that the duration of sedimentation for Case A is longer than that for Case B.

The location and bed morphology of the end of the backwater varies under the same inlet flow conditions and different downstream water levels. The location and direction of upstream flow varies under different locations and morphology, resulting in flow conditions under which there are large differences in sedimentation. Therefore, the sedimentation under Case A occurs close to the right bank of the river, whereas sedimentation under Case B occurs close to the left bank of the river. Because the location of sedimentation under Case A is less constrained than that under Case B, the sedimentation shape under Case A is short and wide, whereas that under Case B is long and narrow. In short, there is an element of randomness in the location and morphology of sedimentation affected by the downstream water level and the fluctuating backwater.

5. Conclusions

The present paper presents a numerical strategy to deal with bed-load erosion and deposition in the fluctuating backwater area using the shallow-water equations and Exner equation solvers. The 2D shallow water hydrodynamic model of the fluctuating backwater area is calculated based on the finite volume method of a Godunov scheme. The bed-load transport and river-bed deformation are calculated using an uncoupled equilibrium sediment transport model. The modelling software was written using the FORTRAN programing language. The present study investigated Longxi River, a small stream in Dujiangyan located in Sichuan Province, as a case study river reach.

To validate the performance of the numerical model, a physical model was constructed at the SKLH of Sichuan University, and was applied for two cases studies. The average water level of river talweg in the longitudinal section and the river-bed morphologies of two randomly-chosen cross sections of the sediment generated by numerical simulation were consistent with the measured value in the physical model, indicating that the numerical model is believable. Actual conditions of the operation of the reservoir were studied to reflect the characteristics of bed-load erosion and deposition in the fluctuating backwater area, including three types: reservoir storage, drawdown of the reservoir, and the continuous flooding process under different water levels. The following results were obtained within the present work:

• Sediment transport is by far the more uncertain process, which is the most significant innovation of this study. This present study shows the implementation that the river channel sedimentation morphology is changed by the change of water level in the downstream reach and provides evidence for the effect of incidental events on river bed morphology, which increases the factors driving the change of river bed morphology and challenges the traditional theory that the shape of a river channel is mainly determined by the upstream water and sediment and the physical boundary conditions of the river channel, rather than random events.
• The sedimentation in the fluctuating backwater area is mainly deposited in the main channel and the difference in elevation of the river-bed between the beach and channel decreases with time. In the river bend, the sedimentation is mainly concentrated on the convex bank, readily resulting in the growth of a convex bank beach. Although the concave bank also experiences siltation, the quantity is relatively minor.
• During the drawdown period of the reservoir, the original sedimentation is scoured, with scouring concentrated over a small width. The flow gradually erodes a deep channel in the river-bed, forming compound channels with a beach and multiple channels, which reshapes the channel of the low flow period. The deposition of bed-load from upstream to downstream and the slope of the longitudinal section of the river bed in the fluctuating backwater area are generally gradually reduced.
• There is an element of randomness in the location and morphology of sedimentation due to the effect of the downstream water level and fluctuating backwater. Under type 3, the location and bed morphology of the end of the backwater vary under the same inlet flow conditions and different downstream water levels. The location and direction of upstream flow are changed under differences in location and morphology, resulting in large differences in sedimentation under different flow conditions.

With further studies and scientific improvements within the topics described above, we believe that 2D numerical modeling of bed-load transport in the fluctuating backwater area of reservoirs can be a useful predictive tool to manage channel engineering and determine potential safety hazards for flood control and river-related engineering construction affected by reservoirs.