The Value of Hydrologic Information in Reservoir Outflow Decision-Making
Abstract
:1. Introduction
2. Case Study and Selected Data
3. Methodology
3.1. Random Forests Algorithm
3.2. Statistical Measurements of Model Performance
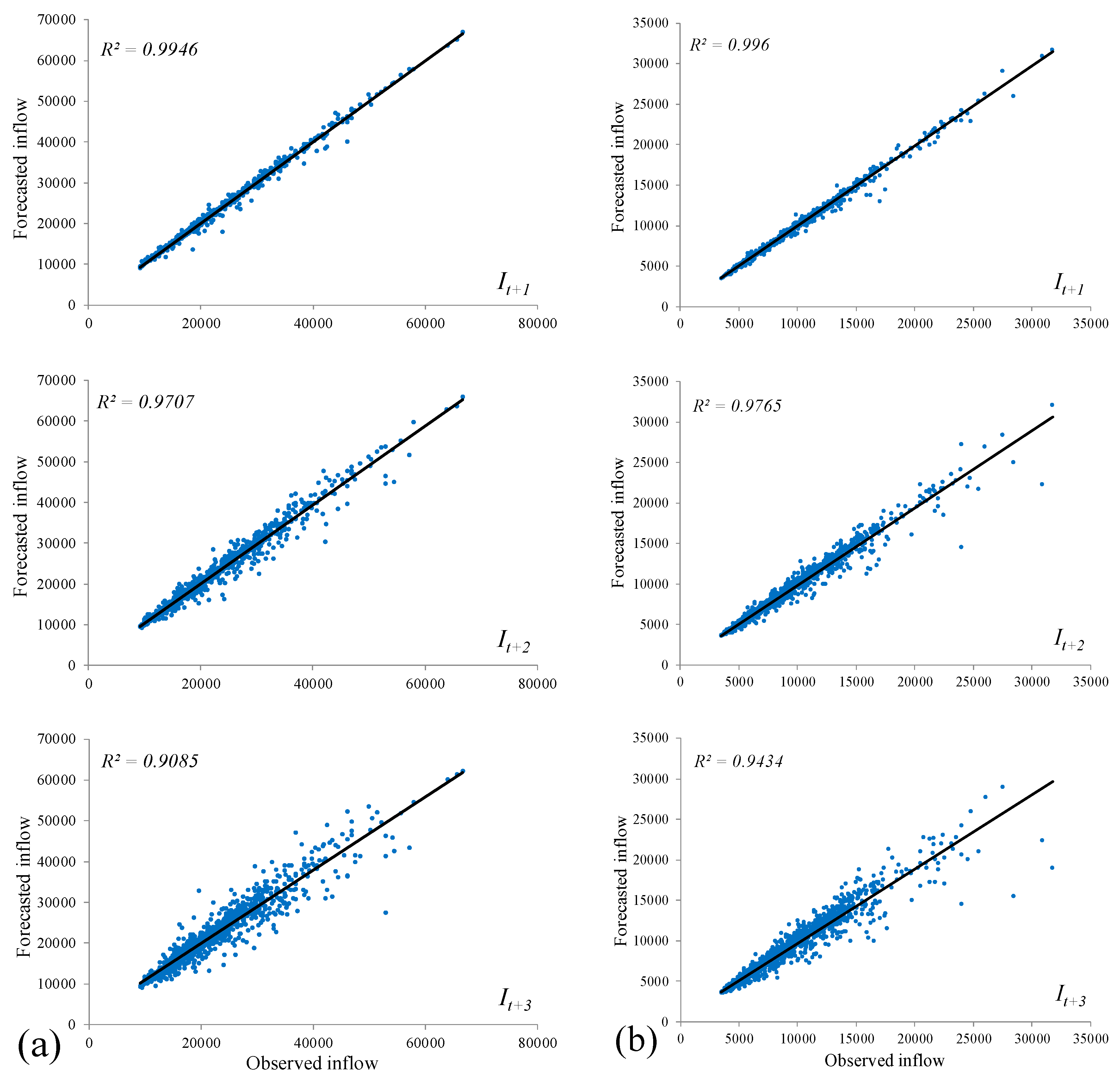
4. Results
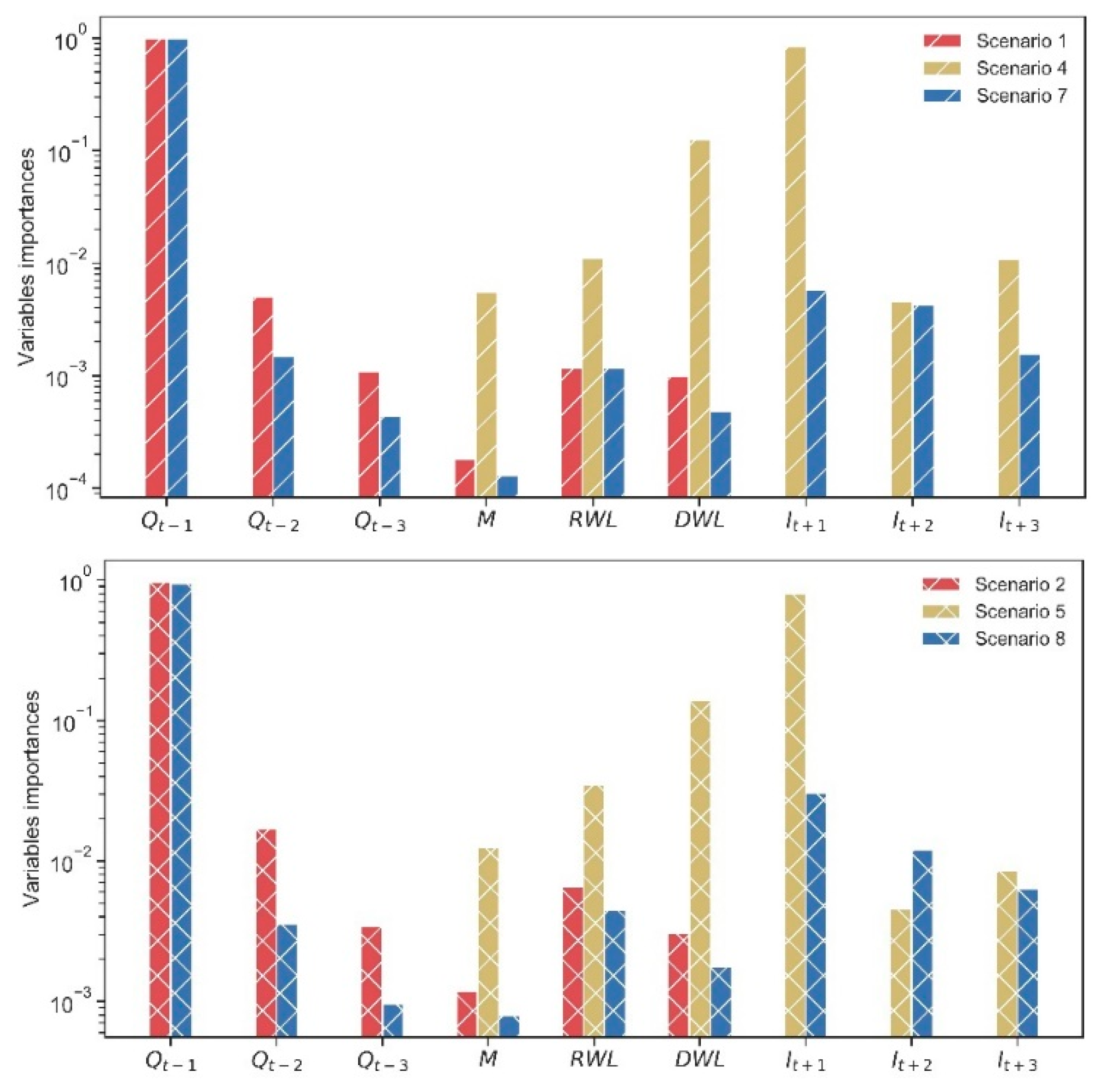
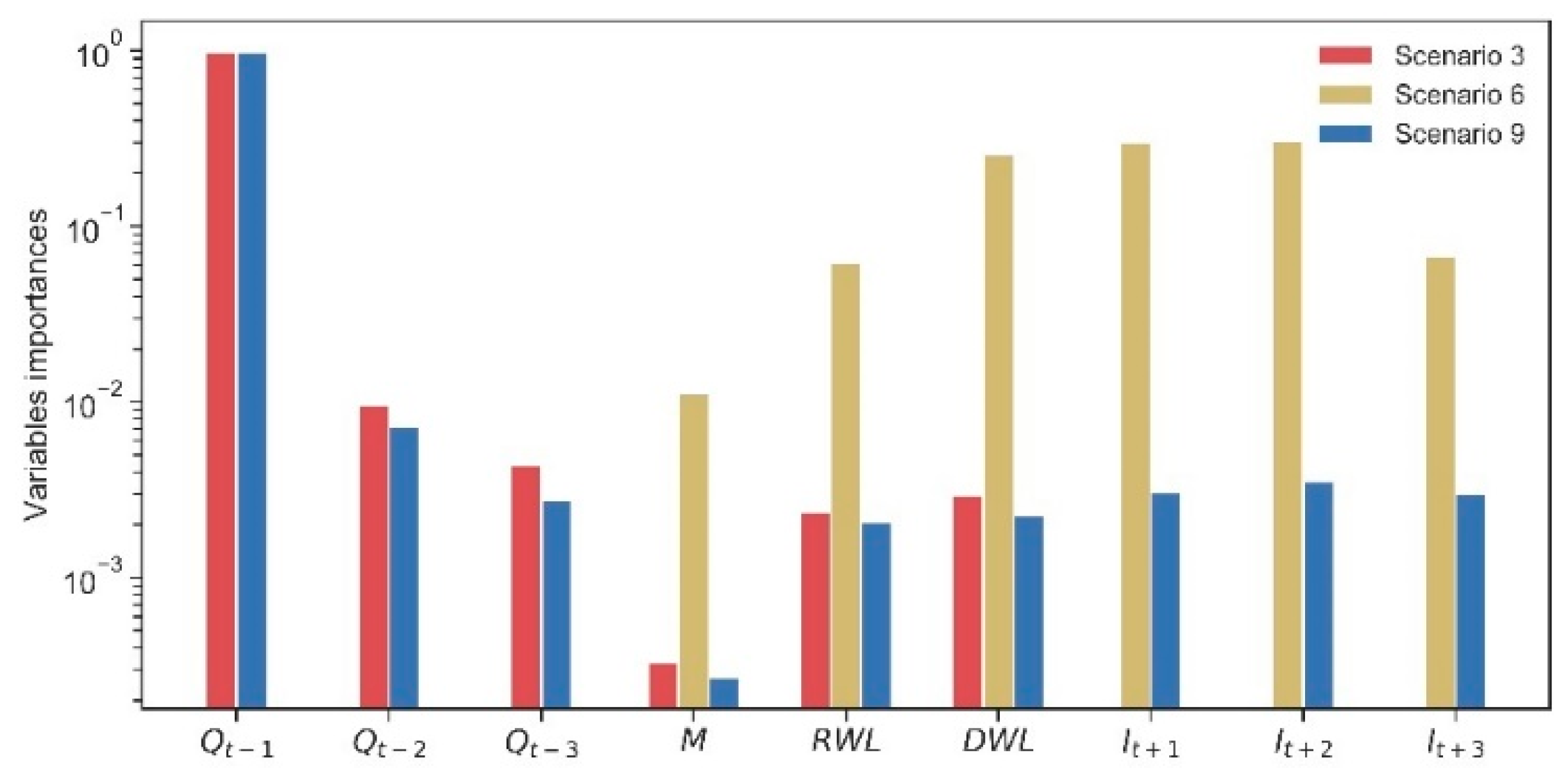
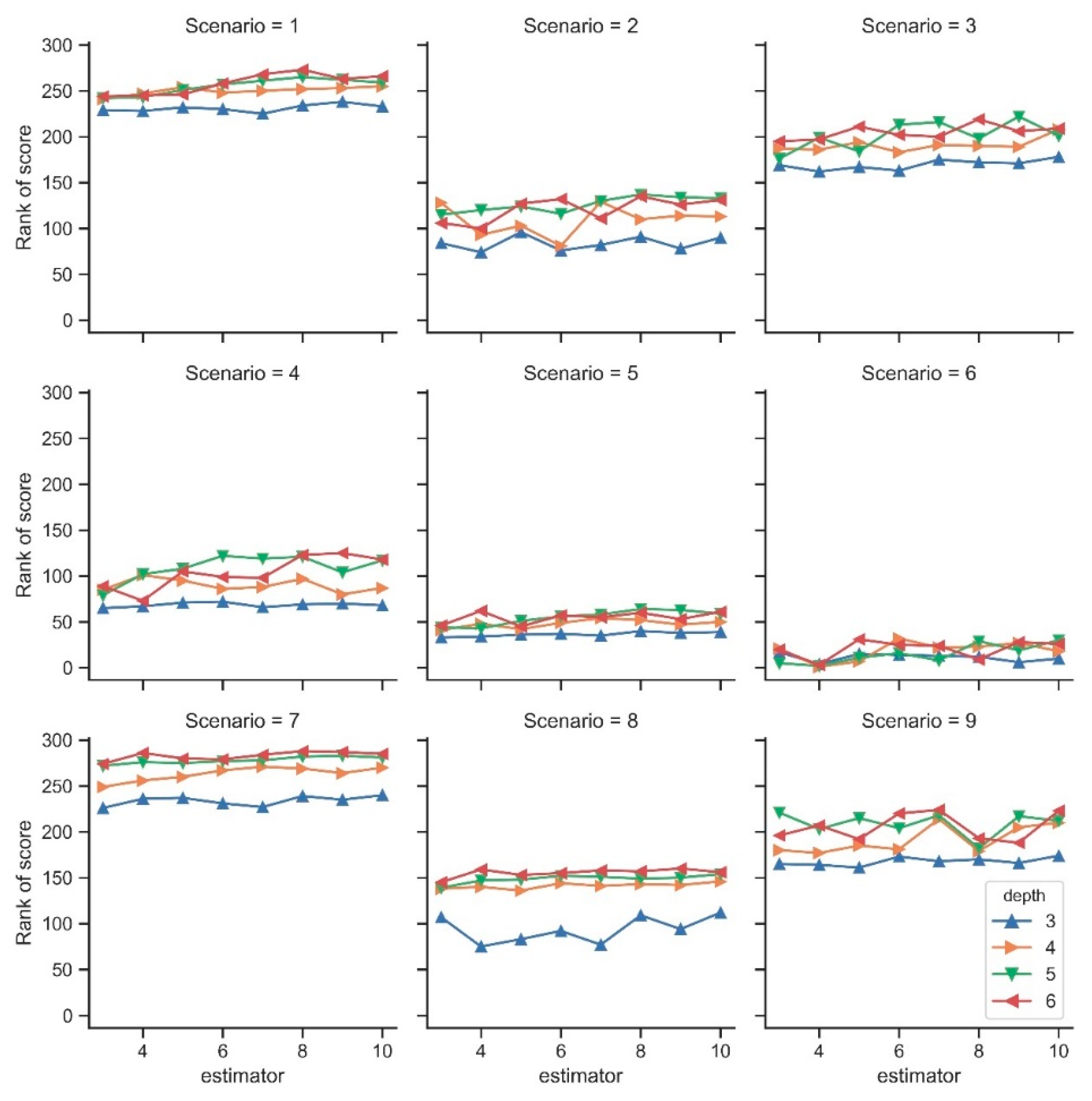
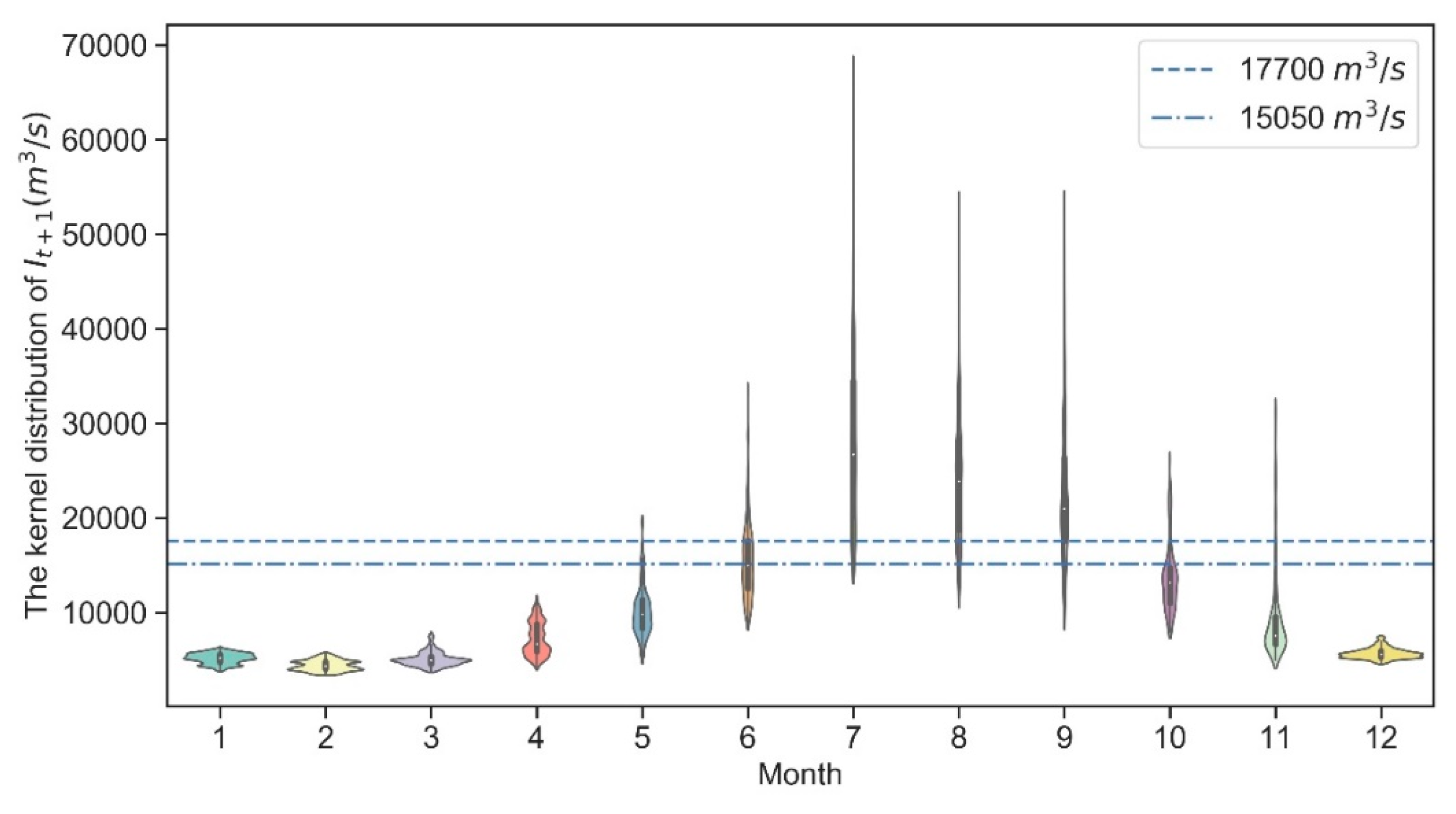
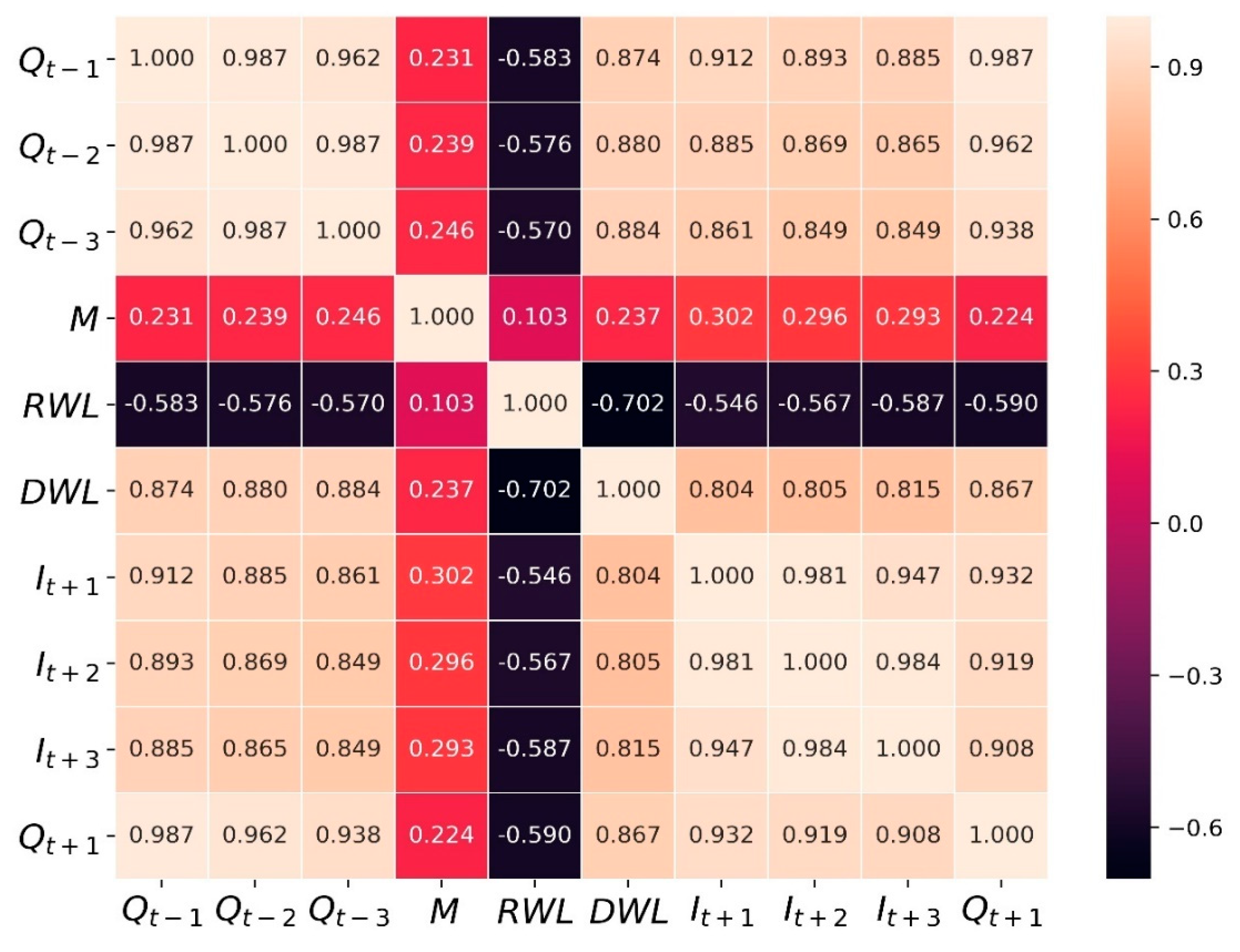
4.1. Candidate Model Parameters and Importance of Input Variables
4.2. Selected Parameters and Simulation Results
- (1)
- Splitting the data into two parts has no improvement on the model’s performance. Compared with scenario 1, scenarios 2 and 3 do not obviously improve the performance of RMSE, NSE and △Qp in three different time periods. For scenarios 4 to 9, the result is also the same.
- (2)
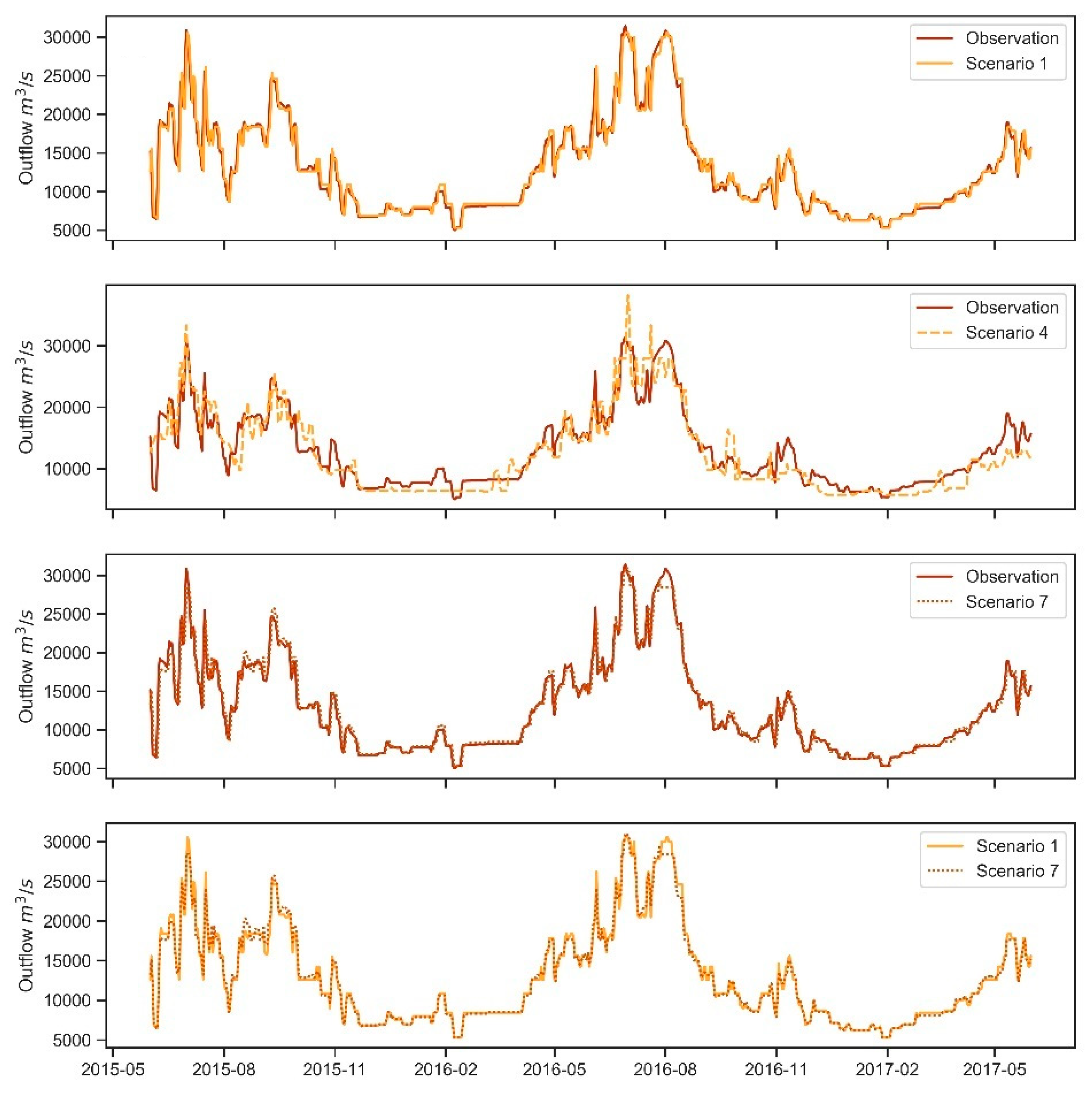
- The future information is effective in a particular scenario and time period. The observed and simulated reservoir outflows of scenarios 1, 4 and 7 are shown in Figure 5. From Table 3 and Figure 5, we can observe that scenario 1 (without future information) performs slightly poorer than the best scenario 7 (with all information). Both of them are far better than scenario 4 (without past information). Comparing statistical performances of scenarios 1 and 7, scenario 7 has obviously increasing more during flood season than non-flood season. There is no significant difference between these two during non-flood season. Further, based on the values of NSE, the scenarios 1 and 7 perform better during non-flood season, while scenario 4 performs much better during flood season.
5. Discussion
5.1. The Impact of Splitting Data Set by Prior Knowledge
5.2. Past Information Is the Most Important Information
5.3. Future Information in Particular Scenario and Time Period
5.4. The Practical Application of This Study
6. Conclusions
- (1)
- The statistical performances of simulation results demonstrate that the RF algorithm can reasonably simulate outflow decisions. The RF with visible physical interpretation and variables importance measure is suitable and helpful for evaluating the value of hydrologic information.
- (2)
- The past outflow is the most important information for reservoir operator decision-making. The forecasted inflow is more important during flood season than non-flood season in outflow decision-making.
- (3)
- The proposed reservoir outflow simulation model is useful for downstream water users and operators of TGR. The value analysis of hydrologic information will help reservoir operators and theoretical optimization researchers of TGR make better use of hydrological information in practice and study.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bessler, F.T.; Savic, D.A.; Walters, G.A. Water reservoir control with data mining. J. Water Res. Plan. Manag. 2003, 129, 26–34. [Google Scholar] [CrossRef]
- Hejazi, M.I.; Cai, X.; Ruddell, B.L. The role of hydrologic information in reservoir operation—Learning from historical releases. Adv. Water Resour. 2008, 31, 1636–1650. [Google Scholar] [CrossRef]
- Corani, G.; Rizzoli, A.E.; Salvetti, A.; Zaffalon, M. Reproducing human decisions in reservoir management: The case of lake Lugano. In Information Technologies in Environmental Engineering; Springer: Berlin, Germany, 2009; pp. 252–263. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; ACM: Pittsburgh, PA, USA, 2006; pp. 161–168. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Yang, G.S.; Wan, R.R.; Dai, X.; Zhang, Y.H. Comparison of Random Forests and other statistical methods for the prediction of lake water level: A case study of the Poyang lake in China. Hydrol. Res. 2016, 47, 69–83. [Google Scholar] [CrossRef]
- Albers, S.J.; Dery, S.J.; Petticrew, E.L. Flooding in the Nechako river basin of Canada: A Random Forest modeling approach to flood analysis in a regulated reservoir system. Can. Water Resour. J. 2016, 41, 250–260. [Google Scholar] [CrossRef]
- Yang, T.; Gao, X.; Sorooshian, S.; Li, X. Simulating California reservoir operation using the classification and regression-tree algorithm combined with a shuffled cross-validation scheme. Water Resour. Res. 2016, 52, 1626–1651. [Google Scholar] [CrossRef]
- Sultana, Z.; Sieg, T.; Kellermann, P.; Müller, M.; Kreibich, H. Assessment of business interruption of flood-affected companies using Random Forests. Water 2018, 10, 1049. [Google Scholar] [CrossRef]
- Tillman, F.D.; Anning, D.W.; Heilman, J.A.; Buto, S.G.; Miller, M.P. Managing salinity in upper Colorado river basin streams: Selecting catchments for sediment control efforts using watershed characteristics and Random Forests models. Water 2018, 10, 676. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, L.; Chen, L.; Wang, D.; Dai, M.; Xu, W.; Yan, T. Water compensation and its implication of the Three Gorges Reservoir for the river-lake system in the middle Yangtze river, china. Water 2018, 10, 1011. [Google Scholar] [CrossRef]
- Ma, C.; Lian, J.J.; Wang, J.N. Short-term optimal operation of Three-gorge and Gezhouba cascade hydropower stations in non-flood season with operation rules from data mining. Energy Convers. Manag. 2013, 65, 616–627. [Google Scholar] [CrossRef]
- Cunge, J.A. On the subject of a flood propagation computation method (musklngum method). J. Hydraul. Res. 1969, 7, 205–230. [Google Scholar] [CrossRef]
- Nash, J. The form of the instantaneous unit hydrograph. Int. Assoc. Sci. Hydrol. Publ. 1957, 3, 114–121. [Google Scholar]
- Ren-Jun, Z. The xinanjiang model applied in china. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Hancock, T.; Put, R.; Coomans, D.; Vander Heyden, Y.; Everingham, Y. A performance comparison of modem statistical techniques for molecular descriptor selection and retention prediction in chromatographic qsrr studies. Chemom. Intell. Lab. Syst. 2005, 76, 185–196. [Google Scholar] [CrossRef]
- Yin, J.B.; Guo, S.L.; He, S.K.; Guo, J.L.; Hong, X.J.; Liu, Z.J. A copula-based analysis of projected climate changes to bivariate flood quantiles. J. Hydrol. 2018, 566, 23–42. [Google Scholar] [CrossRef]
- Yin, J.B.; Guo, S.L.; Liu, Z.J.; Yang, G.; Zhong, Y.X.; Liu, D.D. Uncertainty analysis of bivariate design flood estimation and its impacts on reservoir routing. Water Resour Manag 2018, 32, 1795–1809. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wu, X.S.; Guo, S.L.; Yin, J.B.; Yang, G.; Zhong, Y.X.; Liu, D.D. On the event-based extreme precipitation across China: Time distribution patterns, trends, and return levels. J. Hydrol. 2018, 562, 305–317. [Google Scholar] [CrossRef]
- Wu, X.S.; Wang, Z.L.; Guo, S.L.; Liao, W.L.; Zeng, Z.Y.; Chen, X.H. Scenario-based projections of future urban inundation within a coupled hydrodynamic model framework: A case study in Dongguan city, China. J. Hydrol. 2017, 547, 428–442. [Google Scholar] [CrossRef]
- Liu, X.Y.; Guo, S.L.; Liu, P.; Chen, L.; Li, X.A. Deriving optimal refill rules for multi-purpose reservoir operation. Water Resour. Manag. 2011, 25, 431–448. [Google Scholar] [CrossRef]
- Guo, S.L.; Chen, J.H.; Li, Y.; Liu, P.; Li, T.Y. Joint operation of the multi-reservoir system of the Three Gorges and the Qingjiang cascade reservoirs. Energies 2011, 4, 1036–1050. [Google Scholar] [CrossRef]
- Li, Y.; Guo, S.L.; Quo, J.L.; Wang, Y.; Li, T.Y.; Chen, J.H. Deriving the optimal refill rule for multi-purpose reservoir considering flood control risk. J. Hydrol.-Environ. Res. 2014, 8, 248–259. [Google Scholar] [CrossRef]
- Mu, J.; Ma, C.; Zhao, J.Q.; Lian, J.J. Optimal operation rules of Three-Gorge and Gezhouba cascade hydropower stations in flood season. Energy Convers. Manag. 2015, 96, 159–174. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Guo, S.L.; Xu, C.Y.; Liu, P.; Qin, H. Deriving joint optimal refill rules for cascade reservoirs with multi-objective evaluation. J. Hydrol. 2015, 524, 166–181. [Google Scholar] [CrossRef]
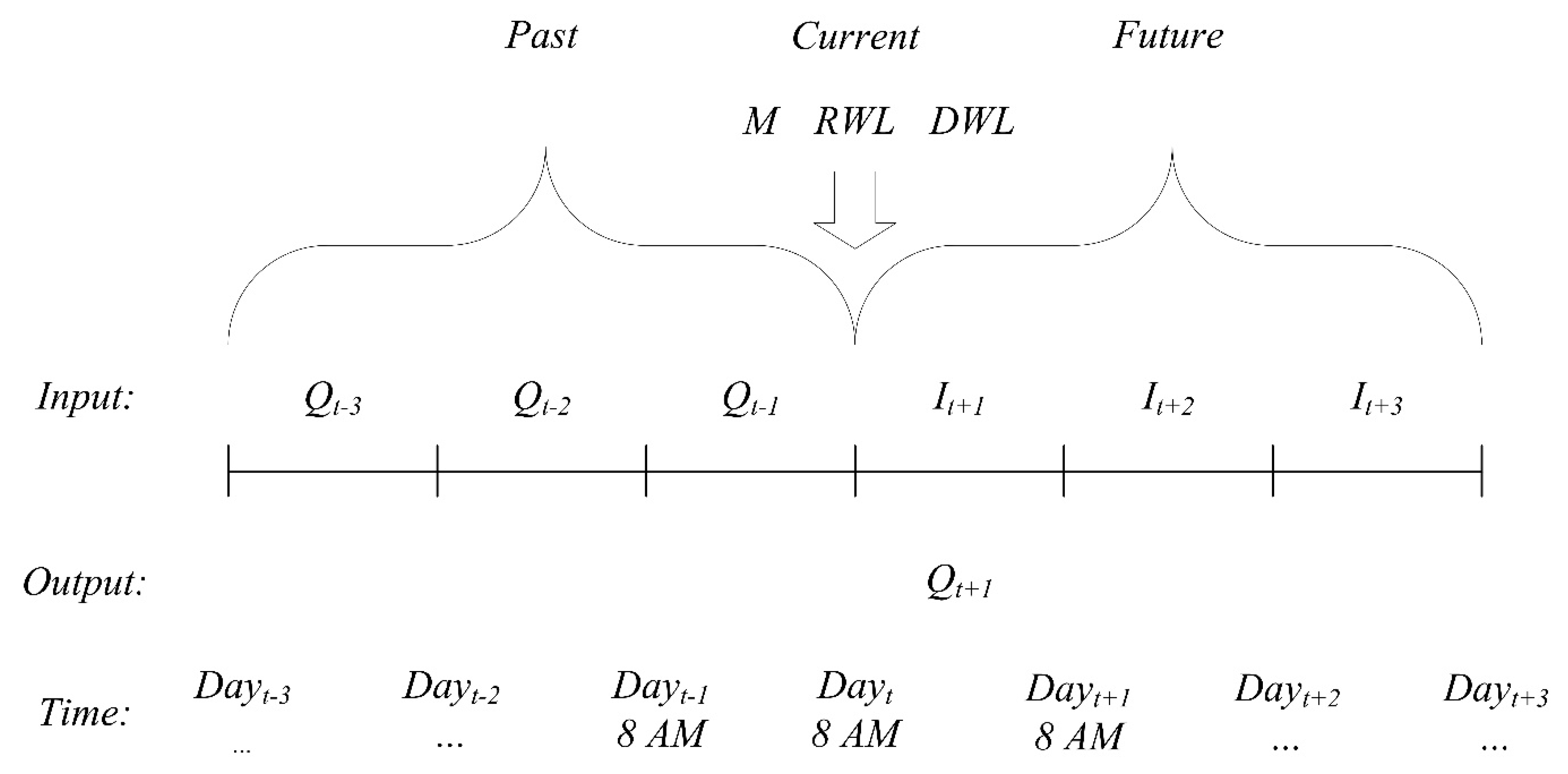
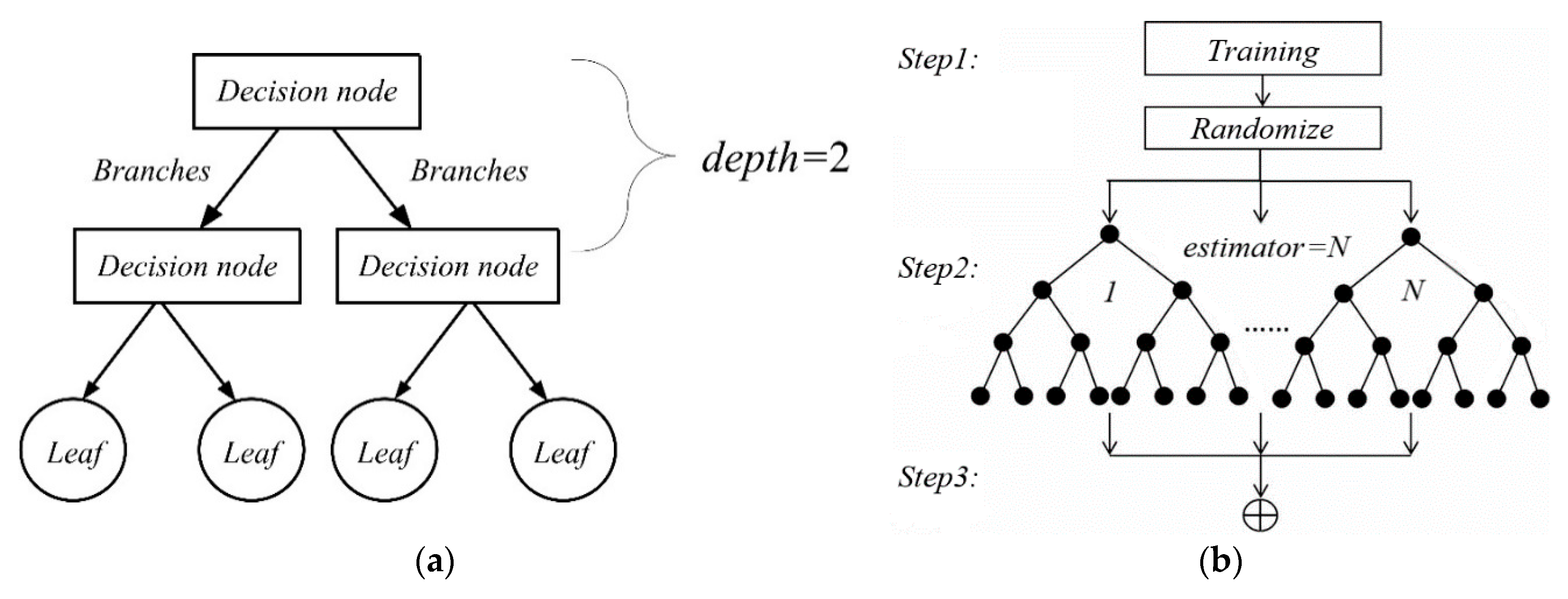

| Information | Input/Output Variable Names | Abbr. | Unit | Resolution |
|---|---|---|---|---|
| Past | past 1-day outflow | Qt−1 | m3/s | Daily |
| past 2-day outflow | Qt−2 | m3/s | Daily | |
| past 3-day outflow | Qt−3 | m3/s | Daily | |
| Current | month | M | Monthly | |
| reservoir water level | RWL | m | Daily | |
| downstream water level | DWL | m | Daily | |
| Future | forecasted 1-day inflow | It+1 | m3/s | Daily |
| forecasted 2-day inflow | It+2 | m3/s | Daily | |
| forecasted 3-day inflow | It+3 | m3/s | Daily | |
| tomorrow average outflow | Qt+1 | m3/s | Daily |
| Combination of Information | All Year | Flood Season | Non-Flood Season |
|---|---|---|---|
| Past + Current | 1 | 2 | 3 |
| Current + Future | 4 | 5 | 6 |
| Past + Current + Future | 7 | 8 | 9 |
| Scenarios | All Year | Flood Season | Non-Flood Season | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE (m3/s) | NSE | △Qp | RMSE (m3/s) | NSE | △Qp | RMSE (m3/s) | NSE | △Qp | |
| 1 | 1225 | 0.959 | 1.9 | 1864 | 0.899 | 1.9 | 717 | 0.950 | 2.2 |
| 2 and 3 | 1181 | 0.962 | 2.5 | 1764 | 0.909 | 2.5 | 732 | 0.948 | 6.5 |
| 4 | 2525 | 0.829 | 7.7 | 3239 | 0.696 | 7.7 | 2077 | 0.587 | 25.9 |
| 5 and 6 | 2506 | 0.832 | 5.0 | 3143 | 0.714 | 5.0 | 2116 | 0.572 | 28.8 |
| 7 | 1141 | 0.965 | 0.9 | 1718 | 0.915 | 0.9 | 690 | 0.954 | 5.4 |
| 8 and 9 | 1195 | 0.961 | 2.4 | 1794 | 0.906 | 2.4 | 729 | 0.949 | 4.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Guo, S.; He, S.; Xu, T.; Zhong, Y.; Sun, S. The Value of Hydrologic Information in Reservoir Outflow Decision-Making. Water 2018, 10, 1372. https://doi.org/10.3390/w10101372
Chen K, Guo S, He S, Xu T, Zhong Y, Sun S. The Value of Hydrologic Information in Reservoir Outflow Decision-Making. Water. 2018; 10(10):1372. https://doi.org/10.3390/w10101372
Chicago/Turabian StyleChen, Kebing, Shenglian Guo, Shaokun He, Tao Xu, Yixuan Zhong, and Sirui Sun. 2018. "The Value of Hydrologic Information in Reservoir Outflow Decision-Making" Water 10, no. 10: 1372. https://doi.org/10.3390/w10101372
APA StyleChen, K., Guo, S., He, S., Xu, T., Zhong, Y., & Sun, S. (2018). The Value of Hydrologic Information in Reservoir Outflow Decision-Making. Water, 10(10), 1372. https://doi.org/10.3390/w10101372






