Flood Mitigation through Optimal Operation of a Multi-Reservoir System by Using Model Predictive Control: A Case Study in Myanmar
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Hydrological and Morphological Data
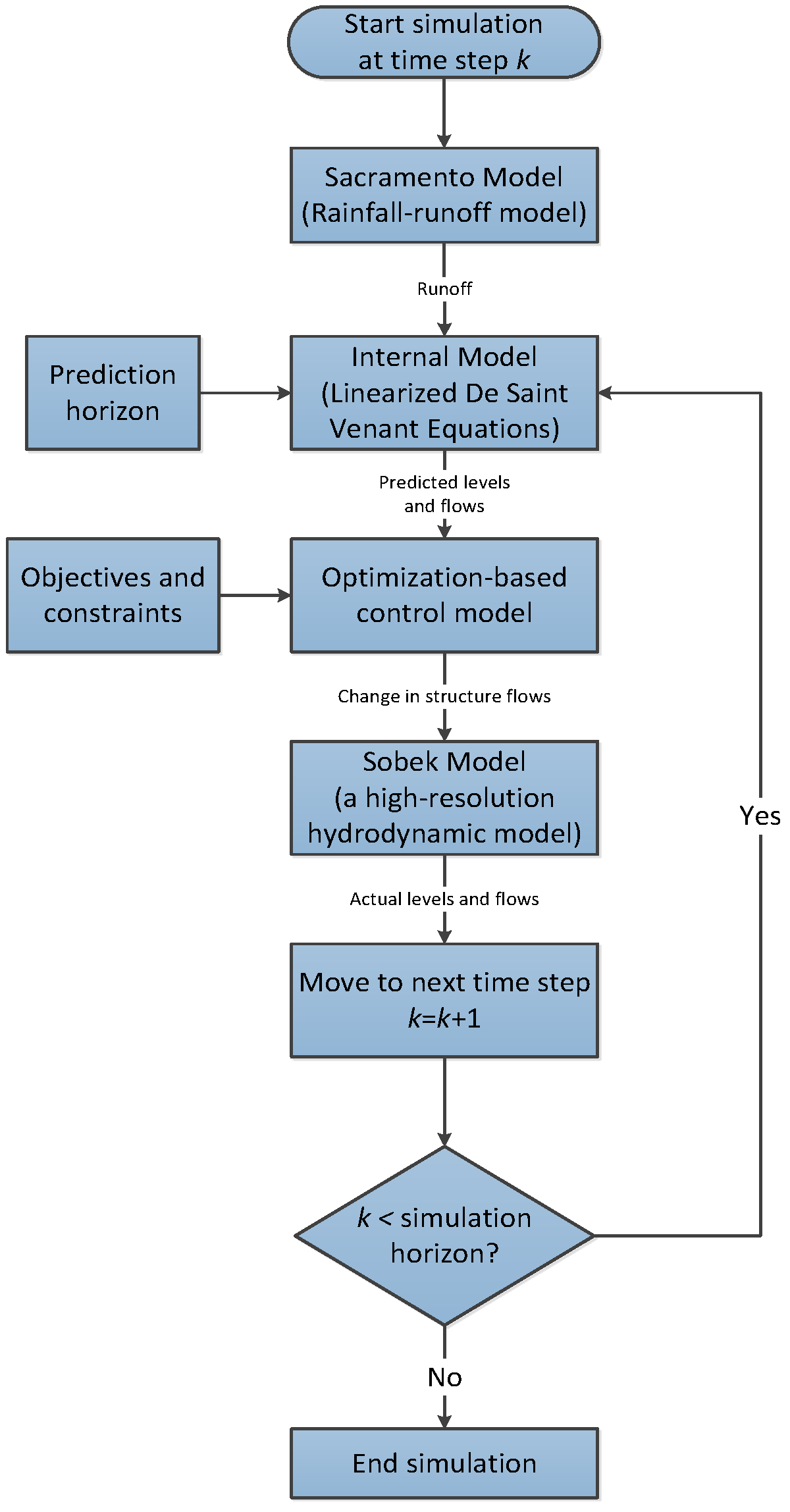
2.3. Methods
2.3.1. Modelling Rainfall-Runoff Process
2.3.2. Simplified Internal Model
2.3.3. Objective Function and Constraints
2.3.4. Modelling the Sittaung River System
3. Simulation Settings and Operation Scenarios
3.1. Performance Indicators
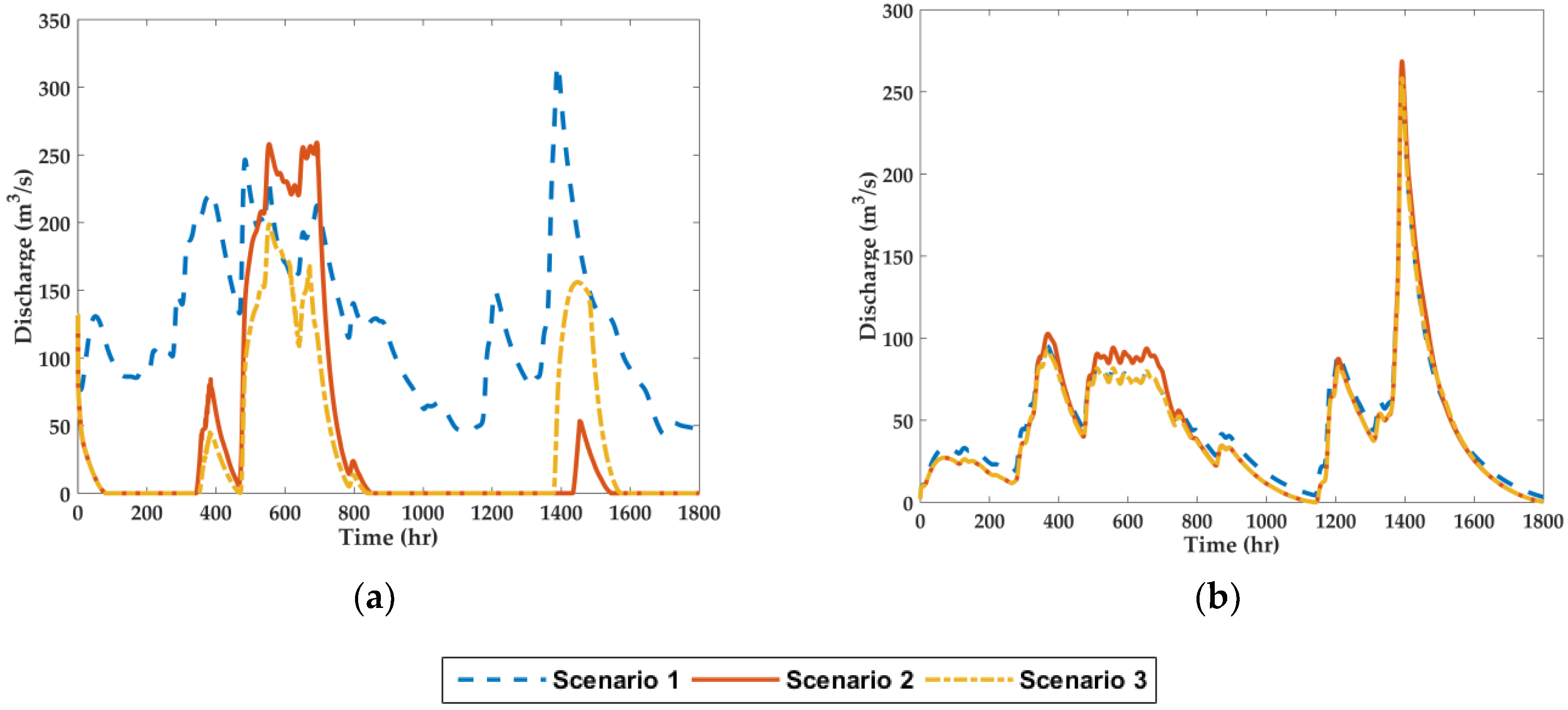
4. Results
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Leithwood, K.A. The Role of Dams in Development. Int. J. Water Resour. Dev. 2002, 18, 9–24. [Google Scholar] [CrossRef]
- Castelletti, A.; Pianosi, F.; Soncini-Sessa, R. Water reservoir control under economic, social and environmental constraints. Automatica 2008, 44, 1595–1607. [Google Scholar] [CrossRef]
- Seibert, S.P.; Skublics, D.; Ehret, U. The potential of coordinated reservoir operation for flood mitigation in large basins—A case study on the Bavarian Danube using coupled hydrological–hydrodynamic models. J. Hydrol. 2014, 517, 1128–1144. [Google Scholar] [CrossRef]
- Lin, N.M.; Rutten, M. Optimal Operation of a Network of Multi-purpose Reservoir: A Review. Procedia Eng. 2016, 154, 1376–1384. [Google Scholar] [CrossRef]
- Che, D.; Mays, L.W. Application of an Optimization/Simulation Model for Real-Time Flood-Control Operation of River-Reservoirs Systems. Water Resour. Manag. 2017, 31, 2285–2297. [Google Scholar] [CrossRef]
- Galelli, S.; Goedbloed, A.; Schwanenberg, D.; van Overloop, P.-J. Optimal Real-Time Operation of Multipurpose Urban Reservoirs: Case Study in Singapore. J. Water Resour. Plan. Manag. 2014, 140, 511–523. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal Operation of Multireservoir Systems: State-of-the-Art Review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mariño, M.A. Multipurpose reservoir operation. 2. Daily operation of a multiple reservoir system. J. Hydrol. 1984, 69, 15–28. [Google Scholar] [CrossRef]
- Niewiadomska-Szynkiewicz, E.; Malinowski, K.; Karbowski, A. Predictive methods for real-time control of flood operation of a multireservoir system: Methodology and comparative study. Water Resour. Res. 1996, 32, 2885–2895. [Google Scholar] [CrossRef]
- Wei, C.C.; Hsu, N.S. Multireservoir real-time operations for flood control using balanced water level index method. J. Environ. Manag. 2008, 88, 1624–1639. [Google Scholar] [CrossRef] [PubMed]
- Camacho, E.F.; Bordons, C. Model Predictive control. In Advanced Textbooks in Control and Signal Processing; Springer: London, UK, 2007; ISBN 978-1-85233-694-3. [Google Scholar]
- Tian, X. Model Predictive Control for Operational Water Management: A Case Study of the Dutch Water System. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Maciejowski, J.M. Predictive Control with Constraints; Pearson Education: London, UK, 2000; ISBN 0 201398230PPR. [Google Scholar]
- Van Overloop, P.-J. Model Predictive Control on Open Water Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Negenborn, R.; van Overloop, P.-J.; Keviczky, T.; Schutter, B. Distributed model predictive control of irrigation canals. Netw. Heterog. Media 2009, 4, 359–380. [Google Scholar] [CrossRef] [Green Version]
- Zafra-Cabeza, A.; Maestre, J.M.; Ridao, M.A.; Camacho, E.F.; Sánchez, L. A hierarchical distributed model predictive control approach to irrigation canals: A risk mitigation perspective. J. Process Control 2011, 21, 787–799. [Google Scholar] [CrossRef]
- Van Overloop, P.-J. Drainage control in water management of polders in the Netherlands. Irrig. Drain. Syst. 2006, 20, 99–109. [Google Scholar] [CrossRef]
- Van Overloop, P.-J.; Weijs, S.; Dijkstra, S. Multiple Model Predictive Control on a drainage canal system. Control Eng. Pract. 2008, 16, 531–540. [Google Scholar] [CrossRef] [Green Version]
- Breckpot, M.; Agudelo, O.; Moor, B. De Flood Control with Model Predictive Control for River Systems with Water Reservoirs. J. Irrig. Drain. Eng. 2013, 139, 532–541. [Google Scholar] [CrossRef]
- Delgoda, D.K.; Saleem, S.K.; Halgamuge, M.N.; Malano, H. Multiple Model Predictive Flood Control in Regulated River Systems with Uncertain Inflows. Water Resour. Manag. 2013, 27, 765–790. [Google Scholar] [CrossRef]
- Ficchì, A.; Raso, L.; Dorchies, D.; Pianosi, F.; Malaterre, P.; van Overloop, P.-J. Optimal Operation of the Multireservoir System in the Seine River Basin Using Deterministic and Ensemble Forecasts. J. Water Resour. Plan. Manag. 2016, 7, 1–12. [Google Scholar] [CrossRef]
- Schwanenberg, D.; Fan, F.M.; Naumann, S.; Kuwajima, J.I.; Montero, R.A.; Assis dos Reis, A. Short-Term Reservoir Optimization for Flood Mitigation under Meteorological and Hydrological Forecast Uncertainty: Application to the Três Marias Reservoir in Brazil. Water Resour. Manag. 2015, 29, 1635–1651. [Google Scholar] [CrossRef]
- Tian, X.; van Overloop, P.-J.; Negenborn, R.R.; van de Giesen, N.C. Operational flood control of a low-lying delta system using large time step Model Predictive Control. Adv. Water Resour. 2015, 75, 1–13. [Google Scholar] [CrossRef]
- García, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice-A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Montero, R.A.; Schwanenberg, D.; Hatz, M.; Brinkmann, M. Simplified hydraulic modelling in model predictive control of flood mitigation measures along rivers. J. Appl. Water Eng. Res. 2013, 1, 17–27. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Negenborn, R.R.; van Overloop, P.-J.; van de Giesen, N.C. De Saint-Venant equations-based model assessment in model predictive control of open channel flow. Adv. Water Resour. 2012, 49, 37–45. [Google Scholar] [CrossRef]
- United Nations. Report on Sittaung Valley Water Resources Development (Technical Report); United Nations: Rangoon, Burma, 1964; (retrieved from the Irrigation Department, Myanmar on 20 May 2015). [Google Scholar]
- Tropical Rainfall Measuring Mission (TRMM) (2011). TRMM (TMPA) Rainfall Estimate L3 3 hour 0.25 degree x 0.25 degree V7, Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: 10.5067/TRMM/TMPA/3H/7 (accessed on 31 October 2016).
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S.; Koren, V.; Zhang, Z.; Smith, M. Toward improved streamflow forecasts: Value of semidistributed modeling. Water Resour. Res. 2001, 37, 2749–2759. [Google Scholar] [CrossRef]
- Boughton, W. The Australian water balance model. Environ. Model. Softw. 2004, 19, 943–956. [Google Scholar] [CrossRef]
- Nielsen, S.A.; Hansen, E. Numerical simulation of the rainfall-runoff process on a daily basis. Nord. Hydrol. 1973. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Dekker, S.C.; Sorooshian, S.; Wagener, T.; Bouten, W. Application of stochastic parameter optimization to the Sacramento Soil Moisture Accounting model. J. Hydrol. 2006, 325, 288–307. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models Part I-A Discussion of Principles*. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Chow, V. Te Open-Channel Hydraulics; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1959; ISBN 0070107769. [Google Scholar]
- Stelling, G.S.; Duinmeijer, S.P.A. A staggered conservative scheme for every Froude number in rapidly varied shallow water flows. Int. J. Numer. Method Fluids 2003, 1354, 1329–1354. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Fluid Mechanics and Its Applications; Springer International Publishing: Cham, Switzerland, 2016; Volume 113, ISBN 978-3-319-16873-9. [Google Scholar]
- Xu, M. Real-Time Control of Combined Water Quantity & Quality in Open Channels. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Banks, J.C.; Camp, J.V.; Abkowitz, M.D. Adaptation planning for floods: A review of available tools. Nat. Hazards 2014, 70, 1327–1337. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Ngo, L.L.; Madsen, H.; Rosbjerg, D. Simulation and optimisation modelling approach for operation of the Hoa Binh reservoir, Vietnam. J. Hydrol. 2007, 336, 269–281. [Google Scholar] [CrossRef]
- SOBEK 2.15 User Manual; Deltares: Delft, The Netherland, 2016.
- Wei, C.C.; Hsu, N.S. Optimal tree-based release rules for real-time flood control operations on a multipurpose multireservoir system. J. Hydrol. 2009, 365, 213–224. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A.J.; Zhou, S.-L. Understanding performance measures of reservoirs. J. Hydrol. 2006, 324, 359–382. [Google Scholar] [CrossRef]
- Raso, L. Optimal Control of Water Systems under Forecast Uncertainty. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Uysal, G.; Alvarado-Montero, R.; Schwanenberg, D.; Şensoy, A. Real-Time Flood Control by Tree-Based Model Predictive Control Including Forecast Uncertainty: A Case Study Reservoir in Turkey. Water 2018, 10, 340. [Google Scholar] [CrossRef]
- Tian, X.; Negenborn, R.R.; van Overloop, P.-J.; María Maestre, J.; Sadowska, A.; van de Giesen, N. Efficient multi-scenario Model Predictive Control for water resources management with ensemble streamflow forecasts. Adv. Water Resour. 2017, 109, 58–68. [Google Scholar] [CrossRef]
- Chiang, P.-K.; Willems, P. Combine Evolutionary Optimization with Model Predictive Control in Real-time Flood Control of a River System. Water Resour. Manag. 2015, 29, 2527–2542. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J. Multi-objective evolutionary algorithm for operating parallel reservoir system. J. Hydrol. 2009, 377, 12–20. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Optimal reservoir operation using multi-objective evolutionary algorithm. Water Resour. Manag. 2006, 20, 861–878. [Google Scholar] [CrossRef]





| No. | Reservoir | Catchment | Storage | Max. Capacity (m3/s) | Purposes | |||
|---|---|---|---|---|---|---|---|---|
| Area (km2) | (106 m3) | Conduit | Spillway | I | F | H | ||
| 1 | Sinthe | 789 | 176 | 15 | 523 | √ | √ | |
| 2 | Yezin | 91 | 90 | 10 | 23 | √ | √ | |
| 3 | Upper Paung Laung | 3168 | 1300 | 100 | 4000 | √ | √ | |
| 4 | Lower Paung Laung | 1551 | 678 | 200 | 3123 | √ | √ | √ |
| 5 | Ngalaik | 328 | 92 | 10 | 400 | √ | √ | |
| 6 | Chaungmange | 265 | 113 | 7 | 74 | √ | √ | √ |
| 7 | Madam | 96 | 45 | 8 | 94 | √ | ||
| 8 | Myohla | 28 | 12 | 4.25 | 51 | √ | ||
| 9 | Swa | 1053 | 267 | 25 | 1487 | √ | √ | |
| 10 | Pathi | 60 | 38 | 3.5 | 156 | √ | ||
| 11 | Kabaung | 1199 | 1084 | 40 | 694 | √ | √ | √ |
| Sum | 8628 | 3895 | - | - | 10 | 8 | 4 | |
| Indicators | Operation Scenarios | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| (Current Operation) | (MPC-Flood Priority) | (MPC-Conservation Priority) | |
| Storage volume (%) | 87 | 67 | 86 |
| Vulnerability (%) | 2.4 | 1.5 | 1.8 |
| Resilience (%) | 1.9 | 2.8 | 2.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Myo Lin, N.; Rutten, M.; Tian, X. Flood Mitigation through Optimal Operation of a Multi-Reservoir System by Using Model Predictive Control: A Case Study in Myanmar. Water 2018, 10, 1371. https://doi.org/10.3390/w10101371
Myo Lin N, Rutten M, Tian X. Flood Mitigation through Optimal Operation of a Multi-Reservoir System by Using Model Predictive Control: A Case Study in Myanmar. Water. 2018; 10(10):1371. https://doi.org/10.3390/w10101371
Chicago/Turabian StyleMyo Lin, Nay, Martine Rutten, and Xin Tian. 2018. "Flood Mitigation through Optimal Operation of a Multi-Reservoir System by Using Model Predictive Control: A Case Study in Myanmar" Water 10, no. 10: 1371. https://doi.org/10.3390/w10101371
APA StyleMyo Lin, N., Rutten, M., & Tian, X. (2018). Flood Mitigation through Optimal Operation of a Multi-Reservoir System by Using Model Predictive Control: A Case Study in Myanmar. Water, 10(10), 1371. https://doi.org/10.3390/w10101371






