Experimental and Simulation Investigation on the Kinetic Energy Dissipation Rate of a Fixed Spray-Plate Sprinkler
Abstract
:1. Introduction
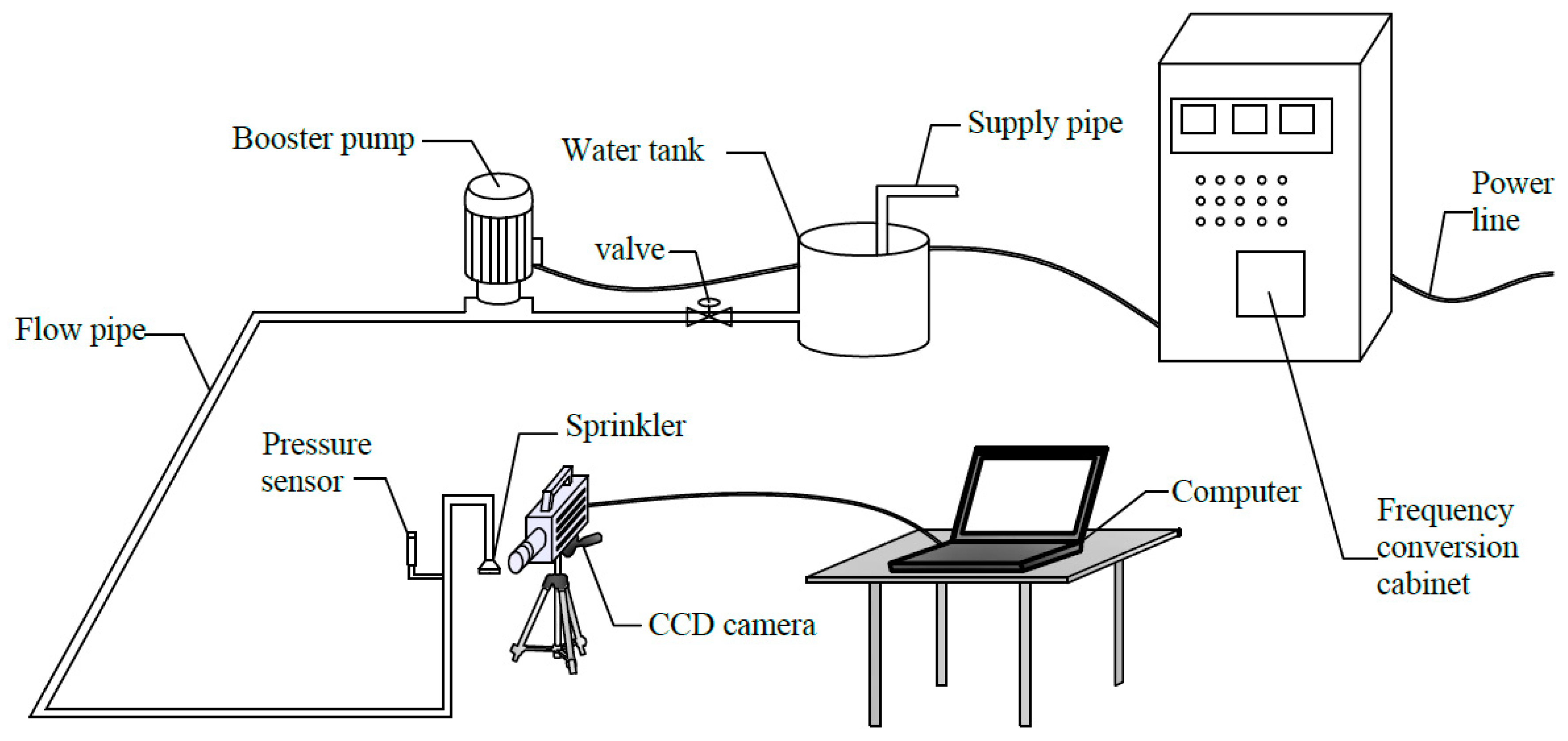
2. Experimental Setup
3. Numerical Simulation
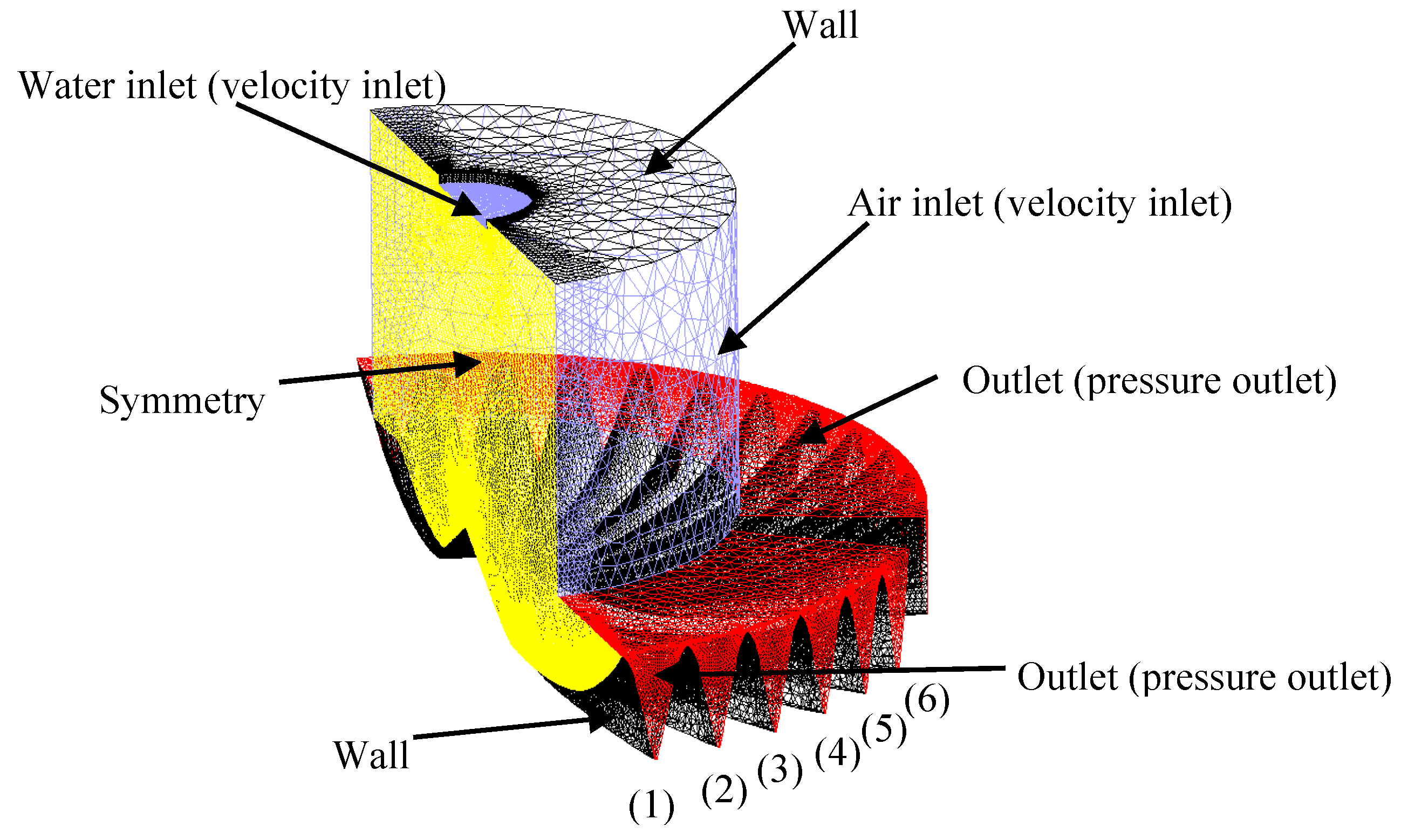
3.1. Description of the Model
3.2. Governing Equations
4. Results
4.1. Comparison of Experimental Results and Simulated Values
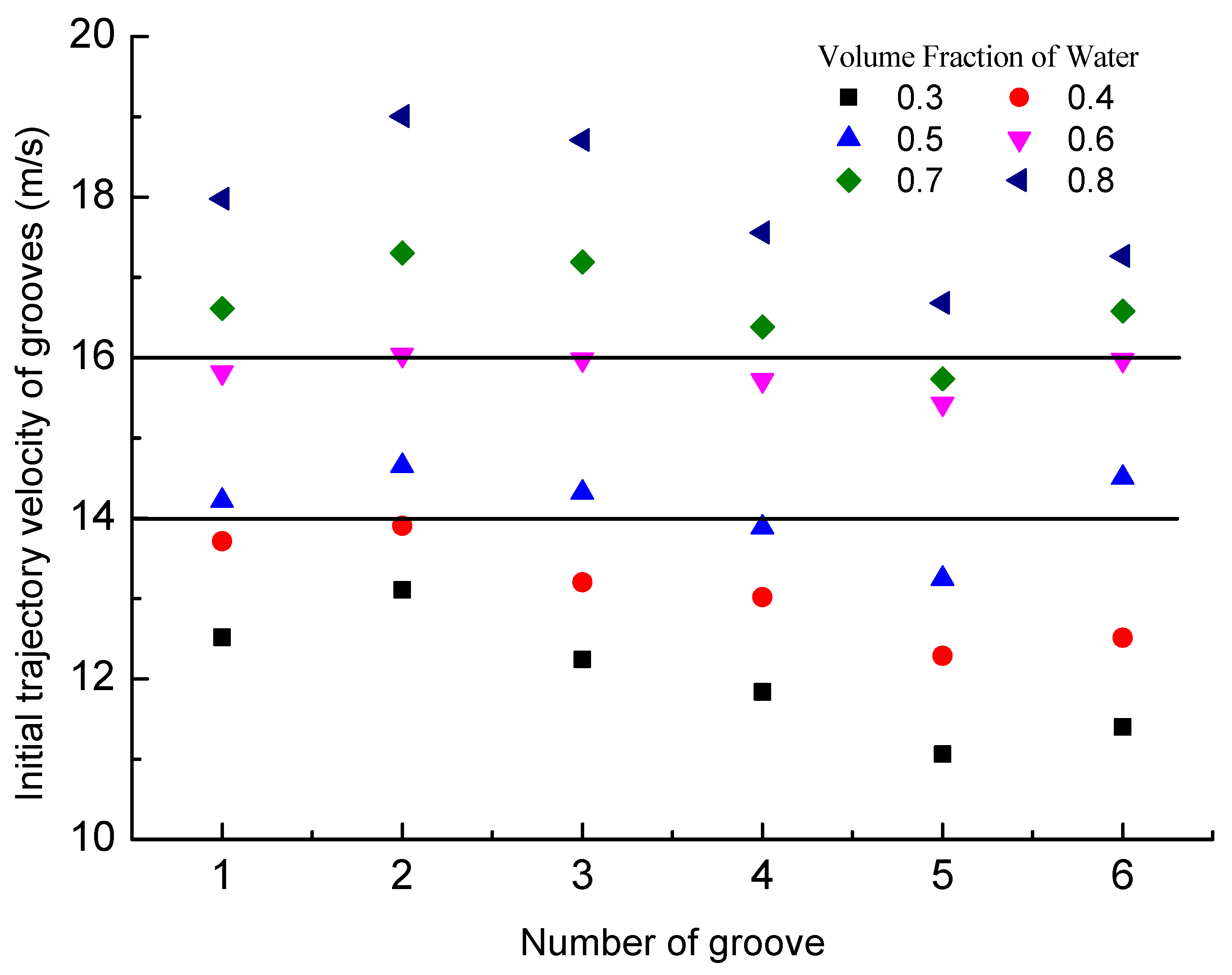
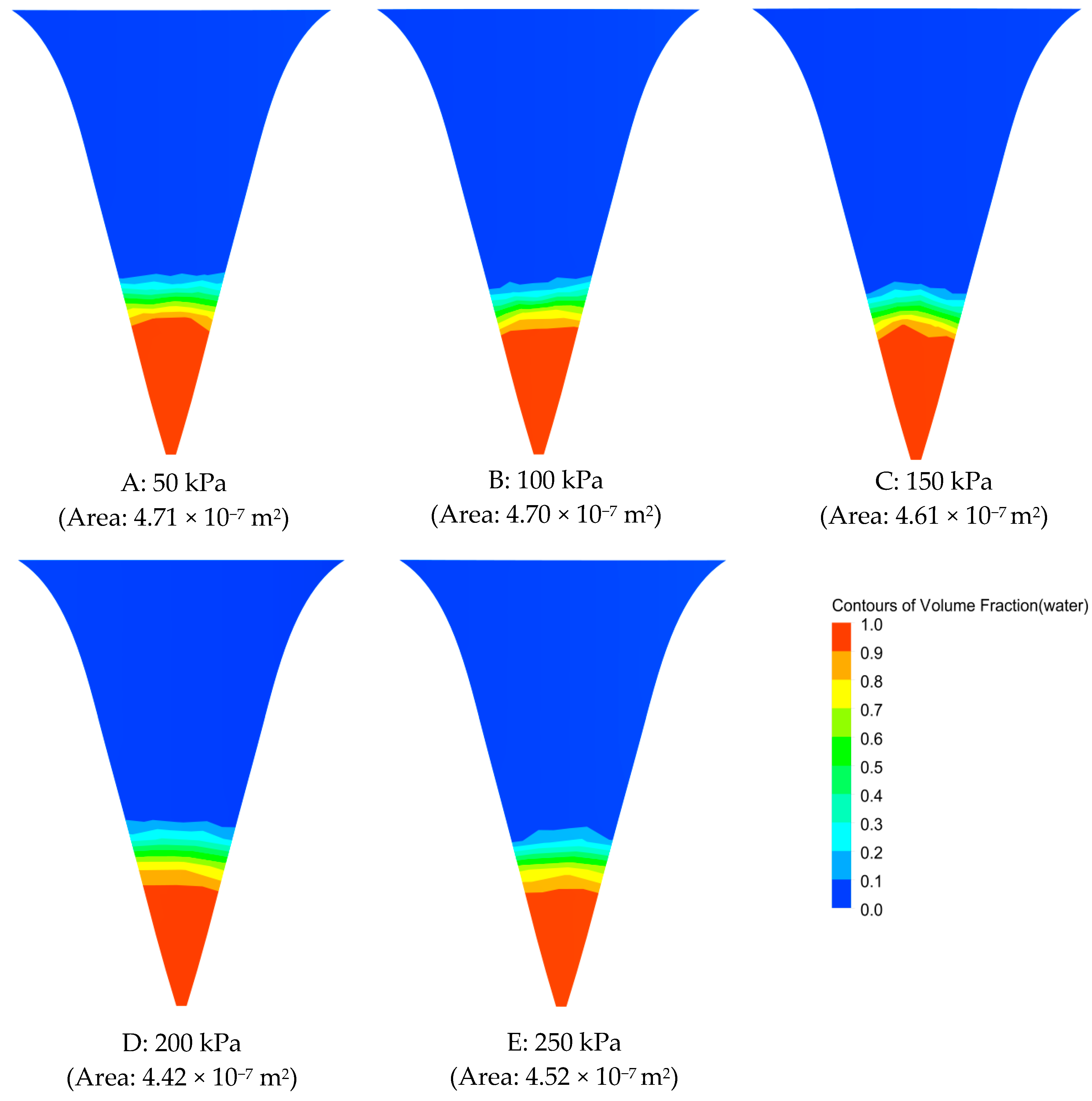
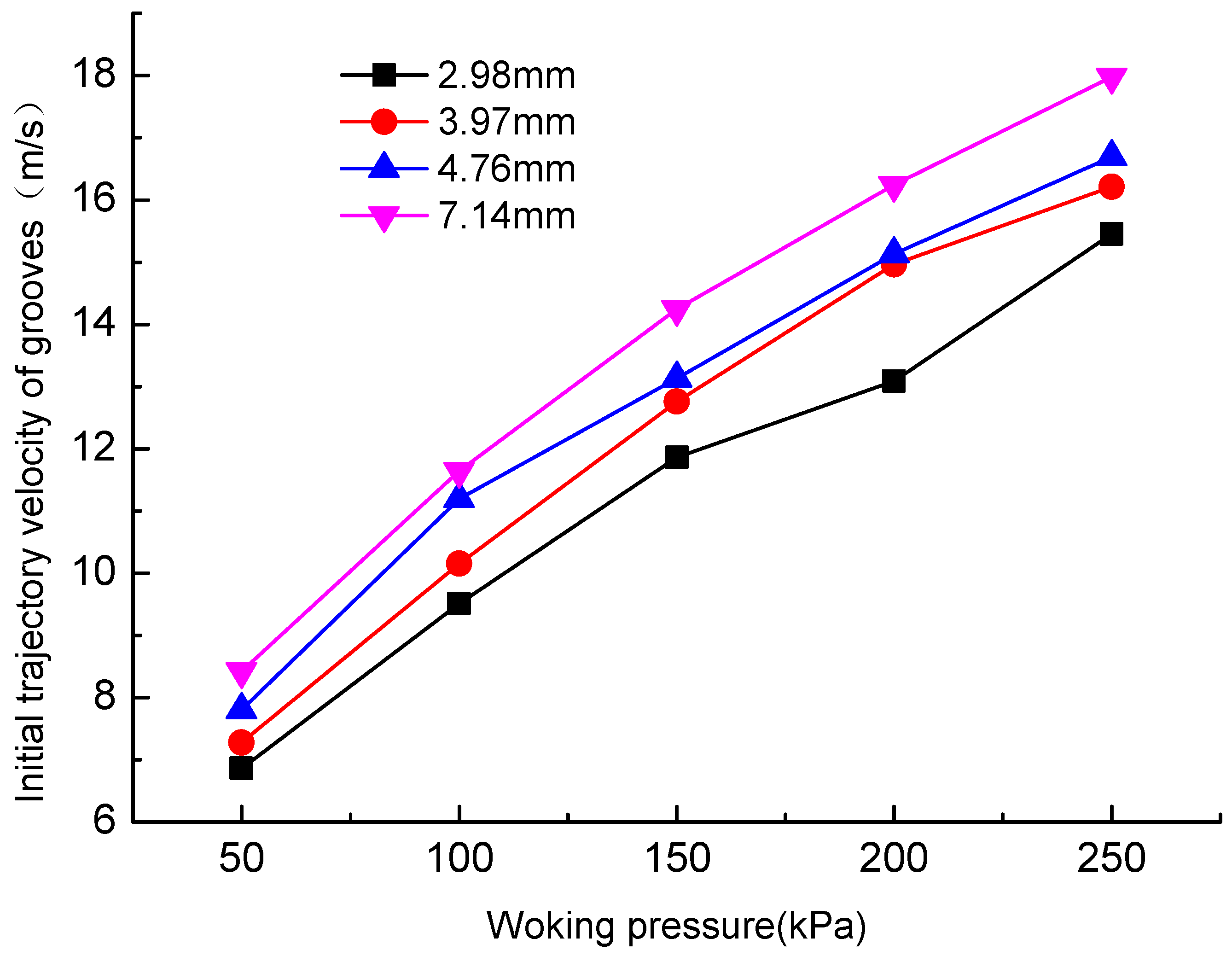
4.2. Fluid-Phase Nephogram and Initial Trajectory Velocity
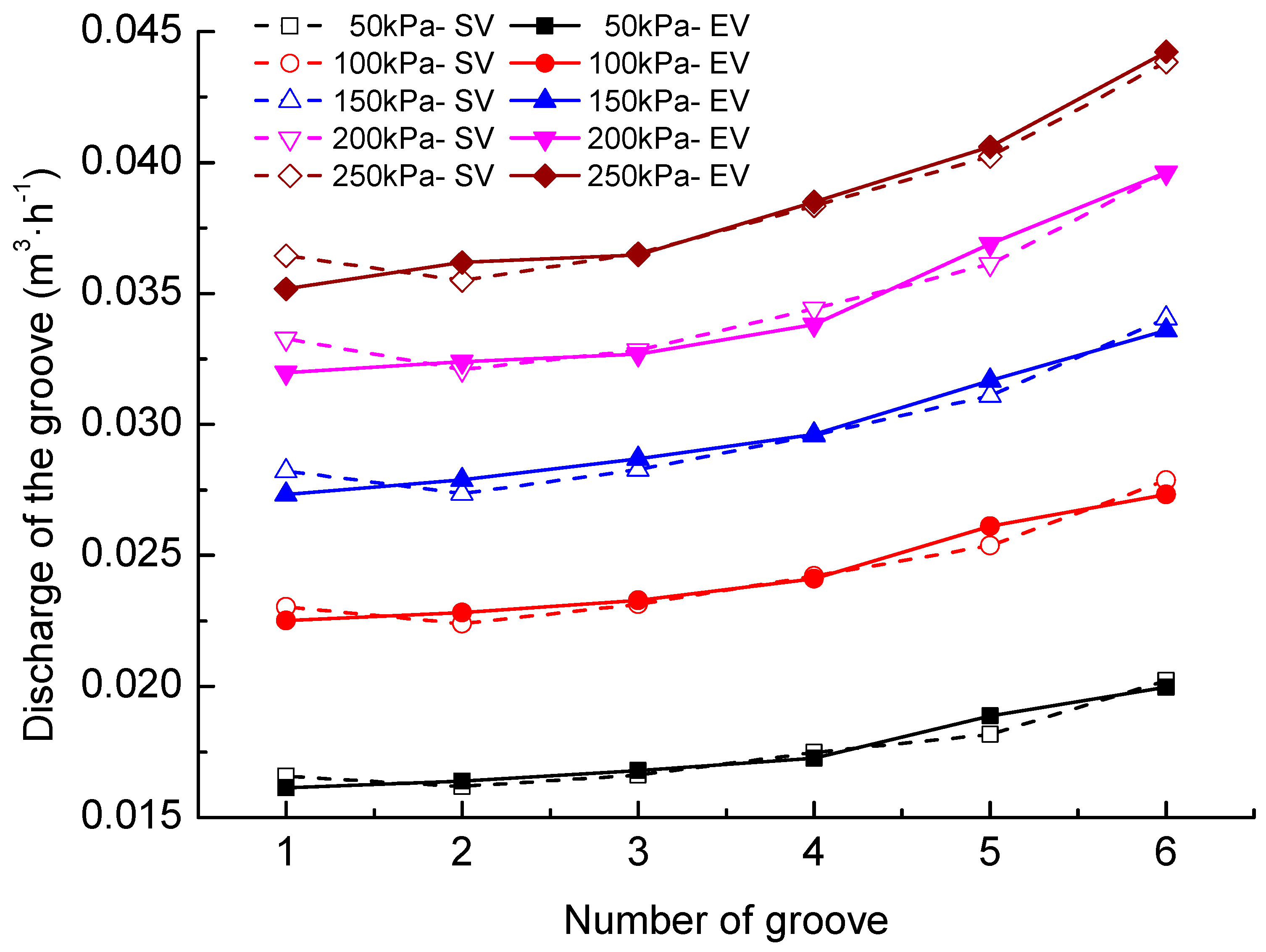
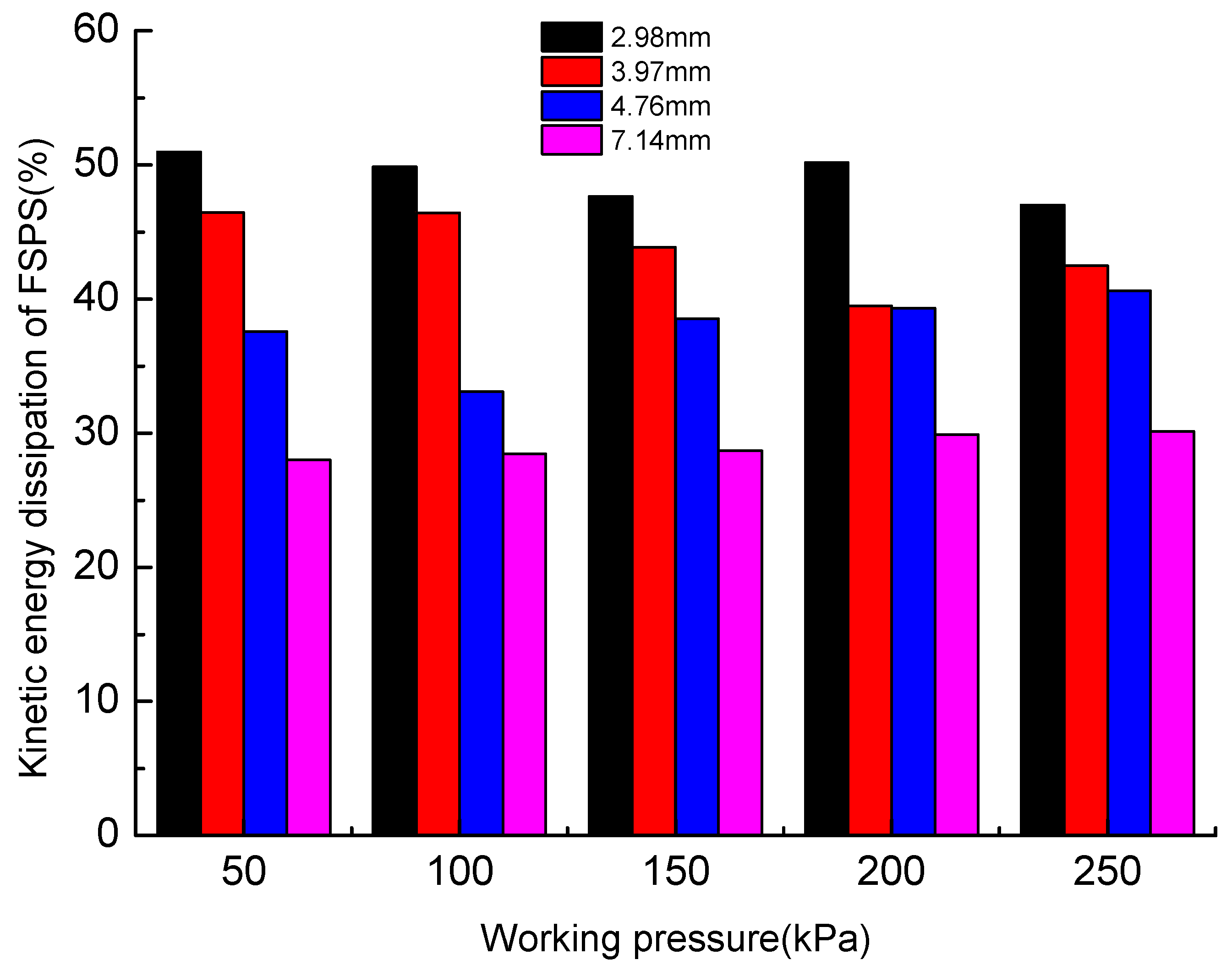
4.3. Kinetic Energy Dissipation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gan, L.; Rad, S.; Chen, X.; Fang, R.; Yan, L.; Su, S. Clock Hand Lateral, a New Layout for Semi-Permanent Sprinkler Irrigation System. Water 2018, 10, 767. [Google Scholar] [CrossRef]
- Kincaid, D.C. Application rates from center pivot irrigation with current sprinkler types. Appl. Eng. Agric. 2005, 21, 605–610. [Google Scholar] [CrossRef]
- Playán, E.; Zapata, N.; Faci, J.M.; Tolosa, D.; Lacueva, J.L.; Pelegrín, J.; Salvador, R.; Sánchez, I.; Lafita, A. Assessing sprinkler irrigation uniformity using a ballistic simulation model. Agric. Water Manag. 2006, 84, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Clemmens, A.J.; Dedrick, A.R. Irrigation Techniques and Evaluations Management of Water Use in Agriculture; Springer: Berlin/Heidelberg, Germany, 1994; pp. 64–103. [Google Scholar]
- Wrachien, D.D.; Lorenzini, G. Modelling Jet Flow and Losses in Sprinkler Irrigation: Overview and Perspective of a New Approach. Biosyst. Eng. 2006, 94, 297–309. [Google Scholar] [CrossRef]
- Faci, J.M.; Salvador, R.; Playán, E.; Sourell, H. Comparison of fixed and rotating spray plate sprinklers. J. Irrig. Drain. Eng. 2001, 127, 224–233. [Google Scholar] [CrossRef]
- Hanson, B.R.; Orloff, S.B. Rotator nozzles more uniform than spray nozzles on center-pivot sprinklers. Calif. Agric. 1996, 50, 32–35. [Google Scholar] [CrossRef]
- Playán, E.; Garrido, S.; Faci, J.M.; Galán, A. Characterizing pivot sprinklers using an experimental irrigation machine. Agric. Water Manag. 2004, 70, 177–193. [Google Scholar] [CrossRef] [Green Version]
- Hills, D.J.; Barragan, J. Application uniformity for fixed and rotating spray plate sprinklers. Appl. Eng. Agric. 1998, 14, 33–36. [Google Scholar] [CrossRef]
- Ouazaa, S.; Latorre, B.; Burguete, J.; Serreta, A.; Playán, E.; Salvador, R.; Paniagua, P.; Zapata, N. Effect of the start–stop cycle of center-pivot towers on irrigation performance: Experiments and simulations. Agric. Water Manag. 2015, 147, 163–174. [Google Scholar] [CrossRef] [Green Version]
- Sayyadi, H.; Nazemi, A.H.; Sadraddini, A.A.; Delirhasannia, R. Characterising droplets and precipitation profiles of a fixed spray-plate sprinkler. Biosyst. Eng. 2014, 119, 13–24. [Google Scholar] [CrossRef]
- Burillo, G.S.; Delirhasannia, R.; Playán, E.; Paniagua, P.; Latorre, B.; Burguete, J. Initial drop velocity in a fixed spray plate sprinkler. J. Irrig. Drain. Eng. 2013, 139, 521–531. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, D.; Lin, Z.; Gong, X.; Wen, Y. Spatial Variation of Application Rate and Droplet Kinetic Energy for Fixed Spray Plate Sprinkler. Trans. Chin. Soc. Agric. Mach. 2015, 46, 85–90. [Google Scholar]
- Ouazaa, S.; Burguete, J.; Paniagua, M.P.; Salvador, R.; Zapata, N. Simulating water distribution patterns for fixed spray plate sprinkler using the ballistic theory. Span. J. Agric. Res. 2014, 12, 850–863. [Google Scholar] [CrossRef] [Green Version]
- Law, W.K.; Wang, H. Measurement of mixing processes with combined digital particle image velocimetry and planar laser induced fluorescence. Exp. Therm. Fluid Sci. 2000, 22, 213–229. [Google Scholar] [CrossRef]
- Kadem, N.; Tchiftchibachian, A.; Pascal, M. Investigation of the Influence of Sprinkler Fins and Dissolved Air on Jet Flow. J. Irrig. Drain. Eng. 2006, 132, 41–46. [Google Scholar]
- Jiang, Y.; Li, H.; Xiang, Q.; Chen, C. Comparison of PIV experiment and numerical simulation on the velocity distribution of intermediate pressure jets with different nozzle parameters. Irrig. Drain. 2017, 66, 510–519. [Google Scholar] [CrossRef]
- Westerweel, J. Fundamentals of digital particle image velocimetry. Exp. Fluids 1997, 23, 1379. [Google Scholar] [CrossRef]
- Willert, C.E.; Gharib, M. Digital particle image velocimetry. Exp. Fluids 1991, 10, 181–193. [Google Scholar] [CrossRef]
- Yan, H.; Ou, Y.; Nakano, K.; Xu, C. Numerical and experimental investigations on internal flow characteristic in the impact sprinkler. Irrig. Drain. Syst. 2009, 23, 11–23. [Google Scholar] [CrossRef]
- Tang, P.; Li, H.; Issaka, Z.; Chen, C. Impact forces on the drive spoon of a large cannon irrigation sprinkler: Simple theory, CFD numerical simulation and validation. Biosyst. Eng. 2017, 159, 1–9. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Jog, M.A. Nonlinear breakup model for a liquid sheet emanating from a pressure-swirl atomizer. J. Eng. Gas Turb. Power 2007, 129, 945–953. [Google Scholar] [CrossRef]
- Liu, G.M.; Huang, L.; Zhang, W.P.; Gao, X.H.; Lin, H.E.; Miao, X.H. Simulation and experiment on the characteristics of exhaust cooling and noise reduction equipment for marine diesel engine. Ship Eng. 2007, 8355, 325–328. [Google Scholar]
- Alhendal, Y.; Turan, A.; Aly, W.I.A. VOF simulation of marangoni flow of gas bubbles in 2D-axisymmetric column. Procedia Comput. Sci. 2010, 1, 673–680. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef] [Green Version]
- Albadawi, A.; Donoghue, D.B.; Robinson, A.J.; Murray, D.B.; Delauré, Y.M.C. Influence of surface tension implementation in volume of fluid and coupled volume of fluid with level set methods for bubble growth and detachment. Int. J. Multiph. Flow 2013, 53, 11–28. [Google Scholar] [CrossRef]
- Meredith, K.V.; Zhou, X.; Wang, Y. Towards Resolving the Atomization Process of an Idealized Fire Sprinkler with VOF Modeling. In Proceedings of the 28th European Conference on Liquid Atomization and Spray Systems, València, Spain, 6–8 September 2017; pp. 257–264. [Google Scholar]
- Kincaid, D.C. Spraydrop kinetic energy from irrigation sprinklers. Trans. ASAE 1996, 39, 847–853. [Google Scholar] [CrossRef]
- Clark, G.A.; Srinivas, K.; Rogers, D.H.; Martin, V.L. Measured and simulated uniformity of low drift nozzle sprinklers. Trans. ASAE 2003, 4, 1–18. [Google Scholar]
- Ramamurthy, A.S.; Tadayon, R. Numerical simulation of flows in cut-throat flumes. J. Irrig. Drain. Eng. 2008, 134, 857–860. [Google Scholar] [CrossRef]
- Aydin, M.C.; Emiroglu, M.E. Determination of capacity of labyrinth side weir by CFD. Flow Meas. Instrum. 2013, 29, 1–8. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, D.; Lin, Z.; Gong, X. Water distribution model of fixed spray plate sprinkler sased on ballistic trajectory equation. Trans. Chin. Soc. Agric. Mach. 2015, 46, 55–61. [Google Scholar]
- Deboerm, D.W. Drop and Energy Characteristics of a Rotating Spray-Plate Sprinkler. J. Irrig. Drain. Eng. 2002, 128, 137–146. [Google Scholar] [CrossRef]

| Working Pressure (kPa) | Nozzle Diameter (mm) | |||
|---|---|---|---|---|
| 2.98 | 3.97 | 4.76 | 7.14 | |
| 50 | 9.80 | 9.95 | 9.87 | 9.92 |
| 100 | 13.43 | 13.87 | 13.69 | 13.76 |
| 150 | 16.39 | 17.03 | 16.75 | 16.88 |
| 200 | 18.54 | 19.23 | 19.42 | 19.40 |
| 250 | 21.22 | 21.38 | 21.65 | 21.51 |
| Groove Number | Working Pressure (kPa) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 100 | 150 | 200 | 250 | |||||||||||
| EV | SV | RD | EV | SV | RD | EV | SV | RD | EV | SV | RD | EV | SV | RD | |
| m s−1 | m s−1 | 100% | m s−1 | m s−1 | 100% | m s−1 | m s−1 | 100% | m s−1 | m s−1 | 100% | m s−1 | m s−1 | 100% | |
| Groove 1 | 7.90 | 7.84 | −0.71 | 11.40 | 11.22 | −1.66 | 13.02 | 13.25 | 1.72 | 14.51 | 15.18 | 4.41 | 15.78 | 16.47 | 4.17 |
| Groove 2 | 7.71 | 7.48 | −3.10 | 11.21 | 10.78 | −4.07 | 12.75 | 12.58 | −1.33 | 15.30 | 14.56 | −5.08 | 14.55 | 15.73 | 7.50 |
| Groove 3 | 7.69 | 7.79 | 1.28 | 11.61 | 11.29 | −2.83 | 13.42 | 13.10 | −2.42 | 15.25 | 15.06 | −1.25 | 15.72 | 16.35 | 3.84 |
| Groove 4 | 7.67 | 7.93 | 3.28 | 11.28 | 11.37 | 0.75 | 12.92 | 13.38 | 3.41 | 16.02 | 15.36 | −4.32 | 16.79 | 16.65 | −0.81 |
| Groove 5 | 7.90 | 7.98 | 1.07 | 11.52 | 11.43 | −0.82 | 12.89 | 13.39 | 3.71 | 16.32 | 15.50 | −5.28 | 15.19 | 16.77 | 9.44 |
| Groove 6 | 7.75 | 7.78 | 0.31 | 10.92 | 11.13 | 1.86 | 12.84 | 13.08 | 1.87 | 15.99 | 15.11 | −5.81 | 15.53 | 16.40 | 5.32 |
| Nozzle Diameter (mm) | Figure: Contour of Water Distribution Pattern | Subfigure: Water Surface Profile of Third Groove |
|---|---|---|
| 2.98 | 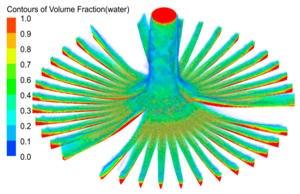 | Area: 2.74 × 10−7 m2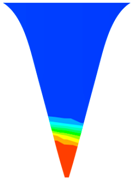 |
| 3.97 | 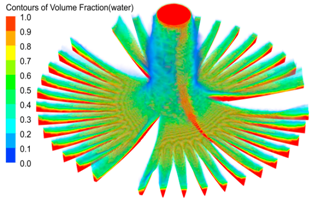 | Area: 4.42 × 10−7 m2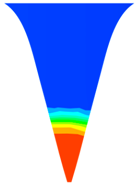 |
| 4.76 | 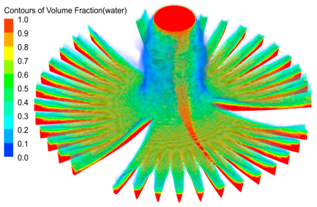 | Area: 6.32 × 10−7 m2 |
| 7.12 | 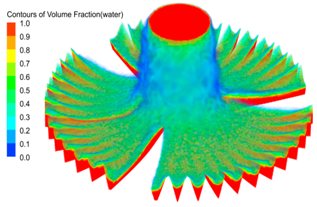 | Area: 1.32 × 10−6 m2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Sun, B.; Fang, H.; Zhu, D.; Yang, L.; Li, Z. Experimental and Simulation Investigation on the Kinetic Energy Dissipation Rate of a Fixed Spray-Plate Sprinkler. Water 2018, 10, 1365. https://doi.org/10.3390/w10101365
Zhang Y, Sun B, Fang H, Zhu D, Yang L, Li Z. Experimental and Simulation Investigation on the Kinetic Energy Dissipation Rate of a Fixed Spray-Plate Sprinkler. Water. 2018; 10(10):1365. https://doi.org/10.3390/w10101365
Chicago/Turabian StyleZhang, Yisheng, Bin Sun, Hongyuan Fang, Delan Zhu, Lingxia Yang, and Zhansong Li. 2018. "Experimental and Simulation Investigation on the Kinetic Energy Dissipation Rate of a Fixed Spray-Plate Sprinkler" Water 10, no. 10: 1365. https://doi.org/10.3390/w10101365
APA StyleZhang, Y., Sun, B., Fang, H., Zhu, D., Yang, L., & Li, Z. (2018). Experimental and Simulation Investigation on the Kinetic Energy Dissipation Rate of a Fixed Spray-Plate Sprinkler. Water, 10(10), 1365. https://doi.org/10.3390/w10101365








