On the Wave Bottom Shear Stress in Shallow Depths: The Role of Wave Period and Bed Roughness
Abstract
:1. Introduction
2. Wind Waves Generated on Finite Depth
3. Numerical Simulation Setup
4. Results and Discussion
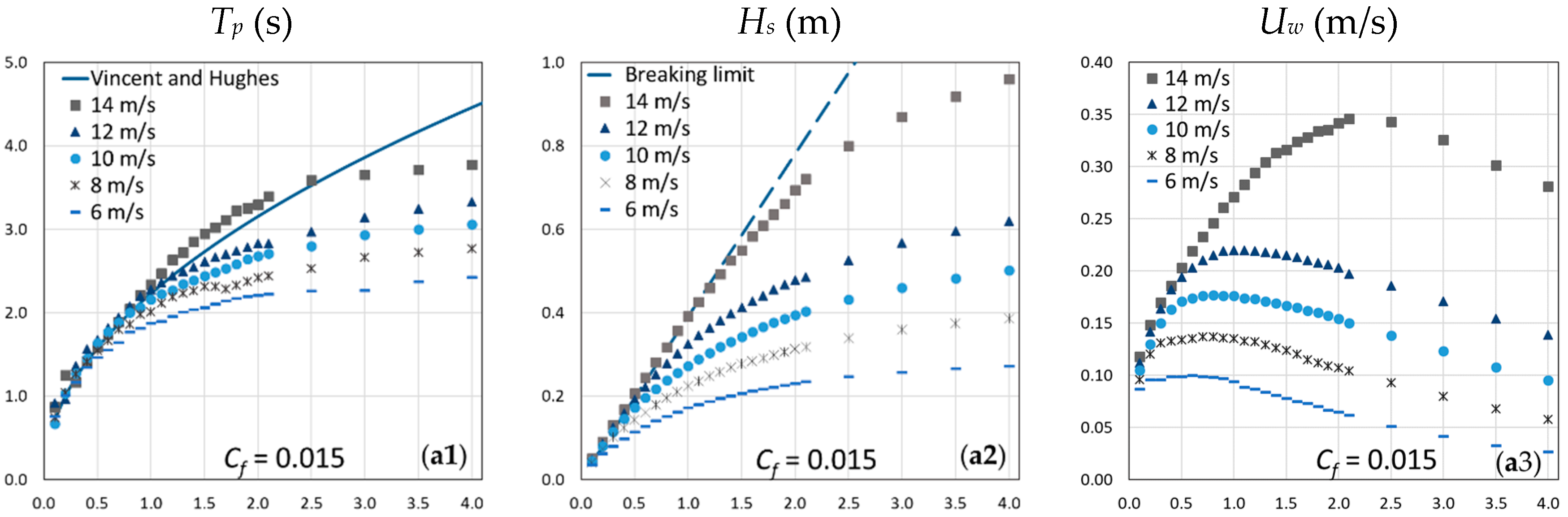
4.1. Main Characteristics of the Wave Field
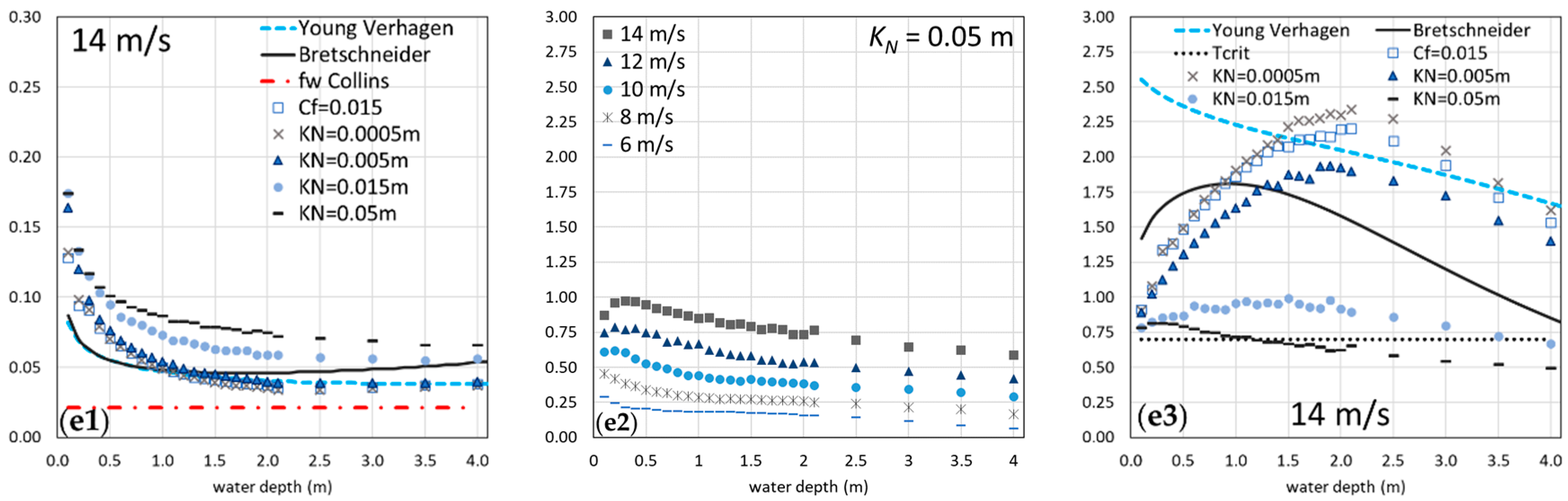
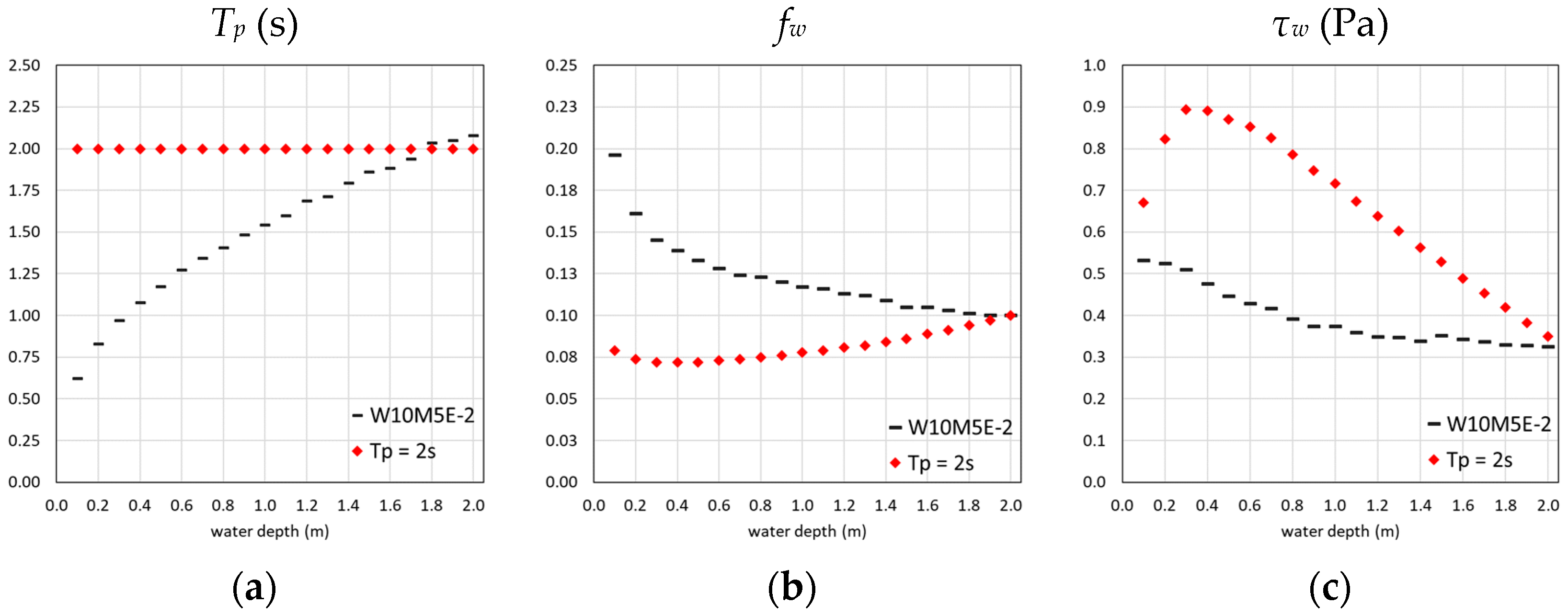
4.2. Analysis of the Bed Shear Stresses
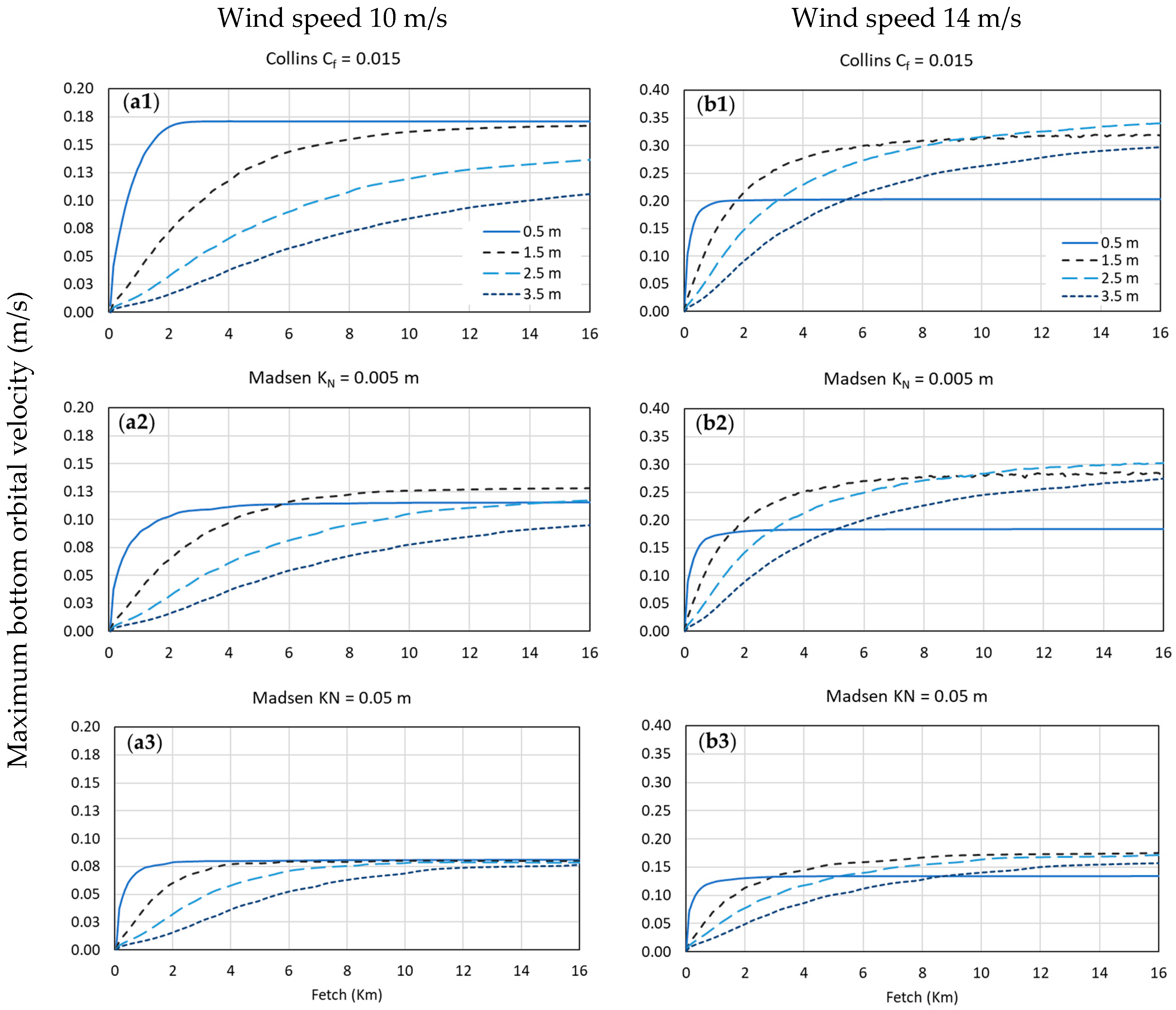
4.3. Considerations on the Fetch Dependence of the Bed Shear Stresses
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Galloway, W.E. Process framework for describing the morphologic and stratigraphic evolution of deltaic depositional systems. In Deltas: Models for Exploration; Broussard, M.L., Ed.; Houston Geological Society: Houston, TX, USA, 1975; pp. 87–98. [Google Scholar]
- Bhattacharya, J.P. Deltas. In Facies Models Revisited; Posamentier Henry, W., Walker Roger, G., Eds.; SEPM (Society for Sedimentary Geology) Special Publication: Broken Arrow, OK, USA, 2006; Volume 84, pp. 237–292. ISBN 9781565761216. [Google Scholar] [CrossRef]
- Wright, L.D.; Coleman, J.M. Variations in morphology of major river deltas as functions of ocean wave and river discharge regimes. AAPG Bull. 1973, 57, 370–398. [Google Scholar]
- Bhattacharya, J.P.; Giosan, L. Wave-influenced deltas: Geomorphological implications for facies reconstruction. Sedimentology 2003, 50, 187–210. [Google Scholar] [CrossRef]
- Ashton, A.D.; Giosan, L. Wave angle control of delta evolution. Geophys. Res. Lett. 2011, 38, L13405. [Google Scholar] [CrossRef]
- Friedrichs, C.L. Tidal flat morphodynamics: A synthesis. In Treatise on Estuarine and Coastal Science; Estuarine and Coastal Geology and Geomorphology; Hansom, J.D., Fleming, B.W., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 3, pp. 137–170. [Google Scholar]
- Friedrichs, C.T.; Perry, J.E. Tidal Salt Marsh Morphodynamics: A Synthesis. J. Coast. Res. 2001, SI 27, 7–37. [Google Scholar] [CrossRef]
- Allen, J.R.L.; Duffy, M.J. Medium-term sedimentation on high intertidal mudflats and salt marshes in the Severn Estuary, SW Britain: The role of wind and tide. Mar. Geol. 1998, 150, 1–27. [Google Scholar] [CrossRef]
- Le Hir, P.; Roberts, W.; Cazaillet, O.; Christie, M.; Bassoullet, P.; Bacher, C. Characterization of intertidal flat hydrodynamics. Cont. Shelf Res. 2000, 20, 1433–1459. [Google Scholar] [CrossRef] [Green Version]
- Roberts, W.; Le Hir, P.; Whitehouse, R.J.S. Investigation using simple mathematical models of the effect of tidal currents and waves on the profile shape of intertidal mudflats. Cont. Shelf Res. 2000, 20, 1079–1097. [Google Scholar] [CrossRef]
- Lanzoni, S.; Seminara, G. Long term evolution and morphodynamic equilibrium of tidal channels. J. Geophs. Res. 2002, 107 C1, 1–13. [Google Scholar] [CrossRef]
- Cappucci, S.; Amos, C.L.; Hosoe, T.; Umgiesser, G. SLIM: A numerical model to evaluate the factors controlling the evolution of intertidal mudflats in Venice Lagoon, Italy. J. Mar. Syst. 2004, 51, 257–280. [Google Scholar] [CrossRef]
- Umgiesser, G.; Sclavo, M.; Carniel, S.; Bergamasco, A. Exploring the bottom shear stress variability in the Venice Lagoon. J. Mar. Syst. 2004, 51, 161–178. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Palermo, C.; Rulli, M.C.; Carniello, L.; Defina, A. Wind waves in shallow microtidal basins and the dynamic equilibrium of tidal flats. J. Geophys. Res. 2007, 112, F02024. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Wiberg, P.L. Importance of wind conditions, fetch, and water levels on wave-generated shear stresses in shallow intertidal basins. J. Geophys. Res. 2009, 114, F03022. [Google Scholar] [CrossRef]
- Callaghan, D.P.; Bouma, T.J.; Klaassen, P.; van der Wal, D.; Stive, M.J.F.; Herman, P.M.J. Hydrodynamic forcing on salt-marsh development: Distinguishing the relative importance of waves and tidal flows. Estuar. Coast. Shelf Sci. 2010, 89, 73–88. [Google Scholar] [CrossRef]
- Green, M.O. Very small waves and associated sediment resuspension on an estuarine intertidal flat. Estuar. Coast. Shelf Sci. 2011, 93, 449–459. [Google Scholar] [CrossRef]
- Carniello, L.; Defina, A.; D’Alpaos, L. Modeling sand-mud transport induced by tidal currents and wind waves in shallow microtidal basins: Application to the Venice Lagoon (Italy). Estuar. Coast. Shelf Sci. 2012, 102, 105–115. [Google Scholar] [CrossRef]
- Shi, B.W.; Yang, S.L.; Wang, Y.P.; Bouma, T.J.; Zhu, Q. Relating accretion and erosion at an exposed tidal wetland to the bottom shear stress of combined current–wave action. Geomorphology 2012, 138, 380–389. [Google Scholar] [CrossRef]
- Zhou, Z.; Coco, G.; van der Wegen, M.; Gong, Z.; Zhang, C.; Townend, I. Modeling sorting dynamics of cohesive and non-cohesive sediments on intertidal flats under the effect of tides and wind waves. Cont. Shelf Res. 2015, 104, 76–91. [Google Scholar] [CrossRef]
- Green, M.O.; Coco, G. Review of wave-driven sediment resuspension and transport in estuaries. Rev. Geophys. 2014, 52, 77–117. [Google Scholar] [CrossRef] [Green Version]
- Fagherazzi, S.; Carniello, L.; D’Alpaos, L.; Defina, A. Critical bifurcation of shallow microtidal landforms in tidal flats and salt marshes. Proc. Natl. Acad. Sci. USA 2006, 103, 8337–8341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fredsøe, J.; Deigaard, R. Mechanics of Coastal Sediment Transport; Advanced Series on Ocean Engineering; World Scientific: Singapore, 1992; Volume 3, 369p. [Google Scholar]
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 1993; 715p. [Google Scholar]
- Madsen, O.S. Spectral Wave-Current Bottom Boundary Layer Flows. Coast. Eng. 1994, 29, 384–398. [Google Scholar] [CrossRef]
- Soulsby, R.L. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford Publications: London, UK, 1997; 249p. [Google Scholar]
- Mariotti, G.; Fagherazzi, S. Wind waves on a mudflat: The influence of fetch and depth on bed shear stresses. Cont. Shelf Res. 2013, 60, S99–S110. [Google Scholar] [CrossRef]
- Collins, J.I. Prediction of shallow water spectra. J. Geophys. Res. 1972, 77, 2693–2707. [Google Scholar] [CrossRef]
- Hsiao, S.V.; Shemdin, O.H. Bottom Dissipation in Finite-Depth Water Waves. Coast. Eng. 1978, 24, 434–448. [Google Scholar] [CrossRef]
- Madsen, O.S.; Poon, Y.-K.; Graber, H.C. Spectral wave attenuation by bottom friction: Theory. In Proceedings of the 21th International Conference Coastal Engineering, Costa del Sol-Malaga, Spain, 20–25 June 1988; pp. 492–504. [Google Scholar]
- Bretschneider, C.L.; Reid, R.O. Change in Wave Height Due to Bottom Friction, Percolation and Refraction; Beach Erosion Board Engineer Research and Development Center (U.S.): Boston, MA, USA, 1954. [Google Scholar]
- CERC (U.S. Army Coastal Engineering Research Center). Shore Protection Manual; U.S. Army Coastal Engineering Research Center: Washington, DC, USA, 1973. [Google Scholar]
- CERC (U.S. Army Coastal Engineering Research Center). Shore Protection Manual; U.S. Army Coastal Engineering Research Center: Washington, DC, USA, 1984. [Google Scholar]
- Vincent, C.L.; Hughes, S.A. Wind Wave Growth in Shallow Water. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 765–770. [Google Scholar] [CrossRef]
- Young, I.R.; Verhagen, L.A. The growth of fetch limited waves in water of finite depth. 1. Total energy and peak frequency. Coast. Eng. 1996, 29, 47–78. [Google Scholar] [CrossRef]
- Hasselmann, K.; Collins, J.I. Spectral dissipation of finite-depth gravity waves due to turbulent bottom friction. J. Mar. Res. 1968, 26, 1–12. [Google Scholar]
- Zijlema, M.; van Vledder, G.P.; Holthuijsen, L.H. Bottom friction and wind drag for wave models. Coast. Eng. 2012, 65, 19–26. [Google Scholar] [CrossRef]
- Pascolo, S.; Petti, M.; Bosa, S. Wave–Current Interaction: A 2DH Model for Turbulent Jet and Bottom-Friction Dissipation. Water 2018, 10, 392. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions, Part I, Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Jonsson, I.G. Wave Boundary Layers and Friction Factors. In Proceedings of the Tenth International Conference on Coastal Engineering, Tokyo, Japan, 5–8 September 1966; pp. 127–148. [Google Scholar] [CrossRef]
- Kamphuis, W. Friction Factor under Oscillatory Waves. J. Waterw. Harb. Coast. Eng. Div. 1975, 101, 135–144. [Google Scholar]
- Myrhaug, D. A rational approach to wave friction coefficients for rough, smooth and transitional turbulent flow. Coast. Eng. 1989, 13, 11–21. [Google Scholar] [CrossRef]
- Ijima, T.; Tang, F.L.W. Numerical Calculation of Wind Waves in Shallow Water. Coast. Eng. 1966, 38–49. [Google Scholar] [CrossRef]
- Petti, M.; Bosa, S.; Pascolo, S. Lagoon Sediment Dynamics: A Coupled Model to Study a Medium-Term Silting of Tidal Channels. Water 2018, 10, 569. [Google Scholar] [CrossRef]
- Carniello, L.; Defina, A.; D’Alpaos, L. Morphological evolution of the Venice lagoon: Evidence from the past and trend for the future. J. Geophys. Res. 2009, 114, F04002. [Google Scholar] [CrossRef]
- Zhu, Q.; van Prooijen, B.C.; Wang, Z.B.; Yang, S.L. Bed-level changes on intertidal wetland in response to waves and tides: A case study from the Yangtze River Delta. Mar. Geol. 2017, 385, 160–172. [Google Scholar] [CrossRef]
- Shi, B.; Cooper, J.R.; Pratolongo, P.D.; Gao, S.; Bouma, T.J.; Li, G.; Li, C.; Yang, S.L.; Wang, Y.P. Erosion and accretion on a mudflat: The importance of very shallow-water effects. J. Geophys. Res. Oceans 2017, 122, 9476–9499. [Google Scholar] [CrossRef]
- Cavaleri, L.; Rizzoli, P.M. Wind wave prediction in shallow water: Theory and applications. J. Geophys. Res. 1981, 86, 10961–10973. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Quasi-linear theory of wind-wave generation applied to wave forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Nielsen, P. Coastal and Estuarine Processes; Advanced Series on Ocean Engineering; World Scientific: Singapore, 2009; Volume 29, p. 345. [Google Scholar]
- Chirol, C.; Amos, C.L.; Kassem, H.; Lefebvre, A.; Umgiesser, G.; Cucco, A. The Influence of Bed Roughness on Turbulence: Cabras Lagoon, Sardinia, Italy. J. Mar. Sci. Eng. 2015, 3, 935–956. [Google Scholar] [CrossRef]
- Wells, J.T.; Kemp, G.P. Interaction of surface waves and cohesive sediments: Field observations and geologic significance. In Estuarine Cohesive Sediment Dynamics; Lecture Notes on Coastal and Estuarine Studies N314; Mehta, A.J., Ed.; Springer: Berlin, Germany, 1986; pp. 43–65. [Google Scholar]
- Whitehouse, R.J.S.; Soulsby, R.L.; Roberts, W.; Mitchener, H.J. Dynamics of Estuarine Muds; Technical Report; Thomas Telford: London, UK, 2000. [Google Scholar]
- Amos, C.L.; Bergamasco, A.; Umgiesser, G.; Cappucci, S.; Cloutier, D.; Denat, L.; Flindt, M.; Bonardi, M.; Cristante, S. The stability of tidal flats in Venice Lagoon—The results of in-situ measurements using two benthic, annular flumes. J. Mar. Syst. 2004, 51, 211–241. [Google Scholar] [CrossRef]
- Bosa, S.; Petti, M.; Pascolo, S. Numerical Modelling of Cohesive Bank Migration. Water 2018, 10, 961. [Google Scholar] [CrossRef]



| Test | Wind Speed (m/s) | Spectral Bottom Friction | Cf | KN (m) |
|---|---|---|---|---|
| W6Col | 6 | Collins | 0.015 | - |
| W6M5E-4 | Madsen | - | 0.0005 m | |
| W6M5E-3 | Madsen | - | 0.005 m | |
| W6M1.5E-2 | Madsen | - | 0.015 m | |
| W6M5E-2 | Madsen | - | 0.05 m | |
| W8Col | 8 | Collins | 0.015 | - |
| W8M5E-4 | Madsen | - | 0.0005 m | |
| W8M5E-3 | Madsen | - | 0.005 m | |
| W8M1.5E-2 | Madsen | - | 0.015 m | |
| W8M5E-2 | Madsen | - | 0.05 m | |
| W10Col | 10 | Collins | 0.015 | - |
| W10M5E-4 | Madsen | - | 0.0005 m | |
| W10M5E-3 | Madsen | - | 0.005 m | |
| W10M1.5E-2 | Madsen | - | 0.015 m | |
| W10M5E-2 | Madsen | - | 0.05 m | |
| W12Col | 12 | Collins | 0.015 | - |
| W12M5E-4 | Madsen | - | 0.0005 m | |
| W12M5E-3 | Madsen | - | 0.005 m | |
| W12M1.5E-2 | Madsen | - | 0.015 m | |
| W12M5E-2 | Madsen | - | 0.05 m | |
| W14Col | 14 | Collins | 0.015 | - |
| W14M5E-4 | Madsen | - | 0.0005 m | |
| W14M5E-3 | Madsen | - | 0.005 m | |
| W14M1.5E-2 | Madsen | - | 0.015 m | |
| W14M5E-2 | Madsen | - | 0.05 m |
| Simulation | W6Col | W8Col | W10Col | W12Col | W14Col |
|---|---|---|---|---|---|
| Equivalent KN (m) | 0.0002 | 0.0004 | 0.0005 | 0.0007 | 0.0011 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pascolo, S.; Petti, M.; Bosa, S. On the Wave Bottom Shear Stress in Shallow Depths: The Role of Wave Period and Bed Roughness. Water 2018, 10, 1348. https://doi.org/10.3390/w10101348
Pascolo S, Petti M, Bosa S. On the Wave Bottom Shear Stress in Shallow Depths: The Role of Wave Period and Bed Roughness. Water. 2018; 10(10):1348. https://doi.org/10.3390/w10101348
Chicago/Turabian StylePascolo, Sara, Marco Petti, and Silvia Bosa. 2018. "On the Wave Bottom Shear Stress in Shallow Depths: The Role of Wave Period and Bed Roughness" Water 10, no. 10: 1348. https://doi.org/10.3390/w10101348
APA StylePascolo, S., Petti, M., & Bosa, S. (2018). On the Wave Bottom Shear Stress in Shallow Depths: The Role of Wave Period and Bed Roughness. Water, 10(10), 1348. https://doi.org/10.3390/w10101348






