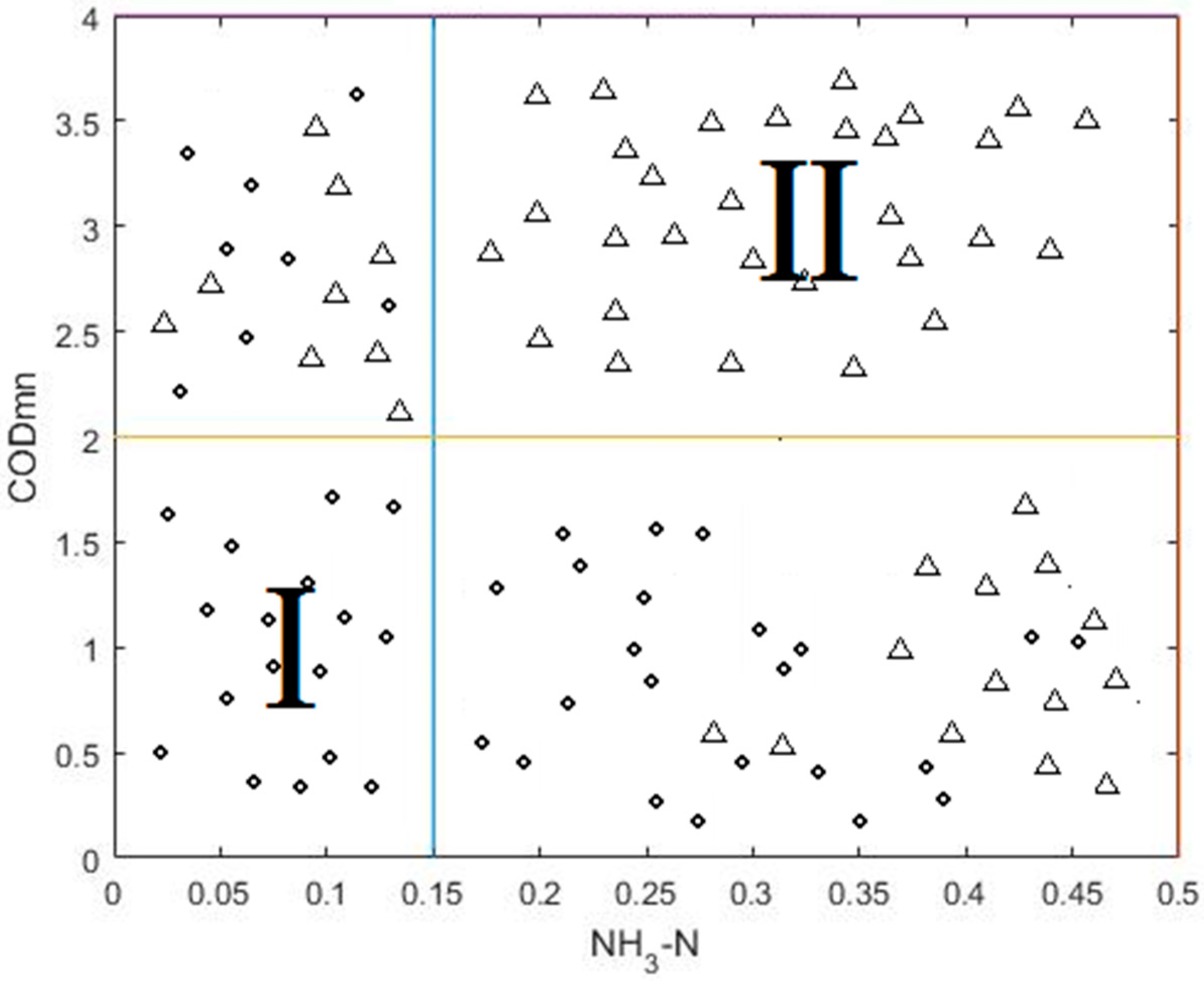
3.3.1. Problems with Existing Membership Functions
(1) Basic architecture issues
In addition to satisfying the requirements of the basic value range (0, 1), the membership function that is required by FSVM is mainly to reflect the requirements of noise reduction and to facilitate the formation of classification planes. Many articles, including [
30,
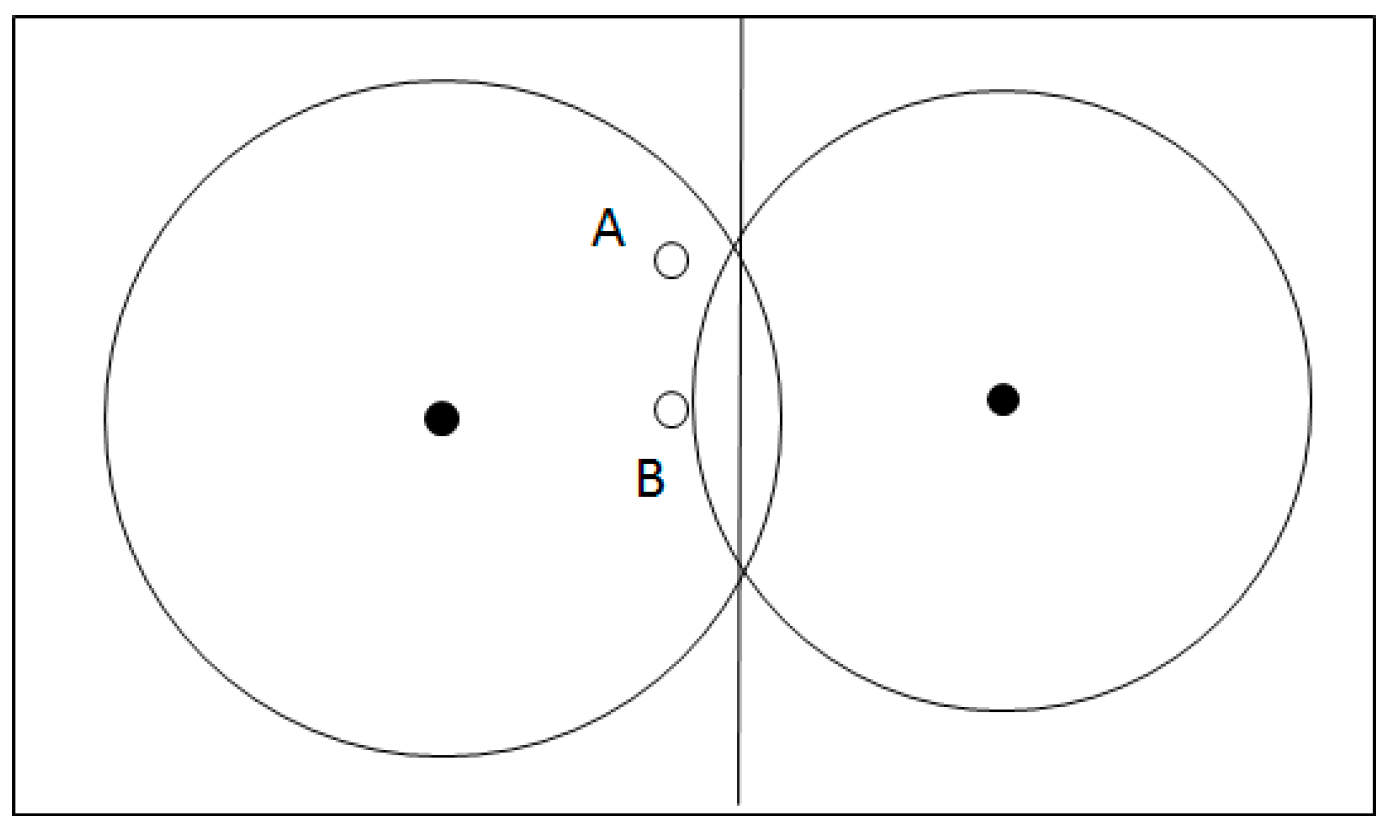
31], construct a hypersphere based on the class center, and design a membership function based on the distance from the sample point to the sample center. To some extent, this method relies heavily on the geometry of the sample distribution. For example, in the case of
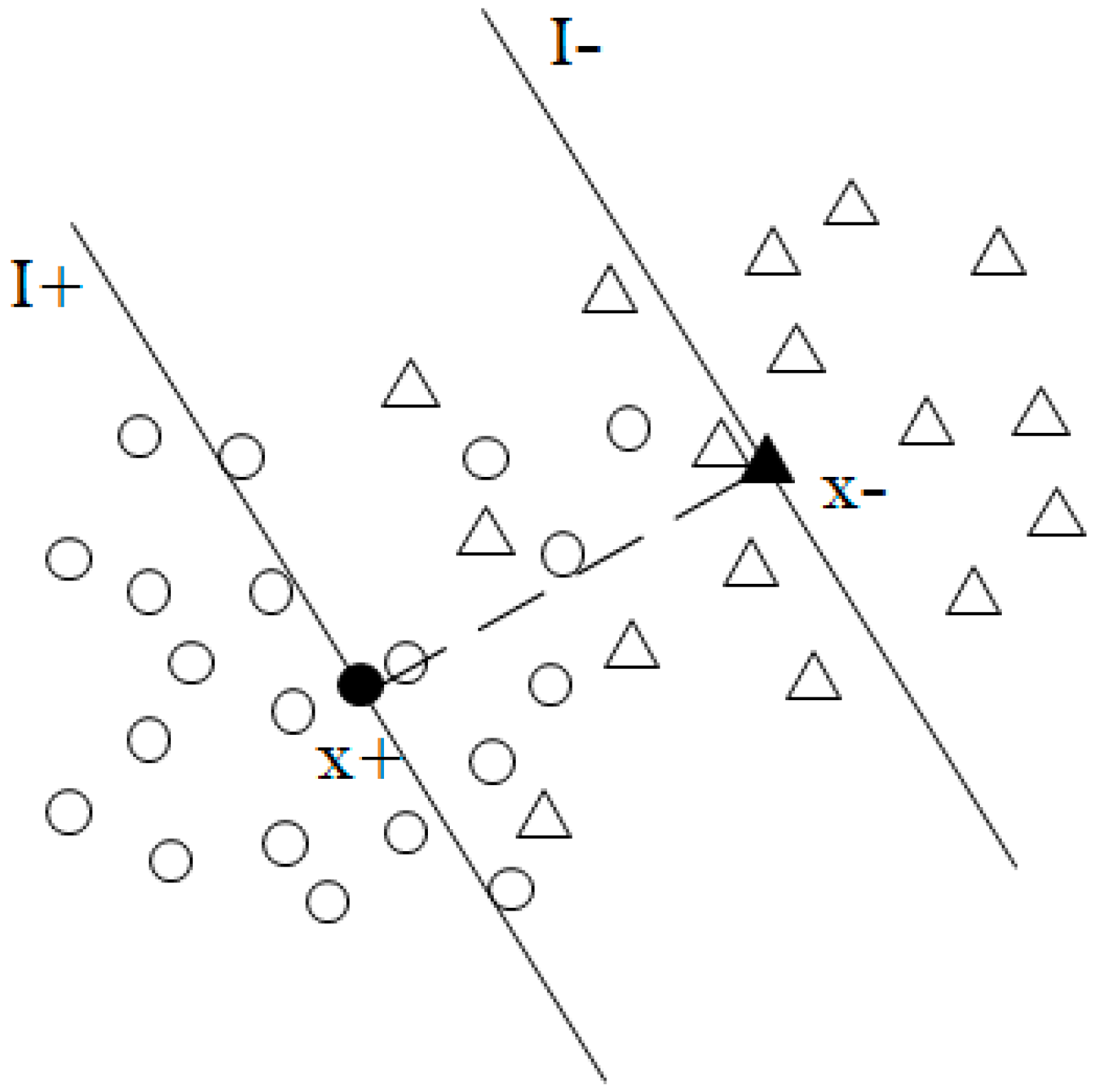
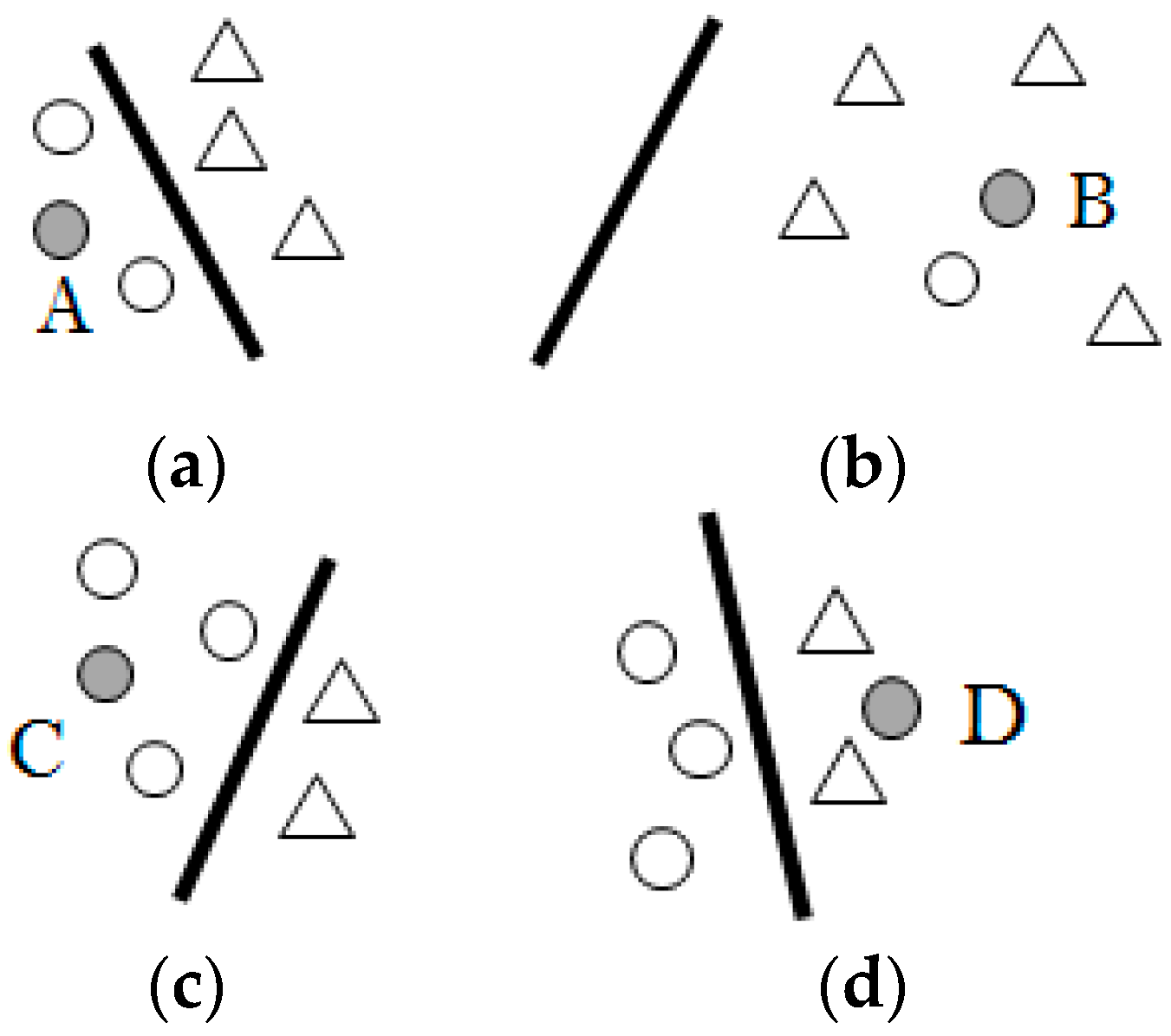
Figure 4 below, the two points A and B contribute the same to the construction of the classification plane, but due to the different distance between the two points and their class centers, the values of membership, as calculated by the above method, based on class center are different.
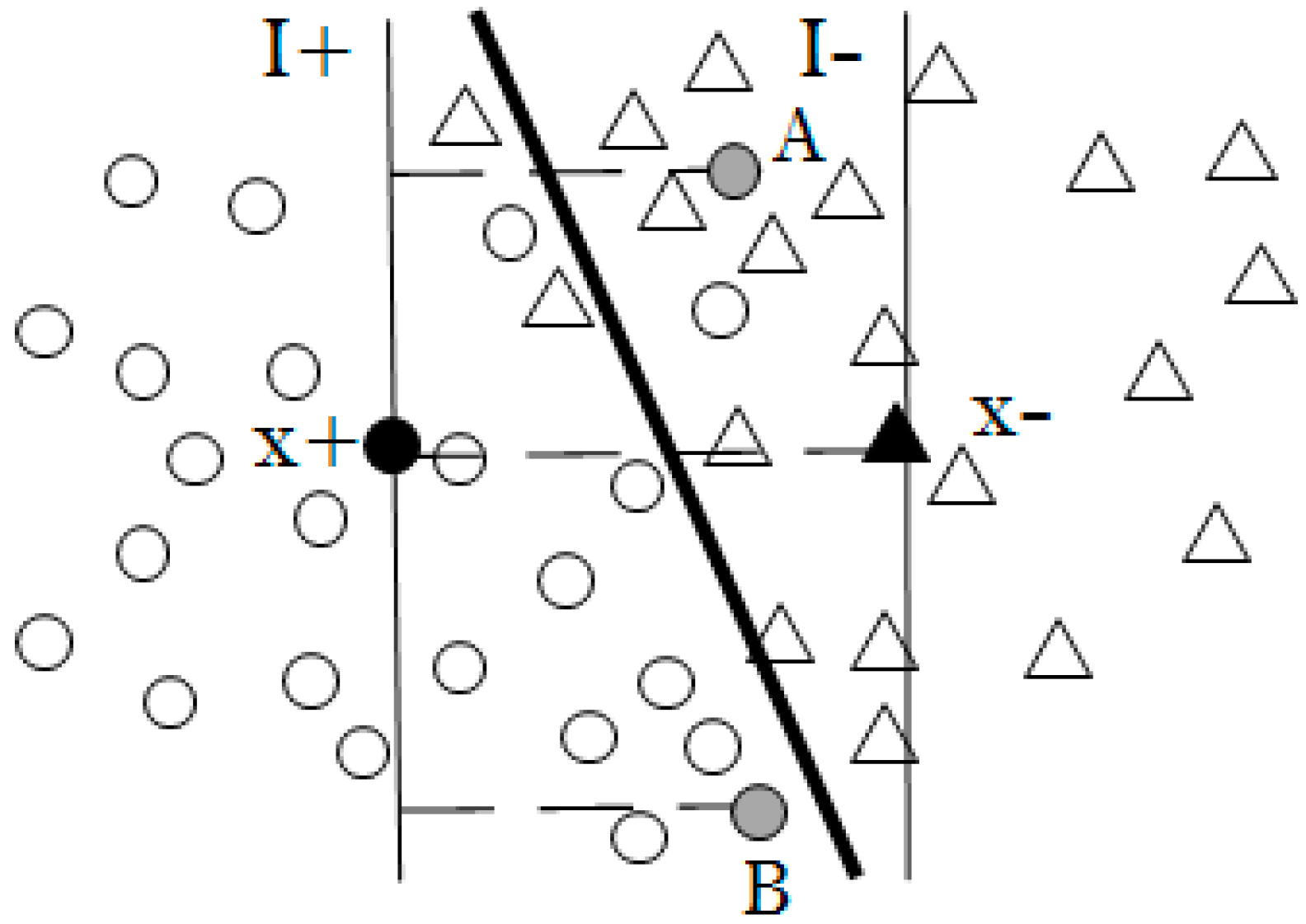
Therefore, this paper decides to use the idea of intra-class hyperplane to design the membership function. As shown in
Figure 5, the class centers
and
are first obtained, respectively. Then the two intra-class hyperplanes are constructed by the normal vector
.
Thus, the membership function considers only the set U′, which includes the sample points inside the two hyperplanes
and
. The sample points outside the hyperplanes are no longer considered, because they do not help in the determination of the optimal hyperplane. The above content is described in Equation (18).
where
is a very small positive number.
(2) The problem of distance-based membership function
The distance-based membership functions that are designed in [
30,
32] are inversely proportional to the distance
, that is, the closer to the center of the class, the larger the value. This design is mainly based on the idea that the closer the point is to the class center, the more it should belong to this class. However, the point outside the boundary of the classification plane satisfies the condition
, and its relaxation variable
, so the value of
C does not affect the classification result. Conversely, such a method makes the
of the useless point that is closer to the center of the class bigger than the
of the point that may be the support vector. Therefore, this paper adopts the idea of membership function that is based on intra-class hyperplane in [
32], and it gives the larger function value to the samples that are closer to the boundary zones between two types.
(3) The problem of compactness-based membership function
In [
30], the author used a parameter
to solve the problem of noise reduction. When the value of
is bigger than the product of
and the distance D between two hyperplanes,
(
is a small positive number). However, if the situation in
Figure 6 below occurs, that is, the final classification plane is not parallel to the two hyperplanes. Here,
or
is the distance from the point A or B to the intra-class hyperplane. Assuming that the final
can make
, the noise A can be successfully excluded, but the B point satisfying
should be a support vector. However, the condition of
is also satisfied, so B is also treated as noise. Therefore, there may be some problems with this method.
In [
32], the author constructed a membership function based on compactness. When
q samples of the nearest
p neighbors of the sample
are not in the same class as
, the centripetal degree is defined as the former one. However, as shown in
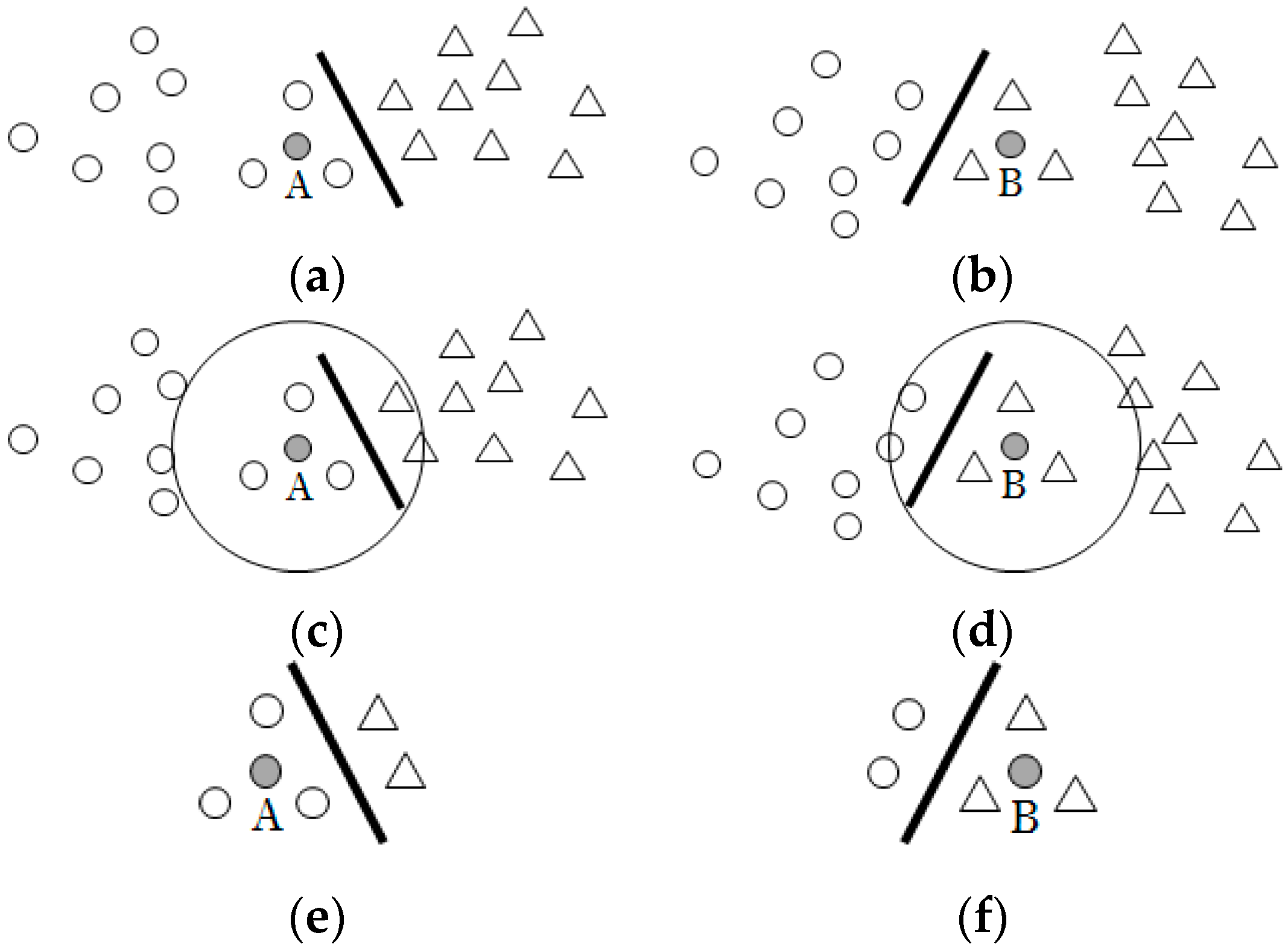
Figure 7, if
p = 5, and the five white points that are shown in
Figure 7e,f are the nearest five neighbors of point A and B, the point A in
Figure 7a has a certain effect on the formation of the classification plane, but the point B in
Figure 7b is obviously a noise point. But, according to the method of [
32], A and B have the same membership.
3.3.2. Improvement Ideas
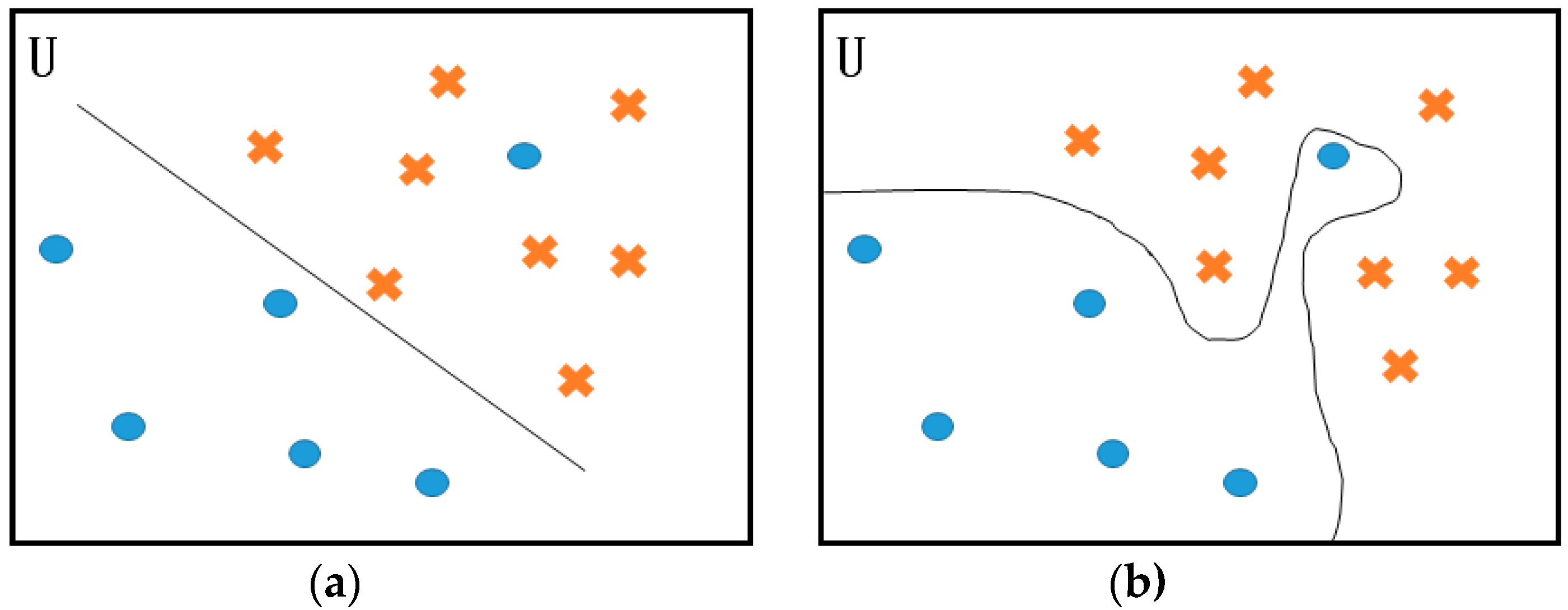
For the case where the neighbors of a sample point are all of the same class of this point or the neighbors of a sample point are all the points of the different class, it can be directly determined. However, there are two main situations for areas where the positive and negative sample points are mixed together. One is that the points are close to the junction area of two types, so most of the samples in this area should be given correspondingly large values. The other is that the point is a noise point inside a certain class, but the categories of its neighbors are not all different from it, so this situation is different from the case, where all of the surrounding points are of different class.
At the beginning, this paper uses the category of the nearest neighbor as the criterion for evaluating whether the point in the mixed area is noise. If the class of the sample point closest to it is the same as its class, it is judged to be a useful point. If the class of the sample point closest to it is different from its class, the point is determined to be noise, namely,
- (1)
When all of the p sample points are not in the class of , is noise, and has no effect on the classification plane formation, so the value of is .
- (2)
When all the p sample points are of the same class as , the function is designed according to the degree of compactness of the points around , so the value of is
- (3)
When only q samples of the p points belong to the same class of , takes the value or , according to the class of its nearest neighbor.
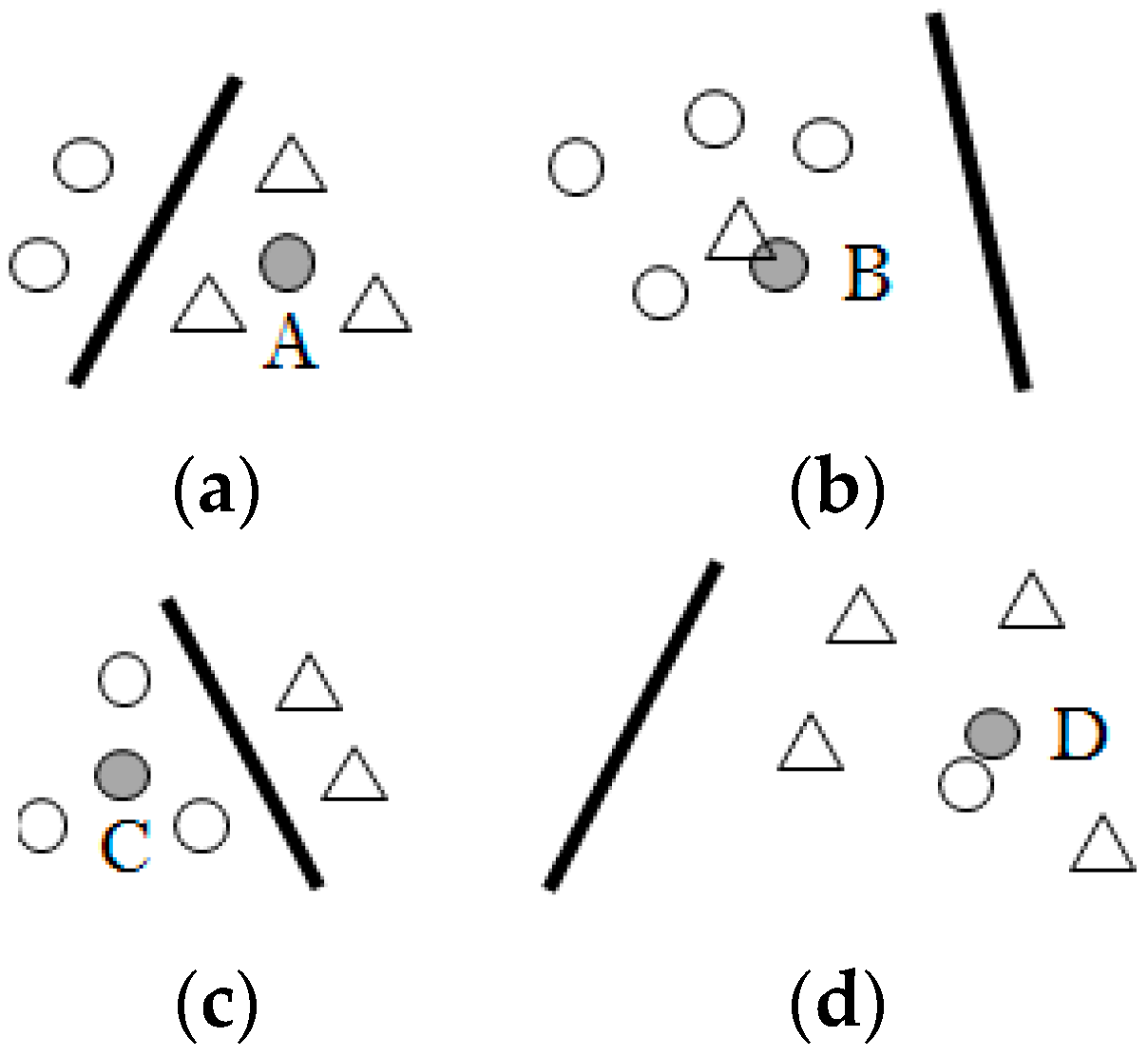
But, in fact, the counterexample, like
Figure 8, can be given. If
p = 5, what appears under normal conditions should be similar to the case of
Figure 8a,c. Since they are close to the classification plane, the two points A and
C do not belong to the cases (1) or (2). Then, according to the class of the nearest neighbor, this method determines that point A is noise, and point
C is useful for determining the classification plane.
However, it is inaccurate to base only on whether ’s nearest neighbor is of the same or different class as . The reason is that although the model in this article can deal with those noise points, they will also interfere with the judgment of the surrounding points. For example, there is a nearest different-class neighbor next to point B. Point B will be judged as noise by this method, but the actual situation is not the same. Similarly, when the two noise points are very close, this method will instead judge point D as the point that contributes to the classification plane. In both cases, other noise points interfere with the determination of the adjacent sample points.
Thus, the situation similar to that in
Figure 8b is first solved here. Although some of the noise isolated from the different-class points is removed by the previous case (1), a different-class point itself still interferes with the determination of the surrounding points. Therefore, this paper decides to treat the judgment of the previous situation (1) as a priori. After finding out the noise points whose neighbors are all the different-class points, the discrimination of case (2) and case (3) no longer consider these noise points in the situation (1).
In addition, in order to solve the situation like
Figure 8d, we must consider the second influencing factor—the number of same-class and different-class points. When a different-class point is the closest neighbor, and the number of surrounding different-class points is more than that of the same-class points, this point is judged as noise (such as point A). When a different-class point is the closest neighbor, but the number of same-class points is more than that of different-class points, the point is judged to be a useful point (such as point B). When a same-class point is the closest neighbor, and the number of same-class points is more than that of different-class points, the point is judged to be a useful point (such as point C). When a same-class point is the closest neighbor, but the number of different-class points is more than that of similar points, the point is judged as noise (such as point D).
However, it was found that in the condition from A to D discussed above, when the number of surrounding different-class points is more than the number of same-class points, the point is judged as noise regardless of the category of its closest neighbor. Thus, the result of this judgment is exactly the same as the method that considers only the number of same-class points and different-class points. The category of the nearest neighbor has no meaning. Therefore, it can be determined as directly based on the number of neighbors in the different class and in the same class.
If a counterexample is also given to this classification method, it should be similar to the case of
Figure 9b,c under normal circumstances. That is, when there are more neighbors of the same class of this point, it should be a normal point. Similarly, when the number of neighbors that belong to the different class of the point is bigger, it should be the noise.
However, for example, the number of different-class points in the neighbors of point A in
Figure 9a is more than that of the same type, but it is not a noise point. Similarly, the number of same-class points around point D in
Figure 9d is more than that of the different class, but it is noise. In fact, this kind of idea that is similar to k-nearest neighbor is acceptable. The most important goal of the function
is to find the noise point, so the method is acceptable that identifies the point, the neighbors of which have more points of the different class, as noise. But, this judgment will be limited by the value of the parameter
p and the local phenomenon interference.
Therefore, another factor to be considered is added here, which is the number of the points belonging to the same class as the point among the three neighbors other than the p nearest neighbors. This factor can avoid the interference of local phenomena on judgment to a certain extent.
In this case, when the number of same-class points in
p neighbors around a point is less than the different-class points, this point should be judged as noise. But, if two or three of the three nearest neighbors, except the
p points are belong to the same category, it proves that the above situation is only a partial phenomenon, so the sample point is judged to be a normal point (such as point A). If only one or none of the three neighbors except the
p points is in the same class, then the sample point is judged to be noise (such as point B). When there are more same-class neighbors of the
p point, if only one or none of the three neighbors except the
p points is in the same class, the sample point is judged to be noise (such as point D). If two or three of the three nearest neighbors except the
p points belong to the same category, the sample point is judged to be a normal point (such as point C). The Equation (19) shows this function:
where if there are two or three points in the three neighbors belonging to the same class as the point
,
= 1. If there are only one or none of the three points in the three neighbors belonging to the same class as the point
,
= −1.
However, in fact, when
= 1, regardless of whether the value of (
is positive or negative, the value of
is
. Similarly, when
= −1, the value of
is
, regardless of the value of (
. Therefore, the value of the function can be only determined by the positive and negative of
, namely,
However, the discriminant of Equation (20), the condition of the three neighbors, except the p points, is actually based on the number of same-class and different-class points around it in essence. The difference between the two judgement conditions is only the value of p. So the addition of three points is actually meaningless. That is, the problem can be solved by using only the idea of the number of same-class and different-class points around the point.
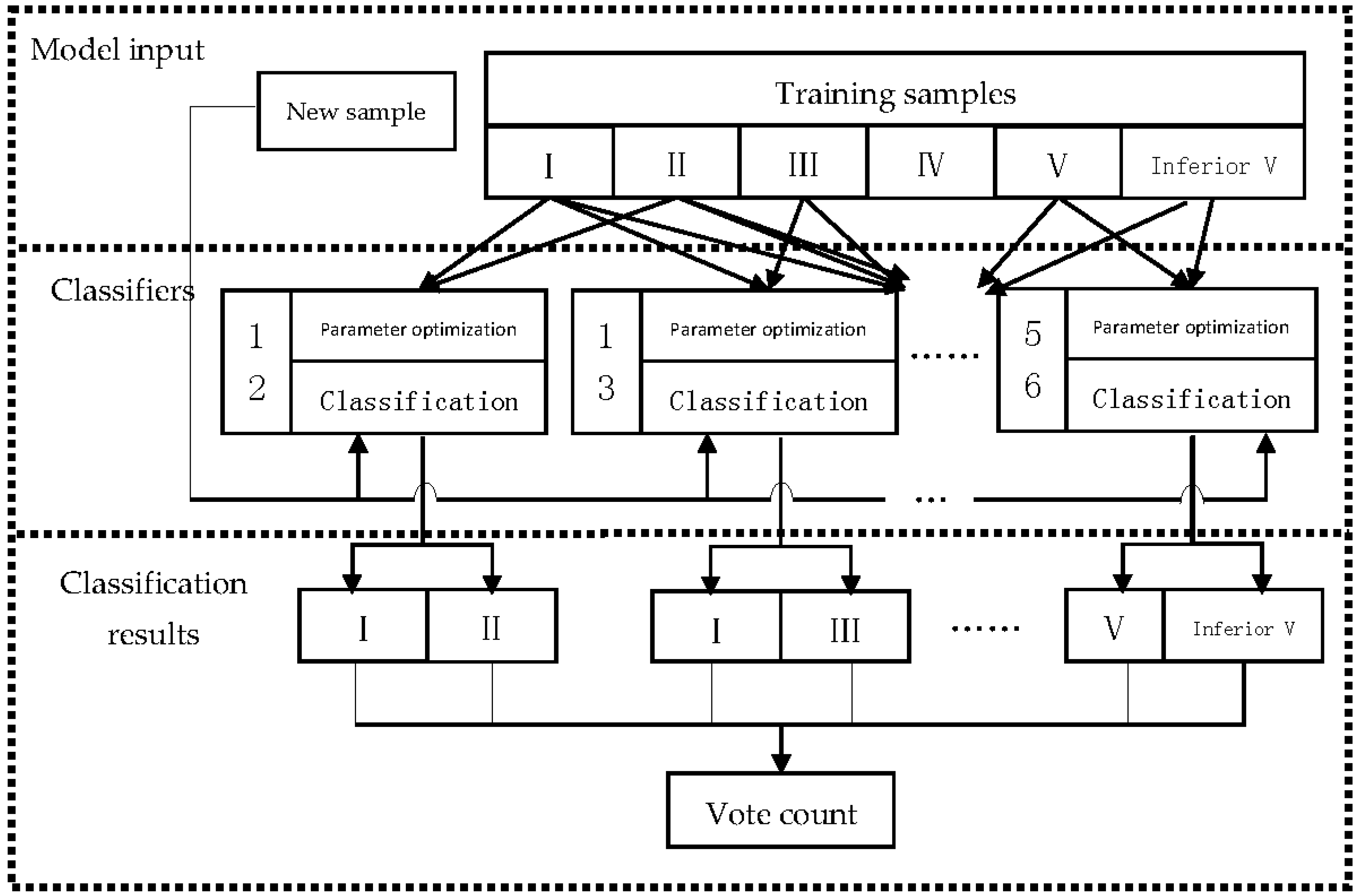
3.3.3. Improved Membership Function
Therefore, based on the above analysis, the membership function of the paper finally combines both the distance and the compactness. The following Equation (21) is the distance-based membership function of this article that is designed for easy classification:
where
t− and
t+ are the total number of positive and negative sample points inside the two hyperplanes, respectively, and
is a small positive number.
When a point is very close to the intra-class hyperplane, it has no effect on the construction of the classification plane, so its membership degree is infinitely close to zero. As the sample point gets closer to the junction zone of the two types of samples, its contribution to the construction of the classification plane is greater. Therefore, its membership is also greater.
However, only one function in the model is obviously insufficient. For example, when a point satisfying the condition is far away from the positive class hyperplane, it is mixed into the negative class sample points. Obviously, it should be a noise point, but the value of the membership function above will be large. Therefore, it is necessary to adjust the above function. To this end, this paper designs another membership function to solve the problem of noise and isolated points.
The following is the improved compactness-based membership function that is proposed in this paper. Here, distance from the nearest p sample points around the sample point to is , , ⋯, , where p is an odd number.
- (1)
When all the
p sample points are not in the same class as
,
is judged as noise and it has no effect on the classification plane formation, namely,
- (2)
Reselect p sample points around the sample point that are closest to it and do not contain the points of the above case (1). This can effectively avoid the interference of a single noise point in some cases (1) to the judgment of surrounding sample points.
When all of the
p sample points at this time are not in the same class as
,
is judged as noise and it has no effect on the classification plane formation, namely,
When all of the
p sample points are of the same class as
, the function is designed according to the compactness of the sample points around
, that is, the tighter the sample point, the larger the
:
When
q points in
p sample points belong to the same class of
, the remaining ones do not belong to this class, the value of
is as follows:
Finally, the formula of the second membership function
is presented, as follows:
So far, the design of in the case (1) and the case a of (2) completes the aim of noise reduction. The design of the function value in b of the case (2) excludes the effect of isolated points. When a point is isolated, its will be very small. The c of the case (2) compensates for the loopholes of the previous two cases a and b. It uses the idea of k-nearest neighbor to make better distinguish the effect of the sample points in the junction area by the appropriate parameter p. At the same time, together with case (1), it also solves the problem left by , that is, by the effect of determining the noise, the function negates the membership value in , which is largely due to being far away from the hyperplane in the class.
Since
only considers the importance of points near the classification plane, it has no ability to handle noise and isolated points. Therefore, this paper constructs
to complete the task of removing noise and isolated points, and it makes up for the defects of
. Thus, the final membership function of this paper is determined, as follows:
When the compactness of the neighbors around the sample point is constant, the closer the sample point is to the junction area, the greater its membership degree. When the distance between the sample points and the hyperplane in the class is constant, the bigger the compactness of the neighbors of the sample point, the greater the membership degree. For the method of the combination of and , since the two functions can compensate each other after the addition, this article does not adopt the addition method. When considering that noise should be directly rejected, this paper uses the multiplication method that is uncompensated.
Now, please have a look at the issues discussed before:
- (1)
For the case of
Figure 4, it is clear that this problem has been solved by using the method of intra-class hyperplane instead of hypersphere. The value of
of the new function is the same for A and B in
Figure 4, but, depending on the situation of the surrounding points of A and B, different
may be given. Finally, the result is the combination of
and
- (2)
For the case of
Figure 5, the new function judges the sample point based on the number of same-class and different-class points around it, rather than the distance to the intra-class hyperplane.
- (3)
For the problem of
Figure 6, the improved effect has been shown in the analysis of the situation in
Figure 9.
Finally, since the model is to be adopted to multi-class classification, the variables are to be converted. These variables include the class centers
and
, distance
between two class centers, condition that determines whether it is inside or outside the hyperplane, the distance
or
between the point and the intra-class hyperplane and the distance
between the sample points.